Topological classification for intersection singularities of exceptional surfaces in pseudo-Hermitian systems

Abstract

Non-Hermitian systems are known for their intriguing topological properties, which underpin various exotic physical phenomena. Exceptional points, in particular, play a pivotal role in fine-tuning these systems for optimal device functionality and material characteristics. These points can give rise to exceptional surfaces with embedded lower-dimensional non-isolated singularities. Here we introduce a topological classification for non-defective intersection lines of exceptional surfaces, where exceptional surfaces intersect transversally. We achieve this classification by constructing a quotient space of an order-parameter space under equivalence relations of eigenstates. We unveil that the fundamental group of these gapless structures is a non-Abelian group on three generators. This classification not only reveals a unique form of non-Hermitian gapless phases featuring a chain of non-defective intersection lines but also predicts the unexpected existence of topological edge states in one-dimensional lattice models protected by the intersection singularities. Our classification opens avenues for realizing robust topological phases.

Introduction

Singularities are ubiquitous and play significant roles in various physical systems in the real world, often accompanied by exotic physical phenomena^{1,2,3,4,5,6,7,8,9,10,11,12,13}. For example, in topological materials, a Weyl point in a Hermitian system acts as a sink or source of the Berry curvature, and two Weyl points with opposite chiralities are connected by a Fermi-arc surface state^1,2,9,11. The existence and stability of singularities can be better understood via topology, and a singularity can be characterized by a topological invariant, such as the Chern number. This invariant is usually encoded in the adiabatic evolution of eigenstates over closed loops or surfaces that enclose the singularity point^5,6,7,8,9,11. Recently, the topology of non-Hermitian systems has attracted growing attention^{14,15,16,17,18,19,20,21,22,23,24,25}. As unique features of non-Hermiticity, exceptional points are singular points on the complex energy plane where both the eigenenergies and the eigenstates coalesce^{14,15,16,17,18,19}. They differ from the usual degeneracies of Hermitian systems, such as Weyl points, Dirac points, and nodal lines, in that they may carry fractional topological invariants^{16,18,19,24,26} and can induce stable bulk Fermi-arcs^22,24 and braiding of eigenvalues²⁶. The non-Hermitian skin effect, manifested by sensitivity of the eigen-spectrum to boundary conditions, is associated with the point gaps in bulk topology^{15,16,17,18,21,23,25}. Recent discoveries of lines, rings, and surfaces of exceptional points have further enriched the classes of topological degeneracies^{27,28,29,30,31}. In particular, high-order exceptional degeneracies, which frequently appear as the cusps of exceptional lines or surfaces, carry a hybrid type of topological invariants in a high-dimensional parameter space³².

In the meantime, significant efforts have been devoted to classifying these exceptional points and related energy band structures. Topological classifications are of particular importance, as they enable predictions of degeneracies in the parameter space whenever the type of energy gaps and the Altland–Zirnbauer symmetry class of a system are known^{14,19,20,33,34,35}. This provides a theoretical framework for predicting non-Hermitian topological phases of matter and for guiding their experimental realizations. In particular, exceptional points can assemble into hypersurfaces in a 3D parameter space, called exceptional surfaces (ESs), which separate exact and broken phases²⁰. ESs are commonly observed in non-Hermitian systems with parity–time inversion (PT) symmetry or chiral symmetry^20,27,28,29 and have broad applications in the design of sensing and absorption devices^31,36. As a subspace of the parameter space, ESs may possess embedded lower-dimensional singularities, which have remarkable properties differentiating them from other points on the ESs. These so-called hypersurface singularities include intersections³⁷, cusps^38,39,40, and swallowtail catastrophes⁴¹. They are symmetry protected and stable against symmetry-preserving perturbations^{31,37,38,39,40,41}. However, despite various important physical phenomena and potential applications, these hypersurface singularities on ESs have never been topologically classified.

In this work, we provide a topological classification for a typical hypersurface singularity in two-band models where exceptional surfaces intersect transversally. We call it a non-defective intersection line (NIL) of the ESs. An NIL commonly appears in generic non-Hermitian systems with PT-symmetry and an additional pseudo-Hermitian symmetry⁴¹. The band structures of such systems feature a gapless configuration of ESs connected at an embedded NIL. We analyze equivalence relations of eigenstates, and discover that the quotient space of the order-parameter space is homotopy equivalent to a bouquet of three circles $M={S}^{1}\vee {S}^{1}\vee {S}^{1}$. The topology of this NIL is thus characterized by the fundamental group of M, which is a non-Abelian free group on three generators. Essentially, we introduce intersection homotopy theory to classify such non-isolated singularities, which is very different from the usual homotopy theory addressing isolated singularities^{6,26,32,33,34,35,40}. Our classification systematically explains exotic physical effects arising from the nontrivial topology of NILs, such as the formation and evolution of a chain of NILs. In addition, our topological description predicts the stable edge states in one-dimensional lattice models protected by a topological NIL, even though they are counter-intuitive for gapless phases and go beyond conventional explanations by Zak phase theory.

Results

Classification with fundamental group

The prototypical Hamiltonian is a two-level system H that is PT-symmetric and preserves an additional η-pseudo-Hermitian symmetry^41,42,43:

$$\left[H,{PT}\right]=0,\eta H{\eta }^{-1}=H$$

(1)

Here, the operator PT can be regarded as complex conjugation with a suitable choice of basis in parameter space, and thus the Hamiltonian can always be gauged to be real. The metric operator η here takes the Minkowski metric $\eta ={{\mbox{diag}}}(-1,1)$^13,41,44,45. More details on pseudo-Hermiticity are provided in Supplementary Note 1. These symmetries imply that the k-space Hamiltonian can be written in the form

$$H\left({{{{{\boldsymbol{k}}}}}}\right)={f}_{2}\left({{{{{\boldsymbol{k}}}}}}\right)i{\sigma }_{2}+{f}_{3}\left({{{{{\boldsymbol{k}}}}}}\right){\sigma }_{3}$$

(2)

where f_2,3 are real-valued functions of three-dimensional (3D) k-space, and σ_2,3 are Pauli matrices. There is no term multiplied by σ₁ due to the above pseudo-Hermitian symmetry. Without loss of generality, we may assume that the term multiplied by the identity matrix vanishes as well, because it does not affect the gapless structure. Such Hamiltonians correspond to physical systems with nonreciprocal hopping of orbitals^41,46,47,48.

In analogy with the Hermitian case⁶, the 2D f_2,3-plane serves as the order-parameter space of all Hamiltonians that preserve the symmetries specified in Eq. (1). In particular, as f_2,3 are real functions on k-space, any exceptional surfaces (ESs) in the 3D k-space correspond to exceptional lines (ELs) at ${f}_{2}=\pm {f}_{3}$ on the 2D f_2,3-plane. The ESs intersect transversally in lines (i.e. the NILs) in the k-space, which in turn correspond to the intersecting point (called a non-defective intersection point, or NIP) of the ELs at the origin ${f}_{2}={f}_{3}=0$. Moreover, a path traced in the 3D k-space maps to a path on the 2D f_2,3-plane, and if the path loops around an NIL in the k-space, the corresponding path in the f_2,3-plane encircles the NIP. Figure 1a shows the gapless structure of the order-parameter space, with red and green lines representing the ELs satisfying ${f}_{2}=\mp {f}_{3}$, respectively. Regions I and III (satisfying $|{f}_{2}| < |{f}_{3}|$) support Hamiltonians with real eigenenergies and are referred to as PT-exact phases. On the other hand, regions II and IV ($|{f}_{2}| > |{f}_{3}|$) are PT-broken phases, where the eigenvalues come in complex-conjugate pairs. The paths α, α‘, β and β‘ begin and terminate at the ELs, and they are located in different regions (Fig. 1a). We aim to classify the NIP at the origin, which is excluded from the plane^20,49. First, the plane punctured at the origin deformation retracts to a circle S¹ (Fig. 1b). Such a mathematical process can be interpreted as a quotient map, which identifies all points along each ray starting from the origin (excluding the origin). This identification is based on the equivalence relation that all points on the ray, namely the Hamiltonians, have the same eigenstates ordered by eigenvalues. Consequently, the upper and lower halves of EL₁ shrink to antipodal points A and A’, respectively, while those of EL₂ to B and B’. Moreover, there are two equivalence relations on the S¹. At point A, the two eigenstates coalesce, which coincides with the coalesced eigenstates at point A’. Therefore, A and A’ should be identified, and one can glue A’ to A via a quotient map. The same procedure applies to B and B’. It is important to note that antipodal points located in the regions where eigenenergies are gapped cannot be identified, because their eigenstates are reversely ordered by the eigenenergies. Such a refined topological discrimination of the strata of the origin, the intersecting lines ${f}_{2}=\mp {f}_{3}$ and the plane is a distinguished feature of intersection homotopy methods^50,51,52. The intersection homotopy method, which is a mathematical technique used to address hypersurface singularities, differs significantly from the conventional homotopy method that focuses on the topology of isolated singularities. In the conventional homotopic loops, the intention is to avoid intersecting singularities^6,49, which inherently makes it incapable of dealing with singularities that are entirely located on ESs (or ELs in 2D), just like our case. When dealing with non-isolated singularities, the parameter space becomes stratified (as described in Supplementary Note 2), and the singular hypersurfaces ESs (or ELs in 2D) that satisfy ${f}_{2}=\mp {f}_{3}$ form a subspace within the parameter space, known as a stratum. Unlike conventional homotopic loops, the intersection homotopic loops do not need to avoid intersecting this stratum [although intersecting NIL (or NIP in 2D) should be avoided because it is our classification target]. In this context, we can define equivalence relations on ESs (or ELs in 2D). This follows and adapts the mathematical notions originated from Goresky and MacPherson’s work and further developed by Gajer^50,51,52. Using the above procedures, we obtain the quotient space of the S¹ in Fig. 1b, which is a bouquet of three circles (see Fig. 1c)

$$M={S}^{1}\vee {S}^{1}\vee {S}^{1}$$

(3)

Fig. 1: Construction of a quotient space under equivalence relations.

a The gapless structure of the order-parameter space (i.e. f_2,3 plane), where EL₁ and EL₂ are exceptional lines satisfying ${f}_{2}=\mp {f}_{3}$, respectively. The nondefective intersection point (NIP) is at the origin where the ELs intersect, with f₂ = f₃ = 0. Regions I and III are PT-exact phases (PT: parity-time inversion), and Regions II and IV are PT-broken phases. b The 2D plane excluding the NIP can deformation retract to a circle S¹, with the upper and lower parts of EL₁ shrinking to A and A’, respectively, and with those of EL₂ to B and B’. c Gluing identified points A with A’, and B with B’, we obtain the quotient space of S¹ in panel b as a bouquet of three circles.

The notion of quotient space has been widely applied in physics, and the basic technique is gluing identified points within the parameter space under well-defined equivalence relations. A prominent example is the first Brillouin zone, which serves as a quotient space. We know that the band dispersions are repetitive with respect to Brillouin zones. Parameters with interspaces being multiples of reciprocal lattice vectors can thus be identified. Moreover, the first Brillouin zone can be further reduced to a quotient space, such as a circle S¹ (in 1D) or a torus S¹×S¹ (in 2D), by gluing together points on the Brillouin zone boundary that share the same eigenvalues and eigenstates. Furthermore, the concept of quotient space has been utilized to classify isolated singularities⁶. More detailed mathematical discussions on quotient spaces can be found in Supplementary Note 2. The fundamental group of M can be calculated as

$${\pi }_{1}\,(M)={\mathbb{Z}}\ast {\mathbb{Z}}\ast {\mathbb{Z}}$$

(4)

which is a free non-Abelian group on three generators. As shown in Fig. 1c, the three generators Z₁, Z₂ and Z₃ of the group can be given by the concatenations of paths αβ, αα‘^–1 and α‘β‘, respectively. These topological invariants associate with the frame deformations of eigenstates along these paths, which are explained in detail in Supplementary Note 3.

To better understand how this group encodes physical information, we now introduce loops (or concatenated paths) in the order-parameter space that carry nontrivial or trivial topological invariants. The concatenated paths characterizing the generators Z₁, Z₂ and Z₃ are shown in Fig. 2a–c, respectively, where the dashed lines with arrow denote quotient maps that glue identified points. We note that the gluing process does not mean the loop passes through the NIP. Each of the concatenated paths corresponds to an S¹ in Fig. 1c, which are loops in the quotient space M generating its fundamental group. In Fig. 2d, a loop in the plane encircling the NIP is also a concatenation of paths αβα‘β‘, which carries the topological invariant Z₁Z₃, an element in the group [Eq. (4)]. Some other nontrivial loops are discussed in Supplementary Note 4. Typical loops carrying the trivial topological invariant are shown in Fig. 2e–g. The loop l does not cut through any EL and is thus confined in a single region, which is always trivial because it cannot enclose any singularity (i.e. the excluded point, NIP). As we transport l upwards past one of the ELs, the loop decomposes into two paths l₁ and l₂ (Fig. 2f). As the endpoints of l₁ (or l₂) can be identified, l₁ (or l₂) becomes a loop in the quotient space M. It is a trivial loop that can shrink to a point without encountering the NIP. Therefore, the concatenation l₁l₂ is also trivial. By further expanding l downwards to cut through the other EL (see Fig. 2g), the loop becomes a product l₁l₃l₄l₅. Since both l₁ and l₄ correspond to trivial loops in the quotient space M, this product is equivalent to the concatenation l₃l₅. In addition, paths l₃ and l₅ are along opposite directions and are homotopic to α^–1 and α, respectively. It is thus not difficult to find out that the product l₁l₃l₄l₅ remains trivial. From the above analysis, we conclude that continuous deformations of a loop (or a path), even encountering ELs (or ESs for 3D), will not change the topology. In contrast, encountering NIPs (or NILs for 3D) will change the topology. Similar conclusions have also been drawn in ref. ⁴¹. Importantly, as can be indicated from the above analysis, a path joining ELs (or ESs) can provide a lot of information on the NIP (see Supplementary Note 4 for adiabatic evolution of eigenstates) even though it appears open in the parameter space, which is substantially different from the situation with isolated singularities. Therefore, if a loop is partitioned into several segments by ELs (or ESs), it is necessary to investigate the evolution of eigenstates along each path before discussing their combined consequence.

Fig. 2: Typical loops carrying nontrivial or trivial topological invariants.

a–c Loops carrying nontrivial topological invariants Z₁, Z₂ and Z₃, respectively, which are the generators of the group [Eq. (4)]. The dashed lines with arrow denote quotient maps, i.e., gluing of identified points. d The loop formed by the concatenation αβα‘β‘ encloses the NIP (NIP: nondefective intersection point), which carries the topological invariant Z₁Z₃. Point A’ in panels a–d denotes the basepoint. e–g Evolution of a loop carrying trivial topological charge. e A loop without touching ELs (EL: exceptional line) is confined within a specific region and is trivial. f Moving the loop l in panel e upwards along the black arrow direction, we see that it becomes a product of paths l₁ and l₂. Both l₁ and l₂ are trivial loops in the quotient space M, and thus the loop as their product is also trivial. g Stretching the loop along the black arrow direction in panel f, we obtain that the loop crosses EL₁ and becomes a product l₁l₃l₄l₅ of paths. The path l₄, similar to l₁ and l₂, corresponds to a trivial loop in the quotient space M. The paths l₅ and l₃ are oriented in opposite directions (labeled by the arrows) and are homotopic to α and α⁻¹, respectively (Fig. 1a). The path product l₁l₃l₄l₅ is thus trivial.

Chain of nondefective intersection lines

Next, based on our topological descriptions, we aim to understand the formation of chain-like structures composed of NILs and their evolution as the Hamiltonian deforms. The chain of singular lines in parameter space is a nontrivial phenomenon which has previously been observed for nodal lines in PT-symmetric Hermitian systems⁶. Here, we show that such an interesting joining phenomenon of singular lines can also occur with NILs, for example,

$${f}_{2}\left({{{{{\boldsymbol{k}}}}}}\right)={k}_{x}{k}_{z},{f}_{3}({{{{{\boldsymbol{k}}}}}})=-{k}_{x}^{2}+{k}_{y}^{2}+{k}_{z}^{2}-d$$

(5)

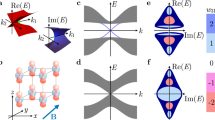
The Hamiltonian exhibits a chain-like structure in k-space as depicted in Fig. 3a(i): a circular NIL located on the plane k_x = 0 is chained to a pair of hyperbolic NILs located on the plane k_z = 0 at two intersecting points. All the NILs (satisfying the equations ${f}_{2}={f}_{3}=0$) are contained in ESs, which are represented by the red (ES₁) and green (ES₂) surfaces (satisfying ${f}_{2}=\mp {f}_{3}$, respectively) corresponding to EL₁ and EL₂ in Fig. 1, respectively. We begin by examining the loop l₆, which encloses the waists of the two ESs and their NILs, and which does not cut through any of the ESs. According to our previous analysis, such a loop, similar to l (Fig. 2e), is topologically trivial. This may not be immediately apparent from the figure, as the ESs and NILs seem to prevent the loop from retracting to a point. However, by changing d from positive to negative, the waists of the ESs first gradually retract to a point [Fig. 3a(ii)] and then open up to form a gap [Fig. 3a(iii)]. The two hyperbolic NILs enclosed by the loop in Fig. 3a(i) thus annihilate each other, consistent with the topological triviality of l₆. Moreover, the trivial loop l₆ enforces the ESs containing the two NILs to remain smooth as the Hamiltonian deforms. This can be explained by ${l}_{6}^{{\prime} }$ [Fig. 3a(i)], which is homotopic to l₆, as they enclose the same NILs, but ${l}_{6}^{{\prime} }$ traverses the ESs. On its plane of cross section, as sketched in Fig. 3b(i), ${l}_{6}^{{\prime} }$ is segmented by the ESs into several paths, where the red and green lines denote the traces of ES₁ and ES₂ on that plane. The topological invariants of the segments along ${l}_{6}^{{\prime} }$ must cancel each other to form a trivial product, which implies that each path l_t, connecting points of a single ES without cutting through the other ES, must carry a trivial topological invariant. This agrees with our previous analysis of l₁, l₂ and l₄ in Fig. 2. As one continues to deform the Hamiltonian (d < 0), the two ESs enclosed gradually become disjoint once the two NILs annihilate [see panels (ii) and (iii) of Fig. 3a–b]. Moving on to the loop l₇ in Fig. 3a(i), we see that it is segmented by the ESs into various paths, as depicted in Fig. 3c(i). This loop can be represented as a concatenation of paths (β^–1α^–1β‘ ^–1α‘ ^–1)2, carrying a nontrivial squared topological invariant (Z₁^–1Z₃^–1)². This invariant prevents the two encircled circular NILs from annihilating each other as d varies in the Hamiltonian [Eq. (5)]. The two NILs merge to a point when d = 0 [Fig. 3a(ii)], dividing the nearby area into eight regions [see Fig. 3c(ii)]. Since the loop is still the product (β^–1α^–1β‘ ^–1α‘ ^–1)², its topological invariant does not change and remains to be squared (Z₁^–1Z₃^–1)². As d varies further, the point splits, and the two NILs become separate in opposite directions, as shown in panel (iii) of Fig. 3a, c. Thus, the squared invariant (Z₁^–1Z₃^–1)² is conserved throughout the deformation of this Hamiltonian. The conservation of the squared invariant (Z₁^–1Z₃^–1)² on l₇ and the trivial invariant on l₆ (or ${l}_{6}^{{\prime} }$) is a necessary condition for the chain of NILs. To observe the chain-like structure of NILs, we can design 3D periodic systems with nonreciprocal hopping between orbitals. The nonreciprocal hopping between orbitals has already been realized in phononic systems and electric circuits with the employment of active devices^41,52. A design of a 3D face-centered cubic (fcc) lattice model, as well as the hopping parameters between orbitals, are shown in Supplementary Note 5. We note that the chain-like structure of NILs is protected by the mirror symmetries k_x ↦ –k_x and k_z ↦ –k_z, and breaking the symmetries will eliminates such a structure. These physical consequences can all be observed based on the design in Supplementary Note 5. The invariant conservation shows that two inannihilable NILs cannot be directly connected by smooth ESs, as one observes in Fig. 3c.

Fig. 3: Explaining the formation of the chain of nondefective intersection lines (NILs) in k-space and its evolution against perturbations with the fundamental group.

a Exceptional surfaces (ES: red and green surfaces) and NILs (black lines) plotted from Eq. (5). The blue loops l₆ and ${l}_{6}^{{\prime} }$ have trivial topological invariants. b Cross sections on the plane containing ${l}_{6}^{{\prime} }$. The enclosed pair of NILs can annihilate each other. Each l_t is a path with its endpoints on the same ES without cutting through the other ES. Similar to l₁, l₂ and l₄ in Fig. 2, l_t carries a trivial topological invariant (the subscript t stands for “trivial”). c Cross sections on the plane containing the orange loop l₇. The NILs enclosed cannot annihilate each other. Red and green lines: ESs; Dark blue dots: NILs; Black dots: intersecting points of loops with ESs (in b and c). The panels (i), (ii) and (iii) correspond to d > 0, d = 0 and d < 0 in Eq. (5), respectively.

Topologically protected edge states

Finally, we demonstrate that an NIL (or NIP) can host topologically protected edge states, which represents a type of bulk–edge correspondence that appears in a gapless non-Hermitian system. This concept may seem counterintuitive, as bulk–edge correspondence is typically discussed in gapped phases^8,11. Specifically, let us consider the following 1D k-space Hamiltonian corresponding to a lattice model,

$$H(k)={\sigma }_{3}\cos k+i{\sigma }_{2}\sin k+v{\sigma }_{0}\cos (k+a)$$

(6)

where σ₀ is the 2×2 identity matrix. The Hamiltonian includes a term proportional to σ₀, which is useful in tuning gaps in projection bands to identify edge states. As can be commonly understood, introducing the identity term does not change the topology of the system and, in particular, the degeneracy features remain. Comparing Eq. (6) to Eq. (1), with k-space represented by a 1D momentum k, we obtain the following correspondence: f₃(k) = cos k and f₂(k) = sin k. The path traced out by (f₂(k), f₃(k)) goes around the NIP as shown in Fig. 4a, and we can see that the 1D Brillouin zone of the lattice model carries the topological invariant Z₁Z₃ (see Fig. 2d). Such a Hamiltonian can be experimentally realized by the 1D tight-binding lattice as shown in Fig. 4b. To observe the topological edge states, we need to consider the band structure and topology of the systems with open boundary condition (OBC) and periodic boundary condition (PBC), respectively. The schematic sample with finite number of unit cells under PBC is shown in Fig. 4b(i), in which the terminal unit cells are connected via the hoppings. The sample under OBC is shown in Fig. 4b(ii), where the terminal unit cells are disconnected. The corresponding real-space Hamiltonian is

$${H}_{r}= \underbrace{\frac{1}{2}({\sigma }_{3}+{\sigma }_{2}+v{e}^{ia}{\sigma }_{0})}_{{t}_{1}}\mathop{\sum}\limits_{j}{c}_{j}^{{{\dagger}} }{c}_{j+1} \\ +\underbrace{\frac{1}{2}({\sigma }_{3}-{\sigma }_{2}+v{e}^{-ia}{\sigma }_{0})}_{{t}_{2}}\mathop{\sum}\limits_{j}{c}_{j}^{{{\dagger}} }{c}_{j-1}$$

(7)

where j denotes unit cell index. The hopping of orbitals is described by two 2 × 2 hopping matrices ${\hat{t}}_{1}$ and ${\hat{t}}_{2}$, whose entries represent the hopping parameters between lattice sites, as shown in Fig. 4c. The hopping matrices satisfy the relation ${\hat{t}}_{1}^{* }={\hat{t}}_{2}$. As can be seen from Eq. (7), the intercell hoppings between adjacent unit cells are non-Hermitian and nonreciprocal, meaning that the two directional hopping matrices ${\hat{t}}_{1}\ne {{\hat{t}}_{2}^{{{\dagger}}} }$. Rather, they have entries that are negatively conjugate to each other ${t}_{1}^{12}=-{({t}_{2}^{21})}^{* }$ and ${t}_{1}^{21}=-{({t}_{2}^{12})}^{* }$. Such tight-binding models can potentially be realized by electric circuits and phononic lattices incorporating active devices^41,53. As the 1D Brillouin zone inevitably cuts through the ELs four times, the band structure undergoes line-gap closing four times, as shown in Fig. 4d. Clearly, the conventional Zak phase, which is commonly used for explaining edge states in gapped 1D systems, cannot be defined in this 1D Brillouin zone. Nevertheless, the two eigenstates experience frame deformation process along each path, evolving from parallel states to antiparallel states (Supplementary Fig. S3b2 in Supplementary Information). This process shows that the relative rotation angle between the two eigenstates is π, which equals an integral

$$\psi ={\oint }_{{l}_{\alpha }}i\left\langle \varphi |{\nabla }_{k}\varphi \right\rangle {dk}$$

(8)

Fig. 4: Topologically protected edge states by the invariant Z₁Z₃.

a A loop circulating the nondefective intersection point (NIP), as the Brillouin zone of the 1D lattice model in Eq. (6), is partitioned into four paths, with α and α‘ residing in exact phases. b Sample designs of the lattice model under periodic boundary condition [PBC: panel (i), terminal unit cells are connected with hoppings] and open boundary condition [OBC: panel (ii), terminal unit cells are disconnected]. Here the black circles denote unit cells and the green bonds denote the hopping matrices connecting adjacent unit cells. The dashed blocks encircle two unit cells, and the structure inside the block is shown in panel c. c Realization of the lattice model. The dashed block shows the internal structure of unit cells and the hoppings (labeled in panel b with dashed blocks). The hopping parameters ${t}_{{{{{\mathrm{1,2}}}}}}^{11}$, ${t}_{{{{{\mathrm{1,2}}}}}}^{12}$, ${t}_{{{{{\mathrm{1,2}}}}}}^{21}$ and ${t}_{{{{{\mathrm{1,2}}}}}}^{22}$ are the entries of the hopping matrices ${\hat{t}}_{1}$ or ${\hat{t}}_{2}$ in Eq. (7). d Eigenvalue dispersions (real part) of the model of Eq. (7) in the 1D Brillouin zone. Since the Brillouin zone cuts through exceptional lines (ELs) four times, the band structure experience gap closing four times. e Joining the trajectories of two bands on the path α forms a loop in Re(E)-f₂-f₃ space l_α, along which the Berry phase is π. This quantized Berry phase is equal to the relative rotation angle between the two eigenstates resulting from frame deformation along α. For the path α‘, joining the two bands forms the loop l_α‘, along which the Berry phase is –π. This is because from α to α‘ the two eigenstates swap due to band inversion at NIP. The relative rotation angle between the eigenstates changes sign. f Plots of projection bands of the 1D lattice model under open boundary condition (OBC, black dots) and periodic boundary condition (PBC, red dots). There exists a pair of edge modes in the line gap for eigenstates along the loops l_α and l_α‘ in panel e. g Field distribution of one edge mode. The lattice model with OBC has 300 periods (600 lattice sites, denoted by Ns). Inset: zoom-in view showing the field distribution near the left edge.

The loop l_α of the integration [Eq. (8)] is shown in Fig. 4e and connects the trajectories of the two eigenvalues along the path α at the ELs. In this context, the loop l_α is in the 3D Re(E)-f₂-f₃ space. Moreover, Eq. (8) represents the conventional Berry phase, which is related to the frame deformation along α. Along the path α‘, the two eigenstates swap in comparison to α, resulting in a relative rotation angle of –π. This means that the Berry phase along the loop l_α‘ given by Eq. (8) is –π (see Fig. 4d). Additionally, the identity term in the Hamiltonian [Eq. (6)] creates a real line gap between the eigenenergies on α and α‘ in the projection band. As a result, if we truncate the 1D system with open boundaries, there will be a pair of edge modes residing in this line gap, as shown in Fig. 4f, where the black and red dots represent the projection bands under OBC and PBC. In broken phases, the eigenenergies form point gaps in the projection band, which lead to the non-Hermitian skin effect as indicated by black dots in the continuum in Fig. 4f. It is shown that the eigenvalues of the skin modes form arcs locate inside the loop of the eigenmodes under PBC on the complex plane. The edge states are separate from any bulk modes and skin modes in the continuum, making them easily distinguishable. The field distribution (amplitude |φ|) of one edge mode is shown in Fig. 4g, where clearly the field is confined at the left edge of the 1D chain (inset).

Conclusion

We have topologically classified a generic non-Hermitian two-level system possessing PT-symmetry and an additional pseudo-Hermitian symmetry which may arise in lattice systems with nonreciprocal hopping^41,46,47,48. These systems feature surfaces of exceptional points that host stable embedded intersection singularities in momentum space. Our study demonstrates that the topology of this gapless structure can be understood by examining the quotient space under equivalence relations of eigenstates, which turns out to be a bouquet of three circles. The fundamental group of this space is isomorphic to a free non-Abelian group on three generators. This classification enables us to predict the formation and evolution of chain-like structures of NILs as the Hamiltonian deforms, based on the conservation of topological invariants. Our work further leads to prediction for the existence of topologically protected edge states in 1D lattice models, which is a remarkable and counterintuitive phenomenon for such gapless phases, going beyond the conventional Zak phase understanding. The methods of quotient space topology and intersection homotopy theory might potentially be extended to systematically classify other hypersurface singularities in non-Hermitian systems, such as high-order exceptional points as cusps^32,40 and more complicated swallowtail catastrophes⁴¹. Our work also proposed a kind of non-Hermitian gapless topological phase of matter, providing pathways for designing systems to realize robust topological non-defective degeneracies in non-Hermitian systems.