Semi-empirical approach to assess externally-induced photoluminescence linewidth broadening of halide perovskite nanocrystals with particle-size distribution

Abstract

Colloidal nanocrystals (NCs) can be used to prepare high-color-purity metal halide perovskites (MHPs) for light-emitting displays. However, the NCs have a finite particle-size distribution, which broadens the linewidth of photoluminescence spectra under strong quantum confinement, and thereby degrades the color purity of the MHPs. This paper presents a simple method to quantify this externally-introduced broadening of linewidth ${{{{{{\boldsymbol{\Gamma }}}}}}}_{{{{{{\bf{SD}}}}}}}$ by combining experimental size-distribution histogram with size-dependent photoluminescence-wavelength (PL-${{{{{\boldsymbol{\lambda }}}}}}$) curve. We develop a semi-empirical method to estimate the other three contributions to the experimentally-measured full-width at half-maximum, ${{{{{{\boldsymbol{\Gamma }}}}}}}_{{{{{{\bf{EXP}}}}}}}$. Namely: the intrinsic linewidth ${{{{{{\boldsymbol{\Gamma }}}}}}}_{{{{{{\bf{LO}}}}}}}$ caused by exciton-longitudinal optical (LO) phonon Fröhlich coupling; the inhomogeneous linewidth ${{{{{{\boldsymbol{\Gamma }}}}}}}_{{{{{{\bf{o}}}}}}}$ caused by imperfections-related scattering, and the broadening ${{{{{{\boldsymbol{\Gamma }}}}}}}_{{{{{{\bf{QC}}}}}}}$ due to the quantum-confinement effect. We show that ${{{{{{\boldsymbol{\Gamma }}}}}}}_{{{{{{\bf{LO}}}}}}}$ of a nanocrystal decreases together with the particle size, disappearing at 1.6 nm radius. Finally, we show that ${{{{{{\boldsymbol{\Gamma }}}}}}}_{{{{{{\bf{LO}}}}}}}$ is correlated with the degree of Fröhlich-polaron formation, hence proportional to the long-range LO-phonon-electron coupling.

Introduction

Metal halide perovskites (MHPs) have spectral tunability that covers ultraviolet to near-infrared wavelengths, high color purity, and low production cost, and are therefore possible next-generation luminescent materials for light-emitting diode (LED) displays^1,2,3,4,5. The high color purity is a consequence of narrow emission linewidths (full-width at half-maximum (FWHM) ≤20 nm), and offers a wide color gamut over 140% of the National Television Standard Committee (NTSC) color standard. These attributes surpass the characteristics of organic emitters (FWHM >40 nm, color gamut <100% NTSC) and inorganic quantum dot (QD) emitters (FWHM ≈30–40 nm, color gamut ≈120% NTSC)⁶.

Early perovskite LEDs achieved bright electroluminescence by using bulk polycrystalline films^2,5. Subsequent perovskite LED technology progressed remarkably by using small nanograins⁵, low-dimensionality layered crystals^7,8, and colloidal perovskite nanocrystals (PNCs)^9,10,11. These approaches boost the quantum-confinement effect by reducing the grain or particle size, and strengthen the excitonic radiative recombination, and thereby increase the photoluminescence quantum efficiency (PLQE)^6,12,13. The use of colloidal PNCs is an effective strategy to increase the PLQEs of MHP crystals^14,15,16,17. This approach uses organic ligands^18,19, which limit growth of MHP crystals and stabilizes them to increase their dispersion stability in solution. MHPs have low exciton-binding energy, so the restriction of PNC size by ligands can overcome exciton dissociation^5,14. Moreover, the MHP crystallization process ends in a solution state, which is weakly influenced by the environment, so colloidal PNCs can be reproducibly coated on a variety of substrates^20,21,22,23.

Both intrinsic and extrinsic factors can affect color purity by broadening the linewidth of the photoluminescence (PL) spectrum $\varGamma \left(T\right)$ at temperature T. For most photoluminescent semiconductors, these factors are divided into four terms^24,25,26: $\varGamma \left(T\right)={\varGamma }_{{{{{{\rm{o}}}}}}}+{\varGamma }_{{{{{{\rm{ac}}}}}}}\left(T\right)+{\varGamma }_{{{{{{\rm{LO}}}}}}}\left(T\right)+{\varGamma }_{{{{{{\rm{imp}}}}}}}$, where ${\varGamma }_{{{{{{\rm{o}}}}}}}$ denotes inhomogeneous line broadening caused by disorder and imperfections-related scattering, and is independent of temperature. ${\varGamma }_{{{{{{\rm{ac}}}}}}}\left(T\right)$ and ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(T\right)$ designate homogeneous line broadening, which arise from phonon scatterings and are dependent on temperature. ${\varGamma }_{{{{{{\rm{ac}}}}}}}\left(T\right)={\gamma }_{{{{{{\rm{ac}}}}}}}T$, where ${{{{{{\rm{\gamma }}}}}}}_{{{{{{\rm{ac}}}}}}}$ is the coupling strength of acoustic phonon and charge carriers. ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(T\right)={\gamma }_{{{{{{\rm{LO}}}}}}}{N}_{{{{{{\rm{LO}}}}}}}\left(T\right)$, where ${{{{{{\rm{\gamma }}}}}}}_{{{{{{\rm{LO}}}}}}}$ is the coupling strength of longitudinal optical (LO) phonon and charge carriers, and ${N}_{{{{{{\rm{LO}}}}}}}(T)=1/\{{e}^{\hslash {{\omega }_{{LO}}}/{{k}_{B}T}}-1\}$ represents the Bose-Einstein distribution function where ${{{\hslash }}{{{{{\rm{\omega }}}}}}}_{{{{{{\rm{LO}}}}}}}$ is the energy of LO phonons. ${\varGamma }_{{{{{{\rm{imp}}}}}}}$ phenomenologically accounts for inhomogeneous scattering from ionized impurities.

A systematic study²⁷ of bulk polycrystalline films of hybrid MHPs MAPbBr₃, MAPbI₃, FAPbBr₃, and FAPbI₃ used the Bose-Einstein distribution function to fit the temperature-dependent FWHM of the PL peak, and thereby demonstrated that linewidth broadening in them at room temperature is primarily caused by long-range Fröhlich coupling between exciton carriers and LO phonons, with scattering ${\varGamma }_{{{{{{\rm{ac}}}}}}}\left(T\right)$ from acoustic phonons and ${\varGamma }_{{{{{{\rm{imp}}}}}}}$ from impurities being minor components^27,28. Thus, the net broadening factor can be expressed as ${\varGamma }_{{{{{{\rm{net}}}}}}}\left(T\right)={\varGamma }_{{{{{{\rm{LO}}}}}}}\left(T\right)+{\varGamma }_{{{{{{\rm{o}}}}}}}$. In their subsequent analysis, however, the temperature-independent imperfections-related scattering ${\varGamma }_{{{{{{\rm{o}}}}}}}$ term was implicitly absorbed in ${\varGamma }_{{{{{{\rm{LO}}}}}}}(T)$ term^27,28. The FWHM of the room-temperature steady-state spectrum of polycrystalline MAPbBr₃ film is $\varGamma \left(\lambda \right)=23.4\ {{{{{\rm{nm}}}}}}$ at $\lambda =538\ {{{{{\rm{nm}}}}}}$ (equivalent to $\varGamma \left(\hslash \omega \right)=100.3\ {{{{{\rm{meV}}}}}}$), which slightly exceeds the high color-purity standard of FWHM ≤ 20 nm. Herein, $\varGamma \left(\lambda \right)$ denotes the FWHM of the PL-$\lambda$ spectrum in which the PL intensity is plotted as function of the PL wavelength, whereas $\varGamma \left(\hslash \omega \right)$ denotes the FWHM of the PL-$\hslash \omega$ spectrum in which the PL intensity is plotted as function of the PL energy ($\hslash \omega$).

In a system of colloidal PNCs that show extraordinarily high PLQEs, the mechanism of the PL linewidth broadening seems to be more complicated than in bulk polycrystalline films due to an additional external factor that arises from the particle-size distribution. If colloidal PNCs are not strictly mono-disperse, an additional broadening mechanism is inevitably introduced because each NC shows a characteristic PL wavelength (PL-$\lambda$) associated with its own size, so a finite size distribution inevitably leads to a finite linewidth in the PL peak. In addition to this external broadening ${\varGamma }_{{{{{{\rm{SD}}}}}}}$ due to the size distribution, one should also consider linewidth broadening ${\varGamma }_{{{{{{\rm{QC}}}}}}}$ due to the quantum-confinement effect, especially for the particle whose radius is smaller than the exciton Bohr radius ${a}_{{{{{{\rm{B}}}}}}}$²⁹. Thus, the net FWHM in the PL-$\lambda$ spectrum of colloidal PNCs at a fixed temperature (e.g., 300 K) can be written as

$${\varGamma }_{{{{{{\rm{net}}}}}}}\left(\lambda \right)={\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)+{\varGamma }_{{{{{{\rm{o}}}}}}}(\lambda )+{\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\lambda \right)+{\varGamma }_{{{{{{\rm{QC}}}}}}}\left(\lambda \right),$$

(1)

where $\lambda$ inside the parenthesis of each broadening term denotes the broadening contribution to the PL-$\lambda$ spectrum. ${\varGamma }_{{{{{{\rm{net}}}}}}}\left(\lambda \right)$ can be directly obtained from the observed broadening ${\varGamma }_{{{{{{\rm{EXP}}}}}}}(\lambda )$ of the experimental PL-$\lambda$ spectrum [i.e., ${\varGamma }_{{{{{{\rm{net}}}}}}}\left(\lambda \right)={\varGamma }_{{{{{{\rm{EXP}}}}}}}(\lambda )$] and ${\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\lambda \right)$ denotes the externally-introduced FWHM that is caused exclusively by the size distribution (Table 1). According to Eq. (1), the FWHM in the photoluminescence angular-frequency spectrum PL-$\omega$ can be written as ${\varGamma }_{{{{{{\rm{net}}}}}}}\left(\omega \right)={\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\omega \right)+{\Gamma }_{{{{{{\rm{o}}}}}}}(\omega )+{\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\omega \right)+{\varGamma }_{{{{{{\rm{QC}}}}}}}\left(\omega \right).$ A QD is a semiconductor nanoparticle that has a diameter less than its Bohr diameter ${D}_{{{{{{\rm{B}}}}}}}(=2{a}_{{{{{{\rm{B}}}}}}})$ and thus shows a strong quantum-confinement effect²⁹. Hereafter, when the corresponding particle has R < ${R}_{{{{{{\rm{c}}}}}}}$, which is the critical size for the onset of the PL blue shift (i.e., the incipient size for weak quantum confinement), we will refer to the particle as a confined nanocrystal (CNC). In an MAPbBr₃ CNC, we found that ${R}_{{{{{{\rm{c}}}}}}}=13.75\ {{{{{\rm{nm}}}}}}$ from the size-dependent experimental PL-$\lambda$ curve (Results and discussion).

Table 1 Three nominal contributions to the size-dependent experimental linewidth of MAPbBr₃ CNCs, expressed in ${{{{{\rm{nm}}}}}}$ value.

Two additional broadening terms, ${\varGamma }_{{{{{{\rm{SD}}}}}}}$ and ${\varGamma }_{{{{{{\rm{QC}}}}}}}$, are thus introduced in colloidally dispersed CNCs, as compared with bulk polycrystalline films²⁷. The linewidth broadening due to these two terms is pronounced at small CNC sizes, which possibly deteriorates the ultrahigh color purity of MHPs. Therefore, it is of significance (i) to estimate the CNC-size-dependent contribution of these two broadening terms and (ii) to consequently find a suitable modal radius for maintaining both high color purity and high PLQE of colloidal PNCs (perovskite nanocrystals). For these purposes, we developed a simple method to extract ${\varGamma }_{{{{{{\rm{SD}}}}}}}$ at a given modal size by combining the experimental size-distribution histogram with the size-dependent PL-$\lambda$ curve. We subsequently developed a semi-empirical method to estimate the other three contributions to the experimentally-measured FWHM, namely, ${\Gamma }_{{{{{{\rm{LO}}}}}}},{\varGamma }_{{{{{{\rm{QC}}}}}}}$, and ${\varGamma }_{{{{{{\rm{o}}}}}}}$. We show that ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ of MAPbBr₃ disappears at the CNC radius $R=1.60\ {{{{{\rm{nm}}}}}}$. The net FWHM ${\varGamma }_{{{{{{\rm{net}}}}}}}$(λ) obtained from the experimental PL-$\lambda$ spectrum effectively remains at a constant plateau value $\left( \sim 23\ {{{{{\rm{nm}}}}}}\right)$ down to $R\approx 4.5\ {{{{{\rm{nm}}}}}}$, then rapidly increases as R decreases further. This result indicates that to maintain ultrahigh color purity of MHPs with high PLQEs, colloidal PNCs should have the modal radius (R_p) not less than $\sim 4.5\ {{{{{\rm{nm}}}}}}$. See Supplementary Table 1 for definition or explanation of various mathematical symbols used in the present study.

Results and discussion

Externally-introduced linewidth broadening due to CNC-size distribution

First, we will illustrate graphically that for a colloidal dispersion having a given CNC-size distribution, characteristic size-dependent variation of the PL wavelength $\lambda$ does greatly alter the shape of the resulting PL-$\lambda$ spectrum by considering two distinct types of the PL-$\lambda$ vs. size ($R$) curve. There exists a unique 1:1 correspondence between the modal CNC size ${R}_{{{{{{\rm{p}}}}}}}$ and the corresponding PL wavelength (Methods). Thus, the CNC-size distribution $g\left(R\right)$ inevitably produces a finite linewidth ${\varGamma }_{{{{{{\rm{SD}}}}}}}=\Delta {\lambda }_{1/2}^{{\prime} }+\Delta {\lambda }_{1/2}$, where $\Delta {\lambda }_{1/2}^{{\prime} }$ and ${\Delta \lambda }_{1/2}$ are respectively the half-widths at half-maximum on the short-λ and long-λ sides in the PL-$\lambda$ spectrum $f\left(\lambda \right)$ (Fig. 1a, b). A linear variation in $\lambda$ across ${R}_{p}$ (Fig. 1c) and a nonlinear variation in $\lambda$ across ${R}_{{{{{{\rm{p}}}}}}}$ (Fig. 1d) would lead to a slightly asymmetric $f\left(\lambda \right)$ spectrum with a ${\Delta \lambda }_{1/2} > \Delta {\lambda }_{1/2}^{{{{\hbox{'}}}}}$ (Fig. 1e) and an asymmetric $f\left(\lambda \right)$ spectrum but with ${\Delta \lambda }_{1/2} < \Delta {\lambda }_{1/2}^{{{{\hbox{'}}}}}$ (Fig. 1f), respectively. The slightly asymmetric $f(\lambda )$ in Fig. 1e occurs because $g\left(R\right)$ is a slightly asymmetric. This analysis predicts the absence of linewidth broadening in the PL-$\lambda$ spectrum $(i.e.,{\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\lambda \right)=0)$ if all CNCs have identical size ($i.e.,\Delta R=0$). However, it should be noted that f(λ) schematically illustrates a hypothetical PL-$\lambda$ spectrum that would be caused exclusively by the CNC-size distribution (Fig. 1e, f).

Fig. 1: Linewidth broadening arising from the polydispersity in CNC-size distribution g(R).

a, b CNC-size distribution $g\left(R\right)$ depends on the size. c Hypothetical linear variation and (d) nonlinear variation in the PL wavelength $\lambda$ across the modal CNC (confined nanocrystal) size would produce (e) a slightly asymmetric $f\left(\lambda \right)$ spectrum that is skewed toward the long-$\lambda$ side of the modal (peak) ${\lambda }_{p}$, and (f) a spectrum with a slight skew toward the short-$\lambda$ side of ${\lambda }_{{{{{{\rm{p}}}}}}}$ for the same CNC-size distribution $g\left(R\right)$. g Schematic diagram that graphically illustrates the relation, ${\varGamma }_{{{{{{\rm{net}}}}}}}\approx {\varGamma }_{{{{{{\rm{LO}}}}}}}+{\varGamma }_{{{{{{\rm{SD}}}}}}}$. Herein, we ignore ${\varGamma }_{{{{{{\rm{QC}}}}}}}$ and ${\varGamma }_{{{{{{\rm{o}}}}}}}$ to simplify our discussion at a conceptual level.

In contrast, a PL-λ spectrum caused by the intrinsic PL broadening ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ should be Lorentzian in the absence of extrinsic broadening ${\varGamma }_{{{{{{\rm{SD}}}}}}}$ (Fig. 1g), where ${\varGamma }_{{{{{{\rm{o}}}}}}}$ is implicitly included in ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ for convenience²⁷. Then, the net linewidth in the real PL-$\lambda$ spectrum is obtained by (i) by shifting the intrinsic Lorentzian ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ spectrum to the short-$\lambda$ side by ${\Delta \lambda }_{1/2}^{{{{\hbox{'}}}}}$ and to the long-$\lambda$ side by ${\Delta \lambda }_{1/2}$ and (ii) adding $\tfrac{1}{2} \, {\varGamma }_{{{LO}}}$ to each of these two shifts caused by the CNC-size distribution (Fig. 1g); i.e., if ${\varGamma }_{{{{{{\rm{QC}}}}}}}$ is negligible, then ${\varGamma }_{{{{{{\rm{net}}}}}}}=(\frac{1}{2}{\varGamma }_{{{{{{\rm{LO}}}}}}}+{\Delta \lambda }_{1/2}^{{{{\hbox{'}}}}})+ ({\Delta \lambda }_{1/2}+\frac{1}{2}{\varGamma }_{{{{{{\rm{LO}}}}}}})={\varGamma }_{{LO}}+({\Delta \lambda }_{1/2}^{{{{\hbox{'}}}}}+{\Delta \lambda }_{1/2})={\varGamma }_{{{{{{\rm{LO}}}}}}}+{\varGamma }_{{{{{{\rm{SD}}}}}}}$.

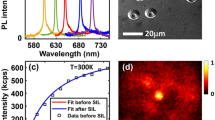
The size distribution of MAPbBr₃ CNCs affects their PL spectrum and associated properties (Fig. 2). As the CNC size decreases, the peak wavelength ${\lambda }_{p}$ gradually decreases in the normalized PL-λ spectrum (Fig. 2a), and the asymmetry of the PL spectrum tends to increase. The spectral asymmetry is very pronounced when the modal diameter ${D}_{{{{{{\rm{p}}}}}}}\,$(2R_p)$\,=2.7\ {{{{{\rm{nm}}}}}}$. PL-$\lambda$ decreases slowly and linearly with decreasing ${D}_{{{{{{\rm{p}}}}}}}$ down to $\sim 9\ {{{{{\rm{nm}}}}}}$ but decreases rapidly below this critical size, showing a pronounced PL blue shift beginning at $\sim 9\ {{{{{\rm{nm}}}}}}$ (Fig. 2b). It can be shown theoretically that there exists a unique 1:1 correspondence between the particle size and the PL wavelength with an increasing tendency of the PL blue shift (moves towards a shorter ${\lambda }_{{{{{{\rm{p}}}}}}}$) as ${R}_{{{{{{\rm{p}}}}}}}$ decreases (Methods). The critical size for the pronounced PL blue shift is close to the exciton Bohr diameter ${D}_{{{{{{\rm{B}}}}}}}(=2{a}_{{{{{{\rm{B}}}}}}})$ which is reported between $8.76\ {{{{{\rm{nm}}}}}}$ (ref. ³⁰) and $10\,{{{{{\rm{nm}}}}}}$ (ref. ²⁹) for MAPbBr₃. This result suggests that the strong quantum confinement (i.e., noticeable degree of the PL blue shift) begins to occur when the modal CNC diameter (radius) is reduced to its ${D}_{{{{{{\rm{B}}}}}}}({a}_{{{{{{\rm{B}}}}}}})$.

Fig. 2: Size-dependent PL spectra and associated properties of MAPbBr₃ CNCs.

a Normalized PL intensity vs. PL wavelength (i.e., PL-$\lambda$ spectrum) of MAPbBr₃ CNCs (confined nanocrystals) having various modal diameters. b Experimentally measured PL wavelength $\lambda$ of MAPbBr₃ CNCs plotted as a function of the modal CNC diameter obtained from the corresponding size-distribution histogram. c Experimentally obtained FWHM (full-width at half-maximum) ${\varGamma }_{{EXP}}$ vs. modal diameter of MAPbBr₃ CNCs. This size-dependent experimental FWHM was obtained directly from the corresponding PL-$\lambda$ spectrum. It can be shown that the difference between the red horizontal ${\varGamma }_{{EXP}}$ line and the blue horizontal line comprises the two independent contributions: $\Delta {\varGamma }_{{{{{{\rm{SD}}}}}}}+\Delta {\varGamma }_{{{{{{\rm{QC}}}}}}}=2.1-0.1=2.0\left({{{{{\rm{nm}}}}}}\right),$ where $\Delta {\varGamma }_{{{{{{\rm{QC}}}}}}}$ represents the difference in ${\varGamma }_{{{{{{\rm{QC}}}}}}}$ between the CNCs with ${D}_{{{{{{\rm{p}}}}}}}=23.7\ {{{{{\rm{nm}}}}}}$ and the CNCs with ${D}_{{{{{{\rm{p}}}}}}}=19.5\ {{{{{\rm{nm}}}}}}$ namely, ${\varGamma }_{{{{{{\rm{QC}}}}}}}=\left(0.2-0.3\right)\,{{{{{\rm{nm}}}}}},$ because $\Delta {\varGamma }_{{{{{{\rm{LO}}}}}}}=18.3-18.3=0.$ d Normalized PL intensity vs. PL frequency (i.e., PL-$\omega$ spectrum) of MAPbBr₃ CNCs having various modal diameters.

The FWHM of the PL-$\lambda$ spectrum is plotted as a function of the modal diameter of MAPbBr₃ CNCs (Fig. 2c). According to the normalized PL-$\omega$ spectra (Fig. 2d), the modal frequency ${\omega }_{{{{{{\rm{p}}}}}}}$ gradually moves towards the onset frequency ${\omega }_{p}=3.575\times {10}^{15}\,{{{{{{\rm{s}}}}}}}^{-1}$ of the PL blue shift as the CNC size increases. Unlike other PL-$\omega$ spectra, the PL-$\omega$ spectrum at ${D}_{{{{{{\rm{p}}}}}}}=2.7\ {{{{{\rm{nm}}}}}}$ is highly asymmetric with (i) a strong skew toward the low-$\omega$ side and (ii) a long tail in the low-$\omega$ side of the peak frequency ${\omega }_{{{{{{\rm{p}}}}}}}$. The main reason behind this anomalous non-Lorentzian behavior will be analyzed theoretically in other section.

Extraction of size-dependent ${{{{{\boldsymbol{\Gamma }}}}}}_{{{{{{\mathbf{SD}}}}}}}$

Transmission-electron microscopy (TEM) images of colloidally dispersed CNCs were captured at various modal diameters of MAPbBr₃ (Fig. 3a), and their modal-diameter-dependent size-distribution histograms were compiled. The degree of size distribution (i.e., polydispersity) in the synthesized MAPbBr₃ CNCs decreased prominently as ${D}_{{{{{{\rm{p}}}}}}}$ decreased; the polydispersity in size, i.e., $\Delta R$ in $g(R)$ (Fig. 1a) was as small as $\sim 1\ {{{{{\rm{nm}}}}}}$ at ${D}_{{{{{{\rm{p}}}}}}}=2.7\ {{{{{\rm{nm}}}}}}$ (Supplementary Table 2, Supplementary Fig. 1).

Fig. 3: Size-dependent characteristics and a simple method of extracting PL-λ curve.

a TEM images of the colloidally dispersed CNCs (confined nanocrystals) for various modal diameters ($2.7\ {{{{{\rm{nm}}}}}}\le {D}_{{{{{{\rm{p}}}}}}}\le 23.7\ {{{{{\rm{nm}}}}}}$) of MAPbBr₃ with the size-distribution histograms for various modal sizes. b Schematic diagrams that illustrate a simple method of extracting the $f\left(\lambda \right)$ curve and the associated FWHM (full-width at half-maximum) using the CNCs assembly with ${D}_{{{{{{\rm{p}}}}}}}=7.5\ {{{{{\rm{nm}}}}}}$ as a standard example. The extracted ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)$ is not the net FWHM of the experimental PL-$\lambda$ curve but is the FWHM of hypothetical $f\left(\lambda \right)$ spectrum, which is caused exclusively by the CNC-size distribution under a nonlinear variation of the PL wavelength $\lambda$ with the CNC size. c Extracted $f\left(\lambda \right)$ spectra of MAPbBr₃ CNCs vs. PL wavelength for nine different modal diameters between $2.7\ {{{{{\rm{nm}}}}}}$ and $23.7\ {{{{{\rm{nm}}}}}}.$ $f\left(\lambda \right)$ curve denotes the $\lambda$-dependent PL spectrum which would be exclusively caused by the CNC-size distribution, and thus is not the $\lambda$-dependent net experimental PL-$\lambda$ spectrum. The extracted result indicates that ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)$ decreases dramatically as modal size increases and tends toward an asymptote of $2.2\ {{{{{\rm{nm}}}}}}$ for ${D}_{p}\ge 19.5\ {{{{{\rm{nm}}}}}}$.

The $f(\lambda )$ spectrum (Fig. 1e, f) can be extracted in a simple manner by combining the experimental size-distribution histogram with the size-dependent PL-$\lambda$ curve (Fig. 3b), where $f(\lambda )$ again denotes a hypothetical PL-$\lambda$ spectrum that is exclusively caused by the CNC-size distribution described by $g\left(R\right).$ ${\varGamma }_{{SD}}(\lambda )$ can be easily extracted from the difference between the two points on the horizontal line that intersects the extracted $f\left(\lambda \right)$ curve at $f\left(\lambda \right)=1/2$ (Supplementary Table 2). For a CNC assembly with ${D}_{p}=7.5{{{{{\rm{nm}}}}}}$ as an illustrative example, ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)=523.6\ {{{{{\rm{nm}}}}}}-517.6\ {{{{{\rm{nm}}}}}}=6.0\ {{{{{\rm{nm}}}}}}$ (Fig. 3b), where ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)$ denotes ${\varGamma }_{{{{{{\rm{SD}}}}}}}(\lambda )$ extracted from the size-dependent PL-$\lambda$ curve combined with the experimental size-distribution histogram (Supplementary Fig. 1). In this way, we extracted $f(\lambda )$ spectra for nine modal diameters (Fig. 3c and Supplementary Fig. 2); ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}(\lambda )$ decreased dramatically as ${D}_{{{{{{\rm{p}}}}}}}$ increased and tended toward an asymptote of $2.2{{{{{\rm{nm}}}}}}$ at ${D}_{{{{{{\rm{p}}}}}}}\ge 19.5{{{{{\rm{nm}}}}}}$. The main reason for obtaining a narrow f$(\lambda)$ spectrum (i.e., small ${\varGamma }_{{{{{{\rm{SD}}}}}}}$) at large modal diameters is that dλ⁄dD decreases significantly as ${D}_{{{{{{\rm{p}}}}}}}$ increases (Fig. 2b) although the polydispersity in the CNC-size distribution increases noticeably as ${D}_{{{{{{\rm{p}}}}}}}$ increases (Fig. 3a). This results in narrow $f(\lambda )$ spectra that have a common linewidth of $\sim 2.2{{{{{\rm{nm}}}}}}$.

However, the correct ${\varGamma }_{{{{{{\rm{SD}}}}}}}$ value for colloidal CNCs having a finite degree of the size distribution is substantially different from ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}$ due to a nonlinearity in the size-dependent PL-$\lambda$ curve. According to our analysis described in Methods, the extracted value ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}$ is significantly overestimated as compared with the correct ${\varGamma }_{{{{{{\rm{SD}}}}}}}$ value with the degree of overestimate designated by ${\Delta }_{R}$. Accordingly, we empirically establish the following equation:

$${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}(\lambda )={\varGamma }_{{{{{{\rm{SD}}}}}}}(\lambda )+{\varDelta }_{R}$$

(2)

It can be shown that ${\varDelta }_{R}=0$ (i.e., ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}={\varGamma }_{{{{{{\rm{SD}}}}}}}$) if the following two requirements are simultaneously satisfied: (i) a symmetric size distribution $g(R)$ with respect to the modal radius ${R}_{{{{{{\rm{p}}}}}}}$ and (ii) a linearity in the size-dependent PL-$\lambda$ curve.

Size-dependent three nominal contributions to net linewidth

The three distinct contributions to the experimental net linewidth, ${\varGamma }_{{{{{{\rm{EXP}}}}}}}\left(\lambda \right)$, vary as the CNC radius varies (Fig. 4a). Here, the three nominal contributions are ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}\,}\left(\lambda \right),{\varGamma }_{{{{{{\rm{QC}}}}}}}\left(\lambda \right),$ and ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}(\lambda )$. ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}\,}\left(\lambda \right)$ in Fig. 4a is not the true intrinsic ${\varGamma }_{{{{{{\rm{LO}}}}}}}(\lambda )$ value but designates an indirect estimate obtained from (i) the experimental ${\varGamma }_{{{{{{\rm{EXP}}}}}}}\left(\lambda \right)$, (ii) the extracted ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)$, and (iii) the theoretically computed ${\varGamma }_{{{{{{\rm{QC}}}}}}}\left(\lambda \right)$ using the following nominal definition:

$${\varGamma }_{{{{{{\rm{EXP}}}}}}}\left(\lambda \right)\equiv {\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)+{\varGamma }_{{{{{{\rm{QC}}}}}}}\left(\lambda \right)+{\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}(\lambda )$$

(3)

where ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)$ absorbs ${\varGamma }_{{{{{{\rm{o}}}}}}}$ term in Eq. (1). The main reason for absorbing ${\varGamma }_{{{{{{\rm{o}}}}}}}$ term into ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)$ is that we are not able to separately evaluate ${\varGamma }_{{{{{{\rm{LO}}}}}}}(\lambda )$ and ${\varGamma }_{{{{{{\rm{o}}}}}}}(\lambda )$ at this stage. It can be shown readily that ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}={\varGamma }_{{{{{{\rm{LO}}}}}}}+\left({\varGamma }_{{{{{{\rm{o}}}}}}}-{\varDelta }_{R}\right)$ (Methods). This signifies that the nominal ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}$ absorbs the ${\varGamma }_{{{{{{\rm{o}}}}}}}$ term²⁷ into ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ but is corrected by the overestimate ${\Delta }_{{{{{{\rm{R}}}}}}}$ made in the experimental extraction of ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}$.

Fig. 4: Three nominal contributions to net linewidth.

a Three nominal contributions to the net experimental linewidth ${\varGamma }_{{{{{{\rm{EXP}}}}}}}\left(\lambda \right)$ (black) of MAPbBr₃ vs. CNC (confined nanocrystals) radius. ${\prime} \lambda {\prime}$ inside the parenthesis of each broadening term indicates that the corresponding PL intensity is displayed as a function of $\lambda$ (not of $\omega$). ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}\,}\left(\lambda \right)$ (red) designates an extracted ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)$ value which is obtained using Eq. (3) and the following three distinct contributions: (i) experimental ${\varGamma }_{{{{{{\rm{EXP}}}}}}}\left(\lambda \right)$, (ii) theoretically computed ${\varGamma }_{{{{{{\rm{QC}}}}}}}\left(\lambda \right)$ (green), and (iii) experimentally extracted ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)$ (blue). We semi-empirically deduced that ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)$ is equal to the correct intrinsic ${\varGamma }_{{{{{{\rm{LO}}}}}}}(\lambda )$ for $R\le 4.95\ {{{{{\rm{nm}}}}}}$. b Semi-empirically deduced size-dependent ${\varDelta }_{R}$ over a wide range of the CNC radius. It shows a constant plateau behavior up to $R=4.95\ {{{{{\rm{nm}}}}}}$ and decays to zero at $R=11.85\ {{{{{\rm{nm}}}}}}$ A non-zero ${\varDelta }_{R}$ indicates that there exists a certain degree of nonlinearity in the size-dependent PL wavelength for a CNC having the radius $R$.

As described in Methods, we estimated ${\varGamma }_{{{{{{\rm{LO}}}}}}}(\lambda )$ and ${\varGamma }_{{{{{{\rm{o}}}}}}}(\lambda )$ separately by comparing ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}(R=11.85\ {{{{{\rm{nm}}}}}})$ with ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(R=4.95\ {{{{{\rm{nm}}}}}}\right),$ where ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}(R=11.85\ {{{{{\rm{nm}}}}}})$ denotes the value of ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}$ at $R=11.85\ {{{{{\rm{nm}}}}}}.$ The semi-empirically estimated ${\Gamma }_{{{{{{\rm{o}}}}}}}$ is $4.8\ {{{{{\rm{nm}}}}}}$ in the PL-$\lambda$ spectrum. In addition, we semi-empirically found that (i) ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)={\varGamma }_{{{{{{\rm{LO}}}}}}}(\lambda ){\equiv \varGamma }_{{{{{{\rm{LO}}}}}}}(R)$ for $R\le 4.95\ {{{{{\rm{nm}}}}}},$ where ${\varGamma }_{{{{{{\rm{o}}}}}}}\approx {\varDelta }_{R}$ and (ii) ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)={\varGamma }_{{{{{{\rm{LO}}}}}}}\left({{{{{\rm{bg}}}}}}\right)+\left({\varGamma }_{{{{{{\rm{o}}}}}}}-{\varDelta }_{{{{{{\rm{R}}}}}}}\right)$ for $R\ge 4.95\ {{{{{\rm{nm}}}}}}.$ Herein, ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(R\right)$ denotes the CNC-radius-dependent intrinsic linewidth solely caused by the exciton-LO phonon coupling (${\varGamma }_{{{{{{\rm{LO}}}}}}}$). ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(R\right)$ is a rapidly decaying function of $R$ varying from $18.3\ {{{{{\rm{nm}}}}}}$ to $0\ {{{{{\rm{nm}}}}}}$ as $R$ decreases from $4.95\ {{{{{\rm{nm}}}}}}$ to $1.60\ {{{{{\rm{nm}}}}}}$ (Methods for details). On the other hand, ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left({{{{{\rm{bg}}}}}}\right)$ denotes the ${\varGamma }_{{{{{{\rm{LO}}}}}}}(\lambda )$ value that corresponds to the bulk grains. It is estimated to be $18.3\ {{{{{\rm{nm}}}}}}$ for MAPbBr₃. ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ for sufficiently coarsened grains in a polycrystalline film probably meets this requirement that ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)={\varGamma }_{{{{{{\rm{LO}}}}}}}\left({{{{{\rm{bg}}}}}}\right)$.

We computed the size-dependent overestimate ${\varDelta }_{R}$ by using the following equation that can be obtained by combining Eq. (2) with Eq. (1): ${\varDelta }_{R}=\left\{{\varGamma }_{{{{{{\rm{LO}}}}}}}+{\Gamma }_{{{{{{\rm{o}}}}}}}+{\varGamma }_{{{{{{\rm{QC}}}}}}}+{\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\right\}-{\varGamma }_{{{{{{\rm{EXP}}}}}}}$. In the case of MAPbBr₃ CNCs, ${\varDelta }_{R}$ lies somewhere between $0$ and $5.8\ {{{{{\rm{nm}}}}}},$ approaching $0$ as the modal radius increases. Semi-empirical calculations (Methods) indicate that ${\varDelta }_{R}$ decreases noticeably with increasing radius beginning at $R=4.95\ {{{{{\rm{nm}}}}}}$ and becomes effectively $0$ at $R=11.85\ {{{{{\rm{nm}}}}}}$ (Fig. 4b). Thus, ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)\approx {\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\lambda \right)$ for $R\ge 11.85\ {{{{{\rm{nm}}}}}}.$ Consequently, ${\Gamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)$ or ${\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\lambda \right)$ reaches a constant plateau value of $2.2\ {{{{{\rm{nm}}}}}}$ as the CNC size increases to ${R}_{{{{{{\rm{c}}}}}}}=13.75\ {{{{{\rm{nm}}}}}}$ (Fig. 4a), where ${R}_{{{{{{\rm{c}}}}}}}$ is the critical radius at which the PL blue shift begins (Table 1).

The quantum-confinement contribution to the linewidth broadening was calculated as²⁹ ${\varGamma }_{{{{{{\rm{QC}}}}}}}\left(\lambda \right)=\frac{3\hslash {\lambda }_{{{{{{\rm{p}}}}}}}}{{\mu }_{{{{{{\rm{o}}}}}}}c{R}_{{{{{{\rm{p}}}}}}}}\left(1-\frac{3{C}_{1}^{{\prime} }}{{{{{{{\rm{\pi }}}}}}}^{2}}\right)=0.544\times {10}^{-11}\left(\frac{{\lambda }_{{{{{{\rm{p}}}}}}}}{{R}_{{{{{{\rm{p}}}}}}}}\right)$, where ${\lambda }_{{{{{{\rm{p}}}}}}}$ denotes the PL wavelength that corresponds to the modal (peak) radius ${R}_{{{{{{\rm{p}}}}}}}$, and ${\mu }_{{{{{{\rm{o}}}}}}}$ designates the effective mass of the exciton ($=0.13{m}_{{{{{{\rm{o}}}}}}}$ for MAPbBr₃)³⁰, where ${m}_{{{{{{\rm{o}}}}}}}$ denotes the free-electron mass ($9.109\times {10}^{-31}\,{{{{{\rm{kg}}}}}}$). ${C}_{1}^{{\prime} }$ is the modified effective Madelung constant for a spherical CNC, and it is modulated from ${C}_{1}=1.786$ by considering the dielectric-confinement effect³¹ that arises from the surrounding low dielectric-permittivity medium. The evaluated ${C}_{1}^{{\prime} }$ value is 1.39 for MAPbBr₃ CNCs dispersed in a toluene²⁹. The three nominal contributions to ${\varGamma }_{{{{{{\rm{EXP}}}}}}}$, namely, ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}\,},{\varGamma }_{{{{{{\rm{QC}}}}}}},$ and ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}$, are listed in the unit of wavelength (${{{{{\rm{nm}}}}}}$) in Table 1 and in the unit of energy (${{{{{\rm{meV}}}}}}$) in Table 2.

Table 2 Three distinct contributions to the size-dependent experimental linewidth of MAPbBr₃ CNCs, expressed in ${{{{{\bf{meV}}}}}}$ value.

Corrected four distinct contributions to net linewidth

The four corrected contributions to ${\varGamma }_{{{{{{\rm{EXP}}}}}}}\left(\lambda \right)$ are plotted as a function of the CNC radius (Fig. 5a). The contribution of ${\Gamma }_{{{{{{\rm{o}}}}}}}$ to ${\varGamma }_{{{{{{\rm{EXP}}}}}}}\left({{{{{\rm{\lambda }}}}}}\right)$ is constant and independent of the CNC radius. The semi-empirically estimated ${\Gamma }_{{{{{{\rm{o}}}}}}}$ is $4.8\ {{{{{\rm{nm}}}}}}$ in the PL-$\lambda$ spectrum (Methods). It can be shown readily that $4.8\ {{{{{\rm{nm}}}}}}$ is equivalent to $21.4\ {{{{{\rm{meV}}}}}}$ in the PL-energy (i.e., PL-$\hslash \omega$) spectrum. This value is substantially smaller than $\sim 30\ {{{{{\rm{meV}}}}}}$ obtained by curve fitting of the temperature-dependent linewidth data of polycrystalline MAPbBr₃ film with the Bose-Einstein distribution function²⁷. The difference of $\sim 8.6\ {{{{{\rm{meV}}}}}} \, ({{{{{\rm{i.e}}}}}}.,30-21.4)$ is due to structural disorders and imperfections presumably introduced during the film-forming processes that include annealing step at ${100}$°C after spin coating²⁷.

Fig. 5: Four distinct contributions to net linewidth.

a Corrected four distinct contributions to the net experimental linewidth ${\varGamma }_{{{{{{\rm{EXP}}}}}}}\left(\lambda \right)$ (black) of MAPbBr₃ vs. CNC (confined nanocrystals) radius, where ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)$ (red) indicates the FWHM caused by the exciton-LO phonon Fröhlich coupling, ${\varGamma }_{{{{{{\rm{QC}}}}}}}(\lambda )$ (green) indicates the FWHM (full-width at half-maximum) caused by the quantum-confinement, and ${\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\lambda \right)$ (blue) denotes the corrected externally-introduced FWHM that is caused exclusively by the CNC-size distribution. b $R$-dependent ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}$ and the reduced long-range Coulomb potential ${\varphi }_{r}\left(R\right)$ (blue) 1over a wide range of CNC radius up to the onset ${R}_{{{{{{\rm{c}}}}}}}$ of the PL blue shift where the weak quantum-confinement effect begins to occur. For $R\le 5.0\ {{{{{\rm{nm}}}}}},$ we used a red solid line to represent the size-dependent ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ because ${\varGamma }_{{{{{{\rm{LO}}}}}}}(R)={\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}$ in this size range, where ${\varGamma }_{{{{{{\rm{LO}}}}}}}(R)$ is used to emphasize the strongly $R$-dependent corrected ${\varGamma }_{{{{{{\rm{LO}}}}}}}(\lambda )$ for $R\le 5.0\ {{{{{\rm{nm}}}}}}$ in the PL-$\lambda$ spectrum. On the contrary, we used a red dashed line for $R > 5.0\ {{{{{\rm{nm}}}}}}$ as this line represents ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}$ rather than the correct intrinsic ${\varGamma }_{{{{{{\rm{LO}}}}}}}({bg}),$ where ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)={\varGamma }_{{{{{{\rm{LO}}}}}}}\left({bg}\right)+({\varGamma }_{{{{{{\rm{o}}}}}}}-{\varDelta }_{R})$ for $R\ge 4.95\ {{{{{\rm{nm}}}}}},$ Herein, we adopt ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}$ values to correlate the size-dependent ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ with ${\varphi }_{r}\left(R\right)$ because we are primarily concerned with the decaying behavior of ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ for the CNC radius smaller than ${R}_{{{{{{\rm{rd}}}}}}}(\approx 5.0\ {{{{{\rm{nm}}}}}})$. The estimated result shows that ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{\left(1s\right)}$(λ) reduces to zero when ${\phi }^{{{{{{\rm{LR}}}}}}}\left(R\right)$ [i.e., ${\varphi }_{r}\left(R\right)$] disappears at ${R}_{{{{{{\rm{p}}}}}}}=$1.6 nm${{{{{\rm{;}}}}}}$ this result suggests that the intrinsic linewidth broadening caused by the exciton-LO phonon coupling is closely correlated with the driving force for the formation of large Fröhlich polarons.

The corrected ${\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\lambda \right)$ was evaluated using size-dependent ${\Delta }_{{{{{{\rm{R}}}}}}}$ (Eq. 4b) and Eq. (2). ${\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\lambda \right)$ shows a rapid increase beginning at $R=4.95\ {{{{{\rm{nm}}}}}}.$ In contrast, ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)$ decreases rapidly with decreasing radius beginning at the same radius, $4.95\ {{{{{\rm{nm}}}}}}.$ However, ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)$ shows a constant plateau value of $18.3\ {{{{{\rm{nm}}}}}}$ beyond this particular size. The most prominent features of Fig. 5a are (i) the rapid decrease of ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)$ with decreasing CNC size, and (ii) the disappearance of ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)$ when the CNC radius decreases to 1.6 nm (i.e., $D=3.2\ {{{{{\rm{nm}}}}}}$). Similar to the present finding, it was reported³² that the long-range Fröhlich interaction decreased with a concomitant narrowing of linewidth in quasi-zero-dimensional ZnO CNCs (~4 nm in average size), as compared with unconfined bulk ZnO crystals. Phonons are long-range collective excitations of lattice vibrations, so this observation can be attributed to the reduced range of translational symmetry³² in the collective excitations.

The R-dependent ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ scales well with the reduced long-range Coulomb potential ${\varphi }_{r}\left(R\right)$ (Fig. 5b). Here, ${\varphi }_{r}\left(R\right)$ is defined as ${\phi }^{{{{{{\rm{LR}}}}}}}(R)/{\phi }^{{{{{{\rm{LR}}}}}}}({\infty })$, where ${\phi }^{{{{{{\rm{LR}}}}}}}(R)$ is the long-range Coulomb interaction potential between the excess electron (or hole) and the ionic lattice in a CNC of radius $R$, which is considered to be the main driving force for the formation of the large Fröhlich polaron^33,34. Here, ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{\left(1s\right)}$ emphasizes the exciton-LO phonon linewidth associated with the PL emission to the exciton’s 1s ground state. The observed scaling between ${\varGamma }_{{{{{{\rm{LO}}}}}}}(R)$ and ${\varphi }_{r}\left(R\right)$ indicates that the ratio ${\varGamma }_{{{{{{\rm{LO}}}}}}}(R)/{\varphi }_{r}\left(R\right)$ is constant and independent of $R$ over a wide range, and suggests a linear correlation between ${\varGamma }_{{{{{{\rm{LO}}}}}}}(R)$ and ${\phi }^{{{{{{\rm{LR}}}}}}}(R)$, where ${\varGamma }_{{{{{{\rm{LO}}}}}}}(R)$ is used to emphasize the strongly $R$-dependent ${\varGamma }_{{{{{{\rm{LO}}}}}}}(\lambda )$ for $R\le 5.0\ {{{{{\rm{nm}}}}}}$ in the PL-$\lambda$ spectrum. Thus, ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(R\right)={\varGamma }_{{{{{{\rm{LO}}}}}}}\left({R;}\lambda \right).$ In the next section, we will clarify theoretically this proposition of the $R$-independent constant ratio.

Correlation of ${{{{{\boldsymbol{\Gamma }}}}}}_{{{{{{\mathbf{LO}}}}}}}(R)$ with the long-range Coulomb potential

The linear correlation between ${\varGamma }_{{{{{{\rm{LO}}}}}}}(R)$ and ${\phi }^{{{{{{\rm{LR}}}}}}}\left(R\right)$ for $R\le 5.0{{{{{\rm{nm}}}}}}$ further suggests that the Fröhlich-polaron radius might affect the variation of the PL linewidth. ${\varGamma }_{{{{{{\rm{LO}}}}}}}(R)$ decreases rapidly when the CNC radius is smaller than a certain critical value ${R}_{{{{{{\rm{rd}}}}}}}\approx 5.0\ {{{{{\rm{nm}}}}}}$ (Fig. 5b). We therefore tested whether ${R}_{{{{{{\rm{rd}}}}}}}$ is correlated with the equilibrium polaron size. The following equation can be obtained for the radius ${r}_{{{{{{\rm{p}}}}}}}$ of the large Fröhlich polarons for a weak or moderate electron-LO phonon coupling³⁵:

$${r}_{{{{{{\rm{p}}}}}}}^{2}=\frac{2{{{\hslash }}}^{2}}{{m}_{{{{{{\rm{b}}}}}}}\left({{\hslash }}{\omega }_{{{{{{\rm{LO}}}}}}}\right)}\left(1-\frac{\alpha }{6}\right),$$

(4)

where ${m}_{b}$ is the effective band mass, which can be approximated by the effective reduced mass of exciton ($0.117{m}_{{{{{{\rm{o}}}}}}}$) and ${\omega }_{{{{{{\rm{LO}}}}}}}$ = ${167\ {{{{{\rm{cm}}}}}}}^{-1}$ for MAPbBr₃ (ref. ³⁶). The dimensionless Fröhlich coupling constant $\alpha \le 2$ is a measure of the degree of the electron-LO or hole-LO phonon coupling that is responsible for the formation of large Fröhlich polarons ($\alpha =1.69$ for MAPbBr₃)³⁶. Plugging these values into Eq. (4) yields ${r}_{{{{{{\rm{p}}}}}}}\approx 6.7\ {{{{{\rm{nm}}}}}}.$ The experimental critical CNC radius for a rapid decrease in ${\varGamma }_{{{{{{\rm{LO}}}}}}}(R)$ is $\sim 5.0\ {{{{{\rm{nm}}}}}}$ (${\equiv R}_{{{{{{\rm{rd}}}}}}}$) (Fig. 5b) and is substantially smaller than the equilibrium polaron radius ($6.7\ {{{{{\rm{nm}}}}}}$). This result suggests that the PL linewidth tends to decrease rapidly when the large Fröhlich polaron is physically confined under the condition that ${R}_{{{{{{\rm{rd}}}}}}} < {r}_{{{{{{\rm{p}}}}}}}$. We will show subsequently that the decrease in ${\varGamma }_{{{{{{\rm{LO}}}}}}}(R)$ with decreasing $R$ is linearly correlated with the reduced driving force ${\phi }^{{{{{{\rm{LR}}}}}}}\left(R\right)$ for the formation of large Fröhlich polarons.

Large Fröhlich polarons are formed by a long-range interaction between an electron and LO phonons^33,37. Similarly, the PL linewidth broadening ${\varGamma }_{{LO}}$ originates from the exciton-LO phonon coupling²⁴. The strength of the electron-LO phonon coupling is expressed by the dimensionless Fröhlich coupling constant $\alpha$ (ref. ³⁷). $\alpha$ is proportional to the long-range Coulomb potential for a bulk state, ${\phi }^{{{{{{\rm{LR}}}}}}}\left(R={\infty }\right)$ (Supplementary Notes 1). ${\phi }^{{{{{{\rm{LR}}}}}}}\left({\infty }\right)$ in a bulk material is given by³⁴

$${\phi }^{{{{{{\rm{LR}}}}}}}(\infty )=-\frac{{{{{{\rm{e}}}}}}}{4{{{{{\rm{\pi }}}}}}\,{\varepsilon }_{o}|{{{{{\boldsymbol{r}}}}}}|}\left(\frac{1}{{\varepsilon }_{r(\infty )}}-\frac{1}{{\varepsilon }_{r(0)}}\right)\equiv -\frac{{{{{{\rm{e}}}}}}}{4\pi \,{\varepsilon }_{o}{\varepsilon }_{r(\infty )}^{{{{{{\rm{eff}}}}}}}|{{{{{\boldsymbol{r}}}}}}|} \, < \, 0.$$

(5)

where $\left|{{{{{\boldsymbol{r}}}}}}\right|$ is the distance between the excess electron (or hole) and the ionic lattice. ${\phi }^{{LR}}$ is the ensemble average of the long-range Coulomb potential operator $\widetilde{\phi }\left(r\right)$, and it is given by^33,37 $\widetilde{\phi }(r)=-\frac{1}{{{{{{\rm{e}}}}}}}\mathop{\sum}\limits_{{{{{{\bf{q}}}}}}}({V}_{{{{{{\bf{q}}}}}}}{a}_{{{{{{\bf{q}}}}}}}^{-}{e}^{+{{{{{\rm{i}}}}}}{{{{{\bf{q}}}}}}{{\cdot }}r}+{V}_{{{{{{\bf{q}}}}}}}^{* }{a}_{{{{{{\bf{q}}}}}}}^{+}{e}^{-{{{{{\rm{i}}}}}}{{{{{\bf{q}}}}}}{{\cdot }}r}),$ where ${a}_{{{{{{\bf{q}}}}}}}^{+}$ and ${a}_{{{{{{\bf{q}}}}}}}^{-}$, respectively, are the creation and annihilation operators for the LO phonon with the wave vector ${{{{{\bf{q}}}}}}$ and energy $\hslash {\omega }_{{{{{{\rm{LO}}}}}}}$. ${V}_{{{{{{\bf{q}}}}}}}$ denotes the Fourier component in the electron-LO phonon interaction Hamiltonian, and its magnitude $|{V}_{{{{{{\bf{q}}}}}}}|$ is proportional to ${\alpha }^{1/2}$. Applying Eq. (5) to a dielectrically-confined CNC of radius $R$, and adopting the effective-action thickness approximation, we eventually obtain the following approximate expression of the Coulomb potential for a dielectrically-confined CNC of radius $R$ (Supplementary Notes 1):

$${\phi }^{{{{{{\rm{LR}}}}}}}\left(R\right)=-\frac{{{{{{\rm{e}}}}}}}{4{{{{{\rm{\pi }}}}}}{\varepsilon }_{{{{{{\rm{o}}}}}}}{\varepsilon }_{r}^{Q}\left|{{{{{\boldsymbol{r}}}}}}\right|}\left[1-\left\{\left(\frac{{\varepsilon }_{r}^{{{{{{\rm{Q}}}}}}}}{{\varepsilon }_{r}^{{{{{{\rm{s}}}}}}}}\right)-1\right\}\left(\frac{{L}_{{{{{{\rm{eff}}}}}}}}{R+{L}_{{{{{{\rm{eff}}}}}}}}\right)\right],$$

(6)

where ${\varepsilon }_{r}^{{{{{{\rm{Q}}}}}}}$ designates the relative dielectric permittivity (hereafter, dielectric constant) of a CNC (or QD) core that is surrounded by a low-permittivity solvent having the dielectric constant ${\varepsilon }_{r}^{{{{{{\rm{s}}}}}}}$, and ${L}_{{{{{{\rm{eff}}}}}}}$ denotes the effective-action thickness of the low-permittivity solvent layer. Thus, the (dimensionless) reduced long-range Coulomb potential is

$${\varphi }_{r}\left(r\right)\equiv \frac{{\phi }^{{{{{{\rm{LR}}}}}}}\left(R\right)}{{\phi }^{{{{{{\rm{LR}}}}}}}\left({\infty }\right)}=1-\left\{\left(\frac{{\varepsilon }_{r}^{{{{{{\rm{Q}}}}}}}}{{\varepsilon }_{r}^{{{{{{\rm{s}}}}}}}}\right)-1\right\}\left(\frac{{L}_{{{{{{\rm{eff}}}}}}}}{R+{L}_{{{{{{\rm{eff}}}}}}}}\right).$$

(7)

The dielectric-confinement effect is negligible at $R={\infty }$, so in obtaining Eq. (7), we implicitly used the asymptotic relation ${\varepsilon }_{r}^{{{{{{\rm{Q}}}}}}}\to {\varepsilon }_{r\left({\infty }\right)}^{{{{{{\rm{eff}}}}}}}$ as the CNC size approaches its bulk value (i.e., as $R\to {\infty }$).

We have shown that this reduced long-range Coulomb potential can be expressed in terms of the dielectric-confinement effect on the exciton-LO phonon coupling contribution to the PL linewidth (Supplementary Notes 1). More explicitly, we have

$$\frac{{\Gamma }_{{{{{{\rm{LO}}}}}}}^{(1s)}(R)}{{\Gamma }_{{{{{{\rm{LO}}}}}}}^{(1s)}(\infty )}=\frac{{\phi }^{{{{{{\rm{LR}}}}}}}(R)}{{\phi }^{{{{{{\rm{LR}}}}}}}(\infty )}\equiv {\varphi }_{r}(R).$$

(8)

Equation (8) indicates that size-dependent PL linewidth ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{\left(1s\right)}\left(R\right)$ is proportional to the reduced long-range Coulomb potential ${\varphi }_{r}\left(R\right)$ because ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{\left(1s\right)}({\infty })$ is $R$-independent constant. This supports the scaling shown in Fig. 5b. In other words, the PL linewidth ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{\left(1s\right)}\left(R\right)$ is directly proportional to the long-range Coulomb potential ${\phi }^{{{{{{\rm{LR}}}}}}}\left(R\right)$ associated with the electron-LO phonon coupling which is needed for the large Fröhlich-polaron formation^33,34. Equation (8) also predicts that the PL linewidth caused by the exciton-LO phonon coupling reduces to zero when the driving force ${\phi }^{{{{{{\rm{LR}}}}}}}\left(R\right)$ for the formation of large Fröhlich polarons disappears at ${R}_{o}( \sim 1.50\ {{{{{\rm{nm}}}}}})$. This prediction accords well with the computational results (Fig. 5b). Thus Eq. (8) shows that the line broadening caused by the exciton-LO phonon coupling can be linearly correlated with the driving force for the formation of large Fröhlich-polarons which arises similarly from the electron-LO phonon coupling.

Computation of R-dependent ${\varphi }_{r}\left(R\right)$ using Eq. (7) requires use of a suitable value of the effective-action thickness ${L}_{{{{{{\rm{eff}}}}}}}$ of the surrounding low-permittivity solvent layer. Using Eq. (6) and the experimental finding that $|{\phi }^{{{{{{\rm{LR}}}}}}}\left(R\right)|=0$ at ${R}_{{{{{{\rm{o}}}}}}},$ we obtain the following approximation: ${L}_{{{{{{\rm{eff}}}}}}}=\frac{{\varepsilon }_{r}^{{{{{{\rm{s}}}}}}}}{\left({\varepsilon }_{r}^{{{{{{\rm{Q}}}}}}}-2{\varepsilon }_{r}^{{{{{{\rm{s}}}}}}}\right)}{R}_{{{{{{\rm{o}}}}}}}\approx 0.43{R}_{{{{{{\rm{o}}}}}}}\approx 0.65\ {{{{{\rm{nm}}}}}}.$ In obtaining this value, we adopt ${\varepsilon }_{r}^{{{{{{\rm{Q}}}}}}}=10.75$ (ref. ³⁰), ${\varepsilon }_{r}^{{{{{{\rm{s}}}}}}}\approx 2.5$ (toluene), and ${R}_{{{{{{\rm{o}}}}}}}=1.5\ {{{{{\rm{nm}}}}}}$ (Fig. 5b). Thus, ${L}_{{{{{{\rm{eff}}}}}}}$ to exert the dielectric-confinement effect on the MAPbBr₃ CNC-core is limited to a short distance ($\sim 0.65\ {{{{{\rm{nm}}}}}}$) from the core surface.

Highly asymmetric PL spectra for ${D}_{{{{{{\mathbf{p}}}}}}} < 3.0\ {{{{{\mathbf{nm}}}}}}$

Considering the experimental observation (Fig. 3a), we adopt the following asymmetric Gaussian-like function $g(R)$ for the normalized CNC-size distribution with respect to its modal size ${R}_{{{{{{\rm{p}}}}}}}$: $g(R)=\exp \{-{(R-{R}_{{{{{{\rm{p}}}}}}})}^{2}/(2{\sigma }_{R}^{2})\}$ for $R\ge {R}_{{{{{{\rm{p}}}}}}},$ where ${\sigma }_{R}$ denotes the standard deviation in the size distribution for $R\ge {R}_{{{{{{\rm{p}}}}}}}$. Similarly, $g(R)=\exp \{-{(R-{R}_{{{{{{\rm{p}}}}}}})}^{2}/(2{\sigma }_{{R}^{{\prime} }}^{2})\}$ with the standard deviation of ${\sigma }_{{R}^{{\prime} }}$ for$\,R\le {{Rs}}_{{{{{{\rm{p}}}}}}}.$ The ratio of these two standard deviations is simply given by the ratio of the two distinct half-widths at half-maximum in g(R), i.e., ${\sigma }_{R}/{\sigma }_{R^{\prime} }=\varDelta {R}_{1/2}/\varDelta {R}_{1/2}^{{\prime} }$ (Fig. 6a, left-hand side).

Fig. 6: CNC-size-dependent asymmetric PL spectra.

a Schematic representation of the asymmetric PL-$\lambda$ spectrum $f$(λ) and the corresponding PL-$\omega$ spectrum f$(\omega )$ which arise solely from the asymmetric CNC-size distribution $g(R)$ for ${D}_{{{{{{\rm{p}}}}}}} < 3.0\ {{{{{\rm{nm}}}}}}\,\left(={R}_{{{{{{\rm{p}}}}}}} < 1.5\ {{{{{\rm{nm}}}}}}\right).$ In this small-$R$ region, all three FWHMs ${\varGamma }_{{{{{{\rm{SD}}}}}}}\left(R\right),{\varGamma }_{{{{{{\rm{SD}}}}}}}$(λ)$,$ and ${\varGamma }_{{{{{{\rm{SD}}}}}}}(\omega )$ are exclusively caused by the CNC-size distribution because ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)=0$ and ${\varGamma }_{{{{{{\rm{SD}}}}}}}(\lambda )\gg {\Gamma }_{{{{{{\rm{QC}}}}}}}(\lambda )$ for ${D}_{p} < 3.2\ {{{{{\rm{nm}}}}}}.$ b Size-distribution function $g\left(R\right)$ and the corresponding $f(\lambda )$ spectrum with a pronounced line broadening for $R < 1.5\ {{{{{\rm{nm}}}}}}$ vs. the size-distribution function $\bar{g}\left(R\right)$ and the corresponding $\bar{f}(\lambda )$ spectrum with a significant linewidth narrowing for the large-$R$ region near ${R}_{{{{{{\rm{c}}}}}}}$ (the onset of the PL blue shift, $13.75\ {{{{{\rm{nm}}}}}}$ for MAPbBr₃). c Symmetric Lorentzian PL-$\omega$ spectrum $I(\omega )$ vs. asymmetric pseudo-Lorentzian PL-$\lambda$ spectrum $I(\lambda )$ for ${D}_{p} >$ exciton Bohr diameter ($\approx 9\ {{{{{\rm{nm}}}}}}$ for MAPbBr₃).

We consider an empirical relation between the (modal) particle size and the PL wavelength to convert the asymmetric g(R) function to the corresponding PL spectrum f(λ). For a limited range of the particle size, the $R$-dependent PL λ of MAPbBr₃ is described by the empirical linear relation (Fig. 2b): $R=a\lambda +b,$ where both $R$ and λ have units of nanometers. Linear regression estimated $a$ = 0.012 (dimensionless) in the vicinity of ${D}_{p}=2.7\ {{{{{\rm{nm}}}}}}$ (i.e., ${R}_{p}=1.35\ {{{{{\rm{nm}}}}}}$) (Supplementary Notes 2). Using this empirical linear relation, we obtain the PL spectrum $f(\lambda )$ that corresponds to a particular CNC-size distribution, $g\left(R\right)$ for$\,\lambda \ge {\lambda }_{{{{{{\rm{p}}}}}}}$:

$$f\left(\lambda \right)=\exp \left\{-{a}^{2}{\left(\lambda -{\lambda }_{{{{{{\rm{p}}}}}}}\right)}^{2}/2{\sigma }_{R}^{2}\right\}=\exp \left\{-{\left(\lambda -{\lambda }_{{{{{{\rm{p}}}}}}}\right)}^{2}/2{\sigma }_{\lambda }^{2}\right\},$$

(9)

where ${\sigma }_{\lambda }\equiv {\sigma }_{R}/a=83.3{\sigma }_{R}\gg {\sigma }_{R}.$ Thus, for the CNC-size distribution centered at ${D}_{{{{{{\rm{p}}}}}}}=2.7{{{{{\rm{nm}}}}}}\,({R}_{{{{{{\rm{p}}}}}}}=1.35\ {{{{{\rm{nm}}}}}})$, the standard deviation of the PL-$\lambda$ spectrum (${\sigma }_{\lambda }$) is substantially bigger than that for the asymmetric CNC-size distribution itself, ${\sigma }_{R}$ (Fig. 6b, left-hand side).

The following relationship can be readily obtained from g(R) and f(λ):

$$\left(\frac{\Delta {\lambda }_{1/2}}{{\Delta \lambda }_{1/2}^{{{{{{\rm{{{\hbox{'}}}}}}}}}}}\right)=\left(\frac{{\sigma }_{R}}{{\sigma }_{{R}^{{\prime} }}}\right)=\left(\frac{{\sigma }_{\lambda }}{{\sigma }_{{\lambda }^{{\prime} }}}\right)=\left(\frac{\Delta {R}_{1/2}}{{\Delta R}_{1/2}^{{{{{{\rm{{{\hbox{'}}}}}}}}}}}\right) > 1.$$

(10)

Equation (10) is only valid for the linewidth broadening that is caused by the CNC-size distribution with ${\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\lambda \right)=\Delta {\lambda }_{1/2}+{\Delta \lambda }_{1/2}^{{{{\hbox{'}}}}}$ (Fig. 6a). The exciton-LO phonon coupling contribution to the net linewidth ${\varGamma }_{{{{{{\rm{LO}}}}}}}(\lambda )$ is 0 at ${D}_{{{{{{\rm{p}}}}}}}=2.7\ {{{{{\rm{nm}}}}}}\,({R}_{{{{{{\rm{p}}}}}}}=1.35\ {{{{{\rm{nm}}}}}})\,$(Fig. 5a). Thus, the experimentally-observed FWHM is primarily determined by the linewidth ${\varGamma }_{{{{{{\rm{SD}}}}}}}$ that is exclusively caused by the CNC-size distribution at ${D}_{{{{{{\rm{p}}}}}}}=2.7\ {{{{{\rm{nm}}}}}}$. Therefore, Eq. (10) explains the observed asymmetric PL-$\lambda$ spectrum at ${D}_{{{{{{\rm{p}}}}}}}=2.7\ {{{{{\rm{nm}}}}}}$ (Fig. 2a) which is skewed toward the long-$\lambda$ side of the modal wavelength ${\lambda }_{p}$. This explanation is consistent with a schematic $f\left(\lambda \right)$ spectrum, which is characterized by $(\Delta {\lambda }_{1/2}/{\Delta \lambda }_{1/2}^{{{{\hbox{'}}}}}) \, > \, 1$ (Fig. 6a).

Contrary to the PL-$\lambda$ spectrum, the PL-$\omega$ spectrum for ${D}_{p} < 3\ {{{{{\rm{nm}}}}}}$ is characterized by skew toward the low-$\omega$ side of the modal frequency ${\omega }_{p}$ (Fig. 2d). We derived $(\Delta {\omega }_{1/2}^{{\prime} }{/\Delta \omega }_{1/2})=({\sigma }_{\omega }/{\sigma }_{{\omega }^{{\prime} }})\approx ({\Delta \lambda }_{1/2}/{\Delta \lambda }_{1/2}^{{{{\hbox{'}}}}})=\{({\sigma }_{R}/a)/({\sigma }_{R}^{{\prime} }/a)\} \, > \, 1,$ which correlates the asymmetry in the PL-$\omega$ spectrum with the asymmetry in the PL-$\lambda$ spectrum or in the CNC-size distribution (Supplementary Notes 2). This relation predicts that contrary to the PL-$\lambda$ spectrum, the PL-$\omega$ spectrum $f\left(\omega \right)$ should show a skew toward the low-$\omega$ side of the modal frequency ${\omega }_{p}$ (Fig. 6a). This prediction concurs with the experimental PL-$\omega$ spectrum at ${D}_{p}=2.7\ {{{{{\rm{nm}}}}}}$ (Fig. 2d), where the ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)$ contribution to the total FWHM is $0$ (Fig. 5a). To quantify this relationship, we considered the degree of asymmetry in the PL-$\omega$ spectrum, which is defined as ${\delta \omega }_{1/2}={\Delta \omega }_{1/2}^{{\prime} }-{\Delta \omega }_{1/2} \, > \, 0$. Several algebraic rearrangements (Supplementary Notes 2) yield

$${\delta \omega }_{1/2}={\Delta \omega }_{1/2}^{{\prime} }-{\Delta \omega }_{1/2}=\left(\frac{{\Gamma }_{{{{{{\rm{SD}}}}}}}\left(\omega \right)}{{\Gamma }_{{{{{{\rm{SD}}}}}}}\left(R\right)}\right)\left({\Delta R}_{1/2}-{\Delta R}_{1/2}^{{{{{{\rm{{{\hbox{'}}}}}}}}}}\right) \, > \, 0.$$

(11)

This relation again predicts that the PL-$\omega$ spectrum is skewed toward the low-$\omega$ side of the modal frequency, and is consistent with the result shown in Fig. 2d at ${D}_{p}=2.7\ {{{{{\rm{nm}}}}}}.$ We have estimated that ${\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\omega \right)=\left\{{\Gamma }_{{{{{{\rm{SD}}}}}}}(\lambda )/{\Gamma }_{{{{{{\rm{EXP}}}}}}}(\lambda )\right\}\cdot {\Gamma }_{{{{{{\rm{EXP}}}}}}}(\omega )=\left(29.2/35.9\right)\times 0.293\times {10}^{15}\,{{{{{{\rm{s}}}}}}}^{-1}=0.238\times {10}^{15}\,{{{{{{\rm{s}}}}}}}^{-1}$ at ${D}_{{{{{{\rm{p}}}}}}}=2.7\ {{{{{\rm{nm}}}}}}\,$(Tables 2 and 3) and found experimentally that ${\varGamma }_{{{{{{\rm{SD}}}}}}}\left(R\right)\approx 1\ {{{{{\rm{nm}}}}}}$ and ${\Delta R}_{1/2}-{\Delta R}_{1/2}^{{{{\hbox{'}}}}}\approx 0.2\ {{{{{\rm{nm}}}}}}.$ Using these values in Eq. (11) predicts ${\delta \omega }_{1/2}\approx 0.05\times {10}^{15}\,{{{{{{\rm{s}}}}}}}^{-1}$, which is much smaller than the modal frequency ${\omega }_{{{{{{\rm{p}}}}}}}=3.97\times {10}^{15}\,{{{{{{\rm{s}}}}}}}^{-1}$ at ${D}_{{{{{{\rm{p}}}}}}}=2.7\ {{{{{\rm{nm}}}}}}.$ Thus, ${\delta \omega }_{1/2}/{\omega }_{{{{{{\rm{p}}}}}}}\approx$ $0.012\ll 1.$ Equation (11) shows that the degree of asymmetry in the PL-$\omega$ spectrum is determined by the degree of asymmetry in the CNC-size distribution,$\,({\Delta R}_{1/2}-{\Delta R}_{1/2}^{{{{\hbox{'}}}}}).$ Equation (11) can be alternatively written as ${\delta \omega }_{1/2}/{\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\omega \right)=({\Delta R}_{1/2}-{\Delta R}_{1/2}^{{{{\hbox{'}}}}})/{\varGamma }_{{{{{{\rm{SD}}}}}}}\left(R\right)\approx \frac{0.2}{1}=0.2.$ Thus, ${\delta \omega }_{1/2}$ is comparable to ${\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\omega \right)$; this indicates a highly asymmetric PL-$\omega$ spectrum at ${D}_{{{{{{\rm{p}}}}}}}=2.7\ {{{{{\rm{nm}}}}}}.$ This prediction accords well with the experimental PL-$\omega$ spectrum (Fig. 2d) at ${D}_{{{{{{\rm{p}}}}}}}=2.7\ {{{{{\rm{nm}}}}}}$.

Table 3 Four distinct contributions to the size-dependent experimental linewidth of MAPbBr₃ CNCs, expressed in ${{{{{\bf{nm}}}}}}$ value.

However, the FWHM value of the present MAPbBr₃ QD at ${D}_{{{{{{\rm{p}}}}}}}=2.7\ {{{{{\rm{nm}}}}}}$ is noticeably larger than that of the MAPbBr₃ QD (with a similar ${D}_{p}$ of $2.12\ {{{{{\rm{nm}}}}}}$) prepared by low-temperature liquid-nitrogen passivation³⁸ to restrain the defects of surface Br vacancy (${V}_{{{{{{\rm{Br}}}}}}}$): FWHM of ~35 nm (Table 1) vs. FWHM < ~20 nm. Here, we refer to as a QD if the corresponding CNC radius is smaller than the exciton Bohr radius (${a}_{{{{{{\rm{B}}}}}}}$). It has been reported that these kinds of vacancy defects can be facilely generated on the surface of perovskite QDs during the fast nucleation and growth steps^39,40. In addition, highly dynamic organic capping agents, such as n-alkylamine or oleic acid used in the present study, cannot stabilize the perovskite QD structure well, easily regenerating ${V}_{{{{{{\rm{Br}}}}}}}$ defects at room temperature^41,42. Considering the restraining effects of liquid-nitrogen passivation and facile defects formation, the observed FWHM broadening of the present MAPbBr₃ blue-emission QD can be attributed not only to a finite CNC-size distribution but also to surface vacancy defects or poor structural stability probably due to organic capping agents.

The most prominent feature of the PL-$\omega$ or PL-$\lambda$ spectrum at ${D}_{p}=2.7\ {{{{{\rm{nm}}}}}}$ is the extended skew toward the low-energy side of the modal frequency (Fig. 2d) but with a small degree of asymmetry at half-maximum (${\delta \omega }_{1/2}/{\omega }_{{{{{{\rm{p}}}}}}}\approx$ $0.012$). This tail-like extended skew is also observed in liquid-nitrogen passivation-treated deep-blue emission QDs³⁸ and suggests that emissive-band tail states with a large tail width exist just below the excited singlet |1S_e〉 state^43,44,45. This type of emission from the band tail states has been reported in all-inorganic halide perovskite, CsPbBr₃, for ultrasmall ($\sim 3\ {{{{{\rm{nm}}}}}}$) CNCs⁴⁵. Photocarriers produced by the above-gap excitation can then relax into the band tail states and then recombine radiatively; the result is a long tail on the low-energy side of the PL peak⁴⁵. Thus, the emission from the band-tail states seems to be mainly responsible for the long tail, whereas the asymmetry in the CNC-size distribution causes the asymmetric PL-$\omega$ spectrum at the half-maximum for modal size smaller than $\sim 3\ {{{{{\rm{nm}}}}}}$ in the MAPbBr₃ CNC (Fig. 2d).

Asymmetric Lorentzian PL-${{{{{\boldsymbol{\lambda}}}}}}$ spectrum for ${D}_{{{{{{\rm{p}}}}}}} > {D}_{{{{{{\rm{B}}}}}}}$

The estimated ${\Gamma }_{{SD}}\left(\lambda \right)$ decreases noticeably as modal size increases and reaches its minimum value at ${D}_{{{{{{\rm{p}}}}}}}=19.5\ {{{{{\rm{nm}}}}}}$ (Fig. 5a). To explain this behavior, we consider the experimental PL-$\lambda$ vs. $R$ curve. Near ${R}_{{{{{{\rm{c}}}}}}}\,\left(=13.75\ {{{{{\rm{nm}}}}}}\right)$, the $R$-dependent PL $\lambda$ is described by an empirical linear relation: $R={a}^{{\prime} }\lambda +{b}^{{\prime} }$, with estimated ${a}^{{\prime} }$ = 3.1 (Supplementary Notes 2). The corresponding hypothetical PL-$\lambda$ spectrum solely caused by the CNC-size distribution can be written as

$$\bar{f}\left(\lambda \right)=\exp \left\{-\frac{{\left({a}^{{\prime} }\right)}^{2}{(\lambda -{\lambda }_{{{{{{\rm{p}}}}}}})}^{2}}{2{\bar{\sigma }}_{R}^{2}}\right\}=\exp \left\{-\frac{{(\lambda -{\lambda }_{{{{{{\rm{p}}}}}}})}^{2}}{2{\bar{\sigma }}_{\lambda }^{2}}\right\}$$

(12)

where ${\bar{\sigma }}_{\lambda }={\bar{\sigma }}_{R}/{a}^{{\prime} }=\frac{{\bar{\sigma }}_{R}}{3.1}.$ Thus, compared with the CNC-size distribution, a significant linewidth narrowing $({\bar{\sigma }}_{\lambda }={\bar{\sigma }}_{R}/3.1)$ is expected in the hypothetical PL-$\lambda$ spectrum near ${R}_{{{{{{\rm{c}}}}}}}$. However, this is in sharp contrast with the pronounced linewidth broadening in the PL-$\lambda$ spectrum for ${D}_{{{{{{\rm{p}}}}}}} < \,3.0\ {{{{{\rm{nm}}}}}}\ ({R}_{{{{{{\rm{p}}}}}}} < 1.5\ {{{{{\rm{nm}}}}}}),$ where ${\sigma }_{\lambda }={\sigma }_{R}/a=83.3{\sigma }_{R}$ (Fig. 6b). This prediction qualitatively accords with the estimated ${\Gamma }_{{{{{{\rm{SD}}}}}}}(\lambda )$ (Table 3): at ${D}_{{{{{{\rm{p}}}}}}}=2.7\ {{{{{\rm{nm}}}}}}\,({R}_{p}=1.35\ {{{{{\rm{nm}}}}}}),{\Gamma }_{{{{{{\rm{SD}}}}}}}(\lambda )\approx 30\ {{{{{\rm{nm}}}}}},$ whereas for ${D}_{{{{{{\rm{p}}}}}}}\ge 19.5\ {{{{{\rm{nm}}}}}}\,({R}_{{{{{{\rm{p}}}}}}}\ge 9.75\ {{{{{\rm{nm}}}}}}\,),{\Gamma }_{{{{{{\rm{SD}}}}}}}(\lambda )\approx 1\ {{{{{\rm{nm}}}}}}.$

MAPbBr₃ has ${D}_{{{{{{\rm{B}}}}}}}\,\left(2{a}_{{{{{{\rm{B}}}}}}}\right)$ between $8.76\ {{{{{\rm{nm}}}}}}\,\left(\approx 9\ {{{{{\rm{nm}}}}}}\right)$³⁰ and $10{{{{{\rm{nm}}}}}}$^29,46. According to our estimate (Fig. 5a, Table 3), the linewidth ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ caused by the exciton-LO phonon Fröhlich coupling dominates over the externally introduced linewidth ${\varGamma }_{{{{{{\rm{SD}}}}}}}$ arising from the CNC-size distribution in this large-R region, where ${D}_{{{{{{\rm{p}}}}}}} > {D}_{{{{{{\rm{B}}}}}}}\approx 9\ {{{{{\rm{nm}}}}}}$: ${\varGamma }_{{{{{{\rm{LO}}}}}}} > 16.2\ {{{{{\rm{nm}}}}}}$ vs. ${\varGamma }_{{{{{{\rm{SD}}}}}}}\approx 0.5\ {{{{{\rm{nm}}}}}}\,$. Thus, the net line-shape in this large-R region is determined primarily by the exciton-LO phonon coupling. Under this condition (${D}_{{{{{{\rm{p}}}}}}} > 9\ {{{{{\rm{nm}}}}}}$), the net line-shape is essentially governed by the symmetric Lorentzian PL-$\omega$ spectrum $I\left(\omega \right)$²⁴.

$$I\left(\omega \right)={I}_{o}\left\{\frac{\left(\frac{{\varGamma }_{{{{{{\rm{LO}}}}}}}(\omega )}{2}\right)}{{({\omega }_{{{{{{\rm{p}}}}}}}-\omega )}^{2}+{\left(\frac{{\varGamma }_{{{{{{\rm{LO}}}}}}}(\omega )}{2}\right)}^{2}}\right\}={I}_{o}\left\{\frac{\left(\frac{\gamma }{2}\right)}{{({\omega }_{{{{{{\rm{p}}}}}}}-\omega )}^{2}+{\left(\frac{\gamma }{2}\right)}^{2}}\right\}$$

(13)

where ${\varGamma }_{{{{{{\rm{LO}}}}}}}(\omega )=2{\Delta \omega }_{1/2}\equiv \gamma$ and ${\Delta \omega }_{1/2}$ denotes the half-width at half-maximum of a given symmetric PL-$\omega$ spectrum. This prediction of the symmetric Lorentzian spectrum is consistent with the experimentally-observed PL-$\omega$ spectra for ${D}_{{{{{{\rm{p}}}}}}}\ge 7.5\ {{{{{\rm{nm}}}}}}$ (Fig. 2d).

We then calculated the line-shape of the PL-λ spectrum in this large-R region. By definition, ω = 2πc/λ, where c is the speed of light, so ${({\omega }_{p}-\omega )}^{2}={\left(2{{{{{\rm{\pi }}}}}}c\right)}^{2}{\left(\frac{1}{{\lambda }_{{{{{{\rm{p}}}}}}}}-\frac{1}{\lambda }\right)}^{2}$; substituting the right-hand side into Eq. (13) and rearranging eventually yields an expression for the normalized PL-λ spectrum $I\left(\lambda \right)\!\!:$

$$I\left(\lambda \right)=\left(\frac{{\gamma }^{{\prime} }}{2}\right)\left(\frac{\lambda }{{\lambda }_{{{{{{\rm{p}}}}}}}}\right)\left\{\frac{\left(\frac{{\gamma }^{{\prime} }}{2}\right)}{{(\lambda -{\lambda }_{{{{{{\rm{p}}}}}}})}^{2}+{\left(\frac{{\gamma }^{{\prime} }}{2}\right)}^{2}}\right\}$$

(14)

where ${\gamma }^{{\prime} }\equiv \frac{{\lambda }_{{{{{{\rm{p}}}}}}}\lambda }{2{{{{{\rm{\pi }}}}}}c}\gamma$. Thus, the modified linewidth $\left(\frac{{\gamma }^{{\prime} }}{2}\right)$ is not constant, but depends on PL wavelength $\lambda$. $I\left(\lambda \right)$ is asymmetric with respect to ${\lambda }_{{{{{{\rm{p}}}}}}}$ (Fig. 6c), although $I\left(\omega \right)$ is symmetric Lorentzian²⁴ with respect to ${\omega }_{{{{{{\rm{p}}}}}}}$ [Eq. (13)]. It can be shown that ${\Delta \lambda }_{1/2} > {\Delta \lambda }_{1/2}^{{{{\hbox{'}}}}}$, where ${\Delta \lambda }_{1/2}\equiv {\lambda }_{1/2}-{\lambda }_{p}$ and ${\Delta \lambda }_{1/2}^{{{{\hbox{'}}}}}\equiv {\lambda }_{{{{{{\rm{p}}}}}}}-{\lambda }_{1/2}^{{{{\hbox{'}}}}}$ (Fig. 6c). Thus, the asymmetric pseudo-Lorentzian PL-$\lambda$ spectrum, which is mostly caused by the exciton-LO phonon coupling for ${D}_{{{{{{\rm{p}}}}}}} \, > \, 7.5\ {{{{{\rm{nm}}}}}}$ (or $> {D}_{{{{{{\rm{B}}}}}}}$), is characterized by skew toward the long-$\lambda$ side of ${\lambda }_{p}$. The PL-$\lambda$ spectra (Fig. 2a) for ${D}_{{{{{{\rm{p}}}}}}}\ge 7.5\ {{{{{\rm{nm}}}}}}$ show this asymmetry. To more quantitatively assess the asymmetry, we define the degree of asymmetry in the PL-$\lambda$ spectrum as ${\delta \lambda }_{1/2}\left(L\right)\equiv {\Delta \lambda }_{1/2}-{\Delta \lambda }_{1/2}^{{{{\hbox{'}}}}} \, > \, 0$, where $\left(L\right)$ is used to emphasize that the spectrum is pseudo-Lorentzian. We derived the following simple relation for the degree of asymmetry (Supplementary Notes 2):

$$\frac{{\delta \lambda }_{1/2}\left(L\right)}{{\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)}=\frac{{\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\omega \right)}{{\omega }_{{{{{{\rm{p}}}}}}}}\ll 1,$$

(15)

In the above equation, ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)$ denotes the FWHM in the pseudo-Lorentzian PL-$\omega$ spectrum, whereas ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\omega \right)$ designates the FWHM in the corresponding Lorentzian PL-$\lambda$ spectrum. For MAPbBr₃ CNCs at ${D}_{{{{{{\rm{p}}}}}}}=19.5\ {{{{{\rm{nm}}}}}},$ ${\omega }_{{{{{{\rm{p}}}}}}}=3.587\times {10}^{15}\,{{{{{{\rm{s}}}}}}}^{-1}$ and ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\omega \right)={\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\hslash \omega \right)/\hslash \approx 0.12\times {10}^{15}\,{{{{{{\rm{s}}}}}}}^{-1},$ where ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\hslash \omega \right)={hc}\ {\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)/{\lambda }_{{{{{{\rm{p}}}}}}}^{2}\approx 82.3\left({{{{{\rm{meV}}}}}}\right)$ with ${\lambda }_{{{{{{\rm{p}}}}}}}=525.1\ {{{{{\rm{nm}}}}}}$ and ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)=18.3\ {{{{{\rm{nm}}}}}}$ at ${D}_{{{{{{\rm{p}}}}}}}=19.5\ {{{{{\rm{nm}}}}}}$. Hence, ${\delta \lambda }_{1/2}\left(L\right)/{\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)=0.033\ll 1.$ This estimate demonstrates that the degree of asymmetry ${\delta \lambda }_{1/2}\left(L\right)$ is much smaller than the FWHM itself [${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)$], and indicates that the PL-$\lambda$ spectrum [Eq. (14)] is only slightly distorted pseudo-Lorentzian.

Conclusions

The use of colloidal perovskite nanocrystals (PNCs) is an effective strategy (i) to achieve color tunability by suitably adjusting the degree of PL blue shift and (ii) to increase the PLQE of MHP crystals by exploiting the quantum-confinement effect. However, the approach of colloidal PNCs inevitably introduces two additional broadening effects on the spectral linewidths, ${\varGamma }_{{{{{{\rm{SD}}}}}}}$ and ${\varGamma }_{{{{{{\rm{QC}}}}}}}$, which possibly deteriorate the ultrahigh color purity of MHPs. The linewidth broadening due to these two factors is pronounced especially at small CNC sizes. Considering these, we develop a simple method to extract ${\varGamma }_{{SD}}$ at a given modal size by combining the experimental size-distribution histogram with the size-dependent PL-$\lambda$ curve (Fig. 3b). We subsequently analyze that due to a nonlinearity in the size-dependent PL-$\lambda$ curve, this extracted linewidth (${\Gamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}$) always overestimates the correct ${\Gamma }_{{{{{{\rm{SD}}}}}}}$ by ${\varDelta }_{R}$ [Eq. (2)]. We develop a semi-empirical method to simultaneously obtain this size-dependent overestimate ${\varDelta }_{R}$ and ${\varGamma }_{{{{{{\rm{o}}}}}}}$. ${\varGamma }_{{{{{{\rm{QC}}}}}}}$ as a function of the CNC size is calculated using our theoretical method. Having obtained (i) the size-dependent ${\varGamma }_{{{{{{\rm{SD}}}}}}}$ and ${\varGamma }_{{{{{{\rm{QC}}}}}}}$ and (ii) a constant contribution of ${\varGamma }_{{{{{{\rm{o}}}}}}}\,\left(\approx 4.8\ {{{{{\rm{nm}}}}}}\right),$ we estimate the contribution ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ of the exciton-LO phonon Fröhlich coupling to ${\Gamma }_{{{{{{\rm{net}}}}}}}$ by applying Eq. (1). We further deduce that ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ for the bulk perovskite grains is $18.3{{{{{\rm{nm}}}}}}$ [Fig. 5a and Table 3]. We show that ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ of MAPbBr₃ decreases as CNC size decreases and disappears at the CNC radius R_p$=1.60\ {{{{{\rm{nm}}}}}}$ [Fig. 5a]. We show that the line broadening caused by the exciton-LO phonon coupling ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ can be linearly correlated with the driving force for the formation of large Fröhlich-polarons which arises similarly from the electron-LO phonon coupling [Fig. 5b].

Methods

Synthesis of perovskite nanocrystals

MAPbBr₃ NCs were fabricated using ligand-assisted reprecipitation in air at room temperature⁴⁶. The precursor solution that contained amine ligands was prepared by dissolving 0.3 mmol of CH₃NH₃Br (Dyesol), 0.4 mmol of PbBr₂ (Aldrich, 99.999%) and 40 μL of n-hexylamine (Aldrich, 99%) in 10 mL of anhydrous N, N-dimethylformamide (DMF, Aldrich, 99.8%). To synthesize medium-sized particles, reagents for precursor and n-hexylamine were dissolved in 5 mL of DMF in the same molar ratio used to synthesize the NCs. Then 10% of the precursor-mixture volume was injected into 5 mL of toluene that included various concentrations of oleic acid (Aldrich, 99%; from 0.5 to 100 μL) under vigorous stirring to induce crystallization. After 10 min, the colloidal solutions were centrifuged at 3000 rpm for 10 min to precipitate large particles. The supernatant was collected, and the precipitate was discarded.

Photoluminescence and transmission electron microscopy measurements

PL spectra of PNCs were acquired using a JASCO FP8500 spectrofluorometer in colloidal dispersion states. The measurements were performed using a 150-W Xenon lamp light source and a photomultiplier tube detector with excitation wavelength of 405 nm. A highly concentrated colloidal dispersion is accompanied by a red shift in the PL spectrum owing to the photon reabsorption⁴⁷; therefore, the PL measurement was conducted in a highly diluted dispersion that did not show any blue shift upon further dilution (Absorbance $< 0.5$ at $405{{{{{\rm{nm}}}}}}$). Perovskite-nanoparticle colloidal dispersions were dropped onto a formvar/carbon supported copper grids right after the PL measurement. TEM measurement was conducted using a Tecnai F20 at an acceleration voltage of 200 kV.

Image cytometry analysis

The size information for each particle was extracted using image-analysis software (ImageJ 1.41n, NIH, USA) except small particles (< 5 nm) due to a low contrast ratio. The obtained bright-field optical TEM images were converted to 8-bit images after adjusting the contrast ratio and brightness. Then the areas were acquired and used to calculate the diameter. More than 400 particles were measured at each nominal size. The small particles (< 5 nm) were close to perfectly circular and uniform, so the diameter of a small particle was directly measured by marking opposite ends. For this measurement, the modal diameter, which corresponds to the peak in the size-distribution histogram, was obtained by measuring more than 200 particles in each.

Semi-empirical estimates of four distinct contributions to net linewidth

We first consider a possible discrepancy between the modal wavelength ${\lambda }_{{{{{{\rm{p}}}}}}}$ and the experimentally measured wavelength ${\lambda }_{{{{{{\rm{ms}}}}}}}$ for a colloid dispersion having a finite size distribution. Nine size-dependent peak values in the PL-$\lambda$ spectra (Fig. 2a) thus actually represent various size-dependent ${\lambda }_{{{{{{\rm{ms}}}}}}}$ values (rather than ${\lambda }_{p}$ values) of MAPbBr₃ CNCs having various modal diameters. ${\lambda }_{{{{{{\rm{ms}}}}}}}$ is sensitive to the nonlinearity in the PL-$\lambda$ vs. CNC size curve (Fig. 2b) and consequently to the size-distribution characteristics of dispersed CNC particles. In contrast, ${\lambda }_{{{{{{\rm{p}}}}}}}$ is an intrinsic property and thus independent of the size-distribution characteristics. In the next sub-section, we will show theoretically that there exists a unique 1:1 correspondence between the particle radius (${R}_{{{{{{\rm{p}}}}}}}$) and ${\lambda }_{{{{{{\rm{p}}}}}}}$ with an increasing tendency of the PL blue shift (moves towards a shorter ${\lambda }_{{{{{{\rm{p}}}}}}}$) as ${R}_{{{{{{\rm{p}}}}}}}$ decreases (Figs. 1d and 2b)⁴⁶. We will show that ${\lambda }_{{{{{{\rm{p}}}}}}} > {\lambda }_{{{{{{\rm{ms}}}}}}}$ if the PL-λ vs. CNC size curve is characterized by a nonlinear variation in λ across ${R}_{{{{{{\rm{p}}}}}}}$ (Fig. 1d). As shown in Fig. 2b, this nonlinear variation in λ applies to the present MAPbBr₃ CNCs dispersion, especially for small CNC sizes.

We examine a colloidal dispersion having symmetrical size-distribution characteristics for dispersed CNCs to show the difference between ${\lambda }_{{{{{{\rm{p}}}}}}}$ and ${\lambda }_{{{{{{\rm{ms}}}}}}}$. We can show that asymmetric size-distribution does not alter our conclusion of the inequality, namely, ${\lambda }_{{{{{{\rm{p}}}}}}} > {\lambda }_{{{{{{\rm{ms}}}}}}}$. Consider a colloidal dispersion having three distinct sizes with a symmetric abundance ratio of $x:1:x$ for simplicity. In this case, $g(R)$ in Fig. 1a is symmetric with respect to ${R}_{{{{{{\rm{p}}}}}}}$. Then, ${\lambda }_{{ms}}$ of this symmetric mixture is given by following equation: ${\lambda }_{{{{{{\rm{ms}}}}}}}=\frac{x\bullet {\lambda }_{p-\Delta }+1\bullet {\lambda }_{p}+x\bullet {\lambda }_{p+\Delta }}{\left(1+2x\right)}$, where ${\lambda }_{{{{{{\rm{p}}}}}}-\Delta }$ denotes the modal wavelength that corresponds to the CNC having the radius of ${R}_{{{{{{\rm{p}}}}}}-\Delta }$. Similarly, ${\lambda }_{{{{{{\rm{p}}}}}}+\Delta }$ denotes the modal wavelength for the CNCs having the radius of ${R}_{{{{{{\rm{p}}}}}}+\Delta }$, where $\Delta$ is a positive constant. If the PL-$\lambda$ curve is characterized by a nonlinear variation in $\lambda$ across ${R}_{{{{{{\rm{p}}}}}}}$ (Fig. 2b), then we write: ${\lambda }_{{{{{{\rm{p}}}}}}-\Delta }={\lambda }_{{{{{{\rm{p}}}}}}}-\varepsilon$ and ${\lambda }_{{{{{{\rm{p}}}}}}+\varDelta }={\lambda }_{p}+{\varepsilon }^{{\prime} }$. In the case of MAPbBr₃ CNCs dispersion, $\varepsilon \, > \, {\varepsilon }^{{\prime} }$ for ${R}_{{{{{{\rm{p}}}}}}}\le 5{{{{{\rm{nm}}}}}} \, ({i.e.,{D}}_{{{{{{\rm{p}}}}}}}\le 10{{{{{\rm{nm}}}}}}).$ Substituting these two relations into the above equation for ${\lambda }_{{{{{{\rm{ms}}}}}}}$ yields

$${\lambda }_{{{{{{\rm{ms}}}}}}}={\lambda }_{{{{{{\rm{p}}}}}}}-\frac{\left(\varepsilon -{\varepsilon }^{{\prime} }\right)x}{\left(1+2x\right)}\equiv {\lambda }_{{{{{{\rm{p}}}}}}}-\Delta \lambda ,$$

(16)

where $\Delta \lambda \equiv \left(\varepsilon -{\varepsilon }^{{\prime} }\right)x/\left(1+2x\right) > 0.$ Thus, ${\lambda }_{{{{{{\rm{p}}}}}}} > {\lambda }_{{{{{{\rm{ms}}}}}}}$. If the PL-$\lambda$ curve were linear, i.e., $\varepsilon ={\varepsilon }^{{\prime} }$, then ${\lambda }_{{{{{{\rm{ms}}}}}}}$ would be equal to ${\lambda }_{{{{{{\rm{p}}}}}}}$.

According to Eq. (16), the measured wavelength for a dispersion having the modal (peak) radius ${R}_{{{{{{\rm{p}}}}}}}$ is ${\lambda }_{{{{{{\rm{ms}}}}}}}$ which is smaller than ${\lambda }_{{{{{{\rm{p}}}}}}}$ by $\Delta \lambda$. Inspecting the extraction diagram for a given size distribution (e.g., Fig. 3b), we can deduce that owing to the inequality ${\lambda }_{{{{{{\rm{p}}}}}}} > {\lambda }_{{{{{{\rm{ms}}}}}}}$, the experimentally extracted FWHM ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)$ which is obtained from the measuring ${\lambda }_{{{{{{\rm{ms}}}}}}}-{R}_{{{{{{\rm{p}}}}}}}\,$(or ${\lambda }_{{{{{{\rm{ms}}}}}}}-{D}_{{{{{{\rm{p}}}}}}}$) curve is bigger than the correct FWHM ${\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\lambda \right)$ obtained by the ${\lambda }_{{{{{{\rm{p}}}}}}}-{R}_{{{{{{\rm{p}}}}}}}\,$(or ${\lambda }_{{{{{{\rm{p}}}}}}}-{D}_{{{{{{\rm{p}}}}}}}$) intrinsic (theoretical) curve. Thus, we can establish: ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)={\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\lambda \right)+{\varDelta }_{R}$ [Eq. (2)], where ${\varDelta }_{R}$ is positive and size-dependent. However, we cannot predict a priori the exact value of ${\varDelta }_{R}$ for a particular CNC radius. In subsequent analysis, we will semi-empirically estimate ${\varDelta }_{R}$ for a wide range of the CNC radius with the help of theoretically computed ${\varGamma }_{{{{{{\rm{QC}}}}}}}(\lambda )$ and show that it is pronounced for small CNC sizes with ${\varDelta }_{R}\ge 4.8{{{{{\rm{nm}}}}}}$. However, it gradually decreases with increasing radius for $R > 5{nm}$ and decays to zero at $R=11.85{{{{{\rm{nm}}}}}}$ (Fig. 4b).

Our next task is to semi-empirically deduce ${\varGamma }_{{{{{{\rm{o}}}}}}}$ and ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left({bg}\right)$, where ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left({bg}\right)$ denotes the correct ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ value that corresponds to the bulk grains ($18.3{{{{{\rm{nm}}}}}}$ for MAPbBr₃). To this end, we first consider the relation between ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}(\lambda )$ and ${\varGamma }_{{{{{{\rm{LO}}}}}}}(\lambda )$. Substituting Eq. (2) into Eq. (1) yields the following relation:

$${\varGamma }_{{{{{{\rm{EXP}}}}}}}={\varGamma }_{{{{{{\rm{QC}}}}}}}+{\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}+{\varGamma }_{{{{{{\rm{LO}}}}}}}+\left({\Gamma }_{{{{{{\rm{o}}}}}}}-{\varDelta }_{R}\right),$$

(17)

where we omitted the notation $\left(\lambda \right)$ for simplicity. Comparing Eq. (17) with Eq. (3) then yields a relation between ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}$ and ${\varGamma }_{{{{{{\rm{LO}}}}}}}$: ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}={\varGamma }_{{{{{{\rm{LO}}}}}}}+\left({\varGamma }_{{{{{{\rm{o}}}}}}}-{\varDelta }_{R}\right)$. This signifies that ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}$ absorbs the ${\varGamma }_{{{{{{\rm{o}}}}}}}$ term²⁷ into ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ but is corrected by the overestimate ${\varDelta }_{R}$ made in the experimental extraction of ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}$. Let us consider a sufficiently large particle in which ${\varDelta }_{R}$ is completely negligible ($R\ge 11.85{{{{{\rm{nm}}}}}}$). This is because the PL wavelength shows a linear variation with the CNC size for $R\ge 10{nm}.$We have: ${\varGamma }_{{{{{{\rm{EXP}}}}}}}\left(\lambda \right)=25.5{{{{{\rm{nm}}}}}},{\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)={\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\lambda \right)=2.2{{{{{\rm{nm}}}}}},{\varDelta }_{R}=0{{{{{\rm{nm}}}}}},$ and the calculated ${\varGamma }_{{{{{{\rm{QC}}}}}}}=0.2{{{{{\rm{nm}}}}}}$ at $R=11.85{{{{{\rm{nm}}}}}}$ (Table 3). Substituting these values into Eq. (17) yields the following simple relation:

$${\varGamma }_{{{{{{\rm{LO}}}}}}}+{\varGamma }_{{{{{{\rm{o}}}}}}}={\varGamma }_{{{{{{\rm{LO}}}}}}}\left({bg}\right)+{\Gamma }_{{{{{{\rm{o}}}}}}}=23.1{{{{{\rm{nm}}}}}}\left({{{{{\rm{PL}}}}}}-\lambda \right)=103{{{{{\rm{meV}}}}}}\left({{{{{\rm{PL}}}}}}-\omega \right),$$

(18)

where ${\varGamma }_{{{{{{\rm{LO}}}}}}}({bg})$ denotes ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ value for the bulk grains. This value ($23.1{{{{{\rm{nm}}}}}}$) nearly coincides with $23.4{{{{{\rm{nm}}}}}}(100.3{{{{{\rm{meV}}}}}})$ of the previous report²⁷ in which ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left({bg}\right)+{\varGamma }_{{{{{{\rm{o}}}}}}}$ was obtained by curve fitting of the temperature-dependent linewidth data with the Bose-Einstein distribution function. In Eq. (18), we replace ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ with ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left({bg}\right)$ because (i) our $({\varGamma }_{{{{{{\rm{LO}}}}}}}+{\varGamma }_{{{{{{\rm{o}}}}}}})$ value of $23.1{{{{{\rm{nm}}}}}}(103{{{{{\rm{meV}}}}}})$ is nearly equal to that of a bulk polycrystalline film²⁷ and (ii) ${\varGamma }_{{{{{{\rm{LO}}}}}}}$ for $R\ge 4.95{{{{{\rm{nm}}}}}}$ has a size-independent constant value of $18.3{{{{{\rm{nm}}}}}}$ (Table 3).

Let us consider the $\left({\varGamma }_{{{{{{\rm{o}}}}}}}-{\varDelta }_{R}\right)$-term appears in Eq. (17) for small CNC sizes. ${\varGamma }_{{{{{{\rm{EXP}}}}}}}\left(\lambda \right)=33.7{{{{{\rm{nm}}}}}},{\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)=32.0{{{{{\rm{nm}}}}}},{\varGamma }_{{{{{{\rm{LO}}}}}}}=0{{{{{\rm{nm}}}}}}$ and the calculated ${\varGamma }_{{{{{{\rm{QC}}}}}}}=1.7{{{{{\rm{nm}}}}}}$ at $R=1.60{{{{{\rm{nm}}}}}}$ (Tables 1 and 3). Substituting these values into Eq. (17) yields: $\left({\varGamma }_{{{{{{\rm{o}}}}}}}-{\varDelta }_{R}\right)=0$ at $R=1.60{{{{{\rm{nm}}}}}}.$ Similarly, ${\varGamma }_{{{{{{\rm{EXP}}}}}}}\left(\lambda \right)=28.9{{{{{\rm{nm}}}}}},{\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)=18.5{{{{{\rm{nm}}}}}},{\varGamma }_{{{{{{\rm{LO}}}}}}}=9.3{{{{{\rm{nm}}}}}}$ and the calculated ${\varGamma }_{{{{{{\rm{QC}}}}}}}=1.1{{{{{\rm{nm}}}}}}$ at $R=2.50{{{{{\rm{nm}}}}}}$. These values also yield $\left({\varGamma }_{o}-{\varDelta }_{R}\right)=0$ at $R=2.50{{{{{\rm{nm}}}}}}.$ We can show semi-empirically that $\left({\varGamma }_{{{{{{\rm{o}}}}}}}-{\varDelta }_{R}\right)=0$ until $R$ increases to $4.95{{{{{\rm{nm}}}}}}$. Therefore, ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}={\varGamma }_{{{{{{\rm{LO}}}}}}}+\left({\varGamma }_{{{{{{\rm{o}}}}}}}-{\varDelta }_{R}\right)={\varGamma }_{{{{{{\rm{LO}}}}}}}$ for small CNC sizes, namely, $1.60{{{{{\rm{nm}}}}}}\le {R}\le 4.95{{{{{\rm{nm}}}}}}.$

We are now in a position to deduce the value of ${\varGamma }_{{{{{{\rm{o}}}}}}}$ by comparing ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}(R=11.85{{{{{\rm{nm}}}}}})$ with ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(R=4.95{{{{{\rm{nm}}}}}}\right),$ where ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}(R=11.85{{{{{\rm{nm}}}}}})$ denotes the value of ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}$ at $R=11.85{{{{{\rm{nm}}}}}}.$ We can write the following equation for the difference in ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}$ between these two sizes by applying the previously deduced relation that ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}={\varGamma }_{{{{{{\rm{LO}}}}}}}+\left({\varGamma }_{{{{{{\rm{o}}}}}}}-{\varDelta }_{R}\right)$:

$$ {\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}} \left(R = 11.85{{{{{\rm{nm}}}}}}\right)-{\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(R=4.95{{{{{\rm{nm}}}}}}\right)=23.1{{{{{\rm{nm}}}}}}-18.3{{{{{\rm{nm}}}}}}\\ = \left\{{\varGamma }_{{{{{{\rm{LO}}}}}}}\left(R=11.85{{{{{\rm{nm}}}}}}\right)+{\varGamma }_{{{{{{\rm{o}}}}}}}\right\}-{\varGamma }_{{{{{{\rm{LO}}}}}}}\left(R=4.95{{{{{\rm{nm}}}}}}\right)\\ = \left\{{\varGamma }_{{{{{{\rm{LO}}}}}}}\left({bg}\right)-{\varGamma }_{{{{{{\rm{LO}}}}}}}\left({bg}\right)\right\}+{\Gamma }_{{{{{{\rm{o}}}}}}}={\Gamma }_{{{{{{\rm{o}}}}}}},$$

(19)

where numerical values in the 2^nd term is taken from Table 1. We use the following facts in simplifying the 3^rd term: (i) ${\varDelta }_{R}=0$ at $R=11.85{{{{{\rm{nm}}}}}},$ (ii) $\left({\varGamma }_{{{{{{\rm{o}}}}}}}-{\varDelta }_{R}\right)=0$ at $R=4.95{{{{{\rm{nm}}}}}}$, as discussed previously. In obtaining the 4^th term, we exploit the following equality: ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(R=11.85{{{{{\rm{nm}}}}}}\right)={\varGamma }_{{{{{{\rm{LO}}}}}}}\left(R=4.95{{{{{\rm{nm}}}}}}\right)={\varGamma }_{{{{{{\rm{LO}}}}}}}\left({bg}\right)$. This is because ${\varGamma }_{{LO}}$ for $R\ge 4.95{{{{{\rm{nm}}}}}}$ has a size-independent constant value of ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left({bg}\right)(=18.3{{{{{\rm{nm}}}}}})$ (Table 3). Thus, we finally deduce that ${\varGamma }_{o}=\left(23.1-18.3\right)\,{{{{{\rm{nm}}}}}}=4.8{{{{{\rm{nm}}}}}}$ from Eq. (19). Plugging this value into Eq. (18) yields that ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left({bg}\right)=18.3{{{{{\rm{nm}}}}}}$ which coincides with the deduced ${\varGamma }_{{LO}}$ value for $R\ge 4.95{{{{{\rm{nm}}}}}}$ (Table 3). Thus, we establish the following relation: ${\varGamma }_{{{{{{\rm{LO}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)={\varGamma }_{{{{{{\rm{LO}}}}}}}\left({bg}\right)+({\varGamma }_{{{{{{\rm{o}}}}}}}-{\varDelta }_{R})=18.3{{{{{\rm{nm}}}}}}+({\varGamma }_{{{{{{\rm{o}}}}}}}-{\varDelta }_{{{{{{\rm{R}}}}}}})$ for $R\ge 4.95{{{{{\rm{nm}}}}}}$. The previous deduction that $\left({\varGamma }_{{{{{{\rm{o}}}}}}}-{\varDelta }_{R}\right)=0$ indicates that ${\varDelta }_{R}$ is effectively constant and is equal to $4.8{{{{{\rm{nm}}}}}}$ for $1.60{{{{{\rm{nm}}}}}}\le {R}\le 4.95{{{{{\rm{nm}}}}}}$ (Fig. 4b).

It is expected that ${\varDelta }_{R}$ decays to zero as the CNC size increases because the PL wavelength shows a linear variation with the CNC size for $D\ge 20{{{{{\rm{nm}}}}}}(R\ge 10{{{{{\rm{nm}}}}}})$ (Fig. 2b). We can compute this decaying ${\varDelta }_{R}$ for large CNC particles by using the following obvious relation that can be obtained by combining Eq. (2) with Eq. (1) and rearranging: ${\varDelta }_{R}=\left\{{\varGamma }_{{{{{{\rm{LO}}}}}}}\left({bg}\right)+{\varGamma }_{{{{{{\rm{QC}}}}}}}(\lambda )+{\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)+{\varGamma }_{{{{{{\rm{o}}}}}}}\left(\lambda \right)\right\}-{\varGamma }_{{{{{{\rm{EXP}}}}}}}\left(\lambda \right).$ Here, we replaced ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left(\lambda \right)$ with ${\varGamma }_{{{{{{\rm{LO}}}}}}}\left({bg}\right)$ having a constant value of $18.3{{{{{\rm{nm}}}}}}$ for $R\ge 4.95{{{{{\rm{nm}}}}}}$. ${\varGamma }_{{{{{{\rm{EXP}}}}}}}\left(\lambda \right)=23.5{{{{{\rm{nm}}}}}},{\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)=2.2{{{{{\rm{nm}}}}}},{\varGamma }_{{{{{{\rm{o}}}}}}}=4.8{{{{{\rm{nm}}}}}}$ and the calculated ${\varGamma }_{{{{{{\rm{QC}}}}}}}=0.3{{{{{\rm{nm}}}}}}$ at $R=9.75{{{{{\rm{nm}}}}}}\,$(Table 1). We obtain ${\varDelta }_{R}=2.1{{{{{\rm{nm}}}}}}$ (Table 3) using these values. Similarly, ${\varGamma }_{{{{{{\rm{EXP}}}}}}}\left(\lambda \right)=24.7{{{{{\rm{nm}}}}}},{\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)=2.2{{{{{\rm{nm}}}}}},{\varGamma }_{{{{{{\rm{o}}}}}}}=4.8{{{{{\rm{nm}}}}}}$ and the calculated ${\varGamma }_{{{{{{\rm{QC}}}}}}}=0.3{{{{{\rm{nm}}}}}}$ at $R=11.25{{{{{\rm{nm}}}}}}$ (Table 1). We obtain ${\varDelta }_{R}=0.9{{{{{\rm{nm}}}}}}$ (Table 3) using these values. Finally, ${\varGamma }_{{{{{{\rm{EXP}}}}}}}\left(\lambda \right)=25.5{nm},{\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)=2.2{{{{{\rm{nm}}}}}},{\varGamma }_{{{{{{\rm{o}}}}}}}=4.8{{{{{\rm{nm}}}}}}$ and the calculated ${\varGamma }_{{{{{{\rm{QC}}}}}}}=0.2{{{{{\rm{nm}}}}}}$ at $R=11.85{{{{{\rm{nm}}}}}}$ (Table 2). We obtain ${\varDelta }_{R}=0{{{{{\rm{nm}}}}}}$ (Table 3) using these values. This prediction that ${\varDelta }_{R}=0{{{{{\rm{nm}}}}}}$ at $R=11.85{{{{{\rm{nm}}}}}}$ accords well with our prediction used previously. The calculated size-dependent ${\varDelta }_{R}$ is displayed in Fig. 4b. ${\varDelta }_{R}$ effectively shows a constant plateau behavior up to $R=4.95{{{{{\rm{nm}}}}}}$ and gradually decreases with increasing radius beyond this size, effectively becoming $0$ at $R=11.85{{{{{\rm{nm}}}}}}.$ Thus, ${\varGamma }_{{{{{{\rm{SD}}}}}}}^{{{{{{\rm{ext}}}}}}}\left(\lambda \right)\approx {\varGamma }_{{{{{{\rm{SD}}}}}}}\left(\lambda \right)$ for $R\ge 11.85{{{{{\rm{nm}}}}}}.$

Nonlinear variation in the degree of PL blue shift with the CNC size

In this section, we will examine the observation that the PL wavelength decreases as the CNC size decreases (Fig. 2b), which is known as the PL blue shift. We will show theoretically that the degree of PL blue shift ($\Delta \lambda$) with decreasing radius is not linear (i.e., $\partial \Delta \lambda /\partial R\ne {constant}$) but is highly nonlinear. This nonlinear variation of the PL wavelength is primarily responsible for a non-zero ${\varDelta }_{R}$. To this end, we first consider the total energy of exciton [${E}_{{{{{{\rm{exc}}}}}}}({R;}\alpha )$] in a CNC having radius $R$. It can be written as^29,48

$${E}_{{{{{{\rm{exc}}}}}}}\left(R{{{{{\rm{;}}}}}}\alpha \right)= \, {E}_{{{{{{\rm{g}}}}}}\left({{{{{\rm{b}}}}}}\right)}+\Delta {E}_{{{{{{\rm{g}}}}}}}\left(R{{{{{\rm{;}}}}}}\alpha \right)={E}_{{{{{{\rm{g}}}}}}\left({{{{{\rm{b}}}}}}\right)}+\frac{{{{\hslash }}}^{2}}{2{\mu }_{o}}\left\{\,\frac{{{{{{{\rm{\pi }}}}}}}^{2}}{{R}^{2}}+{\left(\frac{1}{\alpha }\right)}^{2}\right\}\\ -\frac{{{{{{{\rm{e}}}}}}}^{2}}{4{{{{{\rm{\pi }}}}}}{\varepsilon }_{o}{\varepsilon }_{r\,}^{Q}}\left\{\frac{{C}_{1}^{{\prime} }}{R}+\frac{{C}_{2}}{\alpha }\right\},$$

(20)

where ${E}_{{{{{{\rm{g}}}}}}\left({{{{{\rm{b}}}}}}\right)}$ denotes the bulk band-gap energy, ${\mu }_{o}$ is the effective reduced mass of exciton, ${\varepsilon }_{r}^{Q}$ designates the dielectric constant of a CNC (or QD) core, and ${C}_{2}=0.498$. The Coulomb interaction coefficient (${C}_{1}^{{\prime} }$) can be viewed as the effective Madelung constant²⁹ for a sphere having radius $R$. Equation (20) is the most elaborate expression of the net exciton energy above the bulk band gap [∆E_g(R;α)], which considers the internal relative motion between the electron and hole in a given exciton by introducing the quantum mechanical e-h correlation term, $\alpha$(ref. ⁴⁸). We consider the size-dependent PL frequency or wavelength as the next step. The total energy of exciton and the bulk band-gap energy under the condition of PL emission can be respectively written as

$${E}_{{{{{{\rm{exc}}}}}}}\left(R{{{{{\rm{;}}}}}}\alpha \right)={{\hslash }}\omega ={hc}/\lambda \, {{{{{\rm{and}}}}}} \, {E}_{{{{{{\rm{g}}}}}}\left({{{{{\rm{b}}}}}}\right)}={{\hslash }}{\omega }_{c}={hc}/{\lambda }_{{{{{{\rm{c}}}}}}},$$

(21)

where ${\lambda }_{{{{{{\rm{c}}}}}}}$ denotes the wavelength that corresponds to the onset of PL blue shift ($527.0{{{{{\rm{nm}}}}}}$ for MAPbBr₃; Tables 1 or 3). In Eq. (21), ${E}_{{{{{{\rm{g}}}}}}\left({{{{{\rm{b}}}}}}\right)}={hc}/{\lambda }_{{{{{{\rm{c}}}}}}}$ represents that the PL emission from the conduction band minimum to the valence band maximum occurs with the characteristic wavelength ${\lambda }_{{{{{{\rm{c}}}}}}}$. Let us now define the degree of PL blue shift in terms of the PL wavelength.

$$\Delta \lambda \equiv {\lambda }_{{{{{{\rm{c}}}}}}}-\lambda =\frac{\lambda {\lambda }_{{{{{{\rm{c}}}}}}}\,\Delta \omega }{2{{{{{\rm{\pi }}}}}}c\,} \, > \, 0,$$

(22)

where $\Delta \omega \equiv \omega -{\omega }_{c} \, > \, 0$. Combining Eqs. (21) and (22) with Eq. (20) yields the following expression:

$$\Delta \lambda =\frac{{{\hslash }}\lambda {\lambda }_{c}\,}{4{{{{{\rm{\pi }}}}}}c\,{\mu }_{o}}\,\left\{\left(\frac{{{{{{{\rm{\pi }}}}}}}^{2}}{{R}^{2}}+{\left(\frac{1}{\alpha }\right)}^{2}\right)-\frac{2}{{a}_{{{{{{\rm{B}}}}}}}}\left(\frac{{C}_{1}^{{\prime} }}{R}+\frac{{C}_{2}}{\alpha }\right)\right\},$$

(23)

where ${a}_{B}$ designates the exciton Bohr radius which is defined by the following equation⁴⁹:

$${a}_{{{{{{\rm{B}}}}}}}=\frac{4{{{{{\rm{\pi }}}}}}{\varepsilon }_{o}{\varepsilon }_{r}{{{\hslash }}}^{2}}{{\mu }_{o}{{{{{{\rm{e}}}}}}}^{2}}={\varepsilon }_{r}\left(\frac{{m}_{{{{{{\rm{o}}}}}}}}{{\mu }_{{{{{{\rm{o}}}}}}}}\right){a}_{{{{{{\rm{o}}}}}}},$$

(24)

where ${m}_{o}$ is the free-electron mass ($9.109\times {10}^{-31}\,{{{{{\rm{kg}}}}}}$), ${\varepsilon }_{{{{{{\rm{r}}}}}}}={\varepsilon }_{{{{{{\rm{r}}}}}}}^{Q}$, and ${a}_{{{{{{\rm{o}}}}}}}$ denotes the Bohr radius for the ground-state 1s orbital of a hydrogen atom $(=4{{{{{\rm{\pi }}}}}}{\varepsilon }_{{{{{{\rm{o}}}}}}}{\hslash }^{2}/{m}_{{{{{{\rm{o}}}}}}}{{{{{{\rm{e}}}}}}}^{2}=0.0529{{{{{\rm{nm}}}}}})$.

We compared the quantum e-h correlation term [$(1/{\alpha }^{2})-(2{C}_{2}/{a}_{{{{{{\rm{B}}}}}}}\alpha )$] with the classical energy term [$({{{{{{\rm{\pi }}}}}}}^{2}/{R}^{2})-(2{C}_{1}^{{\prime} }/{a}_{{{{{{\rm{B}}}}}}}R)$] to find a possibility of further simplification. For this purpose, we adopted the following semi-empirical correlation between $\alpha$ and $R$ (ref. ²⁹): $\alpha =-0.27R+2.0{a}_{{{{{{\rm{B}}}}}}}$ for $R < 2.3{a}_{{{{{{\rm{B}}}}}}}$. Since ${a}_{{{{{{\rm{B}}}}}}}$ of MAPbBr₃ is $\sim 5.0{{{{{\rm{nm}}}}}}$ (refs. ^29,46), this linear correlation is valid for $R < 11.5{{{{{\rm{nm}}}}}}.$ Let us examine the attractive quantum e-h correlation term at $R=4.95{{{{{\rm{nm}}}}}},$ where a rapid increase in the degree of PL blue shift (i.e., $\Delta \lambda ={\lambda }_{c}-\lambda$) is observed (Fig. 2b). Thus, $(1/{\alpha }^{2})=1/{\left(-0.27R+2{a}_{{{{{{\rm{B}}}}}}}\right)}^{2}=+0.0133{{{{{{\rm{nm}}}}}}}^{-2}$ and $(2{C}_{2}/{a}_{{{{{{\rm{B}}}}}}}\alpha )=2{C}_{2}/\left\{{a}_{{{{{{\rm{B}}}}}}}\times \left(-0.27R+10.0\right)\right\}=+0.0230{{{{{{\rm{nm}}}}}}}^{-2}.$ This leads to $(1/{\alpha }^{2})-(2{C}_{2}/{a}_{{{{{{\rm{B}}}}}}}\alpha )=-0.0097{{{{{{\rm{nm}}}}}}}^{-2}$ at $R=4.95{{{{{\rm{nm}}}}}}.$ On the other hand, the net repulsive classical energy term is $({{{{{{\rm{\pi }}}}}}}^{2}/{R}^{2})-(2{C}_{1}^{{\prime} }/{a}_{{{{{{\rm{B}}}}}}}R)=\left\{\left(9.870/24.503\right)-\left(2\times 1.39/5.0\times 4.95\right)\right\}=+0.2905{{{{{{\rm{nm}}}}}}}^{-2},$ where 1.39 is used for the ${C}_{1}^{{\prime} }$ value²⁹. Thus, the classical energy term is 30 times bigger than the e-h correlation term in their magnitudes at $R=4.95{{{{{\rm{nm}}}}}}.$ Considering this, we write the following approximation in the vicinity of $R=4.95{{{{{\rm{nm}}}}}},$ where a rapid change in the degree of PL blue shift ($\Delta \lambda$) is observed (Fig. 2b).

$$\Delta \lambda \approx \frac{{{\hslash }}\lambda {\lambda }_{{{{{{\rm{c}}}}}}}\,}{4{{{{{\rm{\pi }}}}}}c\,{\mu }_{{{{{{\rm{o}}}}}}}}\left\{\,\frac{{{{{{{\rm{\pi }}}}}}}^{2}}{{R}^{2}}-\frac{{2C}_{1}^{{\prime} }}{{a}_{{{{{{\rm{B}}}}}}}R}\,\right\} \, > \, 0$$

(25)

Equation (25) predicts that the degree of PL blue shift is inversely proportional to ${R}^{2}$, indicating a very rapid nonlinear increase in $\Delta \lambda (={\lambda }_{{{{{{\rm{c}}}}}}}-\lambda )$ with decreasing radius. The nonlinearity in $\Delta \lambda$ can be shown more clearly by taking partial differentiation:

$${\left(\frac{\partial \Delta \lambda }{\partial R}\right)}_{\alpha }\approx -\frac{{{\hslash }}\lambda {\lambda }_{{{{{{\rm{c}}}}}}}\,}{2{{{{{\rm{\pi }}}}}}c\,{\mu }_{{{{{{\rm{o}}}}}}}{R}^{2}}\left\{\,\frac{{{{{{{\rm{\pi }}}}}}}^{2}}{R}-\frac{{\,C}_{1}^{{\prime} }}{{a}_{{{{{{\rm{B}}}}}}}}\,\right\} \, < \, 0$$

(26)

Here, we are concerned with the variation of $\Delta \lambda$ for ${R}\le {R}_{c}(=13.75{{{{{\rm{nm}}}}}})$. Thus, the value inside the parenthesis ($\eta$) of Eq. (26) is always positive: $\eta \, > \, \left\{\left(9.87/13.75\right)-\left(1.39/5.0\right)\right\}\,{{{{{{\rm{nm}}}}}}}^{-1}=0.43{{nm}}^{-1}.$ Equation (26) shows that ${\left(\partial \Delta \lambda /\partial R\right)}_{\alpha }$ is not constant but its magnitude increases very rapidly with decreasing radius.

Finally, we will show that there exists a unique 1:1 correspondence between the modal CNC size ${R}_{{{{{{\rm{p}}}}}}}$ (or ${D}_{{{{{{\rm{p}}}}}}}$) and the modal wavelength ${\lambda }_{{{{{{\rm{p}}}}}}},$ where ${\lambda }_{{{{{{\rm{p}}}}}}}$ actually denotes a particular wavelength (${\lambda }_{{{{{{\rm{p}}}}}}}$) that corresponds to the peak in the PL-$\lambda$ spectrum: e.g., ${\lambda }_{{{{{{\rm{p}}}}}}}=524.0\,{{{{{\rm{nm}}}}}}$ for ${R}_{{{{{{\rm{p}}}}}}}=4.95\,{{{{{\rm{nm}}}}}}$ (Table 1). We can directly obtain the following relation that shows a unique 1:1 correspondence between ${\lambda }_{{{{{{\rm{p}}}}}}}$ and ${R}_{{{{{{\rm{p}}}}}}}$ from Eq. (23):

$${\lambda }_{p}=\frac{{\lambda }_{c}}{\left[1+\frac{{{\hslash }}{\lambda }_{c}}{4{{{{{\rm{\pi }}}}}}c\,{\mu }_{{{{{{\rm{o}}}}}}}}\left\{\left(\frac{{{{{{{\rm{\pi }}}}}}}^{2}}{{R}_{{{{{{\rm{p}}}}}}}^{2}}+{\left(\frac{1}{{\alpha }_{{{{{{\rm{p}}}}}}}}\right)}^{2}\right)-\frac{2}{{a}_{{{{{{\rm{B}}}}}}}}\left(\frac{{C}_{1}^{{\prime} }}{{R}_{{{{{{\rm{p}}}}}}}}+\frac{{C}_{2}}{{\alpha }_{{{{{{\rm{p}}}}}}}}\right)\right\}\right]}$$

(27)

where the quantum e-h correlation parameter at ${R}_{{{{{{\rm{p}}}}}}}$ is denoted by ${\alpha }_{{{{{{\rm{p}}}}}}}.$ As discussed previously, it is given by the following semi-empirical relation for ${R}_{{{{{{\rm{p}}}}}}} \, < \, 2.3{a}_{{{{{{\rm{B}}}}}}}$ (ref. ²⁹): ${\alpha }_{{{{{{\rm{p}}}}}}}=-0.27{R}_{{{{{{\rm{p}}}}}}}+2.0{a}_{{{{{{\rm{B}}}}}}}$. This semi-empirical correlation indicates that the denominator of Eq. (27) is a functional of ${R}_{{{{{{\rm{p}}}}}}}$. Thus, there exists a unique 1:1 correspondence between ${\lambda }_{{{{{{\rm{p}}}}}}}$ and ${R}_{{{{{{\rm{p}}}}}}}$.