Introduction

Charge order is prevalent in materials exhibiting strong electronic correlations and pronounced electron–phonon interactions. This phenomenon is observed in various systems such as cuprate high-temperature superconductors1,2,3, colossal magnetoresistive manganites4, transition-metal dichalcogenides (TMDs)5,6,7, and more recently, kagome lattice metals8,9. Charge order is usually associated with unconventional quantum phases, which highlights the importance of charge order in understanding and manipulating novel phases of matter. Besides the fundamental aspect, layered quantum materials with charge order have also been widely studied and proposed to be potential candidates for next-generation electronic devices. However, the lack of room-temperature charge-order materials has limited the development of charge-order-based electronic devices. Thus, it is of importance both from fundamental and technological aspects to find more materials with room-temperature charge orders.

Along these lines, several kagome metals8,9,10,11,12,13,14,15,16,17 have appeared as promising platforms to study unconventional correlated quantum phases, including charge order. There are three material classes of kagome lattice systems that were recently shown to exhibit charge order: the AV3Sb5 (A = K, Rb, Cs)9,18,19 family of materials, ScV6Sn620,21,22,23,24,25 and FeGe26,27,28. AV3Sb5 exhibits two correlated orders: charge order below Tco  ≃ 80–110 K and a superconducting (SC) instability below Tc  ≃ 1–3 K29,30,31. The system ScV6Sn6 has a similar vanadium structural motif as AV3Sb5 and exhibits charge order below Tco  ≃ 90 K, however it is not superconducting down to the lowest measured temperature. FeGe is a correlated magnetic kagome system and exhibits an A-type antiferromagnetic (AFM) order below 400 K and a charge order below 100 K. The unique features of AV3Sb5 and ScV6Sn6 are the emergence of possibly time-reversal symmetry (TRS) breaking chiral charge orders with both magnetic8,11,21,32,33,34,35,36,37,38,39,40,41,42,43,44 and electronic anomalies45,46. Theoretically, these features could be explained by a complex order parameter realizing a higher angular momentum state, dubbed unconventional36,47,48,49,50,51,52,53,54,55,56,57, in analogy to superconducting orders. It is important to note that the charge order temperature in the above-mentioned kagome-lattice metals is limited to ≃100 K, and to the best of our knowledge, no report of charge order at room temperature exists so far.

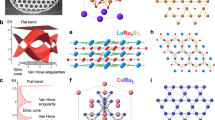
A much less explored kagome lattice system is LaRu3Si215,16,17,58,59,60,61. The structure of LaRu3Si2 contains kagome layers of Ru sandwiched between layers of La and layers of Si having a honeycomb structure (see Fig. 1a)15,16. The superconductivity in LaRu3Si2 is fully gapped17 and has the highest SC transition temperature Tc  ≃ 7 K among the kagome-lattice materials. Using first-principles calculations, we previously found that the normal state band structure features a kagome flat band, Dirac point, and Van Hove point formed by the Ru-dz2 orbitals near the Fermi level (see Fig. 1b). The electron-phonon coupling induced critical temperature Tc, estimated from the phonon dispersion17, was found to be much smaller than the experimental value. Thus, the enhancement of Tc in LaRu3Si2 was attributed to the presence of the flat band, and the van Hove point relatively close to the Fermi level as well as to the high density of states from the narrow kagome bands17. Regarding the normal state properties, there is no report on either magnetic order or charge order in this system. Anomalous properties58,60 in the normal state were inferred from thermodynamic measurements in LaRu3Si2, such as the deviation of the normal state-specific heat from the Debye model, non-mean field like suppression of superconductivity with magnetic field, and non-linear field dependence of the induced quasiparticle density of states (DOS). Previous studies have identified two potential structures for LaRu3Si2 at room temperature: the P6/mmm (space group No. 191) and P63/m (space group No. 176). Our phonon dispersion calculations for both suggest that the P6/mmm structure is inherently unstable. This is evidenced by the appearance of three imaginary phonon modes in the kz = π plane (see Fig. 1c), particularly at the A (0, 0, \(\frac{1}{2}\)) point, indicating a propensity for this structure to transition into an a × a × 2c configuration, akin to the P63/m structure, to resolve this instability. Upon undergoing the a × a × 2c transformation, the phonon dispersion for the P63/m structure still displays two negative modes (see Fig. 1d), now relocated to the kz = 0 plane. One of these modes exhibits a flat dispersion within the kz = 0 plane, suggesting that the P63/m structure, while more stable than the P6/mmm, may still be prone to in-plane structural reconstruction to reach a state of greater stability. These soft dispersions20,21,22,23,24,25 signal the potential for charge-order phenomena, although the exact nature of the most stable in-plane reconstruction remains undetermined by density functional perturbation theory (DFPT) calculations alone.

Fig. 1: High-temperature crystal structure, band structure and phase diagram.
figure 1

a Top view of the atomic structure of LaRu3Si2. The Ru atoms construct a kagome lattice (middle-size circles), while the Si (small-size circles) and La atoms (large-size circles) form a honeycomb and triangular structure, respectively. Structures were plotted using the VESTA visualization tool83. b The band structure (black) and orbital-projected band structure (red) for the Ru-dz2 orbital without spin-orbit coupling along the high symmetry k-path, presented in conformal kagome Brillouin zone (BZ). Calculation was done for the P63/m structure. The width of the line indicates the weight of each component. The blue-colored region highlights the manifestation of the kagome flat band. Arrows mark Dirac point (DP) and van Hove singularity point (VHS) formed by the Ru-dz2 orbitals near the Fermi level. c The phonon dispersion in the bulk of LaRu3Si2 is characterized by the P6/mmm structure through the local density approximation. d The phonon dispersion in the bulk of LaRu3Si2 is characterized by the P63/m structure through the local density approximation. The green-colored regions in panels c and d highlight the presence of imaginary phonon modes, one of which exhibits a flat dispersion.

Full size image

In order to explore the possibility of a structural phase transition and the formation of charge order, we investigated three microcrystalline samples of La(Ru1−xFex)3Si2 (x = 0, 0.01, 0.05) as well as a large single crystal of LaRu3Si2 via X-ray diffraction (the experimental details of which may be found in the methods section). The experiments reveal charge order with a propagation vector of (\(\frac{1}{4}\), 0, 0) in undoped LaRu3Si2 as well as Fe-doped La(Ru1−xFex)3Si2 samples with x = 0.01 and x = 0.05, setting in well above room temperature (TCO,I  ≃ 400 K). The charge order transition is preceded by a structural phase transition with \({T}_{{{{{{{{\rm{str}}}}}}}}}\,\simeq\) 600 K from the high-temperature hexagonal P6/mmm phase (space group (SG) No. 191) to the low-temperature orthorhombic Cccm phase (SG No. 66). Furthermore, a second set of charge order peaks with a propagation vector of (\(\frac{1}{6}\), 0, 0) sets in below TCO,II  ≃ 180 K in the x  = 0.01 sample and possibly in the x = 0 sample below TCO,II  ≃ 80 K, showing competition with the primary charge order.

Results

Previous reports for both pristine and doped LaRu3Si215,59,62,63 have some discrepancy regarding the room temperature structure, represented either by a small hexagonal cell (P6/mmm, a ≃ 5.6 Å, c  ≃ 3.5 Å) (see Supplementary Note 1 and Supplementary Fig. 1) or a large hexagonal cell (P63/m, a ≃ 5.6 Å, c ≃ 7.1 Å) (see Supplementary Fig. 2). Above 600 K, we found, from our single crystal diffraction experiments, that the crystal structure can indeed be described using a small hexagonal cell (P6/mmm, a × a × c, HT-hex) (see Supplementary Fig. 1). The results of the refinement are summarized in the Supplementary Tables 1–5 (CCDC deposition number is 2289106). Attempts to introduce Fe in the Ru position for the x = 0.01 Fe-doped sample yield 1.6(1)%, which agrees with the nominal value of 1% Fe-doping. Another peculiar feature is the presence of 5.6(2)% vacancies in the Si position.

Although the high-temperature model described above fits the diffraction data well, it features oblate thermal ellipsoids for Ru and Si atoms (Supplementary Table 5). This, together with pronounced diffuse scattering within the (0, 0, l = odd) reciprocal space planes (see Fig. 2d, e, I, j, n), indicates the proximity to a phase transition. Indeed, upon cooling below 600 K, we observe evolving Bragg peaks corresponding to the doubling of the initial unit cell along the c-axis (a × a × 2c, LT-hex), indicative of a structural phase transition (see also Supplementary Note 2 and Supplementary Fig. 5). The diffraction pattern follows hexagonal symmetry (Rint = 1.24% for P6/mmm Laue symmetry) in agreement with the P63/m space group (SG No. 176), previously inferred from powder data15. Attempts to solve the crystal structure in this space group or any other down to P1 are unsuccessful, which is likely an indication of twinning upon the structural phase transition. The structure can be described in the space group Cccm (No. 66) as three interpenetrating orthorhombic twins (\(a\times \sqrt{3}a\times 2c\)) propagated by the six-fold axis present in the parent high-temperature phase. The refined twin fractions are close to \(\frac{1}{3}\), which effectively mimics the six-fold symmetry of the diffraction pattern.

Fig. 2: Cascade of charge orders in La(Ru1−xFex)3Si2.
figure 2

Reconstructed reciprocal space along the (0 0 1) direction at 3 r.l.u. (reciprocal lattice units), performed at various temperatures for undoped a–e, as well as Fe-doped samples with x = 0.01 f–j, and x = 0.05 k–o. Arrows indicate the reciprocal space vectors. Orange, green, and blue circles mark the Bragg peak, primary charge order CO-I peak, and secondary charge order CO-II peak, respectively.

Full size image

Below ~400 K, the diffuse scattering is clustered into another set of sharp diffraction spots. Besides the main reflections, there are satellites corresponding to q1 = (\(\frac{1}{4}\) 0 0), q2 = (0 \(\frac{1}{4}\) 0) and q3 = (\(\frac{1}{4}\frac{-1}{4}\) 0) relative to the a × a × 2c cell (see Fig. 2c–e, Supplementary note 1 and Supplementary Fig. 4); the refined deviations from the rational fractions are within 3σ. The diffraction pattern thus represents a 4 × 4 × 1 superstructure (see Supplementary Fig. 3) of the parent diffraction pattern existing above ~400 K; all reflections can be indexed using a 4a × 4a × 2c supercell. Similar to the case of LT-hex, the structure can be solved in this supercell in an orthorhombic unit cell (Cccm, 40 symmetrically independent atoms), assuming twinning by the six-fold axis. The disadvantage of this description is that it also accounts for higher-order satellite peaks besides q1, q2, and q3, including cross-satellites (2q1, q1q2, etc.), which are practically unobservable. This hints at the possibility of describing the CO-I phase with a smaller cell. Indeed, the initial supercell can be reduced to \(a\times 2\sqrt{3}a\times 2c\) or \(a\times \sqrt{3}a\times 2c\) with q = (0 \(\frac{1}{2}\) 0) cell without losing observable reflections. Here, q = (0 \(\frac{1}{2}\) 0) corresponds to a high symmetry direction (DT line) in the Brillouin zone. Within this cell, the structure can be described as modulated in superspace group Cmmm(0b0)s00. Superlattice peak intensity appears below TCO,I  ≃ 400 K for undoped LaRu3Si2 (Fig. 2a–e) as well as Fe-doped La(Ru1−xFex)3Si2 samples with x = 0.01 and x = 0.05 as shown in Fig. 2a–e, f–j, and k–o, respectively. The charge order features for the x = 0.05 sample look broader, as compared to x = 0 and 0.01 samples, and do not coalesce into sharp diffraction peaks right below ≃400 K. This indicates that the effect of Fe-doping is to introduce disorder into the charge order. Another set of reflections evolves at positions corresponding to \({q}_{1}^{{\prime} }\) = (\(\frac{1}{6}\,0\,0\)), \({q}_{2}^{{\prime} }\) = (0 \(\frac{1}{6}\,0\)) and \({q}_{3}^{{\prime} }\) = (\(\frac{1}{6}\frac{-1}{6}\,0\)), which is most pronounced for the x = 0.01 sample with TCO,II  ≃ 180 K. Since the relation between these two sets of ordering vectors is unclear (multi-phase vs. multi-q ordering) we refrain from speculating on the possible models of superstructure ordering.

Comparison of models for HT-hex (at 670 K), LT-hex (at 470 K) and CO-I (at 250 K) phases is provided in Fig. 3a–i. The HT-hex phase features an undistorted planar kagome net comprised of Ru atoms alternating with Si/La planes (Fig. 3a,d,g). The distances within the Ru-kagome net are 2.844(4) Å. Alternatively, this structure can be viewed as packing of La polyhedra comprised of 6 Si atoms (d(La–Si) = 3.284(5) Å) and 12 Ru atoms (d(La–Ru) = 3.357(3) Å) reinforced by short Si–Ru contacts (d(Si–Ru) = 2.424(6) Å). The transition to the LT-hex phase is mainly due to in-plane displacement of Si atoms, distortion of the environment of La, and very small out-of-plane displacements of 2/3 of Ru atoms (Fig. 3b, e, h). In particular, this leads to very weak corrugations of the ideal kagome net with shortening and elongation of Ru–Ru distances (4 × 2.8431(7) Å + 2 × 2.853(1) Å), still retaining a nearly ideal hexagonal Ru-plane. Upon further cooling and transition into the CO-I phase, there occurs a strong disproportionation of bonds, resulting in the emergence of short and long Ru–Ru bonds, which is to say, a bond or charge order is established. The Ru–Ru distances are in the range of 2.832(1)–2.868(1) Å. In Fig. 3c, f, i, the distances below 2.845 Å are marked as short, and the distances above 2.845 Å are marked as long. So, our comprehensive analysis shows that the structural phase transition at \({T}_{{{{{{{{\rm{str}}}}}}}}}\,\simeq\) 600 K leads to a minimal distortion of the Ru kagome plane, thereby preserving a nearly ideal kagome lattice structure, and charge order is established only below TCO,I  ≃ 400 K. Charge ordering results from the ordering of Ru–Ru bonds, a phenomenon of particular interest due to the Ru-dz2 orbital’s formation of a distinctive kagome band structure, suggesting a potential link between charge ordering and the underlying physics of the kagome lattice.

Fig. 3: Quantitative insight into various phases.
figure 3

General projection of the kagome net at 670 K (HT-hex) (a), 470 K (LT-hex) (b), and 250 K (CO-I) (c), projection perpendicular to the kagome net at 670 K (d), 470 K (e), and 250 K (f), projection along the kagome net at 670 K (g), 470 K (h) and 250 K (i). In panels c, f, i, the distances shorter than 2.845 Å are categorized as short and illustrated with a red line. The distances >2.845 Å are categorized as long and illustrated with a blue line.

Full size image

Figure 4a and b outline four distinct temperature regions for La(Ru1−xFex)3Si2 by following selected main and supposedly superstructure reflections. Namely, Fig. 4a and b show the temperature dependences of the intensities of the (2 −3 5) (hexagonal setting) Bragg peak and the charge-order peak intensities, respectively, for x = 0, 0.01, and 0.05 samples. By tracking the relative intensity of CO-I and CO-II peaks for the different doped samples, we find that in the x = 0.01 case, there is a clear decrease in the scattered intensity from the CO-I phase at the same temperature where the scattered intensity from the CO-II phase appears. The intensity of the peaks from the CO-II phase increases while the intensity of the peaks from the CO-I monotonously decreases until they achieve equivalent intensities at 80 K. This implies that the two charge-ordered phases compete. We note that the onset of this additional modulated structure CO-II appears to be enhanced in the x = 0.01 Fe-doped sample, occurring at 180 K, while weak peaks become visible below 120–100 K in the pristine sample. The intensity of the CO-I phase seems to reach a peak at 120 K and decrease from 120 to 80 K in the undoped material, suggesting that the onset of the CO-II phase may be at lower temperatures. No signatures of coherent or diffuse scattering at \(\frac{1}{6}\) periodicity are observed in the x = 0.05 Fe-doped sample, which is most likely due to disorder-induced broadening of the charge order peaks. The intensities of the (2 −3 5) (hexagonal setting) Bragg peak for x = 0, 0.01, and 0.05 samples (see Fig. 4a) show a clear slope change around TCO,I  ≃ 400 K and an additional slope change with an increase in (2 −3 5) intensity below TCO,II  ≃ 180 K for all three samples. Increase of Bragg peak intensity across TCO,II is most pronounced in the x = 0.01 sample in which a clear indication of \(\frac{1}{6}\) charge order is observed. Figure 5 presents a phase diagram summarizing the charge order and superconducting transition temperatures for La(Ru1−xFex)3Si2. This diagram indicates that the onset of the CO-I phase remains constant despite Fe doping, although the superconducting transition temperature Tc is strongly suppressed. However, the effects on the CO-II phase and its interaction with superconductivity are not yet clear, indicating the need for further low-temperature experimental investigations.

Fig. 4: Structural phases and charge orders in La(Ru1−xFex)3Si2.
figure 4

Temperature evolution of the Bragg intensity (a) and charge order satellite peak intensities (b). The error bars represent the standard deviation of the fit parameters.

Full size image
Fig. 5: Phase diagram of La(Ru1−xFex)3Si2.
figure 5

The Fe-doping evolution of the superconducting transition temperature Tc (data are taken from our previous work ref. 61), charge order transition temperatures TCO,I, TCO,II and structural phase transition temperature \({T}_{{{{{{{{\rm{str}}}}}}}}}\). The plots include error bars that indicate the standard error. The standard error is a measure of the variability or precision of a sample mean.

Full size image

Discussion

Before concluding, we clarify our use of the term ‘charge order’, initially defined to describe Peierls-type instabilities64 characterized by periodic charge density fluctuations without changes in atomic positions. It was shown65 that original Peierls construction about purely electronically driven charge order is unlikely to apply to real materials. Even in prototypical charge-ordered materials like NbSe266,67, TaSe2, TiSe268, and CeTe3, Peierls conditions are hardly fulfilled. Instead, charge order transitions were shown to be driven by the concerted action of electronic and ionic subsystems, i.e., a momentum-dependent electron–phonon coupling plays an essential part (provided that the electronic degrees of freedom enhance the electron–phonon matrix elements). Giant electron–phonon coupling associated with charge order was also observed in copper oxide superconductors69. In summary, charge order in crucial materials like cuprates and TMDs seems to be the result of synergy between electronic and ionic subsystems. This synergy is likely present in the LaRu3Si2 and other kagome metals as well22,23,36,48,70. In accordance with more recent literature, such as on AV3Sb5, ScV6Sn6, and FeGe, we use the term ‘charge order’ to encompass a variety of phenomena, including both electronic and atomic modulations with incommensurate or extended periodicity. Specifically, we apply this term to denote the static and long-range Ru–Ru bond order observed in La(Ru1−xFex)3Si2. Our study does not imply a purely electronic origin of this order65 since, in actual materials, the formation of charge density waves is a complex process involving both lattice distortions and electronic instabilities.

Experimental realizations of charge order in the kagome lattice have long been awaited. It was not until recently when studies into the family of kagome metals AV3Sb5 (A = K, Rb, Cs)9,18,19,29,30,31, ScV6Sn620,21 and magnetic FeGe26,27,28 revealed charge-ordered states. However, the charge-ordering temperature in all these materials is limited to ≃100 K, i.e., well below room temperature. Also, among the above-mentioned systems it is only the AV3Sb5 family of materials that shows superconductivity. In these systems, charge order strongly competes with superconductivity and has a negative effect on both the superconducting critical temperature and the superfluid density. Therefore, the maximum SC transition temperature, in the presence of charge order, was reported to be ≃3 K. Here, we report the discovery of the cascade of charge orders in La(Ru1−xFex)3Si2 (x = 0–0.05): the one with a propagation vector of (\(\frac{1}{4}\), 0, 0), setting in well above room temperature (TCO,I  ≃ 400 K) and a second one with a propagation vector of (\(\frac{1}{6}\), 0, 0), setting in at lower temperatures, which competes with the primary charge order. Moreover, the system LaRu3Si2 exhibits the highest superconducting critical temperature Tc ≃ 7 K and the highest superfluid density17 among the known bulk kagome-lattice superconductors. This implies that in this system, both charge order and superconductivity are somewhat optimized, irrespective of the mechanism involved. Fe-doping does introduce significant disorder to the charge-ordered state and leads to the full suppression of superconductivity with xFe,cr = 0.0561. Our results classify the bulk superconductor LaRu3Si2 as the kagome-lattice system with charge order above room temperature. This finding, combined with the three-dimensional character of superconductivity, unlike the mainly two-dimensional properties of AV3Sb5, positions LaRu3Si2 as an outstanding model to study the inherent mechanisms and to analyze the relationship between charge order and superconductivity. Moreover, to the best of our knowledge the system LaRu3Si2 has the highest long-range charge-order temperature among the superconducting materials. The importance of this discovery of above room temperature charge order is not limited to kagome lattice materials, and we anticipate will have a broader impact. Previous research in quantum materials has unearthed complex interactions between charge order and electronic phases, including direct competition with superconductivity or mediation of colossal magnetoresistance, which highlights the importance of charge order in understanding these novel phases of matter. It’s also noteworthy that the series of phase transitions observed in LaRu3Si2 bear a resemblance to those in cuprates, like the La2−xBaxCuO41 system with x = 1/8, and in TMDs6,7. These phenomena encompass structural phase transitions, charge ordering, and superconductivity. However, unlike the cuprates where charge order manifests as stripe order, LaRu3Si2 exhibits charge ordering in the form of bond order, similar to patterns observed in other Kagome systems and certain TMDs, such as IrTe26,7. The comparison of LaRu3Si2 with cuprates and TMDs becomes particularly fascinating, given the higher charge order transition temperatures in LaRu3Si2.

Besides the fundamental aspect, room-temperature charge order may be useful in charge order-based electronic devices71,72. Switching between various material phases near room temperature is a promising step toward next-generation electronic and optoelectronic technologies. There is an example of an oscillator based on an integrated TaS2–boron nitride–graphene device, which utilizes the charge order phase transition71. Previous works have also discussed the implementation of charge order transition-based devices72 for information processing and radiation-hard applications. In theory, such devices can be fast, low-power, and immune to proton and X-ray radiation. Also, the quasi-two-dimensional structure of LaRu3Si2 naturally leads to the question of whether thin layers or even monolayers can be exfoliated. Thin films would allow the formation of Moire structures by gating, stacking, or twisting, promising exciting future developments. This could also facilitate the further exploration of superconducting and charge-ordered phases.

Having established the existence of high-temperature charge order in the kagome material LaRu3Si2, our study opens up exciting avenues for future quantum materials research. In the kagome compounds, ScV6Sn620,21,22,25 and AV3Sb5 (A = K, Rb, Cs)29,32,33,44,47,49,73,74,75, the interplay of electronic and phononic contributions in the formation of charge order have been at the heart of the scientific discourse. It seems clear that both the low-energy fermiology as well as the phononic instabilities have to be considered to explain the charge order with its unconventional properties, such as chiral charge order that can be sensitively manipulated by strain and magnetic fields. While charge order in this context means a translation symmetry breaking instability (Q ≠ 0 order), there exists the equally relevant possibility of an intra-unit cell (Q = 0) charge order in which low energy electronic states are involved. The loop current phases of the Haldane honeycomb model76 or the Varma model77 for the cuprate superconductors are prominent examples. Following this line of thought blurs the boundaries between structural transitions and charge orders. It is thus imperative to study the electronic response and electronic structure of LaRu3Si2 in more detail to unveil its connections with the changes in structural motifs found in this work.

Methods

Sample preparation

The samples of La(Ru1−xFex)3Si2 were synthesized from high-purity Si lump (purity 99.999+%, Alpha aeser), low-oxygen vacuum remelted Fe lump (purity 99.99%, Alpha aeser), Ru pellets (purity 99.95%, Alpha aeser), and La ingot (purity 99.9%) via arc melting using Zr pellets as an oxygen getter. The melted buttons were flipped three times to ensure melt homogenization. In order to suppress the second phase LaRu2Si2, an additional 15% Ru was added to each melt (as mentioned previously59,62,63) in order to attain nominal compositions as La(Ru1−xFex)3.45Si2. Single crystals of La(Ru1−xFex)3Si2 were extracted from arc-melted buttons.

Polycrystalline sample of LaRu3Si2 was prepared by arc-melting mixtures of lanthanum, ruthenium and silicon in a purified argon atmosphere. The polycrystalline materials with excess Ru obtained were used to grow single crystal of LaRu3Si2 by the Czochralski method, using a commercial tetra-arc furnace (TAC-5100, GES). Our X-ray measurements indicate a single phase of hexagonal LaRu3Si2 phase.

Single crystal diffraction measurements

Single crystalline samples were selected from the large undoped crystal and from crushed chunks of the arc-melted samples washed in dilute HCl for 5 min before being flushed in deionized H2O and ethanol, followed by acetone to dry them. Following this, we selected single crystalline samples that had faceted sides and a typical size of 30–100 μm. These were then mounted on a small-diameter (10 μm) MiTeGen loop or a quartz capillary and centered within the X-ray beam. Diffraction measurements were carried out using the laboratory STOE STADIVARI single crystal diffractometer at the Paul Scherrer Institute. Measurements were carried out in the temperature range between 80 and 700 K, using the combination of the CryoStream (constant N2 gas flow) and HeatStream (constant Ar flow of 0.8 L/min). The micro-focused source was a Mo Kα X-ray with a wavelength of 0.71073 Å. The detector was a Dectris EIGER 1M 2R. The exposure time was set to 10 s per frame, and the coverage was calculated through the program X-Area78. Data reduction and correction were done with the X-Area package. The peaks were identified by the X-Area software (typically taking a minimum Intensity/σ ≥ 25), and then the lattice parameters were refined. From this, we were able to integrate the intensities and extract individual Bragg peak and CO peak intensities for each q-vector (modulation). These intensities were corrected by beam-out and frame scaling and then further by spherical correction (where the absorption μ and sample radius were inputs). From this, we were able to identify the strongest CO satellite intensities and follow them with temperature. We also used the X-Area software to perform reconstructions in the reciprocal space of the collected data (see Fig. 2) in order to visually identify changes in the charge order periodicity and structure. We used the software JANA2020 for data refinement and μ calculation79. The large single crystal of LaRu3Si2 was also measured at room temperature in the hard X-ray beamline (P21.1, PETRA III) at the DESY facility, and the superlattice peaks due to charge order were identified.

Density functional perturbation theory

Density functional perturbation theory (DFPT) method is based on the harmonic approximation of phonons, which inherently does not account for temperature variations80. Consequently, DFPT is unable to directly predict temperature-dependent properties. The observed negative phonon energy in our results just suggests a potential for structural instability rather than predicting a specific temperature for a structural phase transition. To accurately determine the temperature at which such transition may occur, alternative methods like the temperature-dependent effective potential method81 or the more recent stochastic self-consistent harmonic approximation method82, are more suitable. These approaches are of great interest for future studies, potentially providing a deeper understanding of the temperature-dependent dynamics of structural phase transitions.