Introduction

Exploiting spin and orbital angular momentum broadens possibilities for wave manipulation1,2,3 and interactions with matter4. The spin angular momentum is associated with circular polarization. In 1992, it was recognized that light beams with a helical phase structure described by exp(ilθ), where l is the topological charge and θ is the azimuthal angle, carry an orbital angular momentum (OAM)5. Unlike the limited spin angular momentum of light with two states, the number of allowable OAM states is theoretically unbounded. Optical vortices carrying different OAMs are orthogonal, creating an ideal space for data transmission with unlimited resolvable channel dimensions6,7,8. OAM’s unique properties have led to extensive research in recent decades9.

In contrast to optical vortices, acoustic waves only carry OAM, since they are essentially scalar pressure fields and are generally considered spinless2,10. Acoustic vortices (AVs) offer advantages such as enhanced object penetration, reduced biological damage11, increased acoustic torque12, and efficient underwater signal transmission13,14. They have drawn significant attention in fields like particle manipulation15,16,17,18, acoustic communication19,20,21, information detection22, asymmetric acoustic transmission23,24, and cross-media transmission25. Given that the generation method significantly influences acoustic vortex (AV) characteristics, it directly impacts related applications. Consequently, extensive research has focused on AV generation methods. Two ways are employed to generate AVs: active and passive. Active methods often utilize active transducer arrays26 and diffraction gratings27. The active uniform circular transducer arrays method offers flexibility in tuning AV’s order and working frequency, with high conversion efficiency. Nevertheless, each transducer necessitates precise digital control, resulting in complex configurations and high power consumption. Passive methods, on the other hand, generate AVs by introducing a plane wave source and using designed structures to control the wavefront of the incident wave source. The spiral phase plate28 efficiently generates AVs but is limited to a single frequency and requires structural dimensions close to the wavelength, making it less compact, particularly for low-frequency AVs. To address this, spiral diffraction acoustic gratings and metamaterial generation methods with subwavelength size characteristics have been proposed. Passive diffraction gratings29,30 have compact structures and a broad working frequency range but suffer from lower conversion efficiency due to the blocking and loss of incident sound energy. Conversely, metasurfaces excel in wavefront control and offer high conversion efficiency. Recent research has explored resonance31,32,33,34, compound labyrinth35, and phase gradient-type metasurfaces36 for AV generation. Some methods reduce metasurface thickness to half a wavelength, while spiral space metasurfaces37 further shrink it to one-third. Nevertheless, these structures have limited flexibility, as they can only generate AVs with a single order at a specific frequency. To address this limitation, reconfigurable metasurfaces have been proposed to achieve tunability of the AV order38,39,40 and working frequency29,33,41,42. However, these methods primarily rely on adjusting or moving structures to modify specific parameters, introducing complexity to the order tunability process. These methods are restricted by the minimum structural thickness determined by the AV’s working frequency, making it challenging to break through the 1/4 wavelength and resolve the conflict between low working frequency and compact structure. Besides, because the passive method requires an incident wave source, it will also cause some problems in the AV application. For instance, similar to optical vortices in remote sensing and metrology43,44,45, there’s extensive research on contactless detection of rotating object information using AV22,46,47,48. Contactless detection of rotational information is performed by directing incident AV onto a rotating object and analyzing the rotational Doppler shift of the scattered vortex waves49. However, the introduction of additional AV waves inevitably raises concerns about the relative size50 of the incident vortex acoustic beam, the rotating object, and their slight misalignment22,51, which collectively impact detection accuracy.

Developing a simple, compact AV generation method without introducing additional incident waves is a promising research avenue, such as utilizing aerodynamic sound sources from simple rotating models like disks. The focus of research on sound radiation from rotating disks is primarily on aerodynamically broadband sound generation52,53,54 and frequencies corresponding to resonant vibrational modes of the disk55,56,57,58. The latter includes the natural frequency, mode shape, and vibration noise during the resonance of the disk under rotating conditions. Regarding the former, three aerodynamic sound sources are produced by rotating objects: turbulent sources (quadrupoles), surface pulsation-induced sources (dipoles), and object motion-related aerodynamic sources (monopoles). When the disk rotates at low Mach numbers, the broad-band sound is due to acoustic dipole sources caused by the turbulent-boundary-layer flow on the disk. The low-frequency part of the spectrum results from a uniform distribution of pressure dipoles over the disk surface52. At high Mach numbers, turbulent sources become the primary aerodynamic sound source59.

Inspired by the broadband dipole sources generated by the disk’s rotation, combining the aerodynamic sound source of the rotating disk with AV generation is expected to address the challenge of reconciling device compactness and convenience with AV’s tunability. Here, based on the acoustic dipole sources generated from the surface of a rotating disk at low Mach numbers, we propose the tunable AV generation method through the interference of dipole sources at the angular frequency and its multiples. It eliminates the need for additional incident sources and waveguide conditions. The characteristics of the AV are explored through numerical simulation. Then, we verify it through experiments and further reveal the amplitude enhancement effect of the generated AVs on the sound field using both plain and roughened disks. Furthermore, we demonstrate the flexible tunability of AVs in working frequency and topological charge by controlling the disk rotation angular frequency. Finally, based on the properties found in the method, the application in the contactless detection of disk rotation information is explored. Our work will drive more related research and may open up perspectives for OAM-based technologies.

Results

Principle and model

In classical acoustics, sound waves are typically generated through the vibration of structures, such as plates, shells, and membranes. However, the sound generation mechanism of aerodynamic sound differs significantly. The Lighthill–Curle theory of aerodynamic sound addresses sound generation in free space and in the presence of static rigid boundaries. Ffowcs Williams and Hawkings extended Lighthill’s acoustic analogy to moving bodies, deriving the governing differential equation. For a rigid body in motion, let \(f(\overrightarrow{y},t)=0\) describe the surface of a moving body where f > 0 outside the body. The governing equation for the determination of the acoustic pressure p′ is the Ffowcs Williams–Hawkings (FW–H) equation59:

$$\frac{1}{{c}_{0}^{2}}\frac{{\partial }^{2}p^{\prime} }{\partial {t}^{2}}-{\nabla }^{2}p^{\prime} =\frac{\partial }{\partial t}\left[{\rho }_{0}{v}_{n}|\nabla f|\delta \left(f\right)\right]-\frac{\partial }{\partial {x}_{i}}\left[{l}_{i}|\nabla f|\delta \left(f\right)\right]-\frac{{\partial }^{2}}{\partial {x}_{i}{x}_{j}}\left[{T}_{ij}H\left(f\right)\right]$$
(1)

Where p′ is the acoustic pressure. ρ0 and c0 correspond to the mean fluid density in an undisturbed medium and the acoustic wave velocity, respectively. vn is the local normal velocity of the body surface, li is the force per unit area on the fluid at the surface of the body. The quantity li is equal to \({P}_{ij}{\hat{n}}_{j}\), where Pij is the compressive stress tensor that includes the surface pressure and viscous stress and \({\hat{n}}_{j}\) is the unit outward normal vector to the surface f = 0. The equation of the form f = 0 defines the surface S. The subscripts of i and j are indices of summation. The Dirac delta and the Heaviside functions are written as δ(f) and H(f) respectively.

The first two inhomogeneous source terms in Eq. 1 are absent in Lighthill’s theory, where the contribution from the remaining term \({\partial }^{2}[{T}_{ij}H(f)]/\partial {x}_{i}{x}_{j}\) represents quadrupole noise due to turbulence60. Tij is Lighthill’s tensor. The first term in the equation arises from the motion of the surface in the normal direction, acting as a monopole source term indicative of volume displacement. Each surface element functions as a small piston acting on the fluid at speed vn. The second term derives from the local surface stress Pij on the body’s surface, representing the net force acting on the fluid due to viscous stress and pressure distribution. It can also be understood as the surface distribution of acoustic dipoles with the intensity density \({P}_{ij}{\hat{n}}_{j}\). The source terms on the right-hand side of the FW-H equation are known as the thickness (monopole), loading (dipoles), and quadrupole terms, respectively61.

Since the disk we studied operates at low Mach numbers, we neglect the thickness and quadrupole source terms in the FW-H equation. These terms become important only for strongly transonic flow and high Mach numbers52,62. Under the above assumptions, the governing equation for the generation of the sound for a moving body is:

$$\frac{1}{{c}_{0}^{2}}\frac{{\partial }^{2}{p^{\prime} }_{L}}{\partial {t}^{2}}-{\nabla }^{2}{p^{\prime} }_{L}=\frac{\partial }{\partial {x}_{i}}\left[{l}_{i}|\nabla f|\delta \left(f\right)\right]$$
(2)

where \({p^{\prime} }_{L}\) denotes the acoustic pressure due to loading (the dipole terms). The solution for the acoustic pressure from Eq. 2 can be derived using the Green function and coordinate transformations.

$$4\pi {p^{\prime} }_{L}\left(\overrightarrow{x},t\right)=\frac{1}{{c}_{0}}\frac{\partial }{\partial t}{\int }_{\!\!\!\! f=0}{\left[\frac{{l}_{r}}{r(1-{M}_{r})}\right]}_{ret}dS+{\int }_{\!\!\!\! f=0}{\left[\frac{{l}_{r}}{{r}^{2}(1-{M}_{r})}\right]}_{ret}dS$$
(3)

where \({l}_{r}={l}_{i}{\hat{r}}_{i}\) is the force on the fluid per unit area in the radiation direction. \({M}_{r}={v}_{r}/{c}_{0}={v}_{i}{\hat{r}}_{i}/{c}_{0}\) is the Mach number in the radiation direction, which is a scalar. vi is the i-component of the surface velocity vector. \({\hat{r}}_{i}\) is the i-component of the unit vector \((\overrightarrow{x}-\overrightarrow{y})/r\), where \(r=|\overrightarrow{x}-\overrightarrow{y}|\). The vectors \(\overrightarrow{x}\) and \(\overrightarrow{y}\) are the source and observer positions, respectively. \(\tau\) and t are the source and observer time, respectively. The subscript ret denotes that the integrand is evaluated at the source or retarded time. Using \(g=\tau -t+r/{c}_{0}\) and the fact that r is a function of \(\tau\) gives

$${\frac{\partial }{\partial t}\Bigg|}_{\overrightarrow{x}}={\left(\frac{1}{1-{M}_{r}}{\frac{\partial }{\partial \tau }\Bigg|}_{\overrightarrow{x}}\right)}_{ret}$$
(4)

This relation allows the time derivation to be taken inside the first integral. Then by using the relations,

$$\begin{array}{c}\frac{\partial r}{\partial \tau }=-{v}_{r},\\ \frac{\partial {\hat{r}}_{i}}{\partial \tau }=\frac{{\hat{r}}_{i}{v}_{r}-{v}_{i}}{r},\\ \frac{\partial {M}_{r}}{\partial \tau }=\frac{1}{{c}_{0}r}\left({r}_{i}\frac{\partial {v}_{i}}{\partial \tau }+{v}_{r}^{2}-{v}^{2}\right),\\ \frac{\partial {v}_{n}}{\partial \tau }=\left(\frac{\partial {v}_{i}}{\partial \tau }{\hat{n}}_{i}+{v}_{i}\frac{\partial {\hat{n}}_{i}}{\partial \tau }\right)\equiv {\dot{v}}_{n}.\end{array}$$
(5)

The final result of the acoustic pressure due to loading is61

$$\begin{array}{c}4\pi {p^{\prime} }_{L}\left(\overrightarrow{x},t\right)=\frac{1}{{c}_{0}}{\int }_{f=0}{\left[\frac{{\dot{l}}_{i}{\hat{r}}_{i}}{r{(1-{M}_{r})}^{2}}\right]}_{ret}dS+{\int }_{f=0}{\left[\frac{{l}_{r}-{l}_{i}{M}_{i}}{{r}^{2}{(1-{M}_{r})}^{3}}\right]}_{ret}dS\\ +\frac{1}{{c}_{0}}{\int }_{f=0}{\left[\frac{{l}_{r}\left(r{\dot{M}}_{i}{\hat{r}}_{i}+{c}_{0}{M}_{r}-{c}_{0}{M}^{2}\right)}{{r}^{2}{(1-{M}_{r})}^{3}}\right]}_{ret}dS\end{array}$$
(6)

The dots on \({\dot{M}}_{i}\) and \({\dot{l}}_{i}\) indicate the rate of variation with respect to retarded time. The above equation is valid for arbitrary object motion and geometry. Near field and far field terms are seen explicitly as 1/r2 and 1/r terms in the integrals, respectively. Besides, dimensional analysis has been used to show the relationship between the acoustic power of the acoustic dipoles of a rotating object and its parameters, such as diameter and rotation rate63.

When we have the required parameters of the disk geometry, motion, and surface pressure distribution, this expression can be solved without being restricted by compactness or far-field assumptions. As shown in Fig. 1, our rotating disk model operates in free space with a 4 mm thickness and a 50 mm radius, controlling the rotational speed within a specified range to meet low tip Mach number requirements. The disk material is photosensitive resin with a Poisson’s ratio of 0.42, density of 1.12 g/cm3, and tensile modulus of 2589 MPa. We use the dipole sources distributed on the rotating disk surface to generate AVs in free space without introducing incident wave sources and waveguide conditions. By the interference of dipole sources at the angular rotation frequency and its multiples, the AVs with different topological charges generate at the corresponding frequency. In the following sections, we demonstrate this AV generation method through numerical solutions and experiments.

Fig. 1: Diagram of the working principle of the tunable acoustic vortex generation without introducing incident wave sources.
figure 1

The disk, rotating at Ω rad/s, generates tunable acoustic vortices through the interference of dipole sources formed by this rotating disk’s surface at the angular frequency and its multiples, resulting in acoustic vortices with different topological charges on both sides of the disk. The red spots represent arbitrary points on the disk surface, illustrating the distribution of acoustic dipoles.

Full size image

Numerical demonstration of the tunable acoustic vortex by rotating disk

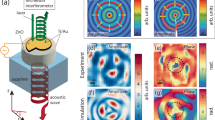
A hybrid numerical approach was used to analyze AV characteristics produced by the interference of dipole sources from a rotating disk operating at 417.8 rad/s. The simulation is run without monopole and quadrupole sources reasonably focusing only on the dipole sources from the disk’s surface. The disk surface is a smooth and rigid wall, eliminating the influence of disk vibration-generated sound waves on the sound field. The simulated phase and amplitude distribution at the cross sections z = 40 mm are illustrated in the first and second rows of Fig. 2a, respectively. The phase changes by 2π, 4π, 6π, and 8π at Ω/2π, 2Ω/2π, 3Ω/2π, and 4Ω/2π Hz, respectively (Ω = 417.8 rad/s), and the central region with near-zero amplitude gradually expanded. It shows that when the radiated frequencies of the dipole sources distributed on the surface of the disk match the disk’s rotational angular frequency and its multiples, the radiated acoustic fields of these dipole sources interfere and generate AV patterns with different topological charges. AV patterns with topological charge l = 1, 2, and 3 are generated at Ω/2π, 2Ω/2π, and 3Ω/2π Hz, respectively. Besides, as the AV working frequency increases, the region with the amplitude center close to zero gradually expands, while the amplitude maximum gradually decreases, and the overall acoustic radiant energy in the vortex plane weakens. For instance, in comparison to the first three-order AVs, the characteristics of the AV formed by interference at 4Ω/2π Hz (when the acoustic radiation frequency of the dipole sources is four times the rotational speed) are not obvious. The main manifestation is that the phase in the region with a smaller radius at the center no longer exhibits the transition from −π to +π, and correspondingly, the amplitude in the center region is no longer zero. In addition, the simulated amplitude contour of the high-order AVs (l = 3, 4) does not exhibit a good doughnut-shaped distribution. This is because the multi-order AVs with lower energy are more prone to diffuse in the free acoustic field.

Fig. 2: Numerical demonstration of the tunable acoustic vortex generation.
figure 2

a Summary of simulated phase (first line), and acoustic amplitude (second line) distributions of Ω/2π, 2Ω/2π, 3Ω/2π, and 4Ω/2π Hz at the cross-section z = 40 mm. b Amplitude–frequency spectrum (normalized with the corresponding maximums). The interference of dipole sources from the rotating disk surface will result in an amplitude enhancement at the working frequency of acoustic vortices, fworking = Ω/2π, 2Ω/2π, 3Ω/2π, and 4Ω/2π Hz. These frequencies correspond to the acoustic vortices pressure distributions for l = 1, 2, 3, and 4, respectively.

Full size image

To further explore the contribution of the generated AV to the acoustic field energy, the spectral characteristics of the AV distribution were analyzed (Fig. 2b). It can be observed that the AV pattern gives an amplitude enhancement at their working frequency, described by the equation

$${f}_{{{{{\rm{working}}}}}}=l{{\Omega}} /2\pi$$
(7)

where fworking is the AV’s working frequency. The sound pressure amplitude at these frequencies experiences significant enhancement. Consequently, the amplitude curve exhibits prominent peaks exclusively at frequencies corresponding to the occurrence of the AV interference pattern, with no discernible peaks present at other frequencies. Besides, the insets in Fig. 2b give the normalized AV acoustic pressure distributions for l = 1, 2, 3, and 4, respectively. From the acoustic pressure distribution (Fig. 2b), it is evident that a greater area proportion of the AV with pressure close to ±1 corresponds to a higher peak. For instance, at 4Ω/2π Hz, the green area with pressure close to 0 occupies most of the detection surface, resulting in the lowest peak at this frequency. Combining Figs. 2a and 2b, it shows that the sound pressure amplitude of each order of AV correlates with the height of the peak value at the corresponding order. For instance, the vortex strength formed by the interference at 4Ω/2π Hz is lower than that of the previous three orders, while the peak at this frequency is also at its lowest value compared to the previous three orders.

To further investigate the three-dimensional spatial distribution characteristics of AVs, we analyze the amplitude fields of the first-order AV at different cross-sections of z = 5, 25, and 50 mm (Fig. 3a). As the axial distance from the disk increases, the region of zero central acoustic pressure amplitude shows the tendency to expand outward, and the maximum amplitude decreases, resulting in an overall reduction in acoustic radiant energy. In Fig. 3b, the sound intensity vector diagram on the z = 25 section at Ω/2π Hz is given. The quantity of acoustic intensity can be calculated from the square of the normal particle velocity at the nodes of the elements. At the center, sound intensity is zero, exhibiting phase singularity characteristics with no directivity. Moving radially outward, sound intensity initially increases, then decreases, with its direction perpendicular to the radial direction. In addition, analyzing the phase, amplitude, and acoustic intensity fields on a three-dimensional spherical surface reveals that the first-order AV characteristics are still achieved on the hemisphere with r = 150 mm.

Fig. 3: Numerically simulated results.
figure 3

a Amplitude distribution of first-order acoustic vortex at z = 10, 25, 50 mm. The unit of sound pressure amplitude is Pa. b The phase, intensity, and amplitude distribution characteristics of the first-order acoustic vortex are presented on the R = 150 mm hemisphere. The sound intensity vector plot on the z = 25 cross-sections is also given.

Full size image

Experimental results

To further explore the AV characteristics using our method, we rotated the disk with a motor in a fully anechoic chamber environment and experimentally demonstrated the AV generation without disk resonance, as shown in the schematic diagram in Fig. 4. In more detail, Fig. 5a illustrates the experimentally measured phase and amplitude fields at z = 40 mm. It is evident that when the radiation frequency of the rotating dipole sources matches the rotational angular frequency or its multiples, AVs are generated through interference. At frequencies of Ω/2π, 2Ω/2π, and 3Ω/2π Hz, corresponding topological charges of 1, 2, and 3 were observed at the rotation speed of 417.8 rad/s (Fig. 5a). The generated AVs significantly enhance the sound field’s amplitude at their working frequency. Only at the frequency where the AV generates, a significant peak appears in the amplitude-frequency spectrum (Fig. 5b), and the working frequency satisfies Eq. 7. The insets reveal that when the frequency is 4Ω/2π Hz, the amplitude and phase fail to meet the criteria for AV characteristics, and consequently, no discernible peak is evident at this frequency.

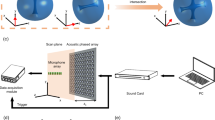
Fig. 4: Schematic diagram of the experimental setup.
figure 4

Sound pressure at a cross-section 40 mm from the front of the disk (z = 40 mm) was measured using two microphones. The center of the area detected by the microphone is coaxial with the center of the disk, differing only in the z-direction distance. Microphone 1 was kept stationary, fixed on a circle with a radius of 50 mm, and served as the phase reference. Microphone 2 was moved to 36 uniformly arranged points on circles with radii of 10, 20, 30, and 40 mm, along with one point at the center, for a total of 145 measurement points. The acoustic vortex phase distribution was determined by calculating the relative phases between microphone 1 and microphone 2 at each measurement point.

Full size image
Fig. 5: Experimental demonstration of the tunable acoustic vortex characteristics.
figure 5

a Summary of phase (first line), and acoustic amplitude (second line) distributions at z = 40 mm for Ω/2π, 2Ω/2π, and 3Ω/2π Hz. b Normalized experimental amplitude–frequency spectrum of the plain disk, and experimental phase and amplitude distributions at 4Ω/2π Hz. The experimental spectrum was tested at locations consistent with the simulation (z = 40 mm and R = 40 mm). c The bars depict the average of phase difference data. The phase value of each measurement for the stationary microphone 1 (Micro 1) is denoted by φ0. At 36 evenly spaced measurement points along the r = 30 mm circle, the phase value for the moving microphone 2 (Micro 2) is denoted as φi (i = 1, 2, 3…36), as shown in the insets. The relative phase value at the ith measurement point is expressed as ∆φi = (φ0 - φi). ∆δi = ∆φi+1 − ∆φi represents the difference in the relative phase between adjacent measuring points i and i + 1. \(\overline{\varDelta {{\phi }}_{i}}={\sum }_{i=1}^{36}\varDelta {\delta }_{i}/36\) represents the average of ∆δi. The value of \(\overline{\varDelta {{\phi }}_{i}}\) under the experiment is shown by the blue bars. The black line represents the variance of ∆δi (i = 1, 2, 3…36). The reference value (red bar) represents the value \(\overline{\varDelta {{\phi }}_{i}}\) under the ideal acoustic vortex phase distribution and is used for comparison with the experimentally generated acoustic vortex.

Full size image

The experimentally measured AV phase field combines the phase information from all measurement points on the detection plane. Each point’s phase value is calculated as the phase difference between the fixed Micro1 (served as a reference phase) and the moving Micro2 during the same measurement, which belongs to the relative phase. To further disclose the factors affecting AV in enhancing sound field amplitude, Fig. 5c illustrates the AV’s stability of various orders at their corresponding working frequencies. We assess their stability by examining the degree of fluctuation (variance) in the phase difference between adjacent measurement points. In our experimental setup, the phase at each measurement point is calculated as the phase difference between a fixed Micro1 and a moving Micro2. We denote φ0 as the phas8e value of each measurement of the fixed Micro1, while φi represents the phase values at the 36 detection points uniformly distributed on the r = 30 mm circle (i = 1, 2, 3…36). ∆φi = (φ0 - φi) represents the relative phase value at the ith measurement point, and ∆δi = ∆φi+1 − ∆φi = (φ0 − φi+1)  − (φ0 − φi) is the difference in relative phase between adjacent measuring points i and i + 1 (∆φ37 = ∆φ1).

For an ideal AV’s phase distribution, the ∆δi values for AVs with topological charges l = 1, 2, and 3 are 10°, 20°, and 30°, respectively (the angle between adjacent measuring points is 10°). These values serve as references to determine whether the AV is generated and its order. It is worth noting that the average value of ∆δi alone cannot indicate the deviation or proximity of the generated AV to the ideal AV. It should be assessed in conjunction with the variance. In Fig. 5c, the average values of ∆δi at Ω/2π, 2Ω/2π, and 3Ω/2π Hz across 36 measurement points are 9.8°, 19.7°, and 29.4°, respectively. These values closely match the reference ∆δi values for l = 1, 2, and 3, indicating the number of phase transitions from −π to +π in an annular loop. Besides, the variances of ∆δi are within 10°, with values of 0.79, 2.42, and 8.61 for these orders, respectively. Combined with the variance, we find that the average value of ∆δi is stable. It indicates that the measured phase closely aligns with the ideal acoustic vortex phase, confirming the successful generation of AVs.

In addition, variance is also an important indicator for measuring the stability of the generated AV. Comparing AVs with the first three-order topological charges, it is evident that smaller variance corresponds to higher amplitude values in the amplitude fields (Fig. 5a) and greater peak values in the spectrum curve (Fig. 5b). This means that the higher the AV stability, the more pronounced the enhanced amplitude effect on the energy of the sound field. For higher-order multiples of the angular frequency, such as 4Ω/2π Hz, the variance of phase differences ∆δi between adjacent measuring points at different detection positions is larger. Simultaneously, the average value \(\overline{\varDelta {{\phi }}_{i}}\) is close to zero, indicating a lack of vortex phase characteristics, as illustrated in Fig. 5b insets. Furthermore, at frequencies that are not multiples of the angular frequency, such as 5Ω/4π and 7Ω/4π Hz, the variances at each measurement point are more pronounced, and a phase distribution with AV phase characteristics cannot be generated in the detection plane. Consequently, no conspicuous peaks appear at these frequencies in the spectrum curve. In summary, AV generation through interference primarily occurs at the low-order multiples of the rotational angular frequency and has a significant enhancing effect on the sound field amplitude. The effect of enhancement is positively correlated with AV stability.

The experimental and simulation results exhibit consistent overall trends. The first difference is that the simulation still shows AV characteristics at 4Ω/2π Hz, corresponding to which there is also a peak at this frequency in the simulation frequency spectrum (Fig. 2b). The main reason for this difference is the simulation can replicate higher-order AVs in the ideal sound propagation environment. However, since the intensity and phase distribution of vortices will be affected by turbulence and change64,65, higher-order AVs with low radiated energy are more susceptible to impact during experimental detection. The rotation of the disk disrupts the initially orderly flow field, this affects the low-energy AV.

The second difference is that at the maximum amplitude in the AV detection plane, the simulation results (Fig. 2a) are lower than the experimental results (Fig. 5a). This is due to the hybrid method used to solve the aeroacoustic problem caused by the disk, which involves certain approximations and simplifications. For instance, SMM (sliding mesh method) technology is utilized in the flow field simulation to rotate the domain surrounding the disk, simulating its real rotation. In the sound field calculation, pressure loading information from the flow field calculation is approximated as sparsely distributed dipole sound sources on the disk surface, rather than directly calculating the entire surface as a dipole sound source. In addition, since the processing accuracy of the plain disk cannot ensure that the surface is smooth, there is a certain roughness compared to the simulation. These factors contribute to the amplitude difference between simulation and experiment to some extent. However, these differences are not critical to the main research goal of our work. Both experiments and simulations have consistently confirmed that AVs with different topological charges can be generated through the interference of dipole sources formed by a rotating disk at the angular rotation frequency and its multiples.

Tunable AVs generated by rotating a disk adhere to Eq. 7. To achieve AVs with different orders at the same frequency, an effective and direct way is to adjust the disk’s rotation angular frequency. In Fig. 6a, we experimented with three different rotation rates. At a disk rotation rate of 139.3 rad/s, AVs with l = 1, 2, and 3 appear at distinct peak frequencies (22.5, 44.5, and 66.5 Hz). The AV’s amplitude is reduced due to the reduced acoustic energy of the dipole produced at lower rotational speeds. Therefore, it cannot effectively mask the broadband noise produced by the disk’s rotation. We observe amplitude fluctuations across the entire frequency band at this rotation rate. At a rotation rate of 208.9 rad/s, different peak frequencies (33, 66.5, 99.5 Hz) correspond to AVs with l = 1, 2, and 3, respectively. Similarly, at 417.8 rad/s rotational rate, varying peak frequencies (66.5, 133, 199.5 Hz) correspond to AVs with topological charges l = 1, 2, and 3 (as depicted in Fig. 5a). It can be observed that at rotation rates of 139.3, 208.9, 417.8 rad/s, corresponding topological charges of 3, 2, and 1 were observed at 66.5 Hz (insets show the phase distribution of the AVs at 66.5 Hz).

Fig. 6: Acoustic vortex characteristics at different rotation rates.
figure 6

a The sonogram of the amplitude–frequency spectrum at different rates. At rotation rates of 139.3, 208.9, and 417.8 rad/s, corresponding topological charges of 3, 2, and 1 were observed at 66.5 Hz. b The mode purity distribution of generated l-order acoustic vortices (l = ±1, ±2, ±3) at different rotation rates.

Full size image

OAM theoretically has infinite dimensions, and AVs with different OAMs are orthogonal. When the AV’s order differs (l1 ≠ l2), their inner product equals zero, denoted as \({\int }_{0}^{2\pi }{e}^{i{l}_{1}\theta }({e}^{i{l}_{2}\theta })d\theta =0\). In the spatial dimension, this independence acts as an information channel, enabling the transmission of multiplexed signals and enhancing the capacity of the acoustic communication system. Figure 6b provides purity information within the AV order mode range from −3 to +3. The mode purity consistently exceeds 90%, indicating that the AV generated by interference has high purity and performs well. The purity definition and calculation can be found in the Methods.

To further enhance the energy of AV generated by this method, hemispheres with a height of 1 mm and a spacing of 7 mm are evenly arranged on the plain disk surface to increase roughness. Compared with the plain disk, the roughened disk enhances the aeroacoustic radiation energy of the dipole52, resulting in higher energy and higher order AVs (l = 1 to 5), as depicted in Fig. 7a. The difference between the results of the plain disk and roughened disk also shows that higher-order AVs with low radiated energy are more susceptible to impact during experimental detection. In addition, Fig. 7a displays the rotation noise amplitude spectrum of the motor without driving the disk. The amplitude is very weak compared to the amplitude generated by the driving disk, which excludes the influence of motor noise on this AV generation method. Figure 7b illustrates the relationship between the working frequency of the AV and the disk rotation rate, which satisfies Eq. 7. By measuring fworking and l, the rotation rate of the object can be measured using the formula \({f}_{{{{{\rm{working}}}}}}=l\varOmega /2\pi\). To enhance the robustness and accuracy of the detection, we can analyze multiple working frequencies associated with different topological charges. Furthermore, the alignment between the AV’s chiral direction and the disk’s steering direction enables the identification of disk steering information by detecting the positive and negative signs of the AV. As shown in the insets, both positive and negative first-order AVs are generated at 66.5 Hz, corresponding to +417.8 rad/s and −417.8 rad/s, respectively.

Fig. 7: Enhanced acoustic vortex energy and rotation information detection based on the rotating disk.
figure 7

a Using a roughened disk generates acoustic vortices with higher energy and higher order (Ω = 417.8 rad/s). Experimental amplitude-frequency spectrum of the roughened disk (red line), amplitude peaks of the plain disk at Ω/2π, 2Ω/2π, 3Ω/2π, 4Ω/2π, and 5Ω/2π Hz (blue point). Rotation noise amplitude spectrum of the motor without driving the disk (green line). The insets display the phase distributions for l = 4 and 5 generated by the roughened disk at frequencies of 4Ω/2π Hz and 5Ω/2π Hz, respectively. The experimental spectrum was tested at locations (z = 40 mm and R = 40 mm). b Detection of rotating information using acoustic vortex amplitude enhancement effect. Values of fworking were measured for different rotation rates and values of l, shown as square points, and were compared to the values predicted from Eq. 7, shown as solid lines. The color represents the values of l from −3 to +3.

Full size image

Discussion

In this work, we propose a method that combines aerodynamic dipole sources with AV generation. This method utilizes the interference of dipole sources from the rotating disk to generate AVs. It offers a compact and convenient approach, resolving the conflict between device compactness and the simultaneous tunability of topological charge and working frequency. It can be confirmed as follows. At low-tip Mach numbers, the broad-band sound is due to acoustic dipole sources from the turbulent-boundary-layer flow on the disk. The low-frequency spectrum results from a uniform distribution of acoustic dipoles over the disk surface52. The thickness and quadrupole source terms in the Ffowcs Williams and Hawkings equation can be neglected since they are important only for strongly transonic flow and high Mach numbers59,61. Therefore, in the simulation, we solve the radiation sound field in free space with only the surface dipole sources of the disk. We demonstrate the tunable AV generation method through the interference of dipole sources at the angular frequency and its multiples, verified through experiments. The agreement between simulation and experiment in the AV characteristics indicates that the simulation is run without monopole and quadrupole sources reasonably focusing only on the dipole sources from the disk’s surface. On the other hand, it is also confirmed that the AV generation depends on the interference of the dipole sources from the rotating disk surface along the propagation direction.

Furthermore, the generated AVs significantly enhance the amplitude of the sound field at its working frequency. The working frequency is equal to the product of the topological charge and the rotation angular frequency, satisfying \({f}_{{{{{\rm{working}}}}}}=l\varOmega /2\pi\). To further disclose the factors affecting AVs in enhancing sound field amplitude, Fig. 5 illustrates the stability of AVs of various orders with different acoustic radiation energy. Experimental results confirmed that the amplitude enhancement effect correlates positively with the AV’s stability, as well as the effectiveness of this method. Taking the first-order AV as an example, the maximum sound pressure amplitude of 0.346 Pa corresponds to a sound pressure level of 81 dB (Fig. 5a). This magnitude is comparable to the Mie resonances structure method34. Consequently, it can be observed that the AV tunability of working frequency and topological charge can be simultaneously achieved with a compactness and convenience model. Compared with current active and passive generation methods, the proposed method overcomes the challenge of balancing device compactness and convenience with flexible tunability in topological charge and working frequency. Our work also addresses the limitations of passive methods in generating low-frequency AVs. By controlling the rotation angular frequencies of the disk, multiple-order AVs can be achieved at the same frequency, with a mode purity exceeding 90%, as shown in Fig. 6. To further explore the spatial characteristics of AV, we demonstrated a first-order AV with spatial AV features on a three-dimensional spherical surface (Fig. 3b).

In addition, by measuring the working frequency and topological charge, the rotation rate and direction of the object can be detected according to Eq. 7. Moreover, the working frequency corresponding to different topological charge orders can be simultaneously analyzed for the detected target rotation speed, enhancing the robustness of rotation speed detection. This non-contact detection method eliminates the need for introducing additional incident AV, avoiding the impact of traditional methods on detection accuracy due to the slight misalignment22 of the incident vortex acoustic beam, the rotating object, and their relative radius size50. At the same time, there are challenges requiring further improvement and resolution. For instance, in acoustic communication applications, AVs diffract from the source in free space, posing challenges for long-distance use. It may also generate redundant orders of AV in multiplexing. Additionally, this method does not address the simultaneous generation of multiple orders at the same frequency. At present, the proposed method needs to be further explored underwater42 and is expected to make up for the shortcomings of some methods that are difficult to apply underwater, such as spiral phase plates and metamaterials. Besides, based on the fact that the dipole sources distributed on the rotating object can reflect its surface topography, the potential for tailoring object structures to achieve desired AV properties and the prospect of surface morphology identification by the analysis of AV fields deserve further research66,67.

In conclusion, the demonstrated method for generating AV enables more versatile characteristics, which provides a blueprint for numerous acoustic OAM-based applications, such as communication, biomedicine, and metrology.

Methods

Mode purity

The calculation of the mode purity by the spiral harmonic power of the different vortex modes is obtained by computing its projection into the spiral harmonics exp(imφ)68. Theoretically, the vortex modes of the AV are orthogonal to each other19, so the generated AV can be expressed as a sum of vortex modes

$${p}_{l}(r,\varphi ,z)={\sum }_{m=-\infty }^{\infty }{a}_{m}(r,z)\exp (im\varphi )/{(2\pi )}^{1/2}$$
(8)

where pl (r, φ, z) is the pressure distribution of the generated AV. The coefficient of the m-order vortex mode is

$${a}_{m}(r,z)=1/{(2\pi )}^{1/2}{\int }_{\!\!\!\! 0}^{2\pi }{p}_{l}(r,\varphi ,z)\exp (-im\varphi )d\varphi$$
(9)

By integrating in the radial direction, the m-order OAM spiral harmonic power Cm is obtained. |am(r, z)|2 represents the orthogonal intensities of pl (r, φ1, z) and pl* (r, φ2, z) over a radius of r (the symbol * denotes the complex conjugate of the corresponding variable), which is given by

$${C}_{m}= {\int }_{\!\!\!\! 0}^{{R}_{0}}{\left|{a}_{m}(r,z)\right|}^{2}rdr=\frac{1}{2\pi {\int }_{0}^{2\pi }{\int }_{0}^{2\pi }\exp [i(l-m)({\varphi }_{1}-{\varphi }_{2})]d{\varphi }_{1}d{\varphi }_{2}}\\ \times {\int }_{\!\!\!\! 0}^{\infty }{A}^{2}(l,r)rdr$$
(10)

where A(l, r) denotes the radial pressure distribution of a single acoustic vortex beam with acoustic vortex mode number l. The mode purity of the m-order vortex mode in the generated AV is represented by the ratio of its spiral harmonic power to the total power. Pm denotes the relative power of the mth OAM. Therefore, the mode purity is expressed as

$${P}_{m}=\frac{{C}_{m}}{{\sum }_{m=-\infty }^{\infty }{C}_{m}}$$
(11)

Numerical simulations

For simulating flow-induced sources from a rotating disk, a hybrid two-step approach is employed. The steady flow is simulated using the Reynolds-averaged Navier-Stokes approach with the SST k–ε turbulent model in FLUENT. Subsequently, unsteady calculations are initialized with the steady solution. It employs the Large Eddy Simulation turbulence model with the WALE subgrid-scale model and a boundary layer grid (y+ ≤ 1). The disk surface is a smooth and rigid wall, eliminating the influence of disk vibration-generated sound waves on the sound field. The disk rotation is modeled using a rotational mesh motion of a cylindrical mesh block, which encloses the disk geometry, while the surrounding mesh remains static. The total grid elements count is 4,409,868, with 1,942,991 elements in the rotational domain and 37,464 on the disk surface. The solution time step is set as 1e−4. When the pressure data of the monitoring points near the disk stabilized in the transient calculation, the pressure pulsation information on the disk surface began to be derived, with a total of 4000 steps. The maximum sound field solution frequency is 5000 Hz with a frequency resolution of △f = 2.5 Hz. In the second step, pressure fluctuations on the disk surface at all time steps are processed using LMS Virtual. Lab software to generate equivalent dipole acoustic sources. The finite element method is employed to calculate the dipole source generated by rotation at a predetermined speed, along with the sound field distribution.

Experiments

The disk is driven by a brushless DC motor, which maintains smooth operation at the set speed. This is achieved through the power supply, controller, and actuator, enabling functions like speed compensation, real-time monitoring, and speed adjustments. The working frequencies of the generated AVs are below the first resonant frequency of the disk. This avoids disk resonance during the experiment, thereby eliminating the influence of sound waves generated by disk vibration on the sound field. Sound pressure information in the z = 40 mm plane is detected using Micro1 and Micro2. Micro1 is fixed on a circle with a radius of 50 mm, serving as the reference sound pressure. There are 145 measuring points on the detection plane, including one at the center and 36 points equally spaced on circles at different radii (r = 10, 20, 30, 40 mm). Micro2 is used to complete measurements by moving to different points, with adjacent measuring points at the same radius set 10° apart. Micro 2 movement is facilitated by glass tubes, rotating cylinders, iron rods, and microphones (shown in Fig. 8). The distance between Micro 2 and the disk is adjusted by the axial movement of the iron rod. Inserting iron rods at different radii of the cylinder allows for changing the measuring radius of Micro 2. Rotating the cylinder adjusts the measurement angle of Micro 2, enabling control over its position within the entire detection plane. The instruments used include the B&K4958-A microphone, a data collector, and a sound card (MOTU 16 A). Due to limitations in the sound card MOTU 16 A’s packaging program, the measured sound pressure amplitude is presented as a relative value. However, this does not affect the observed characteristics of AV generation, such as working frequency and topological charge number. At the same time, the AV phase, obtained through the difference between micro 1 and micro 2 under the same measurement, remains unaffected by the absolute or relative value of the sound pressure amplitude. To obtain actual acoustic vortex radiation energy values, we utilized M + P Vibpilot-8 experimental equipment, which is capable of measuring sound pressure values directly. The results from both sets of equipment consistently demonstrate the generation rules for AVs, confirming that AVs with different topological charges can be generated through the interference of dipole sources formed by a rotating disk at its angular rotation frequency and its multiples.

Fig. 8: Experiment setups.
figure 8

Measurement of the modulated acoustic vortex in a fully anechoic chamber environment. The sound pressure data is obtained using two microphones (Micro), a data acquisition, a personal computer (PC), and a sound card. The disk is driven and controlled by a brushless direct current motor, power supply, controller, and actuator. The inset provides a partially enlarged view of the microphone detection process, scaled at 1:50.

Full size image

We Fourier-transformed the test data without compensating and noise-filtering the microphone response. During measurements, the computer simultaneously records sound pressure data from both Micro1 and Micro2 using the sound card and data acquisition. Fourier transform is applied to obtain sound pressure amplitude and phase information at each measuring point. The amplitude field data on the detection plane comes from Micro2, while the phase field data is calculated as the phase difference between Micro2 and the reference Micro1. We used linear interpolation to draw the AV amplitude and phase based on data from 145 measuring points in the detection plane. This process allows for the detection of AVs generated by the rotating disk. Besides, the phase transition from π to −π does not go directly from red to blue, resulting in a phase regression artifact (Fig. 5a). This is the result of the low resolution (36 phase data are detected equidistantly in one circle) and the use of linear interpolation during the experiment.