Introduction

Group living is widespread in the natural world1 and confers many advantages to individuals, such as increased survival from predators2,3, enhanced foraging efficiency4,5, or improved communication and decision making6,7. Yet, it also plays a key role in the transmission of diseases and genetic traits8,9. The formation, maintenance, and disbanding of groups depend not only on the interactions among individuals but also on the characteristics of the surrounding environment, such as its spatial or temporal heterogeneity10. For instance, while large group sizes are advantageous for foraging in homogeneous environments, the presence of a patchy landscape of resources compels individuals to adopt smaller group formations as an adaptive strategy to ensure sufficient resources for all members11,12.

Recently, active colloids have emerged as a useful tool for studying collective behaviour in living matter13,14. These artificial systems, unlike natural ones15,16,17, have the advantage of evolving on short timescales. Moreover, they are tuneable, and their small sizes make data acquisition more convenient. Previous studies have investigated the role of the interaction among individual active colloids in group formation, such as those due to attraction18,19,20, repulsion21, alignment22,23, reorientation24,25, or perception26,27 and communication28,29. The role of physical features in the environment on group formation has also been explored, such as the presence of obstacles30,31,32,33,34,35 or of a disordered confining potential36. Although it is the key environmental factor shaping group dynamics in living matter10, the influence of a heterogeneous distribution of resources on collective phenomena is not yet fully understood. Indeed, while work exists that studied the effects of a linear gradient in the energy source of active colloids37,38,39, real-world landscapes of resources hardly follow linear gradients and the impact of complex energy distributions on group dynamics is largely unknown.

Here, we use phototactic active colloids moving in a spatially complex distribution of resources, generated optically, to investigate the role of patchy landscapes in the dynamics of group formation and cohesion. Our findings demonstrate a non-monotonic relationship between patch size and group dynamics; specifically, we observed that groups become smaller and more stable when the patchiness of the energy landscape is comparable to the size of the particles.

Results

Individual dynamics

As phototactic active particles, we used monodispersed silica colloids (diameter d = 4.77 ± 0.20 μm) half-coated with a 90 nm carbon layer (Methods). These particles self-propel in a water–2,6–lutidine critical mixture when exposed to light. The propulsion arises from the critical mixture’s local demixing, induced by the carbon heating upon light absorption21,37,38,39,40,41,42.

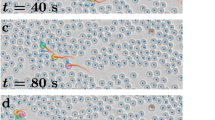
We created a complex two-dimensional energy source landscape with controllable spatial heterogeneity by shining a laser on an optical diffuser, generating a diffraction pattern of randomly distributed light patches. Known as speckle pattern, the intensity of these light patches follows a negative exponential probability distribution43,44. The energy density of the landscape and the typical size of its patches (σe) can be precisely controlled by optical means–Supplementary Fig. 1 and Methods for details. σe is defined as the full width at half maximum of the landscape’s autocorrelation. Figure 1a shows a typical example of a particle trajectory in a complex illumination. What can be qualitatively observed is that an active particle tends to navigate in the energy landscape by spending most of its time in the low-illumination areas–in other words, it performs negative phototaxis. This property of the individual trajectories has a direct consequence on group formation, with a group being defined as a collection of more than two particles in contact. As shown in Fig. 1b, in a heterogeneous energy landscape (σe ≈ d), active particles tend to form smaller groups compared to the case of a homogeneous illumination (σe → ∞). Under both illumination conditions, the average local power density (I = 0.1 μWμm−2) was kept the same by matching the incoming power and envelope size Supplementary Fig. 2.

Fig. 1: Active particles in complex energy landscapes.
figure 1

a Trajectory of an active particle in a spatially complex distribution of energy, with high light intensities in green. The particle self-propels, avoiding the most intense illumination. The trajectory displays the particle’s centre position over 50 minutes. b, c As the particles prefer to stay in the dark areas, the group size appears to be determined by the spatial characteristics of the environment--σe, i.e. the average size of the energy patches. Groups are smaller when the patchiness of the environment is comparable to the particles' dimensions than in homogeneous environments, as shown in b and c, respectively. Particles in groups (more than two individuals) are coloured pink, while isolated particles and pairs are grey.

Full size image

In order to explain the collective behaviours illustrated in Fig. 1, we first need to better understand the statistics of the dynamics of the individual particles on the underlying energy landscape. Figure 2a shows quantitatively that particles perform negative phototaxis. By comparing the light intensity at locations visited by the particles along their trajectories with the overall distribution of the energy landscape, we can observe that particles tend to avoid the most intense light regions. Delving deeper, Fig. 2b shows that as active particles navigate the darker, low-energy channels of the light landscape, they tend to align perpendicular to the light intensity gradient. This is due to their continuous interactions with the two-dimensional gradient, channelling their trajectories between high-energy patches and causing them to move perpendicular to the gradient–i.e. along low-intensity areas. This is evidenced by the emergence of a peak at an angle α = π/2 in Fig. 2b. Here, α represents the angle between the particle’s instantaneous velocity and the local intensity gradient, as illustrated in the inset of Fig. 2b. This result goes beyond previous observations in one-dimensional light gradients, which associated α = π (α = 0) with negative (positive) phototaxis39.

Fig. 2: Statistics of single particle trajectories on a complex two-dimensional energy landscape.
figure 2

A complex two-dimensional energy landscape (σe = 5 μm) affects the particles' spatial occupancy and motion dynamics. a Histogram comparing the distribution of the light intensity in the locations visited by the particles with the intensity distribution of the energy landscape. b Particles tend to move perpendicular to the gradient of the illumination (α = π/2). α, illustrated in the inset, is the angle between the velocity of the particle (v) and the intensity gradient (∇I). Scalebar = 5 μm. c A lower mean squared displacement (〈Δr2〉) for σe = 5 μm reflects avoidance of high-energy areas compared to a more homogeneous environment (Gaussian illumination, σe → ∞). The inset shows the long-time diffusive behaviour. Shaded areas indicate standard deviations on the mean squared displacement. Data was obtained from averaging at least 20 trajectories, each lasting 45 min.

Full size image

A complex energy landscape determines not only the preferential orientation of the active colloids but also their speed, with a decrease in average value from 0.095 ± 0.012 μms−1 in a homogeneous illumination to 0.068 ± 0.005 μms−1 in a landscape with σe = 5 μm (Supplementary Fig. 3). Both in homogeneous energy landscapes37,38 and in one-dimensional light gradients39 a linear increase of the velocity with the light intensity was observed after a given activation energy. This is also reproduced in two-dimensional gradients when the illumination has a Gaussian profile (σe → ∞ in Supplementary Fig. 3a). In this case, the local value of the gradient is relatively low, making it comparable to the previously reported linear cases also in terms of particles’ orientation with respect to the gradient (α = π in Supplementary Fig. 4a), and the observed migration towards the outer region of the illumination (σe → ∞ in Fig. 3b)37,38,39. However, when the heterogeneity of the landscape is comparable to the size of the particles (σe = 5 μm in Supplementary Fig. 3b) the velocity shows a less marked increase with the light intensity. This results from local values of the light gradient which are much stronger than in the previous cases (Supplementary Fig. 3b,d). Active particles do indeed experience an aligning torque proportional to the light gradient37,38,39, which, in turn, is proportional to the local light intensity. The aligning torque is a consequence of breaking the axial symmetry of the velocity field around the particle45 and it forces the colloids to change direction and reduce speed near high-energy regions, as evidenced by the decrease of the speed in function of the gradient seen in Supplementary Fig. 3b, d. This torque-induced reorientation and avoidance of high-energy zones reduce the mean squared displacement of active particles in a complex landscape when compared to a Gaussian illumination, as seen in Fig. 2c. Specifically, the torque decreases the mean squared displacement at intermediate times as colloids are forced to stay in the low-energy regions and at long times as it limits the available space they can explore. The mean squared displacement, despite the decrease, exhibits a superdiffusive transition followed by a long-time return to diffusion in both scenarios, as for typical active colloids14. However, the long-time diffusion coefficient decreases from 2.45 ± 0.09 μm2s−1 to 1.14 ± 0.04 μm2s−1 when moving from a homogeneous to a complex energy landscape.

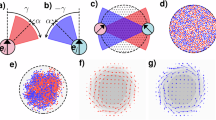
Fig. 3: Modelling the dynamics of active particles in complex energy landscapes.
figure 3

A torque and spatial heterogeneities in the energy landscape determine the dynamics of the active particles. Simulated trajectories (in pink) of individual active particles with (a) different torque values (Ω) for a fixed σe = 5 μm, and (b) environment heterogeneity (σe) for a fixed Ω = 6. c In a complex environment (σe = 5 μm), increasing the torque causes the particles to avoid high-energy areas. d In the presence of a torque, particles move more perpendicular to the gradient (α = π/2). e The difference in the effective diffusion coefficients between complex and Gaussian illuminations observed in the experiments is most accurately described by Ω = 0.6. f Role of the heterogeneity of the energy landscape (σe) on the effective diffusion coefficient (Deff(σe)) for a fixed value of the torque (Ω = 0.6). The effective diffusion coefficient, normalised to its value for a Gaussian illumination, is minimised when the spatial variation of the landscape is comparable to the size of the particles. In e, f, the standard deviation of the data matches the scatter point size. All simulations averaged 150 particles over 50 min each.

Full size image

To disentangle the role of the torque (represented by the dimensionless parameter Ω, Fig. 3a) exerted by the field gradient and the heterogeneity of the energy landscape (σe, Fig. 3b) on the microscale dynamics, we employed a particle-based model that includes an aligning torque proportional to the gradient of the optical field (Methods)37,38,39. Figure 3c confirms how the presence of a torque prevents particles from accessing the high energy regions, with a cutoff in energy that decreases as the torque increases. The emergence of this behaviour coincides also with a preferential orientation of the particles’ velocity perpendicular to the gradient of the illumination, whereas at Ω = 0 the orientation shows a relatively weak dependence on the gradient (Fig. 3d). Our model further validates that under a two-dimensional Gaussian illumination, the preferred orientation relative to the gradient (α = π in Supplementary Fig. 4b) is governed by the effect of the torque. Additionally, as depicted in Fig. 3e, the discrepancy in the long-term behaviour of the mean squared displacement between σe = 5 μm and σe → ∞ in Fig. 2 can be attributed to the torque. In a complex illumination, an increase in torque restricts access to regions of higher energy, thereby reducing the mean squared displacement.

The mean squared displacement also depends on the spatial heterogeneity of the environment, as shown in Fig. 3f in terms of effective diffusion coefficient at a fixed value of torque (Ω = 0.6). In particular, Fig. 3f shows that when σe is on a similar length scale to the particle size, it significantly reduces the long-time diffusion coefficient. In contrast, in the asymptotic scenarios where energy variations occur on scales significantly smaller or larger than the particle size, the differences in long-term diffusivity become less pronounced. This effect is because when light patches are much larger than the particles, the energy landscape appears homogeneous to them. Similarly, when variations are much smaller, particles cannot resolve the spatial complexity of the environment and perceive an averaged field. This maximises the interaction with the environment when variations align with particle size.

Group formation

To study the impact of the differences in individual trajectories on the collective behaviour of active systems we performed experiments with a higher concentration of particles ( ≈ 4%, compared to ≈ 0.1% in Fig. 2). When the concentration of active particles increases, they are more likely to collide with each other, slowing down and forming groups. A group lasts until the propulsion direction of one of the individuals points outside the cluster and its speed is such that it can escape the group by winning over the short-range attraction among particles20,21.

A heterogeneous energy landscape plays a key role in the formation of groups. As illustrated in Fig. 4a, particles tend to aggregate, and eventually separate, in the dark regions of the optical landscape where their motility is lower. In complex energy landscapes, groups exhibit greater durability, with the average rate of aggregation and fragmentation events minimised when the spatial heterogeneity matches the individual particle scale (Fig. 4b). The torque does indeed play a dual role in group dynamics. Firstly, it makes encounters between individuals more difficult by causing particles to linger in low energy regions for longer periods of time, which reduces the rate of aggregation. Secondly, once groups have formed, the torque orients particles toward areas of low energy, causing them to face inward the cluster and reducing the likelihood of fragmentation. The role of the torque is further confirmed by Supplementary Fig. 5a, where decreasing it leads to (i) an overall increase of the rates and ii) a smaller difference in rates between homogeneous and complex energy landscapes.

Fig. 4: Group formation analysis.
figure 4

Comparison of group formation in energy landscapes with different spatial characteristics, i.e. different sizes of the energy patches (σe). a Experimental trajectories showing an example of group aggregation and fragmentation in a complex landscape with σe = 5 μm, with the start marked by a filled circle and the end by a transparent one. When the patchiness of the landscape is comparable to the dimension of the particles, it reduces both the rate of individual exchange between them and the group size, b, c, respectively. In both panels of c, the insets show the distribution of sizes for different spatial heterogeneities. In b, the error bars represent the standard deviation of the data.

Full size image

The patchiness of the landscape also has a significant impact on group size, as demonstrated in Fig. 4c and Supplementary Video 1 and 2 for experiments and simulations, respectively. As individuals tend to avoid high energy regions, groups tend to grow until they fill the space confined between adjacent high-energy patches. The data presented in Fig. 4c support this qualitative relationship, revealing that complex energy landscapes with heterogeneity comparable to the particle size lead to a reduction in the group dimension. The interplay between the dimension of the energy patches and the group size is strongly influenced by the torque exerted by the gradient of resources. Decreasing the torque provides colloids with more freedom to move, enabling larger groups to form, as depicted in Supplementary Fig. 5a, b.

Notably, the differences in group dynamics depicted in Fig. 4 cannot be solely attributed to a lower average motility of active particles in complex landscapes–as depicted in Fig. 2 and Supplementary Fig. 3 in terms of the dynamics of individual colloids. Even when the mean squared displacement in a homogeneous energy landscape is reduced to match that in patchy ones (as shown in Supplementary Fig. 5c, d), disparities persist in both group dimension and stability. This further demonstrates that the spatial complexity of the energy landscape plays a critical role in shaping group dynamics.

Finally, the results presented in Fig. 4 are not restricted to disordered environments. In particular, they do not depend on the details of the spatial distribution of energy sources, but rather on its characteristic length. As shown in Supplementary Fig. 6, the collective behaviour of active colloids in periodically-distributed energy patches shows the same trends in function of σe of Fig. 4, both in terms of size and stability of groups.

Conclusion

In summary, we studied the effect of heterogeneous energy landscapes on the dynamics of group formation in active particles by leveraging optical tools. We found that by manipulating the spatial complexity of the landscape, we can control the size of groups and the exchange of individuals between them. Our results could open avenues in understanding the dynamics of active matter systems in resource-limited settings. In austere resource conditions (e.g., patchy environments), smaller groups may optimise the use of resources, yet their augmented stability and diminished individual exchange could potentially impede the flow of information among groups. Depending on the task at end, this could prove detrimental (e.g. in swarms of communicating robots46,47 and stigmergic systems35,48) or beneficial (e.g. to curtail the transmission of diseases in biological active matter49). As our experimental approach provides a versatile and precise method to modulate the spatial dynamics of the energy landscape using light, it could be instrumental in studying search strategies in the presence of limited resources. Its applicability could span various contexts, ranging from animal foraging, to guiding robots through complex search-and-rescue missions, to testing crowd escape dynamics, and refining colloidal self-assembly.

Methods

Materials

Glass capillaries were purchased from CM Scientific (5005-050 and 5001-050 for single particle and cluster experiments, respectively). The lutidine was purchased and used as received: 2,6-lutidine (≥99%, Sigma-Aldrich). Deionised (DI) water (≥18 MΩ ⋅ cm) was collected from a Milli-Q purification system. Aqueous colloidal dispersions (5% w/v) of silica (SiO2) colloids, used for sample preparation, were purchased from Microparticles GmbH. Additionally, carbon rods measuring 300 mm in length and 6.15 mm in diameter were procured from Agar Scientific and subsequently cut to a length of 50 mm and tapered for the coating of Janus particles through sputtering.

Particles fabrication

Janus particles were synthesised from SiO2 colloids with a diameter of d = 4.77 ± 0.20 μm. Initially, a monolayer of colloids was deposited on a clean glass slide by evaporating a 40 μL droplet containing a 2.5% w/v dispersion of the colloids in DI water. Subsequently, an automatic carbon coater (AGB7367A, Agar Scientific) was employed to coat the particles with a 90 nm thick layer of carbon. The thickness of the carbon layer was confirmed through atomic force microscopy (AFM) measurements. After coating, sonication was performed to dislodge the half-coated particles in DI water from the glass slide, facilitating their use for sample preparation. To reduce the interaction between particles, and the sticking of the particles to the substrate, the Janus colloids were functionalised with bovine serum albumin (BSA, Sigma Aldrich). This was done by replacing the water solvent of the colloidal suspension with a 1%w/v water solution of BSA. Prior to utilisation, the colloidal dispersions underwent centrifugation at 1000 relative centrifugal force (RCF) for 3 min, resulting in the formation of a pellet. The supernatant was subsequently discarded and replaced with a solution containing 28.6% w/v of water and 2,6-lutidine. This purification procedure was repeated three times to ensure the removal of any remaining BSA water solution from the original dispersion.

Sample preparation

In single-particle experiments (Figs. 1 and 2), a suspension of Janus particles was confined in a rectangular capillary with a width of 500 μm, a length of 50 mm, and a thickness of 50 μm. The capillary was then sealed by applying a UV-curable glue to avoid evaporation and drifts. In the multiple-particles systems (Fig. 4), we reduced the sample’s thickness by using a capillary with a width of 100 μm, a length of 50 mm, and a thickness of 10 μm. The reduced thickness mitigates potential convection effects that could arise from a higher number of particles, leading to increased heating.

Experimental setup

Supplementary Fig. 1 shows a schematic of the experimental setup. A laser (Oxxius 532 nm, 300 mW of maximum output power) and a diffuser (1°, Newport 10DKIT-C1) are used to illuminate the Janus particles with a random optical field, also known as speckle. The laser is directed to the sample via two mirrors (M1, M2) and a 4f-lens configuration (L1=L2, Thorlabs, LA1461-A-ML, f = 250 mm) illuminating the back aperture of a 10x objective (Nikon, N10X-PF, NA = 0.3). By changing the position of the diffuser and that of the sample, it is possible to control both the dimension of the speckle grains and the size of the illumination envelope. To create a Gaussian illumination, we removed the diffuser and one lens (L1) to image the beam on the sample. The illumination envelope was fixed to be close to the acquisition area of the camera (≈200 × 200 μm2 and ≈100 × 100 μm2 in the single and multiple particles experiments, respectively) and it was kept the same for different patchiness of the landscape (Supplementary Fig. 2). The intensity of the laser–controlled by a half-waveplate (FOCtek, WPF212H) and a polarising beam splitter (FOCtek, BSC1204) was then adjusted to have a comparable energy density in the different optical landscapes, i.e. different values of σe. The active particles were imaged with a 20x objective (Nikon, N20X-PF, NA = 0.5) and a tube lens (L3, Thorlabs, LA1805-A-ML, f = 30 mm) on a camera (Basler, acA5472-17 μm). A white LED (Thorlabs, MWWHF2), for simplicity not depicted in Supplementary Fig. 1, coupled to a fibre (Thorlabs, M28L01) is used for imaging. The particles’ dynamics were analysed by reconstructing their trajectories from videos (typically of the duration of 50 min at 2 frames per second) using a homemade code based on the python package Trackpy50,51. The position of the sample was controlled in three dimensions using an xyz-stage (Thorlabs, RB13M/M). The z-coordinate was adjusted with a stepper motor (Thorlabs, ZFS25B). For all experiments, the suspension of Janus particles was kept close to the critical temperature of the water-lutidine mixture (\({T}_{\exp }\simeq 3{1}^{\circ }{{{{{{\rm{C}}}}}}},\Delta T\simeq {3}^{\circ }{{{{{{\rm{C}}}}}}}\)) by a heater driven via a temperature controller (Thorlabs, HT19R and TC200, respectively).

Numerical model

We numerically implemented an Euler-Maruyama time integrator for the evolution of the positions ri and orientations ϕi of each particle i in two dimensions, defined by the following equations, based on ref. 39:

$${\dot{{{{{{{\bf{r}}}}}}}}}_{i}(t)=v({{{{{{{\bf{r}}}}}}}}_{i}){{{{{{{\bf{n}}}}}}}}_{i}-\frac{1}{{\gamma }^{{\prime} }}{{\sum}_{j\ne i}}\nabla V\left(\left\vert {{{{{{{\bf{r}}}}}}}}_{i}-{{{{{{{\bf{r}}}}}}}}_{j}\right\vert \right)+\sqrt{2D}{{{{{{{\boldsymbol{\xi }}}}}}}}_{i}(t),$$
(1)
$${\dot{\phi }}_{i}(t)=\omega ({\phi }_{i},{{{{{{{\bf{r}}}}}}}}_{i})+\sqrt{2{D}_{r}}{\xi }_{i}^{\phi }(t),$$
(2)

where \({{{{{{{\bf{n}}}}}}}}_{i}=(\cos (\phi ),\sin (\phi )),{{{{{{{\boldsymbol{\xi }}}}}}}}_{i}\) and \({\xi }_{i}^{\phi }\) represent Gaussian white noise. The translational and rotational diffusion coefficients D and Dr are defined as

$$D=\frac{{k}_{B}T}{{\gamma }^{{\prime} }},\quad {D}_{{{{{{{\rm{r}}}}}}}}=\frac{{k}_{B}T}{{\beta }^{{\prime} }},$$
(3)

where \({\gamma }^{{\prime} }=\frac{16}{3}\pi \eta d\) and \({\beta }^{{\prime} }=\frac{8}{7}\pi \eta {d}^{3}\) are respectively the translational and rotational friction coefficient, corrected by taking into account a distance from the substrate s = d/235, and η = 2.1 × 10−3 Pa s is the viscosity of water-lutidine. The torque ω, which is defined as:

$$\omega ({\phi }_{i},{{{{{{{\bf{r}}}}}}}}_{i})=\frac{\Omega d}{D}v({{{{{{{\bf{r}}}}}}}}_{i})\left[\nabla v({{{{{{{\bf{r}}}}}}}}_{i})\times {{{{{{{\bf{n}}}}}}}}_{i}\right]\cdot {\hat{e}}_{z},$$
(4)

where the adimensional prefactor Ω determines whether the torque steers the particle towards the light (Ω < 0) or away from it (Ω > 0). The value of Ω that best fits the experimental change in the long-time mean squared displacement is Ω = 0.6 (Fig. 3e). V is a 6–12 Lennard-Jones potential with cutoff distance at five colloid diameters d and depth ϵ ≃ 8kBT. This value was chosen by fitting the experimental cluster aggregation and fragmentation rates for a Gaussian illumination. The intensity speckle field was generated by adding a Gaussian envelope to a scaled Fourier transform of a white noise map to match the specific characteristics of the optical fields in experiments: average intensity per unit of area and grain size. This intensity field was then translated into a motility field using the results from39. The gradient of the motility field acting on the particle \(\nabla v({\vec{r}}_{i})\) was averaged over the square area where the particle is inscribed. Regarding the periodic landscapes discussed in Supplementary Fig. 6, they were generated as a grid pattern with a distance between energy sources of 2σe, with each energy sources having a Gaussian distribution profile of width σe. This sets the average extension of the dark regions to be comparable with the size of the energy sources and with σe–therefore characterising the periodic environment with a single length scale. Note that in the case of a speckle field, the environment is fully-characterised by σe, as the size of the dark (low-energy) regions is directly comparable with the grain size.

Cluster analysis

We defined the clusters by measuring all distances among particles and then creating bonds between all the particles with distances smaller than the cutoff radius 1.25d. Similarly to refs. 20,35, clusters made of 2 particles (i.e. dimers) were disregarded in the analysis as they are unstable in time. We determined whether a cluster survives from one timestep to the next by confronting its particles with those of all the clusters in the next timestep. We consider any of these clusters to be the same as a previous one if it satisfies two properties: (i) that more than half of its particles are shared with the old cluster (i.e. the cluster has not decreased more than half in size); (ii) that at least half of the particles of the new cluster are also present in the old one, i.e. the cluster has not grown more than double in size. We calculated mainly two properties regarding clusters for each experiment: the cluster size and the monomer acquisition/loss rate. The first is simply the average number of monomers for each cluster, while the second is defined as the number of monomer acquisition/loss events (i.e. the number of times clusters receive/lose a single monomer during the experiment) normalised by the total experiment time and the average number of particles.