Introduction

Iron oxides have been extensively investigated at extreme conditions as they are fundamentally important materials for geoscience, physics and applied technologies1,2,3,4,5,6,7. Wüstite (Fe1-xO) is of great interest to solid-state physics and chemistry because of its electrical, magnetic, structural, and non-stoichiometric properties. As a member of transition metal monoxides, the high-pressure and high-temperature behavior of Fe1-xO will provide insight into the properties of other transition metal monoxides (CoO, NiO). Its high-pressure and high-temperature behavior is also important for Earth sciences, because Fe1-xO is considered to be one of the main iron-bearing phases in the lower mantle as a component of (Mg,Fe)O. Although chemically very simple, Fe1-xO is known to undergo a series of structural, electronic, and magnetic transformations at high pressures and high temperatures8,9,10,11,12,13,14,15,16,17,18,19,20.

Fe1-xO is a paramagnetic insulator with NaCl structure (B1, Fm\(\bar{3}\)m) at ambient conditions and undergoes a magnetic ordering transition at around 190 K with concomitant structural distortion to a rhombohedral structure (rB1)21. For nearly stoichiometric wüstite, cooling down to 10 K results in a distortion to a monoclinic C2/m structure22. Upon compression at room temperature, Fe1-xO transforms to the rB1 phase at 17-25 GPa23, which is the same as the rhombohedral structure observed at low temperatures. However, its behavior at higher pressures is still contradictory. A further phase transition from the rB1 to a hexagonal B8 phase (P63/mmc) has been proposed upon heating above 70 GPa8,10,17,24. On the other hand, Kantor et al. revealed a monoclinic Fe1-xO with P21/m space group at 80 GPa after heating at ~ 2000 K by quasi-single crystal X-ray diffraction13. Computational predictions for Fe1-xO also suggested that rB1 Fe1-xO is not stable above 65 GPa and should transform to either a trigonal phase with P3221 space group9,25 or a monoclinic phase with C2/m space group26.

The electronic and magnetic properties of Fe1-xO have been investigated by X-ray emission spectroscopy18 and Mössbauer spectroscopy11,16 up to 200 GPa. The B1 to rB1 phase transition, similarly to that transition at low temperature, is accompanied by the emergence of the long-range magnetic ordering. The antiferromagnetic ordering in Fe1-xO was also reported in the B1 phase at around 5 GPa11, indicating the magnetoelastic coupling may not be a key factor driving cubic-to- rhombohedral phase transition in Fe1-xO. With increasing pressure, X-ray emission spectroscopy shows that Fe1-xO remains in the high-spin state up to 143 GPa18. First-principles computations also predict that the collapse in the magnetic state of Fe1-xO occurs above 200 GPa8. On the other hand, Mössbauer spectroscopy studies locate the onset of the spin crossover at around 90 GPa16,27. The reported pressure dependence of Néel temperature, TN, of Fe1-xO is also contradictory. For instance, Badro et al. argued that Fe1-xO has a maximum TN(~420 K) at ~50 GPa18, while Kantor et al. reported a monotonic increase of the TN with pressure, with a much higher TN, ~ 1100 K at 50 GPa28.

The observed controversies are further complicated by the non-stoichiometric nature of Fe1-xO which contains Fe2+ sublattice vacancies, together with Fe3+ ions present on interstitial sites of the cubic phase. The latter tend to form clusters with the Fe2+ vacancies29,30, and the clusters can greatly influence the properties of Fe1-xO, such as the B1 to rB1 phase transition pressure31, the bulk magnetic structure29,32 and the order-disorder transition below its melting temperature19. In addition, it has been suggested that pressure can tune the Fe3+/ΣFe ratio and, consequently, the stoichiometry that further complicates the picture14.

To solve the abovementioned contradictions, we have conducted a systematic study of the structural transitions, electronic and magnetic properties of Fe1-xO by mean of complementary methods of powder and single crystal X-ray diffraction (XRD) and synchrotron Mössbauer source (SMS) spectroscopy in resistive- and laser-heating diamond anvil cells (DACs) up to ~94 GPa and ~1700 K (Fig. 1). We investigated pressure-temperature conditions for the formation of the rhombohedral and monoclinic high-pressure phases of Fe0.94O, as well as their TN and spin transition pressure.

Fig. 1: Magnetic and structural transitions in the Fe0.94O system.
figure 1

The blue solid line represents boundaries between the paramagnetic phases and phases with long-ranged magnetic ordering based on the synchrotron Mössbauer source spectra from this study. Below 40 GPa, the boundary overlaps with the rB1 to B1 phase transition boundary. Blue circles represent phases with long-range magnetic ordering. Gray circles represent paramagnetic phases. Red circles represent phases with the presence of the charge-transfer Fe2.5+ component. Fe0.94O undergoes a phase transition from the rB1 to the monoclinic phase (mC4-model) at ~ 39 GPa and room temperature with no detectable changes in the magnetic properties. Black dash lines show the high-pressure and high-temperature phase diagram of Fe1-xO based on the data from refs. 10,17. The color gradients present the uncertainty of the phase boundary from our data. The magnetic phase boundaries proposed by refs. 18,28. are also presented as short-dashed and dotted lines. In contrast to previous reports10,17, the B8 phase was not observed in our study. The error bars of the pressure and the temperature arise from the pressure change during the measurement and the estimated standard deviations of fittings, respectively. The error bars are smaller than the symbol size if not shown.

Full size image

Results

High-pressure X-ray diffraction

In situ high-pressure single-crystal and powder XRD measurements were conducted up to ~ 78 GPa at room temperature. The volumes of Fe0.94O per formula unit as a function of pressure are plotted in Fig. 2 for all observed phases. All source data in the main figures have been uploaded as Supplementary Data 1. The refined unit-cell parameters and structural details of different phases of Fe0.94O at various pressures are listed in Supplementary Table 1 and Supplementary Data 2 and 3. We observe a phase transition of Fe0.94O from the cubic (B1) phase (Z = 4) to the rhombohedral (rB1, Fig. 3a) phase (Z = 3) upon compression. The transition is evident by a clear splitting of the diffraction reflections at ~ 18 GPa, in line with previous observations13,23. The difference in the volume between our experiment and the results from ref. 23. should be related to different pressure mediums (Ne vs He) and stoichiometry (Fe0.94O vs Fe0.93O). Some of the previous studies suggest that the rB1 phase is stable at least up to 120 GPa at room temperature8,10,17. However, our single-crystal XRD shows that the rB1 phase can be preserved only up to ~ 39 GPa, when more reflections occur (Fig. 3b) and the structure can no longer be refined as the rB1 phase, indicating a further decrease in the symmetry of Fe0.94O. We first solved the structure as a monoclinic phase with C2/m space group (Z = 2; a = 4.84(1) Å, b = 2.73(1) Å, c = 2.99(1) Å, β = 124.06(7)°) hereafter referred to as mC4 model (following Pearson Symbol) (Fig. 3b and Supplementary Table 1). However, the detailed examination of the reciprocal lattice planes shows the presence of some weak reflections that are forbidden for the C2/m space group (dash circles in Fig. 3b). Thus, we additionally refined the structure in a monoclinic P21/m space group, hereafter referred to as mP4. Both structural models yielded discrepancy factors (R1) of ~ 5% or less (Supplementary Table 1) at 42.6 GPa. The R1 for the mC4 model does not change with increasing pressure, however, the model with the P21/m space group becomes worse with increasing pressure and the R1 reaches ~ 14% at 78 GPa, indicating the low quality of the refinement of the structure in this space group (Supplementary Table 1). We do not see any further transitions upon compression up to 78 GPa. At the same time, laser heating at 1700(200) K and 78(2) GPa results in the enhancement of the intensity of the reflections forbidden for the mC4 structure in the quenched sample (Fig. 3c). Solving the structure, yields the mP4 phase with the lattice parameters a = 4.67(6) Å, b = 2.65(1) Å, c = 2.95(2) Å, β = 123.70(12)°, V = 30.40(50) Å3 and Z = 2 (Fig. 3c and Supplementary Tables 1 and 2). The differences between the two monoclinic phases with formally the same P21/m space group are discussed in the Discussion section.

Fig. 2: Unit cell volume per formula unit (V/Z) as a function of pressure for Fe0.94O polymorphs.
figure 2

B1-cubic phase (Z = 4), rB1-rhombohedral phase (Z = 3), mC4-monoclinic phase refined in C2/m space group (Z = 2), mP4-monoclinic phase with P21/m phase space group (Z = 2) obtained after the laser heating, SC-single crystal. Experimental data from ref. 23 are shown for the comparison. Error bars, estimated standard deviations of fittings, are smaller than the symbol size for both pressure and volume.

Full size image
Fig. 3: Examples of reciprocal lattice planes \((h\bar{2}l)\) and crystal structures of different Fe0.94O polymorphs.
figure 3

The appearance of more reflections indicates the transitions from the rhombohedral rB1 (a) to the monoclinic phase (mC4-model) upon compression (b), and ultimately to the monoclinic mP4 phase upon heating (c). Dash blue circles in (b) present the reflections forbidden for the C2/m space group (please refer to the discussion section for details). Positions of the structural reflections are highlighted by red, blue and green circles and indexed. The unmarked reflections in (b) and (c) are reflections from twins of the sample. Blue and red spheres represent iron and oxygen atoms, respectively. Dashed lines indicate the unit cell. The structures are visualized using the Vesta 3 software52.

Full size image

We do not detect any discontinuity in the unit cell volume across the transition from the rB1 to the room temperature monoclinic phase (mC4-model) (Fig. 2). The pressure-induced changes of relative lattice parameters a/a0, b/b0, c/c0 and β angle of the mC4 are plotted in Supplementary Fig. 1a. The interatomic distances of mC4 Fe0.94O are given in Supplementary Fig. 1b and Supplementary Table 1. There is only one symmetry non-equivalent site for iron and oxygen in the rB1 phase. However, Fe-O and Fe-Fe distances split upon transition to the monoclinic phase due to the greater distortion of the octahedra compared to rB1. The transformation to the mP4 phase after the heating results in a further distortion of the structure (Supplementary Fig. 1b–d). Such a distortion is a result of compression of material electronic density and has effects on the magnetic properties of Fe0.94O (please refer to the Discussion section below for details).

High-pressure Mössbauer spectroscopy

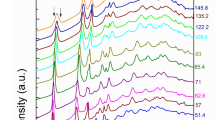
Mössbauer spectra of Fe0.94O were measured up to 94(1) GPa at room temperature. The selected spectra are shown in Fig. 4 and Supplementary Fig. 2. The Mössbauer spectra from 0.5 to 15 GPa at room temperature can be well fitted by the superposition of one doublet and one singlet with relative areas of 90(1) % and 10(1) %, respectively (Fig. 4a and Supplementary Fig. 3). The doublet and the singlet can be assigned to Fe2+ and Fe3+ respectively based on their center shift (CS) values5,6. The CS of both components decrease monotonously with pressure (Fig. 5 and Supplementary Table 3), which is consistent with the volume decrease of the FeO6 octahedron under pressure (Supplementary Fig. 1). We note that the line widths of the spectra have an abrupt increase at 15 GPa and are roughly twice as large as that at 0.5 GPa (0.88(5) vs 0.42(1) mm/s) (Supplementary Figs. 2 and 4), indicating the onset of magnetic ordering in Fe0.94O at 15 GPa.

Fig. 4: Selected synchrotron Mössbauer source spectra of various phases of Fe0.94O at indicated pressures and room temperature.
figure 4

For the crystallographic description of the phases please refer to the main text. Solid lines show the model fits, the percentage bars in all panels indicate the relative absorptions, and the residuals of the fits are indicated below each spectrum (a–f). Sextet with an exponential distribution of the magnetic field is used to fit the magnetic component above 80 GPa (e, f).

Full size image
Fig. 5: Hyperfine parameters of Fe0.94O under pressure.
figure 5

a the center shift (Gray symbols are data collected after the heating) (b) the quadrupole splitting, and (c) the hyperfine magnetic field of the magnetic sextets. The error bars represent estimated standard deviations of fittings. The error bars are smaller than the symbol size if not shown.

Full size image

With further compression, Fe0.94O becomes magnetic above ~ 17 GPa, consistent with the B1 to rB1 phase transition detected in our XRD experiments. Previous studies reported only one sextet that was assigned to Fe2+ in the rB1 phase12,16. However, the high resolution of our data allows to unambiguously identify under fitted part of the spectra near the first line if the spectra are fitted with only one sextet (Supplementary Fig. 5), indicating that the second sextet is needed at pressures above 17 GPa to fit the data (Fig. 4b–d and Supplementary Fig. 5). We determine the CS for the dominant sextet at this pressure to be δCS = 0.94(2) mm/s, the quadrupole shift (QS) to be ε = 0.23(2) mm/s, and the hyperfine magnetic field to be Bhf = 33.85(5) T. From the Mössbauer parameters, we can attribute this sextet to Fe2+. For the second minor sextet, we find the CS to be δCS = 0.68(3) mm/s, the QS to be ε = −0.24(3) mm/s, and the hyperfine magnetic field to be Bhf = 34.0(3) T. We compare the CS of the minor sextet with those reported for various iron oxides, e.g., δCS = 0.29 mm/s for octahedral Fe3+ ions in hematite (α-Fe2O3)6, δCS = 0.67 mm/s for octahedral mixed-valence Fe2.5+ ions in magnetite (Fe3O4) (ref. 4. and references therein) and δCS = 0.94 mm/s for Fe2+ from this study. Based on these values, the above-determined value of δCS = 0.68 mm/s for the minor magnetic sextet in Fe0.94O should correspond to an oxidation state of Fe2.5+, i.e. of nominally one Fe2+ ion exchange of one extra electron with the nearest Fe3+, forming a charge transfer component Fe2.5+ between those two iron ions. Such an assignment is further supported by an excellent agreement of the relative abundances of Mössbauer spectral components (Supplementary Fig. 3). Before the magnetic ordering, the abundance of Fe2+ and Fe3+ components are 90(1)% and 10(1)%, respectively. The abundance of Fe2+ decreases to ~ 80(1)% and Fe2.5+ assigned contribution occupies ~ 20(2)% (10% from Fe3+ and another 10% from Fe2+) after the emergence of the charge transfer component (Supplementary Fig. 3). Upon pressure increase, the relative abundance of the Fe2.5+ component in the rB1 phase remains unchanged within the error bars. At pressures above 40 GPa, i.e. after the transition to the monoclinic phase, the relative abundance of the Fe2.5+ component decreases from ~ 20(2)% at 40 GPa to ~7(1)% at 77.9 GPa (Supplementary Fig. 3), indicating the breakdown of the Fe2+-Fe3+ pairs. This component can still be detected until 77.9 GPa (Fig. 4c, d and Supplementary Fig. 3) and then the spectra can be well fitted by one sextet with parameters corresponding to Fe2+ (Fig. 4e). There is no evidence of the component that could be assigned to Fe3+ after the breakdown of the Fe2+-Fe3+ pairs. Likely, the Fe3+-defects start to be involved in the dynamic exchange of electrons within all iron ions, on a timescale too fast for the Mössbauer technique to detect individual valence states. At the same time, a sextet with the exponential distribution of the magnetic field is needed to fit the Fe2+ component above 83 GPa, and a minor nonmagnetic singlet emerges in the center (δCS = 0.60(7) mm/s) of the Mössbauer spectrum. The singlet cannot be properly fitted on the spectrum at 83 GPa because of its low relative abundance but becomes pronounced at 94 GPa (Fig. 4e, f and Supplementary Fig. 2). The appearance of the singlet represents the onset of the spin transition in Fe0.94O, which is in good agreement with former experiments16.

High-pressure and high-temperature Mössbauer spectroscopy

The magnetic properties of Fe0.94O under high-pressure and high-temperature conditions have been studied by SMS spectroscopy up to 1230(80) K and 78.8(20) GPa to identify its Néel transition temperature (Figs. 1 and 6 and Supplementary Fig. 6). We found that the Fe2.5+ oxidation component can be preserved when heated to moderate temperatures and that pressure has a great effect on its thermal stability (Figs. 1, 6 and Supplementary Fig. 6). For instance, the Fe2.5+ component disappears when the temperature increases to 390(21) K at 21 GPa, indicating the temperature-induced breakdown of the Fe2+-Fe3+ pairs. Upon compression, the breakdown temperature increases, reaching ~ 420(31) K at 41 GPa (Fig. 1). We observe distinct changes in the behavior of the charge-transfer component above and below 40 GPa at the high temperature. Even if heated well above the breakdown temperature, quenching of the rB1 phase to room temperature below 40 GPa results in the re-formation of the charge transfer component (Fig. 6a–c). On the contrary, quenching the monoclinic phase above 40 GPa results in the irreversible breakdown of the Fe2+-Fe3+ pairs, and the resulting spectra can be well fitted by one sextet (Fig. 6d–f). This may be explained either by the different heating temperatures, which was about ~ 100 K lower at pressures below 40 GPa (Fig. 1), or, more likely, by the phase transition from the room temperature monoclinic phase (mC4-model) to the mP4 phase. The spectra with the absent Fe2+-Fe3+ component, require exponential distribution of the magnetic field for the single magnetic component (Fig. 6b–e, f), similar to the spectra that we collected upon room-temperature compression at higher pressures (Fig. 4e, f).

Fig. 6: Representative synchrotron Mössbauer source spectra of Fe0.94O at the indicated pressures and temperatures.
figure 6

a, b, c: rhombohedral (rB1) phase; (d, e, f): monoclinic phases. Solid lines show the model fits, the percentage bars indicate the relative absorptions, and the residuals of the fits are indicated below each spectrum. The spectrum in (f) is fitted by a sextet with a distribution of the magnetic field.

Full size image

We performed a room-temperature compression of the phases quenched from high temperatures to compare the behavior of their magnetic properties with those of unheated phases. The representative SMS spectra at pressures above 55 GPa are shown in Fig. 7. The spectrum of the phase quenched at 55 GPa from ~ 900 K can be fitted with one sextet with δCS = 0.78(1) mm/s (Fig. 6b), consistent with the CS of the Fe2+ component (Fig. 5). The residuals suggest the presence of the minor singlet in the center of the spectrum, however, its relative abundance is too low for a proper fit. Upon compression to 66.2 GPa at room temperature, the singlet in the center of the spectrum becomes more pronounced (Fig. 7d). We do not observe such a component in the spectra from unheated samples (Fig. 7c). With further compression to 78.8 GPa, the relative abundance of the singlet increases at the expense of the magnetic sextet (Fig. 7d–f), however, the heating cycle does not change its relative abundance, suggesting that the appearance and the increase of the relative abundance of the singlet are related to the pressure increase but not to the subsequent temperature treatment. To clarify the origin of the distinct behavior between heated and unheated samples, we performed XRD measurements on the sample that was laser-heated at 78.8 GPa. The powder XRD pattern matches well the mP4 phase detected by our single crystal XRD experiment after the laser heating (Supplementary Fig. 7), indicating that the distinct behavior is related to different monoclinic structures of Fe0.94O. The Mössbauer hyperfine parameters (CS, QS and hyperfine magnetic field) of the magnetic component of both monoclinic phases are similar (Fig. 5). We also note a minor mixed-valence iron oxide phase (Fe25O32) resulting from the partial decomposition of Fe0.94O upon laser heating at high temperature (Supplementary Fig. 7). We conducted a SMS experiment on Fe25O32 and the spectra of Fe25O32 are more complex33 (more Fe sites in its structure) and completely different from that of FeO (Fig. 7f). We think the amount of this phase is too tiny, so it is not possible to detect individual contributions associated with this phase on the SMS spectra in our experiments.

Fig. 7: Representative synchrotron Mössbauer source spectra of two monoclinic Fe0.94O phases.
figure 7

For the monoclinic phase before heating (mC4 model) (a, c, e), the spectra contain the Fe2+ and Fe2.5+ sextets. For the monoclinic phase after heating (mP4 phase) (b, d, f), the spectra only contain one sextet at 55 GPa (b) and one singlet emerges at 67.4 GPa (d, f). The relative abundance of the singlet increases with pressure (f). Solid lines show the model fits, the percentage bars indicate the relative absorptions, and the residuals of the fits are indicated below each spectrum.

Full size image

Discussions

It has been reported that the satellite reflections originating from an incommensurate superstructure of Fe3+ defect clusters disappear around 14.0 GPa34. This long-range order-disorder transition of defect clusters may be related to the formation of the Fe2+-Fe3+ pairs by charge transfer that we can clearly identify after the B1-rB1 transition. Our data demonstrate that iron atoms responsible for the Fe2.5+ charge transfer component are magnetically ordered (Fig. 4b). This is in agreement with the neutron scattering data which also confirmed that the cations within the interstitial clusters appear to be weakly ferromagnetic, and their spins are correlated to the spins of the octahedral cations closest to them29. There is a remarkable difference between the low-temperature and high-pressure behavior of Fe3+ defects in Fe0.94O: there is no evidence of the charge-transfer Fe2+-Fe3+ component in the rB1 phase upon cooling down to 78 K at ambient pressure and Fe3+ can be detected as an independent component in Mössbauer spectra32. Thus, the formation of Fe2+-Fe3+ pairs is likely sensitive to the distance between the Fe3+ defects and the nearest Fe2+ atom, as pressure has a much stronger effect on the distances than temperature. An exponential distribution of the magnetic field of the Fe2+ component is required to fit the spectra above ~ 80 GPa upon cold compression and above 40 GPa after heating, when the Fe2+-Fe3+ component disappears (Figs. 4e, 6b–f, and 7f), and following by the onset of spin crossover in the sample. Thus, we think the onset of the spin transition is likely related to the broadening of the spectrum, the breakdown of the Fe2+-Fe3+ component, as well as the changes in volume, cell parameters, and the c/a ratio at 85 GPa observed in the literature35.

It is useful to analyze the sequence of phase transitions observed in this study in terms of group-subgroup relationships. In Fig. 8a, we plot the isotropy subgroup tree of the parent FeO rock-salt type structure, for the k = (1,0,0) modulation vector, i.e. the vector to the X point of the Brillouin zone of the parent structure. Every subgroup box contains the relevant irreducible representation (irrep), i.e. a certain distortion required to obtain this subgroup from the parent Fm\(\bar{3}\)m group. All irrep labels are given relative to the parent face-centered cubic unit cell. Since the ambient pressure structural transitions in FeO are related to the magnetic ordering we also plot the group-subgroup graph of the relevant magnetic space groups on the right. The magnetic structures experimentally found in FeO have propagation vector q = (1/2,1/2,1/2), i.e. the L point of the Brillouin zone. Note that the magnetic irreps start with the m letter.

Fig. 8: Group-subgroup relationships and the amplitudes of distortion modes of FeO polymorphs.
figure 8

a Graph of isotropy subgroups for the modulation vector k = (1,0,0) between the parent space group Fm\(\bar{3}\)m (B1-phase) and subgroup P21/m (mP4 phase), the phases observed in this work are highlighted by green frames. We also show the corresponding magnetic space groups (highlighted with the red frame) observed for wüstite with neutron diffraction on the right. Magnetic space groups are labeled according to the Belov-Neronova-Smirnova (BNS) notation. b The pressure dependence of the amplitudes of the distortion modes (the standard supercell-normalized amplitude). We plot here only the data for the \({\Gamma }_{5}^{+}\) strain mode and both \({X}_{3}^{-}\) and \({X}_{5}^{-}\) displacive modes, for other modes see Supplementary Table 4. The data points after the laser heating are marked by stars. In preparation of this figure we used ISODISTORT tool53 at the ISOTROPY software suite and Bilbao Crystallographic Server54.

Full size image

As an example of how to use the scheme in Fig. 8a let us consider the P4/nmm subgroup. To undergo a phase transition to this subgroup, the parent Fm\(\bar{3}\)m group should be distorted by the \({X}_{3}^{-}\) distortion mode which will be the order parameter with the (0,a,0) direction for this phase transition. Note that this subgroup can also include every distortion mode of its parent supergroups, i.e. the \({\Gamma }_{3}^{+}\) and \({\Gamma }_{1}^{+}\) modes, because these modes do not change the symmetry of the P4/nmm subgroup, so they are symmetry-allowed in this subgroup and can have some non-zero values but are normally much lower than the primary mode \({X}_{3}^{-}\). As another example, let’s take the Pmmn subgroup. There is no main mode in this case but this subgroup will be adopted if any combination of the \({X}_{3}^{-}\), \({X}_{2}^{-}\), and \({\Gamma }_{5}^{+}\) (0,a,0) is present. However, if only one of these modes has a non-zero value we end up in P4/nmm, P42/nmc, or Immm, respectively.

Overall, the scheme in Fig. 8a shows the list of mathematical possibilities for the given modulation/propagation vector. Only the boxes highlighted by the green frames correspond to the experimentally observed phases. The correspondence between the green and red boxes, designated by thick blue arrows, basically shows what an X-ray or neutron diffraction experiment with a particular FeO phase would show, respectively.

The B1 to rB1 transition, concomitant with the onset of the magnetic ordering with irrep \({{mL}}_{2}^{+}\) and magnetic propagation vector q = (1/2,1/2,1/2) (Fig. 8a), was extensively studied at ambient and high pressures. Our experimental data seem to be consistent with the analysis in Carpenter et al.36 and Zhang et al.37, where it was shown that this phase transition is driven by magnetic ordering, and a linear-quadratic coupling between structural and magnetic order parameters was concluded. Interestingly, the C2/m monoclinic phase, equivalent to the monoclinic mC4 model identified upon room-temperature compression in our study, was reported based on powder neutron diffraction data for the nearly stoichiometric FeO at 10 K and ambient pressure22. In this case magnetic structure is described by the \({P}_{S}\bar{1}\) magnetic space group and involves two \({{mL}}_{2}^{+}\) and \({{mL}}_{3}^{+}\) modes.

In our data we see weak additional reflections (Fig. 3b), forbidden for the C-centered lattice, therefore, strictly speaking, we observe the mP4 phase at room temperature above 40 GPa. In this case the primitive unit cell is doubled in volume so the transition from rB1 to mP4 structure has to involve irreps with non-zero modulation vector, namely k = (1,0,0) (Fig. 8a). The mode decomposition analysis of the mP4 phase (Fig. 8b) reveals two active displacive modes (\({X}_{5}^{-}\) and \({X}_{3}^{-}\)), that are related to the displacement of iron and oxygen atoms from their high-symmetry positions.

Upon compression at room temperature, the displacive \({X}_{5}^{-}\) and \({X}_{3}^{-}\) modes have comparable amplitudes in the investigated pressure range (Fig. 8b). Thus, we can conclude that the rB1 to mP4 phase transition has two superposed primary order parameters and this phase transition has to proceed in a first-order manner. Indeed, above 35 GPa we observe clear signs of phase coexistence which apparently is responsible for the anomalous decrease in the \({\Gamma }_{5}^{+}\) mode amplitude before the rB1-to-mP4 phase transition (Fig. 8b). Upon laser heating at 78 GPa we observe a small increase in the amplitudes of some strain modes (Fig. 8b and Supplementary Table 4) but the two-fold increase of the amplitude for both displacive modes. This discontinuous displacement of iron and oxygen atoms and differences in electronic properties between the two mP4 phases, thus, could be interpreted as an isostructural phase transition induced by laser heating.

It is an interesting question if the mP4 phase observed in our study upon the room temperature compression is related to the C2/m phase found in Fjellvåg et al.22. The magnetic structure reported by them is a subgroup of the rB1 magnetic structure with two q = (1/2,1/2,1/2) active irreps \({{mL}}_{2}^{+}\) and \({{mL}}_{3}^{+}\) (Fig. 8a). These irreps cannot be magnetoelastically coupled to the k = (1,0,0) \({X}_{5}^{-}\) and \({X}_{3}^{-}\) modes in the mP4 phase, meaning that the rB1-to-mP4 phase transition can be driven by structural instability instead. Therefore, the magnetic structure in the mP4 phase can either remain the same as in the rB1 phase or it can differ from that in both the rB1 and C2/m phases. The smooth variation of hyperfine parameters in Fig. 5 seems to support the former alternative.

Interestingly enough the mP4 phase could be relevant to the ambient pressure FeO if the line of the rB1-to-mP4 phase transition has a slope similar to the B1-to-rB1 transition in P-T phase diagram (Fig. 1). Therefore, it could be possible to detect the mP4 phase in the non-stoichiometric wüstite with a high-resolution X-ray diffraction at ambient pressure and low temperatures.

Numerous investigations have been focused on the phase transitions of Fe1-xO under pressure and temperature10,17, and claim that the rB1 phase is stable up to 120 GPa at room temperature. However, most of the studies were conducted utilizing powder XRD. The quality of powder XRD data from DACs significantly limits the detection of phase transitions with small structural distortions due to peak broadening at high-pressures, undesirable contributions from diamonds and pressure media, etc. The high-pressure single-crystal XRD has seen rapid progress during the last decade and the single-crystal datasets, in general, are much less affected by the abovementioned problems. Based on the single-crystal XRD, we detected a monoclinic distortion of Fe0.94O above 40 GPa (Fig. 3b). Recently, Dobrosavljevic et al. documented that the defect structure of Fe1-xO undergoes an order-disorder transition at pressures above 30 GPa and at temperatures several hundred kelvins below melting19. We compared our XRD pattern with that presented in Dobrosavljevic et al.19 and verified that the pattern of the ordered phase at 65 GPa matches that of the mP4 phase observed in this study. Thus, the satellite reflections upon heating in Dobrosavljevic et al.19 should be related to the formation of the mP4 phase together with some mixed valence iron oxides2, rather than be a sign of the order-disorder defect transition. This indicates that the mP4 phase of Fe1-xO may have a wide emergence field, with pressure from 30 GPa to 140 GPa and a temperature from a thousand to several hundred kelvins below melting. Moreover, we did not find any evidence of the B8 phase in our experiments even though we heated FeO at the presumed stability field of the B8 phase8,10. As discussed by Kantor et al. the reflections of the B8 phase are very close to the monoclinic phases of FeO13. The pure B8 phase has only been reported if synthesized at pressures above 120 GPa15,24, while the XRD patterns of the samples synthesized at lower pressures always show the coexistence of B8 and B1 or rB1 phases8,10. Thus, our data, combined with the results of Kantor et al.13 and Dobrosavljevic et al.19, and in line with computational predictions9,25, suggest that at pressures below at least 80 GPa Fe1-xO crystalizes in a monoclinic phases both at room and high temperatures (Fig. 1).

Our data demonstrate that the distortion of rB1 to monoclinic phases at high pressure does not lead to any noticeable changes in the Mössbauer spectra, particularly for the Fe2+ component (Figs. 4 and 5). The weak dependence of the magnetic properties from the lattice distortions has also been shown for other transition metal monoxides, for example in CoO26,38.

The CS of the singlet observed in the laser-heated mP4 phase above 60 GPa (Figs. 5a and 7d) matches the CS values for the low-spin ferrous iron16, suggesting that the spin transition onsets in the mP4 phase already at ~ 66 GPa. The room temperature compression of the unheated sample indicates that the room temperature phase (mC4 model) of Fe0.94O onsets the spin transition at ~ 94 GPa (Fig. 4f). Thus, there is about a 30 GPa offset in the spin transition pressure between the two monoclinic phases. The difference in the Fe-O bond lengths and distortion of iron octahedra might explain the difference in the offset pressure for the spin transition.

We determined the Néel transition temperature (TN) of Fe0.94O by following the temperature dependence of the hyperfine magnetic field Bhf (Fig. 1 and Supplementary Fig. 8). It has been shown that in Fe0.94O the normalized Bhf is proportional to the sublattice magnetization and its temperature evolution correctly provides the Néel transition temperature28. The evolution of the hyperfine magnetic field Bhf of Fe0.94O with temperature for different FeO phases is presented in Supplementary Fig. 8. The magnetic field decreases with increasing temperature until the spectra collapse to a paramagnetic doublet (Supplementary Figs. 6 and 8). The collapse temperature below 40 GPa matches the rB1 to B1 transition temperature (Fig. 1) further supporting the linear-quadratic coupling between structural and magnetic order parameters upon B1 to rB1 transition39. The kink in the slope of the pressure dependence of TN above 40 GPa is most likely related to the rB1 to the monoclinic phase (Fig. 1). The temperature dependence of TN determined by X-ray emission spectroscopy18 shows much lower values of TNcompared to our study but is very close to the stability field of the Fe2.5+ component detected in our experiment (Fig.1). Our results show a slightly weaker pressure dependence of the Néel transition temperature compared to that reported by Kantor et al.28 (Fig. 1). The discrepancy is likely related to the difference in the experimental conditions - it has been shown that the pressure dependence of TN is strongly sensitive to non-hydrostatic pressures39. While we were using small single crystals embedded in the Ne gas pressure transmitting medium, Kantor et al. utilized a powder sample mixed with NaCl or ruby powder or the Ar gas as a pressure medium all of which are much less hydrostatic at the examined pressures28.

Conclusions

We investigated the structural transition and related magnetic properties of Fe0.94O using powder and single-crystal XRD and SMS spectroscopy up to 94 GPa and 1700 K. The rhombohedral distortion of the B1 phase reveals the formation of the Fe2+-Fe3+ pairs caused by the interplay between the defects Fe3+ with the nearest Fe2+ atoms. The charge transfer Fe2.5+ component can be preserved up to 80 GPa and 400 K. We have identified a monoclinic distortion in Fe0.94O at pressures above 40 GPa, with different structural models describing the data before and after the laser heating. The two monoclinic structures of Fe0.94O show a 30 GPa offset in the spin transition pressure due to the different distortion of the iron octahedra. No evidence for the B8 phase was found up to the highest pressure-temperature conditions in our study. Group theory analysis shows that the high-pressure mP4 monoclinic phase observed in this study is not related to the low-temperature ambient-pressure phase of stoichiometric wüstite. Altogether, our investigation demonstrates further complexity of the high-pressure behavior of the simple FeO binary oxide, which may provide insights into the properties of transition metal monoxides26.

Methods

Sample synthesis and preparation

Fe1-xO sample was synthesized by reducing Fe2O3 (96% enriched in 57Fe) in a gold capsule at 1293 K in a CO-CO2 gas mixture with log(fO2) = −14.6 for 16 h12. The cubic unit cell dimension is 4.307(7)Å, which corresponds to the composition Fe0.945O (hereafter FeO) according to the equation a = 3.856 + 0.478 ∗ (1–x)12.

The high-pressure experiments were performed utilizing BX-9040 and membrane-type diamond anvil cell41. Diamonds with 250 and 150 μm culets were employed to reach pressures above 94 GPa. Compression chambers were prepared from 200 μm thick Re gaskets pre-indented to about 30 μm thickness and laser drilled with holes of 125 μm and 75 μm, respectively. Gold and/or ruby were loaded as pressure calibrant42,43. Ne was loaded at 1.2 kbar and served both as a pressure-transmitting medium and thermal insulator for laser heating.

High-quality single crystals of Fe0.94O were pre-selected using single-crystal X-ray diffraction. The quality of crystals in the first DAC decreased with increasing pressure, thus, we measured powder XRD with those crystals. One of the crystals in the second DAC preserved its high quality until 78 GPa and after laser heating, allowing for conducting single crystal XRD on this crystal (Fig. 2).

XRD under pressure

The powder and single-crystal XRD experiments were conducted at the ID15b beamline of the European Synchrotron Radiation Facility (ESRF), Grenoble, France (MAR555 detector, wavelength λ = 0.4100 Å) and at the Extreme Conditions Beamline P02.2 of PETRA III, DESY, Hamburg, Germany (PerkinElmer XRD1621 flat panel detector, λ = 0.2902 Å). The X-ray spot size depended on the beamline settings and varied from 1 to 4 µm. The wide X-ray diffraction images for preliminary analysis were collected during continuous rotation of DACs typically from –30° to 30°; while step-scan data collection experiments were performed by narrow 0.5 scanning of the same angle range. Integration of the reflection intensities and absorption corrections were performed using CrysAlisPro software. The structures were solved by the direct method and refined in the isotropic approximation by full-matrix least-squares refinements using SHELXS and SHELXL software44,45, respectively. Double-side laser-heating set-up at P02.2 was used for temperature-quenched single-crystal X-ray diffraction at 78 GPa46. One tiny piece of Au was loaded right next to the sample as a pressure marker and we always measured the center of the Au and sample to minimize the pressure gradient. Pressure was measured before and after data collection to get the pressure change during the measurement.

Mössbauer spectroscopy under extreme conditions

SMS spectra were recorded at the Nuclear Resonance Beamline ID18 of the ESRF using the (111) nuclear reflection of a 57FeBO3 single crystal mounted on a Wissel velocity transducer driven with a sinusoidal wave form47. The source provides 57Fe resonant radiation at 14.4 keV within a bandwidth of 15 neV (0.31 mm/s) which is tunable in energy. The X-ray beam was focused down to 13 × 4 μm2 (vertical × horizontal) with Kirkpatrick-Baez mirrors. The linewidth of the SMS and the absolute position of the CS relative to α-Fe were controlled before and after each measurement with a K2Mg57Fe(CN)6 reference single-line absorber. The velocity scale was calibrated using 25-μm-thick natural iron foils.

Below 30 GPa, high-temperature experiments were performed up to 540(40) K by resistive heating of using a Pt coil placed around the gasket. A K-type thermocouple attached to the diamond and sat close to a sample chamber was used to determine temperatures. Higher temperatures were achieved by employing a modified version of the portable double-sided laser heating system48,49. The surface temperature was measured by the standard spectroradiometry method employing an IsoPlane SCT 320 spectrometer with a PI-MAX®4 1024i ICCD camera from Princeton Instruments. Typical collection times for each collected spectrum ranged from 5–10 min to 1–10 h depending on pressure-temperature conditions and the desired statistics. SMS spectra were fitted using full transmission integral taking into account the exact shape of the SMS instrumental function. The fitting procedure was done in SYNCmoss software50. We employed the Gaussian distribution of magnetic field for the magnetic components to account for irregularities of the local environment related to non-stoichiometry. Note, that due to the linear polarization of the synchrotron X-ray beam, the intensities of the lines in the magnetic sextet deviate from the 3:2:1:1:2:3 ratio. Due to the low relative abundance of the Fe2.5+ component, we constrained the ratio between the lines of the Fe2.5+ component to be equal to that of the main Fe2+ component. Exponential distribution of the magnetic field50 was employed the fit the magnetic component after the breakdown of Fe2.5+ component and the onset of the spin crossover. The temperature of the sample was calculated from the temperature-induced changes of the CS as: T = A (CS0- CS) + T0, where CS0 is the center shift at the reference temperature T0 (300 K here), CS is the measured center shift at temperature T and A is a constant characteristic of each compound. Details can be found in ref. 5. The A constant in FeO was derived from a least-squares fitting of the ambient pressure data51 from 873 to 1183 K, yielding A = 1753(25) K mm−1s−1.