Introduction

Resonant X-ray interactions, providing high cross sections and selectivity to the interacting element, chemical site, as well as quantum state, are widely employed in characterization techniques such as X-ray absorption (XAS) near edge structure (XANES), various resonant electron and ion spectroscopies, resonant inelastic X-ray scattering (RIXS) and anomalous scattering (diffraction). These weak field methods are commonly applied especially at synchrotrons, but also in small-scale laboratories. On the other hand, a number of novel ultrafast and nonlinear characterization techniques have been enabled by the development of X-ray free electron lasers (XFELs) within the past couple of decades, producing few-to-sub-femtosecond pulses of X-rays with unprecedented intensities through the self-amplified spontaneous emission (SASE) process. These include e.g., coherent core-excitation1, stimulated X-ray emission (and Rabi oscillation)2,3 and stimulated X-ray Raman scattering4,5,6,7, and resonant XFEL interactions play a role also in single particle imaging experiments8 where they are explored as means to enhance the ultrafast diffraction signal strength9.

At XFELs, multiple X-ray photons can be absorbed into a single molecule even within the typical few-fs lifetimes of core-hole states, which has enabled X-ray pump/X-ray probe schemes and multi-core ionization experiments with increased chemical sensitivity10,11,12,13,14. In certain conditions, photoionization(s) have been accompanied by resonant excitation in the same event, including the “hidden resonances” of ionic states2,15,16,17,18 that can also be exploited as excited state probes19,20. The possibility of inducing multiple resonant excitations in a single pulse can then naturally be also hypothesized. Such processes have already been realized in the XUV regime, in the context of establishing interatomic decay mechanisms and nanoplasma formation in rare gas clusters21,22,23, but have been less explored in the X-ray regime. The ultrafast resonant excitation of multiple core-level electrons at X-ray FELs could enable state and site-selective production of exotic neutral multi-core hole states at high interaction cross sections (also in a time-resolved fashion), which are inaccessible in single photon processes other than via weak electronic correlations24,25. These kinds of processes could generally be viewed as an extension of the traditional single photon XAS technique into multidimensional XAS, provide opportunities for control of core-electron dynamics, and have been discussed also in relation to potential future applications of two-dimensional coherent X-ray spectroscopy26,27. In addition, modeling non-linear X-ray interactions remains a theoretical and computational challenge, and there is a demand for benchmark experimental data to assess different theoretical approaches. In this context, small molecules are particularly well-suited for precision measurements.

In the sequential framework, each subsequent core excitation however occurs at a different resonance energy, due to the rearrangement of the molecular electronic configuration upon each excitation. This sets a requirement for the incident photon bandwidth, along with the high pulse intensity needed to surpass the few-fs core-hole lifetime. This situation is different from a multi-excitation scheme mediated by a virtual state (direct two-photon absorption), which has also been predicted and realized experimentally in the XUV regime in Ne dimers28,29. However, as shown in recent calculations27,30, the shifts between subsequent resonances from different atomic sites can be relatively small, just a couple of eV even for the excitation of neighboring atoms in a small molecule. Thus, an ultrashort XFEL pulse with a typical SASE bandwidth of a few eVs should be able to simultaneously cover the resonance energies of sequential excitations. The relatively small shifts between subsequent core-resonances can appear surprising when contrasted with the better-studied off-resonant multi-core ionization processes, where each subsequent core-ionization threshold increases much more significantly (~10 eV). Clearly, while in multi-core ionization the molecule’s charge state is directly increased by each photon, in the multi-resonant pathway the neutral charge state of the molecule is preserved (for the core-excited state lifetime). Besides, the resonant pathway also provides higher interaction cross sections and better selectivity for the excited sites30.

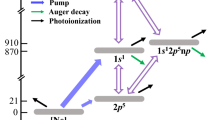
Herein, we report on the experimental observation of a resonant double-core excitation process30 in the molecule N2. Exploiting the naturally broad SASE bandwidth from the SASE3 branch of the European XFEL, two 1σ core-level electrons are promoted to the degenerate \(1{\pi }_{g}^{* }\) lowest unoccupied molecular orbitals with a single X-ray pulse. The process results in a neutral K−1K−1V2-type two-site double core hole (ts-DCH) state, which is identified by observing its characteristic single- and double participator decay channels, respectively abbreviated as DCH-SP (double core hole spectator/participator) and DCH-PP (-participator/participator). Double spectator (DCH-SS) transitions are also prominent but not analyzed in this work, as they appear at lower kinetic energies and are more challenging to isolate from overlapping single photon channels. The double excitation scheme and the monitored DCH-PP and DCH-SP decay channels are illustrated in Fig. 1. Additionally, calculated potential energy curves (PECs) of the ground state (GS), single core hole (SCH) and ts-DCH states involved in the DCH-PP scheme are shown in Fig. 2. The doubly excited state has bound state character, with a shallow dissociation potential and an elongated equilibrium bond distance compared to the GS.

Fig. 1: Resonant double-core excitation process and its characteristic decay channels.
figure 1

A schematic illustration of the resonant double-core excitation process and of the monitored double (DCH-PP) and single participator (DCH-SP) decay channels in N2. For simplicity, the diagram for the double excitation step on the left only represents the dipole allowed partial determinant of the final state \({\Psi }_{DCH}({\scriptstyle{1}\atop}{\Sigma }_{g}^{+})=(\phi (1{\sigma }_{g}^{-2})-\phi (1{\sigma }_{u}^{-2}))/\sqrt{2}\) (see “Introduction”).

Full size image
Fig. 2: Potential energy curves.
figure 2

Calculated simplified potential energy curve diagram of the neutral GS (black), SCH (orange), and ts-DCH (blue) states, and of the cationic valence and core ionized final states resulting from SCH-P and DCH-PP, respectively. Equilibrium bond distances are marked by the small vertical bars, and dissociation potentials by the shaded areas.

Full size image

N2 is a homonuclear diatomic molecule, with a GS of gerade parity (\({\scriptstyle{1}\atop}{\Sigma }_{g}^{+}\)). The degenerate core orbitals can be expressed using either localized (1s1,2) or delocalized (1σg,u) representations. The delocalized picture predicts a small lifting of degeneracy between the 1σg and 1σu (~100 meV), which has been verified with photoelectron spectroscopy31. In addition, core excitation to a single core excited state of ungerade parity, \(1{\sigma }_{u}^{-1}{\pi }_{g}^{* 1}\) (1Πu), was verified in a RIXS measurement where X-ray emission is only occurring from states that satisfy dipole selection rules32. Thus, we likewise employ the delocalized core orbitals picture in our study of sequential core excitations. It has been shown extensively (e.g., ref. 31 and references therein) that this choice requires a proper treatment of electron correlations, which is done using a multiconfigurational description (see “Methods”). However, we can also provide a simplified orbitals picture that captures the relevant symmetry implications in our study. Starting from the \({\scriptstyle{1}\atop}{\Sigma }_{g}^{+}\) GS, and absorbing two photons, dipole selection rules allow for gerade final states of \({\scriptstyle{1}\atop}{\Sigma }_{g}^{+}\) or 1Δg symmetry. In N2, the DCH states of interest have a \({\pi }_{g}^{* 2}\) configuration for the excited electrons, which split into 1Δg, \({\scriptstyle{1}\atop}{\Sigma }_{g}^{+}\) and \({\scriptstyle{3}\atop}{\Sigma }_{g}^{-}\) gerade terms. This implies that the double core hole part of the final states also has to be of gerade parity. Here, we turn to the description of DCH states reported by Cederbaum et al.33. They identified four possible DCH configurations, two of which are singlets with \({\scriptstyle{1}\atop}{\Sigma }_{g}^{+}\) symmetry, i.e., gerade parity, and of interest here. When rewriting these two gerade configurations with localized orbitals33, it becomes clear that one of them corresponds to a single-site DCH (ss-DCH) configuration and the other to a ts-DCH configuration. In our experiment, the two sequential core excitations must occur at fairly similar photon energies, which excludes the ss-DCH case where the second excitation requires  ~60 eV higher energy. Thus we are left only with the ts-DCH option, where the two excitations are separated only by a couple of eV. The ts-DCH wavefunction is of the type \({\Psi }_{DCH}({\scriptstyle{1}\atop}{\Sigma }_{g}^{+})=(\phi (1{\sigma }_{g}^{-2})-\phi (1{\sigma }_{u}^{-2}))/\sqrt{2}\) 33, which in combination with the two excited electrons in the \({\pi }_{g}^{* }\) orbitals produces three dipole-allowed final states: two equivalent 1Δg states (X, Y-degeneracy), and one \({\scriptstyle{1}\atop}{\Sigma }_{g}^{+}\) state.

In the following sections, we first show the calculated sequential GS to SCH and SCH to ts-DCH resonant core-excitation spectra, after which we discuss the experimental results. Using electron time-of-flight spectroscopy, and scanning the central X-ray photon energy over the resonance region, we observe the DCH-SP and DCH-PP decay channels. Their kinetic energies are found in good agreement with high-level theoretical calculations, as well as with experimental binding energy references of their respective final states. In addition, the partial electron yield curves of the DCH-SP (and DCH-PP) transitions are shown to be energetically in good agreement with the calculated core-excitation energies. The X-ray pulse duration in our experiment is estimated to be 8–10 fs (see “Methods”). This is slightly longer than the  ~6 fs lifetime of the mediating SCH state34, and hence we finally also briefly discuss the potential influence of core hole decay and ultrafast nuclear dynamics between subsequent resonant absorption events. Detailed descriptions of the experiment and calculations are included in Methods.

Results

Resonant double-core excitation spectrum

Figure 3a presents the calculated absorption spectra yielding the SCH and ts-DCH core excited states in N2. The GS to SCH state calculation (yellow) well reproduces the experimental ion yield reference35 from synchrotron radiation (SR) that is also plotted36. The ts-DCH absorption (orange) is calculated from the first two strongest SCH vibrational states with equal population. The 1Δg and \({\scriptstyle{1}\atop}{\Sigma }_{g}^{+}\) components are shown also separately, and the former has been multiplied by a factor of 2 to account for the X, Y-degeneracy. The calculated lifetime widths are 122 meV for the SCH state (in good agreement with experiment34), and 317 meV (1Δg) or 297 meV (\({\scriptstyle{1}\atop}{\Sigma }_{g}^{+}\)) for the ts-DCH states. These widths are more than twice that of the SCH state, i.e., more than expected through simple statistical probabilities, and are likely a sign that orbital contraction increases wavefunction overlap in the ts-DCH states. In plotting the SCH → ts-DCH spectrum the sum of the initial SCH and final ts-DCH state widths is applied. It is seen from the figure that the 1Δg state excitation energy is  ~2.5 eV lower than the SCH excitation energy, while the state excitation is  ~0.6 eV higher than the 1Δg states. Our calculations thus show that all of the resonances fall well within the  ~3.7 eV average bandwidth (FWHM) of pulses available at EuXFEL, and can thus be excited by a single XFEL shot (see Supplementary Fig. 10).

Fig. 3: Calculated absorption spectra and measured partial electron yields.
figure 3

a Calculated resonant core excitation spectra of N2, from the ground (GS) to the SCH state (yellow), and from the SCH state to the ts-DCH state (orange). An experimental SCH ion yield reference from Flesch et al.35 measured with SR is also plotted (gray line). The calculated core excitation spectra have been shifted by +0.25 eV to match the SR reference. b Experimental partial electron yields for SCH-P and DCH-SP decay at low and high X-ray intensities, corresponding to the marked areas “A” to “D” in Fig. 4a, b.

Full size image

Auger electron spectra

The main results of this work are shown in Fig. 4. Electron kinetic energy spectra were recorded with three TOF analyzers installed at 90°, 54.7°, and 0° relative to the X-ray polarization axis37, as the central photon energy was scanned over the \(1\sigma \to 1{\pi }_{g}^{* }\) resonance in steps of 0.5 eV. Figure 4a, b shows results from the vertical TOF analyzer (90∘) as 2D-maps for both low (~1013 W/cm2) and high (~1017 W/cm2) X-ray intensities, respectively. The intensity was varied by changing the X-ray focal spot size. In order to better emphasize the nonlinear contributions, the color scales of the maps are saturated for the high counts. Our focus here is on the highest electron kinetic energies, where the DCH-SP and DCH-PP features appear, and therefore a strong retardation field (−370 V) was applied to optimize the resolution. In Fig. 4c, 1D-slices from the low and high-intensity maps in (a, b) are shown, corresponding to the areas “E” and “F” marked by the dashed lines, respectively. In Fig. 4d, the calculated SCH and ts-DCH decay spectra, performed using the delocalized core orbital bases, are shown for comparison. For ts-DCH, only the first step decays were calculated (the second decay steps make no contribution in the presented kinetic energy range). The calculations were broadened to the experimental resolution (~0.6 eV, an upper limit obtained from the width of the SCH-P transition). For ts-DCH, the total decay spectrum is calculated assuming 2:1 occupation of the 1Δg and \({\scriptstyle{1}\atop}{\Sigma }_{g}^{+}\) doubly excited states, respectively, i.e., assuming equal occupation of states and considering the X,Y-degeneracy of 1Δg. The two spectral components are plotted also separately. Note that while the spectra shown in Fig. 4 were obtained at 90° to the polarization axis, the calculations correspond to the total decay rates over the full solid angle, which may cause a small discrepancy. Results from the two other electron analyzers installed at 0° and 54.7°, as well as results at a lower retardation (−330 V) covering a broader kinetic energy range, are shown in Supplementary Figs. 1–6. Besides having varying contributions from direct photoionization channels, the relative intensities of the individual decay lines also show angular dependency38. The full calculated spectra at a broader kinetic energy range are shown in Supplementary Fig. 7.

Fig. 4: Resonant Auger electron spectra.
figure 4

a, b Experimental electron kinetic energy vs. photon energy -maps at low and high X-ray intensities, respectively. The kinetic energy resolution is  ~0.6 eV. c Line spectra from the low intensity (“E”) and high intensity (“F”) measurements, extracted along the correspondingly marked areas in the 2D-maps (a, b) above. On the top, the same spectra are also shown with  10× multiplication, offset for clarity. The SCH-P, as well as the DCH-PP and DCH-SP features are marked. d Calculated SCH and ts-DCH decay spectra. e Experimental synchrotron radiation X-ray photoelectron spectroscopy (SR XPS) reference data from Ueda et al.31 (1σ−1) and Kempgens et al.42 (1σ−1v−11π*1), plotted in the kinetic energy scale EK = 2hν − EB, and scaled arbitrarily in terms of intensity. The partial electron yields extracted along the marked areas “A” to “D” in (a, b) are plotted in Fig. 3b.

Full size image

The low-intensity measurement mostly contains signals from SCH states which are well-known from earlier works38,39,40. The intense peak at  ~384 eV and the shoulder on its high energy side result from SCH participator (SCH-P) decay to the 1\({\pi }_{u}^{-1}\) and 3\({\sigma }_{g}^{-1}\) final states, respectively. These resonant features overlap with dispersive signals corresponding to the single-photon ionization of the valence electrons leading to the same final states (more prominent in the detector along the polarization axis shown in Supplementary Figs. 3 and 6). These features are well reproduced in the SCH calculations, as seen from the comparison of Fig. 4c, d. The steeply rising intensity seen at the low energy end in the experiment is due to spectator transitions (see Supplementary Figs. 4–6).

At high X-ray intensity, additional signatures are observed in the experiment. The two broad features with maxima around  ~380.5 eV and  ~389 eV are respectively assigned to the DCH-SP and DCH-PP decay from doubly excited states. The same regions have only minimal counts in the low-intensity measurement, which likely are faint contributions of the same processes.

Discussion

The observed DCH-SP and DCH-PP line positions are in good agreement with the calculations. Note that the calculations are carried out in the GS geometry and do not account for vibrational and lifetime broadening effects, which are unique for each transition. The SCH-P transition at  ~384 eV does not disperse with the photon energy, due to the broad incident X-ray bandwidth and finite width of the first \(1{\pi }_{g}^{* }\) resonance (Fig. 3). The peak is also quite narrow because the PECs of the core-excited and final ionic states (see Fig. 2) are closely parallel, and transitions with Δv = 0 have maximum intensity39,40. In contrast, for the DCH transitions the bond lengths of the doubly excited states are significantly larger than for the final cation (Fig. 2), especially for DCH-PP since both anti-bonding electrons are removed, and so the calculation should underestimate the peak widths. It is also apparent from those PECs that the transition energy for DCH-PP at the GS geometry, where our calculation is performed, is larger than that at the equilibrium distance of the ts-DCH state (by  ~1.5 eV for DCH-PP), which could help explain the blue shift in the calculated DCH-PP kinetic energy with respect to the experiment in Fig. 4. Additionally, the spectral widths are also connected to the timescale of the double excitation pathway vs. that of nuclear motion, and further complexity can arise from the fact that the larger lifetime width of the ts-DCH state is similar to the vibrational spacing, a situation known to induce strong lifetime-vibrational interference effects41). The assessment of such effects is beyond the scope of the present work.

The results can also be compared with synchrotron radiation X-ray photoelectron spectroscopy (SR XPS) data of single photon ionizations leading to the same final states as DCH-PP and DCH-SP, 1σ−1 and 1σ−1v−11π*1 shake-up (v stands for the 1πu orbital, or to a lesser extent to the 3σg orbital42), respectively. XPS data from Ueda et al.31 (hv = 600 eV) and Kempgens et al.42 (hv = 458 eV) are thus plotted36 in Fig. 4e, assuming 2-photon absorption at present since our process involves two sequential resonant excitations (kinetic energy EK = 2hν − EB, with hν set to hv = 399.7 eV, the center of curve C in Fig. 3b; EB is the binding energy). These XPS lines are in fair agreement with the assigned DCH-SP and DCH-PP features in energy, further supporting their assignment. Note that broadening via the several eV wide double absorption pathway is not reflected in the XPS data, in contrast to the present measurement. The 1σ−1 state is also marked in the 2D maps in Fig. 4a, b by the diagonal dashed lines, dispersing with the photon energy.

We also make a comparison of partial electron yields (PEYs) with the calculated absorption spectra in Fig. 3b, which also support the double-excitation mechanism. The PEY curves are extracted along the marked areas “A” to “D” from the 2D maps in Fig. 4a, b, and correspond to the DCH-SP and SCH-P yields at low and high intensities. As for the SCH-P yield, the DCH-SP yield likewise shows a clear resonant behavior. However, the PEY maximum of DCH-SP (and DCH-PP, not plotted) is red-shifted from the SCH resonance, in full agreement with our calculations in Fig. 3a. In the double excitation process, both resonances must be simultaneously covered by the finite bandwidth of the pulse. Thus the experimental DCH-SP yield maximum is expected to be higher in energy than the maximum in the calculated absorption spectrum for the second excitation step, in agreement with our observation that the maximum is found between the two calculated absorption bands.

It should be considered that the same final states as in DCH-SP (1σ−1v−11π*1) and DCH-PP (1σ−1) could potentially be produced also through competing sequential pathways, where resonant core excitation is followed by valence photoionization. For example, GS → 1σ−11π*1 → 1σ−1. These alternative channels should however show the same photon energy dependence as the SCH-P yield, because the valence ionization step is non-resonant. Therefore, the clear red shift observed in the PEY (Fig. 3b) suggests that the double resonant pathway is more dominant in the present conditions. This is reasonable given that the cross-section of valence ionization is much lower relative to that of resonant core ecitation in our energy range. We do observe a faint dispersive character in the DCH-PP line especially in the 2D map measured at 0∘ relative to the polarization axis (Supplementary Figs. 3 and 6), which may be due to this alternative process.

One also notices a shape change in the SCH-P PEYs between low (B) and high intensities (D). This is likely due to the saturation of the excitation, and can involve a complex competing interplay between the sequential resonant excitation, stimulated emission, and photoionization processes30.

Because the microchannel plate detectors of the electron TOF analyzers are also sensitive to X-ray/UV photons (seen near the zero time-of-flight position), we also obtained total photon yield curves, shown in Supplementary Fig. 8. The total photon yield does not discriminate between emission from SCH and ts-DCH states, but in line with the PEYs, a distinct red-shift and a broadening effect is observed in the high-intensity measurement for the photons as well. This suggests that X-ray emission spectroscopy could also be employed as a probe for the formation of these neutral double core-excited states.

The formation of ts-DCH states should be reflected also in measurements of partial ion yields (PIYs), which are shown in Supplementary Fig. 9. \({{\rm{N}}}_{2}^{+}\) is the exclusive product of SCH-P decay43, while from ts-DCH states it can be produced only by involving a very low probability (≪1%) fluorescence step, which makes it a good probe of the single resonant absorption pathways. Nonlinear processes are seen as higher yields of the multiply charged fragments in the high-intensity measurement, and the maxima of N2+ and N3+ yields show a distinct red-shift which is qualitatively similar to that seen in the DCH-SP (“C” curve) and DCH-PP PEYs (Fig. 3). PIYs however only record final charge states and thus are not selective to any specific electronic state. As such, the PIYs could be sensitive also to alternative excitation schemes that can be readily excluded in the electron spectra. This includes resonant core-excitation of valence ionized \({{\rm{N}}}_{2}^{+}\) where 1σu → 3σg and \(1{\sigma }_{u}\to 1{\pi }_{g}^{* }\) transition energies have been measured at 394–395 eV and 401–405 eV44,45 from the 3σ−1 GS, respectively. Additionally, although prior to core hole decay not much dissociation is expected given the bound geometries of all core excited states (see Fig. 2), the pulse duration in our experiment is slightly longer than the core-hole lifetimes (especially of ts-DCH), and ultrafast dissociation to neutral N and ionic Nn+ fragments and their potential excitation can also be considered. Contributions to the electron signal in the DCH-SP and DCH-PP region from core-excitation of these species can be excluded because either the excitation energies lie outside of the region of interest46, or because the decay electrons fall at lower kinetic energies. In particular, because of the higher second ionization potential, the decay of core excited states from any ionic species would clearly produce electrons with lower kinetic energies than from the neutral ts-DCH molecular states. These alternative 2-photon excitation schemes could on the other hand be more strongly reflected in the PIYs, which seriously complicates their interpretation. Coincident electron-ion detection could greatly improve their usefulness, also as a way to isolate the non-linear components in the electron signal. Using X-ray pulses much shorter47 than the core-hole lifetime and ultrafast dissociation mechanisms on the other hand would simplify the creation of the neutral double core-hole molecular states, and make it possible to study their evolution via a time-resolved absorption measurement30. The slowly rising intensity seen on the higher energy side of the \(1{\pi }_{g}^{* }\) resonance in the PIYs of the atomic fragments is attributed to higher excitations48.

Conclusions

In conclusion, the production of neutral ts-DCH electronic configurations through the resonant double-core excitation process30 was showcased for N2, using intense few-fs X-ray pulses. The findings are supported by the good agreement between electronic structure calculations and the experimentally observed electron kinetic energies and partial electron (and photon and ion) yield absorption profiles of the nonlinear signatures. Such high cross-section and highly selective resonant double (or multi-) core excitation processes should occur universally in XFEL irradiated molecules due to the naturally broad SASE bandwidth. Future experiments may realize resonant core pump/resonant core probe schemes, and also obtain a higher degree of control and resolution with two-color pulses49, including resonantly exciting different elements, as well as creating ss-DCHs. Interestingly, in polyatomic molecules, even the order in which the different atomic sites are preferentially excited should be controllable, as the absorption energetics are accordingly dependent30. All these advanced schemes have the potential to efficiently trigger localized electronic and nuclear dynamics, and follow them in time. Additionally, ultrafast nuclear dynamics following single or double core excitation, preceding core-hole decay, are also of general interest. Measuring decay products (radiative or non-radiative) following core-excitation has long been used to infer ultrafast dissociation mechanisms50,51, and doubly-core-excited states can be expected to exhibit even faster dynamics52, which in turn will be imprinted in the decay spectrum. Since processes like DCH-SP and DCH-PP are specific to the doubly-core-excited states and not directly sensitive to the photon bandwidth of the incoming pulse, we expect that they will be most sensitive to these dynamics. In addition, the shorter lifetimes of the DCH states will improve the time resolution of experiments using them as observables (such as a proxy for XAS), for example using the proposed reconstruction of vibrational wavepackets in a photochemistry experiment from Wang et al.53. We also note that the large bandwidth of the exciting pulse need not represent a limitation to the ultimate energy resolution of the experiment, provided the incident spectrum can be measured on a shot-to-shot basis. Using advanced correlation techniques, it has been shown that high-resolution XAS spectra can be recovered through spectral ghost imaging techniques for example54. It will be interesting to generalize these correlation methods to non-linear XAS techniques. Because of the sequential nature of the excitation processes, interesting questions exist related to their dependence on the spectral chirp. A rarely considered property of XFEL beams, spectral chirp has the potential to be used as a way to control the interaction between the pulse and the sample under study, in a similar manner to the optical regime. First experimental demonstrations of frequency chirp control are appearing55, and double resonant excitations could provide an ideal test case for applications. Finally, extending those studies to temporally coherent, sub-femtosecond pulses47, would, on top of providing better-defined interaction conditions, allow exploring any emerging coherent dynamics that could for example rise from interferences between the decay pathways and direct photoemission, akin to those proposed for nonlinear single resonant core-excitation56,57,58,59.

Methods

Theoretical calculations

In modeling the double excitation process and accompanied electron spectra, the restricted active space self-consistent field (RASSCF) multiconfigurational electronic structure method60,61 and its second-order perturbation theory correction to correlation energy (RASPT2)62,63 have been used. All electron structure calculations in this work were performed in the OpenMolcas software package64. Unless stated otherwise, all calculations in this work were calculated with the ANO-L-VQZP basis set in combination with the Cholesky-based resolution of the identity auxiliary basis65.

Vibrational XANES spectra and PECs

The XANES spectra were calculated at the RASSCF (14, 2, 0; 2, 8, 0) level of theory. This uses the RASSCF(n, l, m; i, j, k) notation, where n, l, and m refer to the total number of active electrons, the maximum number of holes allowed in RAS1, and the maximum number of electrons allowed in RAS3, respectively; i, j, and k refer to the number of orbitals in the RAS1, RAS2, and RAS3 subspaces, respectively. RAS1 contains both the N 1σu and 1σg core orbitals, and RAS2 contains the 5 remaining double occupied orbitals, 2σg, 2σu, 2 × 1πu, and 2σg and an additional 3 virtual orbitals, 2\(\times 1{\pi }_{g}^{* }\) and 3\({\sigma }_{u}^{* }\). The highly excited state and double excited state schemes66 were applied to RAS1 to generate the single and double core excited states, respectively. The dynamic correlation was included with the multistate-restricted active space second-order perturbation theory (MS-RASPT2)62 with an imaginary shift of 0.1 a.u. The transition dipole moments between the ground to SCH and SCH to ts-DCH states were calculated using the restricted active space state interaction (RASSI) method67.

The vibrationally resolved XANES spectra were computed using the FCclasses software program68 using the adiabatic Hessian model within the Franck-Condon approximation. The excitation to the ts-DCH state used a pre-vibrationally excited SCH state comprised of the first two vibrational states69. For the PECs the same electronic structure calculation as the XANES calculations was used at bond lengths every 0.05 Å. The C2v point group symmetry was applied to the XANES and PEC calculations.

Electron spectra

The decay spectra of the SCH and ts-DCH (first step only) states were computed using RASSCF/PT2 wavefunctions for the bound states and the spherical continuum for ionization (SCI) model for the continuum wavefunction and to calculate the partial Auger-decay rates. The SCI method70,71 in the SCAMPI code72 explicitly considers the continuum electron wavefunction by numerically solving the radial Schrödinger equation in the spherically averaged potential of the bound state cation. The bound wavefunctions of SCH and ts-DCH states involved in the spectra were computed with a RASSCF (14, 2, 2; 2, 5, 2) active space, where the N 1σu and 1σg core orbitals were placed into RAS1 with the maximum number of holes set to 2, the five remaining double occupied orbitals, 2σg, 2σu, 2 × 1πu and 2σg were placed into RAS2 and the two unoccupied virtual orbitals, 2\(\times 1{\pi }_{g}^{* }\) placed into RAS3 with the maximum electrons set to 2. The same active space is employed for the SCH and ts-DCH spectra, so a theoretically consistent method is used to evaluate the energy shift of the participator decay channels on an equal footing. However, this active space differs from the XANES calculation by using one less virtual orbital and restricting the number of electrons in the active virtual space to 2, in order to limit the number of possible configurations in the calculation of the final states. 225 and 355 states have been respectively included in the state-averaged RASSCF calculations of the final cation states for the SCH and ts-DCH decay channels. Single-state RASPT2 was applied with an imaginary shift of 0.1 a.u. The calculation of the partial Auger decay rates by the SCI method applied strong orthogonality approximation and neglected the one electron contributions to the partial rates calculation. The SCI method involves a numerical solution to the one-electron radial Schrödinger equation using a spherically averaged potential that includes Slater exchange70,71. A set of orthonormal molecular orbitals produced by a development version of the RASSI module in the OpenMolcas64 was used in the calculation. The maximum angular momentum quantum number used in the partial wave expansion of continuum electron wavefunction was 16. The SCI method assumes the detection of all electrons emitted in any direction, which is best measured at the magic angle. Comparison between the measurements at the magic angle (Supplementary Fig. 2) and perpendicular (Fig. 4) to the X-ray polarization however indicates little angular dependence in our case.

Analysis of the SCH state natural orbitals and occupation numbers has revealed that the core hole is localized on a single N atom. Therefore, the origin of the continuum wave function in the SCI calculation has been centered on the same atom. The DCH states studied herein are ts-DCH states. In order to have a balanced description of the DCH decay from both atomic sites, the origin of the SCI continuum wave function has thus been placed at the center of the molecular bond.

Experimental details

Overview

The experiment was carried out at the SASE3 soft X-ray branch at the European XFEL (Schenefeld, Germany), which was operating at an electron energy of 8 GeV, allowing access to the Nitrogen K-edge energy range. The X-ray pulses were delivered in trains containing 30 pulses each, at 10 trains per second, to an effective 300 Hz operation. Electron spectra were recorded at the Atomic-like Quantum Systems end station of the Small Quantum Systems (SQS) instrument using three identical electron time of flight (TOF) analyzers37, installed at 0° (horizontal), 90° (vertical), and 54.7° (magic angle) with respect to the horizontal X-ray polarization axis. The solid acceptance angle of each analyzer is 0.14% of 4π37. The vertical analyzer could be quickly reconfigured to operate also as an ion TOF mass spectrometer. A continuous flow of N2 was introduced through a small needle to the interaction point. Nonlinear signatures are identified by comparing results with high and low intensities, obtained by varying the X-ray focal spot size at the interaction point. Compared to flux attenuation using e.g., filters or a gas attenuator, this approach presents the advantage of conserving a high average flux at low intensity, as well as the harmonic content. The photon energy was calibrated to the well-known SCH resonance with the low-intensity beam40. The electron TOF to kinetic energy and transmission calibrations were done in reference to Ne 2p photoelectrons measured at varied photon energies, with binding energy from refs. 73,74,75 and cross sections from ref. 76. Jacobian corrections were applied to the intensity in converting the spectra from TOF to E scale.

X-ray bandwidth and pulse duration

Before the main experiment, the spectral span of 2000 FEL shots was individually characterized from the dispersion on an imaging screen using a 50 l/mm grating that was temporarily inserted into the beam path77. The results are shown in Supplementary Fig. 10, including a few examples of the single-shot spectra. A broad energy distribution is seen in each single shot trace, highlighting that both N2 resonances can indeed be well covered in a single XFEL pulse. The FWHM of the total distribution (X-ray bandwidth) is extracted as  ~3.7 eV. These spectral measurements were also used to extract an average value of 8–10 fs for the X-ray pulse duration using statistical methods78,79.

X-ray spot size and intensity

An estimate for the spot sizes and intensities is obtained from the beamline’s optical arrangement. A  ~2.9 × 6.2 mm (Ver. × Hor.) beam size was recorded at an imager close to the KB mirror position. The nominal beam FWHM is  ~2.5 μm at optimal focus at 400 eV (calculated through ray tracing80), corresponding to the high-intensity measurement, with 3.0 m vertical and 1.8 m horizontal focal distances. For the low-intensity measurement, the focal distance was increased by approx. 130 mm for the vertical mirror and 120 mm for the horizontal mirror. From a simple geometric consideration, the spot size at the interaction point is then \(s=\frac{\delta f}{f}\cdot (w-n)+n\), where f is the horizontal or vertical focal distance, w is the corresponding width at the mirror, and n is the nominal focal size. This suggests that the spot size is roughly 130 × 380 μm in the low-intensity measurement. Typical pulse energy measured in the gas monitor detector upstream of the KB mirror was  ~500 μJ, and assuming a 90% transmission for each of the two mirrors, the energy at the interaction point is  ~400 μJ. For a 10 fs pulse, the upstream average power density of 1 × 1011 W/cm2 is concentrated to 3 × 1017 W/cm2 (with a two times higher peak intensity) in the high-intensity measurement or to 4 × 1013 W/cm2 in the low-intensity measurement. Further information on the beamline’s focal characteristics can be found in Mazza et al.80.