Introduction

Spin-orbitronics based on spin-orbit coupling (SOC) offers a promising pathway to power-efficient devices, with spin-orbit torque (SOT) being a typical example1,2. In conventional heavy metal/ferromagnet (HM/FM) bilayers, spin currents generated by spin Hall effect (SHE)3,4 and spin-current-induced SOT2,5,6 have been widely studied. Recently, orbital current carrying orbital angular momentum (OAM) of electrons has introduced promising strategies for both basic research and applications7,8,9. And various OAM-related effects have been intensively studied including the orbital Hall effect (OHE)10,11,12,13, orbital Rashba effect14,15,16, orbital magnetoresistance17, orbital Hanle effect18. Furthermore, research has demonstrated significant SOT arising from the orbital currents in light metal/ferromagnet (LM/FM) bilayers19,20,21,22, in contrast to spin-current-induced SOT. These discoveries highlight the possibility of classifying SOT based on the underlying angular momentum (spin or orbital torque). Unlike SHE depending on SOC23,24, a charge-orbital current conversion by OHE relies on the orbital texture, i.e., the nonuniform distribution of orbital angular momentum in the momentum space12,25. Thus, OHE can occur in both HM and LM materials, even with weak SOC. Moreover, first-principles calculations revealed significant OHE in HMs including Pt, W and Ta13,26, with the orbital Hall conductivity exceeding that of spin. This opens exciting possibilities for exploiting the synergy between spin and orbital torques to enhance the efficiency of SOT in HM/FM multilayers.

Investigating orbital torque in HM/FM bilayers remains a challenge due to the interference of spin torque, hindering its potential applications. Therefore, it is crucial to develop methods for separating and enhancing the contribution of orbital torque to the total SOT in HM/FM systems. As shown in Fig. 1a, spin current generated by HM is fully absorbed by the HM/FM interface and converted into spin torque. Due to rapid dephasing and decay caused by strong scattering from magnetic moments27,28,29, spin torque acts as an interface effect independent of the FM layer thickness in ideal circumstances30,31,32. In contrast, orbital current exhibits a slower decay and longer SOT conversion length within 3d-FM21,22,33. And thicker FM layers are often employed in LM/FM bilayers13,21,22 (Fig. 1b) to improve conversion. Consequently, the HM/FM interface acting as natural spin filter can spatially separate orbital current from mixed angular momentum. Furthermore, the separated orbital current can be readily detected by introducing an additional capping layer with strong SOC to convert the orbital current into orbital torque. Previous studies have shown the effectiveness of strong SOC materials for efficient orbital torque manipulation34,35,36. Moreover, the various in the total SOT caused by varying the thickness of center FM layer can help distinguish spin and orbital torque contributions. This separation allows for further manipulation and utilization of orbital torque in future applications.

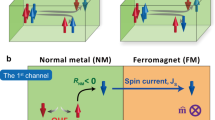
Fig. 1: Schematic illustrations of the spin and orbital currents in HM/FM multilayers.
figure 1

a, b Spin (a) and orbital (b) currents transport and conversion in HM(LM)/FM. Blue straight and red curved arrows indicate spin and orbital angular momentums, respectively. Yellow curved arrows represent the flow of angular momentum. Black arrows denote the magnetic moment, and the small arrows near magnetic moment indicate spin (blue) and orbital (red) torques. For the spin current (a), it generates spin torque at HM/FM interface and undergoes dephasing. For the orbital current (b), it is converted into orbital torque by FM with weak SOC. c Spin and orbital transports in our HM/FM/FMSOC structure, and their contribution to SOT. The behavior of spin current is like in a. However, orbital current will pass through the FM without SOC and be converted into orbital torque after entering the FM layer with SOC.

Full size image

In this study, we propose a HM/FM/FMSOC multilayers structure shown in Fig. 1c to study the OHE and separate orbital torque. Here, HM is Pt or β-Ta generating both spin and orbital currents. FM is 3d metal Co with weak SOC, and FMSOC is CoPt alloy or Co/Pt bilayer with strong SOC. The spin current is fully absorbed at the HM/FM interface, resulting in a FM-thickness-independent spin torque. While the orbital current diffuses through the FM layer and subsequently generates SOT in the FMSOC layer, leading to a FM-thickness-dependent orbital torque. Thus, the orbital torque in HM systems is quantitatively separated. Furthermore, the synergistic operation of orbital and spin torque for magnetization switching and the enhanced SOT efficiency by 110% are achieved. Our study unlocks possibilities for exploiting the synergistic operation of orbital and spin torque for future applications in magnetic devices.

Results and discussion

Samples and measurement

A series of samples, Pt(5)/Co(t)/CoPt(2), Ta(5)/Co(t)/CoPt(2), Pt(5)/Co(t)/Pt(1) with varying Co thickness \({t}_{{{\rm{Co}}}}\), along with their control groups Pt(5)/Co(t), Co(t)/CoPt(2) and so on were deposited on thermally oxidized Si substrate via magnetron sputtering, where all thicknesses are in nanometer. Subsequently, all samples were patterned into Hall bar devices using photolithography and Ar+ etching for electrical transport measurement, as illustrated in Fig. 2a. The saturation magnetization of Co and CoPt alloy is 1092 emu cm-3 and 525 emu cm-3, respectively, with further details provided in Supplementary Note 1. Anomalous Hall effect (AHE) measurement detailed in Supplementary Note 2 were performed to determine the AHE resistance and magnetic easy axis. Most samples exhibits in-plane magnetization, except for Pt(5)/Co(t) with \({t}_{{{\rm{Co}}}}\) ≤ 1 nm, Pt(5)/Co(t)/Pt(1) with \({t}_{{{\rm{Co}}}}\) ≤ 2 nm, Pt(5)/Co(1)/Al(1)/Pt(1) and Pt(5)/Co(1)/Pt(5). To evaluate SOT efficiency, two harmonic Hall methods with consistency, sweeping field and rotating field method37,38, were employed to measure the damping-like and field-like SOT effective fields \({\mu }_{0}{H}_{{{\rm{DL}}},{{\rm{FL}}}}\) for in-plane and out-of-plane magnetization samples, with additional details provided in Supplementary Note 3. Figure 2b shows the first and second harmonic Hall resistance \({R}_{{xy}}^{{\mathrm{1,2}}\omega }\) of out-of-plane sample Pt(5)/Co(1)/Pt(1), where \({R}_{{xy}}^{1\omega }\) takes on parabolic shape and \({R}_{{xy}}^{2\omega }\) is linear. And Fig. 2c. shows the \({\mu }_{0}{H}_{{{\rm{DL}}}}\) of Pt(5)/Co(1)/Pt(1) and Pt(5)/Co(1) as obtained from \({R}_{{xy}}^{{\mathrm{1,2}}\omega }\) under different current density in bottom HM \({J}_{{{\rm{HM}}}}\). The \({\mu }_{0}{H}_{{{\rm{DL}}}}\) increases linearly with \({J}_{{{\rm{HM}}}}\), and Pt(5)/Co(1)/Pt(1) has higher \({\mu }_{0}{H}_{{{\rm{DL}}}}\) due to orbital torque, despite the spin current generated by top Pt(1) attenuating SOT. Furthermore, Fig. 2d reveals various dependency of \({\mu }_{0}{H}_{{{\rm{DL}}}}\) on Co thickness induced by orbital torque in sample series Pt(5)/Co(t)/CoPt(2), Pt(5)/Co(t) and Pt(5)/Co(t)/Pt(1). Note that the \({t}_{{{\rm{Co}}}}^{* }\) in Fig. 2d represents the equivalent Co thickness considering the total magnetic moment, implying that Co(t)/CoPt(2) is treated as Co(t + 1). Ideally, when the angular momentum of spin current is fully absorbed in HM/FM interface, the \({\mu }_{0}{H}_{{{\rm{DL}}}}\) is expected to be linear to \(1/{t}_{{{\rm{Co}}}}^{* }\)30,31,32 as observed in Pt(5)/Co(t) series. However, deviations from this linear relation are observed in Pt(5)/Co(t)/CoPt(2) and Pt(5)/Co(t)/Pt(1) series as \(1/{t}_{{{\rm{Co}}}}^{* }\) increases. This deviation indicates the presence of an additional orbital torque contribution that does not originate solely from the HM/FM interface. In order to accurately analysis the contribution of orbital torque, we calculated SOT efficiency \({\xi }_{{{\rm{DL}}},{{\rm{FL}}}}\) and it can be expressed by Ref. 39

$${\xi }_{{{\rm{DL}}},{{\rm{FL}}}}=\frac{2e}{{{\hslash }}}\frac{{\mu }_{0}{H}_{{{\rm{DL}}},{{\rm{FL}}}}}{{J}_{{{\rm{HM}}}}} {\sum}_{i}{M}_{{{\rm{s}}}}^{i}{t}_{{{\rm{FM}}}}^{i}$$
(1)

where \(e\) is elementary charge, \(\hslash\) is reduced Plank constant, \({\mu }_{0}\) is vacuum permeability, \({M}_{{{\rm{s}}}}^{i}\) and \({t}_{{{\rm{FM}}}}^{i}\) are the saturation magnetization and thickness of the i-th FM layer, respectively. The sum of \({M}_{{{\rm{s}}}}^{i}{t}_{{{\rm{FM}}}}^{i}\) means the total magnetic moment of Co and CoPt with ferromagnetic coupling. \({J}_{{{\rm{HM}}}}\) is obtained by the current shunting in HM layer, with further details provided in Supplementary Note 4.

Fig. 2: Extraction of the damping-like effective field in HM/FM multilayers.
figure 2

a Schematic illustration of electric transport measurement of Hall bar device and multilayer structure. b First and second harmonic Hall resistance \({R}_{{xy}}^{{\mathrm{1,2}}\omega }\) with respect to in-plane field \({\mu }_{0}{H}_{x}\) of Pt(5)/Co(1)/Pt(1) and their fitting curves, the three \({R}_{{xy}}^{2\omega }\) curves are the results under different current density \({J}_{{{\rm{HM}}}}\). c Damping-like effective field \({\mu }_{0}{H}_{{{\rm{DL}}}}\) of Pt(5)/Co(1)/Pt(1) (red) and Pt(5)/Co(1) (brown) with respect to \({J}_{{{\rm{HM}}}}\). The three points with different \({J}_{{{\rm{HM}}}}\) of Pt(5)/Co(1)/Pt(1) correspond to the three \({R}_{{xy}}^{2\omega }\) curves in b. d Different relation between equivalent Co thickness \({t}_{{{\rm{Co}}}}^{* }\) and \({\mu }_{0}{H}_{{{\rm{DL}}}}\) when \({J}_{{{\rm{HM}}}}\) is 1 MA cm-2. The \({\mu }_{0}{H}_{{{\rm{DL}}}}\) of Pt(5)/Co(t) (brown) is linear to \(1/{t}_{{{\rm{Co}}}}^{* }\). But for Pt(5)/Co(t)/CoPt(2) (blue) and Pt(5)/Co(t)/Pt(1) (red), the \({\mu }_{0}{H}_{{{\rm{DL}}}}\) deviates from this linear relation. Error bars in c and d represent the standard deviation uncertainties and are smaller than the markers.

Full size image

Orbital torque in Pt/Co/CoPt and Ta/Co/CoPt

The difference in \({\xi }_{{{\rm{DL}}}}\) between Pt(5)/Co(t) and Pt(5)/Co(t)/CoPt(2) caused by orbital current is shown in Fig. 3a. For Pt(5)/Co(t), the \({\xi }_{{{\rm{DL}}}}\) is approximately 0.11 and slightly increases from 0.105 to 0.115 with \({t}_{{{\rm{Co}}}}\), consistent with literature reports30,39,40. However, for Pt(5)/Co(t)/CoPt(2), the \({\xi }_{{{\rm{DL}}}}\) increases from 0.085 of Pt(5)/Co(0.8)/CoPt(2) to a constant 0.115 with \({t}_{{{\rm{Co}}}}\), indicating that Pt(5)/Co(t)/CoPt(2) has similar \({\xi }_{{{\rm{DL}}}}\) to Pt(5)/Co(t) when the Co layer attains sufficient thickness. Additionally, there is no significant difference in \({\xi }_{{{\rm{FL}}}}\) shown in Supplementary Note 5, consistent with the literature report41. The \({\xi }_{{{\rm{DL}}}}\) of Pt(5)/Co(t)/CoPt(2) with thin Co layer deviates from that of Pt(5)/Co(1), which can be explained as the former containing positive spin contribution \({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}\) and negative orbital contribution \({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}\) with different transport properties. Owing to Pt’s positive spin Hall conductivity \({\sigma }_{{{\rm{SH}}}}^{{{\rm{Pt}}}}\) and orbital Hall conductivity \({\sigma }_{{{\rm{OH}}}}^{{{\rm{Pt}}}}\), Pt(5) generates positive spin and orbital currents13,26. Spin current induces positive spin torque and decoherence within a few atomic layers at the Pt/Co interface27,28,29, resulting constant and \({t}_{{{\rm{Co}}}}\)-independent \({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}\) (~ 0.11) as seen in Pt(5)/Co(t). In contrast, orbital current is converted into orbital torque \({\xi }^{{{\rm{OH}}}}\propto {\sigma }_{{{\rm{OH}}}}{\eta }_{{{\rm{LS}}}}\)19,20 under SOC, where \({\eta }_{{{\rm{LS}}}}\) is effective conversion coefficient associated with SOC. This implies that orbital current efficiently diffuses through the Co layer with weak SOC, then enters CoPt(2) layer with strong SOC and induces negative orbital torque (\({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}\) < 0), as shown in Fig. 3b. Consequently, the \({\xi }_{{{\rm{DL}}}}\) decrease for Pt(5)/Co(t)/CoPt(2) with thin Co layers, and it converges to that of Pt(5)/Co(t) when the Co layer is sufficiently thick for the orbital current to decay completely. Furthermore, the small orbital conversion induced by Co can explain the roughly unchanged but slightly increased \({\xi }_{{{\rm{DL}}}}\) in the Pt(5)/Co(t) series.

Fig. 3: Separation and manipulation of damping-like SOT efficiency in Pt/Co/CoPt and Ta/Co/CoPt.
figure 3

a, c Damping-like SOT efficiency \({\xi }_{{{\rm{DL}}}}\) of (a) Pt(5)/Co(t) (brown), Pt(5)/Co(t)/CoPt(2) (blue) and (c) Ta(5)/Co(t)/CoPt(2) (green) with different Co layer thickness \({t}_{{{\rm{Co}}}}\), and their SOT contribution of spin torque \({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}\) (light violet shading) and orbital torque \({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}\)(light orange shading). Where the curve is the fitting of diffusion equation. The \({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}\) and \({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}\) in Pt(5)/Co(t)/CoPt(2) (a) have inverse sign, orbital torque leads to a decrease in \({\xi }_{{{\rm{DL}}}}\). And the \({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}\) and \({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}\) in Ta(5)/Co(t)/CoPt(2) (c) have same sign, orbital torque causes \({\xi }_{{{\rm{DL}}}}\) increase. As \({t}_{{{\rm{Co}}}}\) increases, \(\left|{\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}\right|\) decreases, and \({\xi }_{{{\rm{DL}}}}\) approaches \({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}\). b, d Schematic illustration of spin (blue straight arrows) or orbital (red curved arrows) current transport and SOT generation in (b) Pt(5)/Co(t)/CoPt(2) and (d) Ta(5)/Co(t)/CoPt(2). Where Pt has positive spin Hall conductivity (\({\sigma }_{{{\rm{SH}}}}^{{{\rm{Pt}}}}\) > 0) and orbital Hall conductivity (\({\sigma }_{{{\rm{OH}}}}^{{{\rm{Pt}}}}\) > 0), Ta has negative spin Hall conductivity (\({\sigma }_{{{\rm{SH}}}}^{{{\rm{Ta}}}}\) < 0) and positive orbital Hall conductivity (\({\sigma }_{{{\rm{OH}}}}^{{{\rm{Ta}}}}\) > 0). Spin current generates spin torque at Pt/Co or Ta/Co interface, and orbital current passes through Co and is converted into negative orbital torque in CoPt alloy with negative conversion coefficient \({\eta }_{{{\rm{LS}}}}\). And the black arrows denote the magnetic moment and SOT induced deflection. Error bars in a and c represent the standard deviation. and indicate spin and orbital angular momentums, respectively.

Full size image

For Ta(5)/Co(t)/CoPt(2), the variation of \({\xi }_{{{\rm{DL}}}}\) with \({t}_{{{\rm{Co}}}}\) exhibits a similar behavior as Pt(5)/Co(t)/CoPt(2). The absolute value \(\left|{\xi }_{{{\rm{DL}}}}\right|\) of Ta(5)/Co(t)/CoPt(2) declines from 0.07 to a constant 0.035, as shown in Fig. 3c. This change of \(\left|{\xi }_{{{\rm{DL}}}}\right|\) can also be explained by the orbital transport and conversion. Ta has negative \({\sigma }_{{{\rm{SH}}}}^{{{\rm{Ta}}}}\) and positive \({\sigma }_{{{\rm{OH}}}}^{{{\rm{Ta}}}}\)13,26. And the negative \({\eta }_{{{\rm{LS}}}}\) of CoPt alloy results in negative orbital torque (\({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}\) < 0), which has same sign as spin torque (\({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}\) < 0). Thus, the orbital current in Ta(5)/Co(t)/CoPt(2) with thinner Co layer enhances total SOT and \(\left|{\xi }_{{{\rm{DL}}}}\right|\) decreases as \({t}_{{{\rm{Co}}}}\) increases, as shown in Fig. 3d. Moreover, the additional negative SOT contribution in both Pt(5)/Co(t)/CoPt(2) and Ta(5)/Co(t)/CoPt(2) with thinner Co layer further indicate that the variation of SOT is not caused by spin-dependent effects. Additionally, to avoid potential impact of HM/FM interface effect on SOT, such as spin transparency42 and spin memory loss43, we bypassed the samples Pt/CoPt and Ta/CoPt with \({t}_{{{\rm{Co}}}}\,\)= 0 ensuring interfacial consistency. And we also excluded samples with ultra-thin Co (\({t}_{{{\rm{Co}}}}\,\)≤ 0.5) to ensure complete spin absorption.

Our disorder CoPt alloy possesses negative \({\eta }_{{{\rm{LS}}}}\), which does not maintain the same sign as the positive \({\eta }_{{{\rm{LS}}}}\) of Co13 or Pt inserting layer34. To further confirm the negative \({\eta }_{{{\rm{LS}}}}\), we measured the SOT of Ru(5)/CoPt(2). Ru has negligible and positive \({\sigma }_{{{\rm{SH}}}}^{{{\rm{Ru}}}}\) and significant positive \({\sigma }_{{{\rm{OH}}}}^{{{\rm{Ru}}}}\)33. However, Ru(5)/CoPt(2) exhibits significant negative SOT, \({\xi }_{{{\rm{DL}}}}\,\)= -0.04, indicating negative \({\eta }_{{{\rm{LS}}}}\), shown in Supplementary Note 6. The negative \({\eta }_{{{\rm{LS}}}}\) could be attributed to the band structure of CoPt alloy. In disorder CoPt alloy, Pt atoms with strong SOC might dominate the orbital torque depending SOC. Moreover, in L10-CoPt, Pt-5d atoms have more occupation in negative spin states near Fermi level44. Thus, the coupling between negative spin states of Pt-5d and orbital current might induce the negative \({\eta }_{{{\rm{LS}}}}\) in disorder CoPt. Similarly, the negative \({\eta }_{{{\rm{LS}}}}\) of GdxCo1-x45 and TbxCo1-x46 could be attributed to the occupation of Gd-5d and Tb-5d in negative spin states47. It should be emphasized that this is just a simple guess. Detailed mechanism analysis requires first principles calculations.

We further checked the SOT of Co(t)/CoPt(2) and the spin mixing conductivity \({G}_{{{\rm{eff}}}}^{\uparrow \downarrow }\) of Pt(5)/Co(t) interface. The \(\left|{\mu }_{0}{H}_{{{\rm{DL}}}}\right|\) of Co(t)/CoPt(2) is less than 5 μT at an average current density of 1 MA cm-2 (Supplementary Note 7). Thus, the spin current generated by CoPt(2)48 or the anomalous spin Hall effect of Co(t) can be disregarded49,50. Additional ferromagnetic resonance (FMR) measurement was used to assess \({G}_{{{\rm{eff}}}}^{\uparrow \downarrow }\), and the details are shown in Supplementary Note 8. The \({G}_{{{\rm{eff}}}}^{\uparrow \downarrow }\) of the Pt/Co interface in Pt(5)/Co(t)/CoPt(2) series decreases from 18 × 1018 to 7 × 1018 m-2 with increasing \({t}_{{{\rm{Co}}}}\). This is not only inconsistent with the change in \({\xi }_{{{\rm{DL}}}}\) of Pt(5)/Co(t)/CoPt(2), but also deviates from the constant \({G}_{{{\rm{eff}}}}^{\uparrow \downarrow }\) in ideal Pt/Co interface. Furthermore, in our experiment Co with different thicknesses was grown on bottom Pt(5), so the Pt/Co interface should remain constant. However, the increased \(\alpha\) could be attributed to the inverse orbital torque, confirmed in YIG/Pt/CuOx by FMR and spin pumping51. The CoPt alloy layer can effectively convert orbital current into torque, suggesting that the CoPt layer might generate orbital current in FMR measurement. This orbital current may cause orbital pumping, leading to an increase in \({G}_{{{\rm{eff}}}}^{\uparrow \downarrow }\) for the samples with thinner Co layer. Conversely, for thicker Co layer, the \({G}_{{{\rm{eff}}}}^{\uparrow \downarrow }\) is similar as Pt/Co interface, i.e., 7×1018 m-2 reported in literature52. In summary, the influence of Pt/Co interface on \({\xi }_{{{\rm{DL}}}}\) can be excluded.

Orbital torque in Pt/Co/Pt

Thin Pt top layer can effectively convert orbital current into SOT and has positive \({\eta }_{{{\rm{LS}}}}\), just as Pt inserting layer34 between non-magnetic layer and FM layer. Figure 4a describes the \({\xi }_{{{\rm{DL}}}}\) of Pt(5)/Co(t)/Pt(1) series, which decreases from 0.14 of Pt(5)/Co(1)/Pt(1) to a constant 0.095 with increasing \({t}_{{{\rm{Co}}}}\). Note that the \({\xi }_{{{\rm{DL}}}}\) of Pt(5)/Co(1)/Pt(1) clearly surpasses Pt(5)/Co(1), consistent with the finding of Chen et al.53. This change of \({\xi }_{{{\rm{DL}}}}\) can be explained by the orbital transport and conversion, as shown in Fig. 4b. The spin current from Pt(5) induce a constant \({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}\) at the lower Pt/Co interface. Whereas, the orbital current from Pt(5) is converted into positive orbital torque \({\xi }_{{{\rm{DL}}}}^{{{\rm{O}}}{{\rm{H}}}}\) by top Pt(1) after passing through Co(t), enhancing the spin torque from lower Pt(5)/Co(1) interface. Moreover, the decay of orbital current in Co layer leads to a decrease in \({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}\) with \({t}_{{{\rm{Co}}}}\). Furthermore, due to the negative spin torque \({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}2}\) generated by top Pt(1) offsetting part of the SOT, the \({\xi }_{{{\rm{DL}}}}\) of Pt(5)/Co(t)/Pt(1) with thick Co layer is lower than that of Pt(5)/Co(t). And the magnitude of \({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}2}\)(~ -0.02) satisfies the SHE strength of the Pt(1) according to the drift-diffusion equation39. In terms of the orbital current conversion in Pt(5)/Co(t)/Pt(1), upper Co(t)/Pt(1) interface might play a key role. This is evident as the \({\xi }_{{{\rm{DL}}}}\) of Pt(5)/Co(1)/Al(1)/Pt(1), with light metal Al spacer layer breaking the upper Co/Pt interface, is only 0.092 (see Fig. 4a), which corresponds to the spin torque contribution \({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}+{\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}2}\)(~ 0.09) in Pt(5)/Co(t)/Pt(1).

Fig. 4: Enhanced SOT efficiency via synergic operation of orbital and spin currents in Pt/Co/Pt and diffusion model.
figure 4

a The \({\xi }_{{{\rm{DL}}}}\) of Pt(5)/Co(t) (brown) and Pt(5)/Co(t)/Pt(1) (red) with different \({t}_{{{\rm{Co}}}}\), and anomalous Pt(5)/Co(1)/Al(1)/Pt(1) (black square) and Co(1)/Pt(5) (black star). The spin torque contribution (light violet shading) come from bottom Pt(5) (\({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}\) > 0) and top Pt(1) (\({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}2}\) < 0). The orbital torque contribution (light orange shading) \({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}\) is positive and the orbital torque from top Pt(1) is ignored here. The total spin torque \({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}+{\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}2}\) and \({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}\) have same sign, i.e., orbital torque increases \({\xi }_{{{\rm{DL}}}}\). The error bars represent the standard deviation uncertainties and are smaller than the markers. b Schematic illustration of spin (blue straight arrows) or orbital (red curved arrows) current transport and SOT generation in Pt(5)/Co(t)/Pt(1). Where Pt has positive spin Hall conductivity (\({\sigma }_{{{\rm{SH}}}}^{{{\rm{Pt}}}}\) > 0) and orbital Hall conductivity (\({\sigma }_{{{\rm{OH}}}}^{{{\rm{Pt}}}}\) > 0). Spin current generates spin torque at lower Pt/Co interface, and orbital current passes through Co and is converted into positive orbital torque at upper Co/Pt interface with positive conversion coefficient \({\eta }_{{{\rm{LS}}}}\). And the black arrows denote the magnetic moment and SOT induced deflection. c Current-induced magnetization switching curve, Hall resistance \({R}_{{xy}}\) with respect to \({J}_{{{\rm{HM}}}}\), of Pt(5)/Co(1) (brown) and Pt(5)/Co(1)/Pt(1) (red). Pt(5)/Co(1)/Pt(1) has lower switching current density and higher \({\mu }_{0}{H}_{{{\rm{k}}}}\), meaning higher switching efficiency. d Orbital torque contribution \({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}\) with respect to \({t}_{{{\rm{Co}}}}\) of three series samples, Pt(5)/Co(t)/Pt(1) (red), Ta(5)/Co(t)/CoPt(2) (green) and Pt(5)/Co(t)/CoPt(2) (blue). They can be fitted well by same diffusion length parameter \({\lambda }_{{{\rm{d}}}}^{{{\rm{Co}}}}\).

Full size image

To further confirm the role of upper Co/Pt interface in orbital torque, we measured the SOT of Pt(5)/Co(1)/Pt(5) and Co(1)/Pt(5). For Pt(5)/Co(1)/Pt(5), \({\xi }_{{{\rm{DL}}}}\) is -0.09 as shown in Supplementary Note 9, consistent with the inference of orbital torque by upper Co/Pt interface. The spin torques by top Pt(5) (\({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}2}\)) and bottom Pt(5) (\({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}\)) cancel out each other, \({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}2}\,\)~ -0.11 and \({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}+{\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}2}\,\)~ 0. Due to the weak \({\eta }_{{{\rm{LS}}}}\) of lower Pt/Co interface, positive orbital current from bottom Pt(5) undergoes decay and generates orbital torque (\({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}\,\)> 0) at the upper Co/Pt interface. Whereas, negative orbital current from top Pt(5) can be directly and more efficiently converted into orbital torque (\({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}2}\,\)< 0) at the upper Co/Pt interface, resulting in \({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}+{\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}2}\,\)~ -0.09. According to the \({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}\,\)~ 0.05 of Pt(5)/Co(1)/Pt(1), \({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}2}\) is approximately -0.14, consistent with the limit of orbital torque caused by bottom Pt(5) at the upper Co/Pt interface (0.15 at \({t}_{{{\rm{Co}}}}\,\)= 0 in the fitting curve of Pt(5)/Co(t)/Pt(1), as shown in Fig. 4a, with more details in next subsection). In addition, similar asymmetric SOT of Pt(5)/Co/Pt(2) and Pt/(2)Co/Pt(5) has also been reported54. And in the report by Huang et al.55, negative SOT was observed in symmetric Pt(t)/Co/Pt(t), and the saturation behavior of negative SOT with respect to \({t}_{{{\rm{Pt}}}}\) in Pt(2)/Co/Pt(t) resembled \({t}_{{{\rm{Pt}}}}\)-dependent OHE56 rather than SHE39. For Co(1)/Pt(5), \({\xi }_{{{\rm{DL}}}}\) is -0.23 as illustrated in Fig. 4a, marking a significant increase of 110% compared to normal bilayer Pt(5)/Co(1). And the \({\xi }_{{{\rm{DL}}}}\) approximately matches the \({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}2}+{\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}2}\,\)~ -0.25. Additionally, this difference in \({\eta }_{{{\rm{LS}}}}\) between upper Co/Pt and lower Pt/Co interfaces is attributed to their structural differences. One evidence is that Pt(5)/Co(1) is out-of-plane magnetization whereas Co(1)/Pt(5) is in-plane magnetization, likely due to interfacial intermixing. This intermixing of upper Co/Pt interface might lead to stronger magnetic proximity effect57. In addition, the change in stacking order might affect the crystal orientation of Pt, contributing to the enhanced magnetic proximity effect at the upper Co/Pt interface58. SOC is crucial for the orbital conversion19,20. Therefore, both interfacial intermixing and magnetic proximity effect involving Pt with strong SOC cause high \({\eta }_{{{\rm{LS}}}}\) and high orbital torque.

In order to verify the assistance of orbital torque in magnetization switching, we measured the current-induced magnetization switching of out-of-plane magnetization sample Pt(5)/Co(1) and Pt(5)/Co(1)/Pt(1). A current pulse with a width of 50 μs was applied, along with an external magnetic field \({\mu }_{0}{H}_{x}\) of 50 mT in the \(x\) axis direction to achieve deterministic switching. The hysteresis loops are shown in Fig. 4c, where the horizontal axis \({J}_{{{\rm{HM}}}}\) represents the current density of the bottom layer Pt(5) considering shunt. The critical current densities of Pt(5)/Co(1) and Pt(5)/Co(1)/Pt(1) are 33 and 28.5 MA cm-2, respectively. Considering the difference in anisotropy field \({\mu }_{0}{H}_{{{\rm{k}}}}\) between the two samples, 0.31 mT for Pt(5)/Co(1) and 0.49 mT for Pt(5)/Co(1)/Pt(1), the macrospin model is employed to further describe current-induced magnetization switching59.

$${J}_{{{\rm{c}}}}=\frac{e}{{{\hslash }}}\frac{{\mu }_{0}{M}_{{{\rm{s}}}}{t}_{{{\rm{Co}}}}}{{\xi }_{{{\rm{DL}}}}}\left({H}_{{{\rm{k}}}}-\sqrt{2}\left|{H}_{x}\right|\right)$$
(2)

According to the macrospin model, the SOT efficiency of Pt(5)/Co(1)/Pt(1) is twice that of Pt(5)/Co(1), indicating the synergistic operation of orbital and spin torque.

Diffusion transport of orbital current

To analyze the orbital current transport and orbital torque in HM(5)/Co(t)/CoPt(2) and Pt(5)/Co(t)/Pt(1), we employed a diffusion model to describe the changes in \({\xi }_{{{\rm{DL}}}}\). If only the orbital current diffusion in the Co layer and orbital conversion in CoPt alloy or upper Co/Pt interface are considered, the effect of orbital current on SOT can be described by

$${\xi }_{{{\rm{DL}}}}={\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}+{\xi }_{{{\rm{DL}}}0}^{{{\rm{OH}}}}{{{\rm{e}}}}^{-{t}_{{{\rm{Co}}}}/{\lambda }_{{{\rm{d}}}}^{{{\rm{Co}}}}}$$
(3)

where \({\lambda }_{{{\rm{d}}}}^{{{\rm{Co}}}}\) is the diffusion length of orbital current in Co. Here, \({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}\) is total spin torque and \({\xi }_{{{\rm{DL}}}0}^{{{\rm{OH}}}}\) means the limit of orbital torque at \({t}_{{{\rm{Co}}}}\,\)= 0, i.e., \({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}={\xi }_{{{\rm{DL}}}0}^{{{\rm{OH}}}}{{{\rm{e}}}}^{-{t}_{{{\rm{Co}}}}/{\lambda }_{{{\rm{d}}}}^{{{\rm{Co}}}}}\). Using this equation to fit the data, the fitting curves shown in the Fig. 3a, c and Fig. 4a describes the data changes well, with the fitting parameters are shown in Tab. 1. It is observed that diffusion length \({\lambda }_{{{\rm{d}}}}^{{{\rm{Co}}}}\) ≈ 1 nm is obviously smaller than Ni22,33. Nevertheless, the saturation behavior at approximately 3 nm of orbital torque in our sample resembles that reported in Co/CuOx by Ding et al.16. Furthermore, utilizing the mean value 0.98 nm for \({\lambda }_{{{\rm{d}}}}^{{{\rm{Co}}}}\) can well fit the \({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}\) without spin torque background, i.e., \({\xi }_{{{\rm{DL}}}}-{\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}\), as shown in Fig. 4d. Therefore, we conclude that the orbital diffusion length is inherently smaller for Co. For the CoPt alloy with strong SOC, the conversion or decay of the orbital current should be faster than that in Co with saturation at 3 nm. Thus, CoPt(2) should be sufficient to convert the orbital current. However, the \(\left|{\xi }_{{{\rm{DL}}}0}^{{{\rm{OH}}}}\right|\) of Pt(5)/Co(t)/Pt(1) (0.15) is significantly greater than Pt(5)/Co(t)/CoPt(2) (0.07). This disparity may stem from the underestimation of \({\lambda }_{{{\rm{d}}}}^{{{\rm{Co}}}}\) and overestimation of \({\xi }_{{{\rm{DL}}}0}^{{{\rm{OH}}}}\) with standard deviation of 0.04 in the fitting of the former, or more decay of orbital current in disordered CoPt alloy. Furthermore, CoPt alloy might not be the optimal candidate for orbital current conversion. However, it is certain that the strength of orbital torque is equivalent to spin torque for Pt, consistent with the results of first-principle calculation13,25 and recent report56. And based on \({\xi }_{{{\rm{DL}}}0}^{{{\rm{OH}}}}\) of 0.15, the effective orbital Hall conductivity \({\sigma }_{{{\rm{OH}}}}^{{{\rm{Pt}}}}\) = 2830 ℏ/2e·Ω-1cm-1. Additionally, it is noteworthy that our Pt-based HM/FM multilayer exhibits higher \({\xi }_{{{\rm{DL}}}}^{{{\rm{OH}}}}\) compared with Cr-based LM/FM multilayer achieving SOT switching34,35.

Table. 1 Fitting parameters of the diffusion model describing orbital torque contribution
Full size table

According to this diffusion model, the fitting curves of \({\mu }_{0}{H}_{{{\rm{DL}}}}\) with respect to \({t}_{{{\rm{Co}}}* }\) shown in Fig. 1d can be expressed by

$${\mu }_{0}{H}_{{{\rm{DL}}}}=\frac{{{\hslash }}}{2e}\frac{{J}_{{{\rm{HM}}}}}{{M}_{{{\rm{S}}}}{t}_{{{\rm{Co}}}}^{* }}\left({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}+{\xi }_{{{\rm{DL}}}0}^{{{\rm{OH}}}}{{{\rm{e}}}}^{-{t}_{{{\rm{Co}}}}/{\lambda }_{{{\rm{d}}}}^{{{\rm{Co}}}}}\right)$$
(4)

Where the first linear term is caused by the spin torque at the bottom Pt/Co interface, and the second nonlinear term is orbital torque generated in CoPt alloy or upper Co/Pt interface.

We further consider the orbital current conversion caused by weak SOC when the orbital current diffuses in the Co layer. Assuming that the orbital torque on Co atoms is directly proportional to the strength of local orbital current, the total orbital torque can be expressed as the integral of the above diffusion equation, the \({\xi }_{{{\rm{DL}}}}\) of Pt(5)/Co(t) can be represented as

$${\xi }_{{{\rm{DL}}}}^{{{\rm{Co}}}}={\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}+{\xi }_{{{\rm{DL}}}0}^{{{\rm{OH}}}}\left(1-{{{\rm{e}}}}^{-{t}_{{{\rm{Co}}}}/{\lambda }_{{{\rm{d}}}}^{{{\rm{Co}}}}}\right)$$
(5)

Using this equation to fit Pt(5)/Co(t) series can obtain \({\lambda }_{{{\rm{d}}}}^{{{\rm{Co}}}}\) = 0.88 ± 0.26 nm, \({\xi }_{{{\rm{DL}}}}^{{{\rm{SH}}}}\) = 0.094 ± 0.004 and \({\xi }_{{{\rm{DL}}}0}^{{{\rm{OH}}}}\) = 0.022 ± 0.004. The \({\lambda }_{{{\rm{d}}}}^{{{\rm{Co}}}}\) closely aligns with that presented in Tab. 1. Thus, the increase of \({\xi }_{{{\rm{DL}}}}\) in Pt(5)/Co(t) might be attributed to the influence of orbital torque. However, it is essential to note the change of easy axis and harmonic measurement method before and after Pt(5)/Co(1), where \({\xi }_{{{\rm{DL}}}}\) changes the most. Incorporating these parameters into the previous fitting may introduce inaccuracies. Hence, we will only consider them as part of a discussion regarding their potential impact.

Conclusions

In conclusion, our HM/FM/FMSOC multilayer structure effectively investigates orbital torque and orbital current transport in HM-FM system. The HM/FM interface adsorbs spin current generating constant spin torque. In contrast, separated orbital current diffuses in 3d-FM with weak SOC and generates orbital torque in FMSOC with strong SOC. In our experiment, Pt(5)/Co(t) without FMSOC layer exhibits constant \({\xi }_{{{\rm{DL}}}}\). Conversely, Pt(5)/Co(t)/CoPt(2), Ta(5)/Co(t)/CoPt(2) and Pt(5)/Co(t)/Pt(1) display \({t}_{{{\rm{Co}}}}\)-dependent \({\xi }_{{{\rm{DL}}}}\), enabling the quantitative separation of spin and orbital torque contributions to total SOT. Moreover, the sign of orbital torque is controlled by the FMSOC layer rather than the HM layer. CoPt alloy has negative \({\eta }_{{{\rm{LS}}}}\), and upper Co/Pt interface with high conversion efficiency has positive \({\eta }_{{{\rm{LS}}}}\). By combining suitable materials, we achieve a 110% enhancement in SOT via the synergy of spin and orbital torques, and improve the efficiency of current-induced magnetization switching in Pt(5)/Co(1)/Pt(1). According to the diffusion model, the orbital diffusion length of Co is 0.98 nm, our Pt-based HM/FM multilayer exhibits \({\xi }_{{{\rm{DL}}}0}^{{{\rm{OH}}}}\) of 0.15 and effective orbital Hall conductance of Pt exceeds 2830 ℏ/2e·Ω-1cm-1. Furthermore, spin pumping measurements hint at possible orbital pumping.

Our innovative multilayer design presents a unique platform for studying the orbital-related effect in strong SHE systems. For example, first-principles calculations predict that non-collinear antiferromagnetic Mn3Ni0.35Cu0.65N has large OHE and orbital torque may be the reason for efficient SOT60, which is difficult for traditional bilayer structure to measure the orbital torque contribution. Moreover, our work provides different perspectives to re-examine the SOT mechanism within HM/FM multilayers. This revelation underscores utilizing synergy of spin and orbital torques in optimizing spintronic devices for efficient manipulation. For example, the [Co/Pt]N multilayer, containing numerous upper Co/Pt interfaces with high \({\eta }_{{{\rm{LS}}}}\), might serve as a more efficient FM. A recent research has demonstrated the orbital torque in [Co/Pt]N61. And the free layer of SOT-MRAM62 can be designed as Pt/[Co/Pt]N/Co/W/CoFeB. Additionally, our study implies the possibility of utilizing the synergy between perpendicular spin and orbital torques to achieve more complex functions, such as field free SOT switching.

Methods

Device fabrication

In our experiment, all samples were deposited on thermal oxidated Si substrate by DC/RF (DC for Ta and Co, RF for Pt and AlOx) magnetron sputtering under 3 mTorr Ar pressure at room temperature. Ta(3) was used as buffer layer to reduce roughness and improve adhesion except Co(t)/CoPt(2) and Co(1)/Pt(5), which use AlOx(3) to eliminate possible SHE and OHE of Ta. And the Ta(3) buffer layer was not calculated in Ta(5) HM layer. The capping layer was AlOx(5) prepared by RF sputtering from Al2O3 target. Hall bar devices with 25 μm width were patterned using photolithography and Ar ion beams etching.

Measurement method

All electrical transport measurement were finished in Physical Property Measurement System (PPMS). Anomalous Hall resistance measurement and current-induced magnetization switching with a pulse width of 50 μs are completed using Keithley current source 6221 and nanovoltmeter 2182 in PPMS. Sweeping field and rotating field harmonic Hall measurement is combining lock-in amplifier SR830 and PPMS. And the saturation magnetization \({M}_{{{\rm{s}}}}\) is measured using vibrating sample magnetometer (VSM) of PPMS. For ferromagnetic resonance (FMR) measurement, the unpatterned sample was tightly attached to the coplanar waveguide (CPW) applied constant microwave. A perturbed magnetic field is applied by a Helmholtz coil and measuring the microwave power by lock-in amplifier can obtain the resonance absorption differential signal with respect to the magnetic field.