Introduction

Simulating fluid dynamics on classical computers at a high Reynolds number (Re) has significant applications in various fields, such as weather forecasting and airplane design. However, it remains challenging due to the wide range of spatial and temporal scales involved in turbulent flows. Its computational cost, scaling with \({{{\mathcal{O}}}}({{{{\rm{Re}}}}}^{3})\) operations for the direct numerical simulation of turbulence1, is prohibitively expensive for engineering applications2,3. The emergence of quantum computing has garnered attention as a potential solution to the computational limitations in classical computing4,5,6,7. Leveraging laws of quantum mechanics such as superposition and entanglement, a quantum processor can manipulate exponentially large degrees of freedom that are intractable on classical computers, making it a promising platform for empowering the next-generation simulation method for fluid dynamics8,9,10. In particular, quantum computing of turbulence, one of the most challenging problems in classical physics11, can serve as a compelling demonstration of quantum utility and practical quantum advantage12,13,14,15.

There have been two major approaches to the quantum simulation of fluid dynamics. Based on solving the governing equations for fluids, hybrid quantum-classical algorithms are proposed10,16,17,18,19,20,21,22,23,24,25,26,27, where quantum computing is employed to handle highly parallelizable operations (e.g., solving linear systems28,29). The efficiencies of these methods are often burdened by the frequent data exchanges between classical and quantum hardwares, as the preparation and statistical measurement of arbitrary quantum state can be more time-consuming than the calculation procedure9,30. Moreover, for the present noisy intermediate-scale quantum (NISQ) devices, the state preparation and measurement (SPAM) errors could accumulate during the time-marching in these algorithms, limiting their accuracy for near-term applications31,32. To alleviate these problems, Hamiltonian simulation, which has been widely used in exploring quantum many-body physics on NISQ devices13,32,33,34,35,36, was proposed as a promising approach to simulate fluid dynamics37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52. In this simulation, a fluid flow is mapped to a quantum system, which can then be evolved and detected on a quantum processor without invoking intermediate quantum state measurement and re-initialization.

However, obstacles remain. First, general fluid dynamics has nonlinear characteristics, while quantum operations except measurement are linear. Incorporating the nonlinearity into a quantum algorithm poses significant challenges. Second, while minimizing the influence of SPAM errors, the Hamiltonian simulation can still be affected by the inevitable errors occurred during the execution of quantum evolution on the NISQ devices. A proof-of-principle demonstration of the capability of the contemporary NISQ devices in simulating fluid dynamics remains elusive. Here we report the end-to-end quantum simulation of two-dimensional (2D) unsteady flows, discretized spatially with up to 1024 grid points, on a superconducting quantum processor. We first consider a simple compressible diverging flow and reveal its dynamics according to the hydrodynamic formulation of the corresponding Schrödinger equation. Then, by involving the two-component wave function, we realize the quantum simulation of a decaying vortex with nonlinear vortex dynamics.

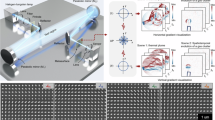
As sketched in Fig. 1, the simulation (referred to as “experiment” below) is implemented with ten qubits on a superconducting processor53,54,55. Through optimizing device fabrication and carefully tuning controlling parameters, we realize median fidelities of 99.97% (99.67%) and 99.3% for parallel single- (two-) qubit gates and measurements, respectively. With the high fidelities and by employing efficient quantum circuits for state preparation and Hamiltonian simulation, we obtain the average density and momentum profiles that well capture key features of the targeting flows. The present study demonstrates the capability of NISQ devices to simulate practical fluid flows, indicating the potential of quantum computing in exploring turbulent flows.

Fig. 1: Schematic for the quantum simulation of fluid dynamics.
figure 1

The initial flow field (exemplified pictorially by a spiral vortex) discretized on a uniform grid in (a) is encoded by the multi-component wave function in (b), followed by state preparation. c Sketch of device topology. Qubits (circles) are arranged in a square lattice and connected through tunable couplers (bars). The ten qubits used here are labeled by Q1–Q5 (blue) and Q6–Q10 (green), encoding the wave function in the x- and y-directions, respectively. d Sketch of the quantum circuit for simulating the 2D unsteady flows. The Hamiltonian simulation is realized by transforming a flow state into the momentum space with quantum Fourier transforms \({\widehat{{{{\rm{QFT}}}}}}_{x}\) and \({\widehat{{{{\rm{QFT}}}}}}_{y}\), applying unitary evolutions \({e}^{-i{\hat{k}}_{x}^{2}t/2}\) and \({e}^{-i{\hat{k}}_{y}^{2}t/2}\), and finally transforming the state back to the coordinate space. The circuit is further compiled with native gate sets (arbitrary single-qubit gates and two-qubit CZ gate) before the experimental execution. e At a given time t, the flow field is extracted by measuring a specific set of Pauli strings.

Full size image

Results

Framework and experimental setup

In our algorithm, we encode the flow state into the nψ-component wave function \({{{\boldsymbol{\psi }}}}\equiv {[{\psi }_{1},\cdots ,{\psi }_{{n}_{\psi }}]}^{{{{\rm{T}}}}}\), with nψ ∈ {1, 2}. Based on the generalized Madelung transform, the flow density and momentum can be extracted as \(\rho \equiv {\sum }_{j = 1}^{{n}_{\psi }}| {\psi }_{j}{| }^{2}\) and \({{{\boldsymbol{J}}}}\equiv \frac{i\hslash }{2m}{\sum }_{j = 1}^{{n}_{\psi }}({\psi }_{j}{{{\boldsymbol{\nabla }}}}{\psi }_{j}^{* }-{\psi }_{j}^{* }{{{\boldsymbol{\nabla }}}}{\psi }_{j})\), respectively37,45,47. Without loss of generality, we set the reduced Planck constant ℏ = 1 and the particle mass m = 1. The fluid velocity and vorticity are defined by u ≡ J/ρ and ω ≡ ∇ × u, respectively. Note that for a single-component wave function ψ, the velocity can be expressed as \({{{\boldsymbol{u}}}}=\frac{i}{2}{{{\boldsymbol{\nabla }}}}\log \frac{{\psi }^{* }}{\psi }\), leading to ω = 0. To introduce finite vorticity, we need nψ = 245. We simulate fluid dynamics by evolving the wave function under the Hamiltonian H = − ∇2/2 + V, where the potential V, which may contain interaction terms among different wave-function components, gives the body force in the fluid flow45. Using the Trotter decomposition56, the evolution of the wave function can be approximated by a series of unitary operators (see Supplementary Note 1 for details).

In this work, we focus on the dynamics of 2D flows without conservative body forces in a periodic box x ∈ [−π, π]2, which is discretized into \({2}^{{n}_{x}}\times {2}^{{n}_{y}}\) uniform grid points. The corresponding wave function of each component can be expressed in the computational basis of nx + ny qubits as

$$\left\vert {\psi }_{j}(t)\right\rangle =\frac{1}{{\parallel {\psi }_{j}\parallel }_{2}}\mathop{\sum }_{l=0}^{{2}^{{n}_{y}}-1}{\sum }_{k=0}^{{2}^{{n}_{x}}-1}{\psi }_{j}({x}_{k},{y}_{l},t)\left\vert k+{2}^{{n}_{x}}l\right\rangle ,$$
(1)

where the coordinates xk = − π + kΔx and yl = − π + lΔy, with \({{\Delta }}x=2\pi /{2}^{{n}_{x}}\) and \({{\Delta }}y=2\pi /{2}^{{n}_{y}}\), respectively. For vortical flows, an additional qubit is required to encode the two-component wave function. In the absence of conservative body forces, the Hamiltonian reduces to \(H=-({\partial }_{x}^{2}+{\partial }_{y}^{2})/2\). The corresponding evolution can be realized without Trotterization as

$${e}^{-iHt}={e}^{i{\partial }_{x}^{2}t/2}{e}^{i{\partial }_{y}^{2}t/2}={U}_{x}(t){U}_{y}(t).$$
(2)

In the computational basis, the evolution operators can be digitized according to

$${U}_{\alpha }(t)={\widehat{{{{\rm{QFT}}}}}}_{\alpha }^{{{\dagger}} }{e}^{-i{\hat{k}}_{\alpha }^{2}t/2}{\widehat{{{{\rm{QFT}}}}}}_{\alpha },$$
(3)

where \({\widehat{{{{\rm{QFT}}}}}}_{\alpha }\) denotes the unitary of quantum Fourier transform along the direction α ∈ {x, y}, and the wavenumber is given by

$${\hat{k}}_{\alpha }=-\frac{1}{2}\left({I}_{{2}^{{n}_{\alpha }}}+\mathop{\sum}_{j=1}^{{n}_{\alpha }}{2}^{{n}_{\alpha }-j}{\hat{Z}}_{j}\right)+{2}^{{n}_{\alpha }}{\hat{Z}}_{1}.$$
(4)

Here, \({\hat{Z}}_{j}\) denotes the Pauli operator of the j-th qubit and \({I}_{{2}^{{n}_{\alpha }}}\) the \({2}^{{n}_{\alpha }}\times {2}^{{n}_{\alpha }}\) identity matrix. See Supplementary Note 2 for detailed derivations. The overall quantum circuit for simulating 2D unsteady flows is shown in Fig. 1d.

We implement the algorithm on a flip-chip superconducting quantum processor53 using ten frequency-tunable transmon qubits labeled as Qj for j = 1–10, as sketched in Fig. 1c. In the simulation, we set nx = ny = 5, corresponding to a solution domain with 25 × 25 = 322 grid points. Each qubit is individually controlled and readout. The nearest-neighboring qubits are capacitively connected through a tunable coupler, which is also a transmon qubit, for turning on and off the effective coupling between the two qubits. The single-qubit gate is realized by applying a 30 ns-long Gaussian-shaped microwave pulse with DRAG correction57. The two-qubit CZ gate, with a length of 40 ns, is realized by carefully tuning the frequencies and coupling strength of the neighboring qubits to enable a closed-cycle diabatic transition of \(\left\vert 11\right\rangle \leftrightarrow \left\vert 20\right\rangle\) (or \(\left\vert 02\right\rangle\))58. The median parallel single- and two-qubit gate fidelities are 99.97% and 99.67%, respectively. See Supplementary Note 3 for details.

Simulation of a diverging flow

As a first example, we demonstrate the quantum simulation of a 2D unsteady diverging flow, which is a simple model of nozzle in compressible potential flow. The flow is initially uniform in the x-direction, with mass concentrated near y = 0, which is described by a density of \(\rho (x,y,0)={e}^{-{y}^{2}}\) and a velocity of u(x, y, 0) = ex. The flow has the vanishing vorticity and can be encoded into a single-component wave function \(\psi (x,y,0)={e}^{-{y}^{2}+ix}\). In practice, we use CPFlow59 to synthesize the quantum circuit for initial state preparation, which fits the native gate set (i.e., arbitrary single-qubit gates and two-qubit CZ gates) and qubit layout topology of our device with minimal numbers of CZ gates. With an optimal depth of 13, the resulting circuit can generate a quantum state with an overlap above 0.999 to the target one in the ideal case (i.e., without any gate errors). After preparing the initial state, we apply quantum circuits of the evolution unitaries with specific times of t = 0, π/4 and π/2, respectively. The evolution circuits are also optimized with CPFlow, leading to a total circuit depth of around 30. To verify the simulation, we fully characterize the flow by measuring both the density and momentum distributions. While the density can be directly measured in the Z basis, the detection of the momentum requires measuring the quantum state in 62 different bases (see Supplementary Note 3 for details).

Figure 2a–c show the experimental data for the evolution of the density contour with streamlines for the diverging flow. Under the symmetry with respect to y = 0, the experimental data (lower half) is compared with the ideal result (upper half) from the exact solution in Eq. (S17) in Supplementary Note 2. The mass diffusion accompanies the momentum diffusion from the central region near y = 0 to lateral sides. The experimental data exhibit qualitative agreements with ideal distributions. The discrepancies are mainly due to quantum gate errors, as even an single-qubit gate error of 5 × 10−4 can cause the stripe-like artifacts in experimental density contours (see Supplementary Note 4). Figure 2d–f plot profiles of ρ as well as two momentum components Jx and Jy. The profiles are averaged in the x-direction due to the homogeneity in x in this diverging flow. Their experimental and ideal results show good agreements. Thus, the quantum simulation on the NISQ device is able to predict unsteady flow evolution. Figure 2g–i present scatter plots comparing ideal and experimental values of ρ, Jx, and Jy at different times. A majority of data points, indicated by red for high data point density, align closely with the diagonal. In Fig. 2g, h, a considerable portion of experimental data falls below the actual values (orange), suggesting the effect of noises akin to filtering on the data. The correlation coefficients between the experimental and ideal values of ρ, Jx, and Jy are 0.954, 0.905, and 0.607, respectively. The notable error for Jy data is likely due to that the small value of Jy is prone to be influenced by noises (detailed in Supplementary Note 4).

Fig. 2: Comparison of experimental results on the superconducting quantum processor with the ideal ones for the 2D diverging flow.
figure 2

Density contours and streamlines are shown at (a) t = 0, (b) t = π/4, and (c) t = π/2. The flow is symmetric about y = 0 (upper panel: exact solution; lower panel: experimental measurement). The streamlines are color-coded by the momentum magnitude. d–f The x-averaged profiles for ρ, Jx, and Jy at t = 0, π/4, and π/2 (dashed lines: exact solution; triangles: experimental measurement with error bars denoting one standard deviation). The density and momentum are obtained with 105 measurement shots, and the experiment is repeated for five times. g–i Scatter plots comparing ideal and experimental values for ρ, Jx, and Jy at t = 0, π/4, and π/2, along with the correlation coefficients (marked at the upper left). Data point density is color-coded by the kernel density estimation (KDE) from low (purple) to high (red) values.

Full size image

Simulation of a decaying vortex

Next, we simulate a 2D vortex, a simple model of tornado and whirlpool, in the Schrödinger flow45 (detailed in Supplementary Note 2). We construct the vortex via rational maps60 in the periodic domain, which features a decaying vorticity profile \(f(r)={e}^{-{(r/3)}^{4}}\) along the radial distance \(r=\sqrt{{x}^{2}+{y}^{2}}\). Denoting the two components of the wave function as ψ+ and ψ−, the initial states \({\psi }_{+}(x,y,0)=u/\sqrt{| u{| }^{2}+| v{| }^{4}}\) and \({\psi }_{-}(x,y,0)={v}^{2}/\sqrt{| u{| }^{2}+| v{| }^{4}}\) are determined by the complex functions u = 2(x + iy)f(r)/(1 + r2) and v = i[r2 + 1 − f(r)]/(1 + r2), respectively.

Our approach transforms the flow characterized by nonlinear vortex dynamics and a distinct body force into a linear two-component Schrödinger equation via the generalized Madelung transformation. Typically, converting nonlinear equations to linear form involves increasing the dimensionality26,61,62, whereas the present approach, similar to the Cole-Hopf transformation63, does not increase the dimensionality. Thus, we solve the linear Schrödinger equation, avoiding the challenge of nonlinearity. However, this merely serves as a demonstrative example of the flow simulation capabilities on NISQ devices. For a general form of the body force, or the Laplacian dissipation for Newtonian fluids in particular48, the associated two-component Schrödinger equation becomes nonlinear. How to solve the nonlinear Schrödinger equations efficiently using quantum algorithms remains an open problem64,65,66. In this flow with V = 0 in the Hamiltonian, the two components of the wave function decouple during the entire evolution, so that we can simulate their dynamics separately without using an additional qubit. The circuits for preparing ψ+ and ψ−, obtained based on CPFlow, have depths of 23 and 27, respectively, which can prepare quantum states with overlaps above 0.993 to the target ones in the ideal case. We then evolve ψ+ and ψ− independently for specific times and measuring the corresponding densities ρ± and momentum J±, with the procedure similar to the diverging flow case. The velocity is then obtained by u = (J+ + J−)/(ρ+ + ρ−), which introduces the nonlinearity for vortex dynamics, and the vorticity is calculated as ω = ∂uy/∂x − ∂ux/∂y.

Figure 3 (a),(b) plot the evolution of the ω-contour and streamlines from experimental and ideal results at t = 0, π/4, and π/2. Initial circular streamlines evolve into spirals with vorticity decay under the body force in the Schrödinger flow. The experimental results in Fig. 3(b) clearly capture the vortex evolution. The vorticity magnitude is underestimated due to quantum gate noises and sampling errors. At the vortex outer edge, the flow field exhibits turbulent artifacts which enhances vortex dissipation. It is accidental to observe that the energy spectrum of the noisy experimental data appears to exhibit the k−5/3 scaling law as in classical turbulence (see Supplementary Fig. S10). Therefore, on the other hand, the NISQ hardware noises could potentially be leveraged to model small-scale turbulent motion67.

Fig. 3: Comparison of experimental results on the superconducting quantum processor with the ideal ones for the 2D vortex.
figure 3

Vorticity contours are depicted for (a) the exact solution and (b) the experimental result. Streamlines are color-coded by velocity magnitude. c Comparison of 〈ω〉θ at t = 0, π/4, and π/2 (dashed lines: exact solution; circles: experimental result with error bars denoting one standard deviation), where 〈ω〉θ denotes the vorticity averaged over the θ-direction in polar coordinates (r, θ). The data is obtained with 105 measurement shots, and the experiment is repeated for five times.

Full size image

The θ-averaged profiles for ω in Fig. 3c show the successful initial construction of the vortex using the two-component wave function. The peak of 〈ω〉θ decays notably faster in the experimental results compared to the exact solution, due to the vortex being displaced from the domain center under spurious turbulent motion and the numerical error in computing ω with differentiation of noisy data.

Discussion

We have conducted experiments on the digital quantum simulation of unsteady fluid flows with a superconducting quantum processor. Our algorithm employs the hydrodynamic formulation of the Schrödinger equation, apt for unitary operations in quantum computing. The computational complexity for the state evolution (detailed in Supplementary Note 5) in Eq. (2) is \({{{\mathcal{O}}}}({n}^{2})\)68, with the total number of qubits n = nx + ny. This represents an exponential speedup over the classical counterpart whose complexity is \({{{\mathcal{O}}}}(n{2}^{n})\). The quantum simulations well capture the evolution of averaged profiles of the density and momentum in the 2D compressible diverging potential flow and the nonlinear decaying process of the 2D vortex. Our results showcase the capability of simulating fluid dynamics on NISQ devices, and indicate the promise of quantum computing in probing complex flow phenomena such as turbulence and transition in engineering applications.

Looking forward, despite the demonstration in the present work, realizing quantum advantage for the simulation of practical fluid flows with NISQ devices remains an outstanding challenge. The quantum representation employed in the present experiment with NISQ devices is tailored from the full quantum representation for the Navier-Stokes equation47, with introducing the artificial body force into the flow. Therefore, methods such as increasing dimensionality69,70,71 should be explored to incorporate the nonlinearity and the non-Hermitian Hamiltonian of a general flow47,72 into the quantum algorithm. In addition, the preparation of initial quantum states for general velocity fields is an open problem46,73. Variational quantum algorithms offer a promising approach to approximate the initial quantum state directly through numerical optimization74. The full characterization of a flow field requires an exponentially large number of measurement shots, and it would be important to find flow statistics that can be measured efficiently without undermining the overall quantum advantage. Finally, the potential inclusion of quantum error correction is desired to fully harness the strengths of the quantum simulation of fluid dynamics.

Methods

Device and experimental setup

The quantum processor was fabricated using the flip-chip recipe, where all qubits and couplers are located on a top chip, and most of the control/readout lines and readout resonators are located on a bottom chip. These two chips have lithographically defined base wirings made of tantalum and junction loops made of aluminum, and are galvanically connected via indium bumps. The processor was loaded into a multilayer printed circuit board enclosure, which was then mounted inside a dilution refrigerator with the base temperature down to 15 mK. There are 11 × 11 frequency-tunable transmon qubits encapsulated in a square lattice on the quantum processor, and the adjacent qubits are connected by tunable couplers for realizing high-fidelity quantum gates which is essential for the experiment.

In this work, we select ten qubits to carry out the quantum simulation, as shown in Fig. 1c. We employ the native gate set {U(θ, φ, λ), CZ} to implement the desired experimental circuits, where U(θ, φ, λ) = Rz(φ)Ry(θ)Rz(λ) denotes a generic single-qubit gate with three Euler angles, and CZ denotes the two-qubit CZ gate that fits the layout topology of our device. By optimizing the control procedure, we realize fidelities of 99.97% and 99.67% for parallel single- and two-qubit gates applied on the ten qubits used in this experiment, respectively.

Quantum representation of fluid flows

We encode the flow states in the nψ-component wave function \({{{\boldsymbol{\psi }}}}\equiv {[{\psi }_{1},\cdots ,{\psi }_{{n}_{\psi }}]}^{{{{\rm{T}}}}}\), for potential flows with nψ = 1 and vortical flows with nψ = 2. With the generalized Madelung transform, the flow density, momentum, and velocity are \(\rho \equiv \mathop{\sum }_{j = 1}^{{n}_{\psi }}| {\psi }_{j}{| }^{2}\), \({{{\boldsymbol{J}}}}\equiv \frac{i\hslash }{2m}\mathop{\sum }_{j = 1}^{{n}_{\psi }}({\psi }_{j}{{{\boldsymbol{\nabla }}}}{\psi }_{j}^{* }-{\psi }_{j}^{* }{{{\boldsymbol{\nabla }}}}{\psi }_{j})\), and u ≡ J/ρ, respectively.

Then, we consider a nψ-component time-dependent Schrödinger equation

$$i\hslash \frac{\partial }{\partial t}{\psi }_{j}=\left(-\frac{{\hslash }^{2}}{2m}{\nabla }^{2}+V\right){\psi }_{j},\quad j\in \{1,\cdots \,,{n}_{\psi }\}$$
(5)

with a real-valued potential V. The continuity equation

$$\frac{\partial \rho }{\partial t}+{{{\boldsymbol{\nabla }}}}\cdot (\rho {{{\boldsymbol{u}}}})=0$$
(6)

follows from the conservation of probability current. The momentum equation is obtained as a standard compressible Euler equation

$$\frac{\partial {{{\boldsymbol{u}}}}}{\partial t}+{{{\boldsymbol{u}}}}\cdot {{{\boldsymbol{\nabla }}}}{{{\boldsymbol{u}}}}=-\frac{1}{\rho }{{{\boldsymbol{\nabla }}}}p-{{{\boldsymbol{\nabla }}}}{U}_{F}+{{{\boldsymbol{f}}}},$$
(7)

with the pressure p, an conservative potential UF, and a body force f. For potential flows, we have p = 0, \({U}_{F}=V/m-{\hslash }^{2}{\nabla }^{2}\sqrt{\rho }/(2{m}^{2}\sqrt{\rho })\), and f = 0. For vortical flows, we have p = ℏζ ⋅ s/m, UF = V/m − ℏ2∣∇s∣2/(8m2ρ2), and f = ℏ∇s ⋅ ζ/(mρ), with the spin vector s ≡ ψ*iψ and a vector ζ ≡ − ∇ ⋅ (∇s/ρ)/4 (see Supplementary Note 1 for details).

Note that in practical fluid flows, the momentum equation does not include the term f. This term can be regarded as an external body force with a dissipative effect45,75. The corresponding “Schrödinger flow” can resemble the viscous flow in terms of the similar flow statistics and structures45.

Circuit optimization

The preparation of an arbitrary n-qubit quantum state generally requires an order of 2n quantum resources76, either circuit depth or ancilla qubits, which is prohibitive for large n on the current device. Besides, the quantum circuits for realizing the QFT require further compilations to adapt the device topology. To circumvent these challenges, we adopt the CPFlow package recently introduced in ref. 59 to reduce the circuit depth for the initial state preparation and the state evolution.

The CPFlow is a variational circuit synthesis method. The program first use the parameterized controlled phase (CP) gates to integrate the discrete search into the continuous optimization procedure. The loss function is carefully designed to balance the fidelity among the optimized template, the target unitary (or state vector), and the circuit depth. After optimization, each CP gate is replaced by an identity (a CZ) gate if its angle lies within a threshold distance away from 0 (or π), or otherwise by their CZ decompositions. Once a prospective circuit is found, it is further optimized to obtained the final result. The fidelities of the optimized circuits and the corresponding depths for different simulation cases are listed in Supplementary Tables S1 and S2.

Detection of flow states

In our experiment, the flow density is obtained by measuring diagonal elements of the density matrix. The matrix elements of the measuring operator are

$${\hat{\rho }}_{j,\,k}^{(m,\,l)}={\delta }_{j,{2}^{{n}_{x}}m+l}{\delta }_{{2}^{{n}_{x}}m+l, \, k},$$
(8)

where the indices \(l=0,1,\ldots ,{2}^{{n}_{x}}-1\) and \(m=0,1,\ldots ,{2}^{{n}_{y}}-1\) denote the discretized coordinates in the x- and y-directions, respectively.

For the momentum, we employ the finite difference method to approximate derivatives. The corresponding measuring operator (non-bounded) is expressed as

$$\begin{array}{rc}{\hat{{{{\boldsymbol{J}}}}}}_{j,\,k}^{(m,\,l)}=\frac{i}{2}&\left[{\delta }_{{2}^{{n}_{x}}m+l, \, k}\left(\frac{{\delta }_{j,{2}^{{n}_{x}}m+l+1}-{\delta }_{j,{2}^{{n}_{x}}m+l-1}}{2{{\Delta }}x}{{{{\boldsymbol{e}}}}}_{x}\right.\right.\\ &\left.+\frac{{\delta }_{j,{2}^{{n}_{x}}(m+1)+l}-{\delta }_{j,{2}^{{n}_{x}}(m-1)+l}}{2{{\Delta }}y}{{{{\boldsymbol{e}}}}}_{y}\right)\\ &-{\delta }_{j,{2}^{{n}_{x}}m+l}\left(\frac{{\delta }_{{2}^{{n}_{x}}m+l+1, \, k}-{\delta }_{{2}^{{n}_{x}}m+l-1, \, k}}{2{{\Delta }}x}{{{{\boldsymbol{e}}}}}_{x}\right.\\ &\left.\left.+\frac{{\delta }_{{2}^{{n}_{x}}(m+1)+l, \, k}-{\delta }_{{2}^{{n}_{x}}(m-1)+l, \, k}}{2{{\Delta }}y}{{{{\boldsymbol{e}}}}}_{y}\right)\right].\end{array}$$
(9)

An intuitive strategy to obtain the momentum is quantum state tomography (QST). However, QST requires an exponentially increasing number of measurements, so it is impractical with a system size as large as ten qubits. Alternatively, we decompose each desired observable as a sum of Pauli strings and pick the necessary Pauli bases to infer expectation values of all required Pauli strings (see Supplementary Note 3 for details). As a result, the number of measurements is reduced to 62 in our work.

Consequently, the embedded flow state including the density and momentum can be extracted with 63 measurements. Each measurement involves 105 single shots to build the probability distribution, consuming approximately 20 s at a sampling rate of 5 kHz. The experiment is repeated five times for each flow case.