Directed motion of cognitive active agents in a crowded three-way intersection

Abstract

Understanding the navigation through semi-dense crowds at intersections poses a significant challenge in pedestrian dynamics, with implications for facility design and insights into emergent collective behavior. To tackle this problem, a system of cognitive active agents at a crowded three-way intersection is studied using Langevin simulations of intelligent active Brownian particles (iABPs) with directed visual perception (resulting in non-reciprocal interactions) and self-steering avoidance—without volume exclusion. We find that the emergent self-organization depends on agent maneuverability, goal fixation, and vision angle, and identify several forms of collective behavior, including localized flocking, jamming and percolation, and self-organized rotational flows. Additionally, we demonstrate that the motion of individual agents can be characterized by fractional Brownian motion and Lévy walk models across different parameter regimes. Moreover, despite the rich variety of collective behavior, the fundamental flow diagram shows a universal curve for different vision angles. Our research highlights the impact of collision avoidance, goal following, and vision angle on the individual and collective dynamics of interacting pedestrians.

Introduction

The collective behavior of active agents is ubiquitous: from eucaryotic cells, bacteria and microbots, to insects, birds, fish, humans, and robots¹. On the mesoscopic and macroscopic size scale, directional sensing (like vision), cognitive information processing, and the adaptation of motion are distinctive features of these processes and the emergent self-organization. An important example of this behavior is collective pedestrian movement, whose understanding is imperative for designing strategies to facilitate smooth pedestrian flow in crowded areas, mitigate crowd-related disasters in confined spaces, and develop effective evacuation procedures². Another key aspect is the goal-oriented motion of the participants. For pedestrian navigation in crowds, typical scenarios are the formation of traffic jams in front of narrow passages and bottlenecks, the interaction of groups in counter flow leading to lane formation, and the self-organization of flows at intersections (see the reviews^3,4 and references therein). Situations like the Shibuya Crossing in Tokyo or mall intersections pose important questions regarding self-organization and the design optimization of facilities. Experiments and simulations of bi-directional flows demonstrate lane formation^5,6,7, while cross flows at an angle result in stripe-like patterns⁸. Four-directional cross-flow experiments^9,10,11,12 and multi-directional crossing scenarios explored through circle antipode experiments^13,14, with participants positioned on a circle and crossing diagonally, have been used to study navigation strategies, conflict avoidance etc.

The importance of understanding the flow of pedestrian crowds has led to the development of various modeling approaches in recent decades, e.g., the force-based models, cellular automaton-based approaches, several physics-inspired models, game theory, optimal control and fluid dynamics (for a more detailed exposition of the different approaches, see refs. ^3,4,15,16 and references therein). The importance of a close interplay between empirical and theoretical investigations has inspired the use of specifically designed laboratory experiments^3,4,17, which generate quantitative results that are important benchmarks for modeling.

However, collective motion and emergent self-organization in crowds and swarms is not unique for pedestrians, but can be observed in many other types of cognitive active agents. Therefore, this behavior can generically be understood as the behavior of interacting self-propelled entities, which places it into the realm of the large field of “active matter”¹⁸, which encompasses systems from cell suspensions and self-propelling colloids to schools of fish and flocks of birds. In this context, the active Brownian particle (ABP) model has been used extensively to understand many intriguing aspects of non-equilibrium physics such as motility-induced phase separation^19,20 and wall accumulation^21,22. Moreover, when equipped with directional environment sensing and self-steering, ensembles of ‘intelligent’ ABP systems (iABPs) can show a rich variety of collective phenomena such as milling, single-file motion, flocking, worm-like swarms, and polar or nematic ordering^23,24,25,26. In pedestrian models, vision-based sensing and cognitive steering have also been identified as key ingredients that determine the emergent collective behavior^27,28,29,30. This suggests the possibility of a unified description of systems of cognitive active agents by iABP models—from pedestrian crowds to animal herds³¹.

Results

Model and cross-stream setup

We investigate here a three-stream intersection scenario (see Fig. 1a), which emulates the crossing of multi-directional flows in a circle. This scenario is designed by incorporating goal-following behavior to each agent to generate active streams, in addition to collision avoidance, creating conditions where particles must navigate through a crowded environment. While this is our primary focus, our model can also be easily applied to well-established bi-directional and cross-flow scenarios and yield qualitatively consistent behavior (see Supplementary Note 3).

Fig. 1: Schematic of intersecting streams and vision-based avoidance.

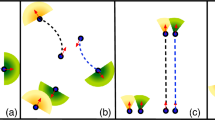
a Simulation setup of a three-way pedestrian crossing. The colors represent different pedestrian types t_i, i.e., pedestrians with different goals (alignment along direction d(t_i)). The human markers show the position of influx, each separated by an angle of π/3 from the other and placed on an interaction circle of radius R_int = 120R₀. The shaded regions depict the regions of ‘successful exits’ (see “Methods”), and the distribution at the inflow indicates the ‘spread’ of each stream leading to an effective interaction zone (dashed circle) R_int/2 (see “Methods”). b Schematic diagram of the (non-reciprocal) vision-based interaction of agents i and j. The vision angle is highlighted in blue, with a vision angle ψ and cutoff 4R₀. c–f Sample trajectories showing the effect of goal fixation and visual avoidance for a vision angle of ψ = π/2. Agents with the same goal direction for c Δ = 1 and d Δ = 2. The blue agent does not ‘see’ the red one and therefore does not react. Agents with opposite goal directions for e Δ = 1 and f Δ = 2. In the cases (e, f), both agents see each other and move away. In all cases, in the initial state at t = 0, the distance between the agents is r = 3R₀.

In contrast to a straightforward two-way flow configuration, pedestrian movement at intersections with multiple streams does not readily organize itself through lane or stripe formation, making it an important case to study. A similar setup with two intersecting streams has been studied experimentally⁹. Since we are interested in the general physical mechanisms of interacting streams, sophisticated models, which usually have several adjustable parameters, are not appropriate. Instead, pedestrians are modeled as intelligent active Brownian particles (iABPs) in two spatial dimensions (see Fig. 1b), which experience a propulsion force f_p acting along their orientation vector e_i, and a friction force  −γv_i with velocity v_i, which implies a constant speed v₀ = f_p/γ. Any individual variability is incorporated as noise in the equation of motion which specifies the dynamics of the position r_i of an iAPB:

$$m{\ddot{{{\bf{r}}}}}_{i}={f}_{p}{{{\bf{e}}}}_{i}-\gamma {\dot{{{\bf{r}}}}}_{i},$$

(1)

where m is the agent mass and γ is the friction coefficient. Each pedestrian is associated with a type t_i, which encodes their goal direction. We employ a self-steering mechanism in the form of a torque that changes the direction of motion as

$${\dot{{{\bf{e}}}}}_{i}=\sqrt{2(d-1){D}_{r}}{{{\boldsymbol{\Lambda }}}}_{i}+\Omega {{{\bf{M}}}}_{{{\rm{vis}}}}+K{{{\bf{M}}}}_{{{\rm{goal}}}},$$

(2)

where D_r is the rotational diffusion coefficient, d is the dimensionality, Λ_i is a Gaussian random process, Ω and K are the strength of the steering torques related to visual perception (M_vis) and goal fixation (M_goal), respectively. The noise acts perpendicular to the direction of motion, so that

$${\Lambda }_{i}={{{\boldsymbol{\zeta }}}}_{i}\times {{{\boldsymbol{e}}}}_{i},$$

(3)

where ζ_i is a Gaussian and Markovian random process with 〈ζ_i(t)〉 = 0 and $\langle {{{\boldsymbol{\zeta }}}}_{i}(t)\cdot {{{\boldsymbol{\zeta }}}}_{j}(t{\prime} )\rangle ={\delta }_{ij}\delta (t-t^{\prime} )$. The agents avoid collisions with each other via ‘vision-assisted’ reorientation of their propulsion direction, which is described by the torque²⁵

$${{{\bf{M}}}}_{{{\rm{vis}}}}=-\frac{1}{{N}_{i}}\sum_{j\in VC}{T}_{ij}\left[{{{\boldsymbol{e}}}}_{i}\times \left(\frac{{{{\boldsymbol{r}}}}_{{{\boldsymbol{ij}}}}}{| {{{\boldsymbol{r}}}}_{{{\boldsymbol{ij}}}}| }\times {{{\boldsymbol{e}}}}_{i}\right)\right],$$

(4)

where r_ij = r_j − r_i is the displacement vector between particle i and particle j, and T_ij is a weight factor,

$${T}_{ij}={e}^{(-| {{{\boldsymbol{r}}}}_{{{\boldsymbol{ij}}}}| /{R}_{0})}[3-{{{\boldsymbol{e}}}}_{i}\cdot {{{\boldsymbol{e}}}}_{j}]/4.$$

(5)

which increases the relative importance of avoiding agents moving ‘head-on’ towards each other (e_i ⋅ e_j = −1), as opposed to co-moving agents (i.e., e_i ⋅ e_j = 1) by a factor 1/2³². Lastly, N_i = ∑_j∈VCT_ij is the normalization factor. The exponential distance dependence in Eq. (5) limits the range of the interaction, such that for high density of agents the effective vision range is R₀. The sum is over all particles j that are in the vision range VC of the agent i, with

$$VC=\left\{\,j| \frac{{{{\boldsymbol{r}}}}_{{{\boldsymbol{ij}}}}}{| {{{\boldsymbol{r}}}}_{{{\boldsymbol{ij}}}}| }\cdot {e}_{i}\ge \cos \psi \,{\mbox{and}}\,| {{{\boldsymbol{r}}}}_{{{\boldsymbol{ij}}}}| \, < \, {R}_{v}\,\right\}$$

(6)

where ψ is the vision angle and R_v > R₀ the ‘full’ vision range. Steering toward the goal is determined by the torque

$${M}_{{{\rm{goal}}}}=\left[{{{\boldsymbol{e}}}}_{i}\times \left({\hat{{\boldsymbol{d}}}}({t}_{i})\times {{{\boldsymbol{e}}}}_{i}\right)\right],$$

(7)

where the unit vector ${\hat{{\boldsymbol{d}}}}({t}_{i})$ is direction toward the goal, with which particle i attempts to align (see Fig. 1a). In two-dimensions, Eq. (2) can be simplified in polar coordinates as

$${\dot{\theta }}_{i}=\sqrt{2{D}_{r}}{\xi }_{i}-\frac{\Omega }{{N}_{i}}\left[\,\sum_{j\in VC}{T}_{ij}\sin ({\phi }_{ij}-{\theta }_{i})\right]+K\sin ({{\Theta }}({t}_{i})-{\theta }_{i})$$

(8)

where ξ_i is a Gaussian random process and ϕ_ij, Θ(t_i), and θ_i are the polar angles of the vectors r_ij, ${\hat{{\boldsymbol{d}}}}({t}_{i})$, and e_i, respectively.

We define the relative maneuverability Δ = Ω/K, which measures the relative strength of visual avoidance to target fixation. The combined effect of alignment and maneuverability is shown in Fig. 1c–f. Pedestrians navigate their movement paths based on visual cues to avoid collisions with others, by adjusting their propulsion direction. For larger relative maneuverability Δ, the agents make sharper turns, see Fig. 1d, f. Importantly, the agents’ vision-based interactions are non-reciprocal for vision angle ψ < π, see Fig. 1c, d. Here the trailing agent notices the leading agent, but not vice versa.

The activity of the agents is described by the dimensionless Péclet number Pe = f_p/(γR₀D_r) = v₀τ_r/R₀, where τ_r = 1/D_r is the rotational diffusion time and v₀ = f_p/γ is the agent velocity. All lengths are measured in units of R₀, time in units of τ_r. The goal fixation is set to K = 8D_r and the vision range R_v = 4R₀. The inflow rate Γ measures the number of agents entering the interaction circle at each inflow per unit time (τ_r). The system is studied for varying relative maneuverability Δ = Ω/K, vision angle ψ, and inflow rate Γ.

We operate in the limit of over-damped motion so that inertial effects are negligible and the self-steering gives a realistic description of pedestrian cognitive motion. In our simulations, agents are modeled as point particles, placing us in the regime of semi-dense crowds, where the volume-exclusion radius σ of an individual pedestrian is much smaller than the vision range R_o, i.e., σ ≪ R₀ and the speed of the agents is roughly constant. By doing so, we specifically focus on isolating and understanding the effects of self-steering on agent dynamics.

Note that the models in our current study and in ref. ³¹ both employ vision-based steering torques to avoid close approach to other particles. However, a crucial difference in the two models are (i) the individual goal-orientation of the motion of all particles, and (ii) the distinction of on-coming and co-moving particles in the steering avoidance. While seemingly minor, these differences significantly impact the emergent collective behavior and long-term dynamics of the agents.

Comparison with “Social-Force” Models—A key feature in our model is that essentially all ‘social’ interactions, such as neighbor avoidance and goal-following, act to reorient the agents heading direction, which is an essential feature governing pedestrian dynamics^33,34. This contrasts with ‘force-like’ interactions, which are typically described by a potential. It is, in fact, intuitive that social interactions like goal following or inter-agent avoidance are non-reciprocal and should be distinguished from “forces”, such as excluded-volume effects or hard-core repulsion. Our model has certain advantages over other models for the specific scenario that we are interested in, i.e., semi-dense crowds, where vision-induced steering dominates over short-range excluded-volume repulsion. There are several more sophisticated pedestrian models that take into account further aspects that are less relevant in this context, the key consideration here is the mitigation of strong inertia effects. Since inertia effects are minimal in semi-dense scenarios, where steering dominates over repulsion, force-based models tend to perform poorly in these conditions, which leads, e.g., to unrealistic behavior like oscillatory motion or “tunneling” of particles. For a more detailed discussion, we refer to refs. ^35,36 and references therein. These problems are avoided by the present model, further highlighting the strengths of our approach.

Dynamic state diagram

The state diagram of the various collective pedestrian movement states as function of relative maneuverability Δ and vision angle ψ is shown in Fig. 2a. At small Δ ≲ 1, agents essentially ignore each other and head directly toward the goal, see Fig. 2b. This behavior corresponds to the case of ‘dumb’ active Brownian particles, and is expected to display activity-induced jamming in the presence of excluded volume effects. Thus, efficient navigation requires pedestrians to have maneuverability Ω larger than goal fixation K, i.e., Δ = Ω/K ≳ 1. The required relative maneuverability Δ increases with decreasing vision angle, as agents see fewer other agents for smaller ψ. As Δ increases for larger vision angles, the pedestrian streams start to avoid each other, which results in a complex motion marked by many scattering events, see Fig. 2c and Supplementary Movie 1. While for two intersecting streams, lane (or stripe) formation occurs³⁷, for three streams the scenario is much more complex and no stable global order exists⁹. The agents rapidly change their direction attempting to avoid other agents leading to noisy and convoluted trajectories. For ψ = π, agents enter a jammed-percolating state, wherein strong clustering is observed and agents cross the interaction regime in groups, see the ‘clustered’ trajectories in Fig. 2d.

Fig. 2: State diagram and agent trajectories.

a State diagram of pedestrian movement states as a function of the relative maneuverability Δ = Ω/K and vision angle ψ. b For small Δ, the agents do not avoid each other significantly, and pass through the interaction zone nearly unhindered. c For intermediate Δ and vision angles ψ ≥ π/2, a scattering regime emerges as the agents attempt to avoid each other while crossing. d For higher Δ, and the largest vision angle ψ = π and relative maneuverability Δ = 8, a jammed, percolating phase develops. e For intermediate Δ and smaller vision angles ψ < π/2, a ‘localized flocking’ regime is found, where agents navigate by aligning with oncoming individuals, forming a local co-moving pedestrian cluster, thus leading to clustering and flocking—as seen by the emergence of parallel trajectories (with different pedestrian types). Here we fix Γ = 1. The solid black lines are a guide to the eye-separating the different phase regimes.

As the vision angle is further decreased, to ψ < π/2, the particle motion drastically changes, see Fig. 2e. In this regime, agents mainly avoid other agents directly ahead of them, implying that their direction of motion changes only for high particle densities, i.e., close to the center of the interaction zone and near the other incoming pedestrian streams. This state is characterized by the presence of parallel trajectories in the interaction zone (see Fig. 2e). Here an agent of one type initially adopts a strategy of polar alignment with the oncoming agents of the other types to avoid “collisions”. The small vision angle is responsible for this flocking-based avoidance mechanism, and has been shown recently in ref. ³¹. Note that the goal-following disrupts the avoidance-induced global flocking state (for vision angle ψ = π/4) without goal orientation³¹.

No pronounced differences are observed for various choices of Pe across all vision angles, which is due to the large goal-fixation (K/D_r = 8).

Cluster-size distributions: percolation and localized flocking

As Δ increases for vision angle ψ = π, the system undergoes a jamming transition due to increased avoidance between agents. Note that the jamming here is not due to volume exclusion, but due to the strong tendency to maintain a large inter-agent distance in all directions. In the jammed state, the agents crowd the interaction regime and form large clusters comprised of agents with the same goal (or type). Clustering is initiated at the inflow; the clusters then extend deep into the interaction region as agents navigate toward their respective goals. Remarkably, the jammed state also exhibits percolation, i.e., the clusters span the length of the interaction zone, see Fig. 3a. The cluster-size distribution for a cluster of size n_c(t_i) (t_i denotes that the clusters contain agents with the same type) shows a power-law decay, with an exponent 2.2, consistent with the percolation universality class³⁸. Therefore, despite of the complex motion and continuously varying environment, the movement from the inflow to the exit can be understood qualitatively under the realm of percolation theory. The broad peak in the cluster-size distribution at n_c(t_i) ≳ 200 represents the cluster formed initially at the inflow that then feeds smaller clusters into the system which make their way to the exit (n_c(t_i) < 100). Note that the percolation in this case is dynamic, i.e., the system shows transient periods of percolating clusters, interrupted by times when the clusters are dispersed, see Fig. 3b.

Fig. 3: Cluster-size distribution and cluster polarization.

a A transition into the percolation state occurs as Δ is increased for vision angle ψ = π, marked by the development of a power law decay of the cluster size distribution P[n_c(t_i)] and the large percolated cluster The peak at large cluster sizes is due to finite system size. Here, clusters of size n_c(t_i) contain agents with the same 'goal' i.e., types, and the distribution is generated by combining the cluster data of all agent types. b The three largest clusters at Δ = 8.0 and ψ = π at two different times for pedestrians of one type. (Left) Clusters are dispersed and the largest cluster is at the inflow. (Right) The largest cluster can feed smaller clusters and reach up to the exit, forming a transiently percolated cluster. c Average cluster polarization P_c (see Eq. (16) in “Methods”) for ψ = π/4 shows an increase with Δ, indicating the development of avoidance-induced flocking. The inset shows the trajectory of two agents exhibiting avoidance-based flocking. d The transition into the localized flocking phase is characterized by a strong increase in both the mean cluster size 〈n_c〉 and the number N_c of clusters. For ψ = π/4, the clustering analysis is performed for all agents, i.e., a cluster of size n_c can contain agents with any goal direction. The distance cutoff R_cut are chosen to be R_cut ≃ R_v and R_cut ≃ R₀ for vision angles ψ = π and ψ = π/4, respectively (see “Methods” section).

In the regime of small vision angles, specifically for ψ = π/4, agents exhibit avoidance-induced flocking behavior. Consider two agents moving toward each other at a small angle, so that only one of them is visible to the other. The ‘aware’ agent initiates a (slight) turn to avoid a collision. However, the unaffected motion of the other agent causes it to repeatedly enter the vision cone of the ‘aware’ agent. Consequently, the aware agent must keep turning away until the other agent is no longer visible to it. This only happens when they move essentially parallel to each other, resulting in the formation of a co-moving cluster, as illustrated in the inset of Fig. 3c. This process repeats when this mini-cluster encounters other agents, who may also align to avoid collision, thereby also becoming part of the cluster (see Supplementary Movie 2). A particle can only leave the cluster if a strong fluctuation disrupts its aligned state. Consequently, an avoidance-induced clustering and flocking state emerges as the strength of relative maneuverability Δ increases.

This phenomenon is characterized in Fig. 3c, d, where a significant increase in the average cluster size 〈n_c〉, number N_c of clusters, and cluster polarization P_c is observed with increasing Δ. For small Δ ≲ 1, polarization remains close to 0.5, indicating a non-flocking state. This occurs due to the random overlap of particles from neighboring streams that do not avoid each other due to the low self-steering avoidance. However, as Δ increases, the clusters achieve a polarization value near unity, signaling the emergence of a flocking/clustering state.

Path length distributions

With increasing relative maneuverability Δ, strong avoidance between agents leads to scattering, and implies larger exit times and broader path-length distributions, as presented in Fig. 4 for various Δ and ψ. The path-length l_p = Σ_t∣dr_t∣ is the length of the entire trajectory of the agent from the inflow till the exit, where dr_t is the displacement at time t. Only ‘successful’ exits, i.e., agents that reach their goal are considered in the analysis (see “Methods” section). For Δ ≲ 1, inter-agent interactions are small, and the path length distribution of nearly straight paths can be estimated to be (see “Methods” section)

$${f}_{L}(\widetilde{{l}_{p}})=\frac{2\widetilde{{l}_{p}}\exp [-(1-{(\widetilde{{l}_{p}})}^{2})/2{(\widetilde{\sigma })}^{2}]}{\widetilde{\sigma }\sqrt{2\pi (1-{(\widetilde{{l}_{p}})}^{2})}},$$

(9)

where $\widetilde{{l}_{p}}={l}_{p}/2{R}_{{{\rm{int}}}}$ and $\widetilde{\sigma }=\sigma /{R}_{0}$ is the normalized variance at the input of the stream. For low Δ, the data matches well with the estimated distribution, see Fig. 4a. However, as Δ increases, the distribution shifts to larger l_p and broadens. This occurs as agents scatter strongly due to high avoidance Δ, leading to longer paths. Agents with lower vision angles reach their destinations in shorter paths, due to fewer scattering events as seen in Fig. 4b, where increasing ψ causes a shift of the distribution to larger l_p, along with the development of a longer tail. The distributions for Δ ≳ 1 and ψ ≥ π/2 follow a log-normal distribution, which is verified by performing a Kolmogorov-Smirnov test with confidence interval of 95%. Notably, log-normally distributed path lengths have been documented in antipode experiments involving pedestrians initiated on a circle¹³. The experimental arrangement closely mirrors the three-stream configuration utilized in our simulations, providing empirical support for the shape of the observed distribution.

Fig. 4: Path-length probability distribution.

Probability distribution P of the path length l_p for a different relative maneuverability (ψ = π/2, Pe = 100) and (b) different vision angles (Δ = 8, Pe = 100). For small Δ, the paths are nearly straight and the probability distribution is well approximated by Eq. (9) (dashed line). In scenarios characterized by high maneuverability (Δ) and large vision angles (ψ), agents traverse longer paths within the interaction sphere to navigate around others. This behavior yields a log-normal distribution for the path length, with the black solid line representing a fitted log-normal model to the data. The path lengths are only determined for trajectories that successfully reach the exit (see “Methods”) and are averaged over different agent types. The data is collected for times 4t₀ < t < 16t₀ and averaged over all agents, where t₀ = 2R_int/v₀.

Dynamics and mean-squared displacement

To better understand the dynamics of the agents, we compute their mean-squared displacement (MSD)

$$\langle {{{\boldsymbol{r}}}}^{2}(t)\rangle ={\langle | {{\boldsymbol{r}}}(t+\tau )-{{\boldsymbol{r}}}(\tau ){| }^{2}\rangle }_{\tau },$$

(10)

where r(t) is the position vector of the particle at time t. The MSD curves (see Supplementary Note 1, Supplementary Fig. S1) indicate that increasing Δ or ψ leads to larger scattering causing a shift of the motion from ballistic to super-diffusive. We also calculate the orientational auto-correlation function

$$C(t)={\langle {{{\boldsymbol{e}}}}_{i}(t+\tau )\cdot {{{\boldsymbol{e}}}}_{i}(\tau )\rangle }_{\tau }$$

(11)

for different Δ at ψ = π/2. For small Δ ≲ 1, the motion is strongly correlated, i.e., the particles hardly change their direction of motion as they have a strong tendency to orient and move toward the goal and do not scatter. For Δ ≳ 1, the auto-correlation function C(t) displays a slow power-law decay, consistent with the super-diffusive behavior observed in the MSD 〈r²(t)〉 = K_αt^α.

The observed functional forms of C(t) and the MSD suggest that the motion of a single agent can be described by fractional Brownian motion (fBM)³⁹ or Levy walk (LW) model^40,41. For fraction Brownian motion

$$C(t)=\frac{d{D}_{H}}{\Gamma (2H-1)}{t}^{2H-2},\langle {{{\boldsymbol{r}}}}^{2}(t)\rangle =\frac{2d{D}_{H}}{\Gamma (2H+1)}{t}^{2H}$$

(12)

where d is the spatial dimensionality, H is the Hurst exponent and D_H measures the strength of the colored noise. For Levy walks with a constant flight velocity and a probability distribution Ψ(τ) ~ τ^−(1+μ) for a flight of time τ, one has

$$C(t)\propto {t}^{-(1+\mu )},\langle {{{\boldsymbol{r}}}}^{2}(t)\rangle \propto {t}^{3-\mu }$$

(13)

where 0 < μ < 1 implies ballistic motion, 1 < μ < 2 super-diffusion, and μ > 2 diffusion. It is crucial to emphasize that in our case the motion is not purely fBM or LW, as the goal-fixation leads to a preference for a certain direction. However, by considering that we have a smaller subset of possible trajectories of an fBM or LW, we can use the model to interpret the behavior of the agents in terms of single particle motion.

We extract both fBM parameters H and D_H along with the Levy walk exponent μ. Figure 5a shows a marginal variation in the Hurst exponent with 0.8 < H < 1, consistent with the super-diffusive/ballistic motion of the agents (α = 2H). A value H > 1/2 indicates the long-memory effect of the noise, a consequence of the goal-oriented motion of the agents. A similar effect is captured in the exponent μ of LW, where measurements indicate 1 < μ < 1.5, implying a slow decay of ψ(τ), long duration of ‘straight’ paths, and super-diffusive behavior. As Δ increases, μ also increases and the probability of longer paths decreases. This is due to more frequent collisions between agents, caused by stronger avoidance behavior.

Fig. 5: Fractional Brownian motion and Lévy walks.

a Hurst exponent H and Lévy walk exponent μ (red) and (b) diffusion coefficient D_H for increasing Δ and different vision angles ψ. c Sample trajectories at Δ = 8 for ψ = π (top) and ψ = π/4 (bottom) in the effective interaction zone R_eff = R_int/2.0 (dashed circle), exhibiting characteristics of fractional Brownian motion and Lévy-like walk, respectively. Only trajectories that successfully reach the exit are considered and we average over all agents.

Notably, for increasing Δ and (or) ψ there is a strong decrease in D_H due to more scattering events, thus implying smaller diffusion coefficient K_α ∝ D_H, see Fig. 5b. Note that the ‘noise’ strength of the fMB is related to the average step length taken by the agent, which decreases for increased scattering. Thus an increase in ‘scattering-induced noise’ causes an decrease in the fBM noise, an important correspondence to keep in mind. The fBM analysis suggests that the interactions lead to an overall decrease in the effective velocity captured via D_H, while the motion is still overall ‘goal-oriented’ i.e., super-diffusive. The motion of agents at narrower vision angles and large Δ are closer to Levy walks, due to longer flight states (i.e., flocking) followed by short reorientation events arising due to avoidance-induced alignment with clusters. At large ψ and Δ, although the overall motion is ballistic, there are hardly any straight paths, and the motion is closer to fBM. This can also be seen by looking at the fixed-time displacement distributions (and trajectories) in the direction ‘perpendicular’ to the goal direction, where the contribution from the scattering (without goal following) can be isolated (see Supplementary Fig. S2). For large δ and vision angles ψ = π and ψ = π/4, the fixed-time displacement distributions are Gaussian and Levy-like, respectively. However, for intermediate values of ψ and Δ, LW or fBM cannot be established (see Supplementary Note 3, Supplementary Figs. S3, S4). This highlights that the comparison of the simulations to these models is largely qualitative.

Notably at (Δ, ψ) = (8, π), the jammed/percolated phase has a larger Hurst exponent H compared to the ‘scattering’ state at (Δ, ψ) = (4, π), despite nearly equal diffusion coefficient D_H. Here, by moving within the percolated cluster, the agents can achieve directed movement with larger long-time memory effects (i.e., large H or small μ) as the agents follow the cluster that has already made its way to the exit, highlighting the unique dynamics of the jammed state (see Supplementary Movie 3). Qualitatively, this phenomenon resembles the behavior of pedestrians joining forces to penetrate through highly congested areas, reflecting a collective strategy to navigate through crowded spaces more effectively. Overall, we conclude that the complex motion involving a combination of noise, goal fixation, and vision-based steering avoidance between several other agents can be described in a mean-field manner by either a fBM or LW description, depending on the vision angle.

Dependence on inflow rate

The (dimensionless) inflow rate Γ, i.e., the number of agents entering at the inflow region per unit time τ_r, is an important parameter that determines the emergent behavior in the interaction regime. Already in the much simpler scenario of single-file motion with volume exclusion, changing the inflow (and similarly the outflow) rate can lead to so-called boundary-induced phase transitions⁴². We focus on the regime of large Δ representing the case of strong avoidance, and study the effect of changing inflow rate on the agent motion for different vision angles ψ.

The fundamental diagram for the pedestrian movement relates flux $J=\rho \bar{v}$ and average velocity $\bar{v}$ to the average density ρ, see Fig. 6a, b. The average density $\rho =N{d}_{{{\rm{neigh}}}}^{2}/{R}_{\,{\mbox{int}}\,}^{2}$ in the interaction region (of radius R_int/2) is measured by approximating the area occupied by each agent by the average minimum separation d_neigh(Γ, ψ) within the vision range R_v (see “Methods”). Since the motion is largely ballistic, we approximate the average velocity as $\bar{v}=\sqrt{{K}_{\alpha }}$. Notably, we observe a collapse of the data for different vision angles onto a single master curve with the characteristic form of the fundamental diagram, i.e., a free-flow regime at low ρ and the jammed state at high ρ. Even without explicit velocity adaptation in our model, we successfully replicate essential features of the fundamental diagram for pedestrian flow⁴³. This implies that the model demonstrates robust properties when examined from a statistical viewpoint. In addition, we conclude from our simulation results that the fundamental diagram holds even for different vision angles.

Fig. 6: Fundamental flow diagram.

Fundamental diagrams of the pedestrian flow measured by performing simulations with different pedestrian inflow Γ for a fixed Δ = 8. a Flux $J=\bar{v}\rho$ and (b) average velocity $\bar{v}$ as a function of the mean agent density ρ. The data collapses onto a single master curve for different vision angles and exhibits the characteristic shape of the fundamental diagram, showing the free-flow (ρ < 0.5) and jammed regimes (ρ > 1). c Agent trajectories for Γ = 4 and ψ = π/2 showing the development of rotational flows and roundabout traffic-like motion. For ψ = π, a jamming transition occurs for large inflow Γ > 0.5, marked by a sudden rise in density (see ρ > 1.0) and a strong reduction in velocity $\bar{v}$. The solid black line in (a, b) is an approximate fit based on the Kladek formula $v(\rho )={v}_{0}\left[1-\exp (-c[{\rho }^{-1}-{\rho }_{{{\rm{jam}}}}^{-1}])\right.$, where v₀ = 1 and we set ρ_jam = 4 and c = 0.4 for a good fit.

In the free-flow regime, we have a steady state and the inflow equals the outflow. However, at ψ = π, a jamming transition occurs around Γ_crit ≈ 0.5, leading to a sudden rise in the average density (ρ > 1.0) (see Fig. 7c, d). In this case, a large number of agents exit close to the entry due to overcrowding in the interaction regime and the outflow saturates. The jamming is triggered by the limited transport capacity in the interaction regime, and thus generally Γ_crit = Γ_crit(R), where R is the system size. This is notably different from boundary-induced phase transitions in one-dimensional systems⁴², which show no system-size dependence. Moreover, the monotonic decay of $\bar{v}(\rho )$ suggests that the free-flow to jamming transition may be understood as motility-induced jamming²⁰, where the repulsive conservative potential of standard ABPs is replaced here by a vision-assisted steering avoidance. At smaller vision angles, the system maintains the free-flow regime even at large inflow, as agents allow for closer proximity (see Fig. 8), preventing congestion. Increasing ρ (i.e., Γ) causes a decrease in the average velocity due to increased scattering in the interaction regime, as seen in Fig. 6b. In particular for the jammed state (ρ ≳ 1.0), a sharp reduction in the velocity is seen. As before, the jammed state has a heightened value of α due to the long-time persistent motion of particles within percolated clusters. It is important to note that in our model, we do not observe a reduction in flow at high densities, with most of the data falling within the ‘free-flow’ regime of the fundamental diagram. This outcome is not entirely surprising, given that our model assumes point-like particles without velocity modulation—an assumption that holds primarily in the semi-dense regime.

Fig. 7: Flow illustration for jamming and roundabout motion.

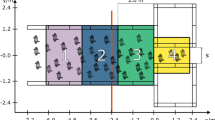
a, b Local density ρ_loc (single stream) with vision angle ψ = π/2 and inflow a Γ = 0.5 and b Γ = 4. As inflow Γ increases, a rotation phase with an asymmetric density distribution develops, as seen in (b). c, d Local density with ψ = π and inflow c Γ = 0.4 and d Γ = 0.6. At Γ = 0.4, there is no jamming, as can be seen by the ‘uniform’ inflow and outflow density lines. However, when Γ ≥ 0.5, the system enters a jammed state, characterized by the depleted outflow lines and enhanced local density at the inflow. In all panels, agents enter at the left and exit at the right, and data is shown for a single agent stream. The local density is estimated as ${\rho }_{{{\rm{loc}}}}={N}_{\delta T}{\tau }_{r}/({\rho }_{0}\delta T{R}_{0}^{2})$, where ${N}_{\delta T}{\tau }_{r}/(\delta T{R}_{0}^{2})$ is the average local density in a region of area ${R}_{0}^{2}$, and N_δT is the total number of agents counted in time δT = 2500τ_r. The data is normalized by the local density at the inflow estimated as ρ₀ = 6Γτ_r/(2πR_intR₀).

Interestingly for ψ = π/2, different movement strategies emerge as the inflow rate Γ is increased. For instance, at Γ = 2.0 and 4.0, a rotation state develops wherein agents follow other agents with the same goal and form a vortex around the center of the interaction, as seen in Fig. 6c and the local density plots in Fig. 7a, b. This rotation state also allows for lower repulsion as each particle is largely aligned with the neighbors, see Eq. (5) in “Methods”. This motion also creates an ‘eye’ in the center, marked by agent depletion (see Fig. 7 and Supplementary Movie 4), suggestive of traffic at a roundabout. This is consistent with the observation of several studies that show the stabilization of pedestrian flows at intersections in presence of an obstacle^27,44. Thus, the self-organized development of the ‘eye’ in the center in our simulations leads to a stabilization of flow. This emergent global state offers insights into discerning effective transport strategies contingent upon the pedestrian volume.

Conclusions

Drawing inspiration from active matter models in biophysics, we have introduced a new approach to simulating pedestrian motion, which employs a vision-based steering mechanism of agents in combination with goal fixation. In contrast to the Social Force Model and its derivatives which employ forces for obstacle avoidance and goal following, we employ non-reciprocal interactions between agents, with local vision-based self-steering through torques that alter the propulsion direction of the agents. The overdamped limit of the Langevin equation mitigates artefacts arising from inertia effects and Newton’s action-reaction principle, which is also inherent in force-based mechanistic pedestrian models. This facilitates a more realistic description of the motion of pedestrians, who ‘steer’ their movement direction, rather than face repulsive/attractive forces, with the former navigation strategy likely dominating in low-density scenarios. Up to now, collision avoidance has been studied theoretically mostly for the much simpler case of bi-directional pedestrian flows. In contrast, we investigate here a multi-stream intersection scenario, inspired in part by recent antipode experiments. The simplicity of our model allows us to isolate the effects of different parameters such as relative maneuverability Δ, vision angle ψ, and inflow rate Γ on the collective dynamics of the agents.

In the state diagram, four classes of motion patterns of semi-dense crowds are obtained, in which agents are weakly interacting, localized flocking, strongly scattering, and jamming. Notably, the jammed state for ψ = π is characterized by percolating clusters, which qualitatively resembles the behavior of pedestrians joining forces to penetrate through highly congested areas. Despite of large differences in the global collective behavior, the complex interplay of inter-agent interactions and goal fixation, the observed super-diffusive motion of the agents can be explained using fractional Brownian motion and Levy walks. For increasing inflow, agents display distinct collective behaviors based on their vision angle, such as the development of roundabout motion at ψ = π/2 and a jammed state at ψ = π. Remarkably, the fundamental flow diagram is found to be universal for different vision angles. Notably, our study captures distinct behaviors such as percolated clusters, roundabout motion, and sub-ballistic movement, even at high relative maneuverability Δ, which can all be directly attributed to the goal-following behavior of the agents, in combination with the distinction between on-coming and co-moving agents in collision avoidance. In contrast, agents without goal orientation, but with similar maneuverability exhibit purely diffusive motion³¹.

Our study lays the foundation for more detailed modeling of systems of interacting cognitive agents, such as pedestrian and animal groups. By introducing additional torques—related to boundaries or local alignment and group-following interactions—various scenarios, including navigation through channels, flocking, and swarming can be studied. We have focused on ‘semi-dense’ crowds, where the assumption of constant speed is a very good approximation. An important next step will be the incorporation of both velocity adaptation and excluded volume effects to generalize the model for higher crowd densities. The former can be addressed in the same spirit as the well-known quorum-sensing mechanism used for ABPs, wherein the agents ‘speed’ depends on the local density of neighbors, and the latter by using Lennard Jones interactions. Lastly, it would be interesting to study experimentally the dependence of the fundamental flow diagram on vision angle.

Methods

Simulation details

All influxes are spaced at the same angular distance from each other and agents enter with frequency v₀/R₀. At each inflow, the start position r₀ = (x₀, y₀) of the incoming agent on the circle is determined by first sampling a number $x^{{\prime} }_{0}$ from a normal distribution $x{{\prime} }_{0} \sim {{\mathcal{N}}}(0,{\sigma }^{2})$ with zero mean and standard deviation σ = πR_int/18 to generate the intermediate point ${{{{\boldsymbol{r}}}}^{{\prime} }}_{0}=({x}_{0}^{{\prime} },{y}_{0}^{{\prime} })$ using ${x}_{0}^{{\prime} 2}+{y}_{0}^{{\prime} 2}={R}_{\,{\mbox{int}}\,}^{2}$. The desired point is then generated by a rotation, ${{{\boldsymbol{r}}}}_{0}={{{\bf{R}}}}_{\theta }{{{\boldsymbol{r}}}}_{0}^{{\prime} }$, where θ = 0, 2π/3, −2π/3 for the red, green and blue streams, respectively. The value of σ determines the approximate interaction radius R_eff, via the relation N_stream(6σ) ≃ 2πR_eff. For our choice of σ = πR_int/18, this results in an effective minimum interaction zone of radius R_eff = R_int/2. An agent crossing the boundary of the interaction zone at any point is removed from the simulation (absorbing boundary).

The equation of motion is solved using the Velocity-Verlet scheme suitable for stochastic systems⁴⁵, with a time step dt = 0.0005τ_r, and a total time of T = 4000τ_r. We ensure overdamped dynamics with the choice of γ = 100, so that m/γ ≪ τ_r.

Path-length distribution for straight paths

In the absence of any interactions, we can estimate the path length distribution using simple geometric arguments. As described in the “Simulation details” section above, the agents are initiated at a position $(x^{{\prime} }_{0},y^{{\prime} }_{0})$ for the central axis of the inflow along y-axis. At each inflow, $x^{{\prime} }_{0}$ is drawn from a Gaussian distribution N(0, σ²), with mean zero and standard deviation σ, and $x^{{\prime}{2}}_{0}+y^{{\prime}{2}}_{0}={R}_{{{\rm{int}}}}^{2}$. The path length for an agent (non-interacting) starting at $(x^{{\prime} }_{0},y^{{\prime} }_{0})$ is then given by L_p = 2L, where $L=\sqrt{{R}_{{{\rm{int}}}}^{2}-x^{{\prime}{2}}_{0}}$. We can estimate the cumulative distribution function F_L(l), i.e., the probability that L ≤ l, as

$${F}_{L}(l) = \, P(L\le l) \\ = \, P(| {x}_{0}| \ge \sqrt{{R}_{{{\rm{int}}}}^{2}-{l}^{2}})\\ = \, 1+\psi (-\sqrt{{R}_{{{\rm{int}}}}^{2}-{l}^{2}})-\psi (\sqrt{{R}_{{{\rm{int}}}}^{2}-{l}^{2}})$$

(14)

where ψ(x) is the cumulative distribution function of x₀. The probability distribution function f_L(l) can then be calculated using ${f}_{L}(l)=F^{{\prime} }_{L}(l)$ to give

$${f}_{L}(l)=\frac{2l}{\sigma \sqrt{2\pi ({R}_{{{\rm{int}}}}^{2}-{l}^{2})}}\exp [-({R}_{{{\rm{int}}}}^{2}-{l}^{2})/2{\sigma }^{2}]$$

(15)

The result in Eq. (15) compared with the simulation data in Fig. 4b of the main text.

Cluster polarization

The average cluster polarization P_c is calculated as

$${P}_{c}={\left\langle \frac{1}{{N}_{c}}\left| \sum_{i\in C}{{{\boldsymbol{e}}}}_{{{\boldsymbol{i}}}}\right| \right\rangle }_{c},$$

(16)

where C represents the set containing indices of particles within the same cluster, e_i is the orientation vector of the particle, N_c is the cardinality of C, and the average is over all clusters.

Fractional Brownian motion

Fraction Brownian motion is a continuous-time Gaussian process X(t) defied as^39,46

$$X(t) = \, \frac{\sigma }{\Gamma (H+1/2)}\left(\int_{0}^{t}{(t-s)}^{H-1/2}dW(s)\right. \\ \quad+ \left.\int_{-\infty }^{0}[{(t-s)}^{H-1/2}-{(-s)}^{H-1/2}]dW(s)\right)$$

(17)

where dW(s) is the standard Wiener process, σ is the noise strength, Γ(z) is the Gamma function, and 1/2 < H < 1 is the Hurst exponent. The Hurst exponent is a measure of the ‘memory’ of the noise, with H > 1/2 for positively correlated increments, H < 1/2 for negatively correlated increments, and H = 1/2 for uncorrelated increments (Brownian noise). Consider R(t) = (X(t), Y(t)) to the be position of the particle at time t, then using the relations

$$\begin{array}{rlr}&{{\boldsymbol{e}}}(t)=\displaystyle\frac{d{{\boldsymbol{R}}}(t)}{dt},&{\sigma }^{2}=\displaystyle\frac{{D}_{H}}{\Gamma (2H+1)},\\ \end{array}$$

(18)

it can be shown that the velocity auto-correlation has the form^46,47,48

$$C(t)=\frac{d{D}_{H}}{\Gamma (2H-1)}{t}^{2H-2}$$

(19)

with the corresponding MSD

$$\langle {{{\boldsymbol{r}}}}^{2}(t)\rangle =\frac{2d{D}_{H}}{\Gamma (2H+1)}{t}^{2H},$$

(20)

where d = 2 is the spatial dimensionality. Here we have assumed that both X(t) and Y(t) are independent Gaussian processes described by Eq. (17).

Nearest neighbor distance

The average nearest neighbor distance d_neigh of agents, is defined as

$${d}_{{{\rm{neigh}}}}={\langle \min ({r}_{ij})\rangle }_{i}$$

(21)

where $\min ({r}_{ij})$ is the distance to the closest neighbor j of particle i and the average is over all particles. Figure 8a shows the plot of d_neigh with Δ for different vision angles. The slope of the curve changes from positive for ψ < π/2 to negative for ψ > π/2, i.e., the minimum separation for small vision ranges decreases for increasing avoidance. This occurs because for small vision angles, localized flocking occurs. Upon alignment, two neighboring agents can be arbitrarily close without noticing the presence of the other. The spatial extent of ‘ignorance’ increases as the vision angle becomes smaller. As soon as ψ > π/2, a least one pedestrian in approaching or co-moving pairs will notice the other, implying the absence of any ‘ignorance’ regimes. This imposes a minimum separation distance d_neigh ≈ R_v equal to the vision range. Similarly, Fig. 8b shows d_neigh for different inflow rates. Clearly, d_neigh depends in a complex way on the inflow, vision angle and relative maneuverability, and thus also implies that the length scales for the analysis of properties such as cluster size distribution and average density must be chosen suitably. Guided by the plots in Fig. 8, we choose R_cut ≃ R_v and R_cut ≃ R₀ for the cluster analysis for vision angles ψ = π and ψ = π/4, respectively. Similarly, for the calculation of the average density at different inflow rates, we assume that each pedestrian occupies approximately an area of $\pi {d}_{{{\rm{neigh}}}}^{2}(\Gamma ,\psi )$. Such a choice becomes necessary, due to the large differences the minimum inter-agent distances for the different parameter choices and the absence of any inherent length scale as we have no excluded volume effects.

Fig. 8: Nearest-neighbor distances.

Mean nearest neighbor distance d_neigh of agents for increasing (a) Δ [fixed Γ = 1] and increasing (b) Γ [fixed Δ = 1] for various vision angles, as indicated.

Characterization of successful exits

For simplicity, we describe the characterization of a ‘successful exit’ for agents from the inflow with the central axis along the y-axis, i.e., the ‘red’ stream in Fig. 1 of the main text. The results hold for other streams via a rotation of the axes. For the center of the stream (the inflow) lying at (0, R_int), i.e., θ₀ = π/2 in polar coordinates, agents exiting the interaction circle for angles θ ∈ (θ₀ + π − δ/2, θ₀ + π − δ/2) are considered to have crossed successfully. Note that here δ is the angular width of the ‘region’ of successful exits, which has a maximum value of δ_max = 2π/N_stream. In the analysis of the data presented in the main text, we have chosen δ = π/2, considering the finite width of the other streams.