Introduction

Excitons are Coulomb bound electron-hole pairs, fundamental excitations in matter that govern the optoelectronic properties in semiconducting materials. Excitons carry energy and momentum, but no net charge and they arise from matter interactions with a moving particle such as photons or electrons. Layered transition metal dichalcogenide (TMDC) semiconductors are of particular interest due to their rich excitonic properties at room temperature1,2,3. Understanding excitons is important to improve our knowledge of transport properties of materials with the ultimate aim to realise the full potential of photonic and optoelectronic applications4,5,6. The coupling of an exciton to the electromagnetic field is called an exciton polariton. Specifically, exciton polariton formation in the strong light–matter coupling regime has been investigated in confined photonic nanostructures7,8,9,10,11,12,13,14,15. Exciton polaritons are of great interest as they have recently been shown to undergo spontaneous coherence to form BoseEinstein (BE) condensates10,16,17,18,19,20 due to their light, bosonic nature. The phenomenon occurs when particles or quasiparticles initially possessing no phase relation become coherent, form a single many-body wavepacket and condensate into the ground level of the entire system once a specific parameter such as temperature threshold is reached. Most commonly, this temperature threshold lies in the nanokelvin range8,10,19, but excitons in TMDCs are thought to be ideal candidates for room temperature BE condensation due to their large binding energy and long lifetimes21,22. Yet there is still a need to understand the underlying coupling mechanism of exciton polariton formation and behaviour in TMDCs at room temperature.

Exciton polariton formation is often studied using a microcavity to trap the photons. However, the nanomaterial itself can act like a microcavity and trap photons. This is due to the confinement within the boundaries of the material and has been demonstrated previously using 2D semiconductors23,24,25. This effect, referred to as self-hybridisation, can be observed in TMDC thin films due to the enormously large background permittivity of the bulk material, for example ϵ∞ = 15 for WSe2. The high refractive index enables an excellent confinement ratio caused by the total internal reflection of the light hosted in the film from the boundaries of the films over a broad spectral and angular range. Coupled modes, such as exciton polaritons in thin TMDCs have so far been investigated using cathodoluminescence25 and scanning near-field optical microscopy (SNOM)26,27, which gave important insights into real-space propagation of exciton polaritons in thicker slabs of WSe2 and MoSe2. Nevertheless, mapping the full energy-momentum dispersion relation of such propagating modes while correlating them to nanoscale structural features has not been accessible to date. A major challenge is that nanoscale light-matter interactions leading to the formation of exciton polaritons are difficult to probe using optical methods, especially optically inaccessible phenomena at large momentum transfer beyond the light cone. Fast electrons, in contrast, can access these excitations28. In the past, conventional electron energy-loss spectroscopy (EELS) techniques implemented in the scanning transmission electron microscope (STEM), referred to hereinafter as STEM-EELS, have enabled direct detection and mapping of excitons at both high spatial and energy resolution29,30,31. However, it is not possible to distinguish between bulk excitons and exciton polaritons using conventional STEM-EELS. Since momentum-resolved EELS (q-EELS) combines high spatial, energy and momentum information, it opens new and exciting opportunities to study optical modes in the electron microscope with the added information of momentum transfer. There have been only very few experimental studies using q-EELS of excitons in TMDCs and those cover different momentum transfer ranges32,33,34,35,36. Most recently, Hong et al.35 included small momentum dispersion measurements of excitons in WSe2, which showed a small shift in the bulk A exciton energy with increasing momentum transfer. Nevertheless, the use of q-EELS is in its infancy regarding the study of dispersion relations of excitons in TMDCs and phenomena such as exciton polariton formation have not been studied to date.

Here we show that using a combination of direct detector technology and high energy resolution STEM-EELS and q-EELS, it is possible to detect and distinguish between bulk excitons and the onset of exciton polariton formation. First, by analysing the intensity distribution with respect to the sample morphology, we show that reflection and transmission of edge exciton polaritonic modes are highly dependent on local geometry such as thickness and presence of edges. In addition, helium ion microscopy was used to pattern structures into the WSe2 and thereby control the local sample geometry and the propagating excitonic modes. Next, we went beyond studying the dispersion of bulk excitons at small q to obtain the full energy-momentum dispersion relation of modes at the onset of exciton polariton formation across the whole Brillouin Zone (BZ) and over a large energy-loss range of several electron-volts. During q-EELS measurements we observed that the electrons accelerated to 60 keV can efficiently couple to excitonic modes in WSe2 thin films of thicknesses of 12 nm as well as monolayers. This allowed to probe the onset of exciton polariton formation in WSe2. Hence, we were able to detect, track and control excitonic modes in WSe2 as well as measure the non-dispersive nature of the energy-momentum distribution in WSe2.

Results

Spatially mapping excitonic intensities in WSe2

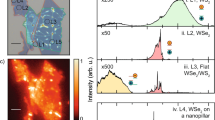
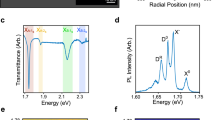
First, WSe2 was imaged and mapped using STEM-EELS and the results are presented in Fig. 1. The high angle annular dark field (HAADF) STEM image in Fig. 1a shows a representative region of thin film WSe2 as analysed for this study. In STEM-EELS, the energy lost by the beam electrons through interacting with the sample is measured. Therefore, the peaks in the energy-loss spectra shown here represent the probability of a certain exciton or exciton polariton creation, where the beam electron is both, the source of the excitation and its probe28,37. There is currently no consensus on the naming of the excitonic peaks with energies above the A exciton in WSe2. Therefore, q-EEL reference spectra were acquired of monolayer (ML) WSe2 (shown in Fig. 1b) and thin film WSe2 (shown in Fig. 1c). The EEL spectrum in Fig. 1b for monolayer WSe2 show the energy-loss peaks associated with the excitons and their Rydberg state excitons for zero momentum transfer (q = 0). Detailed band structure calculations for WSe2 have been published elsewhere35,38. Like in other TMDCs, the A, B excitonic peaks originate from the valence band splitting and this splitting is expected to be large in W-based materials due to the stronger spin-orbit coupling (SOC) compared to molybdenum-based materials39. For monolayer WSe2 the splitting has been calculated to be 0.4 eV using ab initio many-body perturbation theory within the GW/BSE approximation39. The first most prominent peak in Fig. 1b is due to the A exciton (at 1.68 eV). Most recently, Hong et al.35 showed that there is significant overlap between the A’ Rydberg state exciton and the B exciton. Hence, the second peak has overlapping contributions from the B exciton (2.15 eV) and the A’ Rydberg state exciton (expected at 2.08 eV). The third prominent peak (here at 2.44 eV) has been assigned as the B’ Rydberg state exciton recently35, however, this has most commonly been referred to as the C0 exciton. The higher energy-loss peaks originate from different C exciton transitions, with some of their exact origins in k-space not determined yet. The fourth and fifth peaks are denoted here as C1 at 2.95 eV (sometimes also called D exciton) and C2 at 3.3 eV (sometimes also called E exciton) and they are thought to originate from the electronic transition of the first valence/conduction band at the Q point and the transitions between the midpoint of KM between the first valence and the second conduction band respectively35. In contrast, the EEL spectrum for thin film WSe2 (shown in Fig. 1c) only shows defined peaks for the A and B excitons (at 1.75 eV and 2.3 eV respectively) and not their Rydberg state excitons. The spectral positions of 2s Rydberg state excitons, which are resolved in the case of the monolayer have been shown to vary with increasing thickness to shift to lower energies40. This shift most likely causes increased overlap with the 1s excitons making it impossible to distinguish the individual states. The second peak observed in the multilayer WSe2 is associated with the B exciton, however the energy does not exactly match any of the peaks found in the monolayer WSe2 (see Fig. 1b). This is not surprising since EEL spectra show a superposition of all losses (and gains) that the primary electrons undergo while passing through the sample. The shifting of the Rydberg excitonic energy positions with thickness would lead to differently overlapping peaks for varying thicknesses of the WSe2. The difference in energy position of the B exciton in the multilayer sample is most likely due to the peak being composed of a superposition of A’ Rydberg states, B excitons and B’ Rydberg states. Furthermore, the C excitonic transitions peaks are also expected to shift with the WSe2 thickness41. Further imaging and STEM-EELS can be found in the supplementary information (SI) (Supplementary Note 1, Figs. 1, 2).

Fig. 1: A and B excitonic intensities are increased on the edge of WSe2 thin films suggesting presence of edge polaritons.
figure 1

a High-angle annular dark-field (HAADF) image of a representative edge region of thin film WSe2 as analysed. b EEL spectrum showing the electron energy-loss in electron volts (eV) versus intensity in arbitrary units (au) of monolayer (ML) WSe2 showing peaks for the A, B excitons (annotated with A, B) and Rydberg state excitons (annotated with A’, B’) as well as the C exciton transitions (annotated with C1 and C2). c EEL spectrum of the thin film WSe2 showing peaks for A, B excitons (annotated with A, B). d HAADF image of an edge region of the thin film of WSe2 showing regions of increasing thickness (black = vacuum, dark grey = thinnest to light grey = thickest region). e A exciton intensity map acquired from STEM-EELS of the region as shown in(d), generated by integrating the spectral intensity in arbitrary units (au) over the A excitonic energy-loss peak (same spatial scale bar as in (d); colours in map: integrated peak intensity in au, where dark blue regions = lowest intensity, bright yellow regions = highest intensity). f B exciton integrated intensity map from STEM-EELS of the region as shown in (d) (same spatial scale bar as in (d); colours in map: integrated peak intensity in au, where dark blue regions = lowest intensity, bright yellow regions = highest intensity).

Full size image
Fig. 2: Controlling excitonic intensities using nanopatterning of thin film WSe2.
figure 2

a High-angle annular dark-field (HAADF) image showing a thin film WSe2 with cuts (arrows) from helium ion microscopy (black = vacuum, darkest grey = thinnest region to lightest grey = thickest region). b Nanoscale map of A excitonic intensity from STEM-EELS, generated by integrating the spectral intensity in arbitrary units (au) over the A excitonic energy-loss peak (dark purple = lowest A excitonic intensity, yellow-white = highest A excitonic intensity). c Individual EEL spectra showing the signature from A and B excitonic peaks from a reference region as well as from various positions around the cuts as shown in (b). d Intensity profiles of the A and B excitonic peaks across the cut region (annotated with boxed region in (b)) show that the intensity of the A and the B exciton peaks are enhanced around the cuts.

Full size image

The HAADF image shown in Fig. 1d represents the edge region of a thin film WSe2, where the black region shows the vacuum and grey regions the WSe2 with terraces of increasing thickness (black = vacuum, dark grey = thinnest to light grey = thickest region). Conventional STEM-EELS maps were acquired of this region of interest and the intensity was integrated over the A and B exciton energy-loss peaks to show the spatial distribution of the intensity of A and B excitonic loss events (Fig. 1e, f with the dark blue regions showing regions of no to low excitonic intensity and the bright yellow showing regions of high intensity). When using conventional STEM-EELS, no momentum transfer information is retained as it is averaged while using the circular aperture selecting a minimum of 1–2 Brillouin zones in the diffraction space. Conventional STEM-EELS mapping can provide spatial distribution of excitonic intensities, but it provides no direct way to distinguish whether bulk excitons, exciton polaritons or a combination of both are detected. It is however possible to indirectly deduce from the intensity variations whether only bulk excitons are detected or a combination of signals. Here, both, the A and B excitonic intensity maps in Fig. 1e, f show a significant increase in intensity in the edge region of the material. Possible explanations for this localised increase include the presence of edge excitons or confinement of modes in the edges leading to edge polaritons42. Furthermore, the intensity of both, A and B exciton energy-loss peaks appear to reduce gradually for terraces of increasing thickness. A reduction of intensity at energy-losses characteristic for bulk excitons is not unexpected when comparing monolayer to multilayer WSe2. The gradual stepwise decrease in intensity with increases in terrace thickness, however, is surprising.

The maps also indicate that the modes are tightly confined to the edges of the material as the intensity of both, A and B excitonic peaks is enhanced at the edges of the material (also see intensity profiles shown in the Supplementary Fig. 2d). This intensity distribution suggests that in fact we are mapping at least in part a propagating mode rather than a pure bulk exciton. The latter would not be affected by variations in the local geometry. We propose that this gradual decrease in intensity with increasing thickness is an indication of a semi-propagating polaritonic mode.

Controlling excitonic intensities by nanopatterning WSe2

Next, we utilised the knowledge of the increased A, B excitonic intensities at the edges of the material to control the excitonic intensities locally. Helium ion microscopy (HIM) was used to cut patterns into the thin film WSe2 and then conventional STEM-EELS mapping was used to study the spatial variations of the excitonic intensities in the nanopatterned thin film WSe2. The resulting cuts are shown in Fig. 2a. The A excitonic intensity map in Fig. 2b shows the integrated intensity of the energy-loss peak associated with the A exciton. Again, this does not allow to directly distinguish between bulk excitons or exciton polaritons, but the intensity variations can provide some insights. It can be observed that its overall intensity is inversely proportional to the thickness of the flake with the thinnest region in the top left-hand side (LHS) in Fig. 2a featuring increased excitonic intensity in Fig. 2b, compared to the thicker regions on the bottom of the field of view. This observation agrees with the unpatterned thin film WSe2 shown in Fig. 1. Furthermore, the A excitonic intensity appears to be enhanced around the cuts. Intensity profiles of the A and B excitonic energy-loss peaks highlight the localisation of the intensity increase of the excitonic peaks around the cuts. This is in agreement with the localisation of the increase in intensity of the A and B excitons near the edges of the thin film WSe2 as shown in Fig. 1. The increase in intensity could be due to the presence of edge polaritons propagating along the edges of the cuts. The individual EEL spectra presented in Fig. 2c show that near the cuts, the energy-loss intensity is high (red spectrum 1 and blue spectrum 3) and the intensity inside the cut is further increased (green spectrum 2) compared to the reference spectrum acquired away from the cuts (from the region annotated with ’ref’ in Fig. 1b). However, the overall peak width is also increased, which suggests the presence of a WSe2 crystal structure with less long-range order in the immediate vicinity of the cuts.

Energy-momentum dispersion across the Brillouin zone

The energy-momentum dispersion relation of the modes in thin film WSe2 was then analysed using both, computational (Fig. 3b) and experimental means (Fig. 3c–h). Prior to the experimental q-EELS, the sample thickness of the regions of interest was assessed43 and all thin film WSe2 presented here were 8–12 nm thick, with the exception of the monolayer and homobilayer presented later. The thin film WSe2 was then analysed by q-EELS using a slit aperture placed in the diffraction plane at the entrance of the spectrometer to select the energy-losses along the high symmetry directions Γ → K and Γ → M. A schematic of the q space of the sample is shown in Fig. 3a. This approach allows to simultaneously acquire spectra along the chosen direction for momentum transfer covering one or more Brillouin zones (BZs). The central diffraction spot is found at Γ and the high symmetry directions denoted with Γ → M (red) and Γ → K (green). Data was also acquired in an offset manner to improve signal-to-noise by centering the slit aperture at Γ′, along Γ′ → M′′ (yellow) to provide data from crystallographic vectors equivalent to Γ → M and therefore referred to hereinafter as Γ → M. We propose that unlike conventional STEM-EELS, q-EELS allows to distinguish between bulk excitons and exciton polaritons. No excitonic loss intensity is expected at finite momentum exceeding 10% of |Γ−Γ′| or |Γ−Γ′′| for bulk excitons, since the dispersion of bulk excitons in TMDCs is known to be limited to very small q only35. For spectra acquired at zero or small momentum transfer, the bulk exciton and exciton polariton signals are overlapping as shown in Supplementary Fig. 4. At large finite momentum transfer, only exciton polaritons have a detectable signature. The energy-momentum (ωq) map along Γ → K (Fig. 3c) as well as along Γ → M (Fig. 3f) show a non-dispersive feature at the energies corresponding to the energies of the A and B excitonic peaks. In the EEL spectra for zero momentum transfer (q = 0), peaks are present at the A, B exciton energies (spectra in Fig. 3d, g), as well as in the summed finite momentum spectra (Fig. 3e, h) along both, Γ → M and Γ → K, albeit at a much reduced intensity. The peak at the A exciton energy is found to be at 1.75 ± 0.01 eV for finite momentum q-EEL spectra along Γ → M and Γ → K (peak fitting can be found in Supplementary Fig. 6). The raw data as well as more processed maps that were treated with Richardson-Lucy deconvolution are shown in the Supplementary Fig. 5 alongside the individual spectra for varying q along Γ → K. Factors such as sample support and acquisition parameters including time and electron beam currents were found to not affect the general appearance of the experimental high q energy-momentum dispersion of WSe2. Complementary simulations were used to assess the expected dispersion at very small q of exciton polaritons. The simulated energy-momentum EELS map for a 10 nm thick sample of WSe2 (Fig. 3b) show that the exciton polariton dispersion of the A and B excitons is expected to be almost flat at small momentum transfer. The computational simulations were repeated for WSe2 of 15 nm, 20 nm, 30 nm and 60 nm thicknesses to assess the effect of thickness and the results are presented in Supplementary Note 2, Supplementary Fig. 9. It was found that for increasing thicknesses, the splitting of the bands (anti-crossing) becomes apparent for thin films of 60 nm thickness. The splitting however, is very small in energy for these thin structures, which is currently not resolvable using q-EELS. Our experimental findings of near flat A, B excitonic dispersions are therefore in agreement with the calculated spectral maps. Both, the experimental and computational findings suggest that we are in the regime of the onset of exciton polariton formation, which contribute significantly to the transport phenomena in thin film WSe2.

Fig. 3: At the onset, exciton polaritonic modes were found to exhibit a near flat momentum-energy dispersion relation in ≈12 nm thin films of WSe2.
figure 3

a Schematic showing the q space of WSe2 and the high symmetry directions along which the energy-momentum maps were acquired. The central diffraction spot is found at Γ and the high symmetry directions are Γ → M (red) and Γ → K (green). Offset data acquisition along Γ′ → M′′ (yellow), equivalent crystallographic vectors to Γ → M (red), improved signal-to-noise. b The calculated energy-momentum q-EELS for a 10 nm thick sample of WSe2 suggest that the exciton polariton dispersion for A and B excitons are expected to be flat for very small momentum q. c Energy-momentum (ωq) map (in log scale) for momentum transfer from |q| = 0.1 × |Γ−Γ′′| to |q| = 0.9 × |Γ−Γ′′| along Γ → K shows a non-dispersive loss feature at the A exciton polariton energy for finite q across the Brillouin zone (arrows). d q-EEL spectra for zero momentum transfer (q = 0) and (e) summed finite momentum q show a peak at the A exciton energy at 1.75 ± 0.01 eV and B exciton energy at ≈2.3 eV respectively. f ωq map (log scale) for momentum transfer from |q| = 0.1 × |Γ−Γ′| to |q| = 0.9 × |Γ−Γ′| along Γ → M shows a non-dispersive feature at the energy corresponding to the A exciton polariton for finite q across the Brillouin zone (arrows). The peak at the B exciton energy (denoted with B) is also showing a non-dispersive behaviour. Again, (g) q-EEL spectra for zero momentum transfer (q = 0) and (h) summed finite momentum q show a peak for A excitons at 1.75 ± 0.01 eV and B excitons at ≈2.3 eV respectively.

Full size image

As a following step, the energy-momentum dispersion relation of the modes was analysed in monolayer WSe2 using q-EELS (Fig. 4). The ωq map of monolayer WSe2 along Γ → K and along Γ → M are shown in Fig. 4a, d respectively. Like in the case of thin film WSe2, both show a non-dispersive feature at the energies corresponding to the A excitons. In the q-EELS for zero momentum transfer, peaks are present at the A exciton energy as well as B and C exciton transitions (shown in Fig. 4b, e). When summing q-EELS for momentum transfer exceeding 10% of the Brillouin zone in both, Γ → K and Γ → M directions (shown in Fig. 4c, f respectively), a peak at the A exciton energy is present albeit at a much reduced intensity compared to the q = 0 spectrum. Hence, the peak at the energy-loss corresponding to the A exciton energy is observed in the summed finite q spectra along both, Γ → M and Γ → K. It is notable that the energy of the second feature corresponds most closely to the B’ Rydberg excitonic state in energy. These findings suggest that propagating exciton polaritonic modes may contribute significantly to transport phenomena, not only in the case of thin film WSe2 as shown above, but also in the case of monolayer WSe2. We also analysed a region where two monolayers were overlapping (also called a homo-bilayer) and found that the feature at the A exciton energy remained detectable beyond the first BZ (see Supplementary Fig. 8). We also found a shift to lower energies by 58 meV for the overlapping monolayer region compared to the monolayer region. When two monolayers overlap with a relative twist between the two lattices to form a homo-bilayer, this leads to the formation of a moiré superlattice44 and the twist-dependent creation of interlayer excitons and shifts in the excitonic energies.

Fig. 4: A near flat dispersion of the A excitonic feature and below gap signal intensity at large momentum transfer suggest contributions from exciton polaritons as well as optically ’dark’ excitons.
figure 4

a Energy-momentum (ωq) map (log scale) for momentum transfer from |q| = 0.1 × |Γ−Γ′′| to |q| = 0.9 × |Γ−Γ′′| along Γ → K shows a non-dispersive feature at the A exciton energy for finite q across the Brillouin zone (arrows) including at the M’ point. b EEL spectra for zero momentum transfer (q = 0) and (c) summed finite q show a peak corresponding to the A exciton energy. Higher energy peaks at energies associated with the B and C exciton transitions are also present in the summed finite q spectrum. d ωq map (log scale) for momentum transfer from |q| = 0.1 × |Γ−Γ′| to |q| = 0.9 × |Γ−Γ′| along Γ → M shows a non-dispersive feature at the energy corresponding to the A exciton for finite q across the Brillouin zone (arrows) including at the M point. e q-EELS for q = 0 as well as (f) for summed finite q exhibit peaks at energies associated with the A exciton energy as well as higher energy excitonic transitions. When comparing spectra shown in (c) and (f) there is also added intensity below the A excitonic energy (blue arrows) along Γ → K, suggesting the presence of dark excitons at finite q contributing to the overall intensity.

Full size image

In addition, added intensity below the A excitonic loss peak in the spectrum for finite q along Γ → K (marked with arrows in Fig. 4c) compared to spectrum for summed finite q along Γ → M (shown in Fig. 4e) could indicate the presence of inter-valley optically ‘dark’ excitons as postulated previously and detected using angle-resolved photoemission spectroscopy (ARPES)45. However, there is a noted absence of more defined features in the regions where optically dark excitons are expected46. This is most likely due to the suppression of the non-radiative decay to dark excitons resulting from the enhancement of the radiative decay via polaritons.

Discussion

Using conventional STEM-EELS mapping we found that variations in the local geometry, including the presence of steps and edges in the thin film TMDC, were significant factors in the varying intensity of the excitonic peaks. These findings were confirmed by similar observations of the nanopatterned sample where a nanoscale pattern was cut into a multilayer WSe2 using HIM. The cuts were found to enhance the intensities of excitonic energy-loss peaks locally. The edges of a 2D material were previously suggested to host edge polaritons47 and their presence is likely an important factor in the enhancement of exciton peak intensities at edges and cuts observed here and shown in Figs. 1, 2. In addition, the intensity enhancement and therefore the edge polaritons were observed to be tightly confined to the edges of the material. The unexpected gradual decrease in excitonic intensity with terrace thickness as described in the first part of the paper however, is not explained by the presence of edge modes alone. We propose that these variations in intensity are due to the contributions from exciton polaritons to the signal. In 2D materials of monolayer to 12 nm thickness there is significant confinement along the direction of electron propagation. The addition of terraces and steps as well as edges and cuts constitute additional geometric confinement to a propagating exciton polariton mode.

Using q-EELS, the A exciton polaritons originating in thin film and monolayer WSe2 were found to remain detectable across the Brillouin zone for large momentum transfer and the energy-momentum dispersion was found to be near flat (Figs. 3, 4). Using calculations, we found that this flat energy-momentum dispersion is expected for exciton polaritons in monolayer and 10 nm thin films of WSe2 (Fig. 3b and in Supplementary Fig. 9) at very small momentum transfer47. When probing a bulk exciton, no feature is expected at large momentum transfer since the energy-momentum dispersion of bulk excitons is expected to be small35. Hence, we attribute the loss feature detected across the BZ along Γ → K and Γ → M to the presence of exciton polaritons. So far, the presence of exciton polaritons has been reported on in studies of thicker TMDCs using optical methods only24,25.

Some questions remain however, regarding why we are consistently observing a near flat dispersion for loss features at large momentum transfer, which resembles that of exciton-polaritons at much smaller momentum transfer. To investigate the possibility that phonons contribute momentum via dual scattering processes, the measurements were repeated at liquid nitrogen temperature, where electron energy gain through phonons is expected to be significantly reduced and electron energy loss through phonons is expected to be slightly reduced (see Supplementary Fig. 7)48,49. Since the cryo q-EELS showed the same signature as in the room temperature measurements, dual scattering through phonon contributions as the main source of the features at large momentum transfer are unlikely. Furthermore, an additional possible source contributing to the signal at large q, could be the presence of excitonic polarons which form when excitons interact with acoustic or optical phonons via coupling to the deformation potentials50. In theory, contributions from non-linearity of the exciton components (through the presence of the holey silicon nitride support film) or from excited state excitons could also contribute to the signal at large q in our setup. Testing either hypothesis is currently out of reach, as well as being highly speculative. Regarding the latter possibility, it is also worth noting that the energy position of the second exciton polariton peak at large momentum transfer for the monolayer WSe2 shown in Fig. 4 appears closer in energy to the peak associated with the excited-state exciton, the B’ Rydberg state exciton, rather than the B exciton. This indicates that we might be detecting excited-state exciton polaritons in WSe2 in the present study. Excited-state excitons have been shown to enhance polariton interaction strength51.

When comparing our results to existing literature, the most recent paper on the topic by Hong et al.35 is the most relevant. The energy-momentum relation of excitons in WSe2 for small finite q < 0.19 Å−1 was measured. Hong et al. found that the A exciton vanishes for q > |Γ− K | /8 or q > 0.18 Å−1. Furthermore, a small shift in energy of the A exciton peaks was observed in the finite q spectra (≈0.1 eV). The main focus of the studies by Hong et al.34,35 was to measure the small dispersion of bulk excitons at small finite q and not exciton polariton formation like in the present study. The techniques employed were aimed at optimising momentum and energy resolution so that the dispersion signal of the bulk excitons, which is known to vanish rapidly at finite q, could be measured. Here, however, we aimed at measuring the full energy-momentum space across the BZ to observe the exciton polariton formation as well as the presence of inter-valley dark excitons. Employing a direct detection camera allows high signal-to-noise spectra to be recorded, including at high q. This allowed to also measure the energy-momentum dispersion of the A, B and even C excitons for higher q. Similarly the studies by Büchner and Knupfer et al.32,33 were based on q-EELS to measure energy-loss spectra of MoS2 for high q up to q = 1.33 Å−1. In these studies however, the high q signal at the energy-loss positions of the A, B excitons was attributed to the presence of dark excitons.

The present study illustrates the importance of nanoscale spatial information for understanding the mechanisms underlying exciton and exciton polariton formation. It highlights the importance of techniques such as electron microscopy which can be very sensitive and provide high resolution in real space, energy and also momentum. The excitonic signal was found to vary on the nanometer scale, making the spatial information crucial to further our understanding of these fundamental transport properties. Using q-EELS, this spatial information can now be combined with energy-momentum dispersion measurements. Techniques such as ARPES measure the dispersion relation of a material on a spatially much coarser scale, potentially averaging over spectral variations induced by specimen inhomogeneities. Our results show that q-EELS in a monochromated electron microscope is very well suited for studying electronic excitations across the entire BZ and may in the future shine light also on other phenomena, such as spontaneous coherence of exciton polaritons. In this context, there is one crucial difference between electron-based and laser-based optical techniques: scanning an electron beam across the sample provides a maximally incoherent source, excluding any potential influence of the coherence of the excitation on the observation. However, one important limitation to address in the future is that currently it is not possible to reliably access relative populations of electronic states using q-EELS. It might however become feasible to access this information in the future. This is beyond the scope of the present work since it requires the theoretical framework to be developed.

To conclude, using conventional STEM-EELS mapping we found that inevitable variations in the local geometry, including the presence of steps and edges in the 2D material are significant factors in the energy-loss peak intensity associated with the A and B excitons in TMDCs. We propose that this is due to the presence of very localised edge polaritons as well as additional geometric confinement leading to exciton polaritons in thin film and monolayer WSe2. Furthermore, the non-dispersive nature of the energy-momentum dispersion relation of exciton polaritons was measured using q-EELS across the BZ and complemented using electrodynamical calculations. The presence of exciton polaritons is of great relevance to many applications of TMDCs, as they greatly affect electrical conductivity and exciton transport in general. Lastly, we showed that HIM nanopatterning represents an opportunity to control and increase excitonic signals. Having nanoscale spatial control over excitonic intensity could be of great benefit for transport applications of TMDCs and offers great potential in tailoring the excitonic response of 2D materials for optoelectronic application. Further exploration of this avenue will be important to take full advantage of this technological opportunity.

Methods

Sample preparation

WSe2 flakes were exfoliated from bulk WSe2 crystals (purchased from HQ Graphene) using scotch-tape on silicon wafers with a 285 nm thick thermal oxide (SiO2/Si) substrate. The dry transfer was done inside a glove box in argon atmosphere, where the optical microscope, the transfer stage and the micromanipulator were controlled from outside. Polydimethylsiloxane (PDMS) and poly(propylene) carbonate (PPC) films were used for the dry transfer of WSe2 due to their favourable viscoelastic and thermoplastic properties. This ensured that high-quality single-layer to few-layer 2D (WSe2) materials were successfully transferred onto holey silicon nitride grids (holey Si3N4 support film of 200 nm thickness, 1000 nm pore sizes). This allowed the further analysis, imaging and patterning of the suspended sample to be done in vacuum without background from the support.

Helium ion microscopy nanopatterning

A Zeiss Orion Nanofab microscope was used to modify the geometry of the 2D structures at the nanoscale using He ion beam milling. A nanopatterning and visualization engine (NPVE) software was employed to generate the patterns. In a next step, Stage-o-mat (a special module of FIB-o-mat52) was used to place the patterns in such a way that unintended ion irradiation in the suspended sample regions was avoided. Referenced optical control images were used for this purpose. An acceleration voltage of 30 keV, a 11 mm working distance, a 20 µm objective aperture, spot size 7, and a beam current of 1.4 pA were used. The line patterns were created using parallel single line cuts with varying distance rastered using a pitch of 0.25 nm and 1 µs dwell time resulting in 20 pC/µm exposure dose.

Electron microscopy

All EEL spectra and images were acquired on a Nion HERMES aberration-corrected high energy resolution monochromated scanning transmission electron microscope at Humboldt-Universität zu Berlin which is equipped with a Dectris ELA hybrid-pixel direct electron detection camera for recording spectra and diffraction patterns. The microscope was operated at 60 keV accelerating voltage.

Conventional electron energy-loss spectroscopy

Conventional STEM-EELS maps shown in Figs. 1 and 2 were acquired with a convergence angle of 10 mrad and a 2 meV/pixel dispersion in the energy-loss direction. The beam current was 9–10 pA after monochromation. In order to improve the signal-to-noise ratio, some energy-resolution had to be sacrificed by limiting the monochromation to a factor of 10 to obtain an energy-resolution of 21–35 meV on the sample. After acquisition of the spatially resolved STEM-EELS maps, the zero-loss-peak (ZLP) was aligned within the Nion Swift software to correct for potential energy shifts. No smoothing was applied to the EEL spectra. The sample thickness was assessed using the log-ratio EELS method43 using data acquired with a convergence angle of 30 mrad. The intensity maps in Fig. 1 were obtained by integrating the intensity of the A and B excitonic peaks in the background-removed EEL spectral maps. The integrated intensity profiles in Fig. 2 were extracted from the background-removed STEM-EELS maps by summing spectra in the y-direction and retaining the spatial information in the x-direction.

Momentum-resolved electron energy-loss spectroscopy

All momentum-resolved EELS (q-EELS) data were acquired using a convergence semiangle of approximately 1.5 mrad. A slit aperture was employed to select the high symmetry directions in the k-space. To increase signal-to-background ratio, recording the undiffracted beam was avoided when possible by selecting equivalent crystallographic vectors. Figure 3f shows such an offset data-set where the slit aperture was aligned to select data starting from Γ′ rather than Γ. The EELS acquisition with the direct electron detector Dectris ELA allowed to obtain data with high-signal-to-background ratio which was crucial to detect low intensity signals such as finite q signatures. In order to acquire ωq maps across 2×|Γ−Γ′| and 2×|Γ−Γ′′| distances of the BZ in each single acquisition with a sufficient signal-to-background ratio, a suitable combination of energy, momentum resolution and acquisition parameters needed to be found. The energy resolution of the individual spectrum was measured using the FWHM of the zero-loss-peak at zero momentum transfer and it was found to be ∆E ≈ 21−51 meV. The momentum resolution was found to be ∆q = 0.023 Å−1 along Γ → M and ∆q = 0.039 Å−1 along Γ → K. The spectral maps were acquired with a dwell time of 60 s each and by adding up individual maps a total acquisition time of 35–40 mins was achieved for each summed map as presented in Figs. 3 and 4. The cryo q-EELS measurements were conducted using a dedicated cryo-transfer holder (Gatan CT3500 TR, Gatan, Munich, Germany) used as a cooling holder. The sample was mounted at room temperature, and the holder was subsequently cooled down with liquid nitrogen once inside the microscope column. All cryo q-EELS measurements were performed at approximately 95 K. The q-EEL spectral maps were aligned using the Nion Swift software. Next, the ZLP was aligned and centered across the maps. No smoothing of the spectra was employed and all spectra are presented in their raw form. The exception is the map of the multilayer in Γ → K direction (shown in Fig. 4), which has been normalised to total intensity of the ZLP to reduce the background intensity. Richardson-Lucy deconvolution was implemented on the same data set within hyperspy53 to show the peak evolution across the BZ (see Supplementary Fig. 5). This was deemed necessary to preserve the low intensity signals of the finite q losses. To obtain the zero momentum transfer (q = 0) q-EEL spectra, the signal was extracted at Γ only. To obtain q-EELS spectra at finite q, the signal was integrated from |q| = 0.2 × |Γ−Γ′| to |q| = 0.8 × |Γ−Γ′| along Γ → M and from |q| = 0.2 × |Γ−Γ′′| to |q| = 0.8 × |Γ−Γ′′| along Γ → K. All ωq maps are shown in log scale with the momentum information being displayed using fractional units of |q|, with |Γ−Γ′| = 1 along Γ → M and |Γ−Γ′′| = 1 along Γ → K.

Computational electron energy-loss spectra

For calculating the electron energy-loss spectra, we modelled the electron as a swift charge distribution propagating through a WSe2 thin film in the direction perpendicular to the surface of the film. The resulting field distributions were calculated from analytical solutions of Maxwell’s equations, based on a vector potential approach and the non-recoil approximation54,55.