Quantifying the in-plane strain influence on second harmonic generation of molybdenum disulfide

Abstract

Quantifying the strain, and even the strain state, is critical for the advancement of strain engineering in microelectronics and optoelectronics fields, whether using the classical semiconductors or emerging two-dimensional materials. Second Harmonic Generation (SHG) has emerged as a potent technique for exploring the optical-mechanical properties of two-dimensional transition metal dichalcogenides (2D-TMDCs). Based on the theoretical framework of SHG, this work analyses the mechanism of different strain states acting on the SHG polarization-intensity spectrum (PIS) of MoS₂. A quantifying method is proposed by establishing the analytic relationship between the in-plane strain components and the petal amplitude ratios (PARs) obtained from detected PIS. After calibrating the key parameters of MoS₂ SHG PIS, a series of biaxial and uniaxial tensile experiments are performed, whose results are mostly agreed with the theoretical expectations, thus verifying the reliability, correctness and universality of the proposed method for quantitively characterizing the strain state of monolayer MoS₂.

Introduction

Exemplified by Molybdenum disulfide (MoS₂), two-dimensional transition metal dichalcogenides (2D-TMDCs) possess unique traits of atomic-scale thickness, flexibility and distinctive direct bandgap characteristics, which have garnered significant attention in various fields such as new energy, flexible electronics and optoelectronics¹. For example, monolayer MoS₂ has found wide-ranging applications in photodetectors², field-effect transistors³, sensors⁴, batteries⁵, and optoelectronic devices⁶ due to its exceptional optical, electrical, thermal, and mechanical properties^7,8,9,10. Besides, the three-fold symmetrical structure of 2D-TMDCs also makes their multiple properties more sensitive to strain compared with graphene¹¹, thereby enabling 2D-TMDCs great potential in strain engineering and broadening their applying prospects in the areas of flexible electronics and optical sensors¹².

However, in practical application, there are still numbers of fundamental issues hindering the further development of MoS₂, and other 2D-TMDCs as well, especially in the aspects of the strain-optical responses and interfacial behaviors, such as interfacial adhesion performance and shear strain between the interface of MoS₂ and substrate^13,14,15. It is crucial to address these issues to enhance the functionality and reliability of devices using 2D-TMDCs, which requires a precisely strain measurement of MoS₂ on a flexible substrate or inside some flexible-based heterostructure.

The strain measurement of a two-dimensional material on a flexible substrate remains a complex yet compelling topic, particularly for what concerns the quantification of the strain state and the detection of all the strain components. Raman and Photoluminescence (PL) have been widely applied for the strain/stress analyses in 2D materials. However, as for a MoS₂ sample, its Raman shift lacks sufficient (quantifiable) sensitivity to the strain. On the other hand, the PL spectrum of MoS₂ only reflect the magnitude of strain. To be exact, PL can detect the sum of principle strain components of MoS₂, but cannot decouple them. It is not only a broad demand, but also an exciting challenge, to realize the quantitative analysis of strain state by some non-contact and non-destructive method at the microscale.

A nonlinear optical method, second harmonic generation (SHG), may become an effective way to measure the strain state of MoS₂. In recent years, owing to the development of ultrafast lasers, a series of nonlinear optical technologies have been proposed, which offered some unique advantages in the investigation fields such as crystallography^16,17,18, biometrics¹⁹, and nonlinear optoelectronics^20,21. As a typical nonlinear optical method, second harmonic generation provides structural information of some crystal materials including most of the 2D-TMDCs. It is because SHG occurs, and only occurs, in the material structure with inversion symmetry breaking²². Generally, an odd-layered 2D-TMDC possess a non-centrosymmetric structure, exhibiting a strong SHG response when excited by ultrafast laser. As a result, SHG is regarded as a promising tool for characterizing various properties of 2D-TMDCs, including layer number²³, crystal orientation^24,25, crystal boundary²⁶, defects^27,28, and strain²⁹.

Several existing theoretical and experimental studies have demonstrated that strain influences the SHG information of MoS₂ and other 2D-TMDCs^{30,31,32,33,34}. In particular, based on the works into the impact of strain on the SHG intensity, most qualitative researches have demonstrated that the introduction of strain effectively influenced the SHG second-order nonlinear susceptibility of materials, facilitating the development and application of related devices, thus highlighting the significance of strain engineering^35,36,37. In turn, the sensitivity of the SHG signal to strain has also made it a powerful tool for characterizing the material strain, which is of great importance for analyzing the service state of materials in related devices and the application of strain engineering in the sensing field. In detail, Lyubchanskii et. al. incorporated the photoelastic tensor into the nonlinear susceptibility^38,39, predicting that the strain can change the emission intensity and polarization angular-resolved shape of SHG. These works preliminarily outlined the theoretical framework of strain-influenced SHG. According to the published studies, Liang et. al. first experimentally showed the strain influence on SHG shape of 2H-MoSe₂ under uniaxial loading⁴⁰, which confirmed the theoretical predictions in the early works of Lyubchanski. Also based on this theory, Mennel et. al. calibrated photoelastic parameters of several types of 2D-TMDCs using the intensity of polarization-resolved SHG under uniaxial loading, achieving the evolutions of SHG intensity spectra with the changes of strains^41,42. Utilizing the calibrated parameters from Mennel et. al., Khan et. al demonstrated the compressive strain amplitude and direction in the folded region of a 5 L WS₂⁴³.

Nowadays, the strain engineering has advanced from the straightforward manipulation of a simple and single strain component to the tunning of comprehensive material properties under complex strain states^44,45. The existing studies indicate that the SHG of MoS₂ is sensitive to both the magnitude and direction of its strain. Nevertheless, these works have still not provided adequate (theoretical or experimental) evidences to demonstrate that the strain of MoS₂ could be measured or quantitatively characterized by using SHG data, nor have they shown its capability for quantifying the state of strain. This is because the SHG intensity detected in experiment is susceptible to diverse environmental and instrumental factors besides the strain influence. Both theoretical models and calibration experiments are challenging to quantitatively determine the analytical relationship between the strain components of MoS₂ and the actually detected intensity of SHG. Specifically, divergent results can be caused across different measurements even on the same sample with the same strain, making it short of robustness and dependability to analyse strain by directly using the original values of the detected SHG intensity. Moreover, the existing experiments mainly concentrate on the SHG of MoS₂ under uniaxial loading state, which only provide a relatively limited perspective. Therefore, it is necessary to establish a general analytical model for the SHG information of MoS₂ under all kinds of strain states, and then to develop a practical method for quantifying the strain state of the measured MoS₂.

This work analyses the mechanism of different strain states acting on the polarization-intensity spectrum (PIS) of SHG. A method based on the petal amplitude ratio (PAR) is introduced to identify the real strain state from the PIS of MoS₂. Numerical and physical experiments under different loading states were carried out to verify the reliability and accuracy of the analysis method proposed in this work.

Methods

Materials and experiments

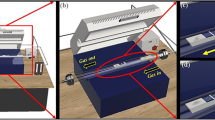
In the experiments, CVD-grown monolayer monocrystalline MoS₂ flakes were produced by 6Carbon Technology Ltd. The side length of quasi-equilateral triangle MoS₂ flakes are about 20 μm. The MoS₂ flakes are transferred onto PET substrate by wet method. Figure 1a shows that numbers of triangle MoS₂ flakes scattered at different positions on PET substrate, some of them are independent of each other. For the substrate, strip shape and cross shape, whose sizes are shown in Fig. 1b, were designed for uniaxial and biaxial tensile loadings, respectively. According to the substrate shapes, the samples were loaded step-by-step by a uniaxial loading device and a biaxial loading device, respectively. The strain in the middle area of the substrate under each loading state was simulated through the finite element method (ANSYS Workbench) and then calibrated through digital image correlation (DIC), whose details are shown in the Supplementary Note 1.

Fig. 1: Second Harmonic Generation (SHG) measurement of MoS₂.

a Micrograph of MoS₂ flakes on PET substrate (The purple dashed line outlines the contour of a triangular monolayer MoS₂ flake). b Schematic of loading and SHG process. Strip and cross shaped substrates are designed. Their sizes are given in this figure. Cross shaped substrate can realize biaxial loading along the pink arrows. MoS₂ flakes are located in the area indicated by the gray square in the middle of the substrates. The red and green wave lines indicate the incident laser (ω) and emitted SHG signal (2ω), respectively. c SHG peak under different polarization angles. The SHG peak position is at 532 nm. As the polarization angle ϕ varies from 0° to 50°, the intensity of the SHG peak first increases and then decreases. The color sequences of the peak lines in order of different ϕ are dark yellow (0°), light blue (10°), green (20°), black (30°), red (40°) and blue (50°), respectively.

The SHG signal of sample was detected using a Witec alpha300R system with a 100X lens and a 1064 nm laser. The obtained SHG peak position is at 532 nm, half of 1064 nm, in the spectrum. The sampling spots were detected in-situ in the center vicinity of each independent triangle MoS₂ flake, as shown in Fig. 1b. All the experiments were performed under the parallel polarization configuration, with a half-wave plate in the common optical path of the incident laser and the emitted light and an analyzer in the emitted light path. The angle of polarization direction (named as polarization angle ϕ) is controlled by rotating the optical axis direction of the half-wave plate with a step of 5° from 0° to 360°. Hence ϕ is from 0° to 720°. Figure 1c displays the SHG peak of MoS₂, along with the variation of the intensity as angle ϕ ranges from 0° to 50°.

Theory of strain characterization using SHG method

Basic theory of SHG

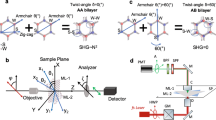
Among kinds of 2D-TMDCs, monolayer MoS₂ has typical SHG behavior. MoS₂ is periodic structure and belongs to P6₃/mmc space group. There is an already established notation of [100] and [010] for its crystallographic directions which can be applied as the crystal coordinate system, as shown in Fig. 2. [100] and [010] axials of the crystal coordinate system also correspond to the ZZ and AC crystal directions of MoS₂, respectively. The polarization vector of the incident laser is denoted as e_m. The initial polarization vector is denoted as e′_m, who has an arbitrary initial angle ϕ₀ relative to [010] direction. Along the direction of e′_m, an experimental coordinate system X′-Y′ is established, shown in Fig. 2. The angle of e_m to X′ axial is set as ϕ. Hence, e_m can be express as below in crystal coordinate system.

$${{{{\bf{e}}}}}_{{\rm{m}}}=[\begin{array}{ccc}\cos (\phi +{\phi }_{0}), &\sin(\phi +{\phi }_{0}), & 0\end{array}]$$

(1)

Fig. 2: The coordinate system based on monolayer MoS₂ sample.

MoS₂ crystal structure is illustrated by the ball and stick model. Cyan and yellow spheres represent Molybdenum (Mo) and Sulfur (S) atoms, respectively. The crystal coordinate system is based on this crystal structure, where the black solid axes denoted [100] and [010] correspond to the ZZ and AC crystal directions of MoS₂, respectively. e′_m is the initial polarization vector, who has an arbitrary initial angle ϕ₀ relative to [010] direction. Along the direction of e′_m, an experimental coordinate system X′-Y′ is established (viz. black dashed axes). Therefore, the angle between the X′ axis and the [010] axis is also ϕ₀. e_m, the blue dashed lines with arrows, denotes the polarization vector of the incident laser. The angle between e_m and X′ axis is defined as ϕ. The black square in the upper right sub-figure represents the unit body of in-plane strain state, where the normal strain ε_xx and ε_yy, and shear strain γ_xy (γ_yx) are shown as black solid arrows, while the principal strain ε₁ and ε₂, are shown as blue dashed arrows, and θ denotes the principal strain angle.

The analyzer vector to the emitted SHG signal is denoted as e_i, whose superscripts “||” and “⊥” correspond to the parallel and the perpendicular polarization configurations, respectively.

$${{{{{\bf{e}}}}}_{{i}}}^{||}=[\begin{array}{ccc}\cos (\phi +{\phi }_{0}), & \sin(\phi +{\phi }_{0}), & 0\end{array}]$$

(2)

$${{{{{\bf{e}}}}}_{{i}}}^{\perp }=[\begin{array}{ccc}-\,\sin (\phi +{\phi }_{0}), & \cos(\phi +{\phi }_{0}), & 0\end{array}]$$

(3)

Besides, ε_xx and ε_yy are the in-plane normal strain components along [010] and [100] direction, respectively. γ_xy is the shear strain component on [010] plane along [100] direction. ε₁ and ε₂ are the in-plane principal strain components (ε₁ ≥ ε₂), and θ is the direction of ε₁ in the crystal coordinate system.

According to the theory of nonlinear optics⁴⁶, the SHG intensity I is described as below equation,

$$I\propto {[{{{{\bf{e}}}}}_{{i}}\cdot {{{\boldsymbol{P}}}}(2{\omega })]}^{2}\propto {[{e}_{i}{\chi }_{ijk}{E}_{j}(\omega ){E}_{k}(\omega )]}^{2}\propto {({e}_{i}{\chi }_{ijk}{e}_{j}{e}_{k})}^{2}$$

(4)

where P(2ω) represents the polarized vector of SHG signal from monolayer MoS₂ sample excited by the incident lights, whose electric field strength vectors are E_j(ω) and E_k(ω), where E_j = E_k = E∙e_m. χ_ijk is named as the second-order nonlinear susceptibility, who is three-order tensor component. When a monolayer MoS₂ sample is free from strain, its symmetry determines that the components of the corresponding second-order nonlinear susceptibility are as follows.

$${\chi }_{111}=-{\chi }_{122}=-{\chi }_{212}=-{\chi }_{221}={\chi }_{0}$$

(5)

where χ₀ is a material constant. Thus, the specific form of SHG under the parallel (or perpendicular) polarization configuration is expressed as a function of the polarization angle ϕ shown in below equation.

$$\begin{array}{c}{I}_{||}={|{\chi }_{0}\cos 3(\phi +{\phi }_{0})|}^{2}\\ {I}_{\perp }={|{\chi }_{0}\sin 3(\phi +{\phi }_{0})|}^{2}\end{array}$$

(6)

According to the Eq. (6), Fig. 3 give the variation curves of SHG intensity with the change of the polarization angle ϕ under the parallel polarization configuration, where the circumferential direction represents the polarization angle and the radial direction represents the SHG intensity. Such kind of curve is named as polarization-intensity spectrum (abbreviated to PIS). In a PIS, curve of intensity value between each two neighboring minimum intensities compose a petal. As shown in the figure, the SHG PIS of monolayer MoS₂ has six petals, where each centrally symmetrical two petals have the same physical meaning according to Eq. (6). These petals are named as P1, P2, P3 and P1′, P2′, P3′ starting from the positive [010] axis counterclockwise. The height of a petal, viz. the maximum intensity inside a petal, is named as petal amplitude. Hence, theoretically, a PIS has 3 independent petal amplitudes at most, denoted as ξ_i (i = 1, 2, 3). In fact, ξ_i are three independent extrema of the PIS. In Fig. 3a, ξ₁ = ξ₂ = ξ₃ when the sample is free from strain. The data of the figures are available in Supplementary Data 1.

Fig. 3: Theoretical polarization-intensity spectrum (PIS) curves under different strain states.

a A PIS curve under the state free from strain. Based on the crystal coordinate system, the six petals of the PIS are named as P1, P2, P3 and P1′, P2′, P3′, respectively, starting from the positive [010] axis counterclockwise. The blue solid line with arrows indicates the height of a petal (petal amplitude ξ). Each PIS curve has 3 independent petal amplitudes denoted as ξ₁, ξ₂ and ξ₃. Examples of PIS curves under different strain states are shown, including (b) uniaxial strain state according to Eq. (14), (c) equal-biaxial strain state according to Eq. (16), (d) non-equal biaxial strain state according to Eq. (17) and (d) non-equal biaxial strain state with shear strain according to Eq. (11). For each strain state, four PIS curve lines from the outside to the inside are depicted in the color order of black, red, blue and green, corresponding to the strain ε_xx value of 0%, 0.1%, 0.3% and 0.5% for (b); the strain ε value of 0%, 0.1%, 0.2% and 0.3% for (c); the strain ε value of 0.1%, 0.2%, 0.3% and 0.4% for (d); the strain (ε, γ) values of (0.1%, –0.2), (0.2%, –0.3), (0.3%, 0.2) and (0.4%, 0.1) for (e). The ratio α between the two normal strain components are both set as 0.5 for (d) and (e).

Strain effect on SHG

When any strain exists, the photoelastic effect is introduced to describe the influence of strain^38,39. The fifth-order photoelastic tensor component p_ijklm demonstrates the strain effect on the nonlinear susceptibility χ_ijk as follows,

$${{{{\rm{\chi }}}}}_{ijk}={{{{\rm{\chi }}}}}_{ijk}^{0}+\Delta {{{\rm{\chi }}}}={{{{\rm{\chi }}}}}_{ijk}^{0}+{{{p}}}_{ijklm}{\varepsilon }_{lm}$$

(7)

where χ⁰_ijk is the susceptibility without strain influence and Δχ is the susceptibility change induced by strain. Considering the symmetry of MoS₂, the photoelastic tensor p has 12 nonzero components expressed by two independent parameters, viz. p₁ and p₂⁴⁷:

$$\begin{array}{c}{p}_{11111}={p}_{1},{p}_{11122}={p}_{2},{p}_{12222}=-{p}_{1},{p}_{12211}=-{p}_{2},\\ {p}_{22122}={p}_{22111}={p}_{21222}={p}_{21211}=-\frac{1}{2}({p}_{1}+{p}_{2}),\\ {p}_{22221}={p}_{22212}={p}_{21121}={p}_{21112}=-\frac{1}{2}({p}_{1}-{p}_{2}).\end{array}$$

(8)

Therefore, the SHG intensity of material under strain is expressed as follows,

$${I}_{s}\propto {[{e}_{i}({\chi }_{ijk}+{p}_{ijklm}{\varepsilon }_{lm}){e}_{j}{e}_{k}]}^{2}$$

(9)

The strain tensor of an arbitrary in-plane strain state, u, usually consists of two normal and one shear components.

$${{{\bf{u}}}}=\left[\begin{array}{cc}{\varepsilon }_{xx} & {\gamma }_{xy}\\ -{\gamma }_{xy} & {\varepsilon }_{yy}\end{array}\right]$$

(10)

where ε_xx and ε_yy are the normal strain components along AC and ZZ directions, respectively, and γ_xy is the shear strain component along ZZ direction. By substituting the strain components into Eq. (9), the relationship between SHG intensity and the polarization angle under arbitrary strain state in parallel polarization configuration for example can be obtained as

$${I}_{||}={\left[\begin{array}{c}{\chi }_{0}\cos 3(\phi +{\phi }_{0})+\frac{1}{2}({p}_{1}+{p}_{2})({\varepsilon }_{xx}+{\varepsilon }_{yy})\cos 3(\phi +{\phi }_{0}) \hfill \\ +\frac{1}{2}({p}_{1}-{p}_{2})({\varepsilon }_{xx}-{\varepsilon }_{yy})\cos (\phi +{\phi }_{0})-({p}_{1}-{p}_{2})\gamma \sin (\phi +{\phi }_{0})\end{array}\right]}^{2}$$

(11)

The relationship can also be expressed by the principal strain components as

$${I}_{||}={\left[\begin{array}{c}{\chi }_{0}\cos 3(\phi +{\phi }_{0})+\frac{1}{2}({p}_{1}+{p}_{2})({\varepsilon }_{1}+{\varepsilon }_{2})\cos 3(\phi +{\phi }_{0})\\ +\frac{1}{2}({p}_{1}-{p}_{2})({\varepsilon }_{1}-{\varepsilon }_{2})\cos (2\theta +\phi +{\phi }_{0}) \hfill \end{array}\right]}^{2}$$

(12)

Equation (11) or Eq. (12) gives a general expression of SHG intensity under an arbitrary strain state in parallel polarization configuration, which is an explicit function taking polarization angle ϕ as independent variable and the components of photoelastic tensor and strain tensor as parameters. Similarly, the SHG intensity under any arbitrary strain state in perpendicular polarization configuration can also be obtained.

Specific examples of strain states are provided as illustrations. Equation (13) describes a uniaxial strain state where only the strain component along the AC direction of the crystal coordinate system is non-zero.

$${{{\bf{u}}}}=\left[\begin{array}{cc}{\varepsilon }_{xx} & 0\\ 0 & 0\end{array}\right]$$

(13)

Hence the SHG intensity under a uniaxial strain along AC direction in parallel configuration can be obtained as Eq. (14),

$${I}_{||}={|{\chi }_{0}\cos 3\phi +{p}_{1}{\varepsilon }_{xx}\cos \phi \cos 2\phi -{p}_{2}{\varepsilon }_{xx}\sin \phi \sin 2\phi |}^{2}$$

(14)

According to Eq. (14), Fig. 3b shows some examples of the PIS curves under different ε_xx. With the increasing of strain ε_xx, each of ξ₁, ξ₂ and ξ₃ diminishes. It should be noticed that ξ₁ > ξ₂ = ξ₃ in this strain state.

When a monolayer MoS₂ sample is under a biaxial strain state (viz. without shear strain component), there is a ratio α between the two normal strain components,

$${{{\bf{u}}}}=\left[\begin{array}{cc}\varepsilon & 0\\ 0 & \alpha \varepsilon \end{array}\right]$$

(15)

When α = 1, the system experiences equal-biaxial strains, whose function of SHG intensity reduces to a straightforward expression as shown Eq. (16).

$${I}_{||}={|{\chi }_{0}\cos 3\phi +({p}_{1}+{p}_{2})\varepsilon \cos 3\phi |}^{2}$$

(16)

The PIS curves under different equal-biaxial strains are shown in Fig. 3c, where ξ₁, ξ₂ and ξ₃ diminish equally with the increasing of strain. While when α ≠ 1 in Eq. (15), the sample is under a non-equal biaxial strain state, the corresponding SHG intensity becomes to Eq. (17),

$${I}_{||}={|{\chi }_{0}\cos 3\phi +\frac{1}{2}({p}_{1}+{p}_{2})(1+\alpha )\varepsilon \cos 3\phi +\frac{1}{2}({p}_{1}-{p}_{2})(1-\alpha )\varepsilon \cos \phi |}^{2}$$

(17)

Some PISs under different non-equal biaxial strain state are given in Fig. 3d. It shows with the increasing of non-equal biaxial strain, all ξ_i diminish and ξ₁ > ξ₂ = ξ₃. As for of all ξ_i in this case, their trends are similar to, but their values are quite different with, those in the case of uniaxial strain in AC direction.

More complexed, when a shear strain component is introduced into the case of non-equal biaxial strain state, viz. an arbitrary strain state, some examples of PISs under this case are shown in Fig. 3e. The three petal amplitudes become unequal to one and another.

In each of Fig. 3, different state and magnitude of strain have different influence on the PIS. In all the cases, each petal has the same shape, and the same amplitude, with that one on its opposite side. Viz. each centrally symmetrical two petals have the same petal amplitude. Hence, it is demonstrated, which has been estimated above, that there are three independent ξ_i. Furthermore, in the crystal coordinate system, the theorical values of ξ_i in PIS are represented at about ϕ + ϕ₀ = 0°, 60° and 120°, respectively, under parallel polarization configuration. Therefore, based on the Eqs. (11) or (12), the three different in-plane strain components can be achieved by measuring the three petal amplitudes ξ_i in actual PIS.

Characterization of strain state

Theoretically, it is possible to achieve all the strain components by analyzing of the PIS curves to achieve all the three ξ_i and then substituting them into Eq. (11) or Eq. (12). However, it is far from practically possible because, as for most of the optical or spectral system, any quantitative analysis based on the detection of absolute optical intensity is lack of feasibility. In detail, any spectrum, like Raman, fluorescence or SHG, is the intensity, a recorded by a detector such as CCD, of the original output of optical signal after passing through numbers of optical elements including but not limited to lenses, reflectors, polarizers, filters, dichroic mirrors, gratings. The reflection, projection or diffraction at each optical element makes this optical signal lose a certain portion of intensity, which is nonlinear in either wavelength or polarization. Then, the detector records the final arrived optical signal with a certain quantum efficiency, which is also nonlinear in either wavelength or polarization. The data given by the detector is actually dimensionless and unitless, or rather arbitrary unit. Besides above universal facts, SHG intensity of any mono-layer MoS₂ excited by a femtosecond laser also lacks sufficient repeatability, especially owing to the focusing differences introduced by different polarizations or sample rotation angles.

This work proposes a method as follows, which makes it is actionable to quantitatively analyse the actual strain state of any mono-layer MoS₂. This method lies on the relative, not the absolute, optical intensity of SHG by introducing the petal amplitude ratio η₁ and η₂, where

$${\eta }_{1}=\frac{\min ({\xi }_{1},\,{\xi }_{2},\,{\xi }_{3})}{\max ({\xi }_{1},\,{\xi }_{2},\,{\xi }_{3})},\,{\eta }_{2}=\frac{{\sum }_{i=1}^{3}{\xi }_{i}}{\max ({\xi }_{1},\,{\xi }_{2},\,{\xi }_{3})}-{\eta }_{1}-1$$

(18)

In practical operation, the original PIS is normalized by dividing the fitted PIS curve by the maximum of this curve. Hence inside the normalized PIS, the biggest value of three normalized petal amplitudes is 1, the smallest one of them is η₁, the left one of them is η₂, shown in Fig. 4a. For instance, Fig. 4b displays several normalized PISs under typical strain states above and the corresponding η₁ and η₂ are in Table 1. For comparison, the principal strain sums of different states are all set as 0.4%. It can be seen from this figure that different strain states correspond to various η₁ and η₂ as well as the relationship between them, even if they have the same sum of principal strains. Figure 4c shows the normalized PISs with the same value of principal strain components but different principal strain directions. The corresponding η₁, η₂ and their angles are presented in Table 2.

Fig. 4: Normalized theoretical PIS curves for petal amplitude ratio method.

a A normalized PIS curve under an arbitrary strain state. The biggest value of three normalized petal amplitudes is 1, η₁ and η₂ are the petal amplitude ratios (η₁ < η₂). The red dashed line divides the PIS curve into two periods, and the petal amplitude ratio should be consistent in each period. Examples of normalized PIS curves under different strain states are shown, including (b) strain states with the same sum of principal strains according to Table 1, (c) strain states with different principal strain direction according to Table 2, (d) uniaxial strain state, (e) non-equal biaxial strain state, (f) non-equal biaxial strain state with principal strain angle θ of 20°. Curves in (d) and (e) are the normalized results of Fig. 3b, d. Curves in (f) are the normalized results according to Eq. (21), where the ratio α′ between the two principal strains is 0.5. Each of the five figures (b), (c), (d), (e) and (f) displays four PIS curves lines, colored in the order of black, red, blue, and green, corresponding to the strain state A, B, C, D of Table 1 for (b); Table 2 for (c); the strain ε_xx value of 0%, 0.1%, 0.3% and 0.5% for (d); the strain ε value of 0.1%, 0.2%, 0.3% and 0.4% for (e); the strain ε₁ value of 0.1%, 0.2%, 0.3%, and 0.4% for (f). ξ₁, ξ₂ and ξ₃ represent the three petal amplitudes of each PIS.

Table 1 Petal amplitude ratio under different strain states with the same sum of principal strain (θ = 15°)

Table 2 Petal amplitude ratio under different strain states with different principal strain direction (ε_θ = 0.3, ε_θ+90 = 0.1)

More detailed, the PISs under uniaxial strain state is set as an example, where Fig. 4d presents the normalized result of Fig. 3b. From the figure, the relationship of η₁ = η₂ remains in all the PISs in this strain state. According to the Eq. (14), petal amplitude ratios are expressed as

$${\eta }_{1}={\eta }_{2}=\frac{{\xi }_{2}}{{\xi }_{1}}=\frac{{\xi }_{3}}{{\xi }_{1}}=\frac{{|1+\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}+\frac{{p}_{2}}{{\chi }_{0}}){\varepsilon }_{xx}-\frac{1}{4}(\frac{{p}_{1}}{{\chi }_{0}}-\frac{{p}_{2}}{{\chi }_{0}}){\varepsilon }_{xx}|}^{2}}{{|1+\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}+\frac{{p}_{2}}{{\chi }_{0}}){\varepsilon }_{xx}+\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}-\frac{{p}_{2}}{{\chi }_{0}}){\varepsilon }_{xx}|}^{2}}$$

(19)

Similarly, for the non-equal biaxial strain state, the normalized PIS is shown in Fig. 4e. Actually, uniaxial strain state can be considered as a special case of non-equal biaxial strain state. It shows that without the shear strain γ, the PIS exhibits axial symmetry. In other words, if η₁ = η₂, the shear strain is absent. In turn, when η₁ is unequal to η₂, there must be the presence of shear strain. For example, if γ is introduced on the basis of the strain state in Fig. 4e, the PISs will transform as shown in Fig. 4f. And according to the Eq. (11), the expressions for the petal amplitude ratios are as follows, where β is the ratio between γ and ε_xx.

$$\left\{\begin{array}{c}{\eta }_{1}=\frac{{\xi }_{3}}{{\xi }_{1}}=\frac{{|1+\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}+\frac{{p}_{2}}{{\chi }_{0}})(1+\alpha ){\varepsilon }_{xx}-\frac{1}{4}(\frac{{p}_{1}}{{\chi }_{0}}-\frac{{p}_{2}}{{\chi }_{0}})(1-\alpha ){\varepsilon }_{xx}-\frac{\sqrt{3}}{2}(\frac{{p}_{1}}{{\chi }_{0}}-\frac{{p}_{2}}{{\chi }_{0}})\beta {\varepsilon }_{xx}|}^{2}}{{|1+\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}+\frac{{p}_{2}}{{\chi }_{0}})(1+\alpha ){\varepsilon }_{xx}+\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}-\frac{{p}_{2}}{{\chi }_{0}})(1-\alpha ){\varepsilon }_{xx}|}^{2}}\\ {\eta }_{2}=\frac{{\xi }_{2}}{{\xi }_{1}}=\frac{{|1+\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}+\frac{{p}_{2}}{{\chi }_{0}})(1+\alpha ){\varepsilon }_{xx}-\frac{1}{4}(\frac{{p}_{1}}{{\chi }_{0}}-\frac{{p}_{2}}{{\chi }_{0}})(1-\alpha ){\varepsilon }_{xx}+\frac{\sqrt{3}}{2}(\frac{{p}_{1}}{{\chi }_{0}}-\frac{{p}_{2}}{{\chi }_{0}})\beta {\varepsilon }_{xx}|}^{2}}{{|1+\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}+\frac{{p}_{2}}{{\chi }_{0}})(1+\alpha ){\varepsilon }_{xx}+\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}-\frac{{p}_{2}}{{\chi }_{0}})(1-\alpha ){\varepsilon }_{xx}|}^{2}}\end{array}\right.$$

(20)

If Fig. 4f is illustrated in the form of principal strain components, Eq. (20) will become into the following expression, where α’ is the ratio between the two principal strains.

$$\left\{\begin{array}{c}{\eta }_{1}=\frac{{\xi }_{3}}{{\xi }_{1}}=\frac{{|1+\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}+\frac{{p}_{2}}{{\chi }_{0}})(1+\alpha ^\prime){\varepsilon }_{1}+\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}-\frac{{p}_{2}}{{\chi }_{0}})(1-\alpha ^\prime){\varepsilon }_{1}\cos (2\theta +120)|}^{2}}{{|1+\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}+\frac{{p}_{2}}{{\chi }_{0}})(1+\alpha ^\prime){\varepsilon }_{1}+\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}-\frac{{p}_{2}}{{\chi }_{0}})(1-\alpha ^\prime){\varepsilon }_{1}\cos 2\theta |}^{2}}\\ {\eta }_{2}=\frac{{\xi }_{2}}{{\xi }_{1}}=\frac{{|1+\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}+\frac{{p}_{2}}{{\chi }_{0}})(1+\alpha ^\prime){\varepsilon }_{1}-\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}-\frac{{p}_{2}}{{\chi }_{0}})(1-\alpha ^\prime){\varepsilon }_{1}\cos (2\theta +60)|}^{2}}{{|1+\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}+\frac{{p}_{2}}{{\chi }_{0}})(1+\alpha ^\prime){\varepsilon }_{1}+\frac{1}{2}(\frac{{p}_{1}}{{\chi }_{0}}-\frac{{p}_{2}}{{\chi }_{0}})(1-\alpha ^\prime){\varepsilon }_{1}\cos 2\theta |}^{2}}\end{array}\right.$$

(21)

As mentioned above, a qualitative method is provided for measuring the strain state. However, if the strain state needs to be quantified, the cases will become more complex. that means, it is necessary to explicitly characterize the quantitative relationship between the two normal strains, as well as the quantitative relationship between any normal strain and the shear strain. In this quantitative process, η₁ and η₂, and the angles of their corresponding petals as well, are directly obtained by SHG experiments. One important fact in this time is that the two measured petal amplitude ratio are relative values, which are free from the influences the optical efficiency of the experimental system and other experimental variables. As seen in the aforementioned derivations (e.g., in Eq. (20)), the specific values of the petal amplitude ratios are functions of the ratio α between the two normal strains and the relationship β between shear strain and normal strain. If the magnitude of the loaded strain or the sum of normal strains is known or measurable (such as using photoluminescence spectroscopy), the strain state can be quantified by analyzing the petal amplitude ratios through the angle resolved SHG experiments and the method proposed in this work. For example, in the non-equal biaxial strain state with shear strain, there are three unknown strain variables, while petal amplitude ratio method provides two individual equations. Photoluminescence spectroscopy provides another one. It is possible to obtain the three strain components by using the two spectral methods in-situ.

Results and discussion

Before characterizing the in-plane strain of the monolayer MoS₂ sample by using SHG, parameters including p₁, p₂ and χ₀ should be calibrated. While, it is particularly challenging to exactly achieve the absolute value of χ₀, which is firmly depending on the equipment and the material used, and hence uncertain or different with one and another each time. While, according to the proposed method above, the absolute SHG intensity χ₀ is not required. Instead, relative photoelastic coefficients p₁/χ₀ and p₂/χ₀ are required to calibrate experimentally. Each of them is free from the influence of SHG equipment.

The calibration was performed under uniaxial tensile loading, since it can provide a more stable and reliable strain state while minimize the impact of shear strain. MoS₂ flakes were stretched along their AC or ZZ crystal directions, respectively. The X′ axial of experimental coordinate system was set along the AC direction of MoS₂ samples, hence ϕ₀ = 0. The PISs detected in experiments at some stages of uniaxial tensile loading are presented in Fig. 5.

Fig. 5: Normalized PISs under different uniaxial tensile loading.

The three sets of petals are sequentially named as P1, P2, P3. In (a), the light red arrows indicate the loading along AC crystal direction. In (b), the light blue arrows indicate the loading along ZZ crystal direction. Dots are results detected in experiments and lines are fitted values. The obtained PISs in (a) and (b) are under the loading strain ε_xx and ε_yy of 0% (black), 0.1% (red), 0.2% (green), 0.3% (blue) and 0.4% (light blue), respectively.

The shape change of each PIS in Fig. 5 matches its corresponding theoretical expectation in terms of trend, where two peaks decrease relatively when the loading is along AC direction, while only one peak decreases relatively when the loading is along ZZ direction. Quantitatively, each individual petal in any PIS was fitted to determine its petal amplitude ξ. Then, petal amplitude ratios corresponding to different loadings were obtained using Eq. (22) as follows,

$${\eta }_{2}^{AC}=\frac{{\overline{\xi }}_{2}}{{\overline{\xi }}_{1}},{\eta }_{3}^{AC}=\frac{{\overline{\xi }}_{3}}{{\overline{\xi }}_{1}},{\eta }_{2}^{ZZ}=\frac{{\overline{\xi }}_{1}}{{\overline{\xi }}_{2}},{\eta }_{3}^{ZZ}=\frac{{\overline{\xi }}_{1}}{{\overline{\xi }}_{3}}$$

(22)

where ${\bar{\xi }}_{1}$ is the mean height of all the P1 petals and so on. Also as depicted in Fig. 5, each PIS exhibits two sets of petals with nearly equal intensity, in agreement with the theoretical relationship. Hence, a single petal amplitude ratio is determined for each loading step by

$${\eta }^{AC}=\overline{{\eta }_{2}^{AC}+{\eta }_{3}^{AC}} \, {{{\rm{or}}}} \, {\eta }^{ZZ}=\overline{{\eta }_{2}^{ZZ}+{\eta }_{3}^{ZZ}}$$

(23)

The relationship between petal amplitude ratio and the actual strain along AC and ZZ direction is demonstrated in Fig. 6 respectively. According to the PIS variation trend, the petal amplitude ratio decreases with the increased strain as the figures displayed. The corresponding expression of petal amplitude ratio for this loading state is in the form of Eq. (19). While, it should be noted that, during the actual uniaxial tensile loading, both ε_xx and ε_yy exist inside the sample due to Poisson’s effect. The ratio α between the two normal strains is set as –0.31 according to the calibration experiments of substrate (Supplementary Fig. 1), which is very close to the Poisson’s ratio of MoS₂, 0.29. Therefore, in Eq. (19), ε_xx is given by the experimental loading, petal amplitude ratio is obtained from the SHG measurement, and p₁/χ₀ and p₂/χ₀ can be regarded as unknown parameters and achieved by fitting the experimental data using Eq. (19).

Fig. 6: SHG petal amplitude ratios change with actual strains.

The tensile loadings are along (a) AC crystal direction and (b) ZZ crystal direction. The black square points represent the experimental results of petal amplitude ratios. The red lines indicate the fitted values, and the fitted slope K_AC = –1.111 ± 0.016 (%^–1) in (a) and K_ZZ = –1.230 ± 0.004 (%^–1) in (b). The error bars mean the standard deviations between the two sets of petals (P2 and P3 in Fig. 5). The error bars are smaller than the symbol size if not shown.

The results of p₁/χ₀ and p₂/χ₀ are –0.560 ± 0.145%^–1 and –1.156 ± 0.116%^–1 respectively in Fig. 5a, –0.552 ± 0.043%^–1 and –1.167 ± 0.034%^–1 in Fig. 5b. And the average results of the two stretching experiments for p₁/χ₀ and p₂/χ₀ are –0.556%^–1 and –1.161%^–1.

Figure 6 also demonstrates that both the η^AC-ε_xx and the η^ZZ-ε_yy relationship turned out to be approximately linear at small uniaxial loading state, which may serve as an index to characterize strain level. The slopes are K_AC = –1.111 ± 0.016%^–1 and K_ZZ = –1.230 ± 0.004%^–1, where K_ZZ is somewhat higher than K_AC. The error bars in the figure mean the standard deviation between the two sets of petals, due to the inevitable slight angular misalignment of loading direction in the loading process or the optical fluctuations.

To verify the correctness of petal amplitude ratio method, biaxial loading experiments were then performed. Four strain states are presented by changing the loading ratio between AC and ZZ direction to acquire the different values of α (Supplementary Fig. 2, 3). Supplementary Fig. 4 demonstrates the PISs under the different strain states with α being 1, 0.81, 0.51, 0.13 respectively.

The experimental results of petal amplitude ratios change with step-by-step actual strains are shown in Fig. 7. Moreover, based on the calibrated parameters, the theoretical relationships between petal amplitude ratio and strain are also simulated under various cases of α with the range from –1 to 1. It can be observed that the experimental results are in good accordance with the values based on the theory given in “Methods” section of this work. According to the experimental and theoretical lines, the petal amplitude ratio achieved under each strain state prominently acts as linearly changing with the strain, especially at small strain state. With α increases, the slope of the η-ε relationship decreases. Until α = 1 (viz. equi-biaxial state), the η-ε relationship becomes a horizontal line. While, when α is greater than 0, the distinction in slopes become more apparent, which furtherly implies the significance of the method in characterizing the biaxial tensile strain.

Fig. 7: Experimental and theoretical results of petal amplitude ratios under strain states with different α.

The square points represent the experimental results of petal amplitude ratios under biaxial loadings. The ratio α between the two normal strain components are 1, 0.81, 0.51, 0.13, –0.31, indicated by the color of pink, green, blue, red and black, respectively. The solid lines represent the theoretical values corresponding to the experimental results, with the α of 1 (pink), 0.81 (green), 0.51 (blue), 0.13 (red), –0.31 (black). The dashed lines represent the theoretical values under other cases of α, including 0, –0.1, –0.5 and –1, indicated by the color of hippie blue, light green, dark yellow and orange, respectively. The error bars mean the standard deviations between the two sets of petals. The error bars are smaller than the symbol size if not shown.

Besides, to observe the impact of shear strain, another experiment under uniaxial tensile loading was also conducted and the form of normal strain components were applied to describe the strain state. To create a complex state with shear strain, a MoS₂ flake with a certain inclination angle was stretched under uniaxial tensile loading as shown in Fig. 8a. According to elastic theory⁴⁸, the resulting strain state is as depicted in Fig. 8b. Then the strain state is transformed into the crystal coordinate system and the shear strain can be obtained as shown in Fig. 8c. In this experiment, the ratio α between ε_xx and ε_yy is set as –0.18. Ratio β between ε_xx and the introduced γ is –0.48.

Fig. 8: The influence of share strain.

A MoS₂ flake (indicated by ball and stick model) is under a uniaxial tensile loading in (a). The blue arrows represent the loading direction and σ is the stress in this loading condition. The black solid line with arrow indicates the [010] crystal direction. The resulting principle strains ε₁ and ε₂ are depicted by the blue dashed arrows around the unit body in (b), where the black solid arrows represent the crystal coordinate system. Then the strain state is transformed into the crystal coordinate system, where normal strains ε_xx and ε_yy, shear strain γ_xy (γ_yx) are indicated by the dashed arrows around the unit body in (c). Normalized PISs under this loading condition is displayed in (d), with the three sets of petals named as P1, P2, P3. Dots are detected experimental results and lines are fitted values. The obtained PISs are under the loading strain ε_xx of 0.12% (black), 0.25% (red), 0.38% (blue) and 0.5% (green), respectively. In (e), the black square points and red round points represent the experimental results of petal amplitude ratios η₁ and η₂, respectively. Black and red solid lines represent the theoretical values of η₁ and η₂, respectively. R₁² and R₂² are the R-Square values for the correlations between experimental data and theoretical results.

PISs were acquired under different loading steps. It can be observed from Fig. 8d that the amplitudes of three sets of petals P1, P2, and P3 in the PISs are all different with the increase of loading, which demonstrates the impact of the shear strain on the SHG of MoS₂. Therefore, in each PIS, the petal amplitude ratio η₁ and η₂ is unequal. By analyzing the PISs under different loadings, two distinct trends of the petal amplitude ratio variation are obtained as indicated by the dots in Fig. 8e. Meanwhile, by substituting α and β into the Eq. (20), the theoretical trends of petal amplitude ratio changes are obtained based on the theoretical model, as the solid lines represent in Fig. 8e. Visually, there is a strong consistency of the experimental and theoretical results. And in terms of quantification, the R-Square values R₁² and R₂² for the correlation between experimental data and theoretical results are 0.962 and 0.979, respectively. It indicates that the experiment not only reflects the impact of shear strain, more importantly, it further proves that the influence of the strain state on the SHG can be quantified.

Therefore, the proposed method demonstrates its potential to quantitively characterize the in-plane strain state of an MoS₂ or other TMDC sample. Additionally, the observed linear change of petal amplitude ratio with the step-by-step loading provides a prospective way to make a non-contact nano-sensor of strain rosette using a TMDC and its PIS of angle-resolved SHG.

Conclusion

This work proposes a method to quantify the strain state of typical monolayer 2D-TMDC such as MoS₂ using the second harmonic generation. Based on the theoretical framework of the SHG, the influences of different strains on the polarization-intensity spectra are analysed. Then, the method of petal amplitude ratio is proposed, which establishes the analytical relationship between the three in-plane strain components of MoS₂ to measure and the petal amplitude ratios obtained from the detected polarization-intensity spectra. A series of experiments were performed, including the uniaxial tensile loading calibration experiments, verification experiments of biaxial tensile loading and uniaxial oblique tensile loading. The results of former are repeatable, which calibrated all the key parameters. The latter shows linear trends of petal amplitude ratios to loaded strains, which are mostly agree with the theoretical anticipations in this work, verified the reliability, correctness and universality of the proposed method to quantitively characterize strain state for TMDCs.