Introduction

ARPES is a powerful tool to observe electronic structures in solid-state materials with the advantage of extremely high momentum and energy resolutions, which has been widely applied in characterization of quantum materials such as superconductors, topological materials, and semiconductors1,2,3,4,5, but limited to homogeneous surfaces of samples. The recently developed spatially resolved ARPES (or called Nano-ARPES) promotes the measurements into relatively inhomogeneous surfaces, such as the surfaces of quasi-one dimensional (quasi-1D) materials, two dimensional (2D) materials and heterostructures, as the beam size can be focused down to sub-micrometer, which is almost two orders of magnitude smaller than it is in the conventional ARPES6,7,8. However, challenges remain for the measurements of spatially resolved ARPES due to the complexity of the surface. The main obstacle is from the positioning of the area of interest, which only relies on the scanning photoemission microscopy (SPEM)8 during spatially resolved ARPES. However, the SPEM data are quite heavy, which need to be well analyzed in order to distinguish the desired regions. In addition, it is rather important to explore the exotic band dispersions during scans even though the signal can be significantly weak. For example, the flat bands in twist graphene and hybridized bands in 2D heterostructures. Generally, the data processing for the purpose that mentioned above is time consuming, which calls for a more efficient and accurate way for improvement, such as data manipulation based on machine learning.

In recent years, machine learning has revolutionized the way in spectra processing9,10,11,12,13,14,15,16,17,18,19,20,21. In particular, it has shown strong capabilities in ARPES data processing, such as super-resolution, de-noising and band structure reconstruction22,23,24,25,26,27. For example, the combination of K-means clustering with Gaussian Process (GP) regression is proposed to reconstruct the experimental phase diagram from as low as 12% of the original dataset size28. Unsupervised clustering algorithms (K-means and fuzzy-c-means) are used to automatically categorize the spatial mapping dataset of YBa2Cu3O7−δ29. The input for the two clustering algorithms is the iEDCs (angle-integrated energy distribution curves), so we refer to these methods as iEDCs K-means clustering and iEDCs fuzzy-c-means clustering in the following. We found that the iEDCs K-means clustering method performs well in extracting the local electronic structures with significant differences, however, it has limited ability in distinguishing subtle differences, such as the different electronic structures caused by different layers and substrates. Besides, the current clustering analysis is mainly focused on resolving the phase distribution in real space (X-Y coordinate), and is not involved in extracting inhomogeneous band structures in the momentum space (E-K coordinate). However, the band stucture in momentum space is likely the more interested section for the researchers, such as band splitting in top valence band of layer dependent few-layer MoS2 in this paper. And usually, the band stuctures are the key to distinguish the subtle difference in real space.

Here, we propose a method called Multi-Stage Clustering Algorithm (MSCA), shown in Fig. 1, which achieves the clustering analysis both in real space and momentum space in spatially resolved ARPES dataset. It applies the clustering algorithms to multi-stage data processing. The K-means clustering results/metrics for real space in different energy-momentum windows are treated as the input of the second round K-means clustering for momentum space. In this way, the energy-momentum windows that exhibit subtle inhomogeneity in real space can be highlighted. The spatial distributions of monolayer and multilayer MoS2, as well as MoS2 based on different substrates (BN or Au) are figured out based on the highlighted energy-momentum windows. Moreover, some subtle band differences, such as band shift or splitting, can still be pointed out by MSCA. Our results demonstrate that the clustering accuracy and identification limit can be significantly improved by MSCA. This is expected to promote the widespread application of machine learning in high-dimensional data clustering processing.

Fig. 1: MSCA (Multi-Stage Clustering Algorithm) workflow.
figure 1

The sample data from DAQ (Data Acquisition) undergoes three clustering processes. The first clustering involves m × n iEDCs (angle-integrated energy distribution curves) K-means clustering processes in real space, conducted within m × n small energy-momentum windows. The result of this clustering is m × n SSE (Sum of Squared Errors) curves. The second clustering employs K-means clustering, using the first clustering result and the associated SSE curves as input. The ROI (region of interest), highlighted in yellow within momentum space, is captured. The third clustering is an iEDCs K-means clustering in real space, based on the energy-momentum windows associated with the captured feature.

Full size image

Results

The spatial mapping dataset we analyzed in this study is from sample MoS2/BN/Au (see Method). The three materials are stacked together, with the layers from top to bottom being MoS2, BN and Au, respectively, and the corresponding optical images are shown in Fig. 2a–c. The monolayer (A) and multilayer (B) MoS2 regions can be identified by optical contrast from the optical image. The truth table for this sample is provided in the Supplementary Note 1. From the truth table, one can see that the real space is mainly divided into 5 partitions: Au, BN, MoS2 on Au (MoS2-Au), monolayer MoS2 on BN (1-MoS2) and multilayer MoS2 on BN (m-MoS2). This truth table is used to calculate the performance metrics of different clustering results in this paper (see Method). For each clustering result, we calculate the Accuracy, Precision, Recall, and F1 score for each partition individually to assess the clustering performance within each partition. Furthermore, we introduce the macro averages for these four metrics by averaging their values across all partitions. Given the success of the K-means clustering method in handling ARPES data28,29, we choose K-means algorithm30 as the methodology in this study. K-means clustering method is a distance-based method that typically uses Euclidean distance or Manhattan distance to measure the similarity among data points and partition the data points into several clusters (see Method). The number of clusters n is a hyperparameter, which needs to be specified in advance. In this paper, we choose the elbow method31 to determine the appropriate number of clusters, which calculates the Sum of Squared Errors (SSE) of different number of clusters (see Method). All SSE curves in this paper consist of SSEs of cluster numbers from 1 to 10. The “elbow” point indicates the number of clusters at which the SSE decrease slows down significantly and it will be chosen as the optimal number of clusters. It should be noted that the number of clusters yielded by the elbow method is typically further evaluated with the silhouette score and gap statistic, and this study can be found in Supplementary Note 2, where results are compared with the elbow method, which has been employed in prior studies29. The elbow method is shown to provide reliable results on the dataset studied. However, the “elbow” point on the SSE curve is difficult to determine, so we ignored to find the absolute cluster number, but rather to compare the results conducted by multiple cluster numbers near the “elbow” to obtain a reasonable number of clusters, similar to the approach in the previous study29. In the following, we discuss the results obtained through iEDCs K-means clustering and MSCA.

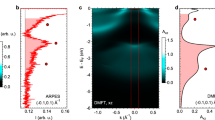
Fig. 2: Unsupervised clustering by iEDCs (angle-integrated energy distribution curves) K-means algorithm.
figure 2

a–c The images of the sample, obtained from an optical microscope, include scale bars represented by black lines to indicate the size: the whole sample, BN and MoS2 (monolayer (A) and multilayer (B)). d iEDCs of all scan points by summing up the number of photoelectrons in the angle (θ) dimension. h The SSE (Sum of Squared Errors) curve of cluster numbers from 1 to 10. e, i, l The spatial distribution results for n = 2, 3, 4, respectively. Different colors represent different phases. In Fig. 2e, the grey area labeled (1) corresponds to Au and the yellow area (2) represents BN and MoS2. In Fig. 2i, the grey area labeled (1) corresponds to Au, the yellow area (2) to BN and the orange area (3) represents MoS2. In Fig. 2l, the grey area labeled (1) corresponds to Au, the yellow area (2) to BN, the orange area (3) to MoS2, and the blue area (4) represents the combined signal from both sides of the edge. f, j, m The mean-EDCs obtained by averaging the cluster members in each cluster for n = 2, 3, 4, respectively. g, k, n The 2D ARPES (angle-resolved photoemission spectroscopy) images obtained by averaging the cluster members in each cluster for n = 2, 3, 4 cases, respectively.

Full size image

iEDCs K-means clustering method

To be consistent with previous study29, the clustering input in this work is the iEDCs of all scan point, obtained by taking an integration over the angle dimension, as shown in Fig. 2d. The clustering results can be seen from SSE curve shown in Fig. 2h. n = 3 seems to be the optimal number of clusters. For a comprehensive inspection, we choose to examine the n-dependence on the clustering results for n = 2, 3, 4. We thus compare the spatial distribution, the mean-EDC averaging the cluster member in each cluster and the 2D ARPES images obtained by averaging the cluster member in each cluster for n = 2, 3, 4 cases in Fig. 2e–n. By comparing the results of n = 2 and n = 3, we can observe that the n = 3 case distinguishes two distinct structures (cluster 2 in Fig. 2k(2) and cluster 3 in Fig. 2k(3)) that are merged together in the n = 2 result (cluster 2 in Fig. 2g(2)). The presence of these two structures is further confirmed in the n = 4 result. In the n = 4 case, it divides the data points into four clusters. The cluster 1, 2 and 3 in n = 4 case are very similar to the clusters in n = 3 case. However for cluster 4, it seems that the band dispersion arises from the signal merge between cluster 1 and 2 (or 3). From the spatial distribution of the cluster 4 in Fig. 2l, one can see that it only locates at the edge between BN and Au, MoS2 and Au. Since the beam size is submicrometer and scan step is 1 micrometer, it is reasonable to conclude that the cluster 4 can be attributed to the conjoint signal from both sides of the edge. We can see from the above results that iEDCs K-means clustering method effectively recognizes the areas of MoS2, BN and Au, but different categories of MoS2 are not distinguished. In order to focus on distinguishing the differences within MoS2, we tried to drive a clustering process only based on the 2D ARPES images belonging to MoS2, the cluster 3 in Fig. 2i. The relevant study can be found in Supplementary Note 3, from where one can see that narrowing down the clustering scope still fails to recognize the different types of MoS2. The performance metrics of n = 6 case in Supplementary Fig. 4e are shown in Table 1.

Table 1 The performance metrics of iEDCs (angle-integrated energy distribution curves) K-means clustering
Full size table

These results indicate that iEDCs K-means clustering method is powerless to finely identify subtle differences such as monolayer and multilayer of MoS2, and whether MoS2 is on substrate Au or BN. We believe this is because the key region for distinguishing between monolayer and multilayer MoS2 lies in specific energy band. While using a wide range of 2D ARPES images or iEDCs as input for clustering would weaken the discrimination capability of the specific band. Therefore, the key to achieving a fine clustering is to identify the specific band in the momentum space and this can be addressed by MSCA.

Multi-Stage Clustering Algorithm(MSCA)

Based on the above discussion, MSCA is developed to capture the subtle features within 2D ARPES image (in the momentum space) to recognize different types of MoS2. The following study is based on the ARPES images belonging to MoS2, the cluster 3 in Fig. 2i. In 2D semiconductors, it is well known that the number of top valence bands at Γ valley is accordance with the number of layers, and such band dispersion divergence is located in the region distributed from kinetic energy (Ek) 94 to 96 eV and angle −5∘ to 5∘ in our MoS2 data. Thus, we emphasize this range and take a relatively larger range, from Ek 92 to 96 eV and angle −15∘ to 5∘, in our fine clustering simulation in order to explore an efficient and general method for identifying the number of layers. To demonstrate the effectiveness of MSCA, we conducted an iEDCs K-means clustering analysis based on this range as a cross-check in Supplementary Note 3 and found that it still could not recognize different types of MoS2.

The concept of MSCA is shown in Fig. 1, which includes three clustering processes. Basically, the momentum space of each scan point is firstly divided into different cells with small energy-momentum (angle) windows, and each cell will go through an iEDCs K-means clustering introduced in the above section, called first clustering. The clustering result (SSE curve) of each cell, will serve as the input for a second clustering, which can divide the momentum space into different regions. The ROI (Region of Interest) will be captured in this way and a third K-means clustering based on the specific feature will finely identify subtle differences in the real space, such as monolayer and multilayer of MoS2 and whether it is on different substrates (BN or Au).

Specifically, we firstly divide the momentum space into 200 cells (20 intervals in Ek direction and 10 intervals in angle direction). Each of cell undergoes an iEDCs K-means clustering with input of iEDCs belonging to the specific momentum space (cell), resulting in 200 SSE curves shown in Fig. 3a. The SSE curve represents the data characteristic of the dataset belonging to a specific cell. Due to the variation of dataset volume and the absolute value across different cells, the absolute SSE values differ significantly. However, the thing we care about is the slope of SSE curve, so all SSE curves are normalized (see Method). Then, 200 normalized SSE curves are utilized as the input for a second K-means clustering and the result is shown in Fig. 3b. Here we examine the clustering results in momentum space for n = 2, 3, 4 in Fig. 3c–e. The range of analyzed momentum space is highlighted in Fig. 3g(2). We found that a region highlighted in yellow exists in all three cases (n = 2, 3, 4). It is independent of the choice of n and appears to be an inherent feature, which means the band shows more pronounced surface heterogeneity in momentum space. Therefore, we conduct an iEDCs K-means clustering (third clustering) only based on the yellow region in n = 3 case. More specifically, the input of third clustering is the iEDCs obtained from energy-momentum windows belonging to the yellow region in Fig. 3d, as shown in Fig. 3h. The SSE curve of the third clustering can be seen from Fig. 3k and the optimal cluster number shows to be 3 or 4. Therefore, we choose to present the clustering results of n = 5 and n = 6 (Include the 2 partitions Au and BN) in Fig. 3f–g and i–j, respectively. Note that the spatial distributions and 2D ARPES images of cluster 1 and cluster 2 are exactly same with the results from Fig. 2i and k, so we only discuss cluster 3-5 in n = 5 case and cluster 3-6 in n = 6 case in the following. In n = 5 case (Fig. 3f, g), it successfully distinguishes the monolayer MoS2 on BN, cluster 4 in Fig. 3f, and the band structure can be clearly identified from the 2D ARPES image in Fig. 3g(2). While the band structure of the other part of MoS2 (cluster 3) is not as clear, and this can be attributed to the fact that the BN surface is atomically flat, while the Au surface is relatively rough. Cluster 5 is located at the interface of different materials and can be attributed to the conjoint signal, which can be demonstrated in its 2D ARPES image. In n = 6 case (Fig. 3i, j), it further distinguishes the multilayer MoS2 on BN (cluster 5), and the difference of band structure between monolayer and multilayer MoS2 can be picked out by zooming in to a small energy-angle window from Ek 94 to 96 eV and angle −5∘ to 5∘ in Fig. 3l. The top valence band of the monolayer MoS2 (Fig. 3l(2)) shows a single band at Γ point, and it splits into double or multiple bands in multilayer MoS2 (Fig. 3l(3)), as seen from the red dash lines, which shows good agreement with theoretical calculation results32,33,34,35.

Fig. 3: Unsupervised clustering by MSCA (multi-stage clustering algorithm) when the momentum space is divided into 200 cells.
figure 3

a 200 normalized SSE (Sum of Squared Errors) curves obtained from first clustering, used as the input of the second clustering. b The SSE curve of the second clustering. c–e The second clustering results in momentum space for n = 2, 3, 4, respectively. The yellow region represents the inhomogeneous bands. The top band corresponds to the top valence band of MoS2 at the Γ valley, while the bottom right corner shows a part of the BN band structure. h The iEDCs (angle-integrated energy distribution curves) obtained from the dataset belonging to the yellow region in Fig. 3d, used as the input of the third clustering. k The SSE curve of the third clustering. f, g The spatial distribution and 2D ARPES (angle-resolved photoemission spectroscopy) images of cluster 3-5 of n = 5 case. Different colors represent different phases. In Fig. 3f, the grey area labeled (1) corresponds to Au, the yellow area (2) to BN, the orange area (3) to MoS2 on Au, the blue area (4) to monolayer MoS2 on BN and the purple area (5) represents the combined signal from both sides of the edge. i, j The spatial distribution and 2D ARPES images of cluster 3-6 of n = 6 case. In Fig. 3i, the grey area labeled (1) corresponds to Au, the yellow area (2) to BN, the orange area (3) to MoS2 on Au, the blue area (4) to monolayer MoS2 on BN, the purple area (5) to multilayer MoS2 on BN and the blue-violet area (6) represents the combined signal from both sides of the edge. l The 2D ARPES images of cluster 3-6 of n = 6 case in energy-angle range from Ek 94 to 96 eV and angle −5∘ to 5∘.

Full size image

We also discuss the dependence of cell numbers on the result. We tried to divide the analysis region into 800 cells (40 intervals in Ek direction and 20 intervals in angle direction) and 1600 cells (40 intervals in Ek direction and 40 intervals in angle direction). The normalized SSE curves, which are the result of first clustering and the input of the second clustering, are shown in Fig. 4a,f for the cases of 800 and 1600 cells, respectively. The corresponding results of the second clustering are shown in Fig. 4b,g. We examine the clustering results in momentum space with n = 2, 3, 4 shown in Fig. 4c–e for 800 cells case and Fig. 4h–j for 1600 cells case. Both cases successfully recognize the yellow feature. Besides, as the number of cells increases, the shape of the feature becomes more similar to the top valence band of MoS2 at Γ valley located in Ek 94 to 95 eV and angle −5∘ to 5∘ in our data. We believe this is exactly the band structure differentiating the number of layers. Based on the feature in n = 3 case with 1600 cells (Fig. 4i), we conduct a third clustering and the result is shown in Fig. 4m. The spatial distributions and 2D ARPES images are shown in Fig. 4k, l or n,o when the chosen cluster number is 5 or 6. The performance metrics when cluster number is 6 are listed in Table 2. The macro Accuracy, macro Precision, macro Recall and macro F1 have improved by about 2%, 6%, 20% and 18%, respectively, compared to n = 6 case of iEDCs K-mean clustering in Table 1. Moreover, the Precision and Recall of each MoS2 partition are enhanced and more balanced. Since MSCA is focusing on distinguishing different types of MoS2, the performance metrics of Au and BN are exactly same with that from iEDCs K-means clustering.

Fig. 4: Unsupervised clustering by MSCA (multi-stage clustering algorithm) when the momentum space is divided into 800 and 1600 cells.
figure 4

a 800 normalized SSE (Sum of Squared Errors) curves obtained from first clustering, used as the input of the second clustering. b The SSE curve of the second clustering. c–e The second clustering results in momentum space for n = 2, 3, 4, respectively. The yellow region represents the inhomogeneous bands. The top band corresponds to the top valence band of MoS2 at the Γ valley, while the bottom right corner shows a part of the BN band structure. f–j The corresponding results of 1600 cells. m The SSE curve of the third clustering based on the dataset belonging to the yellow region in Fig. 4i. k, l The spatial distribution and 2D ARPES (angle-resolved photoemission spectroscopy) images of cluster 3-5 of n = 5 case. Different colors represent different phases. In Fig. 4k, the grey area labeled (1) corresponds to Au, the yellow area (2) to BN, the orange area (3) to MoS2 on Au, the blue area (4) to monolayer MoS2 on BN and the purple area (5) represents the combined signal from both sides of the edge. n, o The spatial distribution and 2D ARPES images of cluster 3-6 of n = 6 case. In Fig. 4n, the grey area labeled (1) corresponds to Au, the yellow area (2) to BN, the orange area (3) to MoS2 on Au, the blue area (4) to monolayer MoS2 on BN, the purple area (5) to multilayer MoS2 on BN and the blue-violet area (6) represents the combined signal from both sides of the edge.

Full size image
Table 2 The performance metrics of MSCA (multi-stage clustering algorithm)
Full size table

Moreover, we can notice that apart from the top valence band at Γ valley, there is another highlighted feature on the bottom right area (angle −15∘ to −10∘, and Ek 92 to 93 eV). We found that this is also a key band structure, which is the valence band of BN to distinguish grain boundaries of BN, as discussed in Supplementary Note 4.

It should be noted that we tried another method by performing auto-correlation analysis between 2D images of all scan points and a specific reference 2D image, but the results are not very satisfactory. The relevant studies and performance metrics can be found in the Supplementary Note 5. By comparing the performance metrics of different methods in this paper, it is evident that the MSCA outperforms other methods. Moreover, for each partition, the similarity in Precision and Recall values indicates that MSCA can effectively avoid misclassifying negative instances as positive while correctly identifying positive instances. This balanced performance is generally considered a desirable feature of a method. Additionally, we also compare the results by fuzzy-c-means clustering method and principal component analysis. These two methods are unable to accurately estimate the appropriate number of clusters, and can not provide correct spatial distributions even when the correct number of clusters is given. However, the fuzzy-c-means algorithm can provide high-purity regions within the same cluster, which appears to be able to differentiate between MoS2 on different substrates. More details can be found in the Supplementary Note 6 and Supplementary Note 7, respectively. As fuzzy-c-means clustering method and principal component analysis cannot clearly indicate the cluster to which each data point belongs, we are unable to discuss their performance metrics. Overall, we believe that each algorithm has its own strengths, and the performance may vary depending on the dataset. The advantage of MSCA lies in its ability to conduct cluster analysis in momentum space and identify band structures. By clustering only based on the band structure, it excludes the influence of other regions, significantly enhancing its discrimination capability.

Discussion

The MSCA is an efficient data processing method for ARPES, which can help to capture the areas of interest, especially suitable for samples with complex band dispersions, and can be a practical tool to any high dimensional scientific data analysis. Generally, It is difficult to complete data selection from tens of thousands of spatial coordinates by humans, especially for the case involving dispersed domain distribution, such as microcrystals and nanowires. And this is exactly where MSCA shines. MSCA, compared to iEDCs K-means clustering method, excels at capturing the inhomogeneous features along a certain dimension, such as band inhomogeneity along sample surface in spatially resolved ARPES. Therefore, the accuracy of clustering will be improved. The iEDCs K-means clustering can only distinguish substrate Au, BN and MoS2. Yet, MSCA can further distinguish the monolayer and multilayer MoS2, as well as whether MoS2 is on BN or Au. The MSCA can act as an experienced researcher automatically searching for spatial inhomogeneous band structures, and highlighting these bands, without the knowledge from previous research work. Besides, MSCA involves both momentum and energy information. Thus the discrimination for subtle band difference can be significantly improved based on the high-dimensional characteristics of ARPES data.

The spatially resolved ARPES will become more powerful with MSCA. We believe that the clustering algorithm performs better than the way extracted band information artificially, especially in low signal-to-noise ratio 2D ARPES images. This can help the researcher to find the region of interest more quickly based on the data with shorter acquisition time. In addition, the system stability is the critical factor for spatially resolved ARPES. Interestingly, MSCA can remove deviated data by monitoring the similarity between each independent acquisition, thus improving the robustness of the spatially resolved ARPES system to low-frequency fluctuations. The whole MSCA process of 20 × 10 cells case only takes about 1 minute, depending on the performance of the computer and dataset. Besides, the clustering process of all cells in the first clustering of MSCA can be highly parallelized, resulting in a speed improvement to the order of seconds and showing the potential for capturing the areas of interest in real time. By combining MSCA with the ARPES data acquisition system, like MAMBA36,37, the data acquisition system of HEPS38 (High Energy Photon Source) in China, it will achieve online fine clustering and band structure extraction, opening an era of efficient ARPES experimental data collection and accelerating the output of various scientific research results.

Method

Introduction to the sample

The sample for Nano-ARPES experiment is MoS2/BN heterostructure prepared on SiO2/Si substrate that coated with Au film. The sample fabrication process is based on dry transfer technique in glove box which has been widely used in other reports. Firstly, thin flakes of MoS2 and BN are exfoliated onto SiO2/Si substrates separately, and the corresponding optical images are shown in Fig. 2a–c. The monolayer (A) and multilayer (B) MoS2 regions can be identified by optical contrast from the optical image. Secondly, the MoS2 flake was picked up by PC/PDMS polymer, followed by BN flake with the accurate alignment. Thirdly, the MoS2/BN heterostructure was placed on Au/SiO2/Si substrate and PC was removed after dissolving in chloroform. Nano-ARPES experiment of MoS2/BN heterostructure was carried out at the ANTARES beamline of synchrotron SOLEIL, France. The sample was annealed in preparation chamber for  ~8 h under  ~ 500 K at the base pressure of 1 × 10−10 mbar. The photon energy we used is 100 eV with a beam size of less than 1 micrometer, and the sample temperature was  ~80 K during the experiment. The photoelectrons were collected with new generation MBS A−1 analyzers equipped with electrostatic lenses allowing Fermi surface mapping to determine the sample orientation. The overall energy and momentum resolution of the experiment were  ~ 35 meV and 0.01 Å−1. The acceptance angle of analyzer is 27∘. During the SPEM, we used the slices of 24 (pixel 24) for each point of angle axis instead of the original 940 (pixel 940), in order to reduce the SPEM data volume. The scan step was 1 micrometer.

Performance metrics

Accuracy, Precision, Recall, and F1 are commonly used metrics in classification tasks to evaluate the performance of a model. These metrics were originally designed for binary classification issues and they need to be carefully analyzed for multi-class issues in this work. To accommodate this, we calculate the Accuracy, Precision, Recall, and F1 score for each class of data separately. For example, when calculating the metrics for the Au partition, we treat the Au samples as positive instances, and all other samples as negative instances. The evaluation of metrics involves several key parameters:

  • – True Positive (TP): This represents the number of instances that were correctly predicted as positive by the model.

  • – False Positive (FP): This indicates the number of instances that were incorrectly predicted as positive by the model.

  • – True Negative (TN): This denotes the number of instances that were correctly predicted as negative by the model.

  • – False Negative (FN): This signifies the number of instances that were incorrectly predicted as negative by the model.

These parameters are used to calculate the following performance metrics:

1. Accuracy: The proportion of all samples that were correctly predicted (both true positives and true negatives) out of the total number of samples, calculated as:

$$\,{\mbox{Accuracy}}=\frac{{\mbox{TP}}+{\mbox{TN}}}{{\mbox{TP}}+{\mbox{TN}}+{\mbox{FP}}+{\mbox{FN}}\,}$$

2. Precision: Measures the proportion of correctly predicted positive samples among all samples predicted as positive, calculated as:

$$\,{\mbox{Precision}}=\frac{{\mbox{TP}}}{{\mbox{TP}}+{\mbox{FP}}\,}$$

3. Recall: The proportion of correctly predicted positive samples among all actual positive samples, calculated as:

$$\,{\mbox{Recall}}=\frac{{\mbox{TP}}}{{\mbox{TP}}+{\mbox{FN}}\,}$$

4. F1 Score: The harmonic mean of precision and recall, providing a balanced evaluation metric, calculated as:

$$\,{\mbox{F1}}=2\times \frac{{\mbox{Precision}}\times {\mbox{Recall}}}{{\mbox{Precision}}+{\mbox{Recall}}\,}$$

Moreover, we also calculate the macro averages of Accuracy, Precision, Recall, and F1 score by averaging the values from each partition. Given the imbalanced nature of the dataset in this paper, where the real area of interest has a smaller dataset compared to the rest, the macro averages provide a more balanced and comprehensive assessment of the model’s overall correctness in classification, ensuring that the performance is not affected by the classes that have a larger number of instances. On the other hand, the Accuracy, Precision, Recall, and F1 scores of each partition provide insights into the model’s performance on specific categories.

K-means clustering

K-means clustering is a widely utilized unsupervised machine learning algorithm that aims to partition a set of observations into a predetermined number of clusters. Consider a dataset comprising n observations X = {x1, x2, …, xn}, the goal of K-means is to classify these observations into m distinct clusters denoted as C = {C1, C2, …, Cm}. This classification is achieved by minimizing the within-cluster sum of squares, which is defined as:

$$W(X,C)={\sum}_{k=1}^{m}{\sum}_{{x}_{i}\in {C}_{k}}| | {x}_{i}-{c}_{k}| {| }^{2},$$
(1)

where ck represents the centroid of cluster Ck, calculated as the mean of all observations in Ck, expressed by the formula:

$${c}_{k}=\frac{1}{{n}_{k}}{\sum}_{{x}_{i}\in {C}_{k}}{x}_{i},$$
(2)

where nk is the number of observations in cluster Ck. The term ∣∣ ⋅ ∣∣ signifies the Euclidean norm. The process of K-means clustering involves iteratively assigning each observation to the nearest cluster centroid and recalculating the centroids based on the current cluster memberships. This iterative process continues until a convergence criterion is met, typically when the assignments no longer change or the change in centroid positions falls below a certain threshold. In this work, the K-means clustering algorithm is developed by Python using the scikit-learn package39.

Elbow method and normalized SSE curve

The elbow method is a heuristic used in determining the number of clusters in a dataset. The basic idea is to run the clustering algorithm (like K-Means) for n different cluster numbers and for each value m, calculate a measure of clustering quality or the total variance within clusters. This measure is often the Sum of Squared Errors (SSE):

$${{{{\rm{SSE}}}}}_{m}={\sum}_{k=1}^{m}{\sum}_{{x}_{i}\in {C}_{k}}| | {x}_{i}-{c}_{k}| {| }^{2}.$$
(3)

As m increases, the SSE typically decreases as the data points are closer to the centroids they are assigned to. However, the reduction rate in SSE curve drops at some point, creating an “elbow” in the plot of SSE versus m. The point where the SSE begins to decrease at a slower rate is considered as the elbow point. The number of clusters m corresponding to this point is taken as the optimal number of clusters. The rationale is that additional clusters beyond the elbow point do not contribute much to the clarity of the clustering. In some scenarios where the focus is on the trend of the SSE curve rather than its absolute numerical values, normalization of SSE curve becomes instrumental. The normalized SSE curve is computed using the formula:

$${{{\rm{Normalized}}}}\,{{{{\rm{SSE}}}}}_{m}=\frac{{{{{\rm{SSE}}}}}_{m}}{\mathop{\sum }_{m = 1}^{m = n}{{{{\rm{SSE}}}}}_{m}}.$$
(4)

This normalization process converts each SSE value into a proportion relative to the sum of SSE values across a defined range of cluster counts. This is particularly useful in comparing clustering outcomes across datasets of differing scales or densities.