Introduction

Charge density waves (CDWs) are quantum states of matter in which the electronic charge density acquires a periodic spatial modulation characterized by one (or more) complex order parameter (OP) \(\psi ={\psi }_{0}{e}^{i{\phi }_{0}}\)1. The electronic ordering epitomizes an instability and is normally accompanied by a lattice reconstruction that lowers the crystal symmetry: both the charge density and the lattice undergo a periodic distortion \(\sim {\psi }_{0}\cos ({{\bf{q}}}\cdot {{\bf{r}}}+{\phi }_{0})\) with collective excitation of ψ0 and ϕ0 named amplitude and phase modes, respectively. According to the original idea outlined in the 1950s by Peierls2 and Fröhlich3 for one dimensional (1D) systems, the instability originates from the divergent behavior of the Lindhard response function χ(q) at the wavevector q = 2kF connecting two opposite sides of the Fermi surface, leading to the so-called Fermi surface nesting (FSN) condition4. However, this picture rarely succeeds in explaining CDWs in real systems with dimensionality greater than 1D. Johannes and Mazin5 demonstrated the extreme fragility of the Peierls transition: small deviations from perfect nesting, given for instance by a finite temperature or by an electron-electron collision term, can easily suppress the instability. Furthermore, using NbSe2, TaSe2 and CeTe3 as prototypical examples of quasi-two dimensional (2D) systems, they showed that a CDW can be thought of as a structural phase transition driven by a momentum-dependent electron-phonon coupling (EPC). These results are in broad agreement with the seminal work of Cowley6, who illustrated that changes in the crystallographic structure will occur if either the EPC or the electronic susceptibility becomes sufficiently large, implicitly establishing that FSN is not a necessary condition to trigger a CDW. For these reasons, the mechanism driving a CDW phase transition in quasi-2D systems is still debated. Although disentangling the electronic order from the lattice displacement seems unachievable due to their inherent coupling, time-resolved spectroscopies employing sub-100 fs light pulses can overcome this issue by exploiting the Born-Oppenheimer approximation, in other words the different response time of electrons and ions to a perturbation lasting less than the natural lattice dynamics7,8,9,10,11,12.

Here, we combine time- and angle-resolved photoemission spectroscopy (tr-ARPES) with computational methods to investigate the dynamics of the CDW amplitude mode (AM) and map the nonequilibrium free energy G(u) of the OP u characteristic of the symmetry-broken state in the quasi-2D CDW material 1T-TaSe2. The photo-induced band structure oscillations probed by tr-ARPES reveal the strong anharmonicity of the AM, which is a fingerprint of lattice instability. A quantitative analysis based on the time-dependent Landau model and density functional theory (DFT) calculations allows us to extrapolate the shape and temporal evolution of the free energy functional, determine the role of electronic screening on the OP and establish the structural nature of the CDW phase transition.

Results

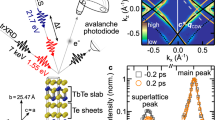
1T-TaSe2 features an incommensurate (ICDW) to commensurate (CCDW) transition at 473 K. The undistorted 1T phase is expected at higher temperatures, although it first transforms into the trigonal prismatic (2H or 3R) polytype above 600 K13. Ab initio calculations of the the undistorted phase14,15,16,17 predict the existence of imaginary phonon frequencies in the acoustic branches along both Γ − M and Γ − K directions of the Brillouin zone (BZ), suggesting that the harmonic lattice term must have an energy maximum rather than a minimum. As a consequence, the crystal undergoes a reconstruction with atomic displacements associated with the AM, which can be clearly seen in Raman experiments18,19 and in oscillations of the electronic bands observed by tr-ARPES7,20. The periodic lattice distortion (PLD) of 1T-TaSe2 consists of a star-like pattern with a \(\sqrt{13}\times \sqrt{13}\) in-plane lattice reconstruction (vectors aC and bC in Fig. 1a). The main displacement involves 12 Ta atoms converging towards the one at the center of each star13. Ta-5d electrons determine the metallic character in the undistorted phase, shaping the large electron-like Fermi surface pockets with elliptical shape centered at the \(\overline{M}\) points of the BZ21,22,23,24, represented by the red dashed lines in Fig. 1b. In our recent work25 we established that, in entering the CDW phase, charge-transfer from the tips to the inner part of each star splits the Ta-dominant states into a fully populated band below EF and an unoccupied one above it. The occupied states are localized on the Ta atom at the center of the star and on its nearest neighbors7 forming a regular hexagon (blue bonds of equal length in Fig. 1a). We will refer to these occupied Ta states as the valence band (VB).

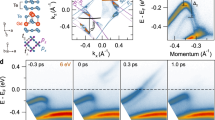
Fig. 1: Periodic lattice distortion, static and dynamic band structure of 1T-TaSe2.
figure 1

a Sketch of the star-like lattice reconstruction in the CDW phase of 1T-TaSe2. For clarity, only the Ta atoms are represented: blue atoms lie at the center of each star, green atoms are their nearest neighbors, yellow atoms lie at the tips of each star. Vectors a and b define the in-plane unit cell of the undistorted phase, aC and bC define the in-plane unit cell of the commensurate reconstruction. b Surface-projected BZ of the undistorted phase: the red dashed lines identify the electron pockets close to the Fermi level. The blue bold line indicates the measured path through the BZ. c Measured ARPES maps along the \(\overline{{{\Gamma }}}-\overline{C}\) direction in equilibrium, before pump arrival. d Photo-induced dynamics of the band structure at k∣∣ ≃ 0.3 Å−1 along \(\overline{{{\Gamma }}}-\overline{C}\). All measurements are performed with the sample at 80 K.

Full size image

In our experimental approach, photo-excitation almost resonant with the charge-transfer gap is provided by 90 fs pulses at 0.6 eV with a fluence of 3 mJ/cm2, while photoemission spectra are acquired with 21 eV pulses produced via high harmonic generation (HHG), granting access to the entire first BZ of 1T-TaSe2 (see Supplementary Note 1). Holding the sample temperature at 80 K, deep in the CCDW phase (TC = 473 K), and employing a fluence of 3 mJ/cm2 (see Supplementary Note 2), we do not observe complete melting of the CDW25, allowing us to study the effects of the photo-induced screening on the OP dynamics. To investigate the largest portion in reciprocal space of the states close to EF, the sample is oriented along \(\overline{{{\Gamma }}}-\overline{C}\) (the midpoint between \(\overline{M}\) and \(\overline{K}\), see Fig. 1b), where the VB is weakly dispersing for k∣∣ < 0.9 Å−1, as shown by the ARPES map in Fig. 1c. The energy distribution curve (EDC) extracted at k∣∣ ≃ 0.3 Å−1 and displayed in Fig. 1d reveals large photo-induced coherent oscillations of the VB, lasting several picoseconds. Identical dynamics are observed over the whole range 0.3 < k∣∣ < 0.9 Å−1 (see Supplementary Note 3). Fitting the EDCs with pseudo-Voigt line profiles comprised of a linear combination of a Gaussian and a Lorentzian we extrapolate the binding energy E − EF of the VB as a function of pump-probe delay.

Figure 2a shows the results of the fitting analysis. Binding energy oscillations as large as 0.12 eV (right vertical axis in Fig. 2a) are converted into lattice displacement (left vertical axis in Fig. 2a) with the help of DFT calculations. The procedure is described in the Supplementary Note 4. The inset in Fig. 2a shows the photo-induced linewidth broadening wL of the Lorentzian component used to fit the EDCs: its prompt increase at the pump arrival is caused by the hot electronic distribution through enhanced electron-electron (ee) scattering processes (wL ~ ℏ/τee) and the subsequent decay with time constant τep ~ 0.7 ps represents the electron-phonon thermalization. The energy shift of the VB towards EF corresponds to a photoinduced expansion of the star triggered by a displacive mechanism25,26. The  ~ 0.5 ps period of the oscillations identifies the AM7,8, corresponding to a coherent expansion and contraction of the star. Here, the most remarkable observation is a strong anharmonicity of the mode frequency. Figure 2b reports Sliding Window Fourier Transform (SWFT) analysis of the oscillations shown in Fig. 2a (see Supplementary Note 5). At early pump-probe delay (<1 ps) the mode softens considerably (ν ≤ 2 THz) and a few picoseconds after the optical excitation it converges to ν ~ 2.2 THz with time constant  ~ τep, indicating that the simple harmonic approximation cannot adequately describe the observed lattice motion.

Fig. 2: Anharmonic coherent lattice dynamics in 1T-TaSe2.
figure 2

a Photo-induced VB oscillations (black symbols) at k∣∣ = 0.3 Å−1 along \(\overline{{{\Gamma }}}-\overline{C}\). Energy scale E − EF (right axis) is converted to lattice displacement scale u − ui (left axis, ui is the steady-state displacement relative to the undistorted phase) with DFT calculations (see Supplementary Note 4). The red solid line is the best fit based on the time-dependent Landau equation (Eq. (3)). The blue dashed line in the transient minimum of the potential, umin(t) (see Methods, Eq. (9)), around which oscillations occur. The inset depicts the photo-induced Lorentzian line broadening wL(t) (cyan symbols) of the EDCs shown in Fig. 1d. The cyan solid line is a phenomenological fit. b Sliding Window Fourier Transform (SWFT) analysis of the oscillations shown in panel (a) within the 0.4–4.8 ps time interval identified by the gray dotted lines. The black symbols mark the maxima of the FFT amplitude, the cyan dashed line is the AM frequency inferred from the solution of the time-dependent Landau equation (see Methods, Eq. (11)).

Full size image

While a reduction of the mode frequency with increasing temperature is generally attributed to anharmonic terms in the potential and is the signature of a lattice instability eventually leading to a structural phase transition6,27,28, here the softening occurs immediately with the photoexcitation, even before the lattice has reached local thermal equilibrium with the electrons, in accordance with previous findings on other quasi-2D CDW systems29. Therefore, the observed time dependence of the mode frequency is not driven by the photo-induced increase of the lattice temperature, but it demonstrates the significant role of the photoexcited out-of-equilibrium electronic distribution in shaping the transient OP potential.

Discussion

The common description of a symmetry-breaking phase transition is the well-known phenomenological model by Landau30, according to which the free energy G of the system is written in terms of powers (up to the 4th) and gradients of the OP. McMillan proposed a development specifically focused on the CDW phases of TaSe2 polytypes31: the charge density ρ of the d-band electrons is represented as a linear combination of three complex OPs satisfying the relation ρ ~ Re[ψ1 + ψ2 + ψ3], with \({\psi }_{i}({{\bf{r}}})={\psi }_{0}{e}^{i{{{\bf{q}}}}_{{{\bf{i}}}}{{\bf{r}}}}\) and qi being three wavevectors of equal length, 120∘ apart. The mutual linear coupling between ψ0, ρ and the PLD u (see Supplementary Note 6 for further details on McMillan’s model) allows the free energy to be written as:

$$\frac{G(u)}{M}=-\frac{\alpha (T)}{2}{u}^{2}+\frac{{\beta }^{{\prime} }}{3}{u}^{3}+\frac{\beta }{4}{u}^{4}$$
(1)

where M is the reduced mass, T is the temperature and α(T) = κ(1 − T/T*) (κ > 0 and β > 0 are phenomenological constants). Neglecting temporarily the third order term, for α(T) > 0 the free energy has the typical double-well shape with one local maximum at u = 0 and two symmetric minima at \({u}_{0}=\pm \sqrt{\alpha /\beta }\). The phase transition occurs at the critical temperature T* above which the double-well potential turns into a single minimum one. McMillan’s model clarifies the physical meaning of the two symmetric minima at  ± u0. In quasi-1D CDW systems such as K0.3MoO332, layered materials with unidirectional CDWs such as TbTe39,29 or quasi-2D CDWs such as 1T-TiSe2 characterized by alternating antiphase-locked distortion of adjacent layers33, the photo-induced “inverted" CDW phase ( + u0) is equivalent to the original one (− u0), differing only by the phase of the OP. On the other hand, in 1T-TaSe2 the third order term in Eq. (1) (that is essential to describe a first order phase transition like the ICDW-CCDW) makes the two minima energetically inequivalent: for \({\beta }^{{\prime} } > 0\), the global minimum at  − u0 corresponds to an electron-like CDW leading to the star-like lattice reconstruction with reduced bond lengths, while for \({\beta }^{{\prime} } < \, 0\) the global minimum at  + u0 would imply a hole-like CDW with an expanded star-like distortion, that is clearly not the ground state of 1T-TaSe2 experimentally observed, although the creation of a photo-induced inverted phase has been recently claimed34. Based on the experimental observation that thermal hysteresis across the ICDW-CCDW transition temperature is negligibly small13 it can be shown that the third order term in Eq. (1) has a minor influence on the dynamics of the order parameter (see Supplementary Note 7). Thus, for the sake of simplicity and following McMillan, we will assume \({\beta }^{{\prime} }=0\) and consider the electron-like solution. When the CDW phase of 1T-TaSe2 sets in below the critical temperature, Ta atomic positions evolve from the unstable local maximum at u = 0 (corresponding to the undistorted lattice with all identical Ta-Ta bond lengths a0) to the local minimum at  − u0, where lattice distortion leads to shorter Ta-Ta bonds a = a0 − u0 and the formation of the star-like reconstruction. The 24 bond lengths within a single star are visualized as a histogram in Fig. 3a. With respect to the undistorted lattice parameter (a0 = 3.461 Å, from DFT), the average value of a (blue and green bonds in Fig. 3a) is 3.275 Å, which allows us to estimate the ground state OP as  − u0 = a − a0 = − 0.186 Å. Using the fact that \({u}_{0}(T=0)=\sqrt{\kappa /\beta }\), then \(\beta =\kappa /{u}_{0}^{2}\) and the “shape” of the double-well potential (up to the proportionality constant κ) can be readily determined, as shown in Fig. 3a (dark red curve), with the local maximum at a0 and two symmetric minima separated by 2u0 = 0.372 Å.

Fig. 3: Free energy functional of the CDW phase in 1T-TaSe2.
figure 3

a Histogram of the 24 Ta-Ta bond lengths within the CCDW star-like reconstruction (the color of the bars correspond to the color of the bonds shown in the inset). The dark red solid line is the double-well potential (Eq. (1)): its local maximum lies at the lattice parameter a0 = 3.461 Å of the undistorted phase, its global minimum is located at u0 = 0.186 Å shorter bond length. b Temporal evolution of the two-component quadratic coefficient A(T, t) = α(T) + η(t) (gray solid line) in Eq. (3), the lattice temperature term α(T) (blue dashed line) and the screening term  − η(t) (red dashed line). The latter is compared with the photo-induced VB Lorentzian line broadening wL(t) (red symbols, same data as inset of Fig. 2a). Analytical expressions of α(T) and η(t) are given in Methods, Eqs. (6)–(8). (c) Photo-induced evolution of the double-well potential: the red solid line is the solution of the time-dependent Landau equation (Eq. 3) that fits the experimental oscillations (same as Fig. 2a), plotted on the G(u, t)/M potential surface.

Full size image

Having established the characteristic shape of the OP potential under equilibrium conditions, now we focus on the description of the photo-induced oscillations reported in Fig. 2. Starting from Eq. (1), the general equation of motion is obtained differentiating G with respect to the OP35:

$$-\frac{1}{M}\frac{dG}{du}=\frac{{d}^{2}u}{d{t}^{2}}+\gamma \frac{du}{dt}$$
(2)

The last term in Eq. (2) includes possible damping of the coherent motion through the phenomenological coefficient γ > 0. During and immediately after pump excitation, a strongly non-thermal electronic distribution develops, modifying the free energy potential (as inferred form the prompt AM softening discussed in Fig. 2b). Consequently, equilibrium parameters such as the temperature and the coefficient α(T) are poorly defined. Landau’s model is still valid provided that α(T) in Eq. (1) is replaced by a time- and temperature-dependent term A(T, t)29,32,35, so that the equation of motion becomes:

$$\frac{{d}^{2}u}{d{t}^{2}}=A(T,t)u-\beta {u}^{3}-\gamma \frac{du}{dt}$$
(3)

The coefficient A(T, t) is unknown, but an analytical form can be deduced on the basis of some phenomenological considerations. Under thermal equilibrium, it is identical to the usual term α(T) that depends linearly on the temperature T. Sub-100 fs light pulses modify the electronic environment on a timescale faster than the period of a lattice vibration, reshaping the potential G(u) within the pump duration. However, a temperature cannot be properly determined until local thermal equilibrium between electrons and lattice is established, which occurs on a timescale  ~ τep. Only after this time lapse, does A(T, t) revert to α(T), possibly with an overall increased temperature. Therefore, A(T, t) significantly differs from α(T) only within the time window 0 < t ≲ τep. Assuming A(T, t) = α(T) + η(t), the prompt AM softening suggests that η(t) < 0 (see Eq. (8) in Methods) and η(t) → 0 with time constant  ~ τep. The univocal candidate is η(t) ∝ − wL(t) with the following physical meaning: the time-dependent coefficient incorporates non-thermal transient processes that weakens the OP potential at the electronic level through screening by hot photo-induced carriers, while α(T) is the usual Landau-like term related to the lattice temperature. Here, we anticipate that enhanced screening by hot electrons can be fully justified on the basis of the Thomas-Fermi model when the density of states develops a gap at the Fermi level, that is typically the case in the CDW phase. Detailed calculations are provided in Methods, Eqs. (4) and (5).

With the explicit forms of α(T) and η(t) and the proper initial conditions (see Methods, Eqs. (6)–(8)), Eq. (3) is numerically solved as a function of only 4 parameters, the values of which are obtained by fitting the AM oscillations. The red solid line shown in Fig. 2a is the fitting curve obtained with the parameters reported in Table 1. Using these values, α(T) and η(t) are quantified and their temporal profiles are shown in Fig. 3b. The pump induces a maximum 40% reduction of the quadratic coefficient A(T, t), ascribed to photo-enhanced electronic screening via η(t). A few picoseconds after the pump arrival, A(T, t) recovers, although its value is 12% lower than prior to the optical excitation due to a  ~ 60 K increase of lattice temperature. The resulting temporal evolution of the free energy G(u, t)/M is reported in Fig. 3c: the prompt change at zero delay shifts the local minimum to higher energy and, most importantly, towards u = 0. Subsequently, the electronic distribution thermalizes with the lattice, η(t) → 0 and the potential relaxes, but it does not reach the initial shape due to lattice heating, as pointed out previously. The optically-induced modification of the potential is the driving force that triggers the oscillations of the OP and the corresponding fitting curve is shown on the G(u, t)/M surface (red solid line in Fig. 3c, same as Fig. 2a). The anharmonic behavior is essentially determined by the time-dependent curvature of G(u, t)/M around its local minimum, as described by Eq. (11) in the Methods. Predicted mode softening matches the experimental result quite accurately (Fig. 2b).

Table 1 Fitting parameters of the oscillations shown in Fig. 2a according to Eqs. (3), (6)–(8)
Full size table

To summarize, starting from the oscillations of the VB triggered by an ultrashort laser pulse in a tr-ARPES experiment, we deduced the free energy governing the OP and its photo-induced dynamics on the basis of the time-dependent Landau equation. We identified the distinct contributions of lattice temperature and transient electronic distribution to the potential landscape. Its shape outlines the lattice reconstruction in the CDW phase that lowers the energy (minimum at a = a0 − u0), while its photo-induced dynamics launches anharmonic oscillations that soften promptly upon the pump arrival. We established that the AM softening is a consequence of the photo-induced weakening of OP potential, which stems from increased screening by the hot electronic distribution excited on a sub-100 fs timescale. We determined that photo-enhanced screening commonly occurs when a local minimum of the density of states appears at the Fermi level, a typical signature of charge-ordered phases. In our previous investigation25, we showed that the CDW gap in the Ta-5d band (along the \(\overline{{{\Gamma }}}-\overline{M}\) direction of the BZ) responds to a sub-100 fs pulse on a time scale matching half the period of the AM, despite the prompt electronic temperature exceeding 103 K (i.e. a transient Lorentzian linewidth exceeding 0.1 eV, Fig. 2a). Combining with the present experimental evidence, we conclude that the CDW is robust against strong electronic perturbation and hot electrons do not substantially alter the CDW, but act indirectly, transiently weakening the OP potential. These facts lead us to conclude that the instability driving the phase transition lies in the lattice degree of freedom rather than the electronic counterpart and firmly endorse the structural origin of the charge-ordered phase in 1T-TaSe2. To further support our conclusion, we recall that previous ab initio calculations revealed imaginary phonon frequencies of the undistorted phase14,15,16,17, symptomatic of lattice instabilities, and moderate peaks in the electronic susceptibility6,36, suggesting poor Fermi nesting. Considering that (i) depletion of states at EF when a CDW sets in and (ii) prompt photo-induced softening of the AM are common features shared by a wide class of quasi-2D CDW systems29, we believe this scenario is not limited to Tantalum dichalcogenides, but has far-reaching validity.

Methods

Time-dependent Landau model: photo-enhanced Thomas-Fermi screening

In solids, electrons screen any bare potential ϕbare by a factor 1/ϵ, where ϵ is the dielectric constant, leading to ϕscr = ϕbare/ϵ. Based on the Thomas-Fermi (TF) model, the components of the dielectric constant in reciprocal space have the following form37:

$${\epsilon }_{TF}(q)=1+\frac{4\pi {e}^{2}}{{q}^{2}}\int-\frac{\partial f}{\partial \varepsilon }g(\varepsilon )d\varepsilon$$
(4)

where q is a wavevector, f is the Fermi-Dirac distribution and g is the density of states (DOS). The previous expression holds in the long wavelength limit (i.e. for small q). At the electronic temperature Te = 0 the derivative of f reduces to  − δ(εF) (the delta function at the Fermi level) and the integral equals g(εF), leading to the well known form of the TF screening. The result does not change at any finite temperature Te > 0 provided that the DOS is not varying much within a range of a few kBTe around εF (see Supplementary Note 7). However, in CDW systems the charge ordering leads to a depletion of states around the Fermi level related to the opening of a gap (or pseudogap). Thus, g(ε) develops a local minimum around εF. In this case, at any finite temperature the integral in Eq. (4) is larger than g(εF) and monotonically increases with Te (see Supplementary Note 8). To a first order approximation ϵ(q) ≈ ϵ0(q) + c(q)kBTe, with both ϵ0(q) and c(q) > 0 being temperature-independent. After replacing kBTe(t) with wL(t) (their temporal profiles are equivalent), the screened potential becomes:

$${\phi }_{scr}=\frac{\phi }{\epsilon }\approx \frac{\phi }{{\epsilon }_{0}+c{w}_{L}}\approx \frac{\phi }{{\epsilon }_{0}}\frac{1}{1+c{w}_{L}/{\epsilon }_{0}}\approx \frac{\phi }{{\epsilon }_{0}}\left(1-\frac{c}{{\epsilon }_{0}}{w}_{L}\right)$$
(5)

(assuming cwL/ϵ0 ≪ 1). The last term in Eq. (5) represents the reduction of the potential induced by hot electrons. If we envisage the harmonic part of the Landau equation as a screened potential, then η(t) ∝ − wL(t) plays precisely the role of the last term in Eq. (5), justifying our hypothesis.

Time-dependent Landau model: analytical forms of the coefficients

Since transient electronic processes are entirely modeled by η(t), in the spirit of the two-temperature model38 we assign the temperature in the coefficient α(T) to the lattice: laser-induced heating leads to a time dependence simply quantified as \(T(t)={T}_{0}+{{\Delta }}T[1-\exp (-t/{\tau }_{ep})]\). In summary:

$$\alpha (T)=\kappa (1-T/{T}^{* })$$
(6)
$$\,{{\mbox{with}}}\,T={T}_{0}+{{\Delta }}T[1-\exp (-t/{\tau }_{ep})]{{\Theta }}(t)$$
(7)
$$\eta (t)=-H\exp (-t/{\tau }_{ep}){{\Theta }}(t)\propto -{w}_{L}(t)$$
(8)

where Θ(t) is the Heaviside step function, T* = 600 K, T0 = 80 K, τep = 0.7 ps. The 4 fitting parameters in Eq. (3) are κ, ΔT, H and γ (all  > 0), while the initial conditions at t < 0 are \({u}_{i}={u}_{0}\sqrt{1-{T}_{0}/{T}^{* }}\) (u0 = − 0.186 Å is the OP at 0 K) and dui/dt = 0. As shown in the main text, the quartic coefficient is \(\beta =\kappa /{u}_{0}^{2}\). Eqs. (3), (6)–(8) are used to fit the VB oscillations in Fig. 2a deducing the values of fitting parameters reported in Table 1. With these values, the potential G(u, t)/M is fully determined and its temporal evolution is shown in Fig. 3c. The transient minimum of the potential well lies at:

$${u}_{min}(t)=-\sqrt{\frac{\alpha (T)+\eta (t)}{\beta }}$$
(9)

and umin − ui is plotted in Fig. 2a (blue dashed line). The second derivative of G(u, t) computed at the local minimum umin(t) provides the curvature of the potential, that is the frequency squared of the AM, \({\omega }_{AM}^{2}(t)\):

$${\frac{1}{M}\frac{{d}^{2}G}{d{u}^{2}} \bigg| }_{{u}_{min}}=-[\alpha (T)+\eta (t)]+3\beta {u}_{min}^{2}(t)$$
(10)
$$=2[\alpha (T)+\eta (t)]={\omega }_{AM}^{2}(t)$$
(11)

ωAM(t)/2π is plotted in Fig. 2b (cyan dashed line), showing an excellent agreement with the experimental SWFT result.