Introduction

The spectrum of hydrogen-like atoms can be calculated very accurately and compared with experiments, making spectroscopy on such systems an invaluable tool for tests of fundamental physics1,2. It plays an important role in the determination of some of the fundamental constants, most notably the Rydberg constant2,3. So far, a variety of hydrogen-like systems have been investigated with precision spectroscopy, e.g., atomic hydrogen4,5,6,7,8,9,10, anti-hydrogen11, muonic hydrogen (where a muon takes the place of the electron)12,13, positronium14, muonium15, and highly-charged ions16,17.

Spectroscopy of the 1S–2S transition in hydrogen-like helium (He+) would open a new route for tests of fundamental physics18,19,20. He+ has a doubly-charged nucleus, making its energy structure much more sensitive to higher-order Quantum Electrodynamic (QED) effects than hydrogen21 by at least one order of magnitude. Moreover, like hydrogen, it can be compared to its muonic counterpart22,23. In 2018 such a comparison between hydrogen and muonic hydrogen spectroscopy led to surprisingly large adjustments in the accepted values of the Rydberg constant and the proton charge radius2. The aforementioned aspects make 1S–2S spectroscopy in He+ very promising18,19,20 for an improved determination of the alpha particle charge radius, for tests of higher-order QED terms better than in hydrogen, or for an alternative measurement of the Rydberg constant to verify its newly accepted value2. An alternative route to measure the alpha particle charge radius is also important given the recent discrepancy of the charge radius difference between the helion and alpha particle from spectroscopy of muonic He+ 23 or neutral electronic helium24.

Despite these prospects, spectroscopy of the two-photon 1S–2S transition in He+ has remained a challenge. A major difficulty is the large 40.81 eV energy difference between the 1S and 2S states25, which requires excitation in the extreme ultraviolet (XUV) range. This precludes the use of conventional continuous wave lasers. Alternatively, pulsed coherent XUV sources have been developed through high-harmonic generation (HHG) of frequency comb (FC) laser light20,26,27,28. However, HHG conversion efficiencies are intrinsically low. This makes excitation by two photons of the same wavelength, the established method for the 1S–2S transition of hydrogen, very challenging in He+ because a high photon flux is required for the simultaneous absorption of two 61 nm photons. As a consequence, laser excitation of the 1S–2S transition has only been reported with a high-power but incoherent free-electron laser source29 that is not suitable for precision spectroscopy.

In this article we report laser excitation of the 1S–2S transition in He+ with a coherent frequency-comb laser-based source. We overcome the previously mentioned challenges by using an asymmetric 2-photon excitation scheme that enhances the 1S–2S transition rate by orders of magnitude compared to a 2 × 61 nm photon scheme. In addition, time-dependent Schrödinger equation calculations enable us to identify the dynamics and confirm the excitation path. Our demonstrated excitation method is an important step toward future precision spectroscopy of hydrogen-like He+, which we pursue based on Ramsey-comb spectroscopy (RCS)30,31,32 with two amplified pulses from an FC laser.

Results and discussion

Description of the 1S–2S excitation process

The principle of our He+ generation and excitation scheme is depicted in Fig. 1. A simplified energy level structure of He and He+ is shown in part a), including the wavelengths that are involved in the excitation process. The 790 nm wavelength (near-infrared, or NIR) corresponds to the pulsed output of an ultrafast amplified FC laser system. All other wavelengths in the extreme ultraviolet (XUV) are obtained by high-harmonic generation of the NIR laser pulses in a jet of argon (see “Methods”). We use 3He instead of the more abundant 4He isotope to avoid false signals from background molecular hydrogen (see “Methods”). The hyperfine structure of 3He has not been taken into account because it is much smaller than the resolution of the current experiment and, therefore, has no noticeable influence.

Fig. 1: Schematics of the He+ 1S–2S experiment.
figure 1

a He+ generation and excitation pathway: first neutral helium is ionized, followed by 1S–2S excitation of He+ and ionization to He2+, all within a single NIR pulse and its harmonics in the XUV. b Schematic representation of the high-harmonic spectrum (logarithmic intensity scale) from the HHG process, showing the relevant harmonics color-coded. Inset: measured relative HHG spectrum in the XUV with linear intensity scale (each data point is an average over 150 laser shots with a typical RMS pulse variation of 8%). Wavelengths above 50 nm are suppressed due to an aluminum filter, and the width of each feature is instrument-limited (see “Methods”). c Outline of the setup, L is an f = 25 cm focusing lens, PV is a pulsed valve, TOF is time-of-flight ion detector, TM pair is a gold-coated refocusing toroidal mirror pair, Al is a 400 nm thick aluminum separator for NIR and XUV, SA is an XUV spectrometer. d Schematic representation of the HHG field generated in the time domain as short XUV bursts (drawn blue and pink for the lower and higher harmonics, respectively) in the central 30 fs of the NIR pulse (red line). Note that in reality the NIR intensity pulse length is 150 fs and, therefore, has an order of magnitude more oscillations than shown in the figure.

Full size image

The excitation sequence starts with neutral helium atoms from a supersonic atomic beam. Those atoms are first ionized to He+ by photons of the 17th harmonic (H17) at 46 nm. Once a He+ ion is produced, it can be resonantly driven from the 1S to the 2S state with one photon from the fundamental NIR beam centered around 790 nm, and one from its 25th harmonic (H25) at 32 nm. The successfully excited He+ ions are further ionized to He2+, predominantly by nine-photon ionization at 790 nm, while the non-excited ions remain singly ionized. We measure the number of He2+ and He+ ions for each laser shot, and the ratio serves as a measure of the 1S–2S excitation probability.

The entire process from He atoms to He2+ ions takes place within the central  ~30 fs of a 150 fs NIR laser pulse, where the highest NIR intensity is present and the highest harmonics are produced (as sub-femtosecond XUV bursts, which is schematically shown in Fig. 1d). In Fig. 1c, a schematic of the experimental setup is shown (more details can be found in the “Methods” section).

Our unequal wavelength scheme leverages the high intensity of the fundamental NIR laser, increasing significantly the excitation rate compared to using two 61 nm photons from a low-intensity XUV beam. Another benefit of our scheme is that the H25 and NIR photons are off-resonant but close to the single-photon (dipole allowed) 1S–2P and 2P–2S transitions, which boosts the 1S–2S excitation rate by nearly two orders of magnitude. The excitation process can be efficient even though the NIR and H25 pulses have a much larger bandwidth of about 6 and 20 THz, respectively, than the 1S–2S natural linewidth of only 84 Hz33. This is possible because, as shown in Fig. 1a, within the spectrum of the NIR and H25 pulses, a range of wavelength combinations are possible that match the 1S–2S energy difference, all contributing coherently to the excitation probability34.

Observation and identification of the transition

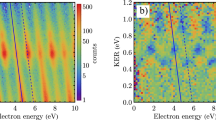
We measure the normalized He2+ signal as a function of the central wavelength of the NIR laser pulse and observe a clear resonance, as shown in Fig. 2a. As mentioned before, the 1S–2S excitation scheme is based on combining one NIR photon and one H25 photon. Given the 40.811 eV excitation energy of the transition in 3He+ 25, we expect a resonance at 789.88 nm when scanning the central wavelength of our NIR laser (which also scans H25 through the HHG process). However, driving the 1S–2S transition and the nine-photon ionization step requires NIR intensities higher than 3 × 1013 W cm−2. This results in an ac-Stark shift of the 1S–2S transition of a few tens of THz, moving the resonance towards longer wavelengths. We use that feature to unambiguously attribute the detected He2+ signal to 1S–2S excitation, by producing several resonance curves at different NIR intensities followed by linear extrapolation of the extracted resonance position to zero intensity—see Fig. 2a, c. We obtain an unperturbed NIR resonant wavelength of 789.97(27) nm, which is consistent with 1S–2S excitation. The extracted wavelength matches our simulations, which take the NIR and much smaller XUV ac-Stark shifts into account. It also excludes resonant excitation of the nearby 1S–2P one-photon transition, as that requires a wavelength of 30.38 nm25 for excitation with one H25 photon, which corresponds to an NIR central wavelength of 759.45 nm. To further corroborate our interpretation of the data, we vary the H25 intensity by varying the argon density in the HHG gas jet, while keeping the NIR intensity constant. A clear linear relationship between the He2+ signal and the H25 intensity is observed, as shown in Fig. 2d, whereas the dependence on the other harmonics (see Supplementary Note 1 and Supplementary Fig. 2) shows a nonlinear behavior. This is further confirmation that a single H25 photon is involved in the excitation process (besides NIR photons), as expected from our excitation scheme.

Fig. 2: Experimental excitation of the He+ 1S–2S transition and comparison with TDSE calculations.
figure 2

a Normalized experimental He2+ signal as a function of the NIR wavelength for several NIR intensities (in 1014 W cm−2). Gaussian fits are used to estimate the center, height, and width of the resonances. b TDSE simulation of the He2+ yield, fitted with Gaussian functions, for several NIR intensities (in 1014 W cm−2). c Fitted center of the resonances from the experiment and the TDSE simulations as a function of the NIR intensity (the vertical error bars are the 1-σ statistical errors based on the fit, the horizontal error bars for the experimental points is the statistical uncertainty of the intensity). The light-blue band represents the uncertainty in the experimental fitted slope due to the uncertainty of the NIR intensity at the position of the helium atoms. d He2+ signal (with 1-σ error bars) as a function of the 25th harmonic intensity, at a NIR central wavelength of 793 nm and an intensity of 0.9 × 1014 W cm−2. The linear relationship indicates that a single 32 nm photon is involved in the excitation process, as expected from our excitation scheme.

Full size image

Comparison with simulations

We can compare the experimental data with simulations based on time-dependent Schrödinger equation calculations (TDSE, see “Methods” and refs. 35,36,37). The calculated yield of He2+ at the end of the excitation pulse is shown in Fig. 2b as a function of the central wavelength, and at different NIR intensities. Resonant He2+ production is observed, and the ac-Stark shift produced by the intense NIR field moves the resonance center toward longer wavelengths, as observed in the experiment. Similarly to the experiment, we fit the center of the simulated resonance for each NIR intensity to construct an ac-Stark shift curve. The result matches the experimental observations within the confidence interval set by the experimental uncertainty on the absolute NIR intensity at the helium atoms—see Fig. 2c.

The simulations also confirm the spectral broadening for higher NIR power as shown in Fig. 2a, b (see also Supplementary Note 2). We can attribute the broadening to a combination of rapid ionization from the 2S state (reducing the lifetime), and a time-dependent ac-Stark shift comparable to the bandwidth of the excitation pulses. This reduces the He2+ signal at the highest NIR power. For the experimental data shown in Fig. 2a, signal saturation is observed but not a reduction for the highest powers. In a second data set (see Supplementary Fig. 4), a decrease of the He2+ signal is actually visible at the highest NIR intensities. This data was measured on a different day, and the effective power in the interaction zone was probably slightly higher due to a different alignment.

The main difference seen between the experimental data and simulations is the maximum excitation probability. In the simulations, it is 10−3 per pulse, while in the experiment it is 10−4. This can be explained by a combination of two effects. First, the spatial intensity variations in the interaction region are not taken into account in the simulations, and secondly, the He+ ion is assumed to be present from the start in the simulation, while in the experiment the ion is first produced sometime during the excitation pulse (for more details see Supplementary Notes 3 and 4).

Excitation dynamics

The TDSE calculations also enable us to follow the dynamical evolution of the electronic wavefunction of He+ during the excitation pulse, as shown in Fig. 3. What is shown is the projection of the total wavefunction on the different bare states (such as the 2S and 2P) of He+. During the NIR pulse, this is a measure of the admixture of those states but not the actual population in these states. Only after the NIR pulse is over can the projection be interpreted as an excited state population. Although the field-free states do not form a proper basis in the strong NIR field, it does provide some insight into the excitation process. It can be clearly seen that during the excitation pulse the strong NIR field induces significant P-character in the electronic wavefunction (mostly 2P and 3P). This is enhanced by the close proximity of the off-resonant single-photon 1S–2P transition in our excitation scheme, which, together with the other 1S–nP and nP–2S dipole-allowed transitions, contributes to boosting the 1S–2S two-photon transition probability. A schematic representation of the excitation process is shown in Fig. 3c. At the end of the laser pulse the induced 2P and higher angular momentum state contributions vanish. Only the resonantly-excited 2S state is significantly populated, and He2+ is produced, as shown in Fig. 3b.

Fig. 3: TDSE simulation of the excitation dynamics and NIR intensity dependence.
figure 3

a Projection on the field-free states of He+ of the electronic wavefunction (for clarity the 1S and P states beyond the 3P are not shown) of a He+ ion during the excitation pulse. This population projection should not be interpreted as real populations but as an indicator of the character of the wavefunction in the presence of the laser fields. The NIR central wavelength is taken at 792 nm with a peak intensity of 0.5 × 1014 W cm−2. b Zoom-in on the electronic wavefunction projections. At the end of the pulse, only the resonantly excited 2S state and He2+ states have a significant real population. c Schematic representation of the excitation process (based on 3He as in the experiment). The presence of the nearby 1S–2P transition of He+, which is dipole-allowed, enhances the two-photon transition probability. The quotes indicate that during the strong NIR pulse the indicated states should not be interpreted as real population. d Simulated 2S, 2P, and He2+ real populations after the excitation pulses. The yield for each state is calculated as a function of the NIR central wavelength, for a NIR intensity of 0.35 × 1014 W cm−2 (dashed lines) and 1.0 × 1014 W cm−2 (continuous lines). Resonant excitation to the 2S state (followed by ionization to He2+) can be seen, while the 2P population remains low and doesn’t exhibit any resonance behavior.

Full size image

One notable feature during the excitation process is the oscillation observed in Fig. 3b, most pronounced in the 2S projection, but also in other state projections. We observe that the modulation depth and period is related to the amount of 2S excitation, though one should be careful with interpretations based on the presented projections when the strong NIR field is present. With NIR light, but without HHG light, and therefore no significant 2S excitation, no oscillations are observed in the simulations.

After the NIR pulse is over, we find that the 2S state is typically populated three orders of magnitude more than the 2P. Other states, such as the 3S and 3P, are populated even less than the 2P. The weak coupling to the 2P state is due to the small spectral overlap of the HHG spectrum with the one-photon 1S–2P transition: H25 and H27 have a bandwidth of about 0.06 nm and correspond to wavelengths of 31.6 nm and 29.3 nm, respectively, well off-resonant from the 1S–2P transition and its excitation wavelength of 30.38 nm25. We also observe in the calculations that for higher NIR intensity, a faster ionization to He2+ leads to a rapid depletion of the 2S population, as shown in Fig. 3d. This leads to the broadening of the resonance as discussed earlier, and again identifies 1S–2S excitation as the main contribution to the He2+ signal. Note that due to the ac-Stark shift and ionization dynamics, the maximum He2+ yield in Fig. 3d occurs at a different wavelength than the peak of the population that remains in the 2S state. This difference vanishes when the NIR intensity approaches zero.

Conclusions

We have observed the 1S–2S transition of singly-ionized helium based on a combination of a powerful NIR ultrafast pulse derived from a frequency comb laser and its 25th harmonic. By performing this experiment with an atomic beam, we could carry out a detailed study of the excitation process. We also performed TDSE simulations of 1S–2S excitation, and the outcomes are consistent with the features seen in the experiment. Our results show that the 1S–2S transition can be significantly and selectively excited with a peak probability of 10−4 per pulse.

Our demonstration paves the way for future precision studies of the 1S–2S transition in He+ and for XUV spectroscopy of highly charged ions for tests of fundamental physics16,18. This could be accomplished by combining the demonstrated excitation method with Ramsey-comb spectroscopy (RCS)30,31,32. In RCS, the transition frequency is measured based on the field-free phase evolution of the atom or molecule between two excitation pulses (derived from an FC laser), making it largely insensitive to the large ac-Stark shifts observed in the present study. In the case of He+ excitation, RCS will require trapping of the ion to restrict its movement so it can interact with two laser pulses that can be up to microseconds apart. Sympathetic laser cooling with a co-trapped Be+ ion18,38 and matching of the period of motion of the He+ ion in the trap with the RCS pulse delay can be used to suppress Doppler and photon recoil effects (see Supplementary Note 5), and we expect that an accuracy of  <10 kHz is feasible. Currently, the uncertainty on the theoretical evaluation of the 1S–2S transition frequency is limited by three contributions: 60 kHz from the uncertainty on the alpha particle charge radius, 42 kHz from higher-order QED terms, and 19 kHz from the uncertainty on the Rydberg constant18. A future RCS precision measurement of the transition frequency would, therefore, enable an improved test of these important contributions.

Methods

Generation of the NIR ultrafast laser pulses

The laser system starts with a Ti:sapphire FC laser, emitting a train of pulses with a repetition rate frep = 125 MHz. Two pulses from the FC laser can be selectively amplified in a noncollinear optical parametric chirped pulse amplifier (NOPCPA) as required for future precision RCS excitation. However, for the experiment reported in this article only one pulse is amplified at a repetition rate of 28 Hz. The NOPCPA is specifically designed for high-phase stability and is similar to the system we used in ref. 39, but based on three lithium tri-borate (LBO) crystals that are pumped with a 532 nm pump laser. The central wavelength of the amplified pulses can be varied between 785 and 800 nm, and the spectral width is adjustable and set to 11.2 nm (with a square spectral profile due to the NOPCPA). This spectrum was observed with an Avantes-AvaSpec-3648 spectrometer, which was calibrated (the resolution and absolute wavelength) with a single mode laser at 791.351 nm, showing an offset of 0.68(20) nm for which the measurements were corrected. The output pulses of the NOPCPA have a duration of about 150 fs (measured using frequency-resolved optical gating40) after compression, close to the Fourier limit. The NIR pulse energy used for all experiments is approximately 1 mJ.

Generation of the extreme-ultraviolet light

High-harmonic generation in an argon jet is used to produce the required XUV light from the 150 fs NIR pulse described in the previous section. For this purpose, the NIR beam is focused with a f = 25 cm lens to a small spot of about 35 μm FWHM to reach the high intensity required for HHG. The focus is placed slightly before the jet to achieve a minimally divergent harmonic beam by phase-matching only the short electron trajectories in the HHG process41. The fundamental NIR pulses and the co-propagating harmonics are refocused together in a pulsed supersonic beam of helium, using a pair of grazing-incidence gold-coated toroidal mirrors. As the NIR beam diverges more strongly than the generated harmonics, an adjustable iris placed after the argon jet allows us to control the NIR intensity in the atomic beam independently of the harmonics. After the interaction region, a 400 nm thick aluminum filter reflects the NIR light out of the vacuum system. This reflected light is used to monitor the NIR pulse energy and stability. Wavelengths below 60 nm are transmitted by the aluminum filter and are either sent onto an Andor Newton CCD camera, or dispersed by an aluminum grating onto a Hamamatsu R5150-10 electron multiplier to measure the harmonic spectrum, see Fig. 1b (inset). With argon as the HHG medium, the cutoff wavelength is close to H25 at 32 nm. The 27th harmonic is strongly suppressed, and all higher harmonics are not observed.

Atomic beam and detection of the excitation signal

A supersonic pulsed beam of helium is produced in a separately pumped vacuum chamber by a piezo-actuated valve with a backing pressure of about 1 bar. The beam is passed through a skimmer with a 3 mm diameter before it reaches the interaction chamber. The NIR and HHG beams are focused on this beam, leading to He+ and He2+ ions. These are detected with a time-of-flight mass spectrometer, in which the arrival time on the ETP AF880 electron multiplier (EM) depends on the charge-to-mass ratio. By digitizing and integrating the EM trace with a DRS4 digitizer board, we record the singly- and doubly-ionized helium signal for each laser shot. As 4He2+ and \({{{{\rm{H}}}}}_{2}^{+}\) ions have virtually the same charge-to-mass ratio, they cannot be distinguished in our detection system. This leads to a significant background signal from trace amounts of H2 in the vacuum chamber and helium bottle. Therefore, we installed a cryogenic recycling system and performed all experiments with 3He.

Data taking and analysis

We record the He+ and He2+ ion signals as a function of the NIR intensity and NIR central wavelength (Fig. 2a, c), or as a function of the H25 intensity (Fig. 2d), and plot the measured number of He2+ counts relative to the He+ signal. The measurement at the highest NIR intensity is an average of two scans. Each data point corresponds to an average of 7500 laser shots typically (some data points are averaged over 2 or 3 series of 7500 shots). To vary the intensity of the NIR beam at the position of the atoms, we vary the NIR power transmitted through the adjustable iris placed after the HHG argon jet (see Fig. 1b). This also changes the size of the refocused NIR beam at the position of the atoms, due to diffraction on the iris. Therefore, to estimate the NIR intensity we monitor both the transmitted NIR power and the size of the beam, using a power meter and a camera, respectively. We select the NIR central wavelength by translating an optical slit placed in the Fourier plane of the pulse stretcher of our frequency comb (before amplification). The pulse length is measured using FROG and kept constant for all our measurements. We assume the interaction happens only when the 25th harmonic is present, which is during the central 30 fs of the 150 fs NIR pulse. Additionally, it is assumed that the XUV focus is much smaller than the NIR focus and that they are overlapped, such that the excitation takes place only in the most intense part of the NIR beam. The intensities shown in Fig. 2a, c are calculated under these assumptions. If some of these assumptions are not correct, the intensity experienced by the He+ ions will be different. We estimate the possible sources of error to be as follows: an up to 10% longer NIR pulse, up to 5% larger focus size, a ±10% error on the power meter reading, and an up to 5% higher than expected optical loss in the vacuum outcoupling of the NIR. These systematic uncertainties are accounted for by the confidence interval displayed in light blue in Fig. 2c of the fitted experimental dependence on NIR intensity. The data shown in Fig. 2a represents one of two recorded sets (see Supplementary Fig. 4b for the second set), while Fig. 2c is based on both data sets. Gaussian fits are used to estimate the center, height, and width of the resonances.

HHG and TDSE simulations

To perform the TDSE calculations, we first calculate the harmonic field using the approach explained in refs. 42,43,44. Since this method only works well for harmonics in the plateau and cut-off region (harmonics higher than H11), the lower harmonics are scaled to match the expected relative strengths45. The full harmonic spectrum is also scaled with a general factor to match an intensity of 2 × 109 W cm−2 for H25, which corresponds to the expected experimental conditions in the interaction zone. The resulting XUV field, together with the fundamental NIR field, is used as input for our TDSE simulations. After integrating over the excitation pulses with a time step of 0.5 attoseconds, a projection of the electron wavefunction is made to identify the population of the bound states and to calculate the ionized (He2+) fraction. Note that resonance enhancement based on two different driving wavelengths has been studied theoretically before in this manner, in the context of HHG in He+ 46.