One-third magnetization plateau in Quantum Kagome antiferromagnet

Abstract

The emergence of nontrivial quantum states from competing interactions is a central issue in quantum magnetism. In particular, for the realization of the quantum spin-liquid state, extensive studies have been conducted on frustrated systems, such as kagome antiferromagnets and Kitaev magnets. Novel quantum states in magnetic fields have remained elusive despite the prediction of rich physics. This can be attributed to material scarcity and the difficulty of precise measurements under ultra-high magnetic fields. Here, in this study, we develop the Kapellasite-type compound InCu₃(OH)₆Cl₃, whose exchange interactions are in appropriate energy scale to comprehensively elucidate the magnetic properties of the frustrated S = 1/2 kagome antiferromagnet. The one-third magnetization plateau was clearly observed. Moreover, the large temperature-linear term in the heat capacity was observed in the magnetic fields, indicating the excitation of gapless quasiparticles in the vicinity of the plateau. These results shed light on the critical behaviors between quantum spin-liquid and -solid in kagome antiferromagnets under high magnetic fields.

Introduction

The physics arising from kagome geometry provides understandings of condensed matter physics. Recently, not only a quantum spin liquid in insulators but also the topological properties of the Dirac point and flat band, and exotic superconductivity have been discussed^1,2,3. In particular, kagome frustrated magnetism research has prioritized quantum spin liquids for a long time. Numerous theoretical models have been proposed for the quantum spin liquid, including Z₂ topological and U(1) Dirac models⁴; however, microscopic properties such as the nature of magnetic excitation spectra have not yet been determined. On the other hand, the observation of spin liquid has been proposed in S = 1/2 kagome antiferromagnet Herbertsmithite (ZnCu₃(OH)₆Cl₂) based on the continuum excitation spectra of inelastic neutron scattering experiments⁵.

Furthermore, the formation of various quantum states in magnetic fields theoretically predicted have been one of the intriguing interests. In the S = 1/2 kagome model considering a nearest-neighbor antiferromagnetic interaction and the Zeeman term in the Hamiltonian, the magnetization jumps due to the collective excitation of resonant hexagonal magnons from the forced ferromagnetic state and (2n + 1)/9 (n = 1, 2, and 3) plateaus of hexagonal magnon crystallization in $\sqrt{3} \times \sqrt{3}$ cells are expected^6,7,8. In addition, a magnon supersolid state just below the 5/9 plateau is expected when an intermagnon interaction is incorporated⁹. These are closely related to macroscopic quantum phenomena based on resonant hexagonal magnon excitations and their bosonic statistics, as well as the localized/itinerant nature caused by interactions between excited quasiparticles. Moreover, the 1/9 magnetization plateau is also anticipated to be a field-induced quantum spin liquid, although the microscopic state is still controversial^10,11. Elucidating these quantum many-body states is of great importance for understanding kagome-frustrated magnetism.

On the other hand, from an experimental perspective, actual quantum kagome antiferromagnets typically possess a large nearest-neighbor interaction J₁ which requires ultrahigh magnetic fields, often exceeding 100 T, to reach the saturation field¹². Thus, it is generally difficult to search for quantum states despite the rich expectations of field-induced quantum states. There are few examples except for a weak anomaly near the 1/3 magnetization in Herbertsmithite around 190 T¹³, a metastable 1/3 plateau in Cu-titmb¹⁴, successive plateaus as candidates of the hexagonal magnon crystallizations in CdCu₃(OH)₆(NO₃)₂·H₂O (Cd-kapellasite)¹⁵, and a 1/9 magnetization plateau in YCu₃(OD)_6+xBr_3-x¹⁶.

Here, we focused on Kapellasite-type compounds as quantum kagome magnets. Because the nonmagnetic ion is located at the center of the hexagon, a finite next-nearest-neighbor J₂ and third-nearest-neighbor J_d across the diagonal of the hexagon are expected. These interactions and the nearest-neighbor interaction J₁ compete, significantly affecting the ground state of kagome magnets and leading to the formation of various magnetic orders, such as Cuboc1 and Cuboc2 structures, even in classical systems^17,18. Moreover, in quantum systems, the formation of spin liquids owing to quantum fluctuations around the phase boundaries is anticipated^19,20. Therefore, the creation of quantum materials in the kapellasite system and the studies of their magnetism will promote the discovery of quantum many-body states such as quantum spin liquids and magnon crystal states, and will greatly facilitate our understanding of the physics of frustrated kagome quantum spin systems. In fact, exotic magnetic states have been observed, such as a spin liquid with Cuboc2 correlations in Zn-kapellasite^21,22, ferromagnetic order with spin fluctuation in Mg-kapellasite²³, the coexistence of negative vector chirality (NVC) order and spin liquid in Ca-kapellasite, and NVC order in Cd-kapellasite and Y-kapellasite^{15,24,25,26,27,28,29,30,31,32,33,34}. In the Y-kapellasite derivative compound Y₃Cu₉(OH)₁₉Cl₈, the dominant antiferromagnetic J₁ has a complicated spatial distribution. From a theoretical consideration of the magnitude and spatial distribution of J₁, phase diagrams that include magnetic phases such as classical spin liquids have been proposed^35,36.

We synthesized a material InCu₃(OH)₆Cl₃ as a member of the Kapellasite-type kagome magnets and successfully found a 1/3 magnetization plateau in high-magnetic fields. In this paper, we report the results of structural analysis, magnetic susceptibility, heat capacity, and high-field magnetization with theoretical calculation of In-kapellasite, which present insights into kagome frustrated magnetism.

Results and discussion

Crystal structure, magnetic susceptibility and heat capacity

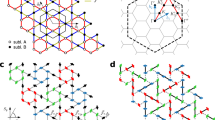
Figure 1 shows the crystal structure of In-kapellasite. In-kapellasite crystalizes in the space group P31m and the lattice constants are a = 11.3235(6) Å and c = 6.0347(4) Å. The kagome layer is composed of edge-shared CuO₄Cl₂ octahedra, in which the $d_{{{\rm{x}}}^{2}{\mbox -} {{\rm{y}}}^{2}}$ orbital of the Cu²⁺ ion is occupied by an unpaired electron. There are threefold rotational axes on the In sites, although each triangle of the Cu²⁺ ions is distorted into an isosceles triangle. Two isosceles triangles exist in the unit cell, one with two long bonds and another with two short bonds. In the ab-plane, they alternately share vertices to form a kagome network with a threefold rotational symmetry. Because the threefold-axes are preserved, symmetry lowering such as the one-dimensionalization of the exchange interaction, which is often observed in kagome systems with monoclinic distortion, is not expected to occur¹².

Fig. 1: Perspective view of the crystal structure of In-kapellasite.

a, b Whole structure and in-plane crystal structure of In-kapellasite. The configuration of $d_{{{\rm{x}}}^{2}{\mbox -} {{\rm{y}}}^{2}}$ orbitals occupied by the unpaired electrons of Cu²⁺ is depicted. c The four sets of Cu-Cu bond distances and Cu-O-Cu bond angles, colored with red, blue, yellow, and green lines. The red bond has the longest Cu-Cu distance and largest Cu-O-Cu bond angle, and the green bond has the shortest distance and smallest angle.

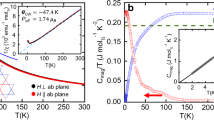
The temperature dependence of magnetic susceptibility measured for randomly oriented single crystals is shown in Fig. 2. It obeys the Curie-Weiss law above 40 K, and the Weiss temperature Θ_W = −10.2 K and effective Bohr magneton number p_eff = 1.89 were estimated from linear extrapolation. The magnetic susceptibility was reproduced well by high-temperature series expansion (HTSE) up to the 15th order, assuming a uniform antiferromagnetic J₁ on a regular kagome network with S = 1/2³⁷. The J₁ and g-values were estimated to be 11.5 K and 2.24, respectively. This interaction is smaller than those of Ca-, Cd-, and Y-kapellasites at 52, 45, and 99 K, respectively^25,32,33. With decreasing temperature, a weak anomaly was observed at approximately 7 K, where the susceptibilities showed further increases, deviating from the Curie-Weiss law. This anomaly was maintained even at a magnetic field of 7 T, although the increase was slightly suppressed upon increasing the magnetic field. No cusps or other anomalies were observed at temperatures down to 2 K.

Fig. 2: Temperature dependence of bulk physical properties in magnetic fields.

a Temperature dependence of magnetic susceptibility and its inverse measured at H = 1 T down to 2 K. The dashed black and solid yellow lines indicate the results of Curie-Weiss and 15th HTSE fitting, respectively. b Low temperature magnetic susceptibility measured in several magnetic fields and heat capacity obtained at H = 0 T. The vertical dotted line indicates the short-range order temperature where the heat capacity shows the broad peak and the susceptibilities suddenly increase. The solid line is an approximated lattice contribution of heat capacity.

The temperature dependence of the total specific heat measured for the small coaligned single crystals is shown in Fig. 3a. A broad peak was observed at T_s = 7 K with zero magnetic field, indicating the formation of an antiferromagnetic short-range order (SRO). A theoretical study predicted characteristic anomalies in heat capacity, where broad peaks and shoulder-like anomaly successively appeared at T/J ~ 0.6 and ~ 0.1, respectively^37,38,39. The SRO temperature T_s /J₁ ~ 0.6 is consistent with the broad peak position of the theoretical expectation. Because T_s corresponds to the temperature at which the magnetic susceptibility increases further as illustrated in Fig. 2b, the enhancement in susceptibility is due to the formation of the SRO. T_s decreases to 4.4 K when applying magnetic fields of up to 8 T, but in stronger magnetic fields the peak temperature increases up to 5 K at 14 T. With the application of magnetic fields, the peak becomes prominent, and more entropy is released. Lower temperature measurements in zero magnetic field revealed a clear peak at T_N = 1.8 K, indicating the development of a magnetic long-range order (LRO). The peak shifts to lower temperatures with increasing applied magnetic field and finally disappears at 8 T. Only a broad peak exists at a low-temperature specific heat above 8 T.

Fig. 3: Temperature dependence of the heat capacity of In-kapellsite.

a Temperature dependence of heat capacity measured in several magnetic fields applied along the c-axis of coaligned small single crystals. The data measured at each field is offset by 0.2. b C/T vs. T² plot in varied magnetic fields. The solid line indicates the linear fitting.

A temperature-linear (T-linear) term is observed under high magnetic fields. At low fields, it is difficult to estimate the T-linear term in the measured temperature region because of the observed divergence in the specific heat associated with the LRO. However, above 10 T, the peak is suppressed, and an extrapolation of the C/T data has a finite value at T = 0, as is clearly seen in the low-temperature region of the 14 T data for the C/T vs. T² plot (Fig. 3b). The coefficient of the T-linear term was estimated to be 59.8 mJ Cu-mol⁻¹ K⁻² at 14 T. T-linear terms in insulators have been observed in some spin liquid candidates, such as κ-(BEDT-TTF)₂Cu(CN)₃⁴⁰, EtMe₃Sb[Pd(dmit)₂]₂⁴¹, and Ca-kapellasite²⁵, and their possible origins have been discussed in accordance with the spinon Fermi surface and anisotropic weathervane excitation in the fluctuating zero-field ground state. In In-kapellasite, gapless magnetic quasiparticles are excited under high magnetic fields, which characterizes the peculiarity of this compound.

To extract the magnetic entropy, we estimated the lattice contribution by fitting the data above 40 K based on the Debye model as shown in Fig. 2b⁴². We found that magnetic entropy of approximately 3 J Cu-mol⁻¹ K⁻¹ was released below 25 K under zero magnetic field. This suggests that approximately half of the magnetic entropy for S = 1/2 remains below T_N, which may appear as a T-linear term for In-kapellsite.

High field magnetization and its theoretical analyses

Figure 4 depicts the results of pulsed high-field magnetization measurements performed on randomly oriented single-crystal samples. The absolute value was corrected by the magnetization data measured with a SQUID magnetometer, and the horizontal axis was normalized by J₁ = 11.5 K. At 1.3 K, the slope of magnetization, dM/dH, decreases at approximately H/J₁ = 0.8 and increases again at approximately H/J₁ = 1.6. Subsequently, a peak is observed at H/J₁ = 3. Since dM/dH becomes small in the field region from H/J₁ = 0.8 to 1.6 and the magnetization value in this region is close to 1/3 of the saturation magnetization (M_s), this magnetization region is considered as a 1/3 magnetization plateau, though it does not show perfect flatness. Recently, the asymmetric plateau melting phenomenon at finite temperatures has been theoretically discussed, in which kagome’s plateau is not essentially flat under finite temperatures^38,39,43. It may be related to the non-flatness of 1/3 plateau in this study, however precise measurements using single crystals would be required to conclude. Similar behavior was observed at 4.2 K, but it was blunted.

Fig. 4: Whole magnetization process of In-kapellasite.

Magnetization curves normalized by the saturation value (Ms) in high magnetic fields (upper panel) and its differential dM/dH (lower panel). The magnetization curve at 4.2 K is offset by 0.3. The absolute value of pulsed magnetization data was corrected by the magnetization data obtained with a SQUID magnetometer at 4.2 K. The horizontal axis H/J₁ is normalized by the nearest-neighbor antiferromagnetic interaction J₁ = 11.5 K determined by the HTSE fitting of magnetic susceptibility. The dashed red line shows the calculated finite temperature magnetization curve assuming uniform nearest-neighbor interaction at T/J₁ = 0.1 by the OFTLM method with N = 36. The dashed-dotted line shows the theoretical curve assuming three nearest-neighbor interactions with the ratio J₁′ (thick, solid, red) : J₁ (thin, solid, blue) : J₁″ (dotted, green) = 2 : 1 : 0.5 of which the spatial distribution is depicted in the inset of the upper panel. The black vertical arrows in the lower panel indicate the starting and terminating magnetic fields of the 1/3 plateau calculated with a DMRG method¹⁰. Blue and purple vertical arrows show the experimental magnetic fields of the 1/3 plateau corresponding to the calculated one. Since the 4.2 K data is blunted, the lower end of the plateau field is determined by the intersection of extrapolated lines as shown in the upper panel. The saturation fields H/J₁ = 3 for both 1.3 K and 4.2 K are determined by the peak top of dM/dH. The weak oscillation of theoretical dM/dH between H/J = 1.5 – 2 in the lower panel is due to the finite size effect.

To better understand this magnetization behavior, we theoretically investigated the effects of finite temperature on the magnetization process of a kagome antiferromagnet with uniform J₁ on a 36-site cluster using the orthogonalized finite-temperature Lanczos method (OFTLM). In Fig. 4, in addition to some finite-temperature calculation results, the magnetization obtained using the grand canonical density matrix renormalization group (DMRG) method at T = 0 with a uniform J₁ is represented by a black solid line¹⁰. We found that the magnetization curve measured at 1.3 K (T/J₁ ~ 0.1) was in good agreement with the theoretical curve at T/J₁ = 0.1, although there was a difference near saturation. This indicates that the magnetic network of In-kapellasite can be regarded as an ideal quantum kagome antiferromagnet consisting of uniform J₁. The difference around the saturation field is due to the Dzyaloshinskii-Moriya (DM) interaction, as observed for Cu benzoate. DM interaction creates a staggered field which significantly blunts the magnetization process near the saturation field; in particular, magnetization exhibits anisotropy depending on whether the external magnetic field is perpendicular or parallel to the staggered magnetic field⁴⁴. Actually, anisotropic behavior was observed in our preliminary magnetization measurements for In-kapellasite. Next, the theoretical magnetization at T = 0, which includes multiple plateaus, was severely blunted by finite-temperature effects, even at T/J₁ = 0.1. To extract information from the magnetization process at finite temperature, we compared the theoretical (T/J₁ = 0.1) and experimental (T/J₁ ~ 0.1 (1.3 K)) dM/dH curves in Fig. 4; in practice, we need to compare the characteristic structure of the dM/dH around the 1/3 plateau and the saturation, where the dM/dH change most significantly. Characteristically, theoretical dM/dH begins to decrease rapidly in the magnetic field where the plateau sets in, takes the smallest value at the end of the plateau, and then shows a peak at saturation. The experimental dM/dH, which decreases from H/J₁ ~ 0.8 (7.0 T) and reaches a minimum at 1.6 (13.7 T) and takes a peak at H/J₁ ~ 3 (25.7 T), shows similar behavior to the theoretical one. The experimental plateau width is comparable to the theoretical width. Moreover, the value of magnetization between 7.0 – 13.7 T was close to M_s/3. The agreement of the experimental and theoretical results indicates that this behavior corresponds to the 1/3 magnetization plateau, which should be a typical example of a 1/3 plateau in S = 1/2 kagome antiferromagnets¹². It is generally difficult to determine the plateau width from experiments at finite temperatures. As demonstrated here, a comparison of magnetization measurements and theoretical calculations for In-kapellasite provides a good guide for determining the plateau width. In contrast, the 1/9, 5/9, and 7/9 plateaus with narrow widths were not observed in our experiments. This is mainly due to the finite temperature effect, which significantly obscures the fine structure of the magnetization curve; thus, further anomalies may be observed by performing magnetization measurements at lower temperatures.

Phase diagram and consideration of magnetic interactions

The above results are summarized in the temperature-field phase diagram in Fig. 5. At zero magnetic field, the antiferromagnetic SRO develops below T_s; subsequently, the LRO is formed below T_N = 1.8 K. This ordered phase is suppressed by magnetic fields of approximately 7 T. However, the SRO persists even at 8 T, although it shifts slightly to lower temperatures. The 1/3 magnetization plateau phase appeared upon the application of magnetic fields above 7 T, which protruded to higher-temperature regions compared to the ordered phase. These results suggest that the magnetic states of the 1/3 plateau and the LRO are not directly related.

Fig. 5: Temperature-field phase diagram of In-kapellasite.

Magnetic phase diagram determined from the bulk magnetization and heat capacity measurements. Solid lines are eye-guides for each phase.

The LRO phase of In-kapellasite is considered to be induced by the DM interaction. The ratio of the DM (D) and nearest-neighbor interaction J significantly affects the ground state of a quantum kagome antiferromagnet, and the theoretical critical point between the quantum spin liquid and the magnetic ordered state is around D/J ~ 0.1⁴⁵. The ratio of D/J₁ = Δg/g ~ 0.12 was estimated using the g-value obtained from the HTSE fitting for In-kapellasite, which should disturb the spin liquid formation and stabilize the LRO. In fact, the Néel temperature 1.8 K roughly agrees with the DM interaction D ~ 1.4 K, supporting the DM induced LRO scenario⁴⁶. The decrease in T_N may be explained by the effective suppression of the DM interaction in the magnetic field, because the energy scale of the magnetic field of 7 T (~ 10 K) is larger than that of the DM interaction. Thus, the magnetism of the system is expected to be dominated by J₁ and the magnetic field. The plateau phase appeared in such a magnetic field regime.

In the case of a triangular lattice antiferromagnet, for comparison, the 1/3 magnetization plateau with the up-up-down (UUD) arrangement is considered as the field-induced spin structure changed from the low-field 120° state, as observed in CsCuCl₃⁴⁷, Ba₃CoSb₂O₉⁴⁸, RbFe(MoO₄)₂⁴⁹, and Rb₄Mn(MoO₄)₃⁵⁰. This indicates that the effects of the temperature as well as magnetic field are very different from that for In-kapellasite. The 1/3 plateau state with the UUD structure in these triangular lattice antiferromagnets is in the LRO state. Thus, the temperature dependence of the heat capacity in the magnetic fields of the plateau region exhibits a clear peak, which indicates the breaking of the translational symmetry of the lattice. On the other hand, in In-kapellasite, the temperature dependence of the heat capacity in the magnetic fields of 10 and 14 T show a broad peak when the plateau state is stabilized. Although there is entropy release upon entering the plateau phase, it is not a typical λ-type peak of the second-order transition. If the 9-sites UUUUUUDDD structure or valence bond crystal state^7,10 is realized in the 1/3 plateau of In-kapellasite with a 9-site structural unit cell, the translational symmetry of the lattice is not broken. We believe this corresponds to the absence of a sharp peak in our heat capacity measurements.

To date, the 1/3 plateau state in quantum kagome antiferromagnets has not been experimentally investigated. In particular, magnetic excitations near the plateau state are quite difficult to predict even with current theoretical treatments. The observation of the 1/3 plateau with exotic excitation represented by the T-linear term at relatively low magnetic fields in In-kapellasite paves the way for the experimental verification of the anomalous properties of quantum kagome antiferromagnets in high magnetic fields such as magnon crystals and magnon BEC, etc.

Finally, we consider the effects of structural distortion. In the Kapellasite series compounds without structural distortion, the Cu-O-Cu bond angle dependence of the nearest-neighbor superexchange interaction strength was investigated using density functional theory (DFT) calculations¹⁹. As shown in Fig. 1, In-kapellasite has four Cu-O-Cu angles between the nearest neighbor Cu²⁺ ions, and thus the four different interactions would be spatially distributed; based on DFT, 114.8°, 111.6°, 110.4°, and 108.6° bonds correspond to magnetic interactions of 60, 33, 27, and 15 K, respectively. The validity of this situation was examined by theoretical calculations of the M-H curve. Because two of the four interactions with bond angles 111.6° and 110.4° are approximately equal to the average magnitude at 30 K, we consider for simplicity that there are three interactions J₁, J₁′, and J₁″ with the ratio of J₁′ : J₁ : J₁″ = 2 : 1 : 0.5. The spatial distributions of these three interactions are shown in the inset of Fig. 4. There are two types of hexagons: hexagons with uniform interactions and hexagons with alternating large and small interactions. This is related to the magnetic model of Y₃Cu₉(OH)₁₉Cl₈, although the spatial distribution of the hexagons differs^35,36. However, when calculating the magnetization process according to this magnetic model, the 1/3 plateau was significantly stabilized, and the calculated magnetization did not reproduce the experimental one, as depicted in Fig. 4.

This result supports the idea that the nearest-neighbor interaction of In-kapellasite is essentially isotropic. This may be attributed to the degree of local orbital overlap caused by structural distortion. Owing to structural distortion, In-kapellasite possesses four nearest-neighbor bond lengths between Cu²⁺ ions, which affects the degree of overlap of the $d_{{{\rm{x}}}^{2}{\mbox -} {{\rm{y}}}^{2}}$ orbitals of the Cu²⁺ ions. This factor also contributes to the magnitude of the superexchange interaction. Accordingly, the contribution of the four Cu-O-Cu bond angles to the superexchange interaction is compensated for by the four bond lengths; for example, bonds with large Cu-O-Cu angles have small orbital overlaps due to large Cu-Cu distances, and vice versa. Therefore, the magnetic network of this system may be considered isotropic, as evidenced by the reproduction of the magnetic susceptibility and magnetization curve by assuming only uniform J₁.

In this study, a temperature-field phase diagram is proposed for the S = 1/2 Kapellasite-type kagome antiferromagnet InCu₃(OH)₆Cl₃ which exhibits a 1/3 magnetization plateau. Importantly, the plateau state with an apparent 1/3 magnetization value is realized. Further microscopic and thermal investigations of this material in magnetic fields are required to lead the frontier of high-field magnetism of frustrated kagome antiferromagnets, such as the characterization of the dynamic properties of the magnetization plateau as a quantum many-body state and the search for a hidden exotic magnetic phase, such as a spin nematic state.

Method

Sample preparation and structural analysis

A crystalline powder sample of InCu₃(OH)₆Cl₃ was synthesized using a hydrothermal technique in a stainless-steel autoclave. Chemical reagents of indium nitride and copper chloride with distilled water and lithium hydroxide as a catalyst were put into the autoclave, and heated for 24 h at 220 °C. Typical particle size of crystal is 0.1 mm in thickness and 0.2 mm in diagonal length.

For crystal structural analysis, a greenish-blue platelet crystal having 0.088 × 0.075 × 0.112 mm was measured at 297 K on a Rigaku Saturn CCD diffractometer with VariMax confocal optical system for Mo Kα radiation. Data were processed and corrected for absorption effects using the REQAB algorithm in the d*trek package of the CrystalClear software suite. The structure was determined using SHELXT⁵¹ and refined using SHELXL-2014⁵² in the WinGX program suite⁵³. A model with an In³⁺/Cu²⁺ mixture was also examined; however, the R values did not improve. The Final R values were R_obs = 3.54% and wR_all = 8.68%.

Physical property measurements

The temperature dependence of the magnetic susceptibility was measured using a SQUID magnetometer (Quantum Design, MPMS) in the temperature region 2 – 300 K in magnetic fields of up to 7 T. Heat capacity measurements were performed by the relaxation method using a Quantum Design PPMS down to 2 K and up to 14 T, and with a self-developed calorimeter below 2 K up to 14 T. Reproducibility of basic physical properties was confirmed with some batches of samples. High-field magnetization measurements at 1.3 and 4.2 K were performed by an induction method in pulsed high magnetic fields of up to 51 T at the Center for Advanced High Magnetic Field Science, Osaka University.

Orthogonalized finite-temperature Lanczos method

The Hamiltonian for the S = 1/2 kagome network with an In-kapellasite-type distortion in a magnetic field is defined as

$$H={\sum}_{\left\langle i,j\right\rangle }{J}_{i,j}{S}_{i}\cdot {S}_{j}-H{\sum}_{i}{S}_{i}^{Z},$$

(1)

where S_i is the spin-half operator at the i-th site, ${S}_{i}^{Z}$ is the z component of S_i, $\left\langle i,j\right\rangle$ runs over the nearest-neighbor spin pairs, ${J}_{i,j}$ corresponds to J₁, J₁′, and J₁″ as shown in Fig. 4, and H is the magnitude of the magnetic field applied in the z direction.

The finite-temperature Lanczos method (FTLM) is useful for analyzing frustrated quantum lattice models⁵⁴. The OFTLM is a more accurate method than the standard FTLM, particularly at low temperatures^55,56. The partition function using standard FTLM is as follows:

$$Z{\left(T,H\right)}_{{{\rm{FTL}}}}={\sum }_{m=-{M}_{{{\rm{s}}}}}^{{M}_{{{\rm{s}}}}}\frac{{N}_{{{\rm{st}}}}^{(m)}}{R}{\sum }_{r=1}^{R}{\sum }_{j=0}^{{M}_{L}-1}{e}^{-\beta {\epsilon }_{j,m}^{\left(r\right)}}\left(H\right){\left|\left\langle {V}_{r,m}|{\psi }_{j,m}^{r}\right\rangle \right|}^{2},$$

(2)

where ${M}_{{\mbox{s}}}$ is the saturation magnetization, N_st is the dimension of the Hilbert subspace with ${S}_{{\mbox{tot}}}^{Z}=m$, R denotes the number of random samplings of the FTLM, ${M}_{L}$ denotes the dimension of the Krylov subspace, |${V}_{r,m}{{\rangle }}$ is a normalized random initial vector with ${S}_{{\mbox{tot}}}^{Z}=m$, and |${V}_{j,m}^{r}{{\rangle }}$ $[{\epsilon }_{j,m}^{(r)}(H)]$ are the eigenvectors (eigenvalues) in the ${M}_{L}$-th Krylov subspace with ${S}_{{\mbox{tot}}}^{Z}=m$. As ${\sum}_{i}{S}_{i}^{Z}$ is a conserved quantity, ${\epsilon }_{i,j}^{\left(r\right)}(H)$ can be expressed as ${\epsilon }_{i,j}^{\left(r\right)}\left(H\right)={\epsilon }_{i,j}^{\left(r\right)}-{mH}$. We define the order of $\{{\epsilon }_{j,m}^{(r)}\}$ as ${\epsilon }_{0,m}^{\left(r\right)}\le {\epsilon }_{1,m}^{\left(r\right)}\le {\epsilon }_{2,m}^{\left(r\right)}\le \cdots \le {\epsilon }_{{M}_{L-1},m}^{\left(r\right)}$. If ${M}_{L}$ is sufficiently large, ${\epsilon }_{0,m}^{\left(r\right)}$ becomes equal to the exact ground state energy ${E}_{0,m}$. However, ${|\langle {V}_{r,m},|,{\psi }_{j,m}^{r}\rangle |}^{2}$ does not converge to the expected value, that is, ${d}_{m}/{N}_{{\mbox{st}}}^{(m)}$, where ${d}_{m}$ represents the degeneracy of the ground state in the subspace with ${S}_{{\mbox{tot}}}^{Z}=m$. Therefore, unless a sufficient number of random samples are considered, the accuracy of $Z{\left(T,H\right)}_{{\mbox{FTL}}}$ will not improve at low temperatures.

In the OFTLM, we first calculate several low-lying exact eigenvectors $|{\Psi }_{i,m}\rangle$ with ${N}_{V}$ levels.

We define the order $\left\{{E}_{i,m}\right\}$ as ${E}_{0,m}\le {E}_{1,m}\le \cdots \le {E}_{{N}_{V}-1,m}$. We then calculate the following modulated random vector:

$$|{V}_{r,m}^{{\prime} }\rangle = \left[I-{\sum }_{i=0}^{{N}_{V-1}}|{\Psi }_{i,m}\rangle \langle {\Psi }_{i,m}|\right]|{V}_{r,m}\rangle$$

(3)

with normalization

$$|{V}_{r,m}^{{\prime} }\rangle \Rightarrow \frac{|{V}_{r,m}^{{\prime} }\rangle }{\sqrt{\langle {V}_{r,m}^{{\prime} }|{V}_{r,m}^{{\prime} }\rangle }}.$$

(4)

The partition function of the OFTLM is obtained as follows:

$$Z{\left(T,H\right)}_{{{\rm{OFTL}}}} = {\sum }_{m=-{M}_{{{\rm{s}}}}}^{{M}_{{{\rm{s}}}}}\left[\frac{{N}_{{{\rm{st}}}}^{(m)}-{N}_{V}}{R}{\sum }_{r=1}^{R}{\sum }_{j=0}^{{M}_{L}-1}{e}^{-\beta {\epsilon }_{j,m}^{\left(r\right)}(H)}{\left|\left\langle {V}_{r,m}^{{\prime} }|{\psi }_{j,m}^{r}\right\rangle \right|}^{2} \right. \\ \left. +{\sum }_{i=0}^{{N}_{V}-1}{e}^{-\beta {E}_{i,m}(H)}\right].$$

(5)

Similarly, in the OFTLM, the magnetization $M{\left(T,H\right)}_{{\mbox{OFTL}}}$ is obtained as follows:

$$M{\left(T,H\right)}_{{{\rm{OFTL}}}}= \frac{1}{Z{\left(T,H\right)}_{{{\rm{OFTL}}}}}{\sum }_{m=-{M}_{{{\rm{s}}}}}^{{M}_{{{\rm{s}}}}} \left[\frac{{N}_{{{\rm{st}}}}^{(m)}-{N}_{V}}{R}\right. \\ \left. \times {\sum }_{r=1}^{R}{\sum }_{j=0}^{{M}_{L}-1}{{me}}^{-\beta {\epsilon }_{j,m}^{\left(r\right)}\left(H\right)}{\left|\left\langle {V}_{r,m}^{{\prime} },|,{\psi }_{j,m}^{r}\right\rangle \right|}^{2}\right. \\ \left. +{\sum }_{i=0}^{{N}_{V}-1}{e}^{-\beta {E}_{i,m}(H)}\right],$$

(6)

Because the final terms in Eqs. (5) and (6) are exact values, they are more accurate than those obtained using the standard FTLM, particularly at low temperatures.

We performed OFTLM calculations for a cluster of 36 sites under periodic boundary conditions with $R=10$, ${N}_{V}=5$, and M_L = 160⁵⁷. Our calculations revealed that there were almost no finite-size effects on the magnetization for T/J > 0.1⁵⁷. Therefore, the analysis of the magnetization curve in this study was sufficiently accurate.