Introduction

Control of dissipationless transport is a core challenge for superconducting electronics, and it is at the heart of several applications, including both classical1 and quantum2 computation. The flow of dissipationless current relies on macroscopic quantum coherence and exploits the phase difference between spatially separated superconducting condensates. The resulting supercurrent cannot exceed a critical amplitude, Ic, above which the superconductor turns into the normal state. In analogy with the semiconducting counterpart, the superconducting diode effect refers to dissipationless current flowing in one direction (+) while the current is driven by dissipative carriers in the opposite direction (−), thereby leading to asymmetric amplitudes of the critical currents \({I}_{c}^{+}\ne | {I}_{c}^{-}|\).

The discovery and design of quantum materials and platforms suitable for non-reciprocal superconducting transport have been developed around the fundamental requirement of realizing the lack of inversion and time-reversal symmetries3,4,5,6,7,8. This condition is, for instance, realized in systems that are naturally equipped with symmetry-breaking crystalline potentials and magnetic interactions, as with noncentrosymmetric or magnetic materials3,4,9,9,10,11,12,13 and related heterostructures14. Alternatively, several implementations exploit external magnetic fields3,15,16,17,18 leading to symmetry-breaking configurations, which yield non-reciprocal superconducting transport. Hence, the current paradigm for superconducting diodes either relies on internal mechanisms19,20,21,22, or on suitably designed external sources to break time and spatial symmetry23,24,25,26.

We propose a general mechanism to achieve non-reciprocal superconducting transport that arises from the back-action of the supercurrent on a reciprocal weak link. Differently from self-field back-action mechanisms10,27, our scheme for supercurrent rectification is magnetic field-free. The idea of exploiting a back-action mechanism not linked to internal or external sources of symmetry-breaking aims at a general design principle suitable for several superconducting platforms. We demonstrate how to achieve a back-action on the supercurrent amplitude via an applied gate voltage to a superconducting weak link. This self-induced effect provides a fundamental path to rectify the supercurrent, thereby leading to a tunable and high-rectification efficiency. The back-action of the supercurrent on the effective gate voltage relies on a control resistor in series with the Josephson element. The gate voltage modifies the supercurrent, which in turn alters the effective gate voltage experienced by the weak link, thereby realizing a retroaction. Our findings set out a general paradigm for the design of all-electrical and magnetic field-free supercurrent rectifiers.

Results

Device concept

The magnitude of the dissipationless supercurrent I through a Josephson element is entangled to the superconducting phase difference ϕ across the junction via the so-called current-phase relation I(ϕ). In its simplest form, it reads \(I(\phi )={I}_{c}\sin (\phi )\), and in generic reciprocal junctions it is an odd 2π-periodic function of ϕ. From the functional form above, it follows immediately the reciprocity of the two critical currents, as depicted in the bottom left sketch of Fig. 1: \({I}_{c}^{+}=\max (I(\phi ))=|{{I}_{c}^{-}}| =| \min (I(\phi ))| ={I}_{c}\). The reciprocity can be violated in systems that concomitantly break inversion and time-reversal symmetry either intrinsically or using applied fields. The concept of a back-action supercurrent rectifier instead relies on a modulation of Ic induced by the flowing current I. For the sake of simplicity, we assume a linear modulation of the form \({I}_{c}={I}_{c}^{0}+\alpha I\), where  −1 < α < 1 represents the back-action strength, and \({I}_{c}^{0}\) is the critical current in the absence of back-action (α = 0). Other monotonic functions Ic(I) bring similar conclusions, provided that Ic and ϕ are factorized in the current-phase relation, i.e., I(ϕ) = f(I)g(ϕ). Solving the self-consistent equation \(I=({I}_{c}^{0}+\alpha I)\sin \phi\) yields \(I(\phi )={I}_{c}^{0}\frac{\sin \phi }{1-\alpha \sin \phi }\), which is a functional form with a non-defined parity, as sketched in the bottom right of Fig 1. It is straightforward to show that the above function is non-reciprocal, with \(| {I}_{c}^{\pm }| =\frac{{I}_{c}^{0}}{1\mp \alpha }\) and rectification efficiency \(\eta \equiv ({I}_{c}^{+}-| {I}_{c}^{-}| )/({I}_{c}^{+}+| {I}_{c}^{-}| )=\alpha\). Hence, in the limit of ∣α∣ ≃1 an ideal rectification can be achieved. The model so far described, though very minimal, captures the essential features of back-action: (i) parity violation of the current-phase relation, (ii) zero spontaneous supercurrent [i.e., I(0) = 0], and (iii) non-reciprocal supercurrent and tunable rectification amplitude (See Supplementary Note for a formal discussion).

Fig. 1: Principle of supercurrent rectifier by supercurrent amplitude back-action.
figure 1

Cartoon of a generic weak link with two superconducting banks (orange) separated by an element with weaker superconductivity (orange with texture). A period of the current-phase relation of the input current injected from the left lead is shown, and it is odd-in-ϕ. The supercurrent coming out from the right lead retroacts on the weak link itself, thereby generating an output supercurrent with no defined parity on ϕ. The odd parity of the input current-phase relation dictates \({I}_{c}^{+}=| {I}_{c}^{-}|\), while the back-action results in an output supercurrent without defined parity in ϕ, so that \({I}_{c}^{+}\ne | {I}_{c}^{-}|\). See the main text for a model of the back-action mechanism.

Full size image

Implementation of a back-action supercurrent rectifier

We now turn to the physical realization of the back-action mechanism. First, we introduce the circuitry that allows the operation of a generic gate tunable Josephson junction as a highly efficient supercurrent rectifier. Later, we present the sample of the experiment and characterize its performance.

Figure 2a shows the schematic of the current-biased setup. The cross represents a weak link whose critical current is measured by sweeping the current bias I till the transition to the normal state is detected by a finite voltage drop V across the weak link. Red and blue bias currents correspond to positive and negative sweep directions, respectively. A third control terminal tunes the critical current via a voltage source at \({V}_{g}^{0}\). The feedback network consists of a control resistor Rc embedded between the weak link and the ground. Thus, the bias current I lifts upward or downward the weak link potential according to its direction, resulting in a polarity-dependent gate voltage, \({V}_{g}={V}_{g}^{0}-I{R}_{c}\).

Figure 2b illustrates the superconducting rectifier principle: at a voltage bias \({V}_{g}^{0}\) for which Ic depends on the gate voltage (i.e., ∂Ic/∂Vg ≠ 0), the critical current for a positive bias current \({I}_{c}^{+}\) (red) differs in modulus from the critical current for a negative bias current \(| {I}_{c}^{-}|\) (blue), thereby resulting in \({I}_{c}^{+}\ne | {I}_{c}^{-}|\). As shown below, the strength of the non-reciprocity depends both on the magnitude of Rc and on ∂Ic/∂Vg , which we shall refer to as transconductance gm. It is worth mentioning that, in general, back-action rectifiers can be designed to operate without a voltage source on the gate, i.e., at \({V}_{g}^{0}=0\). In non-symmetric systems (\({I}_{c}({V}_{g}^{0})\ne {I}_{c}(-{V}_{g}^{0})\)), the supercurrent polarity-dependent gate voltage IRc promotes rectification at any \({V}_{g}^{0}\), making the battery on the gate unnecessary.

Fig. 2: Setup for the back-action supercurrent rectifier.
figure 2

a Circuit schematic to realize a supercurrent rectifier by back-action mechanism. The cross represents a weak link measured in a current-biased (I) setup by monitoring the voltage drop across it (V). A gate electrode at nominal voltage \({V}_{g}^{0}\) tunes the critical current of the weak link nearby. A control resistor in series, Rc, modifies \({V}_{g}^{0}\) into \({V}_{g}={V}_{g}^{0}-I{R}_{c}\), depending on the sign of the current bias I. b Effect of the circuitry presented in a on a representative critical current vs. gate voltage trace. At a certain gate voltage bias \({V}_{g}^{0}\), the positive critical current \({I}_{c}^{+}\) (red dot) at \({V}_{g}^{+}\) differs from the negative critical current \({I}_{c}^{-}\) (blue dot) at \({V}_{g}^{-}\) resulting in a finite diode effect, i.e., \({I}_{c}^{+}\ne | {I}_{c}^{-}|\). c, Scanning electron micrograph of a niobium (Nb) strip (orange) with a nanoconstriction (characteristic dimensions l ~ 80 nm and w ~ 180 nm) to implement the superconducting weak link. The gate voltage \({V}_{g}^{0}\) is applied through a side gate (light blue) located at distance g ~ 50 nm. d Experimental gate voltage dependence of the average critical current \(\langle {I}_{c}\rangle =({I}_{c}^{+}+| {I}_{c}^{-}| )/2\) recorded at T = 1 K with Rc = 2 kΩ.

Full size image

This scheme is implemented with a nanosized constriction of a superconducting stripe patterned from a niobium (Nb) thin film. Such type of weak link, called Dayem bridge, has shown a reduction of the critical currents up to full suppression under the action of a strong gating effect28,29,30. Next to other metallic platforms, such as superconducting nanowires31,32,33, superconductor-normal metal-superconductor Josephson junctions34,35, and hybrid semiconductor-superconductor weak links36,37,38,39,40,41, Dayem bridges typically display larger critical currents, often reaching fractions of mA, which translate into higher transconductance gm and, ultimately, in improved rectification efficiencies. To date, the proposed mechanisms to account for the phenomenology of gate-controlled supercurrent in metals can be grouped into two main categories: i) the supercurrent is suppressed by the nonequilibrium distribution of electronic or phononic excitations which can be induced either by field emission or by leakage currents 32,33,42,43, ii) the supercurrent suppression arises from the impact of the surface electrostatic potential on the superconducting order parameter44,45,46,47,48,49. In this regard, since the back-action mechanism discussed here requires a direct coupling of the gating to the amplitude of the supercurrent, it is valid independently of the mechanism guiding the gating of the supercurrent.

A micrograph of a typical supercurrent rectifier sample is shown in Fig. 2c. A constant-thickness strip of niobium (orange) is interrupted by a constriction of length l ~ 80 nm and width w ~ 180 nm. A side electrode (cyan colored) is placed at a distance g ~ 50 nm. See ref. 50 and Methods for basic electrical characterizations and further fabrication details. Figure 2d displays the modulation of the average critical current \(\langle {I}_{c}\rangle =({I}_{c}^{+}+| {I}_{c}^{-}| )/2\) as a function of the gate bias \({V}_{g}^{0}\) at T ≃ 1 K. As in former experiments, a plateau is followed by a bipolar decay of the critical current, which is roughly linear in gate voltage \({V}_{g}^{0}\) up to its full suppression at \(| {V}_{g}^{0}| \simeq 40\) V. The critical current modulation occurs along with a tiny gate-delivered leakage current of a few pA at the onset of the damp of Ic up to a few nA at full suppression (see Supplementary Fig. 1).

Figure 3a–e demonstrates that non-reciprocity of the critical currents emerges for finite gate voltages via a series resistor and can be easily tuned in amplitude. We show the switching currents while sweeping the biasing current from zero to positive values (\({I}_{c}^{+}\), blue dots) or from zero to negative values (\(| {I}_{c}^{-}|\), orange dots) as a function of the nominal gate voltage \({V}_{g}^{0}\). The control resistor Rc ranges from 2 kΩ to 22 kΩ. As Rc increases, the data sets of positive and negative critical currents move apart. The non-reciprocal component of the critical current, \({{\Delta }}{I}_{c}={I}_{c}^{+}-| {I}_{c}^{-}|\), is plotted in Fig. 3f–j for the same values of Rc. The curves are odd-in-\({V}_{g}^{0}\) but nonmonotonic, with peaks at ≃±32 V that increase in magnitude with Rc. The observed shift and skewness of \({I}_{c}^{\pm }({V}_{g}^{0})\) in Fig. 3a–e results from the offset in the gate voltage due to the current flowing through the resistor. Since the gate voltage for complete Ic suppression does not depend, at first order, on Rc, yielding an increase or decrease of the slope \(\partial {I}_{c}/\partial {V}_{g}^{0}\), depending on the polarity of both the critical current and the gate voltage.

Fig. 3: Back-action supercurrent rectifier characterization.
figure 3

a–e Gate voltage dependence of the switching current for positive \({I}_{c}^{+}\) (blue dots) and negative \(| {I}_{c}^{-}|\)(orange dots) bias current for different values of the control resistor Rc. The diode effect results in \({I}_{c}^{+}\ne | {I}_{c}^{-}|\) and is enhanced by the increase of Rc from 2 kΩ to 22 kΩ. f–j, \({{\Delta }}{I}_{c}={I}_{c}^{+}-| {I}_{c}^{-}|\) as a function of \({V}_{g}^{0}\) obtained from the data in a–e. k Quasi-symmetric behavior the critical currents obtained by normalizing the gate voltage with the back-action contribution, \({V}_{g,c}^{\pm }={V}_{g}^{0}-{I}_{c}^{\pm }{R}_{c}\) for Rc = 12 kΩ. Similar plots for all the configurations (variation of Rc or temperature) are in Supplementary Fig. 2. l, Transconductance \({g}_{m}=\partial \langle {I}_{c}\rangle /\partial {V}_{g}^{0}\) as a function of gate voltage \({V}_{g}^{0}\) for different bath temperatures T. Color code is given in the inset where the maximum transconductance \({g}_{m}^{max}\) versus temperature T is plotted. m Rectification efficiency η evaluated at its maximum value (ηmax) as a function of \(-{R}_{c}{g}_{m}^{max}\). Black dots are measured at T = 1 K by varying Rc, while the color dots are obtained via tuning gm by temperature. Data converge to null rectification, thereby validating the back-action at the origin of the supercurrent rectifier. The red dashed line is a reference to the basic model of linear dependence of the critical current on the supercurrent amplitude, which yields −Rcgm = d〈Ic〉/dI = α.

Full size image

To further confirm the role of the control resistor in driving the supercurrent non-reciprocity, we display the critical currents with respect to the gate voltage normalized by the back-action contribution in Fig. 3k. By defining \({V}_{g,c}^{\pm }={V}_{g}^{0}-{I}_{c}^{\pm }{R}_{c}\), positive and negative critical currents become identical within the experimental accuracy (see also Supplementary Fig. 2).

As previously outlined, the transconductance gm plays a key role in the performance. Figure 3l shows the evolution of \({g}_{m}=\partial \langle {I}_{c}\rangle /\partial {V}_{g}^{0}\) as a function of the gate voltage for Rc = 2 kΩ and different bath temperatures (see also Supplementary Fig. 3). gm exhibits a peak at \(| {V}_{g}^{0}| \simeq 32\) V and can be tuned by the temperature (see the inset for a maximum of gm at different temperatures). Its decrease at high T can be ascribed to temperature-induced decay of the critical current50.

Finally, it may be convenient to estimate the strength of the back-action. For the toy model developed in the first section, the parameter α weights the dependence of the critical current on the supercurrent and the rectification. The analogous quantity in our experiment is—Rc gm, a dimensionless parameter that quantifies dIc/dI. Figure 3m shows the rectification efficiency evaluated at its maximum ηmax as a function of \(-{R}_{c}{g}_{m}^{max}\). A linear trend is observed, as in the model where η = α (see Supplementary Fig. 4). Black dots are obtained at 1 K by changing the control resistor Rc, whereas the data next to the axes origin are measured by tuning the transconductance gm by changing the bath temperature (color code as in Fig. 3l). Remarkably, our device reaches a quasi-ideal rectification efficiency, ηmax ≃ 88% for Rc = 22 kΩ at T = 1 K.

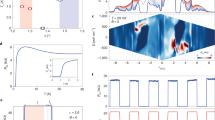
We now demonstrate possible applications of our device as a half-wave rectifier with tunable polarity. Figure 4a presents a color plot of I–V characteristics as a function of the gate voltage \({V}_{g}^{0}\) for a control resistor Rc = 22 kΩ. The yellow vertical lines define three working regimes depending on the gate voltage: no sizable rectification, marked by a conventional (reciprocal) Josephson junction symbol; and two non-reciprocal regimes with dominant negative or positive supercurrent, corresponding to the left and right region of the plot respectively. Therefore, the system operates as a quasi-ideal supercurrent rectifier whose polarity can be changed by simply inverting the sign of the gate voltage.

Fig. 4: Tunability of polarity and half-wave rectification.
figure 4

a Contour plot of the voltage drop V versus biasing current I and gate voltage \({V}_{g}^{0}\) measured at 1 K for Rc = 22 kΩ. Yellow lines mark three regions: the central one, where reciprocal transport takes place, and the device behaves as a Josephson reciprocal element (cross symbol), and two external areas beyond the lines, where the polarity-dependent rectification behavior is achieved. At \(| {V}_{g}^{0}| \simeq\) 32 V, very large rectification efficiency (η ≃ 88 %) is achieved. b, Half-wave rectifier of the input AC current (upper panel). At \({V}_{g}^{0}=33\) V and for Rc = 12 kΩ, the output voltage follows the current only in the negative semi-period (i.e., when the weak link is dissipative, white bands); on the contrary, V = 0 in the positive semi-period of I when the Dayem bridge is superconducting (grey bands). White and grey bands slightly differ in width as the rectification is not ideal. The AC biasing current has an amplitude of 0.4 mA and frequency of 1 Hz.

Full size image

In the right quadrant of Fig. 4a, the weak link is predominantly superconducting with a positive bias current but dissipative with a negative bias current. This opens the possibility of exploiting the device as a half-wave rectifier for AC currents. In principle, this idea holds for supercurrent diodes with any rectification efficiency, till the applied current amplitude lies between \(| {I}_{c}^{-}|\) and \({I}_{c}^{+}\). However, having a quasi-ideal rectification efficiency, like in our case, widens the range of amplitudes of the injected AC current to be rectified, which greatly relaxes the limitations in applications. Figure 4b shows the half-wave rectified voltage output V(t) (black trace) and the applied current I(t) of amplitude 0.4 mA and frequency 1 Hz (red sinusoidal signal) measured at \({V}_{g}^{0}=33\) V for Rc = 12 kΩ. A zero-voltage output occurs for I(t) > 0 (superconducting state, gray bands), while the system follows the applied current signal for I(t) < 0 (dissipative state, white bands).

To show the generality of our work, we have realized the same scheme on a different superconducting platform: an epilayer InAs-based Josephson junction51. Here, the gate-controlled supercurrent arises from the charge depletion in the semiconducting weak link. The device is presented in Supplementary Fig. 5, and exhibits rectification up to 70% with an improvement in the power consumption arising from the lower critical current of the Josephson device. More importantly, the system operates without any additional voltage source in the gate electrode due to the asymmetric transconductance with \({g}_{m}({V}_{g}^{0}=0)\ne 0\).

Now, we discuss the technological aspects of the back-action supercurrent rectifiers and their potential impact in the field. Possible routes to increase the transconductance gm and thus the rectification efficiency comprehend the decrease of the gate voltage required for complete supercurrent suppression, the increase of \({I}_{c}({V}_{g}^{0}=0)\), and the modification on the profile of Ic vs \({V}_{g}^{0}\). Geometrical designs and material engineering can both be leveraged. Increasing \({I}_{c}({V}_{g}^{0}=0)\) can be accomplished in wider Dayem bridges or semiconductor stacks specifically conceived. The development of dedicated Ic vs \({V}_{g}^{0}\) profiles or the reduction of the gate voltage for supercurrent suppression looks more challenging in metallic systems. The reciprocal pancake-like critical current behavior has resulted in a common feature regardless of the material or sample geometry, and complete suppression, which typically requires tens of volts52. The latter is also a drawback for implementing gate-controlled superconducting logic circuits 53 that rely on the transistor output voltage to drive the gate of the following element. By contrast, a diode logic family based on back-action supercurrent transistors might lift such constraints by operating at lower gate voltage in the non-reciprocal regime.

Non-reciprocal dissipationless transport has been successfully used as an efficient tool to pinpoint breaking symmetries in novel materials. Our back-action schemes can be exploited to enhance the rectification efficiency that normally exhibits low values for a better understanding of the underlying mechanism or to explore polarity-dependent phenomena. However, the field of superconducting diodes has rapidly progressed in developing platforms aimed at enhancing efficiency and applications for quantum technology54. Currently, scalability and integration, major limiting factors, have been addressed in vortex-based55 and ferromagnetic56 diodes shunted by dissipative elements. In our approach, the resistor can be placed at any stage of the cryostat, effectively minimizing the heat load. In this context, the superior performance and magnetic-free back-action rectifier offer a significant advance in the field compatible with extremely field-sensitive qubits or in noisy magnetic environments30.

Conclusions

In summary, we have proposed and implemented a supercurrent back-action rectifier. To date, most efforts devoted to lifting the odd parity in the current-phase relation in superconducting weak links rely on magnetic exchange interactions 57,58 and magnetic fields in combination with sizable spin-orbit coupling39,59,60,61, or nonequilibrium conditions62. Instead, the original class of devices presented here counts on the self-induced effect of the supercurrent amplitude to break the parity condition. Though intrinsically reciprocal, supercurrent transport across the metallic weak link is made non-reciprocal by the retroaction of the bias current on the weak link itself. This results in tuning the critical current by a gate voltage-sensitive to the current polarity. The rectification efficiency is easily adjustable and can be boosted nearly to one. Such reduction of fabrication complexity, combined with the absence of magnetic fields, represents a clear asset for scalability and integration with other superconducting devices, making our platform attractive for next-generation superconducting electronics.

The generality of the scheme is also demonstrated in a hybrid semiconducting-superconducting field-effect transistor. The substantial decrease in power consumption and the absence of a gate voltage source are real assets for Josephson-based back-action supercurrent rectifiers as a building block in future non-reciprocal superconducting technologies.

We expect similar devices to be implemented on all the superconducting platforms adjustable by other control knobs, such as phonon-controlled Josephson junctions63,64, flux-retroacted superconducting quantum interference devices65, or quasiparticle injection-driven superconducting transistors66,67,68,69,70. Finally, other functionalities are expected beyond the linear back-action approximation used in this work for rectification improvements or multi-valued circuits.

Methods

Sample fabrication

Nb strips and constrictions are patterned by e-beam lithography on AR-P 679.04 (PMMA) resist. PMMA residuals are removed by O2-plasma etching after developing. Nb thin films of 25 nm thickness were deposited by sputtering at a base pressure of 2 × 10−8 Torr in a 4 mTorr Ar (6N purity) atmosphere and liftoff by AR-P 600.71 remover. Details of the fabrication of InAs-based Josephson junction can be found elsewhere51.

Transport measurements

Transport measurements were carried out in filtered (two-stage RC and π filters) cryogen-free 3He-4He dilution refrigerators by a standard 4-wire technique. DC current-voltage characteristics were measured by sweeping a low-noise current bias positively and negatively, and by measuring the voltage drop occurring across the weak links with a room-temperature low-noise pre-amplifier. The switching currents and error bars were obtained from 10 to 20 reiterations of the IV curves, and their accuracy is mostly given by the current step set to \({{\Delta }}I < 0.002{I}_{c}({V}_{g}^{0}=0)\), where Ic is the switching current of the Nb nanobridge. Joule heating in the system is minimized by automatically switching the current off once the device turns into the normal state. A delay between sweeps was optimized to keep the stability of the fridge temperature lower than 50 mK. Furthermore, no changes in the switching currents (up to the accuracy given by the standard deviation) were observed in different cooling cycles, by changing the order of the sweeps, or by adding an extra delay in the acquisition protocol, thereby concluding that hysteretic behavior or local heating is negligible. The gate-nanobridge current Ig was acquired by using a low-noise voltage source and a 10−11 A/V-gain low-noise current amplifier in a two-wire configuration.