Introduction

Extensive research has focused on the detection of spin currents facilitated by the inverse spin Hall effect (ISHE) for the spin-charge conversion1,2,3,4,5,6. The compensated magnetism of antiferromagnets supports only spin-neutral currents, making the generation and detection of spin currents challenging7,8,9. The realization of the ISHE is of significant importance for the detection of spin currents. However, the microscopic physical mechanisms of ISHE are still unclear, which greatly impedes further understanding of the physical origins of ISHE.

ISHE is intrinsically linked to spin–orbit coupling (SOC), and investigating SOC is instrumental for a deeper understanding of ISHE. By modulating the Berry curvature, a sign inversion of the spin Hall conductivity (SHC) can be induced, see Supplementary Note 1. Vardeny et al. discovered the ISHE in organic semiconductors with tunable SOC1. SOC manipulates electron spins without an external magnetic field, crucial for advancements in spintronics and the spin Hall effect (SHE)10. Systems with microscopic electric fields exhibit bulk inversion asymmetry and structural inversion asymmetry (SIA), leading to Dresselhaus and Rashba interactions. Crystalline materials leveraging Rashba11 and Dresselhaus12 SOC generate momentum-dependent spin–orbit fields, disrupting original spin state degeneracy and creating complex spin configurations.

Rashba SOC, with its linear wave vector k, produces concentric circular Fermi surfaces and distinct chiral spin textures, as shown in Supplementary Note 2. Introducing a nonlinear Rashba term generates out-of-plane spin texture13,14,15,16,17. The spin texture modulates zero-field spin–orbit torque in vertically magnetized systems18, enabling the exploration of transport phenomena like intrinsic SHE19,20,21, spin supercurrent in superconductors22, anomalous Hall effect23, spin-to-charge conversion, and nonlinear transport effects24. The substantial Rashba effect serves as an effective remedy for enhancing the efficiency of spin-to-charge current conversion, which is imperative for the design of high-conversion efficiency spintronic devices that do not require the influence of an external magnetic field. The rare Rashba effect observed in the 3D bulk system25 will significantly facilitate the design and application of non-volatile memory components and logic computation.

Here, we will unveil the substantial Rashba spin-splitting hidden within the antiferromagnetic (AFM) bulk structure of the intrinsic magnetic topological insulator MnBi2Te4 and its physical correlation with the ISHE. Firstly, we conduct a computational assessment of the substantial Rashba splitting, polarization, and structural stability of the MnBi2Te4 with broken \({{{\mathcal{I}}}}\)-symmetry. In addition, by transforming the type of spin-splitting, we will significantly enhance the SHC and induce the ISHE. Concurrently, we further explore the relationship between the ISHE phenomenon and the spin distribution across the energy bands. Furthermore, by constructing an effective model, we will provide a rational explanation for the mechanism of Rashba spin-splitting in MnBi2Te4, emphasizing the robustness of the system’s topological properties in response to variations in spin-splitting.

Results and discussion

Physical depiction of ISHE

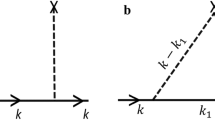
We first propose a corresponding physical depiction for how to achieve the ISHE in Supplementary Note 1. As shown in Fig. 1, the observed SHC reversal can be attributed to changes in spin-splitting and spin distribution within the energy band. Considering the charge current \({j}_{C}^{z}\) in the out-of-plane z direction, it generates spin currents \({j}_{x}^{sy}\) along the  + x direction and \({j}_{y}^{sx}\) along the  − y direction in the xz and yz planes, respectively. The MnBi2Te4 system with broken \({{{\mathcal{I}}}}\) symmetry is used to achieve ISHE, resulting in non-zero SHC values such as \({\sigma }_{xz}^{y}\) and \({\sigma }_{yz}^{x}\) in these planes. In Rashba splitting, \({\sigma }_{xz}^{y} < 0\) and \({\sigma }_{yz}^{x} > 0\), whereas in Lifshitz splitting, the pattern reverses. In contrast to Rashba splitting, which has only one valence band peak, Lifshitz splitting, arising from the phenomenon of Lifshitz transition, exhibits two peak values in both valence bands26. The reversal in the SHC sign is closely tied to the transition of bulk energy bands from Rashba-type splitting to Lifshitz-type splitting.

Fig. 1: The physical correlation between spin Hall conductivity (SHC), spin-splitting types, and spin distribution.
figure 1

a Schematic diagram illustrating the relationship between electron spin orientation, spin current, and charge current in SHC devices. b SHC signals as a function of the type of spin-splitting (Rashba and Lifshitz) and spin distribution in the band structure. The \({j}_{C}^{z}\) represents the charge current in the z direction. And \({j}_{x}^{sy}\) and \({j}_{y}^{sx}\) denote the spin currents along the x and y orientations, respectively, where sy and sx indicate the spin directions. In the SHC \({\sigma }_{\beta \gamma }^{\alpha }\), α, β, and γ correspond to the directions of spin, spin current, and charge current, which can be arranged in any combination of x, y, and z.

Full size image

In addition, the evolution of spin distributions during this transition is further explored. For example, along the K-Γ-K2 path, the spin orientations of the two valence bands near the Fermi level shift from a simple  < ↑↓↑↓ > in Rashba-type splitting to a more intricate  < ↑↑↓↑↓↓ > in Lifshitz-type splitting. This change in spin distribution may be due to external factors like pressure, which compresses the bulk energy band and results in two distinct energy band peaks in a Lifshitz-type splitting. As the second-highest occupied valence band moves upward, the spin orientation changes regularly, subsequently influencing the SHC. We establish a direct link between observations of spin currents and the nature of energy band spin-splitting. Many studies have detailed methods for detecting spin currents2,3,7,8,9,27,28,29,30,31,32,33,34,35, and our approach of linking ISHE with spin distribution will aid in this detection.

Experimentally, the direction of the spin current can be predicted based on the valence band features (Rashba or Lifshitz splitting) observed near the Fermi level through angle-resolved photoemission spectroscopy (ARPES), providing crucial insights into the challenging observation of SHC in AFM systems. The occurrence of Lifshitz transitions can be confirmed experimentally by observing changes in Fermi surface features under temperature control36,37,38, chemical doping or substitution39,40, or applied pressure41,42 through ARPES. For example, Zhang et al. observed a Lifshitz transition in the topological insulator ZrTe5 through ARPES, where the Fermi surface at the Γ point evolved from a hole pocket to an electron pocket under temperature variation. Here, we focus on the R-MBT system with inversion symmetry breaking to study the SHC properties during the transition from Rashba to Lifshitz spin-splitting. It is worth noting that, although early studies based on group theory have proposed such inversion symmetry-breaking structures for MnBi2Te443, further experimental investigations (e.g., high-resolution transmission electron microscopy (TEM) or local scanning tunneling microscopy (STM)) are still needed to reveal the potential Te sublattice displacement structure.

Structure and symmetry

The typical MnBi2Te4 configuration consists of a principal van der Waals hexagonal phase layered structure within the \({D}_{3d}^{5}\) (No. 166) space group44. In nonmagnetic ordering, MnBi2Te4 exhibits mirror symmetry Mx, three-fold rotation symmetry C3z, \({{{\mathcal{I}}}}\), and time-reversal symmetry \({{{\mathcal{T}}}}\). The AFM-z ordering disrupts the Mx and \({{{\mathcal{T}}}}\) symmetries but is preserved by the combined symmetry \(S={{{\mathcal{T}}}}{\tau }_{1/2}\), where τ1/2 denotes half-lattice translational symmetry. As shown in Fig. 2a, the MnBi2Te4 SL connects two Bi-Te octahedral layers, Layer1 and Layer2, with the Mn atomic layer serving as the inversion center, maintaining \({{{\mathcal{I}}}}\) symmetry. Introducing appropriate lattice shifts to the Te atomic layer at the octahedral layer edges results in the violation of \({{{\mathcal{I}}}}\) symmetry, transforming MnBi2Te4 from the \(R\bar{3}m\) phase to the P3m1 (C3v) phase (referred to as R-MBT), as shown in Fig. 2b. R-MBT structure was also achieved in a previous study by altering the layer stacking pattern of MnBi2Te443. The correspondence between the representations of D3d and C3v can be expressed as D3d → C3v: A1i → A1, A2i → A2, Ei → E (i = g, u)45, outlining the symmetry-breaking process driven by interlayer displacement.

Fig. 2: Crystal structure, band structure, and the first Brillouin zone.
figure 2

MnBi2Te4 with a \(R\bar{3}m\) space group and b P3m1 space group. c Phonon spectrum and projected energy band structure, containing an inset image of MnBi2Te4 with the P3m1 space group (where blue and red represent Bi-p and Te-p orbital contributions, respectively). d First Brillouin zone with the projections of (001) and (110) planes.

Full size image

Polarization feature and stability

In R-MBT, polarization is typically induced by the SIA. The polarization in AFM-ordered R-MBT is comparable to materials like BaTiO346 and HfO2 in the Pca21 and Pmn21 phases47, as detailed in Supplementary Note 3. Like the pyroelectric material CaBaCo4O748,49,50, the polarization in R-MBT can be tuned by controlling magnetic order. Phonon spectrum calculations confirm the stability of R-MBT, as shown in Fig. 2c, alongside the projection of bulk bands from the A-type AFM MnBi2Te4. Near the Γ point, the energy band inversion indicates topological nontriviality, with Rashba spin-splitting as a prominent feature.

Rashba spin-splitting

The spin-splitting phenomenon in this stable system with polarization is quite pronounced. In R-MBT,the conduction and valence bands near the Fermi level exhibit significant Rashba splitting, with \({\alpha }_{R}^{\,{\mbox{VBM}}\,}\) = 4.631 eVÅ and \({\alpha }_{R}^{\,{\mbox{CBM}}\,}\) = 4 eVÅ, surpassing BiTeI51 and comparable to systems like PtBi2, KSnSbxBi1−x, and others52,53,54, as detailed in Supplementary Note 4. Figure 3a, b show Rashba and Lifshitz band spin-splittings, which can transition by altering Rashba strength. Fermi surfaces in Fig. 3c, d also confirm Rashba splitting. The robust Rashba splitting is evident from the C3z rotational symmetry and alternating chirality in the Fermi morphology and spin texture at different energy cross-sections, as shown in Fig. 3e–g and Supplementary Fig. S2. It is noteworthy that when the spin-splitting changes from Rashba to Lifshitz, the chirality of the highest pair of valence bands transitions from the opposite (see Fig. 3e) to the same (see Supplementary Fig. S3 at the energy cut EF − 0.175). The physical essence of this change in chirality is induced by the redistribution of spin caused by the deformation of the compressed band structure, see Supplementary Note 5. Despite the bulk bandgap opening in R-MBT due to layer dislocations, a topological surface state ensures an isotropic helical spin texture at the Fermi level, as shown in Fig. 3f. At the (EF + 0.1) and (EF − 0.12) eV cross-sections, the nested bands exhibit spin textures with opposite chirality, reaffirming the presence of Rashba spin-splitting. These computational findings are instrumental in guiding experimental observations and are likely to yield comparable ARPES results. We attribute the physical origin of the Rashba spin-splitting to the intrinsic electric field induced by the electrostatic potential differences between atoms.

Fig. 3: Schematic diagrams of two spin-splitting types and evidence of Rashba splitting.
figure 3

a Rashba and b Lifshitz band splits. Momentum \({k}_{\,{\mbox{CBM, VBM}}\,}^{\Gamma -k,\Gamma -{k}_{2}}\), kf, kL and energy \({E}_{\,{\mbox{CBM, VBM}}\,}^{\Gamma -k,\Gamma -{k}_{2}}\), Ebc dependent on specific paths for conduction band minimum (CBM) and valence band maximum (VBM). Fermi surface of the Rashba splitting band on c valence band (81 and 82) d conduction band (83 and 84). The color bar reflects the Fermi velocity values, with red indicating the maximum and blue indicating the minimum. Fermi surface and Spin textures under different energy cross-sections, which are e (EF − 0.12), f (EF), and g (EF + 0.1) eV (each cross section is marked with a dashed line in 3a).

Full size image

Effective model construction

To understand how structural \({{{\mathcal{I}}}}\) breaking triggers Rashba band spin-splitting in MnBi2Te4, we developed tight-binding (TB) and k ⋅ p models to reproduce the energy band profiles from density functional theory (DFT) calculations, as detailed in Supplementary Notes 6, 7. The constructed TB model primarily relies on nearest-neighbor hopping parameters tl (l = 1–4) and next-nearest-neighbor parameters r1, r3. The imaginary terms t1 and r1 play a major role in achieving spin splitting, while t2, t3, and r3 significantly influence the degree of splitting, as detailed in Supplementary Note 7.

Based on system symmetry, the k ⋅ p model for the R-MBT system has been meticulously constructed. The magnetic space group of the A-type AFM configuration is Pc3c1 (MSG = 158.60). The system’s 12 symmetry operations include six under time reversal, encompassing the identity matrix E, out-of-plane triple rotational symmetries \({C}_{3z}^{+}\) and \({C}_{3z}^{-}\), and in-plane mirror symmetries M100, M010, and M110. The energy bands near the Fermi level unfold at the Γ point as a double Γ4. The conduction and valence band Hamiltonians are derived in Supplementary equation S12 under the Γ4 unitary operation \({C}_{3z}^{+}\), M100, and the anti-unitary transformation \(E| 00\frac{1}{2}^{\prime}\). These k ⋅ p model Hamiltonians convert efficiently into a Pauli matrix representation, as shown in Eq. (1), with Γi,j = σi ⊗ σj (i, j = 0, 1, 2, 3), where σi and σj are Pauli matrices. Furthermore, based on Supplementary equation S12, the Hamiltonian of the R-MBT system is primarily modulated by the constant terms C0,i (i = 1–4), first-order terms C1,j(j = 2, 3, 4), and second-order terms C2,k(k = 6, 7, 8). The imaginary coefficient C2,6 is crucial for inducing Rashba splitting, which will become zero in Lifshitz-type splitting; however, Lifshitz-type splitting will increase the coefficient C2,7 associated with the term \({k}_{x}^{2}+{k}_{y}^{2}\). Fine-tuning specific parameters aligns the energy band structure with DFT calculations. For Rashba-type splitting, parameters are C0,1 = 0.0578, C0,2 = 0.0252, C0,3 = − 0.0045, C1,2 = 0.1, C1,3 = 0.0248, C2,6 = 0.004, C2,8 = 0.0105, with others set to zero. For Lifshitz-type splitting, parameters are adjusted to C0,2 = 0, C1,2 = − 0.01, C1,3 = 0.05, C1,4 = − 0.045, C2,7 = − 0.06, C2,8 = 0.03. The energy band results from TB and k ⋅ p models are compared with DFT calculations as presented in Supplementary Fig. S5.

$${{{\mathcal{H}}}}(k) = \,({C}_{0,3}+{C}_{2,3}{k}_{z}^{2}+{C}_{2,8}({k}_{x}^{2}+{k}_{y}^{2})){\Gamma }_{0,0}\\ +{C}_{1,4}{k}_{y}{\Gamma }_{0,1}+{C}_{1,4}{k}_{x}{\Gamma }_{0,3}\\ + ({C}_{0,2}+{C}_{2,2}{k}_{z}^{2}+{C}_{2,7}({k}_{x}^{2}+{k}_{y}^{2})){\Gamma }_{1,0}\\ + {C}_{1,3}{k}_{y}{\Gamma }_{1,1}+{C}_{1,3}{k}_{x}{\Gamma }_{1,3}+{C}_{1,1}{k}_{z}{\Gamma }_{2,0}\\ +({C}_{2,4}{k}_{y}{k}_{z}+2{C}_{2,6}{k}_{x}{k}_{y}){\Gamma }_{2,1}\\ +({C}_{2,4}{k}_{x}{k}_{z}-{C}_{2,6}({k}_{x}^{2}-{k}_{y}^{2})){\Gamma }_{2,3}\\ +({C}_{0,1}+{C}_{2,1}{k}_{z}^{2}+{C}_{2,5}({k}_{x}^{2}+{k}_{y}^{2})){\Gamma }_{3,0}\\ +{C}_{1,2}{k}_{y}{\Gamma }_{3,1}+{C}_{1,2}{k}_{x}{\Gamma }_{3,3}$$
(1)

Topological properties and SHC

The Rashba SOC exerts a profound influence on the topological properties and the quantum spin Hall effect of topological insulators, with its potential to facilitate dissipationless spin currents in quantum computing being particularly remarkable. To further investigate the topological properties and SHC of the R-MBT system, the (110) planes of both types of spin-splitting have gapless topological surface states protected by the S symmetry (see Fig. 4). Both types of spin-splitting exhibit topological properties with Z2 = 1. Unlike Rashba splitting, Lifshitz splitting has identical left and right terminal surface states on the (110)plane. In the (001) plane, surface states clearly demonstrate the differences between the two types of spin-splitting in the valence band, with a significant surface bandgap in one terminal state. Transforming Rashba-type splitting into Lifshitz-type splitting results in a larger surface bandgap in the (001) plane.

Fig. 4: Topological surface states and SHC components of the two splitting types.
figure 4

Surface states and SHC of a–e Rashba-type and f–j Lifshitz-type energy band splits. From left to right, the left and right terminal surface states of the (110) and (001) planes, respectively, and the SHC in each direction.

Full size image

The crystalline structure of R-MBT belongs to the \(3m1^{\prime}\) magnetic point group, with three sets of non-zero SHC tensor elements, \({\sigma }_{\beta \gamma }^{\alpha }\), where α, β, and γ can be x, y, or z. These elements describe the spin current’s polarization along α and the spin current in β induced by an electric field in γ. The SHC of R-MBT reveals relationships like \({\sigma }_{yz}^{x}\)=\(-{\sigma }_{xz}^{y}\), \({\sigma }_{zx}^{y}\)=\(-{\sigma }_{zy}^{x}\), and \({\sigma }_{xy}^{z}\)=\(-{\sigma }_{yx}^{z}\), shown in Fig. 4e, j. At the Fermi level, the highest SHC values for Rashba-type and Lifshitz-type spin-splittings are \({\sigma }_{zx}^{y}\)=\(-{\sigma }_{zy}^{x}\)=70 (ℏ Se−1cm−1) and 208 (ℏ Se−1cm−1), respectively. While the SHC of R-MBT is lower than that of Pt (2280 (ℏ Se−1cm−1), it is closer to α-Ta (−142) and β-Ta (−389)55. The intrinsic SHC near the Fermi level of the topological insulator (Bi/Sb)2(Te/Se)3 ranges between 50 and 100 (ℏ Se−1cm−1), with spin torque levels comparable to those of surface interaction56. Transitioning from Rashba-type to Lifshitz-type spin-splitting reverses the signs of SHCs \({\sigma }_{yz}^{x}\) and \({\sigma }_{xz}^{y}\). We propose an ISHE with SHC sign reversal, explained in Fig. 1. Meanwhile, the behavior of the sum of Berry curvature, which reverses orientation after the transition of the splitting type, is shown in Supplementary Fig. S7.

Conclusion

We propose a theoretical ISHE phenomenon dependent on spin distribution and spin-splitting type, identifying MnBi2Te4 as an ideal material to observe this effect. Firstly, we attribute the SHC sign-reversal to changes in spin distribution, induced by the competition between opposite spin components within the same energy band under an external field. Then, it reveals significant Rashba spin-splittings of up to 4 eVÅ and 4.61 eVÅ in the conduction and valence bands of R-MBT, respectively. Next, we identified an electric polarization of up to 0.51 C per m2 in R-MBT with both in-plane and out-of-plane linear AFM ordering, and up to 0.37 C per m2 with linear ferromagnetic ordering. This polarization remains consistent regardless of magnetic ordering orientation. The phonon dispersion spectrum confirms the stability of the R-MBT system. Additionally, Rashba splitting is substantiated through analysis of Fermi surface morphology and spin textures across various energy cross-sections. Moreover, symmetry analyses and calculations allowed us to establish TB and k ⋅ p models for the R-MBT system. Our investigations indicate that the system retains non-trivial topological properties as Rashba splitting transforms into Lifshitz splitting, manifesting gapless topological surface states in specific planes safeguarded by S symmetry. Finally, the conversion of band splitting type significantly broadens the SHC platform, profoundly influencing the system’s transport behavior. Importantly, the non-zero SHCs from in-plane spin currents \({j}_{x}^{sy}\) and \({j}_{y}^{sx}\), induced by the out-of-plane charge current \({j}_{C}^{z}\), exhibit an inverse relationship with changes in spin-splitting type.

Methods

First-principles calculations were done using Vienna ab initio simulation package57,58, with projector augmented-wave59 and a Perdew–Burke–Ernzerh-type generalized gradient approximation function60. The truncation energy of the plane wave basis is set to 350 eV. The SOC is taken into account in all our calculations. the Monkhorst–Pack k-point grid centered on Γ is set to 9 × 9 × 3. The software61,62,63 used for post-processing calculations is detailed in Supplementary Methods.

Supplementary information. The definitions of spin Hall conductivity, origins of Rashba SOC, calculation details, and analyses of polarization, Rashba splitting, berry curvature, and spin distribution, as well as the construction of the TB and k ⋅ p models.