Perturbation-induced nonreciprocal transmission in nonlinear parity-time-symmetric silicon micromechanical resonators

Abstract

Parity-time (PT) symmetric systems featuring balanced gain and loss, when biased in a broken phase, can produce nonreciprocal transmission in the presence of nonlinear gain. However, the weak coupling in the broken phase leads to high insertion loss during transmission. Here, we demonstrate an approach to achieve nonreciprocal transmission in PT-symmetric silicon micromechanical resonators operating in an exact phase. In our approach, PT-symmetry breaking due to external perturbations to the loss resonator results in exponential growth and decay modes. The presence of the nonlinear gain suppresses the exponential growth mode. As a result, the nonreciprocal transmission is achieved while keeping the system at the strong coupling region. The coupling strength, perturbation, and gain nonlinearity of the system can be electrically tuned. The system shows 8 dB of nonreciprocal transmission with the insertion loss less than 5 dB and the isolation more than 13 dB. Our approach demonstrates the ability to manipulate nonreciprocal transmission and opens a door towards the development of electronic isolators and circulators on silicon substrate.

Introduction

PT-symmetric systems^1,2 featuring balanced gain and loss manifests as two distinguished phases depending upon their coupling strength, i.e., an exact phase with real eigenvalues and a broken phase with complex-conjugate eigenvalues. They have been demonstrated on various physical platforms, including optic and photonic^3,4, electronic⁵ and microwave⁶, acoustic^7,8, as well as mechanical⁹ and micromechanical¹⁰ platforms. On the basis of the platforms, the PT-symmetric systems have initiated a number of exotic effects and applications^11,12. In particular, they promise applications for the nonreciprocal transmission of optical^13,14, acoustic¹⁵, and electrical signals^16,17,18,19. The nonreciprocal transmission can be intuitively understood in the presence of nonlinear gain. The response of gain and loss sides depends on the amplitude of the signal propagating through them. In general, more powerful signals undergo more severe attenuation owing to the nonlinear gain. Signals incident from the gain side experience the nonlinear gain region with greater amplitude, undergoing more attenuation, while signals entering from the loss side enter the nonlinear region with lesser amplitude, and suffer less attenuation. From this, the PT-symmetric systems are usually biased at the broken phase^{13,14,15,16,17,18,19,20}, where they yield one eigenstate with exponential growth and the other with exponential decay. As a result, the exponential growth is suppressed, leading to the non-reciprocal transmission. However, the coupling between the gain and loss side is weak when the PT-symmetric systems are biased in the broken phase, resulting in high insertion loss during transmission.

Silicon micromechanical resonators possess excellent features like small size, high quality factor, low power consumption, low cost batch fabrication, and integrability with integrated circuits technology. On the basis of the reciprocal transmission of the silicon micromechanical resonators, they have been commercially developed for timing and frequency control^21,22,23. Given that the miniaturization of nonreciprocal devices such as isolators is needed in modern communication technology, it is significant to explore silicon micromechanical resonators for nonreciprocal transmission. In this article, we show that the insertion loss of a standard PT-symmetric system with balanced gain and loss can be drastically reduced provided that the loss resonator is judiciously modified so as to support the non-reciprocal transmission. We have implemented our scheme on PT-symmetric silicon micromechanical resonators¹⁰.

Results and discussion

Operation principle of nonreciprocal transmission

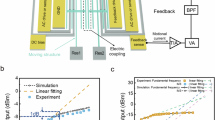
As shown in Fig. 1a, b, a PT-symmetric system consists a pair of electrically-coupled identical silicon micromechanical resonators. The gain resonator is achieved by a positive feedback circuit loop. The coupling between the gain and loss resonator can be electrically tuned so that the PT-symmetric system is initially biased at an exact phase. Perturbations to the spring constant of the loss resonator can be introduced by adjusting the voltage across two electrodes. Without the perturbation, real eigenvalues at the exact phase correspond to stable oscillations, while the perturbation causes PT symmetry to break, leading to complex-conjugate eigenvalues corresponding to exponential growth and decay modes. The presence of nonlinear gain suppresses the exponential growth so as to achieve the non-reciprocal transmission.

Fig. 1: Schematic of PT-symmetric micromechanical resonators for nonreciprocal transmission.

a Schematic of mass (m)—spring constant (k)—damping (c) representation for PT-symmetric resonators. One resonator has a loss and the other has a gain. k_c is the coupling strength. The spring constant $k$ of the loss resonator is adjusted to $k(1+\delta )$ where $\delta =\varDelta k/k$ is the perturbation. The forward transmission is considered to be from the loss to the gain resonator. b Schematic of a pair of electrically coupled beam resonators in this study. Res2 and Res1 correspond to gain and loss resonator, respectively. The electrostatic coupling voltage produces an equivalent electrostatic spring k_c. The feedback loop consists of trans-impedance amplifier (TIA), voltage amplifier (VA), bandpass filter (BPF), automatic gain control (AGC), and phase shifter (PS). The motional current generated by the gain resonator flows into the feedback loop, and then returns as the form of electrostatic force. A DC (direct current) voltage is applied on the loss resonator as the perturbation δ. c Microscope image of our fabricated silicon micromechanical resonators. The gold part is the electrode for feedback, coupling, perturbation and AC path, respectively. The plates in the black dotted frame are electrically coupled. d Real and imaginary parts of the normalized resonant frequency as a function of perturbation.

Figure 1a depicts a schematic of two coupled silicon micromechanical resonators used in this study. The system dynamics are described by:

$$\left\{\begin{array}{c}m\frac{{d}^{2}{x}_{L}}{{{dt}}^{2}}+c\frac{d{x}_{L}}{{dt}}+k{x}_{L}+{k}_{c}\left({x}_{L}-{x}_{G}\right)=0\\ m\frac{{d}^{2}{x}_{G}}{{{dt}}^{2}}-{c}_{s}\frac{d{x}_{G}}{{dt}}+k{x}_{G}+{k}_{c}\left({x}_{G}-{x}_{L}\right)=0\end{array}\right.$$

(1)

where the two resonators are identical with mass m, spring constant k, and uncoupled resonance frequency ${\omega }_{0}=\sqrt{k/m}$, respectively. They are coupled with coupling strength $\mu ={k}_{c}/k$, where k_c is the coupling spring constant. The loss resonator exhibits a loss factor $\gamma =c/\sqrt{{km}}$, while the gain resonator exhibits a gain factor ${g}_{s}={c}_{s}/\sqrt{{km}}$, where c and c_s are the damping coefficient and gain coefficient, respectively. Taking ${x}_{L,G}\propto {e}^{i\omega t}$, where x_L and x_G are the displacements of the loss and gain resonator, respectively, the resonant frequencies (eigenvalues) are then given by (see “Methods” and Supplementary Note 1):

$${\lambda }_{\pm }=1+\frac{\mu }{2}+i\frac{\gamma -{g}_{s}}{4}\pm \frac{1}{2}\sqrt{{\mu }^{2}-{\left(\frac{\gamma +{g}_{s}}{2}\right)\!}^{2}}$$

(2)

where $\lambda =\omega /{\omega }_{0}$ is the scaled the angular frequency. For a delicate balance of PT-symmetric silicon micromechanical resonators, where ${g}_{s}=\gamma$, there are two distinct phases, determined by a coupling strength μ relative to the loss. In the exact phase $\mu \, > \,\gamma$, the coupling between the gain and loss resonators is sufficiently strong, and the resonant frequencies are real, which is characterized by equal magnitudes for the superposition oscillations in the gain and loss sides. In the broken phase $\mu \, < \,\gamma$, the coupling is weak so that the system can no longer remain in equilibrium, and the resonant frequencies become complex with a single real frequency and conjugate imaginary parts, which indicates that it grows exponentially in one mode and decays exponentially in the other. When $\mu =\gamma$, the resonant frequencies are merged, i.e., exceptional points (EPs) appear at which the eigenvalues and the corresponding eigenstates coalesce^10,11,12. In the broken phase, the aforementioned non-reciprocal transmission was achieved in the presence of nonlinear gain^{13,14,15,16,17,18,19,20}.

In our scheme, the system is set at the exact phase so as to reduce insertion loss during transmission. To this end, a perturbation is applied to the loss resonator, and the spring constant of the loss resonator is adjusted to $k+\varDelta k=k(1+\delta )$, where $\delta =\varDelta k/k.$ Solutions to Eq. (1) under the perturbation yield (see “Methods”):

$${\lambda }_{\pm } = \, 1+\frac{\mu }{2}+\frac{\delta }{4}+i\frac{\gamma \,-\,{g}_{s}}{4}\\ \pm \frac{1}{2}\sqrt{{\mu }^{2}-{\left(\frac{\gamma \,+\,{g}_{s}}{2}\right)}^{2}+\frac{{\delta }^{2}}{4}+i\frac{\delta }{2}({g}_{s}+\gamma )}$$

(3)

The perturbation causes the PT-symmetric system to break, leading to an exponential growth mode and an exponential decay mode even in the exact phase where $\mu =\gamma$. Figure 1d depicts the real parts ${R}_{e}\left({\lambda }_{\pm }\right)$ and imaginary parts ${I}_{m}\left({\lambda }_{\pm }\right)$ as a function of perturbation δ under $\mu =\gamma ={g}_{s}$. In contrast to the broken phase without perturbations, the real parts of the two resonant frequencies differ from each other. Owing to the presence of nonlinear gain, however, the exponential growth mode $\left({\lambda }_{-}\right)$ ultimately dominates the performance of the system.

We define the forward transmission as from the loss to the gain resonator (Fig. 1a). The nonreciprocal ratio (${R}_{{nr}}$) is defined as the ratio of forward to backward transmission. It is given by (see “Methods”):

$${R}_{{nr}}=\left|\frac{\left(2s-\delta -2i{g}_{b}\right)\left(2s+\delta +2i\gamma \right)-4{\mu }^{2}}{\left(2s-\delta -2i{g}_{f}\right)\left(2s+\delta +2i\gamma \right)-4{\mu }^{2}}\right|$$

(4)

with

$$s={R}_{e}\left[\sqrt{{\mu }^{2}-{\left(\frac{\gamma +{g}_{s}}{2}\right)}^{2}+\frac{{\delta }^{2}}{4}+i\frac{\delta }{2}\left({g}_{s}+\gamma \right)}\right]$$

where ${g}_{s}={g}_{f}$ for the forward transmission and ${g}_{s}={g}_{b}$ for the backward transmission, respectively. The gain is a nonlinear function of the displacement amplitude, as a result, it is different between the forward and backward transmission. Equations (1) and (4) are derived according to the displacement amplitude of the resonators. Experimentally, the driving and detection of the resonators were performed by capacitive transduction. Accordingly, the transmission of AC (alternating current) voltage signals is achieved (see Supplementary Note 5).

Experiments and results

To demonstrate our scheme, based on the simulations by using SPICE (Simulation Program with Integrated Circuits Emphasis) (see Supplementary Fig. S3, Table S2 and Note 8), we fabricated silicon micromechanical resonators on silicon-on-insulator (SOI) wafer (see “Methods”), as shown in Fig. 1c. Experimentally, the signal input and output were achieved through the capacitive transduction between electrodes. The two resonators were electrostatically coupled by applying polarization voltages across them (see Supplementary Note 6). The loss of the resonators was adjusted by pressure in a vacuum chamber. The nonlinear gain was achieved by a feedback loop (Fig. 1b) which consists of trans-impedance amplifier (TIA), voltage amplifier (VA), bandpass filter (BPF), automatic gain control (AGC), and phase shifter (PS). The specific parameters of feedback loop are presented in Supplementary Table S1. The feedback loop gathers the motion current from the gain resonator and returns a feedback voltage on the electrode, which is equivalent to negative damping. Perturbations were achieved by applying a direct current (DC) voltage to the electrodes situated outside the loss resonator. The resonators were placed in a vacuum chamber.

Figure 2a shows the measured output amplitude of the gain resonator as a function of frequency under different perturbation voltages of 0 to 6 V with the input amplitude being 15 mV, when the system was biased at $\mu =\gamma$. Initially, the perturbation voltage was set to ${V}_{{pert}}=0$ (i.e., $\delta =0$), and according to theoretical predications it should indicate a single resonance peak for ${g}_{s}=\gamma$. In the measurement, however, the gain was set slightly less than the loss, resulting in the appearance of double resonance peaks at $\mu =\gamma$. This setting was employed in order to avoid the occurrence of self-oscillation owing to the positive feedback loop, accordingly, the resonators were operated under a forced vibration. As the perturbation voltage increases, the resonance peak corresponding to λ_- gradually magnifies, while the resonance peak corresponding to λ₊ tends to disappear due to the exponential decay (see Supplementary Fig. S1 and Note 2). The observed shift in resonance frequency is consistent with the theoretical prediction. The forward and backward transmission was measured by exchanging input and output ports. Figure 2b, c shows the measured transmission with the perturbation δ = 0 and δ = 0.003, respectively. The perturbation δ is calculated according to the perturbation voltage (see Supplementary Note 7). Initially, the system was biased at an exact phase close to EPs, and the real parts of the resonant frequency are different, resulting in a mode splitting of the observed transmission spectrum. The transmission is reciprocal in this case (Fig. 2b). However, when a perturbation voltage was applied to the loss resonator, the unequal suppress in the gain resonator between the forward and backward inputs results in non-reciprocal transmission (Fig. 2c).

Fig. 2: Transmission measurements of PT-symmetric micromechanical resonators.

a Output amplitude as a function of frequency under various perturbation voltage. b Output amplitude as a function of frequency without perturbation. The transmission is reciprocal. c Output amplitude as a function of frequency with perturbation (δ = 0.003). The transmission is nonreciprocal. All measured results were obtained at μ = γ = 9 × 10⁻⁴ with input amplitude of 15 mV.

We evaluate the performance of our nonreciprocal system including nonreciprocal ratio, insertion loss, and isolation as the system parameters are varied.

Non-reciprocal ratio

Figure 3a shows the nonreciprocal ratio as a function of perturbation δ corresponding to perturbation voltage V_pert. As the perturbation increases, the non-reciprocity becomes more pronounced. Theoretically, the larger perturbation induces more significant non-reciprocity. In fact, however, large perturbations, corresponding to voltages across the electrodes of loss resonator, lead to nonlinearity of resonators²⁴, causing the resonant frequency to shift. In our arrangement, the maximum non-reciprocal ratio of 8 dB was observed at δ = 0.003. Figure 3b shows the nonreciprocal ratio as a function of input amplitude. As described in the above, the nonreciprocal ratio is related to the input amplitude. For small input amplitudes, the gain is under the saturation threshold and almost linear, and the transmission is almost reciprocal. For large input amplitudes, the gain of the gain resonator is significantly lower for the backward input than the forward input due to the saturation, leading to nonreciprocal transmission. The inset in Fig. 3b emphasizes the measured non-reciprocal ratio from 7.5 mV to 15 mV, which is consistent with simulations. Accurate experimental results were not obtained for smaller or larger input amplitudes since it is challenging to capture signals with excessively small inputs, and excessively large inputs results in a stiffness softening of the resonator²⁴. Therefore, in our experiments, the maximum non-reciprocal ratio obtained is 8 dB at μ = γ = 9 × 10⁻⁴ with perturbation δ = 0.003 and input amplitude of 15 mV.

Fig. 3: Measured nonreciprocal performances of PT-symmetric micromechanical resonators.

a The non-reciprocal ratio as a function of perturbation δ corresponding to perturbation voltage V_pert, where simulated (black square) and measured (yellow circle) results are indicated. The parameters were set at μ = γ = 9 × 10⁻⁴ with input amplitude of 15 mV. b The non-reciprocal ratio as a function of input amplitude, where simulated (black square) and measured (yellow circle) results are indicated. The inset shows the measured nonreciprocal ratio for input amplitudes of from 7.5 mV to 15 mV, where simulations and experiments are consistent. The parameters were set at μ = γ = 9 × 10⁻⁴ and δ = 0.003. c Measured insertion loss (yellow square) and isolation (blue circle) as a function of frequency. Δf = f − f₀ is the difference between the operating frequency f and the fundamental resonance frequency f₀, where f₀ = 106.7 kHz. Measured results were obtained at μ = γ = 9 × 10⁻⁴, δ = 0.003, and input amplitude of 15 mV.

Insertion loss and isolation

Figure 3c shows the insertion loss and isolation as a function of frequency under the aforementioned conditions. It is demonstrated the insertion loss of 5 dB, the isolation of 13 dB, and the non-reciprocal ratio of 8 dB. Moreover, the FWHM (full-width at half-maximum bandwidth) was measured to be less than 5 Hz, indicating that a quality factor (Q) is greater than 2 × 10⁴. The obtained quality factor is much higher than that implemented by piezoelectric acoustic waves¹⁵ or LC (inductor-capacitor) resonators^16,17,18,19, which has significant advantages in narrowband nonreciprocal transmission. The fundamental resonant frequency (f₀) of silicon micromechanical resonators has been extended to a few GHz with appropriate designs^25,26,27, though we utilized resonators with f₀ = 106.7 kHz to demonstrate the non-reciprocal transmission of PT-symmetric silicon micromechanical resonators.

Conclusions

We have reported a scheme of non-reciprocal transmission on the basis of silicon micromechanical resonators operating at an exact phase. In our experiments, we used silicon resonators with an operating frequency of 106.7 kHz, but the frequency could be extended to a few GHz by geometrically scaling the design. Furthermore, perturbations instead of external voltages applied could be also implemented by designing the proper stiffness of the loss resonators. In addition, the high-quality factor could enable the narrowband nonreciprocal transmission of precise signal processing. The proposed scheme offers a non-magnetic and non-reciprocal platform that is well-suited to the demands of modern communication systems.

Methods

Coupled-mode equations for silicon micromechanical resonators

Taking ${x}_{L,G}={a}_{L,G}{e}^{i\omega t}$, where x_L and x_G, a_L and a_G, are the vibration displacement and amplitude of the loss and gain resonator, respectively, Eq. (1) is rewritten as²⁰:

$$\left[\begin{array}{cc}-{\lambda }^{2}+i\lambda \gamma +1+\mu & -\mu \\ -\mu & -{\lambda }^{2}-i\lambda {g}_{s}+1+\mu \end{array}\right]\left[\begin{array}{c}{x}_{L}\\ {x}_{G}\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$$

(5)

Assuming the condition of weak coupling, i.e., $\mu \,\ll\, 1$, Eq. (5) then reduces to:

$$\left[\begin{array}{cc}-\lambda +i\frac{\gamma }{2}+1+\frac{\mu }{2} & -\frac{\mu }{2}\\ -\frac{\mu }{2} & -\lambda -i\frac{{g}_{s}}{2}+1+\frac{\mu }{2}\end{array}\right]\left[\begin{array}{c}{x}_{L}\\ {x}_{G}\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$$

(6)

Solving Eq. (6) yields Eq. (2).

When a perturbation is applied to the loss resonator, the spring constant of the loss resonator is adjusted to $k+\varDelta k=k(1+\delta )$, where $\delta =\varDelta k/k.$ Equation (6) is modified to:

$$\left[\begin{array}{cc}-\lambda +i\frac{\gamma }{2}+1+\frac{\mu }{2}+\frac{\delta }{2} & -\frac{\mu }{2}\\ -\frac{\mu }{2} & -\lambda -i\frac{{g}_{s}}{2}+1+\frac{\mu }{2}\end{array}\right]\left[\begin{array}{c}{x}_{L}\\ {x}_{G}\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$$

(7)

Solving Eq. (7) yields Eq. (3).

Nonreciprocal ratio of silicon micromechanical resonators under perturbations

We apply a time-harmonic input force $f\left(t\right)=F{{{{\rm{e}}}}}^{{{{\rm{i}}}}{{{\rm{\omega }}}}{{{\rm{t}}}}}$ where F is the amplitude of the force added to the loss resonator for the forward transmission and to the gain resonator for the backward transmission, respectively. Equation (7) is rewritten as, for the forward and backward transmission, respectively:

$$\left[\begin{array}{cc}-\lambda +i\frac{\gamma }{2}+1+\frac{\mu }{2}+\frac{\delta }{2} & -\frac{\mu }{2}\\ -\frac{\mu }{2} & -\lambda -i\frac{{g}_{f}}{2}+1+\frac{\mu }{2}\end{array}\right]\left[\begin{array}{c}{a}_{L}\\ {a}_{G}\end{array}\right]=\left[\begin{array}{c}\frac{F}{2k}\\ 0\end{array}\right]$$

(8a)

$$\left[\begin{array}{cc}-\lambda -i\frac{{g}_{b}}{2}+1+\frac{\mu }{2} & -\frac{\mu }{2}\\ -\frac{\mu }{2} & -\lambda +i\frac{\gamma }{2}+1+\frac{\mu }{2}+\frac{\delta }{2}\end{array}\right]\left[\begin{array}{c}{b}_{G}\\ {b}_{L}\end{array}\right]=\left[\begin{array}{c}\frac{F}{2k}\\ 0\end{array}\right]$$

(8b)

where ${g}_{f}$ and ${g}_{b}$ are the gain for the forward and backward transmission, respectively. Owing to the presence of nonlinear gain, the exponential growth mode $\left({\lambda }_{-}\right)$ in Eq. (3) ultimately dominates the performance of the system. Inserting ${\lambda }_{-}$ into Eqs. (8a) and (8b), respectively, one can obtain the forward transmission a_G/F and the backward transmission b_L/F. The non-reciprocal ratio (${R}_{{nr}}$) is defined as ratio of the forward to backward transmission ${R}_{{nr}}=\left|\left({a}_{G}/F\right)/\left({b}_{L}/F\right)\right|=\left|{a}_{G}/{b}_{L}\right|$, i.e., Eq. (4). Supplementary Note 3 provides details.

Nonlinear gain factor

The electrostatic force driving the resonator is²⁸:

$$f\left(t\right)=\frac{\varepsilon A}{{d}^{2}}{V}_{\!\!{dc}}{v}_{{in}}$$

(9)

where V_dc is the DC voltage across the gap, v_in is the AC driven voltage, A and d are the area and the gap of the driving electrode and the resonator, and ε is the dielectric constant, respectively.

The motional current from the resonators is expressed as:

$${i}_{s}=\frac{d({V}_{\!\!{dc}}C)}{{dt}}={V}_{\!\!{dc}}\frac{\partial C}{\partial x}\frac{\partial x}{\partial t}\approx {V}_{\!\!{dc}}\frac{\varepsilon A}{{d}^{2}}\frac{{dx}}{{dt}}$$

(10)

As shown in Fig. 1c, the motional current from the resonator undergoes conversion into a voltage by TIA, and then amplified by VA and AGC. The resulting feedback voltage in the gain resonator is given by²⁰:

$${v}_{f}={A}_{T}{A}_{v}{A}_{n}{V}_{\!\!{dc}}\frac{\varepsilon A}{{d}^{2}}\frac{d{x}_{G}}{{dt}}$$

(11)

where A_T is the conversion coefficient of TIA, Av, and An are the factor VA, and AGC, respectively. From Eqs. (9) and (11), the feedback driving force applied on the gain resonator is:

$${F}_{f}={A}_{T}{A}_{v}{A}_{n}{\left({V}_{\!\!{dc}}\frac{\varepsilon A}{{d}^{2}}\right)}^{2}\frac{d{x}_{G}}{{dt}}$$

(12)

The dynamic equation of the gain resonator, given the feedback force, is as follows:

$$m\frac{{d}^{2}{x}_{G}}{{{dt}}^{2}}+c\frac{d{x}_{G}}{{dt}}+k{x}_{G}+{k}_{c}\left({x}_{G}-{x}_{L}\right)={F}_{f}$$

(13)

By Eqs. (12) and (13), the gain coefficient is:

$${c}_{s}={A}_{T}{A}_{v}{A}_{n}{\left({V}_{\!\!{dc}}\frac{\varepsilon A}{{d}^{2}}\right)}^{\!\!{2}}-c$$

(14)

The parameter of the feedback loop is set to ensure Eq. (14) manifests as negative damping. And ${g}_{s}={c}_{s}/\sqrt{{km}}$ exhibits nonlinearity because of the nonlinear factor A_n. The nonlinear gain can be fitted (Supplementary Fig. S2 and Note 4).

Fabrication of silicon micromechanical resonators

The micromechanical resonators were prepared on SOI wafers by deep reactive ion etching. The specific process flow can be found in Supplementary Fig. S3 and Note 9. The dimension parameters of the resonators are shown in Supplementary Table S3.

Measurement set-up

Micromechanical resonators were mounted to the adapter board with electrical connection established by bonding gold wires to the pads on the adapter board. The setup was placed within a specially designed vacuum chamber with the tunable pressure range of 8 mtorr to the atmospheric pressure. The resonator is electrically connected to the external device through a vacuum adapter located on the chamber. The measurement process is facilitated by the sweep module and HF2TA accessories of Zurich HF2LI. The Zurich HF2LI averages the 20 samples to ensure the accuracy of the measurement. The DC bias on resonators and power of the circuit are provided by RIGOL DP800 Power Supply.

The photograph of the experimental set-up is shown in Supplementary Fig. S4 and Note 10.