Introduction

Quantum information is a significant extension of classical information field and provides another perspective for understanding the quantum world. Many quantum information protocols have no classical counterparts, while some natural processes in classical information are forbidden in quantum cases by the so-called no-go theorem. A typical quantum example is quantum teleportation1,2, in which an unknown quantum state is transferred from one place to another without physical transmission of the object itself. Quantum teleportation was prompted by the famous no-cloning principle (the first no-go theorem), which states that no physical process can perfectly duplicate any pure state3,4. In addition to no-cloning theorem linked to the linearity of the quantum world, there is also the no-deleting theorem5 from the unitarity of the quantum. They are limiting that the quantum information can be neither created nor destroyed. The no-cloning theorem has an extension, the no-propagation theorem6, which introduces the incompatibility of the local identity channels. Arising from the black-hole information paradox, the no-hiding theorem7 proves that hiding quantum state in quantum correlations is impossible. Recently, a no-go theorem, no-masking principle8, was found in quantum information masking (QIM). Both no-hiding theorem and no-masking principle are associated with the conservation law of quantum information. They all investigate whether the isometry exists which from original Hilbert space to bipartite Hilbert space. For the hiding case, quantum information from one of the subspaces of the bipartite Hilbert space is independent of original quantum state. While for the masking case, quantum information from any subspace is independent of original quantum state9.

QIM provides a methodology to hide quantum information from subsystems and to spread it over the nonlocal correlation in multipartite systems. The initial information can be reconstructed from this correlation. Initially, no-masking principle8 stipulated that quantum information pertaining to an arbitrary qubit state could not be masked in a bipartite quantum system while hidden from its subsystems. Subsequently, various studies of the maximal maskable set of quantum states10,11,12,13 were reported. This no-masking theorem tells us that complete QIM, which enables to mask the quantum information to the maximally mixed state of an arbitrary qubit state, is impossible in a bipartite scenario. However, recent theoretical studies show that complete QIM is realizable in multipartite scenarios8,14,15, implying that no-masking principle is significantly different from other no-go theorems. In practical experiments, QIM of a special set of qubit states has been demonstrated12,13, while achieving complete QIM for all states on the Bloch sphere remains an ongoing challenge.

More than just a no-go theorem in quantum theory, QIM is intimately connected to various quantum information processing tasks, such as quantum state identification16, quantum bit commitment17,18, and quantum secret sharing (QSS)19. And it is deeply rooted in fundamental principles such as conservation of information20. The primary objective of QSS is to share secret quantum information in a system involving as many participants as possible and where the full initial information must be obtained with the cooperation of multiple participants19,21,22. Many attempts to share information in quantum systems have been reported in the literature, such as experimental realizations of classical information23,24,25,26 and quantum information in three-27,28 or four-party systems29. However, the experimental realization of QSS with more participants is still a challenge.

Since quantum information tasks such as QSS can be seen as an expression of the versatility and scalability of QIM. Both the deepening of theoretical understanding in the realm of QIM and advancements in experimental realization have played important roles in propelling the field of QSS forward. In 2018, the proof of the unmaskability theorem provided valuable insights to help dealers choose substrates for secret sharing of classical or quantum information8. In 2021, the realization of photonic masking machines contributes to the proposal of QSS scheme that is independent of entanglement between receivers and is not affected by decoherence12. Here, we not only experimentally demonstrate complete QIM, but also implement QSS with up to six participants experimentally realistic, which is based on the extension of the most frugal case.

Results

Complete QIM

For a set of quantum states \(\{{\left\vert a\right\rangle }_{k}\}\) in the Hilbert space H1, a unitary operator \({{{\mathcal{S}}}}\) performs the mapping

$${{{\mathcal{S}}}}:{\bigotimes }_{j = 1}^{n-1}{\left\vert 0\right\rangle }_{j}\otimes {\left\vert a\right\rangle }_{k}\to {\left\vert \Phi \right\rangle }_{k},$$
(1)

where \(\{{\left\vert \Phi \right\rangle }_{k}\}\) is in the Hilbert space \({\bigotimes }_{j = 1}^{n}{H}_{j}\). All Hj (j = 1, . . . , n) have the same dimension as H1. If any local system Hj contains no information about \({\left\vert a\right\rangle }_{k}\), \({{{\mathcal{S}}}}\) is said to be a masker that masks quantum information in \(\{{\left\vert \Phi \right\rangle }_{k}\}\), and this QIM process refers to complete QIM. The unitary property of \({{{\mathcal{S}}}}\) implies that the initial information can be extracted from \(\{{\left\vert \Phi \right\rangle }_{k}\}\).

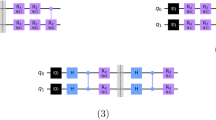
Here we propose complete QIM to mask an arbitrary qubit state \({\left\vert \gamma \right\rangle }_{1}={\alpha }_{0}{\left\vert 0\right\rangle }_{1}+{\alpha }_{1}{\left\vert 1\right\rangle }_{1}\) (where the amplitudes satisfy ∣α0∣2 + ∣α1∣2 = 1) in four qubits, which is the minimal number of qubits required to achieve the complete QIM for a qubit14. Qubits 2 and 3 are initially prepared in the Bell state of \({\left\vert \varphi \right\rangle }_{23}=\frac{1}{\sqrt{2}}{(\left\vert 00\right\rangle +\left\vert 11\right\rangle )}_{23}\). Our complete QIM is realized in three steps. First, a controlled-not (CNOT) gate \({{{{\mathcal{C}}}}}_{21}\) is operated on qubits 1 and 2 (where qubit 2 acts as the control qubit and qubit 1 is the target qubit). Then the three-qubit state becomes \({\left\vert \Phi \right\rangle }_{123}=\frac{1}{\sqrt{2}}[{\alpha }_{0}(\left\vert 000\right\rangle +\left\vert 111\right\rangle )+{\alpha }_{1}(\left\vert 011\right\rangle +\left\vert 100\right\rangle )]\). Thus, the reduced density matrix of qubit 1 is \({\rho }_{1}=\frac{1}{2}\left[I+2{{{\rm{Re}}}}({\alpha }_{0}{\alpha }_{1}^{* }){\sigma }_{x}\right]\), and qubits 2 and 3 are in the maximally mixed states with ρ2 = ρ3 = I/2, where I and σx are the identity and Pauli matrices, respectively. In the first step, the CNOT gate \({{{{\mathcal{C}}}}}_{21}\) masks the diagonal terms representing the amplitude of qubit 1.

To further obscure the remaining non-diagonal coherent terms, the second step involves introducing an ancillary qubit A, prepared in \(\left\vert 0\right\rangle\). In the third step, a CNOT gate \({{{{\mathcal{C}}}}}_{1A}\) is operated on qubits 1 and A (where qubit 1 acts as the control qubit and qubit A is the target qubit). Then the 4-qubit masked state is in the form of

$${\left\vert \Phi \right\rangle }_{A123}=\frac{1}{\sqrt{2}}\left[{\alpha }_{0}(\left\vert 0000\right\rangle +\left\vert 1111\right\rangle )+{\alpha }_{1}(\left\vert 0011\right\rangle +\left\vert 1100\right\rangle )\right].$$
(2)

We can see that all the four local states are maximally mixed with ρA,1,2,3 = I/2, indicating that the initial quantum information is spreading over quantum correlation in \({\left\vert \Phi \right\rangle }_{A123}\) and the complete QIM is achieved. The most basic scheme in a 4-qubit system can be formulated as

$${{{{\mathcal{C}}}}}_{1A}{{{{\mathcal{C}}}}}_{21}{\left\vert 0\right\rangle }_{A}{\left\vert \gamma \right\rangle }_{1}{\left\vert \varphi \right\rangle }_{23}={\left\vert \Phi \right\rangle }_{A123}.$$
(3)

We choose the polarization degree of freedom (DoF) of photons to carry qubit information for qubit 1. The quantum state to be masked can be substituted with the polarized state of the photon following the correspondences of \(\left\vert H\right\rangle \leftrightarrow \left\vert 0\right\rangle\) and \(\left\vert V\right\rangle \leftrightarrow \left\vert 1\right\rangle\), with \(\left\vert H\right\rangle\) and \(\left\vert V\right\rangle\) indicating the horizontally and vertically linear polarization states of the photon, respectively. Qubit 2 and 3 are also encoded in the polarization DoF, while the ancillary qubit A is encoded in the orbital angular momentum (OAM) DoF with the correspondences of \(\left\vert +1\right\rangle \leftrightarrow \left\vert 0\right\rangle\) and \(\left\vert -1\right\rangle \leftrightarrow \left\vert 1\right\rangle\), where \(\left\vert +1\right\rangle\) and \(\left\vert -1\right\rangle\) refer to the right-handed and the left-handed OAMs of  + ℏ and  − ℏ. Then the 4-qubit masked state can be represented as: \({\left\vert \Phi \right\rangle }_{A123}=\frac{1}{\sqrt{2}}[{\alpha }_{0}(\left\vert +1HHH\right\rangle +\left\vert -1VVV\right\rangle )+{\alpha }_{1}(\left\vert +1HVV\right\rangle +\left\vert -1VHH\right\rangle )]\). \({\left\vert \Phi \right\rangle }_{A123}\) is entangled in three photons with four DoFs, which is called the hyperentangled state.

Here, we show that our scheme includes both complete QIM and unmasking process to reconstruct the masked information, which is quantum teleportation in the 4-qubit system, as shown in Fig. 1. The \({\left\vert \Phi \right\rangle }_{A123}\) can be unmasked back to qubit 1 by using the inverse operation \({({{{{\mathcal{C}}}}}_{1A}{{{{\mathcal{C}}}}}_{21})}^{{{\dagger}} }={{{{\mathcal{C}}}}}_{21}{{{{\mathcal{C}}}}}_{1A}\). Similar operations can unmask the quantum information to any of the four parts according to the symmetry of \({\left\vert \Phi \right\rangle }_{A123}\). For example,

$${{{{\mathcal{C}}}}}_{13}{{{{\mathcal{C}}}}}_{32}{\left\vert \Phi \right\rangle }_{A123}={\left\vert \varphi \right\rangle }_{A1}{\left\vert 0\right\rangle }_{2}{\left\vert \gamma \right\rangle }_{3}$$
(4)
Fig. 1: The complete QIM process in the 4-qubit system.
figure 1

The two steps of QIM and unmasking can compose the process of quantum teleportation. For the QIM scheme, the initial state which is encoded in the polarization and represented by the green and blue spheres will pass through the two CNOT gates C21 and C1A and the initial state will be completely masked in the 4-qubit hyperentangled state. The protocol of unmasking will transmit the initial state to an arbitrary qubit and finish quantum teleportation. The photon pair (photon-2, photon-3) is prepared in the Bell state of \(\frac{1}{\sqrt{2}}{(\left\vert HH\right\rangle +\left\vert VV\right\rangle )}_{23}\).

Full size image

reconstructs the initial state in qubit 3. Furthermore, two arbitrary high-dimensional QIM in the 4-qubit system and an odd high-dimensional QIM version in the tripartite system are shown in Supplementary Note 1.

We indicate that the total masking scenario for a single qubit that we propose for the no-masking theorem can be generalized to quantum information encoded in multipartite systems. In a multipartite systems, if the quantum information is encoded in a direct product state, we can attach a set of masking systems to each qubit to achieve the total QIM. If the quantum information is in an entangled state between different systems, any subsystems will be in a mixed state, which is a mixture of different pure states. Since our QIM scheme applies to any pure state on the Bloch sphere, it also applies to their mixed states. For entangled systems, we can also match the masking systems for each subsystem and perform masking procedures to finalize the total QIM. The total QIM is an unitary process, and the unmasking can be implemented by the inverse operation, which is also a unitary process. So that our scenario can be extended to more multipartite systems.

Complete QIM enables QSS and quantum teleportation

Since masking protocols can be viewed as a basis for QSS8, our QIM protocol, in which the arbitrary initial state \({\left\vert \gamma \right\rangle }_{1}\) can be masked in the minimal Hilbert space with the help of the Bell state \({\left\vert \varphi \right\rangle }_{23}\) and an ancillary qubit A, can be easily scaled up in multipartite systems with an arbitrary number of participants involved. This enhanced scalability makes QSS implementation more straightforward.

Starting from our masked state \({\left\vert \Phi \right\rangle }_{A123}\), the second and third steps in our complete QIM scheme can be iterated multiple times to add more qubits involved. The involved CNOT gates are operated on the added qubits and the existing qubits, where the added qubits are the target qubits, and the control qubits can be any qubits of the existing sharing states. To illustrate, let us consider an example of a 6-qubit QSS state. On top of the masked state \({\left\vert \Phi \right\rangle }_{A123}\), we add two qubits \({2}^{{\prime} }\) and \({3}^{{\prime} }\) prepared in \(\left\vert 0\right\rangle\) and do the gate operation \({{{{\mathcal{C}}}}}_{2{2}^{{\prime} }}\) and \({{{{\mathcal{C}}}}}_{3{3}^{{\prime} }}\), respectively. Then the 6-qubit QSS state can be written as

$${\left\vert \Phi \right\rangle }_{A12{2}^{{\prime} }3{3}^{{\prime} }}=\frac{1}{\sqrt{2}}\left[{\alpha }_{0}(\left\vert 000000\right\rangle +\left\vert 111111\right\rangle )+{\alpha }_{1}(\left\vert 001111\right\rangle +\left\vert 110000\right\rangle )\right].$$
(5)

Like the complete QIM, the quantum teleportation in quantum information science is another protocol that requires the arbitrariness of qubit state, i.e., the state set covering the whole Bloch sphere. Quantum information schemes and their extensions are widely studied30,31,32,33,34,35 and applied in various branches of quantum information from fundamental quantum physics such as loophole-free test of Bell inequality violation36 to practical applications such as quantum repeater37 and quantum networks38,39,40. So far, the implementation of quantum teleportation in multiparty systems remains an intriguing and open area of research.

Our work reveals that quantum teleportation can be viewed as a combined process of complete QIM and unmasking. Besides the general unmasking approach above, in the 2⊗6 system given by Eq. (5), the unmasking process can be achieved by some simple Hadamard gates. This process is simpler than the standard paradigm of unmasking. First, the six qubits in the entangled state are divided into two groups (A, 1) and \((2,2{\prime} ,3,3{\prime} )\). Then, the Hadamard gates are executed on all qubits of the group except for the qubit that receives the initial information, and the qubits without Hadamard gate operation can acquire the initial state by a local operation indicated by a measurement on the computational basis of the qubits of the other group. The details of the unmasking process to an arbitrary subsystem are shown in Supplementary Note 2.

Experiment of complete QIM process

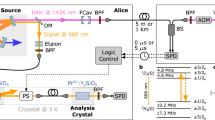
We consider the physical realization of complete QIM. The polarization degree of freedom (DoF) of photons is used to carry qubit information. The quantum state to be masked can be substituted with the polarized state of the photon following the correspondences of \(\left\vert H\right\rangle \leftrightarrow \left\vert 0\right\rangle\) and \(\left\vert V\right\rangle \leftrightarrow \left\vert 1\right\rangle\), with \(\left\vert H\right\rangle\) and \(\left\vert V\right\rangle\) indicating the horizontal and vertical polarizations of the photon, respectively. The experimental setup for arbitrary qubits QIM is shown in Figure 2. The femtosecond (fs) laser with a central wavelength of 390 nm and a repetition rate of 80 MHz pumps successively one single 2 mm-thick β-barium borate (BBO) crystal and standard Kwiat source (i.e., glued two 0.6 mm-thick BBO crystals with perpendicular optical axes) for type-I spontaneous parametric down-conversion (SPDC)33,41, among which the first photon pair (photon-1 and photon-trigger) is prepared in the product state \(\left\vert HH\right\rangle\) pumped by \(\left\vert V\right\rangle\), and the second photon pair (photon-2 and photon-3) is the Bell state of \(\frac{1}{\sqrt{2}}{(\left\vert HH\right\rangle +\left\vert VV\right\rangle )}_{23}\) pumped by \(\left\vert H+V\right\rangle\), which is regarded as the masking channel. The photon-1 is used to prepare the state that will be masked and its twin photon serves as a trigger to herald the photon-1. Furthermore, we utilize two DoFs of a single photon to encode qubits, namely, the polarization and orbital angular momentum (OAM). The ancillary qubit A is encoded as OAM DoF of the photon-1.

Fig. 2: Experimental setup to mask an arbitrary qubit and 6-qubit QSS.
figure 2

An ultrafast fs laser beam successively passes through two separate sources. The first one is a single BBO crystal to generate correlated photon pair \(\left\vert HH\right\rangle\) and the other one is standard Kwiat source to generate the entangled photon pair\(\frac{1}{\sqrt{2}}{(\left\vert HH\right\rangle +\left\vert VV\right\rangle )}_{23}\). SC-YVO4 and TC-YVO4 represent spatial compensation (SC) and temporal compensation (TC) YVO4 crystals. The polarization CNOT gate is combined by three PDBSs and two HWPs. AQ (auxiliary qubit, see “Methods” for details) is the combination of a q-plate sandwiched by QWPs and prepares the OAM polarization entanglement. OTPC (the OAM-to-polarization converter, see “Methods” for details) is utilized to read the photonic OAM qubit. 6-qubit QSS is realized when the combination of AQ and OTPC acts on both photon-2, photon-3 simultaneously.

Full size image

To prepare an arbitrary initial state of \({\left\vert \gamma \right\rangle }_{1}\) for masking, the photon-1 passes through a half-wave plate (HWP) sandwiched between two quarter-wave plates (QWPs) to achieve an arbitrary unitary polarization rotation, which can map an initial state to any point on the Bloch sphere. In our QIM scenario, the photon-1 undergoes three steps: two CNOT gates and introduction of an ancillary qubit. We apply the first CNOT gate \({{{{\mathcal{C}}}}}_{21}\) on the photon-1 and photon-2 to mask the diagonal elements of the reduced density matrix of the initial state, where the photon-1 is the target qubit and the photon-2 serves as the control qubit. The CNOT gate with a success probability of 1/9 is composed of the controlled-phase (C-phase) gate and two Hadamard gates (HWP at an angle of 22.5∘), as shown in Fig. 2. The C-phase gate is combined by three polarization-dependent beam splitters (PDBSs) with one primary PDBS (TH = 1 and TV = 1/3) and two secondary PDBSs (TV = 1 and TH = 1/3)42. In our experiment, the process fidelity of the CNOT operation43,44 is measured to be \(F\in \left[0.87\pm 0.02,0.92\pm 0.01\right]\) (see Supplementary Note 3).

The subsequent CNOT gate \({{{{\mathcal{C}}}}}_{1A}\) is performed on different DoFs of photon-1, namely, polarization and OAM, where polarization DoF is the control qubit and OAM DoF (qubit A) acts as the target qubit, with the correspondences \(\left\vert +1\right\rangle \leftrightarrow \left\vert 0\right\rangle\) and \(\left\vert -1\right\rangle \leftrightarrow \left\vert 1\right\rangle\), where \(\left\vert +1\right\rangle\) and \(\left\vert -1\right\rangle\) refer to the right- and the left-handed OAMs of  + ℏ and  − ℏ. The interfered photon-1 passes through the sandwich structure of a QWP, a q-plate, and a QWP. Such an architecture45 can easily make \(\left\vert H\right\rangle\) photon carry the OAM of  + ℏ, while \(\left\vert V\right\rangle\) photon carries the OAM of  − ℏ, i.e., \({\left\vert g\right\rangle }_{A}{\left\vert H\right\rangle }_{1}\to {\left\vert +1\right\rangle }_{A}{\left\vert H\right\rangle }_{1}\) and \({\left\vert g\right\rangle }_{A}{\left\vert V\right\rangle }_{1}\to {\left\vert -1\right\rangle }_{A}{\left\vert V\right\rangle }_{1}\) (see “Methods” for details), where \(\left\vert g\right\rangle\) represents the Gaussian mode of the photon. Then the desired masked 4-qubit hyperentangled state in Eq. (2) can be generated.

After completing the QIM process, one needs to analyze the masked quantum information by the projection measurement of the final state. Polarization qubits 1, 2, and 3 are read out with a standard polarization analyzer, which consists of one HWP, one QWP, and one polarizing beam splitter (PBS). For the qubit A, which is encoded in OAM, a swap gate is employed to transform the OAM information to polarization. Subsequently, another polarization analyzer is used46. Finally, the photons are collected by single-mode fibers (SMFs) and sent to the single-photon avalanche detectors for four-fold coincidence counting.

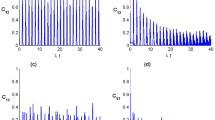
The density matrix of any point on the Bloch sphere can be expressed as a linear superposition of the Pauli matrices12,47. To reveal that our work can be completely masked for any qubit on the Bloch sphere, we select 16 initial states (see Supplementary Note 4 for their details). Figure 3a shows all the selected 16 initial states by the two-dimensional ‘Map’ representation instead of the three-dimensional Bloch sphere, which is prepared by combining QWP, HWP, and QWP (for details, see Supplementary Note 4). We measure the fidelity of the hyperentangled states after QIM for each initial state by representing the density matrix of the hyperentangled state with the identity and Pauli matrices and measuring the corresponding expectation values. The average fidelity of the masking-resulted states is 0.84 ± 0.01 (see Supplementary Note 4 for the fidelities of all the 16 states). The initial state \(\left\vert H\right\rangle\) after QIM is the 4-qubit GHZ state. Figure 3b illustrates the measurement results under the computational basis \(\{\left\vert H\right\rangle ,\left\vert V\right\rangle \}\) to calculate the population and the expectation values of the corresponding entanglement witness operators to calculate the coherence. With the calculated population and coherence, we can easily obtain the fidelity46. We present the reduced density matrices of the masked qubits after passing the first and second CNOT gates in Fig. 3c, respectively. The reduced density matrices can be obtained by measuring the expectation of the three Pauli matrices as the measurement operators. After the first CNOT gate, the diagonal terms in the reduced density matrices of the qubits represent the amplitudes that have been masked. For some states, however, the non-diagonal terms representing the coherence terms are still not completely masked. After the second CNOT gate, the reduced density matrix of any single qubit is the maximally mixed state. We calculate the trace distance \(T({\rho }_{i},{\rho }_{j})=\frac{1}{2}{{{\rm{Tr}}}}| {\rho }_{i}-{\rho }_{j}|\)47,48,49,50 from the masked qubit to the maximally mixed state with \(T\in \left[0.12\pm 0.02,0.03\pm 0.02\right]\). This outcome indicates that the information of any single qubit is masked in the 4-qubit hyperentangled state and no information about the initial state can be obtained from any single qubit (see Supplementary Note 4 for details).

Fig. 3: Experimental results for the complete QIM of the arbitrary qubit.
figure 3

a The 16 initial states selected on the Bloch sphere, for implementing the QIM experiment, are mapped to the “Map” representation for clarity. b For the initial state \(\left\vert H\right\rangle\), QIM result is 4-qubit GHZ state. We show the four-photon coincidence counts in \(\{\left\vert H\right\rangle ,\left\vert V\right\rangle \}\) basis and the expectation values of \({M}_{\theta }^{\otimes 4}={(\cos \theta {\sigma }_{x}+\sin \theta {\sigma }_{y})}^{\otimes 4}\) obtained by the measurement in the basis of \(\frac{1}{\sqrt{2}}(\left\vert H\right\rangle \pm {e}^{i\theta }\left\vert V\right\rangle )\), where θ = kπ/4 (k = 0, 1, 2, 3). The error bar indicates 1 standard deviation (obtained from the Poissonian statistics of the detected four-photon counts). c The reduced density matrix of the qubit carrying the initial quantum information at the different stages of the QIM process: before QIM (initial), passing through the first CNOT gate (partially masked), and after QIM (masked).

Full size image

Furthermore, building upon the foundation of complete QIM in the 4-qubit system, we further repeat the second and the third steps twice in our QIM scheme to introduce two ancillary qubits \(2{\prime}\) and \(3{\prime}\), which are encoded in the OAM DoF of the photon-2 and photon-3, respectively. Then we perform the CNOT gates \({{{{\mathcal{C}}}}}_{22{\prime} }\) and \({{{{\mathcal{C}}}}}_{33{\prime} }\) via AQ, as shown in Fig. 2. This configuration allows us to prepare the 6-qubit QSS state shown by Eq. (5). We share the six states (\(\left\vert +\right\rangle\), \(\left\vert -\right\rangle\), \(\left\vert R\right\rangle\), \(\left\vert L\right\rangle\), \(\left\vert H\right\rangle\), and \(\left\vert V\right\rangle\)) within the 6-qubit QSS system. Figure 4a presents the measurements of the trace distance from the reduced density matrix of each qubit to the maximally mixed state with the average trace distance of 0.06 ± 0.03. For every qubit, we measure the reduced density matrices by the expectation values of the Pauli matrices. In our proposal, the initial state being shared can be recovered to any qubit by local operations and classical communication. We transfer the six initial states to A, 1, 2, \(2{\prime}\), 3, \(3{\prime}\) qubits, respectively. The data shown in Fig. 4b produces the average teleportation fidelity of 0.85 ± 0.03, which is obtained by the projection measurements on the unmasked qubit. The fidelity of the unmasking process is mainly limited by the first CNOT gate \({{{{\mathcal{C}}}}}_{21}\). Using deterministic CNOT gate or increasing the visibility of quantum interference can further improve the fidelity. Unmasking process in a 4-qubit system is demonstrated (see Supplementary Note 5 for details).

Fig. 4: QIM enables 6-qubit QSS.
figure 4

a We share six eigenstates of three Pauli matrices into a 6-qubit hyperentangled system and show the trace distance of the reduced density matrix of each qubit from the maximally mixed state. b The experimental results of unmasking. We pass each of the six initial states to six different qubits and display the fidelity of each process. The error bar indicates 1 standard deviation (obtained from the Poissonian statistics of the detected four-photon counts).

Full size image

Conclusion

We have proposed two QIM schemes for the 4-partite system and one for the tripartite system, going beyond no-masking theorem. Experimentally, we have verified the existence of a complete quantum masker in the 4-qubit system and meticulously tested the theoretical predictions, therefore extending the QIM scheme to the multiqubit regime and providing a solid foundation for future verification of high-dimensional quantum information processing51,52,53,54,55,56,57,58,59,59,60. We present an experimental implementation of QIM-based 6-qubit QSS, which also shows the wide application prospect of QIM in the information security. In ref. 15, a stronger version of k-uniform QIM in multipartite systems has been proposed, which requires that the original information remains inaccessible to any subset of subsystems containing k or fewer participants. Our work can be regarded as a 1-uniform QIM, and stronger QIM is expected in the future.

Methods

Introducing the ancillary qubit and \({{{{\mathcal{C}}}}}_{1A}\)

The operations in the second and third steps of QIM could be written as following:

$$\left(\alpha {\left\vert H\right\rangle }_{1}+\beta {\left\vert V\right\rangle }_{1}\right){\left\vert g\right\rangle }_{1} \mathop {\to} \limits_{ {{{\rm{introducing}}}}\,{{{\rm{qubit}}}}\,A}^{{{{\rm{second}}}}\,{{{\rm{step}}}}} \left(\alpha {\left\vert H\right\rangle }_{1}+\beta {\left\vert V\right\rangle }_{1}\right){\left\vert +1\right\rangle }_{A}\\ \mathop {\to} \limits_{{{{\rm{CNOT}}}}\,{C}_{1A}}^{{{{{\rm{third}}}}\,{{{\rm{step}}}}}}\alpha {\left\vert H\right\rangle }_{1}{\left\vert +1\right\rangle }_{A}+\beta {\left\vert V\right\rangle }_{1}{\left\vert -1\right\rangle }_{A}$$
(6)

In the experiment, the introduction of the ancillary qubit A encoded in the orbital angular momentum (OAM) degree of the photon-1 and the implementation of the second CNOT gate \({{{{\mathcal{C}}}}}_{1A}\) are together implemented by the combination of a q-plate sandwiched by two quarter-wave plates (QWPs) in the following state transfer process:

$$\left(\alpha \left\vert H\right\rangle +\beta \left\vert V\right\rangle \right)\left\vert g\right\rangle \mathop {\to }\limits^{1{{{\rm{st}}}}\,{{{\rm{QWP}}}}}\left(\alpha \left\vert L\right\rangle +\beta \left\vert R\right\rangle \right)\left\vert g\right\rangle \mathop {\to }\limits^{{{{\rm{q}}}}-{{{\rm{plate}}}}}\alpha \left\vert R\right\rangle \left\vert +1\right\rangle +\beta \left\vert L\right\rangle \left\vert -1\right\rangle \\ \mathop {\to }\limits^{2{{{\rm{nd}}}}\,{{{\rm{QWP}}}}}\alpha \left\vert H\right\rangle \left\vert +1\right\rangle +\beta \left\vert V\right\rangle \left\vert -1\right\rangle .$$
(7)

All the above three processes in expression (7) are deterministic, therefore, the overall operation in the second and third steps of QIM is also in a deterministic manner.

OTPC: the OAM-to-polarization converter

The OAM-to-polarization converter (OTPC) is combined by a HWP, an interferometer, a Q-plate and a QWP as shown in Fig. 2. The interferometer consists two double-path PBS, two Dove prisms rotated by  ± π/8 with respect and an HWP. States transform in the interferometer obey the following rules from the input mode to the output mode:

$$\left\vert H\right\rangle \left\vert +1\right\rangle \to {e}^{i\pi /4}\left\vert V\right\rangle \left\vert -1\right\rangle ,\\ \left\vert H\right\rangle \left\vert -1\right\rangle \to {e}^{-i\pi /4}\left\vert V\right\rangle \left\vert +1\right\rangle ,\\ \left\vert V\right\rangle \left\vert +1\right\rangle \to {e}^{-i\pi /4}\left\vert H\right\rangle \left\vert -1\right\rangle ,\\ \left\vert V\right\rangle \left\vert -1\right\rangle \to {e}^{i\pi /4}\left\vert H\right\rangle \left\vert +1\right\rangle .$$
(8)

The transform process is guided by polarization DOF and such a transform is deterministic. Therefore, the state transform in the interferometer is also in a deterministic manner. Then, the state conversion process by our element of OTP could be written step by step in the following form:

$$ \left\vert H\right\rangle \left(\alpha \left\vert +1\right\rangle +\beta \left\vert -1\right\rangle \right)\\ \mathop {\to }\limits^{{{{\rm{HWP}}}}}\frac{1}{\sqrt{2}}\left(\left\vert H\right\rangle +\left\vert V\right\rangle \right)\left(\alpha \left\vert +1\right\rangle +\beta \left\vert -1\right\rangle \right),\\ \mathop {\to }\limits^{{{{\rm{interferometer}}}}}\frac{1}{\sqrt{2}}\left[\alpha {e}^{i\pi /4}\left\vert V\right\rangle \left\vert -1\right\rangle +\beta {e}^{-i\pi /4}\left\vert V\right\rangle \left\vert +1\right\rangle +\alpha {e}^{-i\pi /4}\left\vert H\right\rangle \left\vert -1\right\rangle +\beta {e}^{i\pi /4}\left\vert H\right\rangle \left\vert +1\right\rangle \right],\\ =\frac{{e}^{-i\pi /4}}{\sqrt{2}}\left[\alpha \left(\left\vert H\right\rangle +i\left\vert V\right\rangle \right)\left\vert -1\right\rangle +\beta \left(i\left\vert H\right\rangle +\left\vert V\right\rangle \right)\left\vert +1\right\rangle \right]\\ \mathop {\to }\limits^{{{{\rm{Q}}}}-{{{\rm{plate}}}}}\frac{1}{\sqrt{2}}\left[\alpha \left(\left\vert H\right\rangle -i\left\vert V\right\rangle \right)+\beta \left(-i\left\vert H\right\rangle +\left\vert V\right\rangle \right)\right]\left\vert g\right\rangle ,\\ \mathop {\to }\limits^{{{{\rm{QWP}}}}}\left(\alpha \left\vert H\right\rangle +\beta \left\vert V\right\rangle \right)\left\vert g\right\rangle .$$
(9)

As every step is deterministic, the whole conversion process is deterministic in the form:

$$\left\vert H\right\rangle \left(\alpha \left\vert +1\right\rangle +\beta \left\vert -1\right\rangle \right)\to \left(\alpha \left\vert H\right\rangle +\beta \left\vert V\right\rangle \right)\left\vert g\right\rangle .$$
(10)