Efficient computation using spatial-photonic Ising machines with low-rank and circulant matrix constraints

Abstract

Spatial-photonic Ising machines (SPIMs) have shown promise as an energy-efficient Ising machine, but currently can only solve a limited set of Ising problems. There is currently limited understanding on what experimental constraints may impact the performance of SPIM, and what computationally intensive problems can be efficiently solved by SPIM. Our results indicate that the performance of SPIMs is critically affected by the rank and precision of the coupling matrices. By developing and assessing advanced decomposition techniques, we expand the range of problems SPIMs can solve, overcoming the limitations of traditional Mattis-type matrices. Our approach accommodates a diverse array of coupling matrices, including those with inherently low ranks, applicable to complex NP-complete problems. We explore the practical benefits of the low-rank approximation in optimisation tasks, particularly in financial optimisation, to demonstrate the real-world applications of SPIMs. Finally, we evaluate the computational limitations imposed by SPIM hardware precision and suggest strategies to optimise the performance of these systems within these constraints.

Introduction

The demand for computational power to solve large-scale optimization problems is continually increasing in fields such as synthetic biology¹, drug discovery², machine learning³, and materials science^4,5. However, many optimization problems of practical interest are NP-hard, which means that the resources required to solve them grow exponentially with the size of the problem⁶. At the same time, artificial intelligence systems, including large language models with a rapidly increasing number of parameters, are leading to unsustainable growth in power consumption in data centers⁷. This has spurred interest in analog physical devices that can address these computational challenges with much higher power efficiency than that of classical computers. Various physical platforms are being explored, including exciton-polariton condensates^8,9,10,11,12, lasers^13,14,15, optoelectronic oscillators^16,17, CMOS ring oscillators^18,19, and degenerate optical parametric oscillators^20,21,22. Many of these platforms are known as Ising machines, which aim to solve an optimization problem called the Ising problem by minimizing the Ising Hamiltonian:

$$H=-{\sum}_{i,j}^{N}{J}_{ij}{s}_{i}{s}_{j}+{\sum}_{i}^{N}{h}_{i}{s}_{i},$$

(1)

where spins s_i = ±1. Although this problem originates from a model of ferromagnetism, where the first term is the coupling term with the coupling strengths determined by matrix J and the second term represents the external magnetic field of strength h, many NP problems have been mapped to it with only polynomial overhead²³, making it highly significant beyond its original context.

Ising machines based on spatial light modulators (SLMs), known as spatial-photonic Ising machines (SPIMs), have shown their effectiveness in finding the ground state of Ising Hamiltonians, mainly due to their scalability²⁴. The principle of operation of SPIM is as follows. A coupling matrix J and a set of random initial spin configuration {s_i} are first encoded by SPIM hardware. SPIM then rapidly computes the current Ising Hamiltonian H through optical means. This Hamiltonian value is then transmitted into a digital computer, which must implement some algorithm that determines how spin configuration will be modified based on the H value. The modified spin configuration is then re-encoded in SPIM hardware, and this iteration continues until H converges to the desired minimum value. Experimentally, current SPIM implementations typically encode the interaction matrix J by modulating the amplitude at each pixel of the incident wave emitted by the laser using an amplitude-modulating mask. The wave is then incident on a reflective SLM that imprints a binary phase shift ϕ_i ∈ {0, π} that corresponds to each spin s_i∈ {+1, −1} onto each pixel of the wave. The Hamiltonian value can be read from a camera device that measures the intensity of the wave. This is used to inform a digital algorithm, such as simulated annealing, to determine how to modify the current spin configuration to find states with lower Hamiltonian. The process of computing Hamiltonian optically and determining the next spin flip digitally continues iteratively until convergence or a sufficiently low energy state has been found. A schematic of this process is shown in Fig. 1.

Fig. 1: Schematic of SPIM.

A laser beam passes through an amplitude-modulating mask encoding the coupling matrix J of the Ising problem and then reflects on a binary-phase-modulating SLM, which encodes the current spin configuration. Intensity measurements of this resultant beam by a charged-coupled device (CCD) camera allow the Hamiltonian H of the current spin configuration to be calculated. Further experimental details can be found in refs. ^15,24,25.

The main advantage of SPIM lies in its ability to rapidly compute the Hamiltonian value of any given coupling matrix and set of spin configurations. In this paper, we mainly study a theoretical model of SPIM, which considers SPIM as optical hardware that provides us with fast access to Hamiltonian values but neglects most experimental details that may limit energy resolution. However, while considering this theoretical model, we also considered the analog hardware nature of SPIM and would consider the implication of its precision limitations on its capability in this paper.

One of the main limitations of current experimental implementations of SPIM is that they primarily use Mattis-type coupling matrices^15,24,25. The Mattis-type matrix J is defined as the outer product of two identical vectors:

$${J}_{ij}={\xi }_{i}{\xi }_{j}.$$

(2)

This formulation results in a rank-1 matrix with N degrees of freedom, where N is the dimensionality of the vector ξ. Still, the coupling matrix of an Ising Hamiltonian can be any real symmetric matrix with zeros on its diagonal in general, encompassing up to N(N − 1)/2 degrees of freedom and a rank that does not exceed N. Hence, this restriction of only using Mattis-type matrices significantly limits the variety of Ising Hamiltonians that SPIMs can effectively realize.

Recent advancements have expanded the types of matrices that SPIMs can implement, thanks to innovations like the quadrature method²⁶, the correlation function method²⁷, and the linear combination method²⁸. The quadrature method separates the amplitude-modulating mask and the SLM into two regions, as shown in Fig. 2a. The first half of the amplitude-modulating mask is denoted by vector ξ while the second half is denoted by η. Both regions of the SLM imprint an identical set of phases {ϕ_i} where ϕ_i ∈ {0, π} (which means that the maximum number of spins allowed for a given SLM is halved), but in the second region, an arbitrarily chosen r-th pixel that encodes spin s_r is imprinted with phase shift of ${\phi }_{r}\in \{\frac{\pi }{2},\frac{3\pi }{2}\}$ instead. This changes the form of coupling matrix elements J_ij to:

$${J}_{ij}=\left\{\begin{array}{l}2{\xi }_{i}{\xi }_{j}-2{\eta }_{i}{\eta }_{j},\quad \,{{\mbox{for}}}\,i=r\,{{\mbox{or}}}\,j=r\,{{\mbox{and}}}\,i\ne j \\ 2{\xi }_{i}{\xi }_{j}+2{\eta }_{i}{\eta }_{j},\quad \,{\mbox{otherwise}}\,\quad \hfill\end{array}\right.$$

(3)

where {ξ_i} and {η_i}, known as quadrature components, are freely chosen by setting appropriate amplitude modulation in the first and second region of the amplitude-modulating mask. This increases the number of free variables to 2N but is still significantly smaller than N(N − 1)/2 for larger N values. Furthermore, for a given coupling matrix J_ij, it is not always clear whether and how it can be decomposed into quadrature components that, when recombined, accurately reproduce the desired matrix.

Fig. 2: Schematics of SPIM variants.

a illustrates the quadrature method²⁶. The amplitude-modulating mask was divided into two regions, encoding vectors {ξ_i} and {η_i} respectively. Spin configurations {ϕ_i} are encoded identically in the two regions on the SLM, but with one arbitrary spin having a phase shift of π/2 relative to all other spins. b illustrates the correlation function method²⁷. The SLM encodes both the spin configurations {ϕ_i} and the Mattis vector elements {ξ_i} by rotating each ϕ_i by an angle $\arccos ({\xi }_{i})$. A function G in the coupling matrix is first inverse Fourier transformed into a distribution function g(u) where u is the spatial coordinate in the focal plane, and then digitally integrated with intensity measurement I to produce the Hamiltonian H. c illustrates the linear combination method²⁸. The coupling matrix is decomposed into a linear combination of many Mattis-type matrices. Each Mattis-type matrix is individually implemented and the intensity measurements from all linear components are summed digitally to produce the overall Hamiltonian.

In contrast, the correlation function method allows for the evaluation of matrices characterized by components of the form

$${J}_{ij}=G({{{{\bf{x}}}}}_{i}-{{{{\bf{x}}}}}_{j}){\xi }_{i}{\xi }_{j},$$

(4)

where G(x_i − x_j) can be an arbitrary function, and x_i is the position of the ith pixel on the focal plane. The Ising Hamiltonian can be effectively evaluated using the correlation function method by calculating the correlation function of measured intensity values from SPIM against a distribution function g, derived via the inverse Fourier transform of the function G(x_i − x_j). The schematics of this method are shown in Fig. 2b. While this method broadens the range of matrices that can be represented, it introduces a limitation: the dependency of the additional factor G solely on the difference between focal plane coordinates x_i − x_j restricts output to matrices representing problems with two-dimensional translation invariance. Consequently, this method can only represent Ising problems with periodic geometrical properties.

The linear combination method, on the other hand, theoretically allows for the representation of arbitrary matrices. This is achieved by decomposing the required coupling matrix into a linear combination of Mattis-type matrices:

$${J}_{ij}={\sum}_{k=1}^{R}{\lambda }_{k}{\xi }_{i}^{(k)}{\xi }_{j}^{(k)}.$$

(5)

Each Mattis-type matrix is then sequentially realized in the SPIM, and all outputs are electronically combined to produce the desired Ising Hamiltonian with the accurate coupling matrix, as shown in Fig. 2c. Given that rank(A + B) ≤ rank(A) + rank(B), and ${{{\rm{rank}}}}({{{{{\boldsymbol{\xi }}}}}^{(k)}}^{T}{{{{\boldsymbol{\xi }}}}}^{(k)})=1$, the rank of J is bounded by R. Theoretically, if rank R = N, any arbitrary matrix J can be represented, although the number of optical adjustments and readouts required also scales as O(N). Therefore, it is crucial to investigate whether computationally challenging problems of fixed rank R, which does not increase with problem size, can be represented. This highlights the potential of SPIM to solve challenging optimization problems that can be mapped to an Ising model with a low-rank coupling matrix.

Many NP-complete problems have already been mapped to Ising models²³; however, for effective implementation on SPIMs, these Ising models must have coupling matrices that are either low-rank or circulant. This paper compares the performance metrics of existing Ising machines and identifies computationally significant problems suitable for efficient implementation on SPIM hardware or other hardware with similar coupling matrix limitations. These include problems corresponding to Ising models with inherently low-rank coupling matrices and discuss the practical limitations of such models due to the increasing precision requirements of SPIM hardware. In addition, we examine the feasibility of finding approximate solutions to computational challenges by approximating them with low-rank Ising models, and apply this method to the portfolio optimization problem in finance. We also introduce a new variant of an NP-hard problem, the constrained number partitioning (CNP) problem, as a suitable benchmark problem for future SPIM hardware, and address translationally invariant problems that can be effectively resolved using the correlation function method with SPIMs.

Results and discussion

SPIM performance, advantages, and generality

By exploiting the properties of light, such as interference and diffraction, SPIMs and other SLM-based devices perform computations in parallel, providing significant speed advantages over electronic systems.

SPIMs use spatial light modulation to emulate Ising problems, which are fundamental to various optimization and machine learning tasks^15,25. They optically compute the Ising Hamiltonian from the phase-modulated image of an amplitude-modulated laser beam. Light incident on the ith site of the spatial light modulator with an amplitude ξ_i is phase-modulated to take Ising spin states. SPIMs can efficiently process all-to-all interactions across tens of thousands of variables, with the computational time for calculating the Ising energy H scaling as ${{{\mathcal{O}}}}(N)$ for N spins^29,30. However, SPIMs are optimized for Ising problems with either rank-one interaction matrices, Eq. (2), or low-rank R interaction matrices, Eq. (5), using multiplexing techniques^28,29. This still offers a computational advantage compared to conventional ${{{\mathcal{O}}}}({N}^{2})$ CPU operations if R ≪ N. Despite the limitations to low-rank problems, using SPIMs and similar devices for combinatorial optimization has a significant advantage over other annealers.

The SPIM optical device comprises a single spatial light modulator, a camera, and a single-mode continuous-wave laser. The power consumption of an SLM (model Hamamatsu X15213 series) is 15 W. The power consumption of a charge-coupled device camera (model Basler Ace 2R) is 5W. The power consumption of a laser (Thorlabs HeNe HNL210LB) is 10 W. Thus, the overall SPIM power consumption is 30 W. This can be compared with the 16 kW needed to run a D-WAVE system³¹.

Table 1 provides a comprehensive comparison of various Ising machines in terms of their scale, programmability, resolution of coupling, time-to-solution (TTS), energy-to-solution (ETS), and power consumption metrics. Compared to the most well-established Ising machines, such as the coherent Ising machine (CIM) and D-Wave, SPIM already demonstrates lower power consumption and good scalability. Furthermore, SPIM can also represent spin couplings with greater resolution, the importance of which will be further explored in Section “Limitation of Low Rank Matrix Mapping”.

Table 1 Ising machine performance comparison

Although this paper focuses on SPIMs, the results apply to other alternative analog Ising machines that use similar methods of generating coupling matrices. Specifically, these machines may also employ SLM and techniques that allow the realization of low-rank interaction matrices through the direct implementation of rank-one matrices or the linear combination of multiple rank-one matrices. The problems we discuss in our paper extend their applicability to various analog computational platforms that share these experimental foundations.

Having established SPIMs’ general performance and benefits, we now focus on a critical subset of problems characterized by inherently low-rank structures.

Inherently low rank problems

Low rank graphs

Given the advantages of optical annealers based on spatial light modulation, as previously discussed, it is crucial to understand the structure of Ising coupling matrices. Every Ising coupling matrix J can be associated with the (weighted) adjacency matrix of an underlying (weighted) graph. One can then define the rank of a graph by identifying it with the rank of its adjacency matrix. For graphs with identical connectivity, the unweighted version will generally have a different rank from the weighted graph. We proceed by surveying some known results about low-rank graphs.

In the unweighted case (corresponding to purely ferromagnetic or antiferromagnetic Ising problems), the structure of low-rank graphs appears to be highly constrained. For example, the only rank two graphs are the complete bipartite graphs. Similarly, the only rank three graphs are the complete tripartite graphs³². The complete graph has full rank but can be reduced to a rank one graph by adding diagonal elements to the adjacency matrix (see Section “Decomposition of Target Coupling Matrix”).

Introducing weights at the edges of the graph can strongly influence the rank. For example, by placing weights on the edges of complete bipartite graphs, any rank between 2 and N can be achieved³³.

Graphs with weights that are  +1 or  −1 are known as signed graphs³⁴. Signed graphs that cluster into k groups of vertices that have a positive coupling to vertices within the group and a negative coupling to vertices outside have been shown to have a rank at most k³⁵.

The examples above show that most known low-rank graphs possess a very special structure which limits the range of computational tasks that can be implemented using such graphs. An example of a hard optimization task with a low rank is given by Hamze et al.³⁶. They proposed constructing Ising problems with tunably hard coupling matrices with exactly known rank. This family of constructed Ising problems is known as the Wishart planted ensemble, and they show a hardness peak for relatively small rank

$$R\approx 1.63+0.073N,$$

(6)

where N is the number of spins. This is not ideal as the required rank will increase linearly with the size of the problem N to produce the hardest problems, but it could still serve as a benchmark for small-scale SPIM-type devices since at N ≈ 100, the hardest problem only has rank R ≈ 8.

Weakly NP-complete problems and hardware precision limitation

Yamashita el al.²⁸ proposed a mapping from the knapsack problem with integer weights to an Ising problem with a coupling matrix J that can be represented by Eq. (5) with rank(J) = 2, which does not grow with the size of the problem. The problem is defined as follows: Given a set of items, each having value v_i and integer weight w_i > 0, we would like to find a subset of the items that maximizes the total value of items in the subset while satisfying a constraint where the total weight of items in the subset is not greater than a given limit W. The optimization version of the knapsack problem with integer weights is known to be NP-hard²³. Hence, it was argued that the linear combination method can efficiently implement the Ising formulation of NP-hard problems on SPIM.

Following a similar mapping strategy, we note that it is possible to use a single rank-1 Mattis-type matrix to represent the NP-complete number partitioning problem (NPP), which can be stated as follows: given a set of N positive numbers, is there a partition of this set of numbers into two disjoint sets such that the sums of elements in each subset are equal? This can be easily mapped to the minimization problem of the Ising Hamiltonian ${H}_{{{{\rm{NPP}}}}}({{{\bf{s}}}})={\left({\sum }_{i}^{N}{n}_{i}{s}_{i}\right)}^{2}$, where n_i are numbers given in the set, and s_i ∈ { −1, +1} are Ising spins, which denote which subset n_i is assigned to. This Ising Hamiltonian has a coupling matrix J_ij = −n_in_j, which is of the Mattis-type, so one would expect that SPIM can readily implement any number partitioning problem without using any special rank-increasing methods mentioned in the introduction.

However, these two examples do not demonstrate that SPIM can efficiently implement computationally intractable NP-hard problems. For a number partitioning problem with N integers in the range [1, S], there exists an algorithm that solves the problem in time scaling like ${{{\mathcal{O}}}}(NS)$³⁷. This is known as a pseudo-polynomial time algorithm because if we consider the number of binary digits L required to represent the largest integer S in the problem, then it is given by $L=\lceil {\log }_{2}S\rceil$. The algorithm has running time scaling like ${{{\mathcal{O}}}}(N{2}^{L})$, which still grows exponentially as L increases.

Problems with such pseudo-polynomial time algorithms belong to the weakly NP-complete class, for which increasing problem size alone (in terms of N for the number partitioning problem) is insufficient to make it computationally hard. These problems are only computationally intractable (i.e., having only an algorithm whose run time grows exponentially) if the number of digits used to represent the maximum input L grows. If the number of digits representing the maximum input is allowed to grow, in both of the above mappings to the Ising Hamiltonian, the number of digits in the coupling matrix elements J_ij will also have to grow.

Hence, to simulate a weakly NP-complete problem whose solution requires exponentially growing resources on a classical computer, the precision of SPIM optical hardware will need to grow to encode larger integers represented by more binary digits L involved in these problems. This is unlikely to be realized in experiments because the precision with which coupling matrices can be implemented in SPIM is a fixed number of significant digits, likely much smaller than problem input sizes of practical interest.

Given that NPP with limited binary precision is not NP-hard, studying the statistical properties of random NPP instances is still interesting because it may inform potential modifications or constraints to the problem that can increase its complexity. Historically, NPP was analyzed by Mertens³⁸, with subsequent extensive rigorous study by Borgs et al.³⁹. It was found that the average hardness of a randomly generated NPP instance, where N integers are uniformly randomly selected from the range [1, 2^L], is controlled by a parameter $\kappa =\frac{L}{N}$. When κ > κ_c, they require ${{{\mathcal{O}}}}({2}^{N})$ operations to solve, but when κ < κ_c, average problem instances require ${{{\mathcal{O}}}}(N)$ operations to solve. We demonstrate a short basic derivation of the critical parameter κ_c = 1 in the limit of N → ∞ below, which is the only parameter responsible for characterizing the phase of the problem, whether it is a “hard” phase (κ > κ_c) or “easy” phase (κ < κ_c).

One can introduce the signed discrepancy D of the numbers, given the binary variables s_i⁴⁰ as

$$D={\sum }_{i=1}^{N}{n}_{i}{s}_{i}.$$

(7)

D can be interpreted as the final distance to the origin of a random walker in one dimension who takes steps to the left $\left({s}_{i}=-1\right)$ or to the right $\left({s}_{i}=+1\right)$ with random stepsizes $\left({n}_{i}\right)$. One can calculate the average number of walks that ends at D as

$$\Omega (D)=\mathop{\sum}_{\left\{{s}_{i}\right\}}\left\langle \delta \left(D-{\sum}_{i=1}^{N}{n}_{i}{s}_{i}\right)\right\rangle,$$

(8)

where 〈 ⋅ 〉 denotes averaging over the random numbers n and δ is the Kronecker-delta function. Just as in a typical random NPP instance, all n_i’s are identically and uniformly selected from the range [1, 2^L], so in subsequent calculations, we use the notation 〈n〉 = 〈n_i〉 for all integer i ∈ [1, N]. For fixed $\left\{{s}_{i}\right\}$ and large N, the distribution of D can be treated as Gaussian with mean

$$\langle D\rangle =\langle n\rangle {\sum}_{i}^{N}{s}_{i}$$

(9)

and variance

$$\left\langle {D}^{2}\right\rangle -{\langle D\rangle }^{2} = N\left(\left\langle {n}^{2}\right\rangle -{\langle n\rangle }^{2}\right)\\ = \frac{N}{12}{2}^{2L}\left(1+{{{\mathcal{O}}}}\left({2}^{-L}\right)\right).$$

(10)

To obtain an explicit expression for the average number of walks that ends at a distance D from the origin, Ω(D), we note that the summation over all {s_i} in Eq. (8) is a summation over all possible random walk trajectories. For a random walk with a large number of steps N, its possible trajectories are dominated by those where ∑_is_i = 0, so in the summation, we only consider such terms and $\left\langle D\right\rangle =0$. Hence, for such terms, to the leading order in L, one can express the probability of the walk ending at a distance D as

$$p(D)=\frac{2\sqrt{3}}{{2}^{L}\sqrt{2\pi N}}\exp \left(-\frac{6{D}^{2}}{{2}^{2L}N}\right).$$

(11)

For a given set of integers {n_i}, the random walk must end at even (odd) D values if ∑_in_i is even (odd). Hence, to approximate the discrete probability distribution of D with the above Gaussian probability density p(D), the probability of ending the random walk at distance D should be 2p(D) for any given D value. Hence we can obtain an explicit expression for the average number of walks that ends at a distance D from the origin, Ω(D):

$$\Omega (D)={2}^{N}2p(D).$$

(12)

One can get:

$${\log }_{2}\Omega (0)=N\left({\kappa }_{c}-\kappa \right),$$

(13)

with the final expression

$${\kappa }_{c}=1-\frac{{\log }_{2}N}{2N}-\frac{1}{2N}{\log }_{2}\left(\frac{\pi }{24}\right).$$

(14)

This value, denoted as κ_c, is crucial for indicating the phase transition. When κ < κ_c, on average, there exists an exponential number of perfect partitions where the discrepancy D = 0; however, when κ > κ_c, none exists.

Another essential aspect of such a simple random walk model is the possibility of tracing the effects of finite size. For instance, even with a relatively small system size of around N ≈ 17 units, the critical value of κ_c ≈ 0.9 is due to the finite-size scaling window of the transition. These effects become more pronounced in hardware systems that operate with limited variables.

This statistical analysis aligns with our previous discussion, which suggested that to generate computationally hard NPP instances, both the number of integers N and binary digits L must increase, which can be challenging in practice. Nevertheless, despite its limitations, NPP is a suitable platform for integrating additional modifications or constraints, making it adaptable for deployment on hardware with limited physical resources.

To modify the NPP so that hard instances can be implemented on precision-limited SPIM hardware, one can consider the so-called constrained number partitioning problem (CNP), which will be discussed in more detail in Section “Constrained Number Partitioning Problem”. It is a variation of the original NPP where, apart from splitting integers into groups with equal sums, we also aim to meet an additional requirement known as a cardinality constraint. This constraint ensures that the difference between the numbers of integers in one group and another equals a specific value.

Limitation of low rank matrix mapping

Our investigation in Section “Low Rank Graphs” suggests that low-rank graphs often exhibit highly constrained connectivity, such as complete bipartite or tripartite graphs. This is expected since a low-rank adjacency matrix represents a low-dimensional manifold with reduced degrees of freedom. Consequently, the problems they represent are not likely to be NP-hard. Section “Weakly NP-Complete Problems and Hardware Precision Limitation” further indicates that to describe a problem which requires exponentially growing time to solve on a classical computer, it is necessary to either allow the rank or the precision of each matrix element to increase with the problem size. This evidence strongly suggests the following hypothesis may be true: “It is not possible to find constant integers L and K such that there exists an Ising problem with coupling matrix J with rank K and maximum input precision $L=\lceil {\log }_{2}\bigl({\max }_{i,j}({J}_{ij})\bigr) \rceil$ such that the number of operations required to find its ground state scales as ${{{\mathcal{O}}}}\left({2}^{N}\right)$, where N is the number of spins in the Ising problem.” Given this understanding, it is still possible to utilize SPIM to tackle NP-hard problems with the following two approaches:

• 1. Find approximate solutions to hard problems by approximating them with a low-rank matrix and then solving the approximate problem with SPIM. This is discussed in Section “Low Rank Approximation”.

• 2. Identify NP problems whose precision requirement L and rank requirement K grow slowly as the problem size N increases while maintaining their hardness. One possible candidate problem is presented in Section “Constrained Number Partitioning Problem”.

Low rank approximation

Building on our understanding of low-rank problems, this section explores the practical application of low-rank approximations.

Decomposition of target coupling matrix

Many strongly NP-complete problems have been mapped to Ising problems with only polynomial overhead²³. However, the resultant coupling matrices usually have no fixed structure beyond being real and symmetric, so a general method to decompose any target coupling matrix J into the form given by Eq. (5) is required. This can be achieved by singular value decomposition (SVD), which decomposes any matrices J into vectors u and v such that ${J}_{ij}={\sum }_{k = 1}^{R}{\lambda }_{k}{u}_{i}^{(k)}{v}_{j}^{(k)}$, where R is the rank of the matrix J. For any symmetric J, it will lead to u = v, so SVD will produce the smallest possible set of Mattis-type matrices that represents the target matrix⁴¹.

However, SVD gives no upper bound to the number of digits required in components of u or v to represent J, so the problem presented in Section “Limitation of Low Rank Matrix Mapping” still exists. It is not possible to guarantee that a given coupling matrix J can be represented by vectors u^(k) whose precision is limited.

In general, the rank of matrix J will be full rank, so R = N where N is the number of spins in the Ising problem. Note that the diagonal entries of coupling matrix J modify the Ising Hamiltonian by a known constant, since $H({{{\bf{s}}}})={\sum }_{i,j}^{N}{J}_{ij}{s}_{i}{s}_{j}={\sum }_{i,j\ne i}^{N}{J}_{ij}{s}_{i}{s}_{j}+{\sum }_{i}{J}_{ii}$. Hence, one might try to construct a coupling matrix ${{{{\bf{J}}}}}^{{\prime} }={{{\bf{J}}}}+{{{\bf{D}}}}$, where D is a diagonal matrix, chosen so that the rank of the coupling matrix ${{{{\bf{J}}}}}^{{\prime} }$ is minimized, and then implement this matrix in SPIM. The ground state of this problem will be identical to that of the original problem.

However, the problem of finding the diagonal entries of a real symmetric matrix that minimizes the number of its non-zero singular values is a variant of the additive inverse eigenvalue problem⁴². As far as we know, this particular variant is still an open problem, and the best current result was demonstrated by Philips⁴³, which showed that with 2^N − 1 free diagonal elements, one can set N eigenvalues to 0. Since a N by N coupling matrix can have maximum rank N but only N free diagonal elements, the rank reduction achieved through varying diagonal elements will likely be exponentially smaller than the maximum rank. Hence, in subsequent discussion, we are not going to make use of this technique. However, in principle, one can always convert a given coupling matrix J into ${{{{\bf{J}}}}}^{{\prime} }$ to slightly reduce its rank and then apply the low-rank approximation technique discussed in the following subsections.

How fields influence rank

Ising-type problems with a magnetic field (i.e., a term linear in the spins in the Hamiltonian) can be reduced to a problem without a field by adding an auxiliary spin. The initial Hamiltonian with external field given in Eq.(1) is equivalent (up to a constant difference) to the following Ising Hamiltonian without external field:

$${H}^{{{{\bf{h}}}}}({{{\bf{s}}}})=-\mathop{\sum }_{i,j=0}^{N}{J}_{ij}^{{{{\bf{h}}}}}{s}_{i}{s}_{j},$$

(15)

with ${J}_{i0}^{{{{\bf{h}}}}}={J}_{0i}^{{{{\bf{h}}}}}=-\frac{{h}_{i}}{2}$ and an additional free constant h₀. The auxiliary spin is fixed as s₀ = 1. What is the rank of this new coupling matrix with respect to the original one? Note that the coupling matrix J^h in Eq. (15) is of the form

$$\left(\begin{array}{rc}{h}_{0}&-{{{\bf{h}}}}/2\\ -{{{{\bf{h}}}}}^{T}/2&{{{\bf{J}}}}\end{array}\right).$$

(16)

As long as h₀ ≠ 0, via elementary row and column operations, one can transform

$$\left(\begin{array}{rc}{h}_{0}&-{{{\bf{h}}}}/2\\ -{{{{\bf{h}}}}}^{T}/2&{{{\bf{J}}}}\end{array}\right)\to \left(\begin{array}{rc}{h}_{0}&0\\ 0&{{{\bf{J}}}}-\frac{1}{4{h}_{0}}{{{{\bf{h}}}}}^{T}{{{\bf{h}}}}\end{array}\right)\,,$$

(17)

and hence

$${{{\rm{rank}}}}\,{{{{\bf{J}}}}}^{{{{\bf{h}}}}}={{{\rm{rank}}}}({h}_{0})+{{{\rm{rank}}}}\left({{{\bf{J}}}}-\frac{1}{4{h}_{0}}{{{{\bf{h}}}}}^{T}{{{\bf{h}}}}\right)\le {{{\rm{rank}}}}\,{{{\bf{J}}}}+2.$$

(18)

Low rank approximation of coupling matrices

Given any Ising problem with external fields, we can convert it into another Ising problem with no external field and a coupling matrix with a rank at most two higher. We can then use SVD to decompose the resultant coupling matrix into the linear combination of Mattis-type matrices. This decomposition, in general, produces N terms, where N is the dimension of the coupling matrix, and the precision of each term is not bounded. Under low-rank approximation, we retain only the K largest λ_k terms in the sum produced by SVD, i.e.

$${\widetilde{J}}_{ij}=\mathop{\sum}_{k=1}^{K}{\lambda }_{k}{\xi }_{i}^{(k)}{\xi }_{j}^{(k)},$$

(19)

where K < rank(J), and $\tilde{{{{\bf{J}}}}}$ is the low rank approximation of the exact coupling matrix J. Because now only an approximate solution is required, the precision in ${\xi }_{i}^{(k)}$ can also be limited by truncating excess digits.

The low-rank approximation method was used by Frieze and Kannan⁴⁴ to find an approximate solution to the strongly NP-complete problem of maximum cut, in which one is required to find a partition of the node set V of a graph G(V, E) such that the partition maximizes the total weight of edges that cross the partition. It was shown that even with the precision in ${\xi }_{i}^{(k)}$ limited to multiples of 1/(∣V∣K²), the proposed algorithm can still find an approximate solution within ${{{\mathcal{O}}}}\left(| V{| }^{2}/\sqrt{K}\right)$ of the maximum cut in time polynomial in ∣V∣. However, this method of using low-rank approximation to find approximate solutions to hard problems remains largely unexplored in the context of Ising machines. It is unclear how the number of Mattis-type matrices K and the truncation of ξ^(k) will impact the quality of approximate solutions found by Ising machines and to what extent these two quantities can trade off against each other to maintain the required quality of the approximate solution.

Low-rank approximation of random coupling matrices

To investigate the feasibility of using a low-rank approximation to find approximate solutions to Ising problems with SPIM, a random interaction matrix for an Ising problem was generated and then decomposed into constituent Mattis-type matrices using SVD. Only matrices corresponding to the K largest singular values λ_k were retained, while the remaining matrices were discarded. Each element of the retained Mattis-type matrices was rounded to the nearest 2^−L. This resulted in a rank K approximate matrix with precision L.

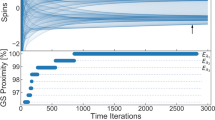
Figure 3 compares the quality of solutions obtained using varying values of K and L. Figure 3a, b show results from the low-rank, limited-precision approximation of a random 1000-vertex unweighted connectivity graph, where each pair of vertices has an equal probability of being connected or unconnected. Figure 3c, d show results from a sparse 3-regular random graph, where each vertex is connected to 3 other random vertices. From Fig. 3a, c, we observe that the quality of solutions obtained from 8-bit precision approximations is indistinguishable from solutions obtained from full-precision calculations, regardless of the rank of the approximate coupling matrix. This suggests that SPIM can still find highly accurate approximate solutions to Ising problems with both dense and sparse coupling matrices, even with limited precision.

Fig. 3: Optimization performance with low rank approximated coupling matrices.

a The energy of approximate solutions is plotted against the rank of the approximate coupling matrix. The exact interaction matrix represents a random, unweighted, undirected graph with 1000 vertices, all with anti-ferromagnetic couplings. The coupling strengths are rounded to the nearest 2⁻⁸ in the approximation. b The energy of approximate solutions is plotted against the precision of the approximate coupling matrix. A full-rank (R = 1000) matrix and two low-rank approximations with ranks R = 256 and R = 64 are used for each precision level. c, d follow the same structure as (a) and (b), but the exact interaction matrix represents a random 3-regular graph, again with all non-zero couplings being anti-ferromagnetic. The semi-transparent bands in (b) and (d) show the 95% confidence interval on mean energy values. Data used to plot this figure can be found in the data tables given in the “Figure 3ab” tab of Supplementary Data 1 file.

This observation is further supported by Fig. 3b, d. It can be seen that with at least 6 bits of precision, SPIM can find low-energy solutions comparable to those found by full-precision machines using the same algorithm. However, the loss of accuracy is more pronounced in dense graphs than in sparse graphs.

The main advantage of SPIM lies in the fast calculation of energy for any given spin configuration. Still, the gradient of energy change with respect to spin flip is not readily accessible to SPIM, so SPIM can only work with gradient-free optimization algorithms. Results shown Figs. 3b, d suggests that given the constraint of available algorithms for SPIM, the precision of at least 6 binary bits will not be a limiting factor of the optimization performance of SPIM hardware.

However, the quality of the approximate solution is highly dependent on the rank of the approximated coupling matrix. In both dense and sparse graphs, the energy of the approximate solution increases rapidly as the rank of the approximate coupling matrix decreases. Therefore, for a general random matrix, the precision of the Mattis-type matrices is not a significant factor in the quality of the approximate solution, but the rank of the approximate matrix is. For a SPIM architecture that computes Ising energy contribution from each rank-1 component by time-multiplexing, this dependence on the rank is likely to lead to much longer computation times per iteration, thus limiting the efficiency of SPIM hardware.

In Section “Low Rank Approximation for Portfolio Optimization”, we discuss a practical application in finance where a low-rank matrix can often approximate the matrix in question, making it suitable for implementation in SPIM hardware.

Low rank approximation for portfolio optimization

Low-rank approximations of covariance matrices S are well studied^45,46,47. If only a small sample of observations is available, and the number of variables N is large, then the sample covariance matrix will include a significant amount of noise. A low-rank approximation can filter out this noise so that the covariances reflect the true underlying structure of the data. Such a technique is commonly used in portfolio optimization⁴⁸, which relies on an accurate covariance matrix between the N assets. In this section, we present a formulation of the portfolio optimization problem for direct encoding into the SPIM hardware, utilizing the low-rank covariance matrix approximation.

Portfolio optimization involves creating an investment portfolio that balances risk and return. The objective is to allocate assets y_i optimally to maximize expected returns μ while minimizing risk φ. The problem is formulated in the Markowitz mean-variance optimization model^49,50,51 with objective function

$$H =(1-\lambda )\varphi -\lambda \mu ,\\ =(1-\lambda ){{{{\bf{w}}}}}^{T}{{{\bf{S}}}}{{{\bf{w}}}}-\lambda {{{{\bf{m}}}}}^{T}{{{\bf{w}}}},$$

(20)

where the scalar λ ∈ [0, 1] quantifies the level of risk aversion, and w_i ∈ [0, 1] with ${\sum }_{i}^{N}{w}_{i}=1$ are portfolio weights that describe the proportion of total investment in each asset. S_ij = Cov(y_i, y_j) is the covariance between the i-th and j-th assets, and m_i is the expected return of asset y_i. The covariance matrix S and return forecast vector m are typically derived from historical time-series data⁵².

Markowitz’s mean-variance portfolio optimization naturally maps to the quadratic unconstrained mixed optimization (QUMO) abstraction⁵³. However, with equal weighting, the problem converts to quadratic unconstrained binary optimization (QUBO). Equal-weighted portfolio optimization, where w_i ∈ {0, 1/q} for q selected assets, has been shown to outperform traditional market capitalization-weighted strategies^54,55,56. In this case, weights w_i can be transformed to Ising spins s_i ← 2qw_i − 1. We extend the model to include a cardinality constraint that limits the portfolio to a specified number of assets, maintaining the QUBO abstraction. This is equivalent to constraining q to a predetermined value. Diversification can be controlled through cardinality constraints, providing an additional mechanism to manage portfolio volatility. The objective function can be expressed as an explicit Ising Hamiltonian

$$H =(1-\lambda ){{{{\bf{w}}}}}^{T}{{{\bf{S}}}}{{{\bf{w}}}}-\lambda {{{{\bf{m}}}}}^{T}{{{\bf{w}}}}+\eta {(q{{{{\bf{1}}}}}^{T}{{{\bf{w}}}}-q)}^{2}\\ ={\sum }_{i,j}^{N}\left(\frac{1-\lambda }{4{q}^{2}}{S}_{ij}+\frac{\eta }{4}\right){s}_{i}{s}_{j}\\ \quad +\mathop{\sum}_{i}^{N}\left(\eta \left(\frac{N}{2}-q\right)-\frac{\lambda {m}_{i}}{2q}+\frac{1-\lambda }{2{q}^{2}}{\sum}_{j}^{N}{S}_{ij}\right){s}_{i}+c,$$

(21)

where parameter η controls the magnitude of the cardinality constraint and c is a constant offset. We can identify the Ising coupling matrix elements as ${J}_{ij}=\frac{1-\lambda }{4{q}^{2}}{S}_{ij}+\frac{\eta }{4}$, and external magnetic field field strength as ${h}_{i}=\eta (\frac{N}{2}-q)-\frac{\lambda {m}_{i}}{2q}+\frac{1-\lambda }{2{q}^{2}}{\sum }_{j}^{N}{S}_{ij}$. By introducing an auxiliary spin to absorb linear fields with the method given in Section “How Fields Influence Rank” and discarding constants, the objective function becomes H = −s^TJ^hs. Realizing portfolio optimization in SPIM architectures requires coupling matrix J to be low rank. This is achieved through low-rank factor analysis (FA), a low-rank approximation technique common in quantitative finance⁴⁵.

To compute coupling matrix J, covariance matrix S is first estimated from historical time-series data on the set of asset returns r(t). However, accurately estimating S from historical data can be challenging due to noise, high dimensionality, and limited data⁴⁶. FA assumes observed data are linearly driven by a small number K of common factors, such that r(t) = c + Bf(t) + ε, where ${{{\bf{c}}}}\in {{\mathbb{R}}}^{N}$ is a constant vector, ${{{\bf{B}}}}\in {{\mathbb{R}}}^{N\times K}$ is the factor loading matrix with K ≪ N, ${{{\bf{f}}}}(t)\in {{\mathbb{R}}}^{K}$ is a vector of low-dimensional common factors and $\varepsilon \in {{\mathbb{R}}}^{N}$ is uncorrelated noise. The unobservable latent variables f(t) capture the underlying patterns shared among the observed variables. FA implies the covariance matrix consists of a positive semi-definite low-rank matrix plus a diagonal matrix such that the transformed covariance matrix is ${{{{\bf{S}}}}}^{{\prime} }={{{\bf{B}}}}{{{{\bf{B}}}}}^{T}+{{\Psi }}$⁴⁷. For low-rank factor analysis, rank(BB^T) ≤ K⁴⁶. The diagonal matrix Ψ becomes a linear field term in the binary formulation, and it follows from Eq. (18) that ${{{{\bf{S}}}}}^{{\prime} }$ remains low rank. Indeed, in the Ising QUBO abstraction with auxiliary variable, coupling matrix J^h has ${{{\rm{rank}}}}\,{{{{\bf{J}}}}}^{h}\le {{{\rm{rank}}}}\,{{{\bf{J}}}}+2\le {{{\rm{rank}}}}\,{{{{\bf{S}}}}}^{{\prime} }+{{{\rm{rank}}}}({{{\bf{1}}}}\otimes {{{{\bf{1}}}}}^{T})+2={{{\rm{rank}}}}\,{{{{\bf{S}}}}}^{{\prime} }+3$. Therefore, the transformed coupling matrix remains low rank.

Covariance matrix S and expected returns vector m are point statistics. We use these to minimize the time-independent objective function (20), or equivalently, the Ising Hamiltonian (21), to obtain the optimal set of portfolio weights. We can then back-test our results on the time-dependent return data r(t) to observe portfolio returns w ⋅ r(t) over time. Figure 4 illustrates the decomposition of the covariance matrix to its low-rank form and shows the proximity of portfolio returns over time constructed in the full-rank and low-rank paradigms. The full universe of stocks can be vast, so decomposing covariance matrices into low-rank forms provides computational advantages in subsequent calculations. For example, the New York stock exchange contains over 2300 stocks, whilst in Fig. 4, we consider only the 503 stocks tracked in the S&P 500 index.

Fig. 4: Portfolio optimization with low rank approximation.

a Frequency histogram of eigenvalues obtained from the covariance matrix of S&P 500 stock data. There are only a few dominating eigenvalues, and most eigenvalues are orders of magnitude smaller than the dominant ones. b Equal-weighted cardinality-constrained portfolios constructed from the full rank covariance matrix S (blue), K = 20 low rank matrix ${{{{\bf{S}}}}}^{{\prime} }$ (orange), and K = 5 low rank matrix (green). The cumulative return percentage of each portfolio is calculated as $\frac{100}{V(0)}{\sum }_{t = 1}^{T}{{{\bf{w}}}}\cdot {{{\bf{r}}}}(t)$, where V(0) is the initial value of the portfolio at t = 0. Here, λ = 0.5, η = 1, and q = 20. The portfolios were built by minimizing Eq. (21) using commercial solver Gurobi. Frequency data for each eigenvalue bin in (a) can be found in Supplementary Data 2 file. The time series data for the full rank, K = 5, K = 20 lines if (b) can be found in the Supplementary Data 3, 4, 5 files respectively.

For a quadratic unconstrained continuous optimization problem, if the coupling matrix is positive semi-definite as the covariance matrix is, then the problem is convex for any linear field term. However, for QUBO problems, even if S and hence J is positive semi-definite, the problem is not necessarily easy to solve. The binary constraint makes the feasible region discrete, not convex, which is why QUBO problems are generally NP-hard. SPIMs derive a temporal advantage over classical computing due to optical hardware implementing fast and energy-efficient computation. This is particularly crucial in high-frequency trading, where optimal portfolios must be calculated over microseconds to minimize latency in placing orders^57,58. We note that while at the moment SPIM hardware is not able to achieve the microsecond time-to-solution (TTS) performance required for high-frequency trading tasks, as shown in Table 1, SPIM is projected to be able to meet this TTS requirement when SLM with higher operating frequency currently under development becomes available.

Constrained number partitioning problem

To further illustrate the utility of SPIMs in tackling complex problems, we introduce the CNP problem, examining its characteristics and computational challenges.

Definition and characteristics of the constrained number partitioning problem

In Section “Weakly NP-Complete Problems and Hardware Precision Limitation”, it was shown that although the Number Partitioning Problem (NPP) can be mapped to an Ising problem with a rank one coupling matrix, its complexity grows as ${{{\mathcal{O}}}}(N{2}^{L})$. Therefore, solving difficult NPP instances would require increasing the precision L of SPIM hardware. The hardness of a random instance of NPP was characterized by Gent et al.⁵⁹ and Mertens⁴⁰, who presented numerical evidence suggesting that the average complexity of a random instance is directly correlated with the probability of a perfect partition. A perfect partition, also known as a perfect solution, is a partition where the difference in the sum of the elements in the two subsets is 0 or 1, meaning that the signed discrepancy D = ∑_in_is_i, as introduced in Eq.(7), is 0 or 1. The studies suggested that when the number of integers N in the problem is large, if the probability of a perfect solution in a random instance tends to 1 (i.e., ${\lim }_{N\to \infty }{\mathbb{P}}\,{({{{\rm{perfect}}}} \, \, {{{\rm{solution}}}})}\,=1$), then the average problem is easy. Conversely, if ${\lim }_{N\to \infty }{\mathbb{P}}\,{({{{\rm{perfect}}}} \, \, {{{\rm{solution}}}})}\,=0$, then the problem is hard. It was rigorously shown that there is a phase transition separating the regimes of the asymptotic existence of a perfect solution, controlled by a parameter κ = L/N, with ${\mathbb{P}}\,{({{{\rm{perfect}}}} \, \, {{{\rm{solution}}}})}\,\to 0$ when κ > κ_c = 1. This analytical study corroborates our previous discussion that when N is large, L must also be large for the problem to be hard.

Borgs et al.⁶⁰ generalized these results to another problem known as the CNP problem. In a random CNP problem, there exists a set of N integers uniformly and randomly chosen in the range [1, 2^L], under the constraint that the set must be partitioned into two subsets whose cardinalities differ by a given value S, known as the bias. The goal is to minimize the difference in the sum of elements in each subset, known as the discrepancy. Given a CNP problem with integers n₁, n₂, . . . , n_N and bias S, it can be mapped to an Ising problem by defining the Ising Hamiltonian

$$H =-{\left(\mathop{\sum }_{i}^{N}{n}_{i}{s}_{i}\right)}^{2}+A{\left(\mathop{\sum}_{i}^{N}{s}_{i}-S\right)}^{2}\\ ={\sum}_{i,j}^{N}\left(-{n}_{i}{n}_{j}+A\right){s}_{i}{s}_{j}-2AS{\sum}_{i}^{N}{s}_{i}+A{S}^{2},$$

(22)

where each spin s_i denotes which subset the number n_i is assigned to. The first term on the first line of Eq. (22) minimizes the discrepancy between sums of two subsets, while the second term enforces the constraint that the cardinalities of subsets must differ by S, as long as constant A is sufficiently large. The second line of Eq. (22) puts the energy into the explicit Ising form, where coupling matrix elements are J_ij = n_in_j − A and there is an external field with field strength − 2AS. By introducing an auxiliary spin as mentioned in Section “How Fields Influence Rank”, the external field term can be subsumed into the coupling term at the cost of increasing the rank of the coupling matrix by up to two and increasing the dimension of the coupling matrix by one. The original coupling matrix has rank two, so this problem will have a coupling matrix of rank up to four when implemented on SPIM hardware, regardless of the number of integers in the problem.

It was found that the probability of a perfect solution for a random CNP instance is controlled by κ and an additional parameter bias ratio b = S/N. It was rigorously shown that asymptotically as N → ∞ when $b > {b}_{c}=\sqrt{2}-1$, it is trivially easy to find the best partition because the bias is so large that it is almost always optimal to assign all largest elements to the smaller subset. This is known as the “ordered” phase. When b < b_c, the probability of existence of a perfect solution has a similar phase transition as in NPP, where ${\mathbb{P}}\,{({{{\rm{perfect}}}} \, \, {{{\rm{solution}}}})}\,\to 0$ when κ > κ_c. However, the critical value κ_c was found to be a function of b, and κ_c moves towards 0 as b increases towards b_c.

This suggests that CNP can be a perfect candidate for implementation on SPIM hardware because an average random CNP instance can be computationally hard even if L ≪ N (i.e., κ ≪ 1) as long as b is sufficiently close to b_c. Two areas need to be explored to establish that this problem is computationally hard and suitable for implementation on SPIM. Firstly, the authors of ref. ⁶⁰ did not rigorously show that the existence of a perfect solution is correlated with the hardness of the CNP problem instance like it is in NPP. Secondly, in a system with finite size N, there will exist a non-zero value of ${\kappa }_{c,\min }$ which leads to the smallest precision L required for the average problem to be hard. This value is obtained when bias ratio b is as close as possible to b_c given that S must be an even or odd integer depending on N. Finite-size effects are likely to make the transition between the easy and the hard phase gradual, with an intermediate region where the probability of having a perfect solution is close to neither 0 nor 1. In the following subsection, we will numerically investigate this phase transition with a finitely sized system and understand the precision requirement for a moderately sized CNP problem that is still computationally hard.

Computational hardness of random CNP instances

As the number of integers N in a CNP problem increases, the probability of finding a perfect partition will undergo a phase transition from 0 to 1, but the critical value of N_c where this happens is expected to increase as bias S of the problem increases because it is increasingly challenging to balance the sums in each subset while fulfilling the constraint of greater cardinality difference. This trend is observed in Fig. 5a. A complete picture of the phase transition landscape is shown in Fig. 5b, which is the probability of the existence of a perfect solution in a random CNP problem with fixed precision L = 12, meaning that all integers are selected uniformly randomly from the region [1, 2¹²], but with various different numbers of integers N and bias S. We can observe a “hard” phase in which the probability of a perfect solution’s existence is low (labeled as region 2 in the color map) and a “perfect” phase in which the probability of a perfect solution’s existence is close to 1 (labeled as region 3). It can be observed that the phase transition between the “hard” and “perfect” phases is not sharp, and there exists an intermediate region where the probability of a perfect solution being present is neither close to 0 nor 1. This can be attributed to the finite system size N. Unlike the theoretical studies presented by Borgs et al.⁶⁰, which depicts the asymptotic behavior when N → ∞, this phase diagram models a finite system implementable in SPIM hardware. From the phase diagram, we observe that region 2, where the probability of a perfect solution’s existence is close to 0, extends into N values much greater than L = 12 used in the simulation. Hence, this numerical experiment suggests that it is possible to realize CNP problem instances with size N much greater than hardware precision L on SPIM and still keep the parameters in region 2, where the probability of a perfect solution being present is very low.

Fig. 5: Perfect solutions in CNP problems.

a The probability of the existence of a perfect solution is plotted against various problem sizes N at fixed values of bias S. b The color map shows the probability of the existence of a perfect solution in a random CNP problem instance with N integers and various bias values, and the integers are chosen uniformly and randomly in the range [1, 2¹²]. The probability at each point in the phase space is calculated over 200 random instances. Three phases are identified in the figure, separated by the orange and red dash lines. Region 1, 2, and 3 correspond to the “ordered”, “hard”, and “perfect” phases proposed in ref. ⁶⁰. Region 1 in the graph is not drawn because it is likely to be trivially easy to find the optimum partition in this region for an average problem instance, so it is not meaningful to investigate the probability of a perfect solution’s existence in this region. Data used to plot (a) and (b) can be found in the data tables given in the “Figure 5a” tab of the Supplementary Data 1 file and in the Supplementary Data 6 file, respectively.

Next, we must understand if problem instances in region 2 represent computationally hard instances. The existing state-of-the-art pseudo-polynomial time algorithm for number partitioning problems is the complete differencing algorithm⁴⁰. As shown in Fig. 6, the algorithm performs the search in a depth-first manner through a tree. The root comprises all integers in a descending order. At each node with more than one element, the node leads to new branches. The left branch takes the difference of the first two elements of the parent node, denoting the decision to assign the two leading elements into two different subsets. The right branch takes the sum of the first two elements of the parent node, denoting the decision to assign the two leading elements to the same subset. The only integer in each leaf node indicates the final discrepancy corresponding to the partition defined by the route from the root to the leaf.

Fig. 6: Schematic search tree of the complete differencing algorithm.

Orange branch leads to the perfect solution, which has the best possible discrepancy of 1. If the algorithm searches from left to right, as shown here, then it will terminate after searching the first branch since the perfect solution will be found, and all other branches will be discarded.

This algorithm has a worst-case time complexity that grows exponentially with N but relies on pruning rules to help it avoid searching through large chunks of the solution space that cannot produce a solution better than the current best-found solution. For example, an entire branch can be discarded when the difference between the largest element and the sum of all other elements exceeds the best-known solution. It is known that for random NPP instances that have size N much greater than the precision limit L, this algorithm, on average, only needs to visit ${{{\mathcal{O}}}}(N)$ number of nodes in the search tree to find the optimal solution. This remarkable reduction in search time from the worst case of ${{{\mathcal{O}}}}({2}^{N})$ to ${{{\mathcal{O}}}}(N)$ is because the probability of the existence of a perfect solution is close to 1 in the average case (when N ≫ L). Hence, the algorithm will likely quickly find the perfect solution, which has the smallest possible discrepancy between sums of the two partitions (0 or 1), and terminate because no better solution is possible, thus pruning away the vast majority of the solution space.

This algorithm has also been adapted for a particular case of CNP known as the balanced number partitioning problem, where the bias S is set to 0⁶¹. The adapted algorithm is still efficient when N ≫ L. This is unchanged from the NNP case - because the algorithm will likely find the perfect solution quickly and terminate before searching an exponential number of nodes in the solution space. Hence, it is reasonable to expect that even in the case of CNP, to avoid searching the exponentially large solution space, there needs to exist exponentially many degenerate optimal solutions scattered in the solution space so that any “good” algorithm can quickly find one of them and terminate before visiting an exponential number of nodes. In other words, if the number of degenerate ground states is not growing exponentially with N, while the total solution space is constantly increasing as 2^N, this suggests that the problem will be computationally hard.

Here, we investigate two versions of the CNP problem. The first is a decision problem: given a CNP instance, determine if a perfect solution exists. The complete differencing algorithm was adapted by enforcing the bias constraint and then used on many random CNP problem instances with given size N and bias S. The number of possible configurations that must be searched before the determination can be made is shown in Fig. 7a. It can be observed that the number of searched configurations first increases exponentially with N before hitting a peak. We note that the average hardness of problems, as indicated by the number of configurations searched, peaks at around the same time as the phase transition from the “hard” phase to the “perfect” phase shown in Fig. 5a. This is because if a perfect solution exists, the algorithm can locate it early on without searching the entire configuration space. If no perfect solution exists, the algorithm will likely have to search most of the configuration space to rule it out. Hence, our numerical test shows that CNP and NPP are likely to behave similarly, with the existence of a perfect solution correlated with the problem being easy.

Fig. 7: Computational hardness of CNP problems.

a The number of configurations the modified complete differencing algorithm must search to determine if a perfect solution exists in a CNP problem instance as a function of size N and bias S. b Degeneracy of the ground state as a function of size N for CNP problems with different bias ratio parameters b. Integers of the CNP instances were drawn uniformly at random from the range [1, 2¹²].

Considering that the random CNP instances used in Fig. 7a have a constant precision limit L = 12, the figure also shows that a random CNP instance can remain hard for greater and greater values of N > L as bias S increases, since even the state-of-art complete differencing algorithm would have to search an exponentially increasing number of nodes before finding the solution. This feature of CNP is particularly useful for SPIM, because it is likely to be far easier to scale up the number of spins in the hardware than to increase the precision of control over their coupling strength in physical hardware.

The second version of CNP problems we investigate is a harder optimization problem: given a CNP instance, find the best partition, regardless of whether it is perfect. Figure 7b shows the degenerate ground states in randomly generated CNP problem instances with different bias parameters b = S/N but with fixed precision L = 12. When N is smaller than L, it can be observed that the number of degenerate ground states did not grow exponentially with N for all values of bias ratio parameters b, which corresponds to the lower-left corner of region 2 in Fig. 5b. When N is larger than L, the number of degenerate ground states grows exponentially with N for smaller values of b. For the largest considered b value of 0.4, the number of degenerate ground states is approximately constant by an order of magnitude, even as the total solution space grows exponentially with N. This strongly suggests that for the largest bias ratio b value, the problem remains computationally hard even as N grows while the precision L is fixed.

Hence, results shown in Fig. 7 suggest that random CNP problems with large bias ratio values can be meaningful benchmark problems for testing the performance of SPIM hardware in solving computationally hard problems because they have limited precision requirements and can be mapped to Ising problem with a low-rank coupling matrix.

Translation invariant problems

Beyond low-rank and constrained problems, translation invariant problems offer another interesting domain for SPIM applications. This section investigates how these problems can be effectively represented and solved using SPIMs.

"Realistic” spin glass

The correlation function method enables SPIM to encode translation invariant (or cyclic) coupling matrices. This type of coupling matrices can be used to study “realistic” spin glasses with nearest-neighbor couplings that live on a hypercubic lattice with periodic boundary conditions in d dimensions^62,63. For d = 1 and d = 2, these systems can be encoded using a modified Mattis-type matrix of the form given by Eq. (4), where

$$G({{{{\bf{x}}}}}_{i}-{{{{\bf{x}}}}}_{j})=\left\{\begin{array}{l}{H}_{G}({{{{\bf{x}}}}}_{i}-{{{{\bf{x}}}}}_{j})\,\quad {\mbox{for}}\,| {{{{\bf{x}}}}}_{i}-{{{{\bf{x}}}}}_{j}| =1\quad \\ 0\, \quad \quad \quad \quad \quad \quad {\mbox{otherwise.}}\,\quad \hfill\end{array}\right.$$

(23)

Here, H_G(k) is an arbitrary function. One could create “glassy” coupling matrices by choosing ${H}_{G}(k)=\cos (\omega k)$ to be sinusoidal with a suitable frequency. That is precisely how (up to decay over distance) the Ruderman-Kittel-Kasuya-Yosida exchange coupling gives rise to the anomalous magnetic behavior measured in dilute magnetic ions in insulators that kick-started the field of spin glasses^63,64,65,66.

A three-dimensional spin glass could be approximated by dividing the focal plane into L × L blocks and connecting nearest-neighbor spins and spins from neighboring blocks. This would modify Eq. (23) to read

$$G({{{{\bf{x}}}}}_{i}-{{{{\bf{x}}}}}_{j})=\left\{\begin{array}{l}{H}_{G}({{{{\bf{x}}}}}_{i}-{{{{\bf{x}}}}}_{j})\,\quad {\mbox{for}}\,| {{{{\bf{x}}}}}_{i}-{{{{\bf{x}}}}}_{j}| ={L}^{\alpha },\alpha \in \{0,1\}\quad \\ 0\,\quad \quad \quad \quad \quad \quad{\mbox{otherwise.}}\,\quad \hfill\end{array}\right.$$

(24)

However, this would add some additional couplings not present in the actual cubic lattice because the nearest neighbors from different blocks in the focal plane are still connected. This method could be iterated to approximate higher dimensional lattices, but it would lead to even more unwanted additional couplings.

Another way to create frustration on a given lattice is to set H_G(k) = 1 identically but add additional anti-ferromagnetic connections to next-nearest neighbors by setting

$$G({{{{\bf{x}}}}}_{i}-{{{{\bf{x}}}}}_{j})=\left\{\begin{array}{l}+1\,\quad {\mbox{for}}\,| {{{{\bf{x}}}}}_{i}-{{{{\bf{x}}}}}_{j}| =1\quad \hfill \\ -1\,\quad {\mbox{for}}\,\parallel {{{{\bf{x}}}}}_{i}-{{{{\bf{x}}}}}_{j}{\parallel }_{1}=2\quad \\ 0\, \quad \quad {\mbox{otherwise,}}\,\quad \hfill\end{array}\right.$$

(25)

where ∥ ⋅ ∥₁ denotes the L₁ norm. Spin models with such coupling are also known as J₁-J₂ models^67,68. Using the correlation function method, these highly frustrated coupling matrices can be realized on SPIM architecture, and the performance of sampling-based algorithms implemented on SPIM for minimizing the Ising Hamiltonian of these spin glasses can be investigated.

Circulant graphs

When an N × N shift matrix P acts on a vector x = (x₁, x₂, …, x_n), the components of x shift such that the order of the x_i change. We describe P as cyclic or circular since each component x_i is shifted by one around a circle. P² turns the circle by two positions, and every new factor P gives one additional shift. P^N gives a complete 2π shift of the components of x and therefore P^N = I_N, where I_N is the N × N identity matrix. A circulant matrix C is a polynomial of a shift matrix. In general

$${{{\bf{C}}}}={c}_{0}{I}_{N}+{c}_{1}{{{\bf{P}}}}+{c}_{2}{{{{\bf{P}}}}}^{2}+\ldots +{c}_{N-1}{{{{\bf{P}}}}}^{N-1},$$

(26)

which always has constant diagonals. The eigenvalues λ of P, given by Px = λx, are the N-th roots of unity. This follows from P^N = I_N to get λ^N = 1. The solutions are λ = w, w², …, w^N−1, 1 with $w=\exp (2\pi i/N)$. The matrix of eigenvectors is the N × N Fourier matrix

$${{{\bf{F}}}}=\left(\begin{array}{ccccc}1&1&1&\ldots &1\\ 1&w&{w}^{2}&\ldots &{w}^{N-1}\\ 1&{w}^{2}&{w}^{4}&\ldots &{w}^{2(N-1)}\\ \vdots &\vdots &\vdots &\ldots &\vdots \\ 1&{w}^{N-1}&{w}^{2(N-1)}&\ldots &{w}^{(N-1)(N-1)}\end{array}\right),$$

(27)

with orthogonal columns. Orthogonal matrices like P have orthogonal eigenvectors, and the eigenvectors of a circulant matrix are the same as the eigenvectors of the shift matrix. All information of a circulant matrix C is contained in its top row c = (c₀, c₁, …, c_N−1), with the N eigenvalues of C given by the components of the product Fc. When the adjacency matrix of an undirected graph is circulant, the eigenvalues are guaranteed to be real. This is because an undirected graph has a symmetric adjacency matrix, and symmetric matrices have real eigenvalues.

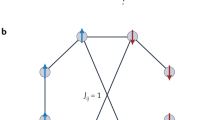
An example of a graph structure with a circulant adjacency matrix is a Möbius ladder graph. This 3-regular graph with even number of vertices N is invariant to cyclic permutations and can be implemented on SPIM hardware with each vertex of the Möbius ladder graph representing an Ising spin. The Ising spins are coupled antiferromagnetically according to the 3N/2 edges of the Möbius ladder graph. Each vertex is connected to two neighboring vertices arranged in a ring, and a cross-ring connection to the vertex that is diametrically opposite, as illustrated in Fig. 8. When N/2 is even, and for large cross-ring coupling, no configuration exists where all coupled Ising spins have opposite signs, and thus, frustrations must arise. The Ising Hamiltonian we seek to minimize is given by Eq. (1) with no external magnetic field and a coupling matrix J given by the Möbius ladder weighted adjacency matrix. The correlation function method can encode the weights of any circulant graph, which for Möbius ladders is given by

$${J}_{ij}=\left\{\begin{array}{ll}-1\quad &\,{\mbox{for}}\,| i-j| =1, \hfill\\ -J\quad &\,{\mbox{for}}\,| i-j| =N/2, \hfill\\ 0\quad &\,{\mbox{otherwise}}\,.\hfill\end{array}\right.$$

(28)

The two types of coupling—neighboring and cross-ring—have different coupling strengths, the former fixed at J_ij = −1 whilst we take the latter as an adjustable parameter J_ij = −J, with J constrained to the domain [0, 1]. The ground state takes two configurations depending on the value of J, as shown in Fig. 8. The two states, denoted S₀ and S₁ have Ising energies E₀ = (J − 2)N/2 and E₁ = 4 − (J + 2)N/2 respectively. For the regime J < J_crit ≡ 4/N, S₀ is the ground state whilst for J > J_crit the energy penalty due to opposite spins having the same Ising spin sign becomes large and the ground state changes to S₁. For even N/2 and canonical shift matrix

$$P=\left(\begin{array}{rc}{{{\bf{0}}}}&{I}_{N-1}\\ 1&{{{{\bf{0}}}}}^{T}\end{array}\right),$$

(29)

where 0 is a column vector of zeros of length N − 1, the weighted Möbius ladder adjacency matrix can be expressed as J = −P − JP^N/2 − P^N−1, where the coefficients of the polynomial in P are c = (0, −1, 0, …, 0, −J, 0, …, 0, −1). The N eigenvalues of J come from multiplying the Fourier matrix F with vector c to give

$$\left(\begin{array}{r}{\lambda }_{0}\\ {\lambda }_{1}\\ {\lambda }_{2}\\ \vdots \\ {\lambda }_{N-1}\end{array}\right)=\left(\begin{array}{r}-1-J-1\\ -w-J{w}^{N/2}-{w}^{N-1}\\ -{w}^{2}-J{w}^{2N/2}-{w}^{2(N-1)}\\ \vdots \\ -{w}^{N-1}-J{w}^{(N-1)N/2}-{w}^{(N-1)(N-1)}\end{array}\right),$$

(30)

which simplifies to ${\lambda }_{n}=-2\cos (2\pi n/N)-J{(-1)}^{n}$. For small J, the first term dominates, and the largest eigenvalue is λ_N/2 = 2 − J. For large J, the second term has an effect, and the largest eigenvalues are ${\lambda }_{N/2\pm 1}=2\cos (2\pi /N)+J$. The eigenvectors of these eigenvalues, projected to the nearest corner of the hypercube [−1, 1]^N, correspond to states S₀ and S₁, respectively. The critical value of J at which λ_N/2 = λ_N/2±1 occurs at ${J}_{{{{\rm{e}}}}}\equiv 1-\cos (2\pi /N)$.

Fig. 8: Ground state Ising spin configurations.

a State S₀ where each neighboring spin alternates, and b State S₁ where there are two positions, opposite on the ring, for which neighboring Ising spins are the same. For J < J_crit, the neighboring couplings dominate, and S₀ is the ground state, whereas for J > J_crit, the cross-ring couplings exert a greater influence and S₁ is the ground state.

Circulant graphs can be expressed as polynomials of shift matrices, from which eigenvalues and eigenvectors are calculated. This allows for a mathematically tractable analysis of the graph structure and its properties, revealing regions of parameter space for which optimization methods can falter. Moreover, circulant graphs are technologically feasible on SPIM hardware when utilizing the correlation function method²⁷. To see how circulant graphs can contain non-trivial structures resistant to simple local perturbations, we note that for Möbius ladder graphs with J ∈ [J_e, J_crit] the eigenvalue corresponding to S₀ is less than that for S₁ despite S₀ being the lower energy (ground) state. Indeed, Cummins et al.⁶⁹ found that gradient-based soft-amplitude solvers, such as the coherent Ising machine^20,21,22, will encounter difficulty in recovering the ground state when J ∈ [J_e, J_crit] with ground state probability decreasing as the spectral gap increases. The transformation from excited state S₁ to ground state S₀ requires N/2 spin flips, representing a significant energy barrier to overcome. Therefore, local perturbations are not enough to bridge the distance between hypercube corners of the ground and leading eigenvalue states. This may be overcome by using SPIM hardware paired with a sampling-based algorithm to provide feedback during each iteration of the minimization process, particularly if multiple SPIMs can be coupled to achieve a massively parallel paradigm that can efficiently sample the phase space of solutions of circulant graphs.

Conclusions

SPIMs are emerging physical computing platforms with distinct strengths and practical constraints, setting them apart from conventional digital computing technologies. As advancements in engineering and materials technology continue, these platforms are expected to see enhanced capabilities. It is, however, imperative to identify problems and methods that can effectively utilize these unique strengths, providing a robust basis for benchmarking their performance. This paper identifies several classes of problems that are particularly well-suited for SPIM hardware. SPIMs are shown to efficiently address practical problems such as portfolio optimization through low-rank approximation techniques. Furthermore, the CNP problem, a variation of the classic number partitioning problem, serves as a valuable benchmark for comparing the performance of SPIMs with that of classical computers. The analytically solvable circulant graph provides insights into the differences in performance between gradient-based algorithms, prevalent in many current Ising machines, and sampling-based algorithms that can be implemented on SPIMs. Additionally, SPIMs have the potential to realize many “realistic” spin glasses, extensively studied within the realm of statistical mechanics, thereby making numerous theoretical models experimentally viable.

Our study also highlights the importance of precision and rank in relation to the constraints of SPIM hardware. While low-rank approximations can render problems more manageable on SPIMs, the precision required for these approximations can impact computational efficiency and the accuracy of solutions. Therefore, future research must explore methods to optimize the balance between rank and precision. Beyond portfolio optimization, SPIMs demonstrate potential in solving various NP-hard problems through innovative mapping techniques. Advanced decomposition methods, such as SVD, enable SPIMs to manage more complex coupling matrices, expanding their applicability across different optimization tasks.

In conclusion, SPIMs represent a promising advancement in computational technologies. By focusing on low-rank approximations, CNP, and the implementation of sophisticated algorithms, this paper sets the stage for future investigations into the capabilities and applications of SPIMs. Continued research and development in this area are crucial for fully realizing the potential of SPIMs, paving the way for novel solutions to some of the most challenging computational problems. The broader implications of this research extend to fields such as finance, logistics, and data science, where SPIMs could significantly enhance performance and efficiency, leading to substantial advancements.

Methods

Simulations on low rank approximation

In Section “Low-Rank Approximation of Random Coupling Matrices”, we first generated a random unweighted, undirected graph with 1000 vertices, all with anti-ferromagnetic coupling, where each edge has an equal probability of having a value of 0 or  −1, and a random 3-regular graph with anti-ferromagnetic non-zero couplings. The coupling matrices then underwent SVD. The approximate Ising coupling matrix was constructed by recombining K Mattis-type constituent matrices with the highest singular values, whose elements were rounded to the nearest 2^−L. The approximate Ising problem was then solved through a simulation of SPIM, where a random group of spins was chosen at each step and flipped, and the new Ising energy of the system was calculated. The spin flips were accepted only if the new Ising energy decreased. As the simulation progressed, larger groups of random spins were chosen to prevent the system from being trapped in local minima of the Ising energy landscape since large clusters of spin flips lead to discontinuous movement in the energy landscape and prevent the system from being bounded by energy barrier surrounding a local minimum. For each set of parameters, 100 different random sequences of spin flips were used to produce the scatter of final energies.

When investigating the application of low-rank approximation on portfolio optimization problems, stock data from 2020-01-01 to 2023-01-01 was used. Low-rank approximated covariance matrices with rank 5 and 20, as well as the full rank covariance matrix S were calculated from stock data by using the factor analysis tools provided by Python software package “PyPortfolioOpt”. Its eigenvalue distribution was then calculated and shown in Fig. 4a. By substituting the covariance matrices into Eq. (21) and minimizing the objective function with commercial optimizer Gurobi, an optimized set of portfolio components were produced, and was then used to produce Fig. 4b.

Simulations on constraint number partitioning problems

CNP problem instances were produced by randomly generating integers in the range [1, 2^L]. In all our investigations, we used a precision limit of L = 12. The complete differencing algorithm, as described in Fig. 6, was adapted to solve the CNP problem by taking into account the bias requirement of the CNP problem. If a branch became too unbalanced in terms of the cardinality of the two subsets that the bias requirement became impossible to satisfy, then the branch would be pruned, so that no computational resources were wasted in searching the impossible branch. The adapted algorithm, like the complete differencing algorithm, is guaranteed to find the perfect solution if it exists. This algorithm was run on 200 different random problem instances for each set of bias and dimension values to produce the probability of existence of a perfect solution for that parameter set. However, to determine the degeneracy of the ground state, regardless of whether the state is a perfect solution, requires the enumeration of the complete solution space to count the total number of degenerate ground state solutions. Hence, the results presented in Fig. 7b were produced by enumerating all possible divisions of the initial integer set.