Introduction

The renowned Dirac equation was introduced to integrate the principles of special relativity and quantum mechanics1,2. It predicts several fundamental phenomena, including negative energy states, which imply the presence of antimatter, spin-1/2 particles, and their associated magnetic moments. Moreover, the Dirac equation has significantly influenced various research fields, notably impacting the study of topological insulators3, which have been among the most prominent topics in condensed matter physics over the past few decades.

The simulation of the Dirac equation has been proposed and realized in various systems4,5,6,7,8,9,10,11. Some simulations of theoretical predictions require stringent experimental conditions, yet they provide an essential understanding of many other physical phenomena. Such challenges have stimulated interest in simulations, particularly for phenomena like the Zitterbewegung (ZBW) effect. ZBW predicts the rapid oscillatory motion of spin-1/2 particles, but the small amplitude (on the order of the Compton wavelength,  ~ 10−12m) and high frequency ( ~ 1021Hz) make experimental observation exceptionally challenging. Consequently, simulating ZBW in artificial systems4,5,6,9,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27, including ultra-cold atoms12,13,14,15, ion traps5,6, and circuit QED4,11, has become essential. Another pertinent example is the Schwinger effect, which describes the creation of electron-positron pairs from the vacuum under the influence of a strong electric field1,28,29,30,31. The Sauter-Schwinger limit indicates that an electric field (E ≈ 1.32 × 1018V m−1) is required to polarize the vacuum, presenting a significant experimental challenge for direct observation. This has driven interest in realizing and analyzing the Schwinger effect in artificial systems. Several analogue and digital simulations of the Schwinger effect have been proposed or demonstrated in systems such as cold atoms32,33,34,35, trapped ions36,37, graphene38,39,40,41,42,43,44, superconducting circuits45,46 and other systems47,48,49,50,51,52,53,54,55.

However, much previous research has focused on 1+1 dimensional models in lattice gauge theory to study confinement, chiral symmetry breaking, and slow dynamics. A comprehensive simulation in higher dimensions could provide profound physical insights while broadening experimental research in quantum simulations38,39,47,48,49,56,57,58,59,60,61. Recently, the simulation of the 3+1 dimensional Dirac particle in a superconducting circuit has been theoretically proposed62, while it is not easy to achieve due to the stringent requirements. Experimental simulations of the Dirac equation in 3+1 dimensions remain lacking.

In this article, we demonstrate the simulation of the Dirac equation in 3+1 dimensions using a diamond-level structure realized with superconducting circuits encoded in the first-excited manifold of the square four qubits. We characterize the nontrivial ZBW effect arising from the spatial interference between the positive and negative energy components for plane waves by measuring the velocity in x and y. Apart from the simulation of the internal four-component spinor dynamics of free Dirac particle, we demonstrate the Schwinger effect by constructing an effective electric field whose strength reaches or even surpasses the Sauter-Schwinger limit. Our experiments characterize the dynamic characteristics of the 3+1 dimensional Dirac equation and prove that our simulation scheme provides a good platform for other physical systems.

Results

Experimental setup

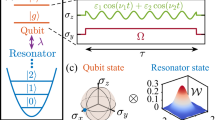
We perform the simulation with four superconducting qubits arranged in 2D squares, where the parameters are specially designed (See Supplementary Note 1). The adjacent qubits are connected by a floating tunable coupler, which is positively and far detuned from qubits, ensuring an adequate coupling strength between two qubits. The qubit frequencies and coupling strength are carefully designed to ensure we can construct the Dirac Hamiltonian via parametric modulation. Each qubit has individual flux and XY control line, and a coplanar waveguide readout resonator is capacitively coupled to the same transmission line, so we can simultaneously measure the state of all qubits with a multi-tone probe microwave.

Constructing Hamiltonian

Next, we show how to analogue simulate the 3+1 dimensions of the Dirac Hamiltonian in our superconducting circuits.

$${H}_{{{{{\rm{D}}}}}}=c{{{{\boldsymbol{\alpha }}}}} \, \bullet \, {{{{\bf{p}}}}}+\beta m{c}^{2}$$
(1)

where α = (α1, α2, α3) and β are four dimensional matrices, holding the following anti-commuting relations αiαk + αkαi = 2δikI4, αiβ + βαi = 0, β2 = I4, i, k = 1, 2, 3(ℏ = c = 1). p = (px, py, pz) and m are momentum and mass of Dirac particle. We simulated the Hamiltonian in the first-excited manifold of four superconducting qubits labelled Qi, i = 0, 1, 2, 3. We map the momentum and mass to the parameters space constructed by the parametric modulation scheme. The constructed Hamiltonian H in the native basis order \((\left\vert 0\right\rangle ,\left\vert 1\right\rangle ,\left\vert 2\right\rangle ,\left\vert 3\right\rangle )\) is shown in the Methods. We use the permutation matrix Up shown below to transform the Hamiltonian into a new basis order \((\left\vert 0\right\rangle ,\left\vert 3\right\rangle ,\left\vert 2\right\rangle ,\left\vert 1\right\rangle )\).

$${U}_{{{{{\rm{p}}}}}}=\left(\begin{array}{cccc}1&0&0&0\\ 0&0&0&1\\ 0&0&1&0\\ 0&1&0&0\end{array}\right).$$
(2)

After the transformation, \({H}_{{{{{\rm{s}}}}}}={U}_{{{{{\rm{p}}}}}}^{{{{\dagger}}} }H{U}_{{{{{\rm{p}}}}}}\), the Dirac Hamiltonian is realized in the supersymmetric representation Hs = ∑i=x,y,z(piσx ⊗ σi) + mσy ⊗ I2, where σi(i = x, y, z) is the Pauli matrix2.

Free Dirac equation

With the constructed Hamiltonian, we can demonstrate the representative properties of the Dirac equation. The first is the spinor dynamics of a Dirac particle, which has a definite momentum value and is a plane wave in the spatial coordinate. Four state amplitudes correspond to the internal spinor components, while the oscillation frequency reflects the energy of particle. For the superconducting circuits with design parameters, the momentum and mass of particles can be adjusted easily. In this experiment, we set p = (1.3 MHz, 0, 0)(we omit 2π hereafter), with mass varying from 0 MHz to 2.6 MHz. Without loss of generality, we initialize the system at the ground state \(\left\vert 0\right\rangle\). We simultaneously measure four qubits and get the corresponding populations to characterize the feature of the spinor dynamics. Figure 1c shows the oscillation pattern of populations with varied masses. The heavier particle has the higher energy, leading to faster oscillation, as illustrated in Fig. 1a. It is worth noting that \(\left\vert 3\right\rangle\) is never populated; the phenomenon can be explained well when we treat the diamond-shape Hamiltonian as a combination of a Λ and a V configuration as shown in Figure 1b. A dark and bright state exists in the V(Λ) subspace, labelled as \({\left\vert D\right\rangle }_{0}({\left\vert D\right\rangle }_{3})\) and \({\left\vert B\right\rangle }_{0}({\left\vert B\right\rangle }_{3})\) respectively. Here \({\left\vert B\right\rangle }_{0}=\frac{{p}_{+}}{E}\left\vert 1\right\rangle +\frac{{p}_{z}+im}{E}\left\vert 2\right\rangle\), where p± = px ± ipy and \(E=\pm \sqrt{| {{{{\bf{p}}}}}{| }^{2}+{m}^{2}}\). The bright(dark) state in the Λ system is precisely the dark(bright) state in the V system; besides, the bright state is orthogonal to the dark state. Therefore, the evolution of free Dirac particle can be described as the Rabi oscillation between \(\left\vert 0\right\rangle\) and bright state \({\left\vert B\right\rangle }_{0}\) in V system, leading that there is no population transfer to \(\left\vert 3\right\rangle\) as shown in the Fig. 1c. The single oscillation frequency indicates that no beat pattern can be explained by the two-fold degeneracy of the Dirac Hamiltonian for both positive and negative eigen-energies  ± E. This degeneracy results in effective two-level dynamics (See Supplementary Note 2). The destructive interference between two transition paths from \(\left\vert 0\right\rangle\) to \(\left\vert 3\right\rangle\) causes the suppressed population in \(\left\vert 3\right\rangle\).

Fig. 1: Free Dirac Equation.
figure 1

a Illustration of the dynamics of four-component spinor. According to the Dirac Hamiltonian, oscillation speeds up with the increase of the particle mass. b The dynamical procedure can be treated as the Rabi oscillation between \(\left\vert 0\right\rangle\) and the bright state \({\left\vert B\right\rangle }_{0}\), which is orthogonal to the dark state \({\left\vert D\right\rangle }_{0}\). They are the superpositions of \(\left\vert 1\right\rangle\) and \(\left\vert 2\right\rangle\), and their probability amplitude varies with mass. c Experimental results(main) and numerical simulation(inset) of the free Dirac equation are demonstrated. The populations of the four states exhibit a single-frequency oscillation with varied evolution time and mass. The colour bar represents the population (shared across all panels).

Full size image

In practice, we observe a slight oscillation of \(\left\vert 3\right\rangle\) with a large mass. The numerical simulation proves this is caused by the deviation of the coupling strength’s phase, which results from the shift of the resonant parametric frequency when all four parametric modulations are applied.

Zitterbewegung effect

Furthermore, we study the ZBW effect, the predicted super-fast rapid oscillation of relativistic particles, which results from the interference between the positive and negative energy solutions of the Dirac equation. Figure 2a illustrates the ZBW procedure, of which the oscillation frequency corresponds to the energy gap. It is believed to be observable in the regime where ∣p∣ ≈ m in 1+1 dimensions11. The velocity operator in the Dirac equation is represented as \({\alpha }_{i}=\Big(\begin{array}{cc}0&{\sigma }_{i}\\ {\sigma }_{i}&0\end{array}\Big)\). The dynamics of the velocity is described by:

$$\frac{d{\alpha }_{i}}{dt}=[{\alpha }_{i},H]/i$$
(3)
Fig. 2: The Zitterbewegung effect.
figure 2

a Illustration of Zitterbewegung in momentum space, the rapid oscillation between eigenstates with opposite eigenvalues. b–d Demonstrations of velocities in the x and y directions with three different masses with dots(Experimental results) and dashed lines(numerical simulation). The frequency of oscillation in the x and y directions can be observed, with momentum \({{{{\bf{p}}}}}=(1.3/\sqrt{2}\,\,{\mbox{MHz}}\,,1.3/\sqrt{2}\,\,{\mbox{MHz}}\,,0)\). e The oscillation frequency of velocities increases with the mass. Measured velocities with different momentum, p = (1.3 MHz, 0, 0) for (f) and \({{{{\bf{p}}}}}=(1.3/\sqrt{2}\,\,{\mbox{MHz}}\,,-1.3/\sqrt{2}\,\,{\mbox{MHz}}\,,0)\) for (g).

Full size image

Our scheme provides larger parameter space than the previous 1+1 dimensional Dirac equation simulation, ensuring we explore more Dirac particle features. In this article, we characterize the ZBW, which is related to complicated commutation relation for the 3+1 dimensional case (See Supplementary Note 4). Without loss of generality, we set pz = 0; the momentum in the x-direction can cause the ZBW in the y-direction and vice versa; the larger mass will also accelerate the ZBW.

We directly measure the velocity by quantum state tomography to demonstrate the ZBW effect. Specifically, we prepare the state \(\left\vert 0\right\rangle\) and system evolves under the free Dirac equation with \({{{{\bf{p}}}}}=(1.3/\sqrt{2}\,\,{\mbox{MHz}},1.3/\sqrt{2}\,\,{\mbox{MHz}}\,,0)\) and different mass values. Before the probe microwave, we apply two simultaneous parametric modulation flux pulses on C1 and C3 to execute two \(\sqrt{\,{\mbox{iSWAP}}\,}\)-like gate (\(\left\vert 0\right\rangle \leftrightarrow \left\vert 1\right\rangle\) and \(\left\vert 2\right\rangle \leftrightarrow \left\vert 3\right\rangle\)) with four different tomography phases φm. Assuming the measured state \(\vert \psi \rangle ={c}_{0}\vert 0\rangle +{c}_{1}\vert 1\rangle +{c}_{2}\vert 2\rangle +{c}_{3}\vert 3\rangle\), the expectation values of velocity in the x and y directions can be written as \({v}_{x}=\langle \psi | {\alpha }_{x}| \psi \rangle =2\,{\mbox{Re}}({c}_{0}^{* }{c}_{1})+2{\mbox{Re}}\,({c}_{2}^{* }{c}_{3})\) and \({v}_{y}=\langle \psi | {\alpha }_{y}| \psi \rangle =2\,{\mbox{Im}}({c}_{0}^{* }{c}_{1})+2{\mbox{Im}}\,({c}_{2}^{* }{c}_{3})\). In the probe procedure, we probe the population or 〈σz〉 of four qubits, we note that \({\langle {\sigma }_{z}\rangle }_{n}^{m}\) represents the expectation value of Qn after the tomography with phase φm = mπ/2, m = 0, 1, 2, 3. We can calculate \({\langle {\sigma }_{z}\rangle }_{i = 0,1}^{m}=| {c}_{2}{| }^{2}+| {c}_{3}{| }^{2}-{(-1)}^{i}2 {\mbox{Im}}\,({e}^{i{\varphi }_{m}}{c}_{0}^{* }{c}_{1})\) and \({\langle {\sigma }_{z}\rangle }_{i = 2,3}^{m}=| {c}_{0}{| }^{2}+| {c}_{1}{| }^{2}-{(-1)}^{i}2\,{\mbox{Im}}\,({e}^{i{\varphi }_{m}}{c}_{2}^{* }{c}_{3})\) with the detailed derivation provided in the Supplementary Note 3. After the measurement, the velocity of the Dirac particle can be calculated from tomography data. For instance, the first term of vx, \(2\,{\mbox{Re}}\,({c}_{0}^{* }{c}_{1})=(-{\langle {\sigma }_{z}\rangle }_{0}^{1}+{\langle {\sigma }_{z}\rangle }_{1}^{1})/2\), can be obtained from the measurement of Q0 and Q1. This term can be estimated using m = 1 or m = 3, the data is redundant, so we average the results for different phases to mitigate the effect of readout error in 〈σz〉. Finally, we can calculate \({v}_{x}=(-{\langle {\sigma }_{z}\rangle }_{0}^{1}+{\langle {\sigma }_{z}\rangle }_{0}^{3}+{\langle {\sigma }_{z}\rangle }_{1}^{1}-{\langle {\sigma }_{z}\rangle }_{1}^{3}-{\langle {\sigma }_{z}\rangle }_{2}^{1}+{\langle {\sigma }_{z}\rangle }_{2}^{3}+{\langle {\sigma }_{z}\rangle }_{3}^{1}-{\langle {\sigma }_{z}\rangle }_{3}^{3})/4\) and \({v}_{y}=(-{\langle {\sigma }_{z}\rangle }_{0}^{0}+{\langle {\sigma }_{z}\rangle }_{0}^{2}+{\langle {\sigma }_{z}\rangle }_{1}^{0}-{\langle {\sigma }_{z}\rangle }_{1}^{2}-{\langle {\sigma }_{z}\rangle }_{2}^{0}+{\langle {\sigma }_{z}\rangle }_{2}^{2}+{\langle {\sigma }_{z}\rangle }_{3}^{0}-{\langle {\sigma }_{z}\rangle }_{3}^{2})\). Within the spatial coordinates, the wave function is separated into positive and negative energy components. Two plane waves move in opposite directions, and their overlap in coordinate space is constant; the interference persists, and the velocity oscillation will never decay without decoherence. Due to the energy decay and pure dephasing in superconducting qubits, we see the decay of velocity oscillation in this experiment.

In Fig. 2, we demonstrate the observed velocities oscillating with different mass and momentum. Specifically, we set a momentum with x- and y- components in Fig. 2b; the velocity oscillations exhibit a higher frequency for particles with greater mass, as shown in Fig. 2c, d. The experiment and simulation data in Fig. 2e indicate that the square of ZBW oscillation frequency ωZ increases linearly with m2. Furthermore, in Fig. 2f, g, we provide a detailed analysis of the relationship between ZBW and commutation relation by measuring the velocity dynamics for different momentum. Oscillations are observed only in vy when momentum is solely in the x-direction. When the momentum in the y direction is reversed relative to Fig. 2b, the oscillation of vx shifts by a phase of π, resulting in it being in phase with vy.

Electric field and the Schwinger effect

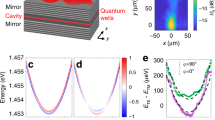
Schwinger effect describes the electron-positron pair production considering the Dirac equation in the presence of a strong electric field. To simulate an electric field \({{{{\boldsymbol{\epsilon }}}}}=-\frac{\partial {{{{\bf{A}}}}}}{\partial t}\), we introduce vector potential A. In this article, we ramp up momentum p to p − eA. In the evolution, an electron in the vacuum and a hole in the Dirac sea are created, as illustrated in Fig. 3a. Notice the similarity between the Schwinger effect and Landau-Zener tunnelling38,39,47,48,49,59,60; we can study this problem from another perspective. In the chirping evolution, the quantum state switches to another energy level when it passes through the avoid-crossing, which means the generation of positive and negative electron pairs. The Landau-Zener rates are extracted from the measured populations63, and they characterize the pair production rate. We practically set the initial momentum pini = (−2.6 MHz, 0, 0), which is ramped to pfin = (2.6 MHz, 0, 0), with a rate ∣ϵ∣ = (2.034 MHz)2. The Hamiltonian has two two-fold degeneracies, which are denoted by \(\{{\left\vert +\right\rangle }_{01},{\left\vert -\right\rangle }_{23}\}\) and \(\{{\left\vert -\right\rangle }_{01},{\left\vert +\right\rangle }_{23}\}\) (see Methods). Two Landau-Zener transitions can proceed independently in two manifolds. Here, we performed an optimal solution in the experiment, preparing the state at \(\left\vert 0\right\rangle\), which is the superposition of the two eigenstates (\({\left\vert +\right\rangle }_{01}\) and \({\left\vert -\right\rangle }_{01}\)), resulting in the Landau-Zener rate can be obtained from the measured population in the manifold of \(\{\left\vert 0\right\rangle ,\,\left\vert 1\right\rangle \}\). In this model, the mass identifies the avoid-crossing gap. As shown in Fig. 3b, for a fixed electric field (fixed ramping rate), the pair production probability decreases with increasing mass, consistent with the Schwinger formula. Fig. 3c, d show the final populations as a function of evolution times and masses. The sum of the population \(\left\vert 0\right\rangle\) and \(\left\vert 1\right\rangle\) reflects the pair production rate, which corresponds with the Landau-Zener model as denoted in Fig. 3e. The population is corrected by readout error mitigation. (See Supplementary Note 5) When the mass is beyond 1.5 MHz, the population increases because the formula of the Landau-Zener rate is not applicable within the experiment parameter.

Fig. 3: Dirac particle in electric fields.
figure 3

a The rapid ramping of the momentum induces an electric field (purple pulse), which is strong enough to depolarize the vacuum and produce the electron-positron pair. A negative energy electron (blue ball) in the Dirac sea is stimulated to a positive energy state (red ball), leaving a hole in the Dirac sea (violet ball). b Schematic of Schwinger effect. The system can be viewed as a two-fold degenerate Landau-Zener model, with no interaction between degenerate states. The electric field depolarizes the vacuum and creates electrons and positrons (holes in the Dirac sea). The minimal gap of 2m determines the minimal chirp rate(electric field) to observe the Schwinger effect. c Experimental results of the populations of four states in the chirping process are demonstrated for different masses, and they are in accord with numerical simulations in (d). In (c) and (d), The colour bar represents the population (shared across all panels). e The remaining population in \(\{\left\vert 0\right\rangle ,\left\vert 1\right\rangle \}\) manifold characterizes the pair production, and it decreases with increasing mass. At large mass, the initial state is not far from the anti-crossing for the finite momentum compared with the gap. Therefore, the deviation from the Landau-Zener transition rate formula in the pink regime is caused by the finite max effective coupling strength.

Full size image

Conclusions

In conclusion, we have demonstrated an analogue simulation of the 3+1 dimensional Dirac equation using superconducting circuits. We mapped the four-component spinors onto the single-excitation manifold of four qubits by applying parametric modulations on four tunable couplers. The dynamics of the Dirac equation were illustrated by simultaneously measuring the population of four states. Furthermore, we directly measured the velocities vx and vy using quantum state tomography and observed the ZBW due to the interference between the positive and negative energy components. The ZBW was demonstrated for both massive and massless free Dirac particles. Additionally, we chirped the momentum of spin-1/2 particles to simulate the Schwinger effect. Owing to the similar dynamics with four levels of Landau-Zener transition, we measured the remaining population in the \(\{\left\vert 0\right\rangle ,\left\vert 1\right\rangle \}\) manifold to characterize the probability of electron-positron pair production. Our experimental results indicate that, due to their high controllability and scalability, superconducting circuits are excellent platforms for simulating the Dirac equation and many other relativistic phenomena that are extremely challenging to observe experimentally.

Methods

Parameters mapping

These effective coupling strengths in the text are introduced by flux parametric modulation (More details see Supplementary Note 1).

The independent real and image part of drive amplitude is related to momentum in different directions pi, i = x, y, z, and mass value m. The coupling strength between \(\left\vert i\right\rangle\) and \(\left\vert j\right\rangle\) is Ωije−iφ, with amplitude Ωij and phase φ. Specifically, we set \({\Omega }_{01}{e}^{-i{\varphi }_{1}}={p}_{x}-i{p}_{y}\), \({\Omega }_{02}{e}^{-i{\varphi }_{2}}={p}_{z}-im\), \({\Omega }_{23}{e}^{-i{\varphi }_{3}}={p}_{x}-i{p}_{y}\) and \({\Omega }_{13}{e}^{-i{\varphi }_{4}}=-{p}_{z}+im\) to construct Dirac Hamiltonian. The Hamiltonian in the native basis order \((\left\vert 0\right\rangle ,\left\vert 1\right\rangle ,\left\vert 2\right\rangle ,\left\vert 3\right\rangle )\) can be written as

$$H=\left(\begin{array}{cccc}0&{p}_{x}-i{p}_{y}&{p}_{z}-im&0\\ {p}_{x}+i{p}_{y}&0&0&-{p}_{z}+im\\ {p}_{z}+im&0&0&{p}_{x}-i{p}_{y}\\ 0&-{p}_{z}-im&{p}_{x}+i{p}_{y}&0\\ \end{array}\right)$$
(4)

Four levels Landau-Zener transitions

In order to elucidate the dynamics in the Schwinger effect experiment, We take the unitary matrix

$$U=\frac{1}{\sqrt{2}}\left(\begin{array}{cccc}1&1&0&0\\ \frac{{p}_{x}+i{p}_{y}}{\sqrt{{p}_{x}^{2}+{p}_{y}^{2}}}&-\frac{{p}_{x}+i{p}_{y}}{\sqrt{{p}_{x}^{2}+{p}_{y}^{2}}}&0&0\\ 0&0&1&1\\ 0&0&\frac{{p}_{x}+i{p}_{y}}{\sqrt{{p}_{x}^{2}+{p}_{y}^{2}}}&-\frac{{p}_{x}+i{p}_{y}}{\sqrt{{p}_{x}^{2}+{p}_{y}^{2}}}\\ \end{array}\right)$$
(5)

to do the unitary transformation, and the Hamiltonian is Hrot = U†HU

$${H}_{{{{{\rm{rot}}}}}}=\left(\begin{array}{cccc}\sqrt{{p}_{x}^{2}+{p}_{y}^{2}}&0&0&{p}_{z}-im\\ 0&-\sqrt{{p}_{x}^{2}+{p}_{y}^{2}}&{p}_{z}-im&0\\ 0&{p}_{z}+im&\sqrt{{p}_{x}^{2}+{p}_{y}^{2}}&0\\ {p}_{z}+im&0&0&-\sqrt{{p}_{x}^{2}+{p}_{y}^{2}}\\ \end{array}\right)$$
(6)

It is clear that when pz = 0 and in the limit ∣p∣ ≫ m, this Hamiltonian is an almost diagonal matrix, the eigenstates can be denoted as \({\left\vert +\right\rangle }_{01}\), \({\left\vert -\right\rangle }_{01}\), \({\left\vert +\right\rangle }_{23}\) and \({\left\vert -\right\rangle }_{23}\), where \({\left\vert \pm \right\rangle }_{01}=(\left\vert 0\right\rangle \pm \frac{{p}_{x}+i{p}_{y}}{\sqrt{{p}_{x}^{2}+{p}_{y}^{2}}}\left\vert 1\right\rangle )/\sqrt{2}\) and \({\left\vert \pm \right\rangle }_{23}=(\left\vert 2\right\rangle \pm \frac{{p}_{x}+i{p}_{y}}{\sqrt{{p}_{x}^{2}+{p}_{y}^{2}}}\left\vert 3\right\rangle )/\sqrt{2}\). Initial state in the manifold \(\{\left\vert 0\right\rangle ,\left\vert 1\right\rangle \}\) can be expressed as the superposition of \({\left\vert +\right\rangle }_{01}\) and \({\left\vert -\right\rangle }_{01}\). Then we chirp the momentum from a negative value to a positive one, the dynamics between \({\left\vert +\right\rangle }_{01}\)(\({\left\vert -\right\rangle }_{01}\)) and \({\left\vert -\right\rangle }_{23}\)(\({\left\vert +\right\rangle }_{23}\)) can be described exactly by Landau-Zener transition. Therefore, the total dynamics of the system are just two independent Landau-Zener transitions. The relationship between the Schwinger effect and Landau-Zener transition is explained in the main text.