Introduction

Understanding how cooperation emerges and persists among unrelated individuals is a fundamental question, as cooperation involves personal costs to benefit others, potentially disadvantaging cooperators relative to selfish individuals1. This puzzle has been examined across multiple disciplines, each offering unique insights into the survival of cooperation. Experimental economists often study cooperation in one-shot, anonymous scenarios to reveal intrinsic cooperative tendencies. Their theories draw on social norms2,3, prosocial preferences4,5, or even attributions of cooperative behavior to confusion or error6,7. In contrast, evolutionary game theory investigates how cooperation can emerge and stabilize as an evolutionary equilibrium through mechanisms such as kin selection8, direct reciprocity9, indirect reciprocity based on reputation10,11, network reciprocity12,13,14, and group selection15. Of these, network reciprocity has been especially influential in explaining how structured populations can sustain cooperation.

Initially studied in regular lattices, network reciprocity proposes that cooperators cluster within networks, reinforcing each other and resisting exploitation by defectors12. This concept has garnered significant attention from researchers in statistical physics, applied mathematics, and computer science, who have further developed theories of cooperation from multiple perspectives. First, researchers have examined how various network structures—such as regular lattices16, scale-free networks17, temporal networks18,19, and higher-order networks20,21,22—affect the conditions under which cooperation survives. A central focus is determining, through mathematical analyses, the conditions under which cooperation persists, often characterized by relationships between the benefit-to-cost ratio and network features like average degree23 or degree distribution heterogeneity24. Second, agent-based simulations have demonstrated how network reciprocity can help resolve evolutionary challenges that are otherwise difficult to overcome in well-mixed populations, such as second-order free-rider problems25 and strong reciprocity, which examines whether punishing defectors and rewarding cooperators are linked traits in individuals26. Third, agent-based models have been applied to coevolutionary games27,28,29, in which strategies, individual traits, or network structures evolve simultaneously, thereby offering valuable insights into the persistence of cooperation under dynamically changing environments 30.

Although analytical methods have significantly advanced the theoretical understanding of cooperation within structured populations23,24, these methods frequently rely on simplifying assumptions, particularly the weak selection assumption. Under weak selection, natural selection processes are approximated as minor perturbations of neutral drift, essentially ignoring higher-order nonlinear evolutionary effects. Agent-based models, by contrast, allow for the simulation of complex and nonlinear dynamics without the restrictive assumptions of weak selection, making them essential for studying spatial evolutionary games under a wider range of conditions and providing insights that complement analytical approaches 31.

However, a significant challenge when using agent-based models to study spatial evolutionary games is the finite-size effect. This refers to random fluctuations arising from limited network sizes, which can lead to unexpected strategy extinction events and make results highly sensitive to network size32,33,34. Traditional methods to address these effects include carefully preparing initial states25 or conducting comprehensive stability analyses of subsystem competition35. While effective, these approaches often require large systems to achieve accurate, size-independent results, significantly increasing computational demands.

Additionally, agent-based simulations often exclude mutations to clearly observe phase transitions, a key focus in statistical physics for studying critical phenomena. While this simplification aids in identifying dynamic transitions, it poses challenges for evolutionary game theory, where stable outcomes must resist invasions by mutant strategies to demonstrate evolutionary robustness. Relying on large network sizes to mitigate finite-size effects increases computational demands and may not accurately represent real-world systems, which are finite and subject to mutations or behavioral noise.

Although some studies have introduced mutations to address finite-size effects36,37,38, the underlying mechanisms remain poorly understood. Specifically, it remains unclear how and why mutation mitigates these effects, and how to determine mutation rates in advance to address finite-size effects for given network sizes. In this paper, we systematically explore whether incorporating mutation can mitigate finite-size effects in agent-based simulations with limited network sizes. We begin with a spatial optional public goods game32, where players choose to cooperate by contributing to a common pool, defect by contributing nothing, or act as loners who opt out and receive a fixed payoff. Contributions are multiplied by an enhancement factor and shared among cooperators and defectors. To test the robustness of mutation in addressing finite-size effects, we introduce a more complex tolerance-based variant of the optional public goods game35,39. In this version, players adopt additional strategies: they cooperate only if the number of defectors in their group remains below a specified tolerance threshold; otherwise, they act as loners. This expansion increases the strategy space to eight distinct strategies, adding complexity to the dynamics.

Focusing on limited network sizes, we first confirm that finite-size effects significantly impact phase boundaries, and our results show that these effects can be effectively mitigated by introducing mutation in agent-based simulations. Specifically, rare mutations help preserve equilibrium stability when the equilibria are inherently stable. However, when equilibria are vulnerable to finite-size effects, we find that introducing a moderate mutation rate maintains competition among strategies by reintroducing those that occasionally go extinct, ultimately yielding results comparable to those observed in large networks. While the efficacy of this approach depends on both network size and mutation rate, our findings suggest that incorporating mutation provides a cost-effective means of mitigating finite-size effects and achieving reliable outcomes without the need for large networks. Given the difficulty of determining an appropriate network size to counter finite-size effects in advance, especially in the absence of prior analytical results, we propose mutation sensitivity analysis as a general strategy for managing finite-size effects and enhancing the reliability of agent-based simulations.

Results

Spatial optional public goods game

Agent-based simulations of the spatial optional public goods game on a 2000 × 2000 square lattice without mutation, as conducted in ref. 32, identify precise critical values of the synergy factor r that delineate distinct phases. Specifically, r = 2 marks the transition from the pure loner phase to a mixed phase of cooperators, defectors, and loners, while r = 4.6005 signifies the shift from the mixed phase to the cooperation-defection phase. These critical values, indicated by arrows in Fig. 1, serve as benchmark outcomes for comparison.

Fig. 1: Strategy frequencies versus synergy factor r for a small network size N = 2002.
figure 1

In spatial optional public goods games, finite-size effects in small networks near phase transition boundaries are addressed by introducing mutation, producing results consistent with larger networks. Dots indicate outcomes without mutation, while solid lines represent outcomes with a mutation rate of μ = 10−6, with the colours blue, orange, and green represent cooperators (C), defectors (D), and loners (L), respectively. Black arrows at r = 2.0 and r = 4.6005 mark critical values from large networks (N = 20002), as reported in ref. 32, separating phases of pure L, C + D + L, and C + D coexistence. Gray regions indicate discrepancies due to finite-size effects.

Full size image

Building on these findings, we ran simulations on a smaller 200 × 200 lattice to examine whether introducing mutation could mitigate finite-size effects (see Methods for details). In the absence of mutation, finite-size effects cause deviations in critical values, as highlighted by the gray regions in Fig. 1. However, incorporating mutation into the simulations effectively mitigates finite-size effects, producing results comparable to those from larger networks. Notably, a mutation rate of μ = 10−6 aligns the critical values of r with those observed in the 2000 × 2000 lattice. Moreover, mutation preserves strategy frequencies in regions unaffected by finite-size effects while simultaneously correcting distortions in the critical regions, thereby improving the robustness of the results.

A closer examination of the evolutionary dynamics reveals that the ability of mutation to promote strategy diversity is critical to mitigating finite-size effects. By enabling the reemergence of strategies that occasionally disappear due to finite-size effects, mutation restores evolutionary dynamics and stabilizes strategy levels to match those observed in large networks. At r = 2.02, finite-size effects in small networks cause to the extinction of defectors (see Fig. 2a), while at r = 4.6, loners disappear entirely (see Fig. 2c). These extinctions disrupt the stable coexistence of three strategies observed in large networks. However, mutation reintroduces these lost strategies, restoring balance. For instance, at r = 2.02, defectors reintroduced by mutation prevent the dominance of cooperation (see Fig. 2b). Similarly, at r = 4.6, reintroduced loners correct the defector-cooperator coexistence observed in small networks (see Fig. 2d). This stabilization ensures that strategy levels closely align with those observed in large networks.

Fig. 2: Adding mutation restores extinct strategies, reproducing outcomes from large populations.
figure 2

The figure shows the frequencies of cooperators (C, blue), defectors (D, orange), and loners (L, green) over time in the spatial optional public goods game on a network of size N = 2002. The top panels (a, b) correspond to a synergy factor of r = 2.02 and bottom panels (c, d) to r = 4.6. The left panels (a, c) display results without mutation, where certain strategies occasionally go extinct due to finite-size effects. The right panels (b, d) show outcomes with mutation introduced at a fixed rate of μ = 10−6, which reintroduces extinct strategies and restores stable coexistence. Horizontal dashed lines represent the stable frequencies of each strategy observed in large populations (N = 20002), as reported in ref. 32.

Full size image

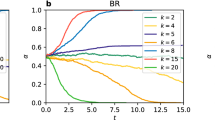
Further analysis across various mutation levels reveals that certain mutation rates effectively mitigate finite-size effects at the phase transition boundaries, with the range of effective mutation rates expanding as the linear system size increases. As shown in Fig. 3, a “window of mutations” exists where the results closely match the reference outcomes from a N = 20002 lattice. For an N = 502 lattice, effective mutation rates range from approximately 10−5 to 10−3 at r = 2.02 and from about 5 × 10−6 to 10−5 at r = 4.6, see Fig. 3a and c. For a larger N = 2002 lattice, these ranges shift to approximately 10−7 to 10−4 at r = 2.02 and remain roughly 10−7 to 10−5 at r = 4.6, see Fig. 3d and f. The upper limit indicates where mutations begin to significantly alter the system’s dynamics, while the lower threshold represents the minimum mutation rate required to address finite-size effects. Mutation rates outside these ranges result in strategy frequencies that deviate significantly from those observed in large networks. Comparisons between N = 502 and N = 2002 reveal that the valid mutation window broadens as the system size increases. This finding suggests that beyond a certain system size, the mutation rate required to mitigate finite-size effects stabilizes at a fixed range, allowing reliable results without further adjustments.

Fig. 3: Strategy frequencies as a function of mutation rate.
figure 3

The figure shows the frequencies of cooperators (C, blue), defectors (D, orange), and loners (L, green) as functions of the mutation rate μ, for two network sizes: N = 502 in (a–c) and N = 2002 in (d–f). Error bars represent standard deviations from 100 independent runs, and horizontal dashed lines represent reference outcomes from a large lattice (N = 20002), as reported in ref. 32. The shaded region highlights mutation rates for which outcomes converge to the large-lattice benchmark. At synergy factors near phase transition points (r = 2.02 in (a) and (d) and r = 4.6 in (c) and (f)), intermediate mutation rates effectively mitigate finite-size effects. In contrast, under stable conditions (r = 3 in (b) and (e)), only high mutation rates alter evolutionary outcomes.

Full size image

A detailed inspection of Fig. 3 further indicates that small mutation rates do not alter evolutionary outcomes in regions where phase transitions are absent. Specifically, when mutation rates remain below approximately μ < 10−3, strategy frequencies closely match those observed in the large lattice, as shown in Fig. 3b and e. However, at higher mutation rates, evolutionary outcomes begin to deviate significantly from the reference results.

Lastly, we evaluated how incorporating fixed intermediate mutation rates can substantially reduce the network size needed to mitigate finite-size effects, despite variability in effectiveness across lattice sizes. Without mutation, finite-size effects persist at r = 2.02 even as the lattice size increases from N = 502 to N = 8002. Strategy frequencies at r = 2.02 remain unchanged across this range and across different realizations (Fig. 4a), but still deviate from those observed on a 2000 × 2000 lattice. At r = 4.6, small discrepancies persist for N < 8002, while results at N = 8002 closely match those from the large reference lattice of 2000 × 2000 (Fig. 4c). These findings highlight the difficulty of mitigating finite-size effects solely by increasing network size, as determining an appropriate lattice size can be challenging, and residual discrepancies may persist even when results appear stable against different network sizes. In contrast, incorporating mutation achieves consistent results with the referenced outcomes in much smaller networks, requiring only N = 2002 at r = 2.02 and N = 502 at r = 4.6 (Fig. 4b and d).

Fig. 4: Strategy frequency as a function of population size N.
figure 4

Error bars represent the standard deviation from 100 independent runs, and horizontal dashed lines represent reference outcomes from a large population (N = 20002), as reported in ref. 32. The colours blue, orange, and green represent cooperators (C), defectors (D), and loners (L), respectively. The shaded region indicates the range of network sizes where mutation-induced outcomes align with those observed in large populations, effectively addressing finite-size effects. Synergy factors are set to r = 2.02 for (a) and (b), and r = 4.6 for (c) and (d). a and c show results without mutation, while (b) and (d) include mutation at a fixed rate of μ = 10−6.

Full size image

Overall, these results demonstrate that incorporating mutation in agent-based simulations with small network sizes effectively mitigates finite-size effects, producing outcomes consistent with the referenced results from large networks (e.g., N = 20002) adapted from ref. 32. However, mutation is not a universal solution; its effectiveness depends on factors such as network size, mutation rate, and key game parameters like the synergy factor. To further validate the robustness and generality of these findings, we extend this approach to the spatial tolerance-based variant of optional public goods games in the subsequent analysis39.

Robustness check: tolerance-based variant of optional public goods game

The tolerance-based variant of public goods games, with its eight competing strategies, introduces significantly more complex evolutionary dynamics and phase transitions compared to the simpler three-strategy optional PGG (see Methods for more details). Simulations reported in ref. 39 used lattice sizes of 2400 × 2400 or larger to ensure that results were independent of network size, reflecting the need for large-scale simulations in the absence of mutation.

Despite the added complexity, our comparative analysis demonstrates that the results of the tolerance-based variant closely align with those of the simpler spatial optional PGG model (see Supplementary Note 1 and Supplementary Figs. 1–5), with two notable exceptions. First, incorporating a mutation rate of μ = 10−6 in agent-based simulations on a square lattice of size 2002 does not fully resolve finite-size effects, leaving a gap compared to results obtained from a 24002 lattice. To conserve computational resources, we did not extend simulations to match the outcomes from the larger lattice. However, adjusting both the network size and mutation rate is expected to achieve consistency with the referenced results, as suggested by Supplementary Figs. 3 and 4. Second, for smaller network sizes (e.g., N = 502, as shown in Supplementary Fig. 3b), identifying an intermediate mutation range that reproduces results consistent with larger networks is not feasible. This observation suggests the possibility of nonlinear or abrupt changes in the width or position of effective mutation windows for certain games, warranting further investigation. Together, these observations underscore the importance of carefully selecting network sizes and mutation rates when employing mutation to address finite-size effects.

Nevertheless, the tolerance-based variant reinforces our main conclusion: mutation enables agent-based simulations on small networks to effectively mitigate finite-size effects, offering a robust approach even in systems with complex evolutionary dynamics. In practice, determining network-size-independent results is often challenging, particularly in the absence of prior analytical insights. To address this, we recommend performing mutation-sensitivity analyses across multiple parameter regimes and network sizes, particularly near critical phase transition boundaries. This approach ensures robust mitigation of finite-size effects without requiring excessively large networks, as in the method of solely increasing network size, and enhances the reliability of simulation outcomes, even in the face of complex dynamics.

Discussions

Our study investigates how mutation can mitigate finite-size effects in agent-based simulations of spatial evolutionary games. Using the spatial optional public goods game and its tolerance-based variant as examples, we demonstrate that introducing mutation into simulations with small networks offers a simple and cost-effective alternative to resource-intensive large networks25,35. We found that rare mutations do not alter evolutionary outcomes when these are stable. When equilibria are affected by finite-size effects, intermediate mutation rates yield results consistent with those from large networks, effectively counteracting finite-size effects. The effectiveness of this approach depends on both network size and mutation rate. While we identify a range of mutation rates that mitigate finite-size effects, and note that this range generally broadens with increasing network size, pinpointing an optimal mutation rate remains challenging without prior knowledge of the true evolutionary outcomes or a reliable analytical benchmark. Furthermore, this effective range is sensitive to population size, game structure, and parameter settings. Nonetheless, our findings highlight mutation as a practical method for mitigating finite-size effects in spatial evolutionary games. As a general guideline, we recommend conducting mutation-sensitivity analyses across parameter regimes and network scales, particularly near critical phase transition boundaries.

The implications of our findings extend beyond the optional public goods game and its specific variant to a broader class of spatial evolutionary games. We focused on the spatial optional public goods game because it is a foundational and classical model that exemplifies finite-size effects and underscores the necessity of large network sizes to mitigate them. The tolerance-based variant, with its eight competing strategies, further underscores the challenges of finite-size effects and serves as a robust test case for evaluating the solutions of subsystem competition35. Finite-size effects are also prevalent in rock-paper-scissors-type Lotka-Volterra systems40,41,42 and other multi-strategy evolutionary games33,43, such as public goods games with peer or pool punishment and multi-strategy extensions of the prisoner’s dilemma. Although we did not extend our approach to other spatial evolutionary games, we propose that incorporating mutation to address finite-size effects is broadly applicable and independent of specific game details. By reintroducing extinct strategies and maintaining fair competition, mutation promotes strategy diversity, offering a viable alternative to relying solely on large networks to enhance strategy survival. Future studies could explore the applicability of this approach to other spatial evolutionary game models and further investigate its potential.

Introducing mutation introduces stochasticity that prevents strategies from going extinct, which may obscure exact phase diagrams and phase transitions—a central focus in statistical physics—but facilitates the study of more complex spatial evolutionary games. While concepts such as phase transitions and self-organization provide valuable insights into complex systems, they often restrict spatial evolutionary game studies to small strategy spaces, typically with four or fewer strategies. This limitation arises because determining phase transition points in games with more complex strategy spaces is challenging due to finite-size effects, particularly in the absence of analytical methods. By shifting the focus from strictly physical phenomena and employing mutation-sensitive analysis to enhance the reliability of agent-based simulations, researchers can explore more intricate evolutionary games on structured networks without requiring extensive computational resources to overcome finite-size effects. For instance, in well-mixed populations, the optional public goods game with a comprehensive punishment set—comprising 24 strategies where cooperators, defectors, and loners can punish one another—shows high levels of antisocial punishment, exceeding those observed in games with limited punishment sets44. While such games have been extensively studied in well-mixed populations, their counterparts on structured networks remain poorly understood and are often constrained to simplified punishment strategy spaces25. We are currently applying this approach to study these complex strategy sets on structured networks, and our work is in progress.

Our findings contribute to the understanding of evolutionary game theory by revealing the nuanced role of high mutation rates in spatial public goods games. We find that high mutation rates can either promote or suppress cooperation, contingent on the enhancement factor, as clearly evidenced by our results in the optional public goods game (Fig. 3) and its tolerance-based variant (Supplementary Figs. 3 and 4). Traditionally, studies of cooperation have focused predominantly on the rare mutation limit, where population states remain close to Nash equilibria, and fixation probabilities of infrequent mutants can be explicitly calculated45,46. However, recent study in direct reciprocity shows that intermediate mutation rates can enhance cooperation by destabilizing defection and fostering diverse, resilient cooperative communities, even when individuals rely on minimal past information47. In structured populations, mutations commonly disrupt cooperative clusters, a phenomenon consistently supported by both weak-selection analyses48,49 and strong-selection simulations50,51. Nevertheless, certain scenarios involving costly expulsion52 or punishment53 illustrate how mutations may facilitate cooperation by promoting cooperative clusters or accelerating prosocial punishment. Our findings, along with these studies, suggest that the effects of mutation on cooperation in spatial evolutionary games remain only partially understood, particularly in complex strategy spaces beyond the traditionally dominant two-strategy models54,55 and structured populations beyond simple lattice-based frameworks. Future research should explore a wider range of network topologies, more intricate spatial game dynamics, and varying selection intensities to deepen our understanding of mutation-driven cooperation.

Our findings have broader implications for addressing finite-size effects in fields like network synchronization and disease spreading56. Traditionally, these fields have relied on methods like finite-size scaling to understand how system behavior depends on network size or have employed large networks to reduce fluctuations57,58,59,60. In contrast, our results suggest that mutation mitigates finite-size effects in evolutionary games by promoting strategy diversity, raising the possibility that analogous diversity-driven or stochastic mechanisms could be beneficial in other contexts. For instance, might variability in oscillator phases or coupling strengths improve synchronization in small networks? Could heterogeneity in transmission rates or recovery times alter epidemic thresholds in limited populations? Exploring these possibilities may deepen our understanding of finite-size effects across disciplines and lead to more robust models in network dynamics.

Methods

The agent-based modeling approach for spatial evolutionary games typically comprises four key components: (i) population structure, (ii) game model, (iii) action selection, and (iv) simulation settings. Below, we briefly describe each of these components.

Population structure

In the simulation, a population of size N is considered and placed on a regular two-dimensional lattice. Each player’s neighborhood followed the von Neumann configuration, meaning each player was connected to four neighbors: left, right, up, and down. Periodic boundary conditions are applied, ensuring that players in the last row (or column) are connected to those in the first row (or column) in a lattice.

Game model

Spatial optional public goods game

In the optional public goods game (PGG), cooperators (C) contribute an amount c to a common pool, defectors (D) contribute nothing, and loners (L) opt out of the game, abstaining from the benefits of public goods while receiving a non-negative payoff σ. The total contributions in the common pool are multiplied by a synergy factor r and distributed equally among participants (excluding loners), regardless of their contributions. The payoff for a player x with strategy sx ∈ {C, D, L} is given by:

$${\Pi }_{{s}_{x}}=\left\{\begin{array}{ll}\frac{rc{n}_{c}}{{n}_{c}+{n}_{d}}-c\quad &\,\text{if}\,{s}_{x}=C\\ \frac{rc{n}_{c}}{{n}_{c}+{n}_{d}}\quad &\,\text{if}\,{s}_{x}=D\\ \sigma \quad &\,\text{if}\,{s}_{x}=L\end{array}\right.,$$
(1)

where nc, nd, and nl denote the number of cooperators, defectors, and loners within the group, respectively, with nc + nd + nl = n, where n = 5 is the group size.

A game group involving a focal player and her four neighbors. In a strict spatial optional PGG, a focal player’s payoff is accumulated over n = 5 games, with PGG groups centered around the focal player and each of her four neighbors, respectively. In the original spatial optional PGG32, only a simplified scenario is considered, where the payoff is determined by single PGG group centered around the focal player. Furthermore, when there is only one participating player in the group (i.e., when nc + nd = 1), the PGG cannot proceed and the participant receives the opt-out payoff σ, akin to that of a loner. We adopt these consistent settings of ref. 32 in our investigation.

Tolerance-based variant of optional public goods game

The tolerance-based variant of the optional public goods game introduces eight strategies39. In addition to traditional cooperators, defectors, and loners, it includes tolerance-based conditional cooperators (Mt). A player adopting strategy Mt acts as a cooperator contribute c to common pool if the number of defectors in the group is below the tolerance level t ∈ {0, 1, 2, …, n − 1}; otherwise, acts as a loner. Furthermore, the adoption of a tolerance-based strategy entails a fixed cost γ, reflecting the expense associated with monitoring the composition of the group.

With respect to the payoff computation for each strategy, the total number of contributors (TC) is given by:

$${n}_{TC}={n}_{C}+\mathop{\sum }\limits_{t = 0}^{n-1}{\delta }_{t}{n}_{{M}_{t}},$$
(2)

where \({n}_{{M}_{t}}\) is the number of players adopted strategy Mt in group, and δt is a indicator function. δt = 1 if the number of defectors in group nd is less than or equal to the tolerance level t, and δt = 1 otherwise. Specifically, a lonely contributor cannot generate the synergistic benefits of collective efforts, so the public pool is not multiplied (equivalent to r = 1), and the public pool only increases by a factor of r (where 1 < r < n) when there are at least two contributors39. The payoff for each strategy in a single PGG is calculated as:

$$\left\{\begin{array}{l} \hskip -70pt {\Pi }_{D}=\frac{r(c\cdot {n}_{TC})}{{n}_{D}+{n}_{TC}} \quad \\ \hskip -65pt {\Pi }_{C}={\Pi }_{D}-c\quad \\ \hskip -90pt {\Pi }_{L}=\sigma \quad \\ \hskip -3pt {\Pi }_{{M}_{t}}={\delta }_{t}{\Pi }_{C}+(1-{\delta }_{t})\sigma -\gamma \quad \end{array}\right..$$
(3)

Following ref. 39, we adopt strict spatial games. A player’s total payoff \({\Pi }_{{s}_{x}}\) with a strategy sx ∈ {C, D, L, M0, M1, M2, M3, M4} is the sum of payoffs accumulated from 5 groups, including the player’s own group and the groups formed by their four neighbors.

Action selection

Following refs. 32,39, we adopt the imitation updating rule for the spatial optional public goods game and the teaching updating rule for the tolerance-based variant. Both rules are similar but differ in perspective: in the imitation rule, focal players learn the strategy of their neighbors, whereas in the teaching rule, focal players enforce their strategy on their neighbors.

Specifically, let \({\Pi }_{{s}_{x}}\) denote the total payoff of a focal player x and \({\Pi }_{{s}_{y}}\) the payoff of a randomly selected neighbor y. The probability of player x imitating the strategy of neighbor y follows the Fermi rule:

$$w({s}_{y}\to {s}_{x})=\frac{1}{1+\exp [({\Pi }_{{s}_{x}}-{\Pi }_{{s}_{y}}+\tau )/K]}.$$
(4)

Similarly, the probability of player x enforcing their strategy sx on neighbor y (or equivalently, the probability of player y imitating player x) is:

$$w({s}_{x}\to {s}_{y})=\frac{1}{1+\exp [({\Pi }_{{s}_{y}}-{\Pi }_{{s}_{x}}+\tau )/K]}.$$
(5)

Here, K represents the irrationality of selection, and τ is the cost of strategy change. Consistent with prior studies, we set K = τ = 0.1 for the spatial optional public goods game, following ref. 32, and K = 0.5, τ = 0 for the tolerance-based variant, following ref. 39.

Inclusion of mutation

We incorporated mutation, or behavioral noise, into the action selection process. With probability μ, the focal player x mutates to another strategy randomly chosen from the available strategy space; Otherwise, the player updates strategy based on Eqs. (4) or (5), depending on specific model. Mutation here can be viewed as analogous to behavioral noise in human behavior models61,62 or to exploration rates in multi-agent systems63,64.

Simulation settings

Simulations were conducted over a series of Monte Carlo time steps. In each time step, a focal player was randomly selected to play the game with all their neighbors. Subsequently, one of the focal player’s neighbors was randomly chosen to play the game with their own neighbors. The payoffs of the focal player and the selected neighbor were then compared to determine the outcome: either the focal player imitates the neighbor’s strategy (imitation rule in the optional PGG model) or enforces their own strategy on the neighbor (teaching rule in the tolerance-based variant). Consistent with the setting of previous refs. 32,39, we fixed c = 1 and σ = 1.

Single simulations ran over 105 time steps, with strategy abundances averaged over the final 5000 time steps. The population size in the study typically consisted of 2002 players, but varied from 502 to 8002 players to examine the influence of network size. Each data point are averaged from 100 independent realizations. Throughout this work, we refer to networks with N = 2002 or smaller as “small networks”, and networks with N = 20002 or larger as ‘large networks’. Intermediate sizes (e.g., N = 8002) are explicitly noted when discussed.