Introduction

The role of mobility in the propagation of epidemics is well-established1. On the one hand, the rapid expansion of global mobility networks has dramatically increased the level of inter-connectivity between regions, accelerating the transmission of infectious diseases2,3,4. On the other hand, the ongoing trends in urbanization and the transition toward more densely populated urban environments further exacerbate the potential for localized disease outbreaks to escalate into epidemics5,6,7. Accurately predicting and mitigating these outbreaks requires a comprehensive understanding of epidemic vulnerability, encompassing factors such as mobility patterns, population susceptibility, healthcare infrastructure, and environmental conditions8,9,10,11,12,13,14,15,16.

In the absence of universally effective vaccines and therapeutics, non-pharmaceutical interventions (NPIs) have become a critical tool in mitigating the spread of epidemics17,18,19. Nonetheless, the suitability of NPIs as optimal responses to epidemic threats hinges on the balance between their expected health benefits and the collateral effects derived from their implementation20,21,22. For instance, policies shaping human mobility during the COVID-19 pandemic were efficient in controlling the exponential growth of cases yet introduced significant socioeconomic challenges23,24,25,26.

Beyond their associated socioeconomic cost, the implementation of NPIs tailored to mitigate a specific epidemic scenario affects the epidemic trajectories of other diseases circulating in the same population. Such effects are always synergistic when both diseases share the same transmission mechanisms, as proven by the reduced prevalence of airborne diseases (ABDs) in the population resulting from the implementation of NPIs designed to contain COVID-19 cases27,28,29. Conversely, quantifying the impact of such policies on other circulating pathogens with different transmission mechanisms, such as vector-borne diseases (VBDs), represents a more intricate problem. Indeed, several empirical studies have reported disparate results of these interventions ranging from potential benefits to negligible effects or even unintended drawbacks30,31,32,33,34,35,36,37,38,39,40.

Numerous theoretical studies have investigated the impact of local mobility on the global transmission of both ABDs and VBDs2,12,41,42,43,44,45,46. However, a holistic understanding of the combined spatial and temporal dynamics of mobility on disease spread remains incomplete42,44,47,48,49,50,51,52,53,54. In this study, we present a unified framework for analyzing both VBDs and ABDs at a large scale. Our approach is grounded in a metapopulation model42,45,55,56 designed to capture the complexity of multi-patch systems. This model incorporates a matrix-based representation of epidemic vulnerability, with each row representing the overall vulnerability of a particular patch. Utilizing the LouBar method57,58, we classify regions into high-vulnerability zones (“hotspots”) and low-vulnerability zones (“suburbs”) based on their population densities. This allows us to identify key areas and relevant mobility flows that shape cities’ vulnerabilities to both types of diseases.

Using this framework and real data from the city of Cali in Colombia, we first demonstrate that interventions proven successful in reducing ABD transmission do not yield comparable outcomes for VBDs. We explain this disparity, by exploring the contagion dynamics of both disease types on a simplifed one-hub-one-leaf mobility network, disentangling the temporal and spatiotemporal components. This approach enables the identification of optimal conditions for the simultaneous control of both ABDs and VBDs in a region. Leveraging this information, we redesign the interventions on the mobility network of the city of Cali, showing that model-informed policies are efficient in containing ABDs while not hampering the control of VBDs. The successful implementation of these strategies using real-world metapopulation data underscores the potential of the model to inform public health interventions for both ABDs and VBDs.

Methods

Data

As a primary illustration, we examine the spread of VBDs and ABDs within Cali, Colombia. This metropolitan area, with a population exceeding 2 million, provides an ideal test case due to its documented history of severe VBD outbreaks. To assess the impact of mobility patterns on disease transmission within Cali, a detailed reconstruction of the city’s resident mobility network was conducted. This reconstruction involved dividing the city into 22 designated administrative districts, or communes ("comunas”). Demographic information on population distribution across these communes was sourced from the local municipality’s census records in 2018. The distribution of both human and mosquito populations across these areas in Cali is further illustrated in Supplementary Fig. 3. Subsequently, mobility flows between these districts were derived from established urban commuting surveys59, resulting in the collection of over 105 individual travel trajectories, which offer a substantial representation of commuting patterns within Cali. This dataset was then used to construct an origin-destination matrix, R whose elements correspond to Rij = Tij/∑lTil, where Tij encodes the population outflows from commune i to j. The elements of R can thus be interpreted as the probability of moving from i to j. In Supplementary Fig. 1a we show the resulting mobility matrix R and in Supplementary Fig. 1b we show the mobility flows on the map of Cali.

To model the vector distribution (mosquito populations) across communes, we consider the container index, encoding the probability of finding Aedes aegypti mosquitoes in recipients distributed across the city. We assume that a high container index corresponds with a large concentration of vectors in this area. Following this rationale, we assume that the ratio between the number of vectors and humans inside each patch in our model is directly proportional to its container index. Although our entomological dataset spans the years 2010 to 2020, all results shown in the main text use the mosquito distribution from 2018 to match the year of the census-based population data. The remaining years are employed in Supplementary Note 9 to assess the robustness of our findings under varying temporal vector distributions.

Hotspot classification

Hotspots are identified using the LouBar method, where hotspots are determined by setting a threshold based on population densities. First, patches are arranged in ascending order of density. A Lorenz curve is then plotted, with the cumulative density of patches on the Y-axis and corresponding patch numbers on the X-axis. The derivative of the curve at its peak point (patch with maximum cumulative density) is extrapolated to intersect the X-axis, determining the threshold patch beyond which all patches are considered hotspots. A patch i qualifies as a hotspot if ρi > ρLouBar, where ρi is the density of patch i and ρLouBar is the threshold density obtained via the LouBar method. All remaining patches are referred to as suburbs. For further details on this method, see Supplementary Fig. 2 where we plot the hotspots in terms of the population density (upper-panel) as well as the container index (ratio of mosquitoes to human population in a given comune).

Epidemic vulnerability

The concept of an epidemic threshold τc is frequently used to determine the minimum level of infectiousness necessary for a pathogen to establish within a population. A higher epidemic threshold signifies increased resistance to disease transmission, whereas a lower threshold suggests heightened vulnerability. In this study, we define epidemic vulnerability as the inverse of the epidemic threshold. Thus, a lower epidemic threshold, indicative of greater susceptibility to disease transmission, equates to a higher level of epidemic vulnerability. Consequently, the epidemic vulnerability, \(\nu ={\tau }_{c}^{-1}\), for a given geographic area (referred to as a “patch”) is defined as the expected number of contagions the population within that area encounters over time, primarily influenced by the population’s recurrent mobility patterns.

To assess the city’s susceptibility to ABDs and VBDs independently, we employ a metapopulation framework. Building on established models for ABDs and VBDs45, we adapt these frameworks to suit the specific context of this study. These models have proven efficient in capturing the heterogeneous distribution of cases across cities/neighborhoods for several real epidemic scenarios, such as the unfolding of the COVID-19 pandemic in the United States46,55 or the endemic propagation of Dengue in the city of Cali45.

The dynamics of ABDs are represented using a generalized Susceptible-Infected-Recovered model, while the Ross-Macdonald model is applied to describe VBD transmission60. Both models incorporate spatial distributions and mobility patterns, fundamental components of metapopulation theory. In this framework, a metapopulation is conceptualized as a network where nodes represent geographic locations (patches) and edges denote population movement between these patches.

Each patch i is characterized by its population size ni, area ai, and vector population mi. These attributes vary across patches, reflecting differences in demographic distribution and vector prevalence. Human and vector populations are assigned to specific patches based on their residence locations, with ni and mi representing the number of humans and vectors residing in patch i. The patches are interconnected, forming a directed, and weighted network encoded in the mobility matrix R. This matrix governs the movement of the human population across the system, while mosquitoes are assumed to remain confined to their respective patches due to their limited dispersal range61.

Coarse-graining real cities into the synthetic hub-leaf metapopulation

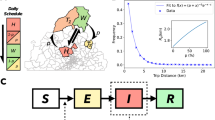
This study adopts a simplified synthetic model designed to isolate universal factors that constrain the effectiveness of mobility-targeted interventions. To reduce the complexity of real urban mobility networks, we apply a coarse-graining procedure that aggregates the system into a two-patch metapopulation comprising a single hub and a single leaf. In this framework, all nodes assigned to the same category—either hotspots or suburbs, as identified via the LouBar method—are assumed to be equivalent in terms of their aggregate contagion dynamics (see Supplementary Fig. 5 for a schematic of the formalism). Figure 1c illustrates the structure of this hub–leaf metapopulation model. The hub is characterized by its human population (nh), area (ah), and vector population (mh), while the leaf is assigned corresponding values nl, al, and ml. To apply this abstraction to a real system such as Cali, we compute effective parameters—β, α, γ, κ, and δ—based on empirical data.

Fig. 1: Effect of mobility-targeted interventions in Cali and a simplified metapopulation model.
figure 1

a Map of Cali showing the spatial distribution of population density hotspots (navy) and suburbs (light blue), along with the mobility network. Edge weights are represented using a red color gradient. b Illustration of a mobility-targeted intervention involving the redistribution of mobility flows from hotspots to neighboring suburbs. The impact of the intervention is quantified by the ratio \(\frac{{\nu }^{{{{{\rm{Mod}}}}}}}{\nu }\), where \({\nu }^{{{{{\rm{Mod}}}}}}\) denotes the recalculated vulnerability after the intervention. Values below 1 indicate a beneficial effect (reduced vulnerability), while values above 1 indicate a detrimental effect (increased vulnerability). c Schematic of the simplified one hub–leaf metapopulation model. The hub aggregates all hotspots and is defined by its human population (nh), mosquito population (mh), and area (ah). The leaf aggregates all suburbs and is characterized by its human population (nl = αnh), mosquito population (ml = βmh), and area (al = γah), with α, β, and γ serving as scaling parameters that relate the leaf to the hub.

Full size image

Following hotspot identification, we define hub-level quantities as: nh = ∑i∈Hni, mh = ∑i∈Hmi, and ah = ∑i∈Hai. Within-hub mobility is defined as \(\kappa =\frac{{\sum }_{i\in H}{\sum }_{j\in H}{R}_{ij}}{{N}_{H}}\), with outward mobility from the hub given by \(1-\kappa =\frac{{\sum }_{i\in H}{\sum }_{j\in S}{R}_{ij}}{{N}_{H}}\), where H and S denote hotspots and suburbs respectively, and NH is the number of hotspot patches. The leaf parameters are scaled relative to the hub using the ratios: \(\alpha =\frac{{\sum }_{i\in S}{n}_{i}}{{\sum }_{i\in H}{n}_{i}}\), \(\beta =\frac{{\sum }_{i\in S}{m}_{i}}{{\sum }_{i\in H}{m}_{i}}\), and \(\gamma =\frac{{\sum }_{i\in S}{a}_{i}}{{\sum }_{i\in H}{a}_{i}}\). This yields nl = αnh, ml = βmh, and al = γah. Within-leaf mobility is computed as \(\delta =\frac{{\sum }_{i\in S}{\sum }_{j\in S}{R}_{ij}}{{N}_{S}}\), with outward mobility from the leaf given by \(1-\delta =\frac{{\sum }_{i\in S}{\sum }_{j\in H}{R}_{ij}}{{N}_{S}}\), where NS is the number of suburban patches. For further details on the model construction, refer to Supplementary Note 3. A summary of parameter definitions and their empirical values is provided in Table 1.

Table 1 Definition of the parameters used in the synthetic model and the corresponding mathematical expressions for deriving them from empirical metapopulation data
Full size table

Results

Effect of mobility-interventions in Cali, Colombia

In Fig. 1a, we present a map of Cali, highlighting hotspot (suburbs) in dark (light) blue. For reference, the population density distribution across communes is provided in Supplementary Fig. 2. One effective (albeit somewhat idealized) mobility-intervention for reducing regional vulnerability to ABDs, as proposed in ref. 55, involves rerouting mobility flows from hotspots to neighboring suburban areas while maintaining the total outflow from each hotspot. For each realization of this modified flow structure, we compute the resulting vulnerability, vmod. In Fig. 1b, we show the distribution of the ratio of modified vulnerability (across 1000 iterations) to the baseline vulnerability calculated from Cali’s empirical mobility network. Note that the contribution of the epidemiological parameters, e.g., the biting rate of mosquitoes or their infectiousness, to the epidemic vulnerability of a population can be separated from that corresponding to the mobility, as shown in Supplementary Note 3. Consequently, the ratio vmod/v exclusively reflects how interventions on the mobility network alter regional vulnerability for a generic VBD. As anticipated, the intervention achieves an average reduction in regional vulnerability of approximately 20% in ABD. This positive effect is attributed to the population density asymmetry within cities; by diverting mobility from dense hotspots to lower-density suburbs, the intervention raises the epidemic threshold through a dilution effect, reducing potential contacts within hotspots and distributing potentially infectious individuals to areas where their impact is minimized.

Conversely, this approach has the unintended consequence of exacerbating vulnerability to VBDs. Hotspots defined by vector abundance (e.g., mosquito populations) do not always align with those based on human population density, although a moderate positive correlation does exist (Spearman correlation coefficient of 0.66; see Supplementary Fig. 2). When evaluating the same intervention under VBD dynamics, we observe an increase in vulnerability of nearly 50%. This finding underscores a key result: a mobility-targeted intervention that is effective for controlling ABDs may have adverse effects when applied to VBDs. This highlights the need to tailor epidemic control strategies to the specific transmission mechanisms of each disease. In Supplementary Fig. 4, we further demonstrate that this double-edged effect persists even under a more practical intervention–restricting individuals who typically commute from suburbs to hotspots to remain within their residential areas. This more feasible policy still benefits ABD control while worsening VBD vulnerability, reinforcing the robustness of our finding.

Our finding—that an intervention effective for one disease type may exacerbate the vulnerability of another within the same region—emphasizes the necessity of thoroughly examining the contagion dynamics of ABDs and VBDs and their interactions with population density and mobility flows. In the case of Santiago de Cali, this interplay could be further investigated by analyzing the relationship between epidemic vulnerability and the structural architecture of its mobility network. However, the inherent complexity of human mobility patterns poses challenges, specifically: (i) extracting actionable insights directly from mobility network analyses, and (ii) generalizing these findings to inform disease control strategies in other urban settings.

To address these challenges, we adopt an alternative approach by focusing on universal factors that constrain the effectiveness of control policies. To do so, we use a simplified synthetic model of two patches, a hub and a leaf, represented in Fig. 1c. In this model, there are three parameters α,γ, β controlling the ratio of populations, areas and mosquito abundance between both areas. Mobility dynamics in this model is governed by two parameters: κ (1 − κ), representing the fraction of hub residents working in the hub (leaf) and δ (1 − δ), encoding the fraction of residents in the leaf working in the leaf (hub). This framework allows us to systematically explore the dependence of urban vulnerability on the parameter space defined by (α, γ, β, κ, δ), facilitating the identification of universal policies that minimize vulnerability across diverse urban environments. Note that any real metapopulation can be coarse-grained into this simple model as detailed in the Methods section.

Contagion dynamics in ABDs

We begin by analyzing the well-established mechanisms governing airborne disease transmission assuming recurrent mobility in our synthetic model. Building on this framework (see Supplementary Notes 3 and 4 for further details), the vulnerability ν of a simplified one-hub-leaf model for ABDs can be expressed as

$${\nu }^{ABD}=\frac{{\Theta }_{h}(\kappa ,\delta )+\frac{{\Theta }_{l}(\kappa ,\delta )}{\gamma }+\sqrt{{\left({\Theta }_{h}(\kappa ,\delta )+\frac{{\Theta }_{l}(\kappa ,\delta )}{\gamma }\right)}^{2}-\frac{\alpha }{\gamma }{\left({\Theta }_{hl}(\kappa ,\delta )\right)}^{2}}}{2},$$
(1)

where Θh(κ, δ), Θl(κ, δ) and Θhl(κ, δ) can be interpreted as hub-, leaf- and cross-vulnerabilities respectively. Their precise mathematical forms are provided in Supplementary Eq. (S26). It is straightfoward to show that νABD is minimized when \(\kappa \approx \frac{1}{\gamma +1}\) and \(\delta \approx \frac{\gamma }{\gamma +1}\).

For our analysis, we simplify the model by fixing γ = 1, ensuring that the hub and leaf regions have equal areas. This approach eliminates the confounding effects of spatial heterogeneity, allowing us to focus on the contagion dynamics. Under this configuration, a homogeneous distribution of the population across the hub and leaf is optimal. Achieving such a distribution requires selecting mobility parameters that promote an even population spread between the regions. Crucially, the initial population ratio between the leaf and hub, represented by α, emerges as a key determinant in this process. (For a detailed analysis of this limiting case and a breakdown of each term in Eq. (1), cf. Supplementary Notes 4 and 5 and Supplementary Figs. 6–8 for illustration.)

In Fig. 2a, we illustrate the vulnerability dynamics for a scenario where α is set to a small value, representing a relatively low population in the leaf compared to the hub. In this regime, the hub exhibits the highest vulnerability, and the system’s behavior is predominantly governed by the mobility parameter κ. For low leaf populations, migration from the hub to the leaf is critical to achieving a more balanced distribution. As κ increases, a greater proportion of the hub’s population migrates to the leaf, reducing vulnerability within the hub. When κ ≈ 0.5, roughly half of the hub population has moved to the leaf, resulting in a near-homogeneous distribution across the two regions. However, as κ → 1, nearly the entire hub population migrates to the leaf, significantly increasing the leaf’s vulnerability and establishing it as the new hotspot.

Fig. 2: Epidemic vulnerability in ABDs.
figure 2

a, b Contour plots illustrating the dynamics of vulnerability in airborne disease (ABD) for different values of the parameter α. The blue dotted contour line indicates the threshold where vulnerability equals 1. In both plots, γ = 1.

Full size image

In epidemiological models, dilution refers to the process of homogenizing population distribution by redistributing individuals across regions. In the context of our ABD model, larger values of α, which correspond to larger leaf populations, reduces the extent of dilution. This reduced dilution elevates overall vulnerability, as reflected by the more intense red hue in the color scale of Fig. 2b. When the leaf-to-hub population ratio approaches 1, both the leaf and hub exhibit equal susceptibility to vulnerability. In this case, any migration from the hub to the leaf requires a proportional counterflow from the leaf to the hub to achieve optimal population homogenization across the two regions.

In Fig. 2b, vulnerability is minimized along the upward diagonal, where κ ≈ δ. This configuration represents a balanced migration regime, where the movement of individuals from the hub to the leaf is counterbalanced by an equivalent flow from the leaf to the hub. Deviations from this equilibrium lead to imbalanced population distributions and increased vulnerability. Specifically, lower κ and higher δ result in an accumulation of individuals in the leaf, causing a sharp increase in its vulnerability. Conversely, higher κ and lower δ lead to a concentration of individuals in the hub, similarly raising its vulnerability. Thus, extreme values of mobility in either direction result in higher overall system vulnerability. In Supplementary Fig. 9, we plot the analog of Fig. 2 for other intermediate values in the range 0 ≤ α ≤ 1 mirroring the trends described here.

Contagion dynamics in VBDs

Next, we analyze the dynamics specific to VBDs. In this context, the vulnerability νVBD represents the average number of indirect contacts an individual has with the rest of the population, mediated by vectors. The corresponding equation for the vulnerability (Details in Supplementary Notes 1 and 2), is:

$${\nu }^{VBD}=\sqrt{\frac{{\widetilde{\Theta }}_{h}(\kappa ,\delta )+\beta {\widetilde{\Theta }}_{l}(\kappa ,\delta )+\sqrt{{\left({\widetilde{\Theta }}_{h}(\kappa ,\delta )+\beta {\widetilde{\Theta }}_{l}(\kappa ,\delta )\right)}^{2}-\alpha \beta {\left({\widetilde{\Theta }}_{hl}(\kappa ,\delta )\right)}^{2}}}{2},}$$
(2)

where once again the terms retain their interpretation as in ABDs, with their precise mathematical forms shown in Supplementary Eq. (S30). We note now the appearance of the term β which quantifies the relative population of mosquitoes in the leaf as compared to the hub ml/mh. The term βmi represents the total number of interactions occurring within patch i, independent of the number of individuals occupying the patch. However, larger effective populations reduce the likelihood of any specific individual being bitten during these interactions, which explains the presence of effective populations in the denominator of the associated expressions. For our subsequent analysis, motivated by the observed correspondence of mosquito- and population density hubs in Supplementary Fig. 2, we simplify the model by fixing β = 0.01, ensuring a higher mosquito population in the hub region, which designates it as a potential hotspot. This configuration allows for an apples-to-apples comparison with the ABD model, where hotspots are similarly characterized by higher densities in their respective critical factors.

In the VBD model, smaller values of α, corresponding to lower leaf populations, reduce the scale of dilution, thereby increasing overall vulnerability. This is reflected by the more intense red hue in the color scale of Fig. 3a. In this regime, the hub and leaf exhibit similar vulnerabilities in the absence of mobility, i.e., when (δ, κ) = (1, 1). As with ABDs, starting from this scenario and reducing κ increases the hub’s vulnerability, as emptying the hub heightens its local exposure. However, mobility also allows hub residents to leave the area, which offsets the increase in local vulnerability, resulting in an approximately constant value of ν = 1 along this axis. Similarly, altering δ to increase the movement of individuals from the leaf reduces the time residents spend in the leaf while increasing its role as a center of transmission. Conversely, when κ approaches 0 and δ is low, the absence of hub residents in the hub amplifies the risk of exposure for the smaller incoming leaf population, leading to heightened overall vulnerability.

Fig. 3: Epidemic vulnerability in VBDs.
figure 3

a, b Contour plots illustrating the dynamics of vulnerability in vector-borne disease (VBD) for different values of the parameter α. The blue dotted contour line indicates the threshold where vulnerability equals 1. In both plots, β = 0.01.

Full size image

For higher values of α, the vulnerabilities of the hub and the leaf in the absence of mobility differ significantly, as β/α ≪ 1. This discrepancy makes the beneficial effects of mobility, primarily through the dilution of hub vulnerability, more pronounced. Specifically, reducing hub vulnerability requires a careful balance between evacuation and dilution strategies. Evacuation involves decreasing κ to promote outflow from the hub and increasing δ to limit inflow from the leaf. In contrast, dilution involves increasing κ to retain the hub population and decreasing δ to encourage migration from the leaf to the hub. Minimizing hub vulnerability necessitates an optimal trade-off between these competing strategies.

Figure 3b illustrates that the optimal balance between evacuation and dilution strategies occurs along the downward diagonal, where κ ≈ 1 − δ. This result can also be derived from Eq. (2), assuming β ≪ 1. Deviations from this equilibrium, such as lower κ and lower δ, lead to increased exposure of the incoming leaf population in the hub due to the reduced size of the hub population. Conversely, higher κ and higher δ result in the hub population being permanently exposed to the disease without adequate dilution from the leaf population. (Refer to Supplementary Fig. 10 for other intermediate values in the range 0 ≤ α ≤ 1).

Mobility-targeted interventions to mitigate urban vulnerability

In the absence of universally effective vaccines and therapeutics, mobility-targeted interventions play a critical role in controlling epidemics. These interventions often involve regulating travel behavior and mobility flows within populations. By studying the contagion dynamics of various diseases, we have uncovered important relationships between epidemic vulnerability and mobility patterns. While strict lockdowns are effective in curbing outbreaks, they come with significant socioeconomic costs. Previous analyses of Fig. 1b demonstrated that redistributing mobility—rather than enforcing complete lockdowns—by shifting flows from hotspots to neighboring suburban regions can aid in controlling ABDs in Cali, though it may exacerbate the spread of VBDs. Building on this understanding, this section examines the potential benefits of reshuffling mobility flows as a NPI strategy for managing both ABDs and VBDs. Based on the derived vulnerability equations, ABD vulnerability, Eq. (1), is minimized at specific mobility parameter values: \(\kappa \approx \frac{1}{\gamma +1}\) and \(\delta \approx \frac{\gamma }{\gamma +1}\). In contrast, VBD vulnerability, Eq. (2), can be reduced over a broader range of mobility parameter values, including δ = 1 − κ, irrespective of population size. These findings are consistent with the contagion dynamics analysis for both disease types across various values of α. The optimal mobility parameter setting for ABDs is a subset of the broader δ = 1 − κ range identified for VBDs.

Next, we investigate two reshuffling strategies: (1) tuning mobility parameters to the specific values \(\kappa =\frac{1}{\gamma +1}\) and \(\delta =\frac{\gamma }{\gamma +1}\), and (2) adjusting mobility parameters within the constrained range δ = 1 − κ, to determine whether either strategy is beneficial for both ABDs and VBDs. To evaluate the effectiveness of these strategies, we generate multiple synthetic networks by exploring the parameter space defined by (α, γ, β, δ, κ). For each network, we calculate the vulnerability ν before and after the intervention, denoted as νMod. By analyzing the resulting histogram of vulnerability ratios, we assess whether the reshuffling strategy is beneficial or detrimental based on the frequency of values less than or greater than 1.

Strategy-I: constraining mobility parameters to the range δ = 1 − κ

Strategy I involves modifying the mobility flows from the leaf such that δ = 1 − κ. Based on our earlier analysis, this intervention is anticipated to reduce vulnerability for VBDs; however, its effectiveness for ABDs is less certain. By performing multiple random iterations across synthetic networks, we observe that for VBDs, the majority of outcomes fall within the beneficial region of Fig. 4a, confirming the expected positive impact of this strategy. In contrast, the results for ABDs are more variable. Approximately half of the computed values lie within the beneficial region, while the remaining half fall in the detrimental region. This mixed outcome underscores the limitations of Strategy I for ABDs, as the precise tuning required to minimize their vulnerability is not consistently achieved. This discrepancy is likely due to the narrower optimal parameter range for ABDs (\(\kappa \approx \frac{1}{\gamma +1}\) and \(\delta \approx \frac{\gamma }{\gamma +1}\)), which Strategy I does not explicitly satisfy. These findings suggest that while Strategy I is a robust approach for reducing vulnerability in VBDs, its application to ABDs is less reliable and may require additional adjustments or complementary interventions to ensure its effectiveness.

Fig. 4: Impact of policies shaping mobility on disease spreading.
figure 4

a Violin plot showing the impact of reshuffling strategy I, which adjusts mobility parameters within the constrained range δ = 1 − κ, on epidemic vulnerability for ABDs and VBDs. b Violin plot illustrating the effect of reshuffling strategy II, where mobility parameters are set to specific values \(\kappa =\frac{1}{\gamma +1}\) and \(\delta =\frac{\gamma }{\gamma +1}\), on epidemic vulnerability for ABDs and VBDs. In both panels, the numerator (νMod) represents the recomputed epidemic vulnerability after reshuffling. The lower zone (values below 1) indicates a beneficial effect, while the upper zone (values above 1) signifies a detrimental effect. All parameters, except for those involved in the reshuffling, are sampled randomly from a uniform distribution.

Full size image

Strategy-II: fixing mobility parameters to \(\kappa =\frac{1}{\gamma +1}\) & \(\delta =\frac{\gamma }{\gamma +1}\)

Our analysis of contagion dynamics reveals that vulnerability to ABDs is minimized at specific mobility parameter values: \(\kappa =\frac{1}{\gamma +1}\) and \(\delta =\frac{\gamma }{\gamma +1}\). These optimal parameters for ABDs fall within the constrained range δ = 1 − κ, where vulnerability to VBDs is also minimized. Consequently, setting these specific mobility parameters is expected to reduce vulnerability for both ABDs and VBDs. This expectation is confirmed by Fig. 4b, where the majority of vulnerability ratios (νMod/ν) fall below 1, indicating that this intervention—referred to as Strategy II—is effective in reducing vulnerability for both disease types.

These findings highlight a direct relationship between vulnerability and the spatial scale (relative area) of the leaf compared to the hub, characterized by the parameter γ. Optimizing mobility based on this ratio emerges as a beneficial policy. Specifically, within-hub mobility (κ) should be adjusted inversely proportional to the relative size of the leaf. For instance, if the leaf area is significantly larger than the hub area (γ ≫ 1), reducing within-hub mobility by migrating the majority of the hub population to the leaf (κ ≈ 0) can decrease disease vulnerability. The larger area of the leaf disperses individuals, reducing contact rates and, consequently, exposure to airborne pathogens compared to the denser hub. Additionally, implementing an outward lockdown in the leaf region (δ = 1) can further minimize vulnerability by preventing the movement of infected individuals back to the hub. This approach ensures that individuals remain in the lower-density environment of the leaf, reducing opportunities for disease transmission. However, when the leaf and hub areas are comparable (γ ≈ 1), complete migration of the hub population and a full outward restriction of the leaf population may not be optimal. In such cases, evenly distributing the population between both patches can yield the best outcome by optimizing the spread of the population and minimizing disease contact rates. Table 2 presents a comprehensive summary of intervention strategies, along with their observed effects.

Table 2 Summary of mobility-targeted intervention strategies and their observed effects
Full size table

Application of mobility-based NPI Strategies to Cali

We now apply the strategies developed for the simplified one-hub-leaf model to the complex mobility network of Cali, demonstrating the practicality and effectiveness of our approach in real-world scenarios. As shown in Fig. 1b, a previously proposed NPI strategy—redistributing mobility between hotspots and suburbs while maintaining total flow volume—proved effective for mitigating ABDs but was detrimental for VBDs in Cali. In the synthetic model, this strategy corresponds to setting κ = 0.

In Fig. 5a, we evaluate the application of Strategy I (described in Supplementary Note 8) to Cali’s complex mobility network. While Strategy I was less effective for ABDs in the one-hub-leaf model, its application to Cali produced predominantly beneficial results, with only a small number of detrimental outcomes. For VBDs, the one-hub-leaf model showed mostly beneficial results, and the application to Cali yielded even more robust outcomes, with all results falling within the beneficial region.

Fig. 5: Application of mobility-based NPI strategies to Cali, Colombia.
figure 5

Violin plots illustrating the impact of reshuffling flows using Strategy-I (a) and Strategy-II (b) on the epidemic vulnerability of Cali.

Full size image

We then applied Strategy II to the complex mobility network of Cali. Strategy II involves setting the mobility parameters \(\kappa =\frac{1}{\gamma +1}\) and \(\delta =\frac{\gamma }{\gamma +1}\). To implement this approach, we first calculated the value of γ for Cali’s network. Extending the definitions of α, β, and γ from the one-hub-leaf model to the complex network, we defined these parameters as the ratios of aggregated values in suburban and hotspot regions. Specifically, γ was calculated as the ratio of the total suburban area to the total hotspot area. For Cali, γ was determined to be 1.43. The application of this strategy is shown in Fig. 5b, with detailed implementation provided in Supplementary Note 8. The results demonstrate that, for both ABDs and VBDs, the vulnerability ratios (\(\frac{{\nu }^{Mod}}{\nu }\)) fall entirely within the beneficial zone. This outcome aligns closely with the results from the one-hub-leaf model, where the majority of vulnerability ratios were below 1, indicating a consistent reduction in vulnerability.

This agreement between theoretical predictions and real-world data suggests that, given the observed commuting patterns, spatial distribution of vectors, and population demographics in Cali, the proposed mitigation strategies can effectively minimize the impact of potential outbreaks of both ABDs and VBDs. These results hold true not just for a specific set of mobility parameter values but across a wide range of parameter combinations, highlighting the robustness and generalizability of our findings.

Discussion

This study presents a unified framework for analyzing the vulnerabilities associated with ABDs and VBDs, integrating theoretical modeling with empirical data to explore how mobility-targeted interventions can be optimized for different transmission dynamics. By combining a coarse-grained hub–leaf metapopulation model with real-world data from Santiago de Cali, Colombia, we assess how human mobility patterns influence epidemic risk and identify intervention strategies that can be jointly effective across disease types.

Our results emphasize the importance of spatial heterogeneity and mobility structure in shaping vulnerability. In the synthetic model, we identify specific parameter regimes—namely, \(\kappa =\frac{1}{\gamma +1}\) and \(\delta =\frac{\gamma }{\gamma +1}\)—that minimize vulnerability to ABDs by balancing intra- and inter-region mobility. For VBDs, a broader range including δ = 1 − κ proves effective, reflecting the indirect nature of vector-human transmission. The overlap of these regimes suggests that coordinated strategies targeting both disease types are feasible when guided by appropriate mobility metrics.

Empirical validation using Cali’s detailed mobility and entomological data confirms the robustness of these findings. Strategy II, which finely adjusts mobility flows based on area ratios, consistently reduces vulnerability for both ABDs and VBDs. While Strategy I, previously proposed to mitigate airborne spread, performs well for ABDs, it leads to a substantial increase in VBD vulnerability. Supplementary Fig. 14 directly visualizes the epidemic threshold for both ABD and VBD, demonstrating how different mobility interventions shift model outcomes in relation to this critical point. These results underscore the epidemiological trade-offs that arise when interventions are designed without accounting for pathogen-specific transmission pathways.

The implications for public health are significant. For ABDs, interventions should focus on reducing crowding in high-density areas by promoting population mixing and limiting mobility among densely connected hubs. In contrast, VBD control strategies should leverage information about local vector ecology and environmental conditions to avoid unintentionally increasing exposure risk. The simplified hub–leaf model provides a tractable abstraction for identifying key regions and optimizing intervention design. To further assess the robustness of our findings, we conducted a longitudinal analysis of vector distributions and intervention outcomes in Cali from 2010 to 2020 (Supplementary Note 9 and Supplementary Figs. 11–13). This extended temporal view demonstrates that our proposed strategies remain effective across varying vector ecologies observed over this decade. We believe that this temporal consistency provides a valuable proxy for empirical robustness in the absence of cross-city comparisons, reinforcing the reliability of the findings and suggesting potential applicability in other urban contexts. Furthermore, the identification of these critical regions can be used to optimize vector control efforts, such as targeted insecticide spraying or larval control, in areas where the model predicts high vector–human interaction and elevated transmission risk.

Nonetheless, limitations remain. The one-hub–leaf model simplifies complex urban networks and omits finer-grained spatial and demographic heterogeneity. Expanding the model to incorporate multiple hubs, dynamic changes in behavior or seasonality, and social determinants of health—such as access to healthcare, economic inequality, and cultural mobility norms—could enhance its practical relevance58,62. The container index, while useful, may introduce spatial bias if vector breeding sites are unevenly distributed. For policymakers operating under uncertainty, frameworks such as the maximum entropy approach63 can help reconstruct early epidemic dynamics and identify priority zones for intervention, even with sparse data.

While our application to Cali offers strong empirical grounding, broader generalizability remains an open question. Future work should extend this framework to additional cities with diverse urban, ecological, and socioeconomic contexts. Expanding the integration of real-world datasets—including healthcare infrastructure, environmental covariates, and behavioral data—will further refine model predictions and improve practical utility. This work bridges theoretical modeling and applied public health, offering a scalable and interpretable tool for designing mobility-targeted interventions. By distinguishing the mechanisms underlying ABD and VBD spread, it lays the groundwork for joint mitigation strategies that are evidence-based, adaptable, and informed by urban structure. Addressing epidemic vulnerability in complex cities will require continued interdisciplinary collaboration, data transparency, and policy innovation.