Introduction

Many complex systems have critical thresholds called tipping points, at which an abrupt shift between qualitatively different states occurs1,2,3,4,5. In biology, critical transitions are associated with asthma attacks6,7, epileptic seizures8,9,10, microbiome dysregulation11,12, depression13,14 and cardiac arrhythmia15,16; in economics, financial markets can form a “bubble” and fall into a recession17,18; in climatology, abrupt shifts in ocean circulation or climate can occur19,20,21,22,23; and in ecology24,25,26, ecosystems can collapse due to their interplay with human behavior, resulting in catastrophic shifts in forests or grasslands27,28,29, eutrophication of lakes30,31,32, collapse of populations33,34 and bleaching of coral reefs35,36. These events typically have tipping points where the system undergoes a qualitative change from one dynamical state to another, and are referred to as critical transitions37.

Countless decisions made by individuals, industries, and policy-makers depend upon the accuracy of early warning signals for critical transitions. Examples range from deciding the rate at which to harvest a population of fish38 to deciding whether to flee a potentially dangerous earthquake39. In 2009, Scheffer and colleagues proposed monitoring the generic indicators' variance and lag-1 autocorrelation to determine whether a critical transition is approaching40. This was motivated by a universal phenomenon called critical slowing down, which occurs in the vicinity of local bifurcations in dynamical systems41,42,43. Critical slowing down is characterized by an increased return time to equilibrium following a perturbation, which, in noisy systems, is manifested as an increase in variance and lag-1 autocorrelation. Rising variance and lag-1 autocorrelation were subsequently found prior to critical transitions in complex systems in cardiology15,37, ecology31,33, the climate21,44,45, engineering46, and geology47, to name a few areas. Many limitations to these generic early warning signals also emerged. They can fail to signal a transition if the time series is too short, too noisy48, or too non-stationary49,50, or if the transition corresponds not to a local bifurcation, but a global bifurcation51, or no bifurcation at all50. The development of more effective early warning signals remains a highly active area of research30,52.

In recent years, deep learning classifiers have been employed for early warning signals37,53,54,55,56,57. These classifiers require a lot of data, which is typically not available in the context of critical transitions. Studies have therefore opted to use synthetic data generated from simulations of mathematical models going through bifurcations—a dataset that can be made as large as needs be53. Given the universal properties of bifurcations41,43, these classifiers have been shown to be effective at predicting bifurcations in real systems, outperforming variance and lag-1 autocorrelation in many cases37,53,55. However, machine learning classifiers are only as good as their training data—this approach is reliant upon the real-world system exhibiting similar properties to one of the bifurcation trajectories contained within the training set. Indeed, it makes the assumption that a bifurcation exists in the first place—something that is not inherent to real-world systems, but rather a property of a mathematical model for the system of interest41.

Ideally, a machine learning classifier would be trained directly on data of the real-world system. To get around the problem of limited data availability58, we propose using surrogate data methods to generate trajectories derived from data of past critical transitions. This way, we can generate a lot of training data (enough to train a machine learning classifier) while also preserving system-specific properties of the data from past critical transitions.

Surrogate data methods have been primarily developed to enable robust statistical evaluations about a system from limited data59,60,61. The method involves creating multiple versions of a time series with the same (or very similar) statistical properties, including the histogram distribution, power spectrum, and autocorrelation function59,62. This allows one to test against a null hypothesis using a larger number of samples. Here, we use surrogate data methods to boost the number of samples with which to train machine learning classifiers. Specifically, surrogate data is generated from data far from (neutral) and near to (pre-transition) the critical transitions, serving as two distinct classes (Fig. 1). We then train machine learning classifiers to distinguish between these two classes. When a classifier assigns a high probability to the pre-transition class, this is interpreted as an early warning signal for a critical transition.

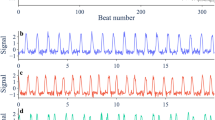
Fig. 1: Illustration of the SDML prediction framework.
figure 1

A Two trajectories (blue) and smoothing (gray) of chick heart aggregates approaching a critical transition. The vertical dashed line marks the onset of the transition. A green background denotes sections of the time series taken as far from the transition ("Neutral'') and red denotes sections close to the transition ("Pre-transition''). The trajectories are divided into training (left) and test (right) trajectories. B Thousands of surrogate time series are generated from the neutral (left) and pre-transition (right) training trajectories. C Machine learning classifiers used for the binary classification problem of distinguishing neutral from pre-transition time series. We use support vector machines (SVM), long short-term memory (LSTM) networks, convolutional neural networks (CNN), and Multi-Head CNN. D The changing trends of indicators prior to the transition in the test trajectory, including variance, lag-1 autocorrelation (AC), and probabilities assigned by the SDML classifier. The arrow illustrates the rolling window (50% of the time series) used for computing early warning signals.

Full size image

This study proposes the surrogate data-based machine learning (SDML) approach for early warning signals of critical transitions. We test the SDML approach on empirical data from geology, climate, sociology, and cardiology, and compare its performance to the widely used generic early warning signals, variance, and lag-1 autocorrelation. We also assess the robustness of SDML approach to different surrogate data methods.

Results

Performance of early warning signals on theoretical model

To test the SDML method on May’s harvesting model experiencing a fold bifurcation (see Methods), the common traits of the bifurcation are required. Thus, we trained the SDML classifier on surrogates of synthetic data generated from simulations of mathematical models going through bifurcations53. To ensure a fair comparison with the previously developed deep learning early warning signals for critical transition53, we retained the identical model architecture and parameter settings, replacing only the synthetic data from the DL classifier with surrogate data of equivalent length and sample size. The SDML classifier was trained on surrogates of synthetic data using 500,000 samples of length 500. The SDML classifier was tested (Fig. 2A) on a harvesting model going through a fold bifurcation, and its performance was compared with variance, lag-1 autocorrelation, and the DL classifier proposed by Bury et al.53. The indicators were monitored progressively as more of the time series was revealed. Variance (Fig. 2B) and lag-1 autocorrelation (Fig. 2C) were considered to provide an early warning signal if they displayed a strong trend (i.e., an increasing trend was taken as a warning signal).

Fig. 2: Trends in indicators prior to a fold bifurcation in the theoretical model using the amplitude adjusted Fourier transform (AAFT) surrogate method.
figure 2

A Trajectory (blue) and smoothing (gray) of a simulation of a harvesting model going through a fold bifurcation. B Variance of residual dynamics after smoothing, computed over a rolling window of size 0.5 times the length of the pre-transition data. C Lag-1 autocorrelation, i.e., AC(1). D Probability assigned to the fold bifurcation by the deep learning (DL) classifier from Bury et al.53. E Probability assigned to the fold bifurcation (or critical transition) by the SDML classifier. The vertical dashed line marks the time at which the system crosses the bifurcation. The gray band shows a catastrophic state. F Performance of confusion matrices for DL classifier. G Performance of confusion matrices for SDML Classifier.

Full size image

The deep learning (DL) classifier of bury et al.53 assigns a probability to each of the four possible outcomes (fold, transcritical, Hopf, and neutral). It is considered to provide an early warning signal when there is a heightened probability of the fold bifurcation (Fig. 2D). The SDML classifier, similar to the DL classifier proposed by bury et al.53, assigns a probability to each of the four possible outcomes. Therefore, a heightened probability assigned to one of the outcomes is taken to provide an early warning signal of that outcome. It is considered to provide an early warning signal when there is a heightened probability of the fold bifurcation (Fig. 2E). The classifier becomes more confident of an approaching critical transition as time goes on, and its assigned fold bifurcation probability increases. The confusion matrix performances of SDML and DL classifiers on test sets are also compared. Confusion matrices summarizing the performance of trained to recognize bifurcation trajectories based on middle portions of the time series (i.e., both left and right sides of the time series are padded with zeros) on test sets for the multi-class classification problem. Cell values show normalized classification rates for each class. In Fig. 2F, the DL classifier on the multi-class classification problem obtains an F1 score of 0.663. In Fig. 2G, the SDML classifier on the multi-class classification problem obtains an F1 score of 0.669. The performance of the SDML and DL classifiers is approximately the same. It is possible that the method can generalize between different systems if they exhibit common traits prior to the transition (e.g., the same type of bifurcation). In future research, we would like to develop methods with surrogate data that can generalize between systems while also addressing the problem of limited data availability.

Rapid transition events

Figure 3 shows rapid transition events in consecutive recordings of three empirical systems: anoxic transitions in the Mediterranean Sea47, paleoclimate transitions63, and transitions in human activity in the pre-Hispanic Pueblo societies64. Surrogate data used for training is generated from historic pre-transition data (shown in green in Fig. 3) and used to predict future periods (shown in blue). In the sedimentary archives from the Mediterranean Sea for core MS21 (Fig. 3A), two critical transition events were observed, i.e., periods S3 and S1. The period S3 represents the historical trajectory used to generate the surrogate data, while period S1 is the future original data of the left-out sample, used for testing. In the sedimentary archives from the Mediterranean Sea for core MS66 (Fig. 3B), four critical transition events were observed, i.e., periods S5, S4, S3, and S1. The periods S5 and S4 are historical trajectories used to generate the surrogate data, while periods S3 and S1 are the out-of-sample future original data, used for testing. In the sedimentary archives from the Mediterranean Sea for core 64PE406E1 (Fig. 3C), seven critical transition events were observed, i.e., periods S9, S8, S7, S6, S5, S4, and S3. The periods S9, S8, and S7 represent historical trajectories used to generate the surrogate data, while periods S6, S5, S4, and S3 are the future original data of the out-of-sample, used for testing. For the paleoclimate transitions (Fig. 3D), four critical transition events were observed, i.e., periods VI, III, II, and I. The periods VI and III are historical trajectories used to generate the surrogate data, while periods II and I are the future original data of the out-of-sample, used for testing. For the construction activity in the pre-Hispanic Pueblo societies (Fig. 3E), five critical transition events were observed, i.e., periods BMIII, PI, PII, Early PIII, and Late PIII. The periods BMIII and PI are historical trajectories used to generate the surrogate data, while periods PII, Early PIII, and Late PIII are the out-of-sample future original data, used for testing. The SDML approach to predicting critical transitions is motivated by two hypotheses: (i) the trajectories leading up to historic and future critical transitions have similar dynamical features; (ii) trajectories far from a critical transition (denoted “neutral”) have different dynamical features to trajectories close to a critical transition (denoted “pre-transition”). If these hypotheses hold, it should be possible to train a machine learning classifier to predict future critical transitions using SDML.

Fig. 3: Time series of rapid transition events for consecutive recordings from three different empirical systems.
figure 3

Sedimentary archives from the Mediterranean Sea for core MS21 at depth 1022 m (A), core MS66 at depth 1630 m (B), and core 64PE406E1 at depth 1760 m (C). D Paleoclimate transitions from Deuterium content expressed as δD (in ‰ with respect to the standard mean ocean water). Time is given as years before present (BP). E Construction activity in the pre-Hispanic Pueblo societies, given as the number of trees felled per year. Vertical dashed lines indicate onsets of rapid transition events. Green lines are historical trajectories used to generate the surrogate data. Red lines are post-transition trajectories, not used. Blue lines are trajectories used for testing the early warning signals.

Full size image

Due to the increasing temperatures and input of excess nutrients to coastal regions, the oceans and seas are losing oxygen. In the geological past, large-scale anoxic events had occasionally triggered mass extinction events, and the current loss of oxygen in the marine field has increased concerns about the recurrence of these types of events. To understand the marine anoxic events, Hennekam et al.47 reconstructed past oxygen conditions in the Mediterranean Sea using redox-sensitive trace elements. The high-resolution anoxia records, based on Mo, indicated a rapid oxic-to-anoxic transition at the start of each sapropel, as shown in Fig. 3A–C. Also, rapid oxic-to-anoxic transitions occurred regularly in the eastern Mediterranean Sea on (multi)centennial time scales. In addition, deoxygenation events in the eastern Mediterranean Sea showed tipping point behavior during which the system abruptly shifted to an anoxic state.

The completion of drilling at Vostok station in East Antarctica has allowed the extension of the ice record of atmospheric composition and climate to the past four glacial-interglacial cycles63. Glacial-interglacial climate changes have been documented by complementary climate records derived from deep-sea sediments, continental deposits of flora, fauna, and loess, and ice cores. The Vostok ice-core record extends through four climate cycles, with the ice slightly older than 400 kyr at a depth of 3310 m, covering a period comparable to that covered by numerous oceanic and continental records. Figure 3D shows the deuterium content of the ice (i.e., a proxy of local temperature change) as a function of the GT4 timescale of the ice. A prominent feature of the glacial-interglacial cycles was the abrupt termination of most glacial periods.

The collapse of civilizations has remained one of the most enigmatic phenomena in human history. To explore the collapse of ancient societies, Scheffer et al.64 leveraged an extraordinarily long and high-resolution time series of Puebloan tree-cutting as a proxy for construction, shown in Fig. 3E. The time series spanned eight centuries and five transitions. The annual-resolution time series of the construction activity demonstrated that repeated dramatic transformations of Pueblo cultures in the pre-Hispanic US Southwest were preceded by signals of critical slowing down.

Performance of early warning signals on experimental and empirical data

We trained and tested the SDML classifier on empirical and experimental data from ecology, climatology, sociology, and cardiology, compared its performance with variance and lag-1 autocorrelation. The indicators were monitored progressively as more of the time series was revealed. Variance and lag-1 autocorrelation were considered to provide an early warning signal if they displayed a strong trend, which was quantified using the Kendall tau statistic. For variance, an increasing trend was taken as a warning signal. For lag-1 autocorrelation, the direction of the trend depends on the frequency of oscillations (θ) at the transition. For θ ∈ [0, π/2), the lag-1 autocorrelation is expected to increase, whereas for θ ∈ (π/2, π], it is expected to decrease65. In the chick heart aggregates, an increase in variance and a decrease in lag-1 autocorrelation is observed prior to the transition15, which could serve as an early warning signal (Fig. 1D). For the test trajectories in the three empirical datasets (Fig. 3), blue), variance and lag-1 autocorrelation showed mixed success at providing an early warning signal. Variance increased prior to the transition in nine out of the twelve cases (Fig. 4, orange) and lag-1 autocorrelation increased in seven (Fig. 4, green).

Fig. 4: Trends in indicators prior to rapid transition events in empirical data using the amplitude adjusted Fourier transform (AAFT) surrogate method.
figure 4

Trajectories correspond to blue traces in Fig. 3. A Anoxic transition (Sapropel S1) obtained from data on the MS21 core. B, C Anoxic transitions (Sapropels S1 and S3) obtained from data on the MS66 core. D–G Anoxic transitions (Sapropels S3 to S6) obtained from data on the 64PE406E1 core. H End of glaciation I (i.e., the end of the last glaciation). I End of glaciation II. J Archeological Period PII. K Archeological Period Early PIII. L Archeological Period Late PIII. (Top) Trajectory (blue) and Gaussian smoothing (gray); (Second down) Variance; (Third down) Lag-1 autocorrelation (AC); (Bottom) probability of an approaching critical transition assigned by the SDML classifier. The quantity N shows the length of data points in the time series before the transition. The arrows indicate the width of the rolling window used to compute early warning signals. The gray bands show transition phases.

Full size image

The SDML classifier assigns a probability to the two possible classes: neutral (far from the transition) and pre-transition (close to the transition). An increase in the probability for the pre-transition class is taken as an early warning signal (Fig. 4, purple). For each case, the probability of a pre-transition state increases over time, thereby providing an early warning signal. Close to the transitions, the classifier becomes very confident of a pre-transition state, with a probability at or close to one. We have calculated the confusion matrix for the AAFT surrogates method (see supplementary Fig. 1) to better visualize and assess the performance of the SDML. These results provide supporting evidence for the hypotheses outlined in this study. Moreover, the SDML approach was effective for five different surrogate data methods (see supplementary Figs. 2–6), demonstrating its robustness to this choice. We have added a performance metric (F1 score) for the SDML classifier [see supplementary Table 1]. We also tested the extent to which Kullback-Leibler (KL) divergence and the Mann-Whitney U-test can differentiate between the neutral and pre-transition time series (see supplementary Table 1) and found that in most cases, there is not enough evidence to claim a significant difference.

These time series, however, do not address how the indicators might perform when faced with a neutral time series where no transition occurs, and whether they might mistakenly generate a false positive prediction of an oncoming state transition53,66. Therefore, we compare the performance of these approaches with respect to both true and false positives using the receiver operator characteristics (ROC) curve. The ROC curve shows the ratio of true positives to false positives as a discrimination threshold is varied. For variance and lag-1 autocorrelation, the discrimination threshold comes from the Kendall tau value. For the SDML classifiers, it comes from the classifiers assigned probability of a pre-transition state. The area under the ROC curve is a measure of performance based on both sensitivity (how many true positives were detected) and specificity (how many false positives were avoided). An AUC of 1.0 indicates a perfect classifier, and an AUC value of 0.5 indicates a classifier that is no better than random.

To construct the ROC curves, we make predictions on both “pre-transition” time series (close to the critical transition) and “neutral” time series (far the critical transition). The ROC curves for variance, lag-1 AC, and the SDML classifier for six evaluations across four study systems are shown in Fig. 5. For the chick heart data (Fig. 5A), the SDML classifier and lag-1 AC equally outperformed variance. For the other empirical datasets, the SDML classifier outperformed both variance and lag-1 autocorrelation in all cases except for the sediment data of the 64PE406E1 core (Fig. 5D), where lag-1 autocorrelation was the best indicator.

Fig. 5: The receiver operating characteristic (ROC) curves showing performance of indicators in the experimental and empirical data using the amplitude adjusted Fourier transform (AAFT) surrogate method.
figure 5

The ROC curves show the SDML classifier (SDML, purple), variance (Var, orange), and lag-1 autocorrelation (AC, green) for the A chick heart aggregates going through a period-doubling bifurcation; B sediment data from the MS21 core, C MS66 core, and (D) 64PE406E1 core showing rapid transitions to an anoxic state in the Mediterranean Sea; E ice core records showing rapid paleoclimate transitions; and F transitions in construction activity in pre-Hispanic Pueblo societies. Performance is assessed on the number of experimental runs (N) for each dataset, with 40 equally spaced predictions made between 60% and 100% (A, B, E, F) or between 80% and 100% (C, D) of the way through the pre-transition data. The area under the curve (AUC) score, denoted by A, is a performance measure. The insets show the proportion of predictions made by the classifier for true pre-transition trajectories. “Pre-tran” means close to a critical transition, and “Neutral” means far from a critical transition. The diagonal dashed black line marks where a classifier works no better than a random coin toss, namely, AUC is 0.5.

Full size image

Discussion

Many complex systems are prone to critical transitions, and data from past transitions is often limited. The majority of research on early warning signals has focused on generic indicators based on properties of bifurcations, and has not incorporated system-specific details, nor information from past transitions. However, data from past transitions contain important system-specific information that should not be neglected. In this paper, we have shown that the limited data available from past transitions can be extended using surrogate data methods to the point where a large enough dataset can be generated to train a machine learning classifier. These trained machine learning classifiers are capable of providing early warning signals for unseen, future critical transitions, despite having only been trained on surrogate data. Moreover, we found that the classifiers outperformed variance and lag-1 autocorrelation in most experimental and empirical test cases among natural systems in cardiology, geology, climatology, and sociology.

The results suggest that the SDML method for early warning signals can be advantageous over generic indicators. There are many scenarios for which generic early warning signals can fail67. Examples include global bifurcations51, out-of-equilibrium (transient) dynamics24, and rate-induced tipping50. These problems stem from generic early warning signals relying on a manifestation of critical slowing down. Critical slowing down involves the degradation of resilience along some dimension of the system’s state space, resulting in a longer return time to equilibrium following a perturbation. For bifurcations with an oscillatory component (e.g., Hopf/period-doubling/Neimark-Sacker), critical slowing down manifests as an increase in variance, and an increase or decrease in autocorrelation depending on the lag time65. For cases such as the onset of alternans in chick heart aggregates, where a period-doubling bifurcation is the likely cause, it seems plausible that the classifier learns about manifestations of critical slowing down specific to period-doubling bifurcations (an increase in variance and decrease in lag-1 autocorrelation). However, the SDML method makes no assumption of a bifurcation—it simply observes past transitions and attempts to extract features that are associated with the approach of a transition. Consequently, for cases where a bifurcation mechanism is not clear, such as for the paleoclimate transitions, learning system-specific features could be key to an effective early warning signal.

Machine learning is a rapidly evolving field, with new algorithms and architectures appearing every year. We have not attempted a comprehensive assessment of the performance of all appropriate types of architecture. We have also not performed hyperparameter tuning on the individual classifiers. Rather, this study is focused on the presentation of a framework to address the problem of limited data availability and demonstration of its baseline capabilities, which can be fine-tuned in future work.

An important consideration in this approach is how to build the training library for the machine learning classifiers. We opted for a simple approach of creating two classes of time series—one containing data far from the critical transition, and the other containing data close to it. More elaborate schemes could be considered in future work, such as having several classes for data at different distances to the transition, or turning the problem into a regression task, where time series are labeled with their distance to the transition.

The data-driven SDML approach relies on good-quality data of past transitions. This is in order to generate high-fidelity surrogate data for the machine learning classifiers. Therefore, rich, high-quality data sources with rapid transition events (e.g., sedimentary archives from the Mediterranean Sea47, paleoclimate transitions44,63, and construction activity in pre-Hispanic Pueblo societies64) and experimental data (e.g., embryonic chick heart cell aggregates37 and thermoacoustic instability experiments46) are invaluable. The SDML approach should not be regarded as a replacement for generic early warning signals, which have been used and enhanced for decades and rigorously tested in many real-world contexts. Rather, our work should be interpreted as evidence that the proposed approach is able to meet the challenges of real-world forecasting problems and has the potential to complement and improve the current best methods.

The SDML approach opens a direction for research on early warning signals, with applications in ecology, climate, finance, energy, and human and biological activities, as well as other complex dynamical systems. The authors believe that machine learning classifiers trained on rich surrogate data of past transitions could be crucial in advancing our ability to prepare for or avert critical transitions.

Methods

Training data generation

The training data consisted of thousands of surrogate data samples, which were generated from data close to and far from critical transitions in the empirical systems. Time series between critical transitions were split at their mid-point, with the earlier half taken as “neutral” and the later half taken as “pre-transition”. The approach of treating data far from the critical transitions as neutral aims to approximate neutral behavior in the absence of explicit neutral data, and it would be more robust to consider samples with no transitions as neutral during the training of the SDML68. Surrogate data were generated for the “neutral” and “pre-transition” sections using a variety of methods, which preserve the histogram distribution and/or the power spectrum of the original data. The surrogate data were labeled according to whether they were far from (neutral) or close to (pre-transition) a critical transition, making up a binary categorization dataset. The methods used to generate surrogate data are listed below.

Random permutation (RP) surrogates

RP surrogates are generated by randomly shuffling the original time series. They possess the same mean, variance, and histogram distribution as the original signal, but any temporal structure is removed69. They therefore possess a different power spectrum and autocorrelation function. RP surrogates were developed to test for temporal structure in a signal.

Fourier transform (FT) surrogates

In contrast to RP surrogates, FT surrogates preserve the power spectrum of the original signal, but not necessarily the histogram distribution. They are generated by taking the Discrete Fourier transform of the original signal, randomizing the phases, and transforming back into the time domain. They remove nonlinear dependencies while retaining all linear information, and so are often used to test for nonlinear structure in a signal. The algorithm for generating Fourier transform surrogate data was provided in Supplementary Note 1.

Amplitude-adjusted Fourier transform (AAFT) surrogates

AAFT surrogates aim to preserve both the power spectrum and the histogram distribution. They are generated similarly to FT surrogates, except a histogram transformation is applied in order match the histogram of the surrogate with the histogram of the original signal60,70. However, this process can introduce spurious harmonics in the power spectrum. Therefore, AAFT surrogates perfectly preserve the histogram distribution, but the power spectrum is slightly distorted.

Iterative amplitude-adjusted Fourier transform (IAAFT1 and IAAFT2) surrogates

IAAFT surrogates were introduced by Schreiber and Schmitz61 to overcome the distortion of the power spectrum in AAFT surrogates. They are generated by iterative replacement of Fourier amplitudes to achieve a closer match between both the histogram distribution and the power spectrum. However, the IAAFT algorithm cannot preserve both the histogram distribution and the power spectrum exactly. There are two versions: IAAFT1, which exactly preserves the histogram distribution, and IAAFT2, which exactly preserves the power spectrum.

Machine learning algorithms

Machine learning algorithms used in this study include support vector machine (SVM), long short-term memory (LSTM), convolutional neural network (CNN), and Multi-Head CNN. We experimented with different algorithms since no single algorithm should necessarily achieve the best prediction performance across different fields and real systems. In this study, we select the best-performing machine learning algorithm for each type of rapid transition event.

The best performing classifier for the MS66 sediment core and the ice core was the SVM, with F1 scores of 1.0 and 1.0, respectively. For the 64PE406E1 sediment core, it was the LSTM, with an F1 score of 0.99. For the MS21 sediment core, it was the CNN with an F1 score of 0.96. Finally, for the chick heart data and the construction activity, it was the Multi-Head CNN, with F1 scores of 1.0 and 0.99, respectively. Implementation details of each algorithm are provided below. In each case, we use default hyperparameter values without hyperparameter tuning.

1) SVM: This is a supervised machine learning algorithm suitable for classification tasks in high-dimensional spaces. SVM works by finding the optimal hyperplane that separates the different classes in feature space. For time series classification, each data point is used as a feature.

2) LSTM: This is a type of recurrent neural network (RNN) that aims at handling the vanishing gradient problem present in traditional RNNs. The LSTM is effective at capturing temporal dependencies in sequential data, making it well-suited to time series classification. We combine the LSTM with fully connected input and output layers. Specifically, we use a dense layer from the input time series to an LSTM layer of 128 neurons. To mitigate overfitting, we add a dropout layer with a dropout rate of 0.5, which is followed by another LSTM layer. Then we add a dense layer with 128 neurons and the ReLU activation function. Finally, we add a dense layer with the sigmoid activation function to output a probability distribution over the two classes.

3) CNN: This is a type of feed-forward neural network that learns features through convolution and can be used for time series classification. We use a CNN with two 1D convolutional layers with 64 filters, a kernel size of three, and the ReLU activation function. They are followed by a dropout layer with a rate of 0.5 and a MaxPooling layer to reduce the dimension. Then, we use a dense layer with the ReLU activation function and 128 neurons. Finally, we use a dense layer to the two output classes with a sigmoid activation function to output a probability distribution.

4) Multi-Head CNN: This algorithm was designed to capture features in the input data occurring on different scales. It does this through having distinct CNN heads, each having a different kernel size. We use three CNN heads. The first is a 1D convolutional layer with 32 filters, a kernel size of three, batch normalization to standardize inputs, and the ReLU activation function. This is followed by a dropout layer for regularization, a MaxPooling layer to reduce the dimensionality, and flattening. The second head is similar, but uses a kernel size of five, aiming to capture patterns over a broader window of input data. It is followed the same sequence of batch normalization, ReLU activation, dropout, max pooling, and flattening blocks. The third head uses a larger kernel size of 11 and 64 filters, designed to capture even broader patterns. The flattened outputs from all three heads are concatenated into a single vector, and then passed through a dense layer with 128 neurons (ReLU activation) and, finally, through the dense output layer with two neurons and sigmoid activation to output a probability distribution.

The LSTM, CNN, and Multi-Head CNN algorithms employed binary cross-entropy as a loss function, which is convenient for binary classification problems, and the Adam optimizer for efficient network weight update. They are then trained using a batch size of 64 for 100 epochs. We use a train/validation/test split of 0.6/0.2/0.2. We used early stopping to prevent overfitting. This terminates the training when the validation accuracy does not improve for more than five epochs. Subsequently, we use the model checkpoint that achieved the highest validation accuracy. We report the F1 score of the model’s performance on the test set, which is a measure that takes into account both sensitivity and specificity. We note that the empirical test data used to generate the ROC curves is not involved in the training process.

Theoretical model used for testing

To test detection of an approaching critical transition (or a fold bifurcation), we use May’s harvesting model with additive white noise40,53,71. This is given by

$$\frac{dx}{dt}=rx\left(1-\frac{x}{K}\right)-h\frac{{x}^{2}}{{s}^{2}+{x}^{2}}+\sigma \xi (t)$$
(1)

where x is biomass of some population, K is its carrying capacity, h is the harvesting rate, s characterizes the nonlinear dependence of harvesting output on current biomass, r is the intrinsic per capita growth rate of the population, σ is the noise amplitude, and ξ(t) is a Gaussian white noise process. Models are simulated using the Euler-Maruyama method with a step size of 0.01. We use parameter values r = 1, K = 1, s = 0.1, h = [0.15, 0.28], and σ = 0.01. In this configuration, a fold bifurcation occurs at h = 0.26. The parameter h is kept fixed at its lower bound for null simulations and is increased linearly to its upper bound in forced simulations.

Experimental and empirical data used for testing

Embryonic chick heart cell aggregates

We used publicly available data from experiments of chick heart cell aggregates that transition to a cardiac arrhythmia15,37. The aggregates were treated with 0.5 μmol–2.5 μmol of E4031, which is a drug that blocks the human Ether-à-go-go-Related Gene (hERG) potassium channel72. Following administration of the drug, in some aggregates, the time interval between two beats began to alternate; namely, there was a period-doubling bifurcation. Such transitions can also occur in the human heart in the form of T-wave alternans, which increases a patient’s risk for sudden cardiac death. The inter-beat intervals were computed as the time between consecutive beats and used in the analysis. The onset of the period-doubling bifurcation has been defined by Bury et al.37 as the first time when the slope of a linear regression of the return map composed of a sliding window of inter-beat intervals is below −0.95 for the next 10 beats. There are 23 time series of aggregates going through a period-doubling bifurcation, and 23 time series from aggregates that did undergo any form of transition. Data were preprocessed as in Bury et al.37, using a Gaussian filter with a bandwidth of 20 beats. Early warning signals were computed using a rolling window of 0.5. In this study, for smoothing and computing generic early warning signals, we used the Python package ewstools73.

Sedimentary archives from the Mediterranean Sea

Hennekam et al.47,74 reconstructed past oxygen dynamics for three sediment cores (MS21, MS66, 64PE406E1) in the eastern Mediterranean Sea. Rapid transitions between oxic and anoxic states occurred regularly in this region in the geological past. Core MS21 spans 2 anoxic events, core MS66 spans 4 anoxic events, and core 64PE406E1 spans 7 anoxic events. The SDML approach was tested on each core separately. The sampling rate provided  ~10 to 50 years resolution, depending on the core, with almost regular spacing between data points. This study performed the same data preprocessing as Hennekam et al.47, where residuals were obtained from smoothing the data with a Gaussian kernel with a bandwidth of 900 years, and early warning signals were computed using a rolling window of 0.5.

Ice core records of paleoclimate transitions

We used data from the Antarctica Vostok ice core, which captures paleoclimate transitions from 420,000 years ago up to present day44,63,75. Out of the eight paleoclimate transitions analyzed by Dakos et al.44, we only consider the four transitions contained within the Vostok ice core since this study requires consecutive transitions contained within a single record. The data were preprocessed as in Dakos et al.44, which involved linear interpolation to make the data equidistant and detrending with a Gaussian filter. Early warning signals were computed using a rolling window of 0.5.

Construction activity in pre-Hispanic Pueblo societies

This data is an annual-resolution time series of number of trees felled, a proxy for construction activity, in pre-Hispanic Pueblo societies64,76,77. The data reveals five transitions in construction activity and subsequent distinct archeological periods. We used the same data preprocessing and rolling window as in Scheffer et al.64. The time series were detrended using a Gaussian filter with a default bandwidth of 30 years, and early warning signals were computed with a default rolling window size of 60 years. The time series for the early and late PIII period were much shorter, therefore, a smaller bandwidth (15 years) and rolling window (20 years) were used in these cases.