A dephasing sweet spot with enhanced dipolar coupling

Abstract

Two-level systems (TLSs) are the basic units of quantum computers but face a trade-off between operation speed and coherence due to shared coupling paths. Here, we investigate a TLS given by a singlet-triplet (ST+) transition. We identify a magnetic-field configuration that maximizes dipole coupling while minimizing total dephasing, forming a compromise-free sweet spot that mitigates this fundamental trade-off. The TLS is implemented in a crystal-phase-defined double-quantum dot in an InAs nanowire. Using a superconducting resonator, we measure the spin-orbit interaction (SOI) gap, the spin-photon coupling strength, and the total TLS dephasing rate as a function of the in-plane magnetic-field orientation. Our theoretical description postulates phonons as the dominant noise source. The compromise-free sweet spot originates from the SOI, suggesting that it is not restricted to this material platform but might find applications in any material with SOI. These findings pave the way for enhanced nanomaterial engineering for next-generation qubit technologies.

Introduction

Qubits based on single localized spins in semiconductor nanostructures represent cutting-edge platforms for quantum information processing, boasting extended coherence times and benefiting from established industrial fabrication techniques¹. Scaling-up spin qubits is challenging because of limitations in all-electrical control and their small electric and magnetic dipole moments. Complex structures such as microstrips or micromagnets are required to facilitate qubit manipulation^2,3. However, the inherent spin-orbit interaction (SOI) in confined semiconductor hole systems^4,5,6,7,8 and in electrons in nanowires (NWs)^{9,10,11,12,13} offers an alternative coupling mechanism: SOI couples spin and charge degrees of freedom, enabling electric-dipole spin resonance^14,15,16,17 and spin-cavity coupling^{9,11,13,18,19,20,21,22,23}.

SOI is particularly relevant in singlet-triplet qubits, where it introduces a hybridization gap, for example, between singlet $\left\vert S\right\rangle$ and spin-polarized triplet $\left\vert {T}^{+}\right\rangle$ states^24,25,26. Recent experiments have demonstrated gigahertz-scale gaps, allowing for reaching the strong coupling limit between these two-level systems and microwave resonators²². These experiments extended the list of systems with strong spin-photon coupling^21,27,28,29 to even charge-parity states.

Despite several reports of SOI-induced material characteristics as a function of the magnetic field orientation^{13,21,30,31,32}, typically, sweet spots optimize coherence and manipulation speed as a function of gate voltages in charge qubits around zero detuning^33,34, which was recently extended to single-spin spin qubit³⁵. Here, we demonstrate that, while remaining at the gate-voltage sweet spot, an additional sweet spot for the total dephasing rate and dipole strength can be found, namely as a function of the orientation of a homogeneous in-plane magnetic field. As the fundamental origin of this additional sweet spot, we identify the inherently strong spin-orbit interaction (SOI) in the host material.

We do so by employing a two-spin singlet-triplet (S-T⁺) TLS in a crystal-phase-defined InAs NW^22,36,37 coupled to a NbTiN resonator^38,39 that is resilient to in-plane magnetic fields. Due to its spin nature, the TLS strongly depends on the magnetic-field orientation. We investigate the TLS properties as a function of the in-plane magnetic field in different orientations relative to the double quantum dot (DQD)^13,21,30,40 which acts like a one-dimensional, global tuning parameter. The coupling between the singlet-triplet TLS and the resonator allows to measure the TLS transition frequency, the vacuum Rabi rate, and the total TLS dephasing rate. Contrary to prevailing expectations, we identify a magnetic field orientation along the nanowire that serves as a compromise-free sweet spot, where a minimal total dephasing rate coincides with a maximal dipolar coupling. These findings are well explained by a theoretical model that suggests phonons as the dominant source of decoherence.

This non-trivial optimization of two TLS parameters with only one external parameter is inherent to systems with a strong SOI and demonstrates the potential of such semiconductor materials. Our results pave the way for future advances in material optimization and enhanced device functionality based on a deeper understanding of the underlying physics.

Results and Discussion

Device

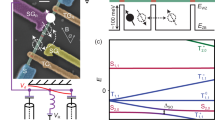
The device is depicted in Fig. 1. Detailed fabrication procedures are outlined in the Methods. This device comprises a superconducting half-wavelength coplanar-waveguide resonator coupled to a DQD formed by in-situ crystal-phase engineering in an InAs NW^22,36,37,41. Figure 1a shows an optical microscopy image of the resonator, fabricated by dry-etching an approximately 10 nm thick NbTiN film, atop a SiO₂ substrate³⁹. The small thickness of the superconducting NbTiN renders the resonator resilient to in-plane magnetic fields^38,39, and the narrow center conductor width, approximately 380 nm, combined with the large kinetic inductance of NbTiN, results in an impedance of 2.1 kΩ. This large impedance enhances the vacuum electric field fluctuation amplitude compared to standard 50 Ω-type resonators, thereby increasing the dipolar coupling to the TLS⁴².

Fig. 1: Superconducting resonator coupled to singlet-triplet two-level system (TLS) in a crystal-phase nanowire (NW).

a Optical microscope image of the device showing a half-wave NbTiN resonator with a characteristic impedance of 2.1 kΩ. In the middle of the center conductor, a dc bias line is connected via a meandered inductor. b False-colored scanning electron micrograph of the crystal-phase NW device (image is rotated by  − 90° with respect to a). The NW is placed at the position indicated in (a), and the purple gate line is galvanically connected to the resonator at its voltage anti-node. Tunnel barriers are highlighted in red. Using the gate voltages V_L and V_R, the device is operated with an even electron filling as depicted schematically. The spin-orbit gap Δ_SO corresponds to the indicated spin-rotating tunnel transition, which forms the TLS. The in-plane magnetic field angle α is varied during the experiments using a vector magnet that controls the magnetic field B. c Level diagram for an even electron occupation as a function of the electrostatic detuning ε in the presence of strong SOI and finite magnetic field exhibiting singlet (S) and triplet (T) states. Subscripts denote the filling of the left and right dots, and the superscript denotes the spin quantum number of the triplet states (see methods). The avoided crossing between the spin-polarized triplet state T⁺ and the low-energy singlet state at ε = ε₀ is detected using the resonator.

The TLS is formed by electronic states in a DQD, with tunnel barriers grown deterministically by controlling the InAs crystal phase during the vertical growth process of the NW^36,37. The barriers are highlighted in the colored SEM image of Fig. 1b in red. The DQD forms within the zincblende segments of the NW, separated by wurtzite tunnel barriers. At finite magnetic fields and in an even electron configuration, the DQD states are singlet and triplet states, as depicted in the energy level diagram in Fig. 1c. The ground state and first excited state comprise a superposition of the spin-polarized triplet $\left\vert {T}^{+}\right\rangle$, with an electron on each dot and the low-energy singlet state $\left\vert {S}_{2,0}\right\rangle$, with two excess electrons on one dot and none on the other. As depicted in Fig. 1c, without spin-flip tunneling, the energy levels would cross at a detuning ε₀ at which the Zeeman energy E_z equals the exchange energy ℏJ,

$${E}_{z}=\hslash J\approx \frac{\hslash }{2}\left({\varepsilon }_{0}+\sqrt{{\varepsilon }_{0}^{2}+4{t}_{c}^{2}}\right),$$

(1)

where t_c is the inter-dot tunnel rate and ℏ denotes the reduced Planck constant. But the finite inter-dot tunnel coupling and a substantial Rashba-type SOI in the zincblende segments⁴¹ result in a spin rotation and in the hybridization of the original eigenstates, with an energy gap ℏΔ_so²⁴. The two hybridized spin levels are split by a spin-orbit gap and constitute a spin-orbit-mediated electric dipole moment that couples to the electric field fluctuations of the resonator. This renders the resonator an effective probe for quantitative measurements of the TLS parameters.

Hybrid system at large magnetic fields

In our experiments, we measure the amplitude A and phase φ of a microwave probe tone transmitted through the resonator, capacitively coupled to the DQD. All measurements are performed at the mixing chamber plate of a dilution refrigerator with a base temperature of 70 mK. In Fig. 2a, the squared normalized transmission amplitude ${(A/{A}_{0})}^{2}$ through the resonator is plotted as a function of the probe frequency ω_p with the DQD tuned into Coulomb blockade, rendering it irrelevant for the measurement. This figure displays probe frequency scans at magnetic-field amplitudes ∣B∣ = 0 mT and ∣B∣ = 100 mT, where the field is applied in-plane. As visible in Fig. 2(a), the transmission through the resonator recorded for ∣B∣ = 0 mT and ∣B∣ = 100 mT does not show any variation, demonstrating that the resonator remains unaffected for the magnetic fields used in our experiments.

Fig. 2: Characterization of the hybrid device.

a Resonator transmission ${(A/{A}_{0})}^{2}$ as function of probe frequency ω_p. Fits to a Lorentzian result in the resonance frequency ω₀/2π = 5.1854 ± 0.0002 GHz, and decay rate κ/2π = 21.2 ± 0.4 MHz independent of the magnetic-field amplitude ∣B∣. The magnetic-field resilience of the resonator enables resonator-based investigation of the double-quantum dot (DQD). b–e Transmission ${(A/{A}_{0})}^{2}$ and phase φ close to resonance frequency as a function of gate voltages V_L and V_R applied to the DQD as illustrated in Fig. 1(b) at zero field and at ∣B∣ = 100 mT. Position and shape of the observed inter-dot transition signal vary as a function of ∣B∣ due to an interaction of the resonator with spinful DQD levels. In the remainder of the manuscript, the DQD detuning ε is varied by applying V_L and V_R along the arrow indicated in (e).

We now prepare the DQD in an even charge state^22,43,44,45 and measure the resonator transmission at a frequency close to resonance. Figure 2b–e depict the transmission amplitude and phase as functions of the gate voltages V_L and V_R for in-plane field amplitudes of ∣B∣ = 0 and ∣B∣ = 100 mT.

Due to the electric-dipolar coupling between the resonator and the DQD, the resonator transmission directly reveals the charge stability diagram of the DQD⁴⁶. At the inter-dot transition (IDT), the Zeeman energy and the exchange energy are degenerate (see Eq. (1)) and the hybridized states couple to the resonator. The IDT can be easily identified, signaled by lines with positive slopes in Fig. 2e.

Both, the position of the IDT in the gate-versus-gate map and the resonator response near the IDT strongly depend on the external magnetic field strength. This susceptibility to magnetic fields arises from the spin-dependent DQD transitions. In the following, we probe the resonator response as a function of electrostatic detuning ε, which is manipulated by varying the gate voltages V_L and V_R along the line indicated in Fig. 2e.

A double sweet spot

The main result of our work is represented by the dependence of the IDT characteristics on the in-plane field orientation. For this we show in Fig. 3a the resonator transmission phase φ close to the resonance frequency, plotted as a function of the in-plane angle α between the NW axis and the magnetic field, illustrated in Fig. 1b and Fig. 3b, and versus the electrostatic DQD detuning ε as defined in Fig. 2e. Similar data for varying magnetic field strength is shown in the SM. Figure 3a reveals that the detuning ε₀, at which the IDT is observed, varies as a function of α. This angle dependence can be understood qualitatively by recognizing that the SOI introduces an anisotropic g-tensor and hence determines the Zeeman energy E_Z and, according to Eq. (1), the position of the IDT ε₀. Furthermore, the phase signal as a function of ε changes continuously from a negative shift in φ at α ≈ π/2 [3π/2] to a double-dip structure at α ≈ π [2π], because the SOI renders the magnitude of Δ_SO and the dephasing rate γ angle-dependent by affecting the overlap of the spin wavefunctions^24,30,40,47. For example, at α ≈ π/2, Δ_so > ω₀, resulting in a dispersive resonator signal. In contrast, at α ≈ π, Δ_so < ω₀ so that an (avoided) crossing between the singlet-triplet TLS and the resonator is observed as function of ε. This crossing experimentally results in a double dip structure in the φ(ε) dependence, framing a positive shift at the center of the IDT, at ε ≈ ε₀.

Fig. 3: Two-level system (TLS) parameters as a function of in-plane field angle at ∣B∣ = 100 mT.

a Phase of the resonator transmission φ as function of electrostatic detuning ε and in-plane magnetic field angle α. The detuning ε, was calculated from the applied voltages, using the gate-to-dot lever arms (see Table 1). The dashed curve corresponds to the position of the inter-dot transition in the theoretical model, ε = ε₀, to which a linear trend was added accounting for a drift of the gate voltage. b Schematic showing the alignment of the magnetic field B with respect to the nanowire (NW), where the NW color scheme represents the crystal-phase structure according to Fig. 1b. c Spin-orbit gap Δ_so as function of α. d Coupling strength g_eff between the TLS and the resonator as function of α. e TLS dephasing rate γ as function of α. When the field is parallel to the NW, α = ± π/2, a compromise-free sweet spot is found where maximal TLS transition frequency and coupling strength coincide with minimal total dephasing rate. c–e are extracted using input-output theory. The streaks symbolize the uncertainty of the fit. This uncertainty is a consequence of the uncertainty of the gate lever arms, which forms the most significant source of uncertainty in our experiment and is stated in the caption of Table 1. All curves overlaid on the data result from the theoretical model described in the main text, using a single set of fit parameters. During the measurement, a charge relocation occurred at a magnetic-field angle α ~1.9π resulting in missing data for α ∈ [0, 0.1π] ∪ [0.19π, 2π) in all subfigures.

Using input-output theory⁴⁸ as described in the Methods, we extract the SOI gap Δ_so, the TLS dephasing rate γ, as well as the effective spin-photon coupling strength g_eff from the dependence of the resonator phase and amplitude on ε. The results are plotted as a function of in-plane angle α in Fig. 3c–e.

Excitingly, we find that, while Δ_so and g_eff are correlated with each other, they are anticorrelated with γ. In particular, when applying the magnetic field parallel to the NW, a compromise-free sweet spot is found, for which the spin-photon coupling strength g_eff is maximal while γ is minimal. To robustly estimate the spin-photon coupling and the dephasing rate at the sweet spot, we average over all extracted values in the interval α ∈ [55°, 125°] ∪ [235°, 305°] and find 〈g_eff〉/2π = 250 ± 15(30) MHz and 〈γ〉/2π = 11 ± 20(400) MHz, where the error corresponds to the statistical (systematic) uncertainty. Here, the large systematic uncertainty originates from the uncertainty of the gate lever arms stated in the caption of Table 1.

Table 1 Free parameters

Theoretical description

In this section, we outline how the effective Hamiltonian yields the dashed white and solid black curves shown in Fig. 3a, c, and d. The consecutive section describes how the decoherence is modeled (black curve in Fig. 3e).

All curves are the result of numerically diagonalizing the Hamiltonian H₅ in Eq. (12) in the Methods that describes the DQD states in proximity to the IDT. Thereby, we take into account an anisotropic g-tensor, identical for both dots, and a spin-orbit vector that is not aligned with the principal axes of the g-tensor. We point out that all curves are obtained from a single set of fit parameter, given in Table 1. The Landé g-factor varies between g = 10.5 and g = 5.25, depending on the field direction. And, taking into account the distance of the two quantum dots, d = 330 nm, the spin-orbit length is found as l_so = 130 nm. These values are consistent with previous experiments^9,49. In Methods Section V C, we describe the DQD model in detail and visualize the g-tensor based on the fitted parameters.

After finding the eigenenergies and eigenstates from diagonalizing the Hamiltonian H₅, we focus on the ground state $\left\vert 0\right\rangle$ and first excited state $\left\vert 1\right\rangle$ with their respective energies E₀ and E₁. These states possess an electric dipole moment which is sensed by the resonator. Because Eq. (1) is only valid for small SOI, which is not the case for certain field alignments, we more generally determine the detuning ε₀, at which the anti-crossing occurs, by identifying the minimum gap for which

$${\partial }_{\varepsilon }({E}_{1}-{E}_{0})=0.$$

(2)

The numerical solution for ε₀ is plotted in Fig. 3a on top of the data (white dashed curve). The variations of the detuning ε₀ of the IDT as function of α is caused by the g-tensor anisotropy. According to Eq. (1), this results in a variation of ε₀ at which the Zeeman energy equals the exchange energy. As a consequence, the detuning ε₀ at which the IDT is observed varies with the g-factor, which in turn is given by the field orientation. Then, we numerically calculate the SOI gap

$${\Delta }_{{{{\rm{so}}}}}={E}_{1}({\varepsilon }_{0})-{E}_{0}({\varepsilon }_{0})\,,$$

(3)

plotted as solid black curve in Fig. 3c. The variation of the SOI gap Δ_so is a consequence of the magnetic field orientation with respect to the anisotropic g-tensor and the spin-orbit vector. To calculate the vacuum Rabi coupling strength g_eff, we assume that the resonator couples to the electric dipole moment of the singlet-triplet TLS via the resonator vacuum fluctuations in the detuning of amplitude δε₀ according to Eq. (11) in the Methods. This gives rise to the dipolar coupling strength as the vacuum Rabi rate

$${g}_{{{{\rm{eff}}}}}=\delta {\varepsilon }_{0}| \left\langle 0\right\vert {h}_{\delta \varepsilon }\left\vert 1\right\rangle |$$

(4)

plotted as solid black curve in Fig. 3d. Here, h_δε is the operator describing small variations of the detuning, given by Eq. (15) in the Methods and evaluated at the center of the IDT, ε = ε₀.

Decoherence

In the experiment, using input-output theory, we utilize the resonator as a probe to extract the total TLS dephasing rate γ, which is plotted in Fig. 3e, and defined by

$$\gamma =\frac{{\gamma }_{1}}{2}+{\gamma }_{\varphi },$$

(5)

where γ₁ is the relaxation rate and γ_φ the pure dephasing rate. The primary sources of decoherence in quantum dots are typically hyperfine-interaction induced dephasing from atomic nuclei^50,51,52, charge noise-induced dephasing^33,34,53,54, or relaxation due to phonons^{55,56,57,58,59,60,61,62,63}.

From our experiments, we extract an unexpected anti-correlation between the spin-photon coupling strength g_eff and the dephasing rate γ. Using our theoretical description, and Bloch-Redfield theory^56,60,64, we investigate various possible decoherence mechanisms as outlined in the Supplementary Note 2. We find that consideration of magnetic noise stemming from nuclear spins or charge-noise due to phonons leads to the correct trend of γ as a function of the in-plane magnetic-field angle α. However, because we identify dephasing rates comparable to the maximum of γ(α) also for a charge qubit at a zero magnetic field, where magnetic noise is irrelevant, we hypothesize that phonons form the dominant noise source in our experiment. Therefore, here, we focus on phonon-mediated decoherence.

Figure 3e and Fig. 4a show the phonon-mediated relaxation ${\gamma }_{1}^{{{{\rm{ph}}}}}(\alpha )$ as a function of the in-plane field angle α overlaid on the measured dephasing rate γ. Considering only the effect of a single gapless, low-energy phonon band gives rise to the analytical functional dependence ${\gamma }_{1}^{{{{\rm{ph}}}}}(\omega )$ as function of phonon frequency, ω. Here, the longitudinal phonon modes couple to the detuning and tunneling through variations in the electrostatic potential due to their deformational interactions. This coupling leads to TLS relaxation (see Supplementary Note 2 for the derivation).

Fig. 4: Phonons as possible decoherence source.

a Measured dephasing rate γ as a function of in-plane angle α (purple). The experimental data is plotted as purple points, and the error bar is given by a purple stripe. The error bars are dominated by the error associated with the gate-lever arm uncertainty. The black curve is the numerically calculated relaxation rate ${\gamma }_{1}^{{{{\rm{ph}}}}}(\alpha )$ originating from deformational phonons (see Section Decoherence). b Analytical relaxation rate ${\gamma }_{1}^{{{{\rm{ph}}}}}(\omega )$ as function of phonon frequency ω (see Equation (27) in Supplementary for details). The TLS operates in the frequency range as indicated with a negative slope of ${\gamma }_{1}^{{{{\rm{ph}}}}}(\omega )$. This explains the anti-correlation between the SOI gap Δ_so and the dephasing rate γ - a possible reason for the compromise-free sweet spot formation.

This dependence is plotted in Fig. 4b. These phonons lead to relaxation when their frequency is close to the TLS transition frequency ω ≈ Δ_so. Because the phonon-mediated relaxation is maximal when the phonon wavelength is comparable to the size of the dots at ω ≈ ω_c, an increase in Δ_so leads to a decrease in ${\gamma }_{1}^{{{{\rm{ph}}}}}$. Therefore, a change in Δ_so as function of α results in the observed variations of ${\gamma }_{{{{\rm{1}}}}}^{{{{\rm{ph}}}}}$. In addition, variations of α result in a change of the electron-phonon coupling strength that enhances this effect and is considered in ${\gamma }_{{{{\rm{1}}}}}^{{{{\rm{ph}}}}}(\alpha )$, plotted as black curve on top of the data in Fig. 4a.

In Supplementary Note 2, we discuss magnetic noise. Additionally, in the Supplementary Note 2, we discuss 1/f-charge noise, which does not capture the functional dependence of γ as a function of the in-plane magnetic field angle α.

Conclusion

We have investigated a singlet-triplet (S-T⁺) TLS strongly coupled to a magnetic-field resilient microwave resonator which we use as a sensitive probe. We extract the SOI gap, the vacuum Rabi rate, and the dephasing rate as function of the in-plane magnetic-field orientation. As the central result, we find a compromise-free sweet spot at which the total TLS dephasing rate is minimal while simultaneously its transition frequency and the dipolar coupling to the resonator are maximal. These experimental findings are well described by our theoretical model that shows that at the compromise-free sweet spot, the TLS is resilient against magnetic noise and phonon-mediated noise, with phonons forming the most likely dominant noise source. Fitting the model, we find an anisotropic g-tensor with a maximal g-factor of g₀ = 10.5 and a spin-orbit length of l_so = 120 nm, consistent with literature^9,49. Our findings demonstrate that, based on the magnetic field as global tuning parameter, optimization of dipole strength and dephasing rate can be not mutually exclusive. Our experimental results and model are very generic and allow for further optimization through synthesis of specifically tailored composite crystals to suppress phonon-induced loss or through a larger resonator frequency. A superconducting resonator combined with input-output theory can be a powerful probe of quantum materials and will enable identifying and optimizing future qubit platforms. Sweet-spot operation might be crucial for large qubit architectures and we anticipate that similar sweet-spots will be identified for qubits in multiple material platforms that rely on large spin-orbit interaction such as hole-spin qubits in Ge^{8,26,65,66,67,68,69}.

Methods

Device fabrication

The fabrication process commences with the sputter deposition of approximately 10 nm of NbTiN on a pristine Si/SiO₂ wafer³⁹. Large structures are patterned utilizing a conventional e-beam protocol and developed at room temperature. Subsequently, the narrow resonator center conductor is patterned in a second e-beam step, followed by development at  −20°C^70,71. Following the dry-etching of the NbTiN film, a NW is deterministically deposited using a micromanipulator. A GaSb-shell that is exclusively present on the zincblende segments of the NW^72,73, allows us to identify the location of the wurtzite tunnel barriers using scanning electron microscopy. After identifying the tunnel barriers, the GaSb shell is removed by wet-etching in MF-319 developer⁷⁴. Consecutively, the contacts and gates are patterned using standard e-beam lithography and thermal evaporation. For the contacts, Ar-milling in the evaporator ensures a good contact, whereas the gates remain isolated by the native oxide on the NW.

Input-output theory

To determine the SOI gap Δ_so, the effective spin-photon coupling strength g_eff, and the TLS dephasing rate γ, we make use of input-output theory that describes the interaction between photons in a resonator and a multi-level system^48,75. Input-output theory allows us to infer the transition frequency, vacuum Rabi rate and dephasing rate of two-level systems formed in a DQD^{21,22,76,77,78,79,80,81}. For the singlet-triplet (S-T+) TLS coupled to a resonator, which is probed in transmission at low power, the linear response of the measured scattering parameter is derived as^22,82

$${S}_{21}(\omega )=\frac{-i\kappa }{\omega -{\omega }_{0}+i\frac{\kappa }{2}-{g}^{2}\left(\frac{1}{\omega -{\omega }_{q}+i\gamma }-\frac{1}{\omega +{\omega }_{q}+i\gamma }\right)}\,,$$

(6)

where ${\omega }_{q}=\sqrt{{\Delta }_{{{{\rm{so}}}}}^{2}+{{\varepsilon }^{{\prime} }}^{2}}$, with ${\varepsilon }^{{\prime} }=\varepsilon -{\varepsilon }_{0}$ the relative electrostatic DQD detuning from the center of the IDT and g = g_effΔ_so/ω_q. ω₀ and κ denote the bare resonator frequency and resonator decay rate and γ is the TLS dephasing. Here we do not apply the usual rotating-wave approximation, preserving the counter-rotating terms, that are relevant for large frequency detuning . To obtain the fit parameters plotted in Fig. 3c–e for every value of field angle α, we fit amplitude and phase of Eq. (6) simultaneously to the measured amplitude and phase as a function of detuning ε. Figure 5 shows amplitude and phase at α = π/2 of the measurement shown in Fig. 3 with the overlaid fit. From this fit, we extract the SOI gap Δ_so, the coupling strength g_eff, and the dephasing rate γ. Repeating a similar procedure for various values of α results in the plots in Fig. 3c–e. The frequency of the resonator ω₀ and the decay rate of the resonator κ as well as the lever arm, which transforms the applied gate voltages into detuning, are determined independently and kept fixed for the fit. When extracting three fit parameters simultaneously, it is crucial to avoid overfitting. In this study, we address the risk of overfitting by fitting both amplitude and phase using a single set of fit parameters. This method results in small point-to-point fluctuations and very small error bars on the extracted parameters, giving us certainty that the fit is accurate. However, these error bars do not fully represent the physical uncertainty of the measurements. The primary source of uncertainty in our experiments arises from the error associated with the gate-lever arm. To determine the error bars shown in Figs. 3 and 4, we propagate the uncertainty of the gate-lever arm through the fitting process and then calculate the two-point systematics.

Fig. 5: Linetrace with input-output theory fit at α = π/2.

a Measured amplitude, A/A₀, as a function of the virtual gate voltage, V_ε which is a linear superposition of the gate voltages V_R and V_L along the detuning direction (arrow in Fig. 2e). Its amplitude is defined such that $| {V}_{\varepsilon }| =\sqrt{{V}_{R}^{2}+{V}_{L}^{2}}$. b Measured phase φ as a function of detuning gate voltage V_ε. The data is a linecut of Fig. 3a at α = π/2. The dashed curves are fits to Eq. (6).

Model of the double quantum dot

The curves plotted in Figs. 3 and 4 of the main text are the result of numerical diagonalization of the effective Hamiltonian of a double quantum dot (DQD) with even occupation close to the avoided crossing between $\vert {T}_{1,1}^{+}\rangle$ and $\left\vert {S}_{2,0}\right\rangle$. Here, for a symbol ${A}_{l,r}^{t}$, A = S denotes the anti-symmetric spin singlet state $\vert S\rangle =(\vert \uparrow \downarrow \rangle -\vert \downarrow \uparrow \rangle )/\sqrt{2}$. A = T denotes the symmetric triplet states, where $\vert {T}^{+}\rangle =\vert \uparrow \uparrow \rangle$, and $\vert {T}^{-}\rangle =\vert \downarrow \downarrow \rangle$ are spin-polarized and $\vert {T}^{0}\rangle =(\vert \uparrow \downarrow \rangle +\vert \downarrow \uparrow \rangle )/\sqrt{2}$ is unpolarized. In our notation, the Zeeman field points in the  − z direction. The subscripts l, r denote the charge occupation of the left and right dot. The (1, 1) → (0, 2) anticrossing is driven by changing the detuning ε between the two dots. For the usual negative exchange splitting between the S and T states, the (1,1) state is preferred at ε < 0 and the state (2,0) is preferred at ε > 0.

The singlet and triplet states in the DQD are $(\vert {S}_{0,2}\rangle ,\vert {S}_{2,0}\rangle ,\vert {S}_{1,1}\rangle ,\vert {T}_{1,1}^{-}\rangle ,\vert {T}_{1,1}^{+}\rangle ,\vert {T}_{1,1}^{0}\rangle )$ and form our basis set. The Hamiltonian including SOI then reads^24,32,83

$${H}_{{{{\rm{DQD}}}}}=\left(\begin{array}{cccccc}{U}_{L}+{U}_{R}+\varepsilon &{U}_{LR}&-{t}_{c}&0&0&0\\ {U}_{LR}&-\varepsilon &-{t}_{c}&0&0&0\\ -{t}_{c}&-{t}_{c}&-{J}_{0}&-\frac{\delta {b}_{x}+i\delta {b}_{y}}{\sqrt{2}}&\frac{\delta {b}_{x}-i\delta {b}_{y}}{\sqrt{2}}&\delta {b}_{z}\\ 0&0&-\frac{\delta {b}_{x}-i\delta {b}_{y}}{\sqrt{2}}&{\bar{b}}_{z}&0&\frac{{\bar{b}}_{x}-i{\bar{b}}_{y}}{\sqrt{2}}\\ 0&0&\frac{\delta {b}_{x}+i\delta {b}_{y}}{\sqrt{2}}&0&-{\bar{b}}_{z}&\frac{{\bar{b}}_{x}+i{\bar{b}}_{y}}{\sqrt{2}}\\ 0&0&\delta {b}_{z}&\frac{{\bar{b}}_{x}+i{\bar{b}}_{y}}{\sqrt{2}}&\frac{{\bar{b}}_{x}-i{\bar{b}}_{y}}{\sqrt{2}}&0\\ \end{array}\right)\,.$$

(7)

Here, U_L/R is the on-site Coulomb energy of the left (L) and right (R) dot, U_LR is the cross-exchange contribution, and J₀ is the Coulomb exchange. And we define the difference and total Zeeman field vectors produced by a magnetic field B as

$$\delta {{{\bf{b}}}}={\mu }_{B}{{{\bf{B}}}}\delta g=\frac{{\mu }_{B}}{2}{{{\bf{B}}}}\left[{\underline{g}}_{L}\underline{R}(-{\theta }_{so}/2)-{\underline{g}}_{R}\underline{R}({\theta }_{so}/2)\right]\,,$$

(8)

$$\bar{{{{\bf{b}}}}}={\mu }_{B}{{{\bf{B}}}}\bar{g}=\frac{{\mu }_{B}}{2}{{{\bf{B}}}}\left[{\underline{g}}_{L}\underline{R}(-{\theta }_{so}/2)+{\underline{g}}_{R}\underline{R}({\theta }_{so}/2)\right]\,,$$

(9)

where $\underline{R}$ is a rotation matrix around the SOI axis by the spin-flip angle θ_so = d/l_so, with d the distance between the dots and l_so the SOI length. For simplicity, we set U_LR = J₀ = 0. Following Ref. ³², we have gauged the spin-flip tunneling contribution into a local redefinition of the Zeeman energy and thus the tunneling amplitude t_c comprises both spin-conserving and spin-flip components. ${\underline{g}}_{L/R}$ are the g-tensors of the left and right dots, parameterized by the unit vector n and the SOI correction factor η ≤ 1,

$${{{\bf{B}}}}\underline{g}={g}_{0}\left[\left({{{\bf{n}}}}({{{\bf{n}}}}\cdot {{{\bf{B}}}})\right)+\eta ({{{\bf{n}}}}\times {{{\bf{B}}}})\times {{{\bf{n}}}}\right]\,.$$

(10)

For describing the experimental results and to limit the number of free parameters, we use identical g-tensors for the left and right dot, $\underline{g}={\underline{g}}_{L}={\underline{g}}_{R}$. A visualization of these g-tensors, based on the Equation (10) and the fit parameters, is shown in Fig. 6.

Fig. 6: Visualization of the anisotropic g-tensor.

a Normalized Zeeman field strength $| {{{\bf{B}}}}\underline{g}| /| {{{\bf{B}}}}|$, where the g-tensor $\underline{g}$ is defined according to Eq. (10). A characteristic peanut shape is exhibited. b Cross-section of a in the x-y plane at z = 0 as a function of the in-plane angle α. The nanowire is aligned parallel to the y axis.

The DQD is coupled to a resonator of frequency ω₀ and bosonic annihilation and creation operators a and a^†, with the effective Hamiltonian H_R = ℏω₀a^†a. The coupling is mediated by the resonator-induced change in detuning of the DQD and thus reads

$$\begin{array}{rc}{H}_{I}&=\delta \varepsilon (\left\vert {S}_{20}\right\rangle \left\langle {S}_{20}\right\vert -\left\vert {S}_{02}\right\rangle \left\langle {S}_{02}\right\vert )({a}^{{{\dagger}} }+a)\,,\end{array}$$

(11)

where δε = V_R∂_Vε depends on the susceptibility of the detuning to the potential applied to the gate and on the zero-point-fluctuations V_R of the potential of the resonator.

Focusing on the (1, 1) → (0, 2) anticrossing at ε ~ ε₀, we neglect the contribution of the singlet $\left\vert {S}_{20}\right\rangle$ which lies at high energy U_R + U_L. We can then easily diagonalize the singlet subsector by accounting for the tunneling between S₁₁ and S₂₀, and we focus on the 5 lowest energy states of the system, comprising the resulting singlets and the three triplets. The effective Hamiltonian reads

$${H}_{5}=\left(\begin{array}{ccccc}J-\varepsilon &0&-\frac{(\delta {b}_{x}^{{\prime} }+i\delta {b}_{y}^{{\prime} })\cos (\theta )}{\sqrt{2}}&\frac{(\delta {b}_{x}^{{\prime} }-i\delta {b}_{y}^{{\prime} })\cos (\theta )}{\sqrt{2}}&\delta {b}_{z}^{{\prime} }\cos (\theta )\\ 0&-J&-\frac{(\delta {b}_{x}^{{\prime} }+i\delta {b}_{y}^{{\prime} })\sin (\theta )}{\sqrt{2}}&\frac{(\delta {b}_{x}^{{\prime} }-i\delta {b}_{y}^{{\prime} })\sin (\theta )}{\sqrt{2}}&\delta {b}_{z}^{{\prime} }\sin (\theta )\\ -\frac{(\delta {b}_{x}^{{\prime} }-i\delta {b}_{y}^{{\prime} })\cos (\theta )}{\sqrt{2}}&-\frac{(\delta {b}_{x}^{{\prime} }-i\delta {b}_{y}^{{\prime} })\sin (\theta )}{\sqrt{2}}&{E}_{z}&0&0\\ \frac{(\delta {b}_{x}^{{\prime} }+i\delta {b}_{y}^{{\prime} })\cos (\theta )}{\sqrt{2}}&\frac{(\delta {b}_{x}^{{\prime} }+i\delta {b}_{y}^{{\prime} })\sin (\theta )}{\sqrt{2}}&0&-{E}_{z}&0\\ \delta {b}_{z}^{{\prime} }\cos (\theta )&\delta {b}_{z}^{{\prime} }\sin (\theta )&0&0&0\\ \end{array}\right)\,,$$

(12)

where $J\approx (\varepsilon +\sqrt{{\varepsilon }^{2}+4{t}_{c}^{2}})/2$ according to Eq. (1) and θ = arctan(2t_c/ε)/2, where the arctan function is defined, such that θ = π/4 at ε = 0. We also fixed the direction of the spin quantization axis such that the triplet subsector is diagonal. This is done by defining the global rotation matrix ${\underline{R}}_{B}$ that maps $\bar{{{{\bf{b}}}}}$ to the z-direction and rotating the δb accordingly, i.e.,

$$\bar{{{{\bf{b}}}}}={E}_{z}{\underline{R}}_{B}{{{{\bf{n}}}}}_{z}\,\to \,\,\delta {{{{\bf{b}}}}}^{{\prime} }=\delta {{{\bf{b}}}}{\underline{R}}_{B}\,.$$

(13)

Here, ${\underline{R}}_{B}$ depends on the direction of the applied B field and on the combined g-tensor of the dots. The prime in δb indicates this choice of reference frame for the spin quantization axis.

The resonator-DQD coupling Hamiltonian H_I in Eq. (11) is related to variations in the detuning δϵ by

$${H}_{I}=\delta {\varepsilon }_{0}{h}_{\varepsilon }({a}^{{{\dagger}} }+a),$$

(14)

with

$${h}_{\varepsilon }=\left(\begin{array}{ccccc}-{\sin }^{2}(\theta )&\sin (2\theta )/2&0&0&0\\ \sin (2\theta )/2&-{\cos }^{2}(\theta )&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0\\ \end{array}\right)$$

(15)

describing small variations of the detuning ε. This leads to the definition of the dipolar coupling strength according to Eq. (4).