All-electric control of skyrmion-bimeron transition in van der Waals heterostructures

Abstract

Two-dimensional van der Waals materials offer a versatile platform for manipulating atomic-scale topological spin textures. In this study, using first-principles and micromagnetic calculations, we demonstrate a reversible transition between magnetic skyrmions and bimerons in a MoTeI/In₂Se₃ multiferroic heterostructure. The physical origin lies in the reorientation of the easy axis of magnetic anisotropy, triggered by the reversal of ferroelectric polarization. We show that the transition operates effectively under both static and dynamic conditions, exhibiting remarkable stability and flexibility. Notably, this transition can be achieved entirely through electric control, without requiring any external magnetic field. Furthermore, we propose a binary encoding scheme based on the skyrmion-bimeron transition, presenting a promising path toward energy-efficient spintronic applications.

Introduction

Topological spin textures, serving as stable information carriers, have gained significant attention due to their potential in spintronic applications^{1,2,3,4,5,6,7,8,9,10}. Among these, magnetic skyrmions, as shown in Fig. 1a, stand out due to their topological protection and energy-efficient manipulation via electric currents^{11,12,13,14,15}. This renders them highly attractive for next-generation classical and quantum spintronic devices^16,17,18. Similarly, bimerons, consisting of meron-antimeron pairs with opposite spin polarities (Fig. 1b), can be viewed as the in-plane counterpart of skyrmions^{19,20,21,22,23,24,25}.

Fig. 1: Structural and magnetic properties of MoTeI monolayer and MoTeI/In₂Se₃ heterostructure.

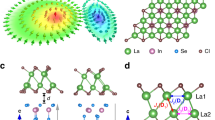
Schematic diagram of (a) skyrmion and (b) bimeron switching in a 2D vdW magnetic layer (top) controlled by ferroelectric polarization reversal (bottom). c Top and side views of the atomic structure of the MoTeI monolayer. d Two spin configurations with opposite chirality, used to determine the in-plane DMI parameters, with red arrows indicating the spin orientations. e Side view of the MoTeI/In₂Se₃ heterostructure, depicting the two distinct polarization states, labeled P↑ (left panel) and P↓ (right panel). Dependence of magnetic anisotropy energy (MAE) on the polar angle θ in the (f) P↑ and (g) P↓ configurations for the MoTeI/In₂Se₃ heterostructure, respectively.

The synthetic versatility and structural robustness of two-dimensional (2D) van der Waals (vdW) materials create a unique platform for exploring atomic-level spin textures, driven by the demand for miniaturization in modern electronics. Since 2019, magnetic skyrmions have been observed in 2D vdW magnets represented by Cr₂Ge₂Te₆²⁶ and Fe₃GeTe₂²⁷, as well as in their heterostructures^28,29. In addition, extensive theoretical and computational investigations have been conducted to predict further 2D vdW materials that can host skyrmions³⁰. Specifically, 2D Janus monolayers, characterized by their intrinsic broken inversion symmetry, exhibit a pronounced Dzyaloshinskii-Moriya interaction (DMI) that stabilizes nonlinear spin textures³¹. This potential becomes particularly promising when combined with 2D ferroelectric (FE) materials^32,33,34 due to the emergence of spin-orbit coupling (SOC). Additionally, the electron reconstruction at the heterointerface provides a nonvolatile electric field, which further mediates magnetic interactions at the atomic scale^35,36,37,38. For example, the magnetic anisotropy interaction can be significantly affected by reversing the FE polarization due to the proximity effect³⁹. This enables control of topological spin textures using an electric field, offering the advantage of low energy dissipation^40,41.

Traditionally, spintronic devices have emphasized a single type of topological textures^1,2,3-either skyrmions or bimerons-determined by material properties. However, there has been a growing focus on their physical correlations^{42,43,44,45,46,47,48,49,50,51,52}, suggesting that integrating different topological spin textures could enhance storage and computing architectures, allowing multiple spintronic components to collaboratively execute complex tasks⁵³. Topological spin textures can be described using homotopy theory⁵⁴ and characterized by the topological charge¹²$Q={(4\pi )}^{-1}\iint {{{\bf{m}}}}\cdot ({\partial }_{x}{{{\bf{m}}}}\times {\partial }_{y}{{{\bf{m}}}})\,{d}^{2}r$, with m being the normalized magnetization vector. For a skyrmion, the boundary conditions are defined as m(r → ± ∞) → (0, 0, ± 1), and for a bimeron they are m(r → ± ∞) → (0, ± 1, 0)⁴². Thus, in an isotropic theoretical model, both skyrmions and bimerons exhibit identical nontrivial topological properties with Q = ± 1 and cannot be deformed continuously into a ground ferromagnetic state⁴². However, the excitation of specific spin textures can be influenced by factors such as anisotropies or external fields that favor either out-of-plane or in-plane spin orientations⁵⁵. Although recent studies have explored skyrmion-bimeron conversions^{46,47,48,49,50,51}, most efforts have focused on metastable scenarios, or relied on pre-patterned anisotropy profiles. The dynamic transitions within transport processes under realistic conditions remains largely unexplored.

In this work, we address this gap by conducting systematic first-principles calculations and micromagnetic simulations to investigate the skyrmion-bimeron transition. The transition is realized through all-electric control and validated within the dynamic motion process, which links the transformation with the widely studied skyrmion-based racetrack memory. The system is 2D vdW heterostructures, composed of Janus monolayer MoTeI and FE monolayer In₂Se₃, as shown in Fig. 1a, b. Through modulation of the ferroelectric polarization in In₂Se₃, we achieve a controllable reorientation of the magnetic anisotropy in MoTeI, switching between in-plane and out-of-plane directions, consequently inducing changes in topological spin textures. We also demonstrate the stability and flexibility of this dynamic transformation and, based on this mechanism, design a racetrack memory-like binary encoder.

Results

Electrical control of magnetic anisotropy in multiferroic MoTeI/In₂Se₃

We started by considering a MoTeI monolayer, whose crystal structure is displayed in Fig. 1c, d with both top and side views, featuring a hexagonal lattice in p3m1 space group. This Janus structure is characterized by a stacking arrangement that arises from the misalignment of the Te, Mo and I layers, with an optimized lattice constant being 4.103 Å. The phonon spectrum (see Supplementary Fig. 1a) exhibits no imaginary frequencies, indicating the dynamic stability of the MoTeI monolayer. The total energy shows negligible fluctuations during the ab intio molecular dynamics (AIMD) simulations at 300 K over 3 ps, with the MoTeI monolayer maintaining structural integrity (see Supplementary Fig. 1b), confirming its excellent thermal stability. The spin Hamiltonian for the MoTeI monolayer is expressed as

$${{{\mathcal{H}}}}=-J\sum\limits_{i,j}{{{{\bf{s}}}}}_{i}\cdot {{{{\bf{s}}}}}_{j}-{{{{\bf{D}}}}}_{ij}\sum\limits_{i,j}{{{{\bf{s}}}}}_{i}\times {{{{\bf{s}}}}}_{j}-K\sum\limits_{i}{({{{{\bf{s}}}}}_{i}\cdot \hat{{{{\bf{z}}}}})}^{2},$$

(1)

where s_i (s_j) is the spin of the ith (jth) Mo atom, J is the exchange coupling constant, D_ij = (D_x, D_y, D_z) denotes the DMI vector, and K is the single ion anisotropy constant. The SOC is included in the calculations of K and D_ij. According to Moriya’s symmetry rules, the reflection planes intersect at the midpoint of bonds between adjacent Mo atoms, orienting each DMI vector perpendicular to the bonding axis. D_ij is defined as ${{{{\bf{D}}}}}_{ij}={d}_{\parallel }(\hat{{{{\bf{z}}}}}\times {\hat{{{{\bf{u}}}}}}_{ij})+{d}_{\perp }\hat{{{{\bf{z}}}}}$, where ${\hat{{{{\bf{u}}}}}}_{ij}$ is the vector connecting s_i and s_j, and d_∥ and d_⊥ are the in-plane and out-of-plane DMI components, respectively. Since the magnitude of d_⊥ is small and its influence on spin textures is negligible in 2D systems, it is omitted in the subsequent calculations. The in-plane component d_∥ is determined by the chirality-dependent total energy difference approach, based on two spin configurations illustrated in Fig. 1d. The exchange coupling constant J was accurately calculated using a 4 × 4 × 1 supercell through the four-state method⁵⁶. Calculations reveal that the MoTeI monolayer serves as a 2D ferromagnet with an interlayer ferromagnetic coupling of 18.95 meV, an in-plane magnetic anisotropy energy (MAE) of −0.21 meV per unit cell, and an in-plane DMI component of 1.24 meV. In addition, MoTeI is identified as an indirect semiconductor with a band gap of 1.72 meV, as illustrated in Supplementary Fig. 2.

To enable non-volatile modulation of the spin Hamiltonian in MoTeI, a multiferroic heterostructure was constructed by vertically stacking the MoTeI monolayer with 2D FE material In₂Se₃, as illustrated in Fig. 1e. The optimized lattice constant of In₂Se₃ is 4.102 Å, consistent with previous experimental and theoretical studies^57,58, and the lattice mismatch of approximately 0.048% results in negligible strain effects in the heterostructure. Given the two stable polarization states (P↑ and P↓) of In₂Se₃, we explored six representative high-symmetry geometric stacking configurations, labeled type-I to type-VI (see Supplementary Fig. 3). To determine the most stable stacking mode among the configurations, we calculated the corresponding binding energy ${E}_{{{{\rm{b}}}}}={E}_{{{{\rm{MoTeI}}}}/{{{{\rm{In}}}}}_{2}{{{{\rm{Se}}}}}_{3}}-{E}_{{{{\rm{MoTeI}}}}}-{E}_{{{{{\rm{In}}}}}_{2}{{{{\rm{Se}}}}}_{3}}$. As shown in Supplementary Table I, type-I exhibits the lowest binding energy across both polarization states, making it the most stable stacking configuration. Thus, type-I stacking configuration is taken as our model system. We also evaluated the potential for realizing ferroelectricity in MoTeI/In₂Se₃ heterostructures. As shown in Supplementary Fig. 4, the transition pathway between P↑ and P↓ states exhibits an energy barrier of 0.71 eV per unit cell, similar to that of conventional ferroelectrics, indicating typical ferroelectricity in this system.

We next examined the magnetic properties of the MoTeI/In₂Se₃ heterostructure. The magnetic parameters for both P↑ and P↓ polarization states, calculated using density functional theory (DFT), are listed in Supplementary Table II, which show no significant variation in J and d_∥ between these states. Figure 1f, g shows the dependence of MAE on the polar angle for both P↑ and P↓ polarization states. As the polarization switches from P↑ to P↓, the easy magnetization axis of the MoTeI monolayer shifts from in-plane (MAE of  − 0.18 meV per unit cell) to out-of-plane (MAE of 0.58 meV per unit cell). We also examined the influence of the ferroelectric layer on the electronic structure of MoTeI. Figure 2a, b presents the layer-resolved partial density of states (PDOS) of the MoTeI/In₂Se₃ heterostructure under the P↑ and P↓ configurations. For the P↑ configuration, MoTeI remains semiconducting, while for P↓, the valence band maximum in the spin-up channel shifts upward, giving rise to a half-metallic state in MoTeI. This transition is electrostatically induced by switching the polarization of the underlying In₂Se₃ layer, and does not involve charge injection or transport through MoTeI. The resulting modulation of spin-resolved band structure provides a non-volatile means of controlling local magnetic configurations.

Fig. 2: Ferroelectric modulation of MAE in MoTeI/In₂Se₃ heterostructure.

Layer-resolved partial density of states (PDOS) of the MoTeI/In₂Se₃ heterostructure in the (a) P↑ and (b) P↓ configurations. c Atomic-resolved magnetic anisotropy energy (MAE) comparison between the intrinsic MoTeI monolayer and the polarized MoTeI/In₂Se₃ heterostructure. Orbital-resolved MAE contributions from Te and I atoms in the MoTeI/In₂Se₃ heterostructure for both (d, e) P↑ and (f, g) P↓ configurations. PDOS of (h) Te and i I atoms within the MoTeI/In₂Se₃ heterostructure. The green arrows indicate the spin-down unoccupied states of the p_x/p_y orbitals and the spin-up occupied states of the p_y/p_x orbitals.

To elucidate the origins of MAE in the MoTeI monolayer and MoTeI/In₂Se₃ heterostructures, we calculated the atom- and orbital-resolved MAEs for different configurations. As shown in Fig. 2c, the results reveal that in both polarization states, Mo, Te, and I atoms are the primary contributors to MAE, while contributions from In and Se atoms are negligible. For both the intrinsic MoTeI monolayer and MoTeI/In₂Se₃ under P↑ polarization, the overall in-plane MAE is primarily determined by substantial in-plane contribution from Te atoms, along with smaller out-of-plane contributions from Mo and I atoms. Under P↓ polarization, the Te atoms’ in-plane contribution decreases considerably, whereas the I atoms’ out-of-plane contribution increases markedly. Consequently, the reorientation of easy magnetization axis from in-plane to out-of-plane is primarily attributed to the MAE contributions of Te and I atoms. Figure 2d–g illustrates the contributions of the coupling between the p-orbital components p_x,  p_y, and p_z of Te and I atoms to the MAE in both P↑ and P↓ states. The atomic-resolved MAE of Te and I atoms are mainly driven by the coupling between the p_x/p_y and p_y/p_z orbitals. The observed reduction in in-plane MAE for Te atoms and out-of-plane MAE for I atoms can be primarily attributed to the coupling of p_x/p_y orbitals. According to second-order perturbation theory^59,60, the MAE can be expressed as

$$\,{\mbox{MAE}}\,= {\sum}_{\sigma ,{\sigma }^{{\prime} }}\left(2{\delta }_{\sigma ,{\sigma }^{{\prime} }}-1\right){\xi }^{2}\\ \times \sum\limits_{{o}^{\sigma },{u}^{{\sigma }^{{\prime} }}}\frac{{\left\vert \langle {o}^{\sigma }| {L}_{z}| {u}^{{\sigma }^{{\prime} }}\rangle \right\vert }^{2}-{\left\vert \langle {o}^{\sigma }| {L}_{x}| {u}^{{\sigma }^{{\prime} }}\rangle \right\vert }^{2}}{{E}_{u}^{{\sigma }^{{\prime} }}-{E}_{o}^{\sigma }},$$

(2)

where ξ is the SOC strength, L_x and L_z are angular momentum operators, and ${E}_{u}^{{\sigma }^{{\prime} }}$ and ${E}_{o}^{\sigma }$ are the energy levels of unoccupied states $\left\vert {u}^{{\sigma }^{{\prime} }}\right\rangle$ with spin ${\sigma }^{{\prime} }$ and occupied states $\left\langle {o}^{\sigma }\right\vert$ with spin σ, respectively. The term ${\left\vert \langle {o}^{\sigma }| {L}_{z}| {u}^{{\sigma }^{{\prime} }}\rangle \right\vert }^{2}-{\left\vert \langle {o}^{\sigma }| {L}_{x}| {u}^{{\sigma }^{{\prime} }}\rangle \right\vert }^{2}$ represents the difference of SOC matrix elements for p-orbitals, as shown in Supplementary Table III. Therefore, the energy gap ${E}_{u}^{{\sigma }^{{\prime} }}-{E}_{o}^{\sigma }$ plays a key role in contributing to the MAE. Figure. 2h, i shows the PDOS of p-orbitals of Te and I atoms in the MoTeI/In₂Se₃ heterostructure. For both Te and I atoms, the unoccupied orbitals are primarily located in the spin-up channel, while the occupied orbitals have contributions from both spin channels. Thus, we focus on the energy gap between the unoccupied spin-up p_x/p_y orbitals and the occupied spin-down p_y/p_x orbitals. Additionally, the PDOS shows that under the P↓ polarization, both the occupied and unoccupied p_x/p_y orbitals of Te and I atoms shift upward. This significant upward shift in the unoccupied p_x/p_y orbitals increase the overall energy gap ${E}_{u}^{{\sigma }^{{\prime} }}-{E}_{o}^{\sigma }$. Since the SOC matrix element difference between the spin-up (spin-down) occupied p_x/p_y and spin-down (spin-up) unoccupied p_y/p_x states is  − 1, the contribution of p_x/p_y orbital hybridization to MAE increases when FE polarization switches from P↑ to P↓. This behavior is consistent with the trends shown in Fig. 2d–g.

Anisotropy-determined equilibrium states of skyrmions and bimerons

In this subsection, we investigated the impact of magnetic anisotropy on equilibrium topological spin textures. The initial state of the system is set to a random magnetization (see Supplementary Fig. 5a), followed by relaxation under out-of-plane anisotropy corresponding to P↓ and in-plane anisotropy corresponding to P↑. The results of the spin configurations are presented in Fig. 3a. It can be observed that skyrmions and bimerons can spontaneously form and reach equilibrium states under zero external magnetic field. Out-of-plane anisotropy favors the formation of skyrmions, whereas in-plane anisotropy favors the formation of bimerons. The presence of half-solitons at the boundaries arises from the periodic boundary conditions (PBC). To further confirm the profiles of the skyrmions and bimerons, we extracted the magnetization components m_x,  m_y, and m_z along the yellow dashed line, as illustrated in Fig. 3b. The colored dots represent the simulation results, and the black lines are analytical curves fitting with⁶¹

$${m}_{z,x}(x)=2\,{\tan }^{-1}\left[\frac{\sinh (d/2w)}{\sinh (x/w)}\right],$$

(3)

where w is the width of the 360° domain wall, treated as a fitting parameter, and d is the diameter of the skyrmion/bimeron, which is 2.8 nm for the skyrmion and 2.1 nm for the bimeron. Given that our simulation results agree well with the theoretical formula, we confirmed that the obtained spin configurations are standard skyrmion/bimeron solitons. To better bridge the gap between theoretical results and real experiments, we also presented the simulated Lorentz transmission electron microscopy (L-TEM) images⁶² of the equilibrium skyrmion/bimeron in Fig. 3a. In the small defocus limit, assuming full electron-wave processing of the electron beam, the L-TEM contrast originates from the underlying spin configurations. It is characterized by the curl of the magnetization along the beam propagation axis $\hat{{{{\bf{z}}}}}$, as given by⁶³

$$I({{{\bf{r}}}},\Delta )=1-(\Delta e{\mu }_{0}\lambda t/\hslash )(\nabla \times {{{\bf{m}}}}({{{\bf{r}}}}))\cdot \hat{{{{\bf{z}}}}},$$

(4)

where I,  Δ,  e,  μ₀,  λ,  t,  ℏ are the normalized intensity, degree of defocus, electron charge, vacuum permeability, electron wavelength, magnetic monolayer thickness, and Planck’s constant, respectively. Here, a sample tilt of 20° was taken to replicate real experiments. These simulated L-TEM images could be compared with previously observed skyrmions and bimerons⁴⁴ and serve to support the experimental validation of our calculations. It should be mentioned that all equilibrium states obtained in the main text were simulated at 0 K, while we also considered the system at finite temperature (see Supplementary Fig. 5d,e). The results indicate that thermal fluctuations induce local spin perturbations in skyrmions/bimerons, but their topological properties remain unaffected.

Fig. 3: Equilibrium States of Skyrmions and Bimerons.

a Spin configurations of equilibrium skyrmions (left column) and bimerons (right column). The yellow dashed lines indicate the direction along the diameter of a skyrmion/bimeron. b The magnetization components m_x,  m_y, and m_z along the diameter direction of equilibrium skyrmions and bimerons. The colored dots represent the simulation results, and the black lines are analytic curves based on Eq. (3). c Simulated Lorentz transmission electron microscopy (L-TEM) images of equilibrium skyrmions and bimerons. Statistics of thirty sets of (d) energy and (e) topological charge data for skyrmion/bimeron relaxed from random magnetization. The dashed lines represent the average values. f Comparison of the average exchange energy E_exch, anisotropy energy E_anis, and demagnetization energy E_demag for equilibrium skyrmions and bimerons. g The average effective field vectors B_eff and anisotropy field vectors B_anis for equilibrium skyrmions and bimerons.

As the relaxation process begins from an initially randomized magnetization, the resulting equilibrium states exhibit inherent randomness. That means the skyrmion/bimeron configurations shown in Fig. 3a-c represent just one of the many possible equilibrium outcomes. To derive a more generalized conclusion, 30 trial numbers were assigned to 30 sets of independent simulations, each set consisting of two opposite polarization states relaxed from random initial condition, which may still converge to slightly different metastable states due to numerical sensitivity and near-degeneracy. Some typical relaxed configurations of the trials are shown in Supplementary Fig. 5b,c. The statistical analysis is shown in Fig. 3d, e, which present the total energy and topological charge, highlighting distinct differences between skyrmions and bimerons despite their inherent randomness. Specifically, the average energy and topological charge are -0.08 eV and -1.5 for skyrmions, and 0.13 eV and 3.1 for bimerons, respectively. These findings suggest that, despite the random variations in individual spin arrangements, the distinction in the topological properties of skyrmions and bimerons remains highly pronounced. Such statistical variation is also consistent with experimental observations, where exact reproduction of identical spin textures is extremely rare, yet their topological and energetic characteristics remain robust. We also noted that the topological charge is reversed in a few instances, this is attributed to the polarity inversion of the skyrmion/bimeron. Figure 3f compares the average values of each of the three energy terms for skyrmions and bimerons: exchange energy E_exch, anisotropy energy E_anis, and demagnetization energy E_demag, with the triangular area approximating the total energy. The lower total energy of skyrmions primarily results from the contribution of E_anis and E_exch terms, whereas bimerons display lower E_demag. In addition to the energy terms, we also calculated the three-dimensional field vectors, as shown in Fig. 3g. It is evident that the effective field B_eff points out-of-plane/in-plane for skyrmions/bimerons. Moreover, the direction of the average anisotropy field B_anis aligns closely with B_eff, differing by only a small angle. This also indicates that the equilibrium configurations of skyrmions and bimerons are indeed determined by magnetic anisotropy.

Dynamic skyrmion-bimeron transformation in a nanotrack

Having demonstrated that the out-of-plane/in-plane magnetic anisotropy induced by P↓/P↑ favors the formation of equilibrium skyrmion/bimeron states, we now examined their dynamic transformation during motion in a nanotrack. A skyrmion is initially positioned at the left end of the nanotrack and begins to move under a continuous in-plane electric current. Electric field pulses are applied at 0.50 ns and 1.55 ns to induce polarization switching in the ferroelectric monolayer, aiming to alter the topological soliton (skyrmion or bimeron) during motion. Figure 4a shows dynamic snapshots of the moving spin configuration on the nanotrack at 0.2 ns, 1.0 ns, and 2.0 ns, visually illustrating the back-and-forth switching between skyrmion and bimeron. Snapshots of the local spin configuration during transitions induced by the voltage pulses are shown in Fig. 4b. It can be observed that a skyrmion smoothly transitions to a bimeron within as short as 0.05 ns, and vice versa. This fast transformation is attributed to the short duration of the polarization switching assumed in our simulations. In practice, ferroelectric switching typically occurs over nanosecond timescales, depending on the profile and duration of the applied electric field pulse. To assess the robustness of our mechanism under such realistic conditions, we performed additional simulations with a slower polarization modulation. As shown in Supplementary Fig. 6a, even when the transition time is extended from 0.05 ns (used in Fig. 4e–g) to 2 ns - a 40-fold increase - the skyrmion-bimeron conversion still proceeds reliably, albeit more gradually. This result confirms the flexibility and dynamical stability of the proposed approach, even under substantially slower, experimentally relevant switching dynamics.

Fig. 4: Dynamic skyrmion-bimeron transition and its application as an encoder.

a Dynamic snapshots of the moving skyrmion/bimeron in a nanotrack, taken at 0.2 ns, 1.0 ns, and 2.0 ns. b Dynamic snapshots of local spin configuration at the moment of skyrmion-bimeron transitions, taken at 0.51–0.55 ns and 1.56–1.60 ns. Time-dependent variations in c position (x, y) and d velocity (v_x, v_y) during the skyrmion/bimeron motion. The colored dots represent the simulation results, and the black lines are analytic curves based on Eq. (5). The green dashed lines mark the moment when the skyrmion-bimeron transitions occur. Time-dependent variations in (e) electric field E_c, (f) total energy E, and (g) topological charge Q during the skyrmion/bimeron motion. A scheme for a dynamic skyrmion-bimeron encoder, with h the electric field as the input signal and i the total energy as the output signal. The output signal is controlled to represent the binary ASCII code of “SKYRMION".

To further analyze the spin dynamics, we extracted the soliton’s position and velocity information, as shown in Fig. 4c, d. Although fluctuations in the soliton’s velocity occur at the transition moment, the overall process can be regarded as uniform linear motion along the nanotrack. Such robustness in the transition arises from the shared topological charge between skyrmions and bimerons. To support the simulation results, we also perform an analytical analysis based on the modified Thiele equation⁶⁴

$${{{\bf{G}}}}\times ({{{\bf{u}}}}-{{{\bf{v}}}})+{{{\mathcal{D}}}}\left(\beta {{{\bf{u}}}}-\alpha {{{\bf{v}}}}\right)={{{\bf{0}}}},$$

(5)

where G is the gyromagnetic coupling vector, ${{{\mathcal{D}}}}$ is the dissipative force tensor, β is the degree of non-adiabaticity, α is the Gilbert damping constant, and v and u are the velocity of the soliton and the conduction electrons, respectively. In the main text, we set α = β to avoid the skyrmion Hall effect, allowing for a more focused study on the skyrmion-bimeron transition. As shown by the solid black line in Fig. 4d, the analytic solutions are v_x ≈ 45 m/s and v_y = 0 (see Methods for details), which agree well with the simulations. Moreover, we also considered the case of α ≠ β (see Supplementary Fig. 6b), which exhibits a pronounced skyrmion Hall effect without disrupting the skyrmion-bimeron transition, further demonstrating the robustness of the transition. In addition to position and velocity, we also recorded the variations in electric field E_c, total energy E, and topological charge Q during motion, as shown in Fig. 4e–g. The coercive field E_c required to switch the FE polarization of In₂Se₃ is approximately 1 V/nm⁶⁵, which is chosen as the peak amplitude for the applied electric field pulse. Notably, as continuous application of the electric field is unnecessary once polarization saturation is achieved, the pulse duration presented here represents the minimum time but can be extended based on practical requirements. By comparing Fig. 4e, f, one may observe that the dynamic skyrmion-bimeron transition alters the system energy without changing the topological charge, providing an advantage for the design of skyrmion-bimeron spintronic devices.

Here, we proposed a scheme for a binary encoder based on the dynamic transformation between skyrmions and bimerons, which is analogous to the racetrack memory. We designated the skyrmion state and bimeron state as binary digits “0” and “1”, respectively, enabling repeated transitions between these states to facilitate switching between “0” and “1”. The input signal is an electric field that is crucial for determining the spin configuration, while the output signal is a physical quantity (such as energy) that reflects the distinction between the two solitons. The time length of each bit is set to 0.2 ns, and different bits are read out using a clocking system. The variations of the designed sets of eight input and output signals are illustrated in Fig. 4h, i. By applying electric field pulses at the appropriate moments, we effectively control the output signal to be eight letters “SKYRMION” in ASCII code, thereby validating the feasibility of this scheme.

Conclusions

In conclusion, we have investigated a reversible transition between skyrmions and bimerons in a MoTeI/In₂Se₃ multiferroic heterostructure. First-principles calculations revealed that the reversal of ferroelectric polarization in In₂Se₃ induces a significant shift in the magnetic anisotropy of the MoTeI monolayer from out-of-plane to in-plane orientations, establishing favorable conditions for the formation of skyrmions or bimerons. Micromagnetic simulations further clarified the equilibrium spin textures and dynamic transformations, with statistical analysis and solutions of the Thiele equation confirming both flexibility and stability of the skyrmion-bimeron transition. Building on these findings, we proposed an all-electric-controlled device resembling a racetrack memory and validated its feasibility. Our results presented a promising pathway toward low-power memory applications in future spintronic devices.

Moreover, while our study focuses on a 2D van der Waals heterostructure, the proposed mechanism of electric-field-induced magnetic anisotropy modulation and topological state conversion may be extended to other quantum magnetic materials beyond two dimensions. This includes systems such as hematite⁶⁶, ruthenates³⁵, and Heusler compounds⁶⁷, where tunable magnetic order and spin-orbit interactions offer promising opportunities for electric control of topological spin textures.

Methods

First-principles calculations

All first-principles calculations were performed using the Vienna Ab Initio Simulation Package (VASP) within the framework of DFT^68,69. The Perdew-Burke-Ernzerhof (PBE) functional, formulated in the form of generalized gradient approximation (GGA)⁷⁰, was employed to describe the exchange-correlation energy. Electron-ion interactions were treated using the projector-augmented wave (PAW) pseudopotential method^71,72, with a plane wave cutoff energy of 500 eV. To eliminate interactions between adjacent periodic images, a vacuum region of 25 Å was added along the z-axis. The k-space integration for all calculations was performed using a 15 × 15 × 1 k-point grid in the 2D Brillouin zone. The criterion of atomic position relaxation was set to 1 × 10⁻⁵ eV/A, and the convergence criterion for electron self-consistency was set to 1 × 10⁻⁷ eV. To account for the strong electron-electron interactions in localized Mo d orbitals, we employed the DFT + U method using Dudarev’s approach⁷³, with an effective Hubbard Coulomb interaction parameter, U_eff, set to 3 eV^74,75,76,77. The DFT-D3 method of Grimme was adopted to describe the interlayer vdW interactions^78,79. The phonon dispersions were calculated using the finite displacement method as implemented in the Phonopy code⁸⁰, employing a 4 × 4 × 1 supercell. The energy barrier and transition pathway for ferroelectric switching were investigated via the climbing-image nudged elastic band (CI-NEB) approach^81,82.

Micromagnetic simulations

The micromagnetic simulations were preformed using the GPU-accelerated finite-difference MuMax3 code⁸³. Only the magnetic monolayer MoTeI is explicitly modeled and discretized into cells sized 0.1 × 0.1 nm² to maximize computational accuracy. For the static case, the simulation universe is 20 × 20 nm², with PBC applied in both x and y directions, and the energy minimum states are obtained using the conjugate gradient method. For the dynamic case, the simulation universe is 100 × 20 nm², with PBC applied only in the y direction, and calculations are performed using the Dormand-Prince solver.

The average energy density of the system is given by

$$\epsilon = \, A{(\nabla {{{\bf{m}}}})}^{2}+D\left[{m}_{z}(\nabla \cdot {{{\bf{m}}}})-({{{\bf{m}}}}\cdot \nabla ){m}_{z}\right]\\ -{K}_{{{{\rm{u}}}}}{({{{\bf{m}}}}\cdot \hat{{{{\bf{z}}}}})}^{2}-\frac{1}{2}{\mu }_{0}{M}_{{{{\rm{s}}}}}{{{\bf{m}}}}\cdot {{{{\bf{H}}}}}_{{{{\rm{dm}}}}},$$

(6)

where A,  D, and K_u are the Heisenberg exchange, interfacial DMI, and magnetic anisotropy constants, respectively. M_s is the saturation magnetization and H_dm is the demagnetizing field. The dipolar interaction is always considered in the micromagnetic simulations. Additionally, a term ${K}_{{{{\rm{u}}}}}{({{{\bf{m}}}}\cdot \hat{{{{\bf{x}}}}})}^{2}$ was incorporated to define an easy axis along the x-direction when stabilizing the bimerons. This modeling choice is consistent with the system’s easy-plane anisotropy and does not affect the generality of the results⁴⁹. To explore the skyrmion-bimeron transition during the current-induced motion, we numerically solved the Landau–Lifshitz–Gilbert (LLG) equation augmented with a spin-transfer (STT) term τ_STT in Zhang-Li form⁸⁴

$${\partial }_{t}{{{\bf{m}}}}=-{\gamma }_{0}{{{\bf{m}}}}\times {{{{\bf{B}}}}}_{{{{\rm{eff}}}}}+\alpha ({{{\bf{m}}}}\times {\partial }_{t}{{{\bf{m}}}})+{\tau }_{{{{\rm{STT}}}}},$$

(7)

$${\tau }_{{{{\rm{STT}}}}}=u\left({{{\bf{m}}}}\times {\partial }_{x}{{{\bf{m}}}}\times {{{\bf{m}}}}\right)-\beta u\left({{{\bf{m}}}}\times {\partial }_{x}{{{\bf{m}}}}\right),$$

(8)

where γ₀ is the gyromagnetic ratio, and B_eff = − (δϵ/δm)/(μ₀M_s) is the effective field. The first term of τ_STT is the adiabatic torque and the second term is the non-adiabatic torque. The STT coefficient is given by u = (gμ_BPj)/(2eM_s)⁸⁵, where g,  μ_B,  P, and j are the Landè factor, Bohr magneton, spin polarization factor, and applied current density, respectively. The current density was set to j = 10¹² A/m² with P = 0.45.

The material parameters used in micromagnetic simulations (Supplementary Table IV) were derived from rigorous DFT calculated parameters (Supplementary Table II) using the following conversion formulas⁸⁶: $A=(\sqrt{3}J)/(2t),\,D=(-\sqrt{3}{d}_{\parallel })/(at),\,{K}_{{{{\rm{u}}}}}=(2K)/(\sqrt{3}{a}^{2}t)$, and ${M}_{{{{\rm{s}}}}}=(6{\mu }_{{{{\rm{B}}}}})/(\sqrt{3}{a}^{2}t)$. Here, t is the thickness of the magnetic monolayer, 3.304 Å for P↓ and 3.309 Å for P↑, respectively. a = 4.10 Å is the lattice parameter of the heterostructure for both P↓ and P↑ states. Polarization switching is modeled by changing the micromagnetic parameters corresponding to the P↓ and P↑ states, instead of introducing an explicit electric field.

Analytical calculation of the Thiele equation

In the modified Thiele equation, the first term describes the Magnus force with ${{{\bf{G}}}}=(0,0,{{{\mathcal{G}}}})$ and ${{{\mathcal{G}}}}=4\pi Q$. The second term represents the dissipative force where the components ${{{{\mathcal{D}}}}}_{ij}={{{\mathcal{D}}}}$ for (i, j) = (x, x) or (y, y) and ${{{{\mathcal{D}}}}}_{ij}=0$ for otherwise.

Thus, the general solutions of Eq. (5) are ref. ⁸⁷

$${{{{\bf{v}}}}}_{\parallel }=\left(\frac{\beta }{\alpha }+\frac{\alpha -\beta }{{\alpha }^{3}{({{{\mathcal{D}}}}/{{{\mathcal{G}}}})}^{2}+\alpha }\right){{{\bf{u}}}},$$

(9)

$${{{{\bf{v}}}}}_{\perp }=\frac{(\alpha -\beta )({{{\mathcal{D}}}}/{{{\mathcal{G}}}})}{{\alpha }^{2}{({{{\mathcal{D}}}}/{{{\mathcal{G}}}})}^{2}+1}\left(\hat{z}\times {{{\bf{u}}}}\right),$$

(10)

where v_∥ and v_⊥ are the components parallel and perpendicular to v, respectively. When the current injects along the  − x direction and α = β, one can obtain v_x = u = (gμ_BPj)/(2eM_s) and v_y = 0.