Introduction

The Kardar–Parisi–Zhang (KPZ) universality class has become a prototypical model for non-equilibrium critical phenomena owing to the ever-increasing list of systems it describes. Initially proposed to model rough geometries in stochastic growth processes1, it is notable for its distinct anomalous diffusion, characterised by a dynamical exponent z = 3/2 and roughness exponent χ = 1/2 in spatial dimension d = 1. Despite the KPZ equation being a classical stochastic equation, its scaling behaviour has been observed in quantum systems, both as a semiclassical description of phase fluctuations in driven-dissipative condensates such as exciton-polaritons2, and in transport properties of the Heisenberg spin chain3,4. In the single-component and one-dimensional case, the KPZ equation is largely considered solved: its solutions can be understood through the Cole–Hopf transformation mapping to a stochastic heat equation with multiplicative noise, its statistical properties are constrained by Galilean and tilt-symmetries directly enforcing χ + z = 2, and its stationary two-point correlators are fully determined5,6.

A natural question to pose is whether KPZ systems1,2,7,8,9,10,11,12,13,14,15 offer multicomponent generalisations16,17. This question has arisen in various cases: dynamic roughening of directed lines16; sedimenting colloidal suspensions18; stochastic lattice gases19,20,21; magnetohydrodynamics22,23; dynamics of fluids and quantum fluids24; dynamics of anharmonic chains on a mesoscopic scale25,26; and proliferating active matter27. It has also been argued that multicomponent KPZ-like equations arise from continuity equations in the non-linear fluctuating hydrodynamics of quantum integrable systems19,28. The isotropic spin chain at finite temperature is an instance of this, where transport properties are modelled by coupled Burgers’ equations29. Multicomponent KPZ is directly relevant to polariton systems30,31,32, which have established themselves as key platforms for realising non-equilibrium critical behaviour13,33,34. Polaritons are hybridised light-matter quasiparticles typically comprising two optically active spin components Jz ∈ {−1, 1}35,36 and a photonic component37. In the absence of external magnetic fields (an in-plane magnetic field can be generated for polaritons via TE-TM splitting in the sample38), condensates support linear polarisation with equal occupations of spin-up and spin-down states36,39,40,41. Most models neglect this spinor structure. However, when including both fields and allowing for intercomponent density-density interactions, it is not a priori true that: each mode’s scaling remains within the KPZ universality class, that a stationary measure exists, or that the dynamics are constrained by Galilean and tilt-symmetries. This means that systems described by multicomponent KPZ do not generally fit within the single-component framework, thus demanding thorough classification while offering an opportunity to realise different phases in non-equilibrium42,43.

In this paper, we investigate the rich physics of multicomponent KPZ, specifically focusing on how it describes the dynamics of the gapless Nambu–Goldstone modes in two-component driven bosonic systems at weak noise in one spatial dimension. We determine the full phase diagram of the linearly-polarised degenerate condensate model with \({{\mathbb{Z}}}_{2}\) inversion symmetry ψ1 ↔ ψ2, highlighting its miscible-immiscible transition. We identify parameter regimes where the effective KPZ equations are unstable, giving rise to a non-thermal vortex turbulent phase. At the physical level, this regime exhibits a modified exponent z = 1 due to phase compactness. We construct the most general \({{\mathbb{R}}}^{2}\)-KPZ equations obeying \({{\mathbb{Z}}}_{2}\) internal symmetries for the unwound phase and probe the infrared physics to one-loop in Wilsonian renormalisation group (RG) using the Martin-Siggia-Rose-Janssen-de Dominicis formalism44,45,46,47.

This maps the stochastic equation to a \({{\mathbb{R}}}^{1+1}\) classical field theory for the phase modes \({({\theta }^{\alpha })}_{\alpha = 1}^{2}\) amenable to perturbative treatment around their Gaussian free theories. In both RG analysis and direct integration of the multicomponent KPZ, we recover the critical exponents z = 3/2 and χ = 1/2 in stable regimes. Additionally, we highlight non-universal effects on the distribution of fluctuations within specific submanifolds, such as the Cole–Hopf line where a non-trivial decoupling transformation exists. This analysis provides a comprehensive understanding of the long-wavelength behaviour of density-coupled condensates, but applies to many other systems.

Results and discussion

Degenerate coupled condensates

Typically, mesoscopic dynamics of driven-dissipative condensates in d = 1 are modelled by coupled stochastic complex Ginsburg-Landau equations (SCGLE) describing the dynamics of the lower polariton branch fields \({({\psi }_{i})}_{i = 1}^{2}\in {\mathbb{C}}\)48

$$i{\partial }_{t}{\psi }_{i} = \left[-({k}_{c}-i{k}_{d}){\partial }_{x}^{2}+({\mu }_{c}+i{\mu }_{d})\right.\\ +\left.({u}_{c}-i{u}_{d})| {\psi }_{i}{| }^{2}+({v}_{c}-i{v}_{d})| {\psi }_{\overline{i}}{| }^{2}\right]{\psi }_{i}+{\zeta }_{i},$$
(1)

where each field ψi has a density-mediated contact interaction with the other component \({\psi }_{\overline{i}}\) where i runs over the spinor components and \(\overline{i}\) denotes the complementary component. The SCGLE can be derived from the Schwinger–Keldysh path integral within the semiclassical approximation of bosonic fields with Markovian couplings to the decay and pumping bath modes49,50. For further details, we refer to Supplementary Note 1. The model describes a classical field driven by a complex Gaussian white noise process with diagonal covariance \(\langle {\zeta }_{i}^{* }(x,t){\zeta }_{j}({x}^{{\prime} },t)\rangle = ({\gamma }_{p}+{\gamma }_{l}){\delta }_{ij}\delta (x-{x}^{{\prime} })\delta (t-{t}^{{\prime} })\). The white noise arises naturally in the Lindbladian formalism in the semiclassical limit after employing a Hubbard-Stratonovich transformation and accounts for fluctuations due to interactions with a Markovian environment. In the vicinity of k = 0, the dispersion is typically taken to be a parabola E(k) = E0 + k2/2mLP, giving the kinetic coefficient kc = 1/2mLP where mLP is the effective polariton mass. Importantly, we introduce a phenomenological diffusion constant kd which suppresses higher momentum modes. Experimentally, this arises due to the momentum dependence of the polariton linewidth15. The momentum-dependent losses turn out to be crucial in determining the universality class of the phase fluctuations in the multicomponent KPZ theory. All parameters in Eq. (1) are real and we impose positivity constraints on the Lindblad operators μd,  ud and effective interactions uc > 0 for a stable condensed solution. The system is driven-dissipative requiring incoherent external pumping to counterbalance photon decay. This gives rise to an effective drive μd = (γp − γl)/2 comprising of the incoherent pump γp minus the single particle losses γl, which is positive in the U(1) spontaneously symmetry broken (SSB) condensate phase. Incoherent pumping is key since it preserves the global phase rotation symmetries unlike a coherent pumping scheme, explicitly locking the phase. The chemical potential μc in driven-dissipative systems is a posteriori determined by the mean field condition as it can be adjusted via a gauge transformation50. The two particle losses ud,  vd > 0 act as gain saturation terms. This model assumes local interactions which is a good approximation for the polariton system.

Miscible-immiscible transition

Before embarking on the analysis of the low-energy theory, we first look at the linear stability of the multicomponent equations and identify unstable regimes, where the mapping to multicomponent KPZ is inappropriate. The derivation of the conditions are presented in the Supplementary Note 1. Equilibrium two-component condensates support a miscible-immiscible transition when the real intercomponent interactions exceed the intracomponent interactions \({v}_{c}^{2} > {u}_{c}^{2}\)51,52,53,54. In this case modulation instabilities cause condensate fragmentation. Non-equilibrium condensates support a similar phase separation14,41 but differ from their equilibrium counterparts in that the linearised SCGLE (1) no longer has four gapless sound modes in its Bogoliubov spectrum but instead has two gapped density modes and two gapless diffusive phase modes. There are two conditions of different physical origin which can drive a miscible transition shown in Fig. 1a, b: (a) the dissipative intercomponent interaction exceeds the intracomponent interactions vd > ud, resulting in the gapped modes becoming dynamically unstable, and (b) when the rescaled intercomponent interaction \({\tilde{v}}_{c}={v}_{c}/{u}_{c}\) does not satisfy

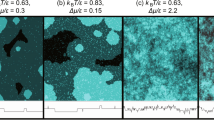
$$-1-{{{\mathcal{R}}}}(k){{{\mathcal{R}}}}(u)(1+{\tilde{v}}_{d}) < {\tilde{v}}_{c} < 1+{{{\mathcal{R}}}}(k){{{\mathcal{R}}}}(u)(1-{\tilde{v}}_{d})$$
(2)

with \({{{\mathcal{R}}}}(k)={k}_{d}/{k}_{c}\) and \({{{\mathcal{R}}}}(u)={u}_{d}/{u}_{c}\), resulting in the gapless modes becoming dynamically unstable. All bare parameters for polaritons which violate this condition conveniently map to Quadrants II and III in Fig. 1, though it is important to emphasise that the low-energy theory cannot simply be described by coupled KPZ, since density fluctuations are not negligible. Within the \({\tilde{v}}_{d}={v}_{d}/{u}_{d} < 1\) region, the miscible transition exhibits two sub-cases depending on whether the intercomponent interaction vc is attractive or repulsive. For repulsive intercomponent interactions vc > 0, tuning \(({\tilde{v}}_{c},{\tilde{v}}_{d})\) outside of the immiscible boundary Eq. (2), gives rise to spatially localised single-component regions. If the interaction is attractive \({\tilde{v}}_{c} < 0\), as shown for the density plot for the simulation in Quadrant III in Fig. 1b, there is no obvious fragmentation and instead the components spatially cluster. However, the density fluctuations are still large and cannot be adiabatically eliminated, making the KPZ mapping unsuitable. Quadrants I and IV support a well-defined ground state manifold. This is shown in Fig. 1c where Quadrants I and IV have small density fluctuations in \({\hat{e}}_{N}\), resulting in dynamics dominated by the Nambu–Goldstone modes tangential to the ground state manifold \({\hat{e}}_{\theta }\). This justifies integrating out the gapped modes in the normal direction \({\hat{e}}_{N}\). On the other hand, Quadrants II and III see smearing in their distributions, indicating that the gapped normal modes cannot be ignored.

Fig. 1: Linear stability of SCGLE modes.
figure 1

a Stability conditions in \(({\tilde{v}}_{d},{\tilde{v}}_{c})\) for Eq. (1) with μd = ud = kd = 1,  uc = 3,  kc = 4 and \(\tilde{{{{\mathcal{R}}}}}(k)={k}_{c}/{k}_{d}\); hence t and x are measured in \({\mu }_{d}^{-1}\) and \(\sqrt{{k}_{d}}\). Tuning \({\tilde{v}}_{c}\) and \({\tilde{v}}_{d}\) allows crossing between quadrants in (b), denoted by the same colours across all subfigures signifying distinct regimes. b Density fluctuations for ψ1,  ψ2 (blue and green respectively) components for parameters in Quadrants (I–IV). c Smoothed histograms of the real and imaginary parts of the field ψ1 at t = 100 for system size 217 giving a geometric interpretation to the dynamics. The Nambu–Goldstone modes are phase fluctuations in the direction \({\hat{e}}_{\theta }\); and the density fluctuations are normal \({\hat{e}}_{N}\) and gapped. In Quadrants II and III, the linear instability results in large fluctuations in \({\hat{e}}_{N}\), which cannot be adiabatically eliminated to arrive at a KPZ equation. The colour bar runs from transparent to unity for the maximum.

Full size image

Low-energy multicomponent KPZ

Instead, if we focus on Quadrants I and IV where the theory is stable against small fluctuations, we expect that the Nambu–Goldstone modes should correctly describe the low-energy behaviour. The theory is invariant under U(1) × U(1) symmetry with independent \({\psi }_{i}\mapsto {e}^{i{\theta }_{i}}{\psi }_{i}\). When μd > 0, each U(1) undergoes spontaneous symmetry breaking. The ground state manifold is given after trivially quotienting out the identity for both U(1) product symmetries and is isomorphic to S1 × S1. The coset construction dictates that the low-energy manifold for Nambu–Goldstone modes from spontaneous symmetry breaking of a group G down to subgroup H (for the ground state) is given by the quotient group G/H. In this case, the low-energy manifold is the trivial quotient group G/{eG} ≅ G. Since the ground state topology is simply two independent compact S1 manifolds, the low-energy theory should be parameterised using the density-phase representation, where θi parameterise the gapless fluctuations. In the adiabatic approximation around the mean field ∣ψ0,i∣2 = ρi = μd/(ud + vd) = − μc/(uc + vc), gapped fluctuations can be integrated out50 giving multicomponent KPZ equations for \({{\mathbb{R}}}^{2}\)-fields \({({\theta }^{\alpha }(x,t))}_{\alpha = 1}^{2}\)

$${\partial }_{t}{\theta }^{\alpha }={D}_{\alpha \beta }{\partial }_{x}^{2}{\theta }^{\beta }+\frac{1}{2}{\Gamma }_{\beta \gamma }^{\alpha }({\partial }_{x}{\theta }^{\beta })({\partial }_{x}{\theta }^{\gamma })+{\zeta }^{\alpha }$$
(3)

driven by a real Gaussian additive white noise \({({\zeta }^{\alpha })}_{\alpha = 1}^{2}\) with symmetric covariance \(\langle {\zeta }^{\alpha }(x,t){\zeta }^{\beta }({x}^{{\prime} },{t}^{{\prime} })\rangle =2{\Delta }^{\alpha \beta }\delta (x-{x}^{{\prime} })\delta (t-{t}^{{\prime} })\). To highlight the difference between the low-energy theory for the phases θα and the SCGLE in Eq. (1), we index the phase fields using Greek letters. Strictly, the phase itself is a compact variable, supporting non-trivial topological excitations such as spacetime vortices (STV) which modify the scaling. For the single-component case in the low-noise regime, compactness does not affect KPZ scaling for significant time windows55. The parameters from the SCGLE mapping have been previously discussed in ref. 48, but we impose a strict \({{\mathbb{Z}}}_{2}\) symmetry with

$${D}_{11} = \, {D}_{22}={k}_{c}{{{{\mathcal{C}}}}}_{1}({u}_{d}{u}_{c}-{v}_{c}{v}_{d})+{k}_{d},\\ {D}_{12} = \, {D}_{21}={k}_{c}{{{{\mathcal{C}}}}}_{1}({v}_{c}{u}_{d}-{u}_{c}{v}_{d}),\\ {\Gamma }_{11}^{1} = \, {\Gamma }_{22}^{2}=-2{k}_{c}+2{k}_{d}{{{{\mathcal{C}}}}}_{1}\left({u}_{c}{u}_{d}-{v}_{c}{v}_{d}\right),\\ {\Gamma }_{22}^{1} = \, {\Gamma }_{11}^{2}=2{k}_{d}{{{{\mathcal{C}}}}}_{1}({v}_{c}{u}_{d}-{u}_{c}{v}_{d}),\\ {\Gamma }_{12}^{1} = \, {\Gamma }_{21}^{1}={\Gamma }_{12}^{2}={\Gamma }_{21}^{2}=0.$$

where \({{{{\mathcal{C}}}}}_{1}={({u}_{d}^{2}-{v}_{d}^{2})}^{-1}\). The structure of the parameters respects the \({{\mathbb{Z}}}_{2}\) symmetry imposed at the level of the SCGLE. In the limiting case where density cross-couplings vanish vc = vd = 0, the system is reduced to two independent KPZ equations. Coupling in the density channels between the condensates vc/d introduces couplings in the off-diagonal terms of the diffusion D12 = D21 and noise matrices Δ12 = Δ21. The Δαβ have non-trivial cross-components, corresponding to correlated white noise fields that simultaneously drive the two phase modes. The correlations are presented in Supplementary Note 1. Requiring the diffusion matrix D to be positive definite is equivalent to the dynamical stability condition given in Eq. (2). A point to stress is that off-diagonal interaction vertices \({\Gamma }_{\beta \gamma }^{\alpha }\) are only generated if kd ≠ 0. In general, there are 8 possible interaction vertices where the upper index details the dynamical equation and the lower indices detail the phase modes involved in the coupling. However, owing to the \({{\mathbb{Z}}}_{2}\) symmetry and due to the nature of the mapping, not all terms are generated giving rise to only 4 degenerate couplings \({\Gamma }_{11}^{1}\), \({\Gamma }_{22}^{1}\), \({\Gamma }_{11}^{2}\), \({\Gamma }_{22}^{2}\). As in the single-component case, the non-linearity vanishes at the equilibrium condition when kd/kc = vd/vc = ud/uc define collinear rays in the complex plane56.

In the spirit of Landau, the effective theory in multicomponent regimes should be described by Eq. (3) with \({{\mathbb{Z}}}_{2}\) symmetry θ1 ↔ θ2 resulting in the degenerate structure of the \({\Gamma }_{\beta \gamma }^{\alpha }\) tensors

$${\Gamma }^{1}=\left(\begin{array}{ll}{\Gamma }_{11}^{1}&{\Gamma }_{12}^{1}\\ {\Gamma }_{12}^{1}&{\Gamma }_{22}^{1}\end{array}\right),{\Gamma }^{2}=\left(\begin{array}{ll}{\Gamma }_{22}^{1}&{\Gamma }_{12}^{1}\\ {\Gamma }_{12}^{1}&{\Gamma }_{11}^{1}\end{array}\right)$$
(4)

and D = DT = Dτ, Δ = ΔT = Δτ where τ denotes the off-diagonal transpose e.g. Δ11 = Δ22. It is insightful to transform Eq. (3) to its normal modes where the rotated fields, denoted by tildes, transform as \({\tilde{\theta }}^{1}=({\theta }^{1}+{\theta }^{2})/\sqrt{2}\), \({\tilde{\theta }}^{2}=({\theta }^{1}-{\theta }^{2})/\sqrt{2}\). These coordinates capture the joint phase and phase difference between the condensates, and have been used in d = 2 + 1 dimension in the study of vortex dynamics42. A full and spin vortex corresponds to windings in the \(\tilde{{\theta }_{1}}\) and \({\tilde{\theta }}_{2}\) fields respectively. Half vortices are topological excitations in the non-rotated coordinates θ1 or θ2 fields individually. The linear equations decouple with diffusion matrices \({\tilde{D}}_{11}={D}_{11}+{D}_{12}\) and \({\tilde{D}}_{22}={D}_{11}-{D}_{12}\). The noise covariance inherits the diagonal structure with \({\tilde{\Delta }}_{11}={\Delta }_{11}+{\Delta }_{12}\) and \({\tilde{\Delta }}_{22}={\Delta }_{11}-{\Delta }_{12}\). Interaction vertices are rank-(1,2) tensors, transforming non-trivially \({\tilde{\Gamma }}_{11}^{1}=({\Gamma }_{11}^{1}+2{\Gamma }_{12}^{1}+{\Gamma }_{22}^{1})/\sqrt{2}\), \({\tilde{\Gamma }}_{22}^{1}=({\Gamma }_{11}^{1}-2{\Gamma }_{12}^{1}+{\Gamma }_{22}^{1})/\sqrt{2}\), \({\tilde{\Gamma }}_{12}^{2}=({\Gamma }_{11}^{1}-{\Gamma }_{22}^{1})/\sqrt{2}\), while other non-linear terms vanish. In the normal mode coordinates and dedimensionalising, the \({{\mathbb{Z}}}_{2}\)-theory maps onto

$${\partial }_{t}{\tilde{\theta }}_{1} = \, {\partial }_{x}^{2}{\tilde{\theta }}_{1}+\sqrt{Z}\left({({\partial }_{x}{\tilde{\theta }}_{1})}^{2}+Y{({\partial }_{x}{\tilde{\theta }}_{2})}^{2}\right)+\sqrt{2}{\zeta }_{1},\\ {\partial }_{t}{\tilde{\theta }}_{2} = \, T{\partial }_{x}^{2}{\tilde{\theta }}_{2}+2X\sqrt{Z}({\partial }_{x}{\tilde{\theta }}_{1})({\partial }_{x}{\tilde{\theta }}_{2})+\sqrt{2T}{\zeta }_{2},$$
(5)

previously studied by Ertaş and Kardar in dynamic roughening of directed lines with unit and normalised Gaussian white noises16,57. Following an equivalent scheme to ref. 58, the adimensionalisation is detailed in Supplementary Note 2 and shows that there are four relevant parameters which determine the scaling behaviour of the modes: the diffusion ratio \(T={\tilde{D}}_{22}/{\tilde{D}}_{11}\), which describes the ratio of the two diffusion constants for the \({\tilde{\theta }}_{2}\) and \({\tilde{\theta }}_{1}\) modes; the interaction ratio \(X={\tilde{\Gamma }}_{12}^{2}/{\tilde{\Gamma }}_{11}^{1}\), describing the relative strength of the cross-term interaction for the \({\tilde{\theta }}_{2}\) mode’s dynamics to the standard KPZ-like term; the interaction ratio \(Y=({\tilde{\Gamma }}_{22}^{1}{\tilde{\Delta }}_{22}{\tilde{D}}_{11})/({\tilde{\Gamma }}_{11}^{1}{\tilde{\Delta }}_{11}{\tilde{D}}_{22})\), which is proportional to the non-linear interaction term from the \({\tilde{\theta }}_{2}\) mode in the \({\tilde{\theta }}_{1}\) dynamics; and the effective KPZ constant \(Z=({\tilde{\Delta }}_{11}{({\tilde{\Gamma }}_{22}^{1})}^{2})/(4\Lambda {\tilde{D}}_{11}^{3})\), which captures the strength of the non-linear dynamics. The noise ratio \(W={\tilde{\Delta }}_{22}/{\tilde{\Delta }}_{11}\) is required to be positive definite to retain its connection to probability and the diffusion constants have to be positive definite to ensure stability. For decoupled \({{\mathbb{Z}}}_{2}\) symmetric KPZ equations with vc = vd = 0, the bare parameters transform to \({\tilde{\Gamma }}_{11}^{1}={\tilde{\Gamma }}_{22}^{1}={\tilde{\Gamma }}_{12}^{2}\), which corresponds to the point X = 1, Y = 1 in Fig. 2.

Fig. 2: Projected RG flows in (X, Y)-plane.
figure 2

The RG flows in Eq. (8) where T = 1, with the Cole–Hopf line X = 1 (red) and a line of fixed points with an emergent fluctuation dissipation relation X = Y (black). For the SCGLE, Quadrant I gives KPZ scaling in both modes, Quadrant IV is an STV-dominated phase, Quadrants II and III have a dynamical instability in the gapless modes, making the mapping inappropriate. Bare parameters which lie on the Cole–Hopf line in Quadrant I flow to the decoupled KPZ fixed point at (1, 1), denoted by the star. The point (0, 0) corresponds to an exceptional point, where \({\tilde{\theta }}_{1}\) and \({\tilde{\theta }}_{2}\) are decoupled in the rotated basis, and thus is an unstable fixed point describing a KPZ mode decoupled from an EW mode. The square at (1, − 1) is a fixed point predicted in Quadrant II where there is a complex Cole–Hopf solution, but is unstable and thus not considered further.

Full size image

We assume a single time-scaling parameter, which is valid in the non-decoupled case within the normal mode space57. Notably, X = 0 is an exceptional point allowing independent time rescaling for both modes \({t}_{1}\mapsto {b}^{{z}_{1}}{t}_{1}\) and \({t}_{2}\mapsto {b}^{{z}_{2}}{t}_{2}\) with z1 = 3/2 and z2 = 2 since we have a KPZ mode decoupled from an Edwards–Wilkinson (EW) mode. This time-scaling condition is equivalent to demanding that in the RG limit, there is one scaling parameter in time with z1 = z2, and the resulting two-point functions take on the scaling form

$$\begin{array}{l}\left\langle {({\tilde{\theta }}_{\alpha }(t,x)-{\tilde{\theta }}_{\beta }(0,0))}^{2}\right\rangle \sim {t}^{\chi /z}{\hat{C}}_{\alpha \beta }(x/{t}^{1/z})\\ \quad \,\, \Rightarrow \quad \left\{\begin{array}{l}\hat{C}(t,0) \sim \hat{A}{t}^{2\beta }\\ \hat{C}(0,x) \sim \hat{B}| x{| }^{2\chi }\end{array}\right.\end{array}$$
(6)

where χ = χ1 = χ2 is the roughness exponent and z is the dynamical exponent with χ = βz. The two-point correlation matrix \(\hat{C}\) is potentially a non-universal scaling function, which additionally may or may not coincide with the single-component case6,28. Tuning the intercomponent interactions allows you to move away from the decoupled point into other quadrants, each representing distinct physical behaviours. Since Quadrants II and III are not relevant for exciton-polaritons, we focus instead on Quadrants I and IV, which lie in the upper half-plane.

Spacetime vortex phase

Even before resorting to RG for scaling analysis, certain pathological behaviours can be identified from the dynamical equations. At large times, the dynamics is dominated by the non-linearities and an instability arises when X and Y do not share the same sign. In this instance, the diffusion and noise are both stable, but the instability is generated by the non-linear terms. This instability arises from the non-hyperbolicity of the linearised long-time dynamics in Quadrants II and IV59. The system is called non-hyperbolic since there are modes which grow exponentially in time. Tuning \(({\tilde{v}}_{c},{\tilde{v}}_{d})\), we can access this instability in Quadrant IV from the SCGLE by choosing bare parameters which satisfy Eq. (2) but violate conditions

$$-1+\frac{{{{\mathcal{R}}}}(u)}{{{{\mathcal{R}}}}(k)}(1+{\tilde{v}}_{d}) < {\tilde{v}}_{c} < 1-\frac{{{{\mathcal{R}}}}(u)}{{{{\mathcal{R}}}}(k)}(1-{\tilde{v}}_{d})$$
(7a)
$$1-\frac{{{{\mathcal{R}}}}(u)}{{{{\mathcal{R}}}}(k)}(1-{\tilde{v}}_{d}) < {\tilde{v}}_{c} < -1+\frac{{{{\mathcal{R}}}}(u)}{{{{\mathcal{R}}}}(k)}(1+{\tilde{v}}_{d})$$
(7b)

for \({{{\mathcal{R}}}}(u) < {{{\mathcal{R}}}}(k)\) and for \({{{\mathcal{R}}}}(u) > {{{\mathcal{R}}}}(k)\) respectively.

In this quadrant, non-hyperbolicity gives rise to large jumps in the phase. In Fig. 3, we analyse the distribution of fluctuations for a non-compact field with X = − 1 and Y = 1, denoted by the five-sided star in Fig. 2, revealing that even at early times the \({\tilde{\theta }}_{1}\) surface exhibits large deviations away from its mean, as evidenced by the large tail to the left. The numerical simulations for Quadrant IV were found to be numerically unstable for times t > 20. The direction of the tail is dictated by the sign of the non-linearity \({\tilde{\Gamma }}_{11}^{1}\). These fluctuations do not fall under those predicted in the single-component case. At the level of the condensate ψi, the surface instability must be reinterpreted in terms of its behaviour in the compact phase space. At the physical level, this triggers the proliferation of spacetime vortices, non-trivial windings in the phase due to compactness. Once these defects are present, the two-point correlations \(\langle {\psi }_{i}^{{{\dagger}} }(x,t){\psi }_{j}({x}^{{\prime} },{t}^{{\prime} })\rangle\) should be exponentially decaying in both time and space. The vortex turbulent regime dramatically modifies the scaling, resulting in growth exponent β = 1/2 and consequently dynamical exponent z = 1 as shown in Fig. 4. A spacetime vortex phase has been observed in the single-component case in the large noise regime, where it was shown that the spacetime vortex density scales as \({{\mathbb{P}}}_{v} \sim {e}^{-A/\Delta }\) with Δ being the noise strength55. However, in the multicomponent case, tuning \({\tilde{v}}_{c}\) reveals a similar exponential dependence in the density of vortices, but importantly the phase transition originates from the intercomponent interactions. Crossing over to Quadrant IV, the activation energy for a vortex decreases sufficiently that spacetime vortices are observable across all time windows as predicted by the linear stability analysis. More detail on the analysis of the spacetime vortex phase can be found in the Supplementary Note 5.

Fig. 3: Unstable phase fluctuations in quadrant IV.
figure 3

Distribution of rescaled fluctuations χ for \({\tilde{\theta }}_{1}\) and \({\tilde{\theta }}_{2}\) in Quadrant IV with X = − 1 and Y = 1 and system size L = 220. a \({\tilde{\theta }}_{1}\) generates skewed fluctuations with a heavy tail to the left. b \({\tilde{\theta }}_{2}\) has symmetric fluctuations but upon the onset of the instability in \({\tilde{\theta }}_{1}\) becomes increasingly kurtotic. The solid red line shows a rescaled Gaussian \({{{\mathcal{N}}}}(0,0.638)\). All the distributions are rescaled in time to have constant variance and zero mean.

Full size image
Fig. 4: Proliferation of spacetime vortices in quadrant IV.
figure 4

SCGLE simulations with parameters vd = 0, kd = ud = μd = 1 and kc = 3, uc = 1.5 and tuning \({\tilde{v}}_{c}\) from 0 to  − 1.2. a Probability of a vortex in the spacetime lattice for unrotated θ1, θ2 as a function of interaction \({\tilde{v}}_{c}\). Inline plot shows that tuning \({\tilde{v}}_{c}\) traces a path in the (X, Y) plane from the decoupled point (1, 1), which lies in Quadrant I (KPZ) in blue to Quadrant IV (STV) in red. b, c The autocorrelation Δ(t1 − t2) of the unwound phase for rotated coordinates \({\tilde{\theta }}_{1}\) and \({\tilde{\theta }}_{2}\), respectively, showing a crossover to the STV regime, when tuning \({\tilde{v}}_{c}\) between 0 to  − 1.2, plotted from bottom to top. In black we plot the expected relationships for Edwards–Wilkinson (EW), KPZ and the spacetime vortex (STV) phase.

Full size image

Renormalisation group analysis

To understand the scaling behaviour presented in each of the quadrants, we appeal to Wilsonian renormalisation group (RG). In this framework, the theory elevates the parameters to functions of the RG scale ℓ. This can be done by iteratively integrating out high-momentum modes for all the fields Λ/b ≤ k ≤ Λ, where Λ is the ultraviolet cutoff regularising the effective theory. The derivation of the RG equations is given in the Supplementary Note 3 in the \({{\mathbb{Z}}}_{2}\) coordinates, but has previously been discussed in ref. 57. The RG equations describe how each of the parameters in Eq. (3) are renormalised as we coarse grain the system to large wavelengths, corresponding to flowing towards the low-energy theory, which should be governed by simple scaling behaviour in critical regimes. This results in a set of coupled autonomous ODEs closing under the \({{\mathbb{R}}}^{4}\)-parameter space:

$$\begin{array}{rcl}{\partial }_{\ell }T&=&-\frac{Z}{\pi }\left(T+XY+\frac{2X((T-3)X-3TY+Y)}{{(1+T)}^{2}}\right)\\ {\partial }_{\ell }X&=&-\frac{4Z}{\pi }\frac{X(X-1)(X-Y)}{{(1+T)}^{2}}\\ {\partial }_{\ell }Y&=&\frac{Z}{\pi }\frac{Y(X-Y)\left(2(5T+1)X+{(1+T)}^{2}Y-4T(1+T)\right)}{T{(1+T)}^{2}}\\ {\partial }_{\ell }Z&=&Z\left(\frac{Z(Y(Y-3X)-2T)}{\pi T}+1\right).\end{array}$$
(8)

The boundary conditions for the RG flows are specified at ℓ = 0, where the parameters assume their initial bare values. The projected flows of X and Y are shown in Fig. 2. From inspection of Eq. (8), the parameters X,  Y cannot change sign under RG, implying that the flows do not cross between quadrants. We have a line of attractive fixed points when X = Y defining a manifold on which there is an emergent stationary measure, which is denoted by the black diagonal line in Fig. 2. Furthermore, the X flow vanishes at X = 1 defining the Cole–Hopf line which is closed under RG. To understand the phase dynamics relevant to polaritons, we can concentrate on Quadrants I and IV since the other quadrants present a physical instability from Eq. (2). In Quadrant IV, the RG suggests that the coupling parameters should vanish with X → 0 and Y → 0, however additionally T → 0, which results in the breakdown of the RG analysis57 as the two modes can be rescaled in time independently i.e. z1 ≠ z2. However, instead we must discount this based on the emergence of an instability from violating conditions (7a) and (7b). Physically for the SCGLE, this quadrant as previously discussed corresponds to a disordered STV phase with z = 1 for both modes. At this point, we focus on the analysis of the coupled SCGLE in Quadrant I.

Fluctuation-dissipation line

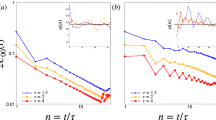
One important characteristic of coupled KPZ is that, in contrast to the single-component case, there is no longer an incidental Gaussian stationary measure in dimension d = 1. A stationary measure arises from a time-independent solution to the Fokker-Planck equation. Ignoring the non-linearity, the Gaussian stationary measure with correlations \(\langle {\partial }_{x}{\theta }^{\alpha }(x){\partial }_{{x}^{{\prime} }}{\theta }^{\beta }({x}^{{\prime} })\rangle ={C}^{\alpha \beta }\delta (x-{x}^{{\prime} })\) must satisfy the Lyapunov condition DC + CDT = 2Δ where C = CT, Δ > 0 and D + DT > 0. The condition that the stationary measure remains time-stationary in the presence of interactions requires that the rescaled interaction vertices \({\hat{\Gamma }}^{\alpha }={({C}^{-1})}_{\alpha \beta }{\Gamma }^{\beta }\) satisfy the cyclicity condition \({\hat{\Gamma }}_{\beta \gamma }^{\alpha }={\hat{\Gamma }}_{\gamma \beta }^{\alpha }={\hat{\Gamma }}_{\gamma \alpha }^{\beta }\)17,28. In Quadrants I and III, the flows project onto the fixed line X = Y where a fluctuation dissipation relation (FDR) is satisfied \({\tilde{\Gamma }}_{22}^{1}{\tilde{\Delta }}_{22}{\tilde{D}}_{11}={\tilde{\Gamma }}_{12}^{2}{\tilde{\Delta }}_{11}{\tilde{D}}_{22}\). On this submanifold, stationarity enforces χ = 1/2 for both components as the measure coincides with the non-interacting theory. Additionally, the one-loop RG predicts KPZ scaling z = 3/2 for both components. Furthermore, numerical integration of initial bare parameters in Quadrant I show that the long-time and large system size dynamics converge to the expected exponents β = 1/3 and χ = 1/2. Along the fixed line, same-time correlations \(\hat{C}(0,| x-{x}^{{\prime} }| )={\hat{C}}_{\alpha \beta }| {{{\bf{x}}}}-{{{{\bf{x}}}}}^{{\prime} }{| }^{2\chi }\) are given by two-sided white noise processes with \({\hat{C}}^{\alpha \beta }={[{D}^{-1}\Delta ]}^{\alpha \beta }\). Under RG, \(\tilde{C}(l)\) is renormalised until it reaches the FDR line. On the FDR line, emergent time-reversal symmetry enforces the non-renormalisation \(\hat{C}(l)={\hat{C}}_{0}{| }_{X = Y}\)60. Consequently, even in the case when \({\tilde{C}}_{0}={\mathbb{1}}\), for \({\tilde{\theta }}_{1},\,{\tilde{\theta }}_{2}\) modes initialised away from X = Y, the respective long-time two-point correlations may not coincide.

Cole–Hopf line

A relevant case of the SCGLE for polaritons arises when the coherent term kc dominates over the relaxation term kd = 0. These parameters map onto the closed X = 1 submanifold denoted by the red line in Fig. 2. A specific sub-case of this is discussed by Funaki et al.17, where crucially the diffusion matrix satisfies T = 1. The line can be split into two distinct behaviours: (a) Y > 0 in Quadrant I, where there exists a real Cole–Hopf solution with fixed point coinciding with FDR and (b) Y < 0 in the unstable Quadrant II, where there exists a complex Cole–Hopf solution1,57. To build up the intuition of the Cole–Hopf line, we first discuss the case of two independent KPZ equations but with correlated noise in the \({{\mathbb{Z}}}_{2}\) coordinates. This scenario is depicted in Fig. 5a, where the flows terminate at a point where W = 1, illustrating that a noise coupling between independent KPZ equations is irrelevant. Along this submanifold, the cross-couplings Γ do not flow. The more general case, where the bare parameters map onto the X = 1 Cole–Hopf manifold, but cross-couplings in the diffusion channels and non-linear vertices are allowed is shown in Fig. 5b. We see that the RG flows go to a point where \({\tilde{D}}_{11}^{* }={\tilde{D}}_{22}^{* }\ \Rightarrow \ {T}^{* }=1\) is recovered at the fixed point, a necessary condition for the existence of a valid decoupling transformation, and \(({\tilde{\Gamma }}_{22}^{1* }{\tilde{\Delta }}_{22}^{* })/({\tilde{\Gamma }}_{11}^{1* }{\tilde{\Delta }}_{11}^{* })=1\). Therefore, the diffusion matrix flows to a form proportional to the identity and the ratio of noises is fixed by the cross-coupling \({\tilde{\Gamma }}_{22}^{1* }/{\tilde{\Gamma }}_{11}^{1* }\). Consequently, at the fixed point, a decoupling transformation exists \({\hat{\theta }}^{\alpha }={s}_{\beta }^{\alpha }{\tilde{\theta }}^{\beta }\)17 with

$$s=\left(\begin{array}{ll}{\tilde{\Gamma }}_{11}^{1* }&{\left({\tilde{\Gamma }}_{11}^{1* }{\tilde{\Gamma }}_{22}^{1* }\right)}^{1/2}\\ {\tilde{\Gamma }}_{11}^{1* }&-{\left({\tilde{\Gamma }}_{11}^{1* }{\tilde{\Gamma }}_{22}^{1* }\right)}^{1/2}\end{array}\right)$$
(9)

where all parameters assume their renormalised values. This leads to two equivalent, but decoupled, KPZ equations at the fixed point in the coordinate system from transformation Eq. (9). For flat initial conditions \(\hat{\theta }(x,0)=0\), the limiting form of the phase is \(\hat{\theta }(x,t)={v}_{\infty }t+{(Mt)}^{1/3}\chi\), where v∞ is the asymptotic growth velocity, M is a non-universal scaling parameter depending on renormalised parameters, and χ is a random variable sampled from a Tracy-Widom (TW) Gaussian Orthogonal (GOE) distribution. The fluctuations in the normal mode coordinates have an additional scaling parameter \({\tilde{\Gamma }}_{22}^{1* }\) with asymptotic forms

$${\tilde{\theta }}_{1}(x,t) = \, \frac{1}{2{\tilde{\Gamma }}_{11}^{1* }}\left[2{v}_{\infty }t+{(Mt)}^{1/3}\left({\chi }_{1}+{\chi }_{2}\right)\right]\\ {\tilde{\theta }}_{2}(x,t) = \, \frac{1}{{2\left({\tilde{\Gamma }}_{11}^{1* }{\tilde{\Gamma }}_{22}^{1* }\right)}^{1/2}}\left[{(Mt)}^{1/3}\left({\chi }_{1}-{\chi }_{2}\right)\right].$$
(10)

\({\tilde{\theta }}_{2}\) has symmetric fluctuations, but unlike a Gaussian, has excess kurtosis shown in the extended tails in Fig. 5d. The kurtosis converges to the expected values at large times. After numerical integration of the multicomponent KPZ with bare parameters X = 1, Y = 2, Z = 25, we rescale the variance of the fluctuations to match a TW-GOE with cumulative distribution F( − 2−2/3x) and \({\langle {\chi }^{2}\rangle }_{c}=0.638\). The distributions of \({\tilde{\theta }}_{1},\,{\tilde{\theta }}_{2}\) are χ1 + χ2 and χ1 − χ2 up to a translation of mean and rescaling of variance. The TW-GOE distribution can be found up to numerical precision from evaluating a generalised Fredholm determinant efficiently using Gauss-Legendre quadrature and rescaling using the Hastings–Mcleod solution to the Painlevé II equation61,62. The distributions of the sums and differences can be subsequently calculated using a numerical convolution of probability density functions. Away from the X = 1 line, there is no obvious decoupling transformation, which makes calculating the analytical form of the fluctuation distribution difficult. Nevertheless, \({\tilde{\theta }}_{1}\) retains an asymmetric profile and \({\tilde{\theta }}_{2}\) retains its inversion symmetry. The distributions can at most depend on two additional parameters T, X. Moving along X = Y starting from 0 at finite time, we see a crossover from Gaussian in \({\tilde{\theta }}_{2}\) at the decoupled point (0, 0) to more kurtotic distributions as shown in Supplementary Fig. S4. Experimentally and numerically, this showcases that for the multicomponent SCGLE when kd = 0, the distribution of fluctuations still has valid subclasses which can be exactly calculated to validate non-equilibrium phenomena.

Fig. 5: Mode decoupling along Cole–Hopf line.
figure 5

a For \({{\mathbb{Z}}}_{2}\) coupled KPZ with only cross-coupling in noise, the fixed point in the (W, Z)-plane (initial condition T = 1, Y = W) is decoupled KPZ in the original \({{\mathbb{Z}}}_{2}\) coordinates. Here \(W={\tilde{\Delta }}_{22}/{\tilde{\Delta }}_{11}\) is the noise-strength ratio, and the fixed point W* = 1 shows that noise cross-coupling is irrelevant. b The flow in the \((T,{\tilde{\Gamma }}_{22}^{1}{\tilde{\Delta }}_{22}/{\tilde{\Gamma }}_{11}^{1}{\tilde{\Delta }}_{11})\)-plane approaches (1, 1), allowing for a decoupling transformation. c, d Fluctuation distributions χ for initial condition (X, Y) = (1, 2). c The field \({\tilde{\theta }}_{1}\) converges to the sum of rescaled TW-GOE distributions (yellow). For comparison, we plot the rescaled TW-GOE distribution \({2}^{2/3}{F}^{{\prime} }\left.(-{2}^{-2/3}{\chi }_{1})\right)\) (black dashed), and its translation (black solid) so that the means coincide. d The field \({\tilde{\theta }}_{2}\) converges to the difference of TW-GOE distributions (yellow), contrasted with Gaussian (red). Insets (c, d) show time convergence of higher order moments κn to their asymptotic values as predicted by Eq. (10) (horizontal lines) with skewness κ3 = −0.207, and kurtosis κ4 = 0.0829 and κ3 = −0.00,  κ4 = 0.0829 respectively for \({\tilde{\theta }}_{1}\) and \({\tilde{\theta }}_{2}\).

Full size image

Experimental visibility

We now place the analytical results in the context of exciton-polariton experiments. The SCGLE description from Eq. (1) serves as a toy model, capturing the mesoscopic dynamics of the lower polariton (LP) branch. However, in many experimental setups, the generalised Gross-Pitaevskii Equation (gGPE) for a polariton condensate coupled to a reservoir of non-condensed particle is often preferred. Both descriptions give a low-lying effective theory described by KPZ in relevant sectors, but can differ slightly in the bare values of the mapped KPZ parameters. The parameters for the gGPE mapping are contained in the Supplementary Note 6 and discussed in Supplementary Fig. S5. In fact, the SCGLE can be realised from the gGPE by integrating out the reservoir in the adiabatic limit. It is important to stress that in this case the intracomponent and intercomponent contact interactions uc/d and vc/d should both contain contributions from the direct contact interactions between the spinor components, as well as cross-scattering terms that arise from interactions between each component and their respective reservoir. These effective interactions mediated by the reservoir arise in the effective equations for ψi, after integrating out the reservoir with multicomponent densities \({\overrightarrow{n}}_{R}={({n}_{R}^{+},{n}_{R}^{-})}^{T}\)63. Typically in many previous works kd = 0 is taken to be zero, and in this case the theory maps directly onto the Cole–Hopf line X = 1 and the effective theory in the RG limit is described exactly by decoupled KPZ. For polaritons, the intercomponent, vc, and intracomponent, uc, interactions are attractive and repulsive respectively. Typically, experimental cross-spin scattering rates are 5−10% of the intraparticle scattering rate implying vc ≈ −0.1uc64,65. If we relax the constraint and allow the diffusion constant kd ≪ kc, the effective theory maps onto the neighbourhood of X = 1, Y = 1. This means that we expect that \({{\mathbb{Z}}}_{2}\) coupled condensates should still approximately have valid subclasses for their phase fluctuations following the TW-GOE distribution. However, the success in experimentally realising 1D Lieb lattices of micropillars with flat-band geometries offers the possibility of tuning the system away from the Cole–Hopf line15,66. In fact, even in the recent 1D observation of KPZ, the scaling ratio kd/kc ≃ 1 suggests that a moderate effective intercomponent interaction can drive the system away from the Cole–Hopf line. Generalising the gGPE model to be multicomponent with \({{\mathbb{Z}}}_{2}\) symmetry, the extracted experimental values map onto the neighbourhood of the FDR line X = Y, when varying the effective intercomponent interaction. In fact, this corresponds to the limit where R(k) ≫ R(u) and the parametric space is mapped to the line of fixed points, given by the fluctuation dissipation relation. At the fixed point, although we expect KPZ scaling in both modes, the distribution of fluctuations does not seem to be described simply by linear combinations of GOE distributions. Flat band geometries may offer additional tunability to explore the entire parameter space since kc ≃ 0, and feasibly the effective theories can lie within Quadrant IV for specific choices of parameters.

Conclusion

We have demonstrated that under one-loop RG flow, in the regime of stability of the d = 1 SCGLE, we recover a stationary measure, enforcing χ = 1/2 and z = 3/2 exponents for both phase components. In particular, by considering the dedimensionalised coordinates, the RG equations naturally close in an \({{\mathbb{R}}}^{4}\)-dimensional parameter space. This clarifies subtleties of the flow equations, showing that a valid Cole–Hopf transformation to decoupled KPZ requires the ratio of diffusion paramters to be unity T = 1. For polaritons, the Cole–Hopf line is relevant when the effective diffusion parameter kd = 0, and the RG flow restores both the fluctuation-dissipation relation and an exact decoupling transformation at the fixed point. Along the fluctuation dissipation line, X = Y, but off the Cole–Hopf line, we expect neither the distribution of height fluctuations nor two-point correlators to fall directly into the single-component KPZ statistics (e.g. linear sums of rescaled GOE distributions). The nature of how these distributions deform smoothly along the fluctuation dissipation line remains an open question and is an avenue for future work. With lattice geometries, our findings are increasingly relevant, since they offer the possibility to explore the entire parameter space, including phase-separation in Quadrants II and III from unstable gapless modes, and a non-thermal spacetime vortex regime in Quadrant IV, characterised by the altered dynamical exponents z = 1. This phase can be accessed by tuning the effective intercomponent interactions into the unstable regime, providing an opportunity to experimentally realise a vortex-dominated phase even in low-noise conditions. This fully determines the phase diagram of the SCGLE, and has repercussions for our understanding of multicomponent KPZ systems more broadly.