Introduction

The interaction of an intense laser pulse with matter results in the emission of multiple forms of radiation, including X-rays, electrons, ions, and positrons. This general observation has motivated three decades of research on laser-based particle acceleration. The prospect of accelerating ions on a compact scale to MeV energies and beyond has potential for many applications, including radiography of transient phenomena and strong electromagnetic fields1, for the ion fast-ignition approach to fusion energy2, and in generating neutron beams3 for non-destructive testing4. It has particularly promising benefits in radiation therapy5 because of the enormous cost of ion radiation therapy based on current technology, which limits the use of this treatment. A fundamental requirement for this application is the acceleration of ions to energies sufficiently high to penetrate human tissue and reach any tumor, which in the case of protons is about 250 MeV6.

The target normal sheath acceleration (TNSA) mechanism of ions7 has been extensively studied in dozens of different experimental scenarios. TNSA relies on high-magnitude electric fields that form between an irradiated target and the electron sheath that develops around it to accelerate ions from surface contaminants. The general phenomenology is that laser systems that deliver higher pulse energies and shorter pulse durations are able to accelerate ions from flat-foil targets to higher energies8. For example, the current record of 150 MeV9 has been achieved using ultrashort laser pulses with 22 J of energy, whereas 0.12 J laser pulses, like the one used for the results presented here, typically reach maximum proton energies of 2 MeV8,10. Prospective applications suitable for such lower energies include radiopharmaceuticals generation either directly11 or through the products of secondary nuclear reactions12,13, and materials analysis techniques such as fast neutron activation14 and laser-driven particle-induced x-ray emission15.

Advanced target designs aimed to enhance TNSA via controlled pre-expansion, localized field enhancement, or increased heating of target electrons include foam layers16,17,18, sub-micron gratings19,20,21, micron-scale channels22,23,24, and micro- or nano-structured wire arrays25,26.

In TNSA, both the lateral and longitudinal (thickness) dimensions of an irradiated target affect the characteristics of the emitted ions. It is generally established that ion energies rise when the target thickness is of the order of the laser wavelength or smaller8. The caveat is that very thin targets would remain intact throughout the interaction to emit ions only when the laser pulse contrast is sufficiently high27. Limiting the transverse size of thick target foils down to 10 s of micrometers was observed to enhance the accelerating gradient of the electron sheath because of electrons refluxing from the edges of the target28,29,30,31,32,33. But in this case, the resulting ion energies still fall short of those produced using sub-wavelength thin foils irradiated with the same laser pulse parameters34,35,36.

Here we report on irradiation experiments of single formations immersed in the focal volume of an intense laser pulse and thinner than half its wavelength. These experiments resulted in proton energies higher than those achieved with any other laser-based method with a similar pulse energy. We show that this effect is not a mere combination of the two aforementioned observations about the dimensions of the target but rather a manifestation of a different and more efficient ability of the laser fields to transfer energy to the electrons that form the sheath. Hints of this dynamics could be gleaned from several experimental results showing enhanced proton emission from irradiated surfaces covered with nanometric or micrometric structures37,38,39,40.

Irradiation of truly isolated targets fully contained within the laser focal volume is mechanically challenging and was demonstrated only by using a Paul trap to levitate single micrometer-scale plastic spheres41,42. These experiments did not result in higher proton energies than those obtained with solid foils but the emitted protons featured a reduced energy bandwidth.

We studied the emission of protons from irradiated micrometric bar targets (μ-bars) made of gold. In a previous work we have shown that the interaction of an intense laser pulse with such μ-bars results in the emission of two beams of MeV-level electrons with a narrow opening angle43. Numerical simulations revealed that these beams consist of trains of attosecond-duration electron bunches, emitted because of the diffraction of the fields around the target. These bunches interact with the laser field over large distances in vacuum, resulting in non-trivial dependence on the focusing geometry44.

Results and Discussion

Experiments

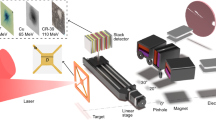
The irradiation geometry (see Methods) is illustrated in Fig. 1a. We irradiated d = 0.2 μm thick, w = 2–10 μm wide μ-bars using 27-fs long p-polarized laser pulses with 120 mJ of energy. These pulses were focused to a 3.5 μm diameter spot, corresponding to a normalized laser amplitude of a0 = 4.6. A scanning electron microscope image of one such target is shown in Fig. 1b. See the Methods section for details about how the μ-bars were fabricated.

Fig. 1: The irradiation setup.
figure 1

a Illustration of the irradiation geometry. Laser pulses focused to a 3.5 μm diameter spot, corresponding to a normalized laser amplitude of a0 = 4.6 were used to irradiate d = 0.2 μm thick, w = 2–10 μm wide μ-bars. The emitted protons were detected downstream using a magnetic spectrometer. b SEM image of a w = 5 μm wide μ-bar suspended over a gap in a Si substrate.

Full size image

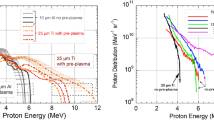
The energy spectra of protons emitted at the laser propagation direction were measured using a Thomson parabola type ion spectrometer (TPIS)45 described in detail in the Methods section. The resulting differential proton spectra for flat foils (black) and μ-bars (w in a color scale) are shown in Fig. 2a. Each curve represents the result of a single irradiation experiment. Two raw spectrograms are shown in insets for an irradiated reference 0.2 μm thick Au foil and a d = 0.2 μm thick, w = 1.8 μm wide μ-bar. The increased signal around the zero-point results from the electron jets that we studied in ref. 43, impinging on the spectrometer wall. The irradiation of narrower μ-bars feature higher proton cutoff energies, reaching beyond 6 MeV for w = 2 μm.

Fig. 2: The effect of the μ-bar width.
figure 2

a Experimentally measured differential proton energy spectra emitted from d = 0.2 μm thick Au foils (black) and μ-bar targets (color scale). The insets in (a) present example raw TPIS traces resulting from irradiation of a foil target and a w = 1.8 μm wide μ-bar. b Compilation of the proton cutoff energies from experiments of various laser and target parameters, as a function of the laser pulse energy (gray) adapted from ref. 8. The results of this work are shown with the μ-bar width indicated in color. c Simulated differential proton energy spectra for the same experimental parameters as in (a), overlaid with snapshots of the transverse electric field (blue-to-red), electron density (green) and space averaged electron and proton energy (color scale). d–f Measured and simulated proton energy cutoffs, peak-values of the electric field in the sheath, and the cone angles of protons emitted with E > 0.5 MeV plotted vs. w. Systematic uncertainties of 5% and 12% are associated with the fitting procedures of the energy cutoffs and cone angles respectively. g Energy resolved virtual source distribution of the protons and (h) the RMS of the emittance for a d = 0.2 μm, w = 2 μm μ-bar.

Full size image

Figure 2 b presents a compilation of the proton cutoff energies in laser acceleration experiments as a function of the laser pulse energy, adapted from ref. 8 and references therein. Also shown are the results of this study for the irradiation of μ-bar targets, where w is indicated with the same color scale as in Fig. 2a. The figure shows that in a common flat-foil irradiation scenario (gray squares), a laser pulse energy higher than 1 J is required to accelerate protons to the same cutoff energies as we achieved using 120 mJ only.

Numerical simulations

The underlying dynamics were revealed by 3D particle-in-cell (PIC) simulations using the EPOCH46 code (see the Methods section for details). In these simulations, d = 0.2 μm thick μ-bars of various widths were irradiated with p-polarized 800 nm wavelength laser pulses having a 30 fs (FWHM) wide Gaussian temporal profile and 120 mJ of energy. The laser pulses were focused to a spot size of 3.5 μm (FWHM), yielding a normalized laser amplitude of a0 = 4.6. The simulation results are presented in Fig. 2c. The differential proton energy spectra for irradiated μ-bar targets in the same parameter range as in Fig. 2a are shown with the same color scale. Overlaid are snapshots taken at t = 0, 60, and 450 fs, for the cases of w = 10 μm and 2 μm wide μ-bars. t = 0 represents the instant in which the peak of the laser field impinges on the μ-bar. The transverse component of the laser field (Ey) is shown in a red-to-blue color scale, with the electron density superimposed in a green color scale. The w = 2 μm μ-bar is narrower than the laser focus and therefore is transversely immersed in the focal volume.

The experimentally observed increase in the proton cutoff energy for narrower μ-bars is captured by the simulation (Fig. 2d). Figure 2e shows how the increased proton cutoff energies for narrower μ-bars are correlated with the sheath field amplitude (snapshots taken at t = 60 fs). The cone angles of E > 0.5 MeV proton beams emitted from d = 0.2 μm μ-bar targets are plotted in Fig. 2f as a function of w. Both the experiment and the simulation feature an increased divergence of the proton beam for the narrowest (w = 2 μm) targets. This geometric effect occurs when both d and w are smaller than the sheath scale length, which is on the order of microns47, so the sheath no longer maintains the target’s aspect ratio.

For narrow μ-bars, the measured proton energy spectra feature flattening in the low-energy region that is not captured by simulations. Simulating the low-energy tail of laser-accelerated ions remains a challenge48, as it often requires extremely high numbers of computational particles to accurately represent a realistic plasma scale-length, when the spatial resolution is limited by computational constraints49. This spectral flattening may stem from several numerically unresolved physical mechanisms, including fast electrons refluxing through the target that induces oscillating charge separation at the rear surface50; the emergence of ion acceleration mechanisms other than TNSA51; and high sensitivity to the detailed density profiles of surface contaminants52.

Strong sheath fields close to the target may modify the proton trajectories following their emission. This affects the ability of a distant observer to determine the spread of their point of origin (their “source size”). To account for this effect, we obtained energy resolved “virtual” source distributions of the proton beam53 by projecting the proton angle at the end of the acceleration phase back to the target plane. These are shown in Fig. 2g for the case of a d = 0.2 μm, w = 2 μm μ-bar, color-coded by the final proton energy, and features a source size smaller than 4 μm2 for E > 4 MeV protons. The normalized r.m.s. values of the two transverse components of the proton beam emittance are shown in Fig. 2h. These were evaluated as \({{{{{\mathcal{E}}}}}}_{y/z}=(p/mc){\sigma }_{y/z}{\sigma }_{{y}^{{\prime} }/{z}^{{\prime} }}\) where \({\sigma }_{y/z},{\sigma }_{{y}^{{\prime} }/{z}^{{\prime} }}\) are the r.m.s. values of the source beam width and divergence angle in the y and z directions54. The large difference between \({{{{{\mathcal{E}}}}}}_{y}\) and \({{{{{\mathcal{E}}}}}}_{z}\) results from the increased horizontal divergence angle of the proton beam, observed both in the experiment and the simulation. This is another consequence of when the sheath no longer maintains the target’s aspect ratio for narrow targets.

So far we discussed how the lateral dimension w of the target plays a role in increasing the emitted proton energies. The effect of the target thickness d on the proton maximal energy is demonstrated in Fig. 3a; a sharp increase of up to 15% in the proton cutoff energy (blue curve) emerge for d < λ/2 targets. This increase in energy is correlated with an increase in the peak value of the sheath electric field (red curve). Some properties of TNSA may be obtained using a simple self-similar isothermal fluid model55,56 in which the proton cutoff energy is given by \({\epsilon }_{{{{{\rm{cutoff}}}}}}=2{T}_{e}ln[{(\tau +\sqrt{{\tau }^{2}+1})}^{2}]\) with \(\tau ={\omega }_{pi}{t}_{acc}/\sqrt{2e}\). Here Te is the temperature of the hot electron population, tacc is an effective acceleration time, and \({\omega }_{pi} \sim \sqrt{{n}_{e}}\) is the ion plasma frequency. The strong dependence of ϵcutoff on Te ~ 〈ϵe〉 is observed in Fig. 3b where the sheath density and average electron energy were sampled at t = 60 fs, 1 μm behind the rear side of the target. For d = 0.2 μm μ-bars, smaller values of w result in higher electron energies that can account for the higher energy cutoff. However, when reducing d for fixed w = 2 μm μ-bars (Fig. 3c), the electron energies do not increase and the source of the increased proton cutoff energies is found to be the rising sheath density. To identify the origin of this thicker sheath, we separated the electron population according to the surface from which they originated. Figure 3d presents sheath density distributions forming around w = 2 μm μ-bars at t = 60 fs. Electrons that initially covered the plasma gradient at the front (x < 0) of the target are shown on the left, and those that originated from the back side (x − d > 0) are shown on the right. For a target thinner than half the laser wavelength (top, d = 0.2 μm), the laser field may simultaneously pull electrons from both the front surface (to the −x direction) and the rear surface (to the +x direction) and the sheath is observed to be a mixture of front and back electrons. However, when the μ-bar is thicker than half the laser wavelength (bottom, d = 0.6 μm), the sheath is observed to consist of front-side electrons only.

Fig. 3: The effect of the μ-bar thickness.
figure 3

a Proton cutoff energies (blue) and the maximal amplitude of the sheath field (sampled at t = 60 fs, red). b The density and average energy of electrons in the sheath sampled at t = 60 fs for d = 0.2 μm and w = 2–10 μm μ-bars. c Same as (b) for w = 2 μm and d = 0.2 to −1.0 μm μ-bars. d Density distributions of the electron sheath forming at t = 60 fs around w = 2 μm, d = 0.2 μm (top) and 0.6 μm (bottom) μ-bars. Electrons originating from the front side or the back side of the target are shown on the left and right, respectively.

Full size image

The inset in Fig. 2(c) features Coulomb expansion of the electron sheath for a w = 2 μm, d = 0.2 μm μ-bar. The drop in proton energies for thicker targets in Fig. 3(a) indicates that the higher proton energies are indeed due to enhanced TNSA rather than to Coulomb explosion (i.e., not from the target ions accelerating themselves by mutual repulsion), since in the latter case proton energies would rise due to the increased stored charge.

Source properties

One of the strong suites of using μ-bar targets for TNSA we identified is the small virtual source size of the protons. This property sets a limit on the spatial resolution when performing proton radiography, a method used for a range of basic research1 and medical applications57. In TNSA off planar foils the virtual source size is of the order of 10 μm53,58,59, while for μ-bars (Fig. 2g) it was found to be smaller than 1 μm for the high energy part of the proton beam. This advantage is further highlighted by the low transverse z component of the proton beam emittance, plotted in Fig. 2h, which drops well below the values typical to planar foil targets ( ~ 10−3 mm mrad54).

Compared to the common irradiation scenario of flat foils, the widest μ-bars we irradiated (w = 6 μm), produce the same absolute spectrum of protons above E > 1.5 MeV (Fig. 2a). Key properties of the resulting proton beams for the cases of foil targets and w = 2 μm μ-bars (the narrowest we irradiated) are given in Table 1. For μ-bars, the 32% lower proton flux at the laser direction is nearly balanced by the increased emission cone-angle (Fig. 2f), yielding similar total proton numbers in both cases. However, the higher proton energies in the μ-bar case correspond to a  ~ 4 times higher coupling efficiency of laser energy to the proton beam, compared to that of conventional foil targets.

Table 1 Comparison of the flux, number and energy conversion efficiency for protons with energy above 1 MeV, emitted from foil vs. μ-bar targets
Full size table

Cascaded acceleration

The use of micrometric formations as targets for TNSA of ions suggests the possibility of cascaded ion acceleration by sequential irradiation of multiple targets. This method has been attempted using solid foils60,61, but because the numerical aperture in this irradiation scenario is on the order of unity, the separation distance between the two targets must be kept close to their lateral dimension to allow a second laser pulse to fit between the targets. Indeed, the separation between the foil targets in those experiments was on the order of millimeters, resulting in a dispersed proton bunch that is much larger than the sheath of the second target, thus making the secondary acceleration inefficient.

We demonstrate numerically the potential of a cascaded proton accelerator composed of micrometric targets in Fig. 4. Two d = 0.2 μm μ-bars are positioned parallel to their w = 2 μm sides, with a separation of 6 μm between them. The targets are irradiated at a 45∘ angle of incidence with two laser pulses, having the same parameters as in the simulations presented in Fig. 3, with the laser energy distributed evenly between them. The second pulse is delayed by Δt = 200 fs with respect to the first, so an electron sheath forms around the second μ-bar at the time of arrival of  ~ 4 MeV protons emitted from the first target. The position of the second μ-bar is chosen at the minimal separation in which the intensity of the first pulse would not induce a sheath around it prematurely, taking advantage of the increased divergence of the proton beam discussed above. Figure 4a shows four snapshot of the transverse component of the laser field (red-to-blue), electron density (green), and the space-averaged proton energy (color scale). The final snapshot demonstrates how the sheath around the second target further accelerates those protons to energies of over 8 MeV. The resulting differential energy spectra of the emitted protons are shown in Fig. 4b. It is also compared to two identical simulations in which the second pulse arrives too early (Δt = 190 fs) or too late (Δt = 210 fs), resulting in lower proton cutoff energies.

Fig. 4: 3D PIC simulation of a cascaded proton accelerator based on the irradiation of two μ-bars.
figure 4

Each μ-bar was irradiated with a 25 fs long, 60 mJ laser pulse at a 45∘ angle of incidence. The second pulse follows the first one with a Δt = 200 fs delay. a Snapshots of the transverse component of the electric field (Ey) are shown in a red-to-blue color scale, with the electron density overlaid in green and the space-averaged energy of protons in a color scale. At t = 240 fs, protons that were emitted from the first μ-bar are observed to be further accelerated by the sheath of the second μ-bar to energies above 8 MeV. b The resulting differential proton energy spectra from the simulation shown in (a) compared to simulations with shorter (Δt = 190) or longer (Δt = 210) delays between the two pulses. The spectra are also compared with those resulting from the irradiation of a single μ-bar with a 25 fs long laser pulse of 60 or 120 mJ.

Full size image

In comparison to the double-foil target experiments discussed above, we may consider for example, a beam of protons emitted from the first target with energies close to 5 MeV, and a 1 μm thick sheath prevailing for 50 fs of effective acceleration time56 around the second target. A 6 μm separation distance will correspond to effective acceleration of 5 ± 0.64 MeV protons, while a 1 mm separation distance will only accelerate protons arriving within 5 ± 0.004 MeV. Target assemblies consisting of multiple μ-bars having set separation distances on the μm scale can be realized using photolithography-based micromachining10. Realization of two foci that are a few μm apart, with a controllable relative delay, can be achieved by spatially dividing the beam into two parts before the final focusing optics, with one part having an adjustable relative angle and front-facing position62. Such an optical manipulator is simple and compact, but it comes at the cost of reduced intensity due to the inherent astigmatic focusing of one of the beams. Alternatively, an astigmatic system can be realized by expanding the beam to a sufficiently large diameter such that different spatial parts of the focusing beam can be steered with the desired relative delay, while keeping the fluence below the optical damage threshold of the optics.

For a given μ-bars separation distance and Δt chosen under the considerations above, the energy gain of protons injected at time tin with respect to Δt to the rear sheath field of the second μ-bar, can be evaluated in the isothermal plasma expansion approximation55: \({m}_{p}v\frac{dv}{dx}=eE(x,{t}_{in})\approx 2{k}_{B}{T}_{e}/(x+{c}_{s}{t}_{in}+\sqrt{2}{\lambda }_{D})\). Here, mp is the proton’s mass, v and x are its velocity and position with respect to the rear surface, λD is the Debye length, and cs is the ion sound speed. For simplicity, we assumed above that the sheath field is quasi-static during the proton’s interaction (i.e., “frozen” at time tin). Separation of variables (x and v) and integration of both sides of the above expression yields: \(\Delta {{{{\mathcal{E}}}}}=\frac{1}{2}{m}_{p}({v}_{\infty }^{2}-{v}_{in}^{2})=2{k}_{B}{T}_{e}\ln \left(\frac{2{c}_{s}{t}_{{{{{\rm{in}}}}}}+\sqrt{2}{\lambda }_{D}}{{c}_{s}{t}_{{{{{\rm{in}}}}}}+\sqrt{2}{\lambda }_{D}}\right)\), where we assumed that the sheath field extends only up to the ion front at x ≈ cstin. This implies an energy gain linear in tin at early times (cstin ≪ λD), \(\Delta {{{{\mathcal{E}}}}}\approx \sqrt{2}{k}_{B}{T}_{e}{c}_{s}{t}_{in}/{\lambda }_{D}\), and asymptotic at late times (cstin ≫ λD), \(\Delta {{{{\mathcal{E}}}}}\approx 2\ln (2){k}_{B}{T}_{e}\).

Practical aspects

A few practical aspects in the irradiation of μ-bar targets need consideration. First, unlike planar targets which are transversely larger than the focus dimensions, μ-bars are more susceptible to intensity drops resulting from the pointing instability of the laser system. Second, while proton production targets in the form of massive rotating disks63, spooled tape64, and jets of liquids, gases, and molecular clusters65,66,67,68 demonstrated target replenishment with Hz – kHz rates, systems designed to deliver micromachined targets mounted on either whole wafers10 or small chips69 operate at sub-Hz rates only and their ability to position targets with submicrometer accuracy in the transverse direction has yet to be demonstrated. The results presented here should motivate the development of liquid jets producing replenishing targets that are bound and stable in the transverse direction within the μm scale.

Targets having a large surface covered with micrometric formations19,20,21,25,26,37,38,40 are naturally more resilient to the laser’s miss-pointing making them simpler and faster to align. This advantage is shared also with many other target designs which manipulate laser absorption to enhance TNSA16,17,18. However, the stochastic nature of the overlap between their micrometric features and the laser field results in an inherent shot-to-shot variability of the accelerated ions. Beyond the increase in the proton energies and the reduced source-size reported here, single-formation targets like μ-bars and levitated spheres41 unveil the interaction dynamics in a straightforward manner by allowing parametric scans over their geometrical features.

Finally, understanding the sensitivity of the acceleration to the intensity of precursor light is paramount to evaluating the scalability of our findings to larger laser systems. This future study will be conducted through time-resolved plasma interferometry of the target’s pre-expansion.

In summary, we discovered that the interaction of an intense laser pulse with an object whose dimensions are transversely immersed in the focal volume and thinner than half the laser wavelength results in enhanced TNSA. The smaller target dimensions provide a small virtual source size and very low emittance. By irradiating 2 μm wide, 0.2 μm thick gold bar targets with 120 mJ of laser energy, we accelerated protons to over 6 MeV, which is three times higher than those obtained with a conventional planar foil target. We note that for the acceleration of ions heavier than H+, other methods such as the Coloumb explosion of molecular clusters68 were able to generate even higher ion energies using the same laser pulse energy.

This irradiation scheme makes possible cascaded acceleration by irradiation of multiple targets with micrometric spacing, which could provide even higher proton energies and optical means to control their spectrum.

Methods

Target fabrication

The targets were free-standing Au bars suspended over rectangular openings in a 250 μm thick Si wafer support. The fabrication process started with a Si wafer pre-coated on its front with a 200 nm thick layer of high-stress Si3N4. The back side of the wafer was spin-coated with layers of resist (MicroChem SF9) and photoresist (MicroChem AZ-1518), on which 3.0 mm × 0.4 mm rectangular gaps were photo-lithographed. The Si was then etched in a 30% KOH solution at 90 °C. The process stopped spontaneously when the inner surface of the front side Si3N4 was exposed. Next, the Si3N4 side of the wafer was spin-coated with layers of the same resist and photoresist. 1.7–10.5 μm wide rectangular openings, which would form the micro-bars, were photo-lithographed over the gaps. The wafer was coated with a 10 nm thick Ti adhesion layer and a 190 nm thick layer of Au. The Si3N4 around the bars was removed by reactive ion etching and immersed in Acetone. Finally, the remaining Si3N4 layer below the Au bars was removed by dry-etching. Illustrations of parts of the process are given in ref. 10.

PIC simulation

We used the fully relativistic EPOCH PIC code46 to carry out the simulations. In these simulations, d = 0.2 μm thick μ-bars of various widths were irradiated with p-polarized 800-nm wavelength laser pulses having a 30 fs (FWHM) wide Gaussian temporal profile and 120 mJ of energy. The laser pulses were focused to a spot size of 3.5 μm (FWHM), yielding a normalized laser amplitude of a0 = 4.6. The 3D simulation space was defined as a (32 μm)x × (20 μm)y × (24 μm)z box divided into (1000)x × (1000)y × (150)z computational mesh cells. We conducted one computationally heavy simulation with a high resolution of (8000)x × (3000)y × (300)z cells to verify the consistency of the results.

The focused laser intensity is sufficient to ionize the target to charge states of up to  ~ Au40+ 70. In the simulations presented in this paper, the bulk of the targets was representative of Au20+ ions and electrons with densities of 30 and 20 × 30 times that of the critical plasma density, respectively. The targets were surrounded on all sides by an exponential density gradient with a scale length of λ/60. This evaluation relies on findings of ref. 71 which studied proton emission from ultrathin Au foils irradiated with similar laser intensity and temporal contrast. Using a simple sonic-expansion model they estimated a scale length in the range of 20–70 nm, which yielded minimal modifications to the resulting proton spectrum. Rerunning the simulations with initial ion charge states in the range of Au4+–Au40+, and with a pre-plasma scale length in the range of λ/80 – λ/40, resulted in an overall shift of the proton energies by a factor of 0.88–1.24, but the dependence on w remained unchanged. Following the results of this sensitivity test, dynamical treatment of the ionization was not simulated to reduce computational load.

An external contaminate layer composed of H+, C4+, and O4+ ions in equal parts was set with a uniform density 30 times that of the critical plasma density over a thickness of 0.1 μm72. The distribution of the composition of the target along the long dimension of the μ-bar was uniform over the range of ∣z∣ < 5.5 μm.

Experimental setup

27 fs long laser pulses of central wavelength λ = 800 nm, with energies of 120 mJ (on-target) and pulse contrast better than 1011 before t = −60 ps73, that are polarized along the width (w) of the bar, were focused using an f/2.5 off-axis parabolic mirror unto d = 0.2 μm thick and w = 2–10 μm wide μ-bars. 70% of the laser energy was measured to be contained within a circle of 3.5 μm diameter, corresponding to a normalized laser amplitude of a0 = 4.6. The laser pointing stability was measured to be 0.43 μm (RMS). See 2nd and 3rd order autocorrelation trace measurements, and a measurement of the focal spot in low power in Fig. 5.

Fig. 5: Laser pulse characterization.
figure 5

a The laser’s temporal profile measured with a sequoia third-order autocorrelator (Sequoia HD, Amplitude Tech.). b The measured (white) and simulated (red) profiles of the focal intensity, overlayed over an x100 magnification image of the focus taken at low-power, with the same scale as the r axis. c The measured (black) and simulated (red) profiles of the laser pulse duration. The measured trace was obtained using a 2nd order autocorrelator.

Full size image

We recorded ion spectra using a TPIS with a similar design to that of Morrison et al.45, operating with an electrode voltage difference of 2 kV. The spectrometer aperture was set to accept ions arriving at a solid angle of 3.56 μsr around the laser propagation direction. A charge-coupled device imaged a CsI(Tl) scintillator74 positioned at the end of the spectrometer. This type of scintillator is very suitable for laser-based particle acceleration experiments, as it is very bright both for MeV-level electrons75 and ions10, and its peak emission is in the visible spectrum (540 nm). Calibration of the position along the parabolic trace of the protons to absolute energy was obtained by taking shots with parts of the scintillator covered by foil filters of known thickness and composition. Figure 6, presents raw TPIS traces for irradiation experiments under identical conditions, for cases in which the scintillator was (a) uncovered, (b) covered with a 11 μm thick Al foil, and (c) covered with a 6 μm thick Ti foil. The edges of the filter foils are indicated by a dashed frame. Using calculated punch-through energy values of protons for each of the filters76, 0.85 MeV for 11 μm thick Al and 0.65 MeV for 6 μm thick Ti, each measurement provides one absolute energy calibration point. We calibrated the conversion of the scintillation signal to an absolute proton dose value by recording spectrometer traces using image plates10,77.

Fig. 6: Position-to-proton-energy calibration.
figure 6

Raw images of TPIS traces for irradiation experiments under identical conditions, for cases where the scintillator was a uncovered, b covered with a 11 μm thick Al foil, and c covered with a 6 μm thick Ti foil. The dashed frame indicates the position of the filter.

Full size image