Introduction

Flat band systems have led the way in exploration of unconventional phenomena in quantum materials with discoveries of superconductivity, spontaneously generated symmetry broken states and heavy fermion physics, most notably in graphene heterostructures1,2,3,4,5,6,7. The unique properties of these systems are driven by strong correlations among slow moving electrons and non-trivial winding of Bloch wavefunctions1,8. In superconductors, this has led to a quantum geometric origin of supercurrent with topologically bounded superfluid weight9,10,11 and coherence length12,13, simulating great interest in flat band superconductivity. However, despite the great interest in these systems, their nonequilibrium properties have only just begun to be explored14,15.

Here, we consider the effect of microwave radiation on superconducting order in flat bands, and in particular show it is possible to use microwave radiaiton to realize a dramatic nonequilibrium enhancement of superconductivity in flat band materials. In conventional superconductors, microwave-enhanced superconductivity was first discovered by Wyatt16 and Dayem17 and elucidated theoretically by Eliashberg18,19, with later refinements by others20,21,22,23,24,25,26,27,28. This counter-intuitive phenomenon can be understood as radiation boiling off thermally available quasiparticles from the superconducting gap edge, driving them to higher energies where their effect on superconducting order is less detrimental. This is known to occur via radiative absorption of microwaves determined by the Fermi velocity, vF of the electrons. It is most pronounced near the critical temperature Tc, given the near phase transition sensitivity and abundant availability of quasiparticles.

In this work we will extend this idea to flat band superconductors and, in particular demonstrate a distinct route towards nonequilibrium superconductivity in which quantum geometric effects play a central role. Our key result is that despite vanishing vF in flat bands, an effective microwave absorption channel in flat bands is enabled by virtual transitions to proximal bands due to cooperative effect of quantum geometry and disorder, see Fig. 1. We demonstrate this inelastic radiative scattering and corresponding microwave enhancement of superconductivity in 1D toy model, and twisted bilayer graphene (TBG), a promising candidate material. With these demonstration we note that superconducting order enhancement is most pronounced (i) near Tc due to availability of abundant thermal quasiparticles (ii) in non-isolated flat bands with large quantum geometry and (iii) in flat bands with sufficient bandwidth allowing sufficient phase space for inelastic radiative scattering. In TBG, we find that a large superconducting gap enhancement of nearly 20%, larger than recently reported values in pump-probe set ups29,30,31 and cavity systems32, may be achievable even at moderate drive strengths due to large microwave-frequency dynamical phase space and pronounced quantum geometry in moiré flat bands. We anticipate such nonequilibrium properties could be readily observed with state-of-the-art microwave circuits, as developed in ref. 33 and recently applied to twisted graphene multilayers34,35.

Fig. 1: Microwave enhancement of superconductivity in flat band superconductors governed by quantum geometry.
figure 1

a A microwave circuit with flat band superconductor for which we have picked twisted bilayer graphene (TBG). b When the superconductor is driven at subgap frequencies the quasiparticle spectrum is cooled-off at band bottom as thermally available quasiparticles are excited to higher energies via inelastic radiative scattering where momentum exhange is provided by disorder. In particular for flat bands, the nonequilibrium excitations are achieved via virtual transitions to proximity bands which are captured in quantum geometry. c The quantum geometric origin of nonequilibrium dyanmics in flat band superconductors is revealed by disorder corrected velocity vertex from where we can obtain the absorption determined by weighted interband quantum connection, see Eq. (7).

Full size image

Results

Nonequilibrium flat band superconductivity

To describe nonequilibrium superconductivity in flat bands, we start by considering a general multiband system which hosts at least one flat Bloch band. The corresponding Hamiltonian satisfies \({\hat{{\mathcal{H}}}}_{{\bf{k}}}{\psi }_{\alpha {\bf{k}}}={\epsilon }_{\alpha {\bf{k}}}{\psi }_{\alpha {\bf{k}}}\) for Bloch state ψαk at energy ϵαk. The superconducting order can be described within the mean-field picture. Assuming SU(2) spin-rotation and time reversal symmetries, we write the Bogoliubov-de Gennes (BdG) Hamiltonian

$${\check{H}}_{{\bf{k}}}^{{\rm{BdG}}}=\left(\begin{array}{cc}{\hat{{\mathcal{H}}}}_{{\bf{k}}}-\mu &{\hat{\Delta }}_{{\bf{k}}}\\ {\hat{\Delta }}_{{\bf{k}}}^{\dagger }&-{\hat{{\mathcal{H}}}}_{-{\bf{k}}}^{T}+\mu \end{array}\right).$$
(1)

where μ is the chemical potential and \({\hat{\Delta }}_{{\bf{k}}}\) is the superconducting gap. Here we distinguish between matrices in Bloch (indicated by a hat \(\hat{\cdot }\)) and Nambu (indicated by a check \(\check{\cdot }\)) space, and use the units where ℏ = kb = c = e = 1. For brevity, we assume s-wave pairing trivial in orbital and band basis, i.e., \({\hat{\Delta }}_{{\bf{k}}}=\Delta \hat{1}\). This implies \([{\hat{\Delta }}_{{\bf{k}}},{\hat{{\mathcal{H}}}}_{{\bf{k}}}]=0\). In this case, \({\check{H}}_{{\bf{k}}}^{{\rm{BdG}}}\) can diagonalized for each band separately to give \({\check{H}}_{{\bf{k}}}^{{\rm{BdG}}}{\chi }_{\pm \alpha {\bf{k}}}=\pm {E}_{\alpha {\bf{k}}}{\chi }_{\alpha \pm {\bf{k}}}.\) The energy eigenvalues are characterized by \({E}_{\alpha {\bf{k}}}=\sqrt{{({\epsilon }_{\alpha {\bf{k}}}-\mu )}^{2}+| \Delta {| }^{2}}\), and the Nambu spinor is written as \({\chi }_{\alpha +{\bf{k}}}={({u}_{\alpha {\bf{k}}},{v}_{\alpha {\bf{k}}})}^{T}\otimes {\psi }_{\alpha {\bf{k}}}\), whereas \({\chi }_{\alpha -{\bf{k}}}=i{\check{\tau }}_{2}{\chi }_{\alpha -{\bf{k}}}\). Here, \({\check{\tau }}_{a}\) is the Pauli matrix in Nambu space and \({u}_{\alpha {\bf{k}}},{v}_{\alpha {\bf{k}}}={[\{1\pm ({\epsilon }_{\alpha {\bf{k}}}-\mu )/{E}_{\alpha {\bf{k}}}\}/2]}^{1/2}\). We fix μ in flat band α, and the superconducting gap can be determined self-consistently using the gap equation

$$\frac{\Delta }{g}=\sum _{{\bf{k}}}\frac{\Delta }{2{E}_{\alpha {\bf{k}}}}\left[1-2{f}_{\alpha {\bf{k}}}\right],$$
(2)

where g is the coupling constant and fαk is the distribution of quasiparticles which is assumed the same for both spin-species with energy Eαk; β = 1/T with T being the temperature.

In presence of microwave drive, quasiparticles absorb energy and redistribute attaining a nonequilibrium distribution. From quasiparticle density of states \(\sim E/\sqrt{{E}^{2}-{\Delta }^{2}}\) and Eq. (2), one can readily see if the quasipartilce distribution decreases around the quasiparticle band edge, the superconducting gap increases. This is particularly pronounced near Tc, and at subgap frequencies (ω < 2Δ) where disruption of superconducitivity by Cooper pair breaking is avoided.

We determine the nonequilibrium quasiparticle distribution perturbatively such that at leading order \({f}_{\alpha {\bf{k}}}\approx {f}_{\alpha {\bf{k}}}^{0}+\delta {f}_{\alpha {\bf{k}}}\) where \({f}_{\alpha {\bf{k}}}^{0}={(1+{e}^{\beta {E}_{\alpha {\bf{k}}}})}^{-1}\) denotes the equilibrium distribution. Here, δfαk captures the effect of microwave driving, and we obtain it by solving kinetic equation in steady state25. This gives \(\delta {f}_{\alpha {\bf{k}}}={\tau }_{{\rm{in}}}{{\mathcal{I}}}_{{\bf{k}}}^{{\rm{rad}}}\) which for ω < 2Δ is determined by the inelastic radiative scattering from χαk to \({\chi }_{\alpha {{\bf{k}}}^{{\prime} }}\) with transition rate \({W}_{\alpha {\bf{k}}\to \alpha {{\bf{k}}}^{{\prime} }}\), captured by the collision integral

$${{\mathcal{I}}}_{{\bf{k}}}^{{\rm{rad}}}=\sum _{{{\bf{k}}}^{{\prime} }}{W}_{\alpha {\bf{k}}\to \alpha {{\bf{k}}}^{{\prime} }}\left[{f}_{\alpha {{\bf{k}}}^{{\prime} }}^{0}-{f}_{\alpha {\bf{k}}}^{0}\right].$$
(3)

Additionally, δfαk depends on inelastic relaxation time of quasiparticles, τin. We use a phenomenological τin in this work, however, often this is determined by interactions of electrons with phonon heat bath20,21. Additionally, it must be noted that the nonequlibrium dynamics are suppressed for extremely flat bands due to suppresssed \({f}_{\alpha {{\bf{k}}}^{{\prime} }}^{0}-{f}_{\alpha {\bf{k}}}^{0}\). Thus, the optimal phase space for inelastic radiative scattering is accessible for ω < W where W is the bandwidth.

Superconducting gap enhancement

We solve for inelastic radiative scattering in Eq. (3), and demonstrate how it enables microwave enhancement of superconducting gap. However, momentum transfer from microwave radiation is negligible and \({{\mathcal{I}}}_{{\bf{k}}}^{{\rm{rad}}}\) for scattering in the same quasiparticle band would vanish due to momentum conservation. Nevertheless, the momentum conservation can be relaxed due to disorder which is known to be crucial in describing electromagnetic absorption in single-band superconductors36. Thus, it is important to consider the combined effect of microwave drive and disorder.

We first consider the effect of microwave radiation which is incorporated by Peierl’s substitution, \({\bf{k}}\to {\bf{k}}-{{\bf{A}}}_{{\rm{ext}}}{\check{\tau }}_{3}\) for a homogeneous electric field described by vector potential Aext. The Hamiltonian that describes the interaction between microwave radiation and quasiparticles, to linear order in field, is thus

$${\check{H}}_{{\bf{k}}}^{{\rm{rad}}}=-\left(\begin{array}{cc}{\partial }_{{\bf{k}}}{\hat{{\mathcal{H}}}}_{{\bf{k}}}&0\\ 0&{\partial }_{{\bf{k}}}{\hat{{\mathcal{H}}}}_{-{\bf{k}}}^{T}\\ \end{array}\right)\cdot {{\bf{A}}}_{{\rm{ext}}}\equiv -{\hat{{\bf{v}}}}_{{\bf{k}}}\cdot {{\bf{A}}}_{{\rm{ext}}}{\check{\tau }}_{0}$$
(4)

where we have introduced the Bloch velocity operator \({\hat{{\bf{v}}}}_{{\bf{k}}}={\partial }_{{\bf{k}}}{\hat{{\mathcal{H}}}}_{{\bf{k}}}\). Typically, this interaction in the single band limit describes conventional radiation-stimulated superconductivity where the absorption is estimated to go as ~∣vF∣2. This conventional paradigm fails for flat bands as vF → 0, quenching microwave absorption in flat band superconductors. In a multiband system however, this problem is circumvented due to the presence of nontrivial band geometry which gives contributions to the velocity vertex off-diagonal in band-space, as \([{\check{H}}_{{\bf{k}}}^{{\rm{rad}}},{\check{H}}_{{\bf{k}}}^{{\rm{BdG}}}]\ne 0\) in general. Given the pronounced role of quantum geometry in flat band superconductivity, we systematically utilize this in our treatment below.

Next, the disorder is accounted by short-range random impurities \({\hat{V}}^{{\rm{imp}}}({\bf{r}})={\sum }_{j}{V}_{j}\delta ({\bf{r}}-{{\bf{R}}}_{j})\) modelled with a Gaussian-distributed field Vj which satisfies \({\langle {V}_{j}^{2}\rangle }_{{\rm{dis}}}={N}_{{\rm{imp}}}{V}_{0}^{2}\)37. Here, Nimp is the impurity concenteration and V0 denotes the strength of disorder. The disorder then enters in to the BdG Hamiltonian as \({\check{H}}_{{{\bf{k}}}^{{\prime} },{\bf{k}}}^{{\rm{BdG}}}\to {\delta }_{{{\bf{k}}}^{{\prime} },{\bf{k}}}{\check{H}}_{{\bf{k}}}^{{\rm{BdG}}}+\check{{\tau }_{3}}{\hat{V}}_{{{\bf{k}}}^{{\prime} },{\bf{k}}}^{{\rm{imp}}}\).

Finally, we proceed to evaluate the transition rate \({W}_{\alpha {\bf{k}}\to \alpha {{\bf{k}}}^{{\prime} }}\) which can be computed using the Fermi’s Golden Rule as

$${W}_{\alpha {\bf{k}}\to \alpha {{\bf{k}}}^{{\prime} }}=2\pi | {{\bf{A}}}_{{\rm{ext}}}{| }^{2}{\left\vert {\chi }_{\alpha {{\bf{k}}}^{{\prime} }}^{\dagger }{\hat{{\mathbf{\Gamma }}}}_{{\bf{k}}{{\bf{k}}}^{{\prime} }}{\check{\tau }}_{0}{\chi }_{\alpha {\bf{k}}}\right\vert }^{2}\delta ({E}_{\alpha {{\bf{k}}}^{{\prime} }}-{E}_{\alpha {\bf{k}}}-\omega ).$$
(5)

We restrict our treatment to processes which remain in the same band around the Fermi surface α for simplicity. The effective velocity vertex \({\hat{{\mathbf{\Gamma }}}}_{{\bf{k}}{{\bf{k}}}^{{\prime} }}\) differs from \({\hat{{\bf{v}}}}_{{\bf{k}}}\), see Eq. (4), in the presence of disorder. Here, \({\hat{{\mathbf{\Gamma }}}}_{{{\bf{k}}}^{{\prime} }{\bf{k}}}\) is obtained by expanding the Bloch states up to leading order in impurity potential. This yields

$${\hat{{\mathbf{\Gamma }}}}_{{\bf{k}}{{\bf{k}}}^{{\prime} }}=\sum _{\beta \ne \alpha }{\hat{{\bf{v}}}}_{{\bf{k}}}^{\alpha \beta }\frac{{\psi }_{\beta {\bf{k}}}^{\dagger }{\hat{V}}_{{{\bf{k}}}^{{\prime} },{\bf{k}}}^{{\rm{imp}}}{\psi }_{\alpha {{\bf{k}}}^{{\prime} }}}{{\epsilon }_{\beta {\bf{k}}}-{\epsilon }_{\alpha {{\bf{k}}}^{{\prime} }}}+\frac{{\psi }_{\alpha {\bf{k}}}^{\dagger }{\hat{V}}_{{{\bf{k}}}^{{\prime} },{\bf{k}}}^{{\rm{imp}}}{\psi }_{\beta {{\bf{k}}}^{{\prime} }}}{{\epsilon }_{\beta {{\bf{k}}}^{{\prime} }}-{\epsilon }_{\alpha {\bf{k}}}}{\hat{{\bf{v}}}}_{{{\bf{k}}}^{{\prime} }}^{\beta \alpha },$$
(6)

which systematically captures the disorder assisted inelastic radiative scattering in a flat band. Importantly, Eq. (6) reveals virtual transitions to proximal bands, enabled by interband velocity matrix elements \({\hat{{\bf{v}}}}_{{\bf{k}}}^{\alpha \beta }\), highlighting the role of Bloch quantum geometry in multiband systems which is particularly relevant in the case of flat bands, illustrated in Fig. 1b, c. The effective velocity vertex can also be obtained by a Schrieffer-Wolff procedure, as for instance recently developed in refs. 38,39; details are relegated to the Supplementary Note 1. Additionally, the modified velocity vertex for conventional contribution (without virtual transitions) is shown in Supplementary Note 2. We simplify Eq. (6) by utilizing \({\check{\tau }}_{0}\) Nambu channel for radiative scattering, and after disorder average

$${W}_{\alpha {\bf{k}}\to \alpha {{\bf{k}}}^{{\prime} }}=2\pi {N}_{{\rm{imp}}}{V}_{0}^{2}| {{\bf{A}}}_{{\rm{ext}}}{| }^{2}{L}_{{\bf{k}}{{\bf{k}}}^{{\prime} }}{\Phi }_{{\bf{k}}{{\bf{k}}}^{{\prime} }}\delta ({E}_{\alpha {{\bf{k}}}^{{\prime} }}-{E}_{\alpha {\bf{k}}}-\Omega )$$
(7)

where \({L}_{{\bf{k}}{{\bf{k}}}^{{\prime} }}={({u}_{\alpha {\bf{k}}}{u}_{\alpha {{\bf{k}}}^{{\prime} }}+{v}_{\alpha {\bf{k}}}{v}_{\alpha {{\bf{k}}}^{{\prime} }})}^{2}\) is given by superconducting coherence factors determining probability of transition based on energy of quasiparticles. Here,

$${\Phi }_{{\bf{k}}{{\bf{k}}}^\prime }={\left| \sum _{\beta \ne \alpha }i{{\mathcal{A}}}_{{\bf{k}}{{\bf{k}}}^\prime}^{\alpha \beta }+({\rm{h.c.}},{\bf{k}}\leftrightarrow {{\bf{k}}}^\prime )\right|^{2}}$$
(8)

is determined completely by the quantum geometry of Bloch bands captured in weighted interband Berry connection, \({\mathcal{A}}_{{\bf{k}}{\bf{k}}^\prime}^{\alpha \beta } = -i{\hat{{\bf{v}}}}_{{\bf{k}}}^{\alpha \beta }{\psi }_{\beta {\bf{k}}}^{\dagger }{\psi }_{\alpha {{\bf{k}}}^\prime} /({\epsilon }_{\beta {\bf{k}}}-{\epsilon }_{\alpha {{\bf{k}}}^\prime })\), modified by the band overlap \({\psi }_{\beta {\bf{k}}}^{\dagger }{\psi }_{\alpha {{\bf{k}}}^\prime}\) due to the scattering by disorder. As such, this vanishes as \({\bf{k}} \to {{\bf{k}}}^\prime\). We find that the presence of proximal bands prevents the quenching of quasiparticle dynamics even though \({v}_{k}^{\alpha \alpha } \sim {v}_{F}\to 0\) in flat bands and enables microwave-enhanced flat band conductivity.

The transition rate in Eq. (7) along with \({{\mathcal{I}}}_{{\bf{k}}}^{{\rm{rad}}}\) in Eq. (3) can be used to obtain the change in quasiparticle distribution, δfk, given which one can compute the change in the superconducting gap. We obtain the change in superconducting gap in the Ginzburg-Landau regime, T ≲ Tc. For a flat band of bandwidth W

$$\frac{\delta \Delta }{{\Delta }_{0}}\approx {a}_{0}^{-1}\sum _{{\bf{k}}}\frac{\delta {f}_{\alpha {\bf{k}}}}{{E}_{\alpha {\bf{k}}}}$$
(9)

where Δ0 is the superconducting in absence of drive, \({a}_{0}={\nu }_{F}[(T-{T}_{c})/{T}_{c}]\tanh ({\beta }_{c}W/4)\) in the limit gW ≲ 1, and νF is the flat band single particle density of states near the Fermi energy. The details to obtain Eq. (9) are presented in Supplementary Note 3.

Gap enhancement in 1D topoogical bands

To elucidate the physical nature of quantum geometry enabled microwave-enhanced flat band superconductivity, we consider a 1D Su-Schreiffer-Heeger (SSH) model which has local singlet s-wave pairing. This is depicted in Fig. 2a, where we consider a 1D bipartite lattice with nearest neighbor intra- and inter-cell hopping, t+ and t−, respectively. In the ordered basis \(\{| k,A\left.\right\rangle ,| k,B\left.\right\rangle \}\), the systems’s Bloch Hamiltonian is

$${\hat{{\mathcal{H}}}}_{{\bf{k}}}^{{\rm{1D}}}=\left(\begin{array}{cc}0&{J}_{k}\\ {J}_{k}^{* }&0\end{array}\right)$$
(10)

where Jk = t+eika/2 + t−e−ika/2 and a is the lattice constant. The key feature of the Hamiltonian in Eq. (10) is the tunable bandwidth with parameter λ = t−/t+. The band structure for different values of λ is shown in Fig. 2a. Evidently, λ → 0 denotes the flat band condition. Note that intraband, \({v}_{k}^{++}=-2\lambda a{t}_{+}^{2}\sin ka/| {J}_{k}|\), and interband, \({v}_{k}^{+-}=(1-{\lambda }^{2})a{t}_{+}^{2}/| {J}_{k}|\), velocity matrix elements are vanish for λ = 0, 1 respectively; we have used  ± to denote bands with energy ϵ± = ±∣Jk∣. The distribution of \({v}_{k}^{++}\) and \({v}_{k}^{+-}\) in the Brillouin zone (BZ) is shown in Fig. 2b and c, respectively. We note large interband velocity matrix element distributed throughout the BZ for flat band which is in contrast to dispersive bands where interband velocity matrix element is concenterated only around the band edge. Finally, we obtain the the change in superconducting order using Eq. (9) in variation with λ, and compare quantum geometric and conventional contributions. δΔ/Δ0 peaks for narrow bands which have sufficient phase space for scattering. It decreases for dispersive bands (larger λ) due to suppressed v+− in most of the BZ. δΔ/Δ0 decreases for extremely flat bands (smaller λ) due to due to vanishing \({f}_{\alpha {\bf{k}}}^{0}-{f}_{\alpha {{\bf{k}}}^{{\prime} }}^{0}\). In constrast, the conventional contribution grows with increasing λ due to increasing v++. The corresponding δΔ0/Δ in variation with bandwidth is shown in Supplementary Note 4.

Fig. 2: Microwave enhancement of superconducting gap in 1D SSH model.
figure 2

a 1D bipartite lattice with nearest neighbor intra- and inter-cell hoppings denoted by t+ and t− respectively. Here, we show the band structure for λ = 0.1 (blue) and 0.8 (red). (b, c) Distribution of intra- and interband velocity matrix elements, \({v}_{k}^{+\pm }\), for values of λ corresponding to dispersion in (a). Reduced bandwidth implies suppressed \({v}_{k}^{++}\). On the other hand, for narrow bands large \({v}_{k}^{+-}\) is distributed throughout the k-space. d Quantum geometry governed superconducting gap enhancement (green) in comparison with the conventional contribution (magneta). Evidently, δΔ/Δ0 due to quantum geometry peaks for narrow bands with sufficient phase space for scattering. It decreases when bandwidth increases (for larger λ), and is suppressed in extremely flat bands (smaller λ) due to vanishing \({f}_{\alpha {\bf{k}}}^{0}-{f}_{\alpha {{\bf{k}}}^{{\prime} }}^{0}\). The conventional contribution increases with increase in λ due to increasing v++. Here we use μ = u, Δ = 0.1u, ω = 0.05u, T/Tc = 0.05 and set \({V}_{0}^{2}{N}_{{\rm{imp}}}{e}^{2}| {\mathcal{E}}{| }^{2}/(\hslash {\tau }^{-1})=0.03{u}^{3}{a}^{-2}\).

Full size image

Gap enhancement in TBG

We now examine the microwave-enhanced superconductivity in a promising candidate system: TBG. It is a particularly attractive venue for microwave enhanced superconductivity due to the flat bands and strong interactions, with typical values of the interaction strength that can even exceed the bandwidth of the narrow bands. Importantly, near magic angle, superconductivity with Tc ≈ 3K emerges around half-filling and its quantum geometric origin has been verified in experiments12,34.

Guided by this we focus on nonequilibrium superconductivity in near-magic angle TBG around half-filling. We model the electrons in this system using the continuum model, and include modest heterostrain and the effects from hBN encapsulation of the graphene layers40. This produces a set of narrow bands tunable by twist angle, see Fig. 3a. For convenience of the reader, details of the Hamiltonian are included in Supplementary Note 5. For superconducting order, we consider s-wave pairing which has been previously used to account for qualitative properties of TBG superconductivity13,41,42. While the microscopic pairing mechanism for superconductivity in TBG is still debatable, the nonequlibrium paradigm proposed here is valid for nodal-less superconductivity, recently observed in TBG34.

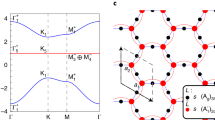
Fig. 3: Microwave enhancement of superconducting gap in twisted bilaye graphene (TBG).
figure 3

a TBG band structure in the moire BZ at various twist angle θ = 1.05° (black), 1.15° (blue) and 1.25° (pink). θ = 1.05° is the magic angle with minimum band width. Here, we include lattice relaxation, hBN encapsulation and strain, and use following parameters (see Supplementary Note 5 for details): tAA = 79.7 meV, tAB = 97.5 meV, δ1 = δ2 = 5 meV, strain = 0.1%. b Variation of superconducting gap enhancement, δΔ/Δ0, with twist angle which is most pronounced at magic angle. We use same parameters as in (a), and chemical potential, μ = 3 meV, inelastic relaxation time τin = 1 ps, \({N}_{{\rm{imp}}}{V}_{0}^{2}=100\) meV2, T/Tc = 0.1, Δ0 = 0.1 meV, ω = 0.05 meV and ∣E∣ = 20 V/cm. c δΔ/Δ0 in variation with tAA (interlayer hopping between same sites) which elucidates the effect of proximity of remote bands. The gap between remote and flat bands is tunable by the relative magnitudes of tAA and tAB (interlayer hopping between different sites). Here we fix tAB as in (a) at magic angle, chemical potential at μ = 5 meV, ∣E∣ = 10 V/cm and vary tAA.

Full size image

We first analyze the effect of bandwidth on quantum geometry determined δΔ/Δ0 in TBG heterostructures. While superconductivity is found only around the magic angle, the twist angle can be used as a knob to tune the bandwidth for illustration. We set the chemical potential in the conduction flat band and numerically investigate the gap enhancement using Eq. (9) in variation with the twist. δΔ/Δ0 is maximum at θ = 1.05° where the bandwidth is minimum and we obtain large δΔ/Δ0 of about 20% for a modest drive strength, see Fig. 3a, b. This is consistent with pronounced optoelectronic THz responses governed by quantum geometry at magic angle43,44,45. To quantify the strength of ∣E∣, assuming an active TBG patch of 50 nm we calculate the corresponding power of around 12 pW for ∣E∣ = 20 V/cm which is consistent with state of the art experiments34,35. Here we have used, \(P={\eta }_{0}^{-1}{{\bf{E}}}_{{\rm{rms}}}\times {\rm{Area}}\) with η0 = 377Ω being the free space impedance and \({{\bf{E}}}_{{\rm{rms}}}=| {\bf{E}}| /\sqrt{2}\). In these calculations, we have modeled the inelastic relaxation of excited quasiparticles by using typical electron-phonon scattering rates in graphene heterostructures (τin = 1ps46). We also comment that the analysis was performed at twist angles at magic angle and above to demonstrate the combined effect of flat dispersion and presence of proximal bands. This is because the increase in dispersion of flat bands below magic angle is accompanied by decreasing gap with the remote bands, and according to Fig. 3 and Eq. (6), δΔ/Δ0 would continue to grow below magic angle. However, the current calculation was contained at mean field level which does not capture the vanishing of superconductivity at angles below magic angle.

Next, we investigate the role of proximal remote bands on the nonequilbrium superconductivity. This is particularly relevant for TBG heterostructures where lab procedures and interactions have been known to cause macroscopic differences in physical properties47,48,49. At a qualitative level, this can be accounted with lattice relaxation effects which can alter the separation between flat and remote bands50,51. Within the continuum Hamiltonian lattice relaxation is parameterized by the ratio between interlayer hopping amplitudes between same and different lattice sites, i.e., tAA/tAB. In Fig. 3c, we fix tAB and show the gap enhancement at different values of tAA. Note that decreasing tAA/tAB reduces the bandwidth of flat bands and pushes remote bands higher in energy (see Fig. S2 for TBG band structure for different values of tAA/tAB). Since, the coherence between energetically far bands is suppressed, we note reduced δΔ/Δ0 for smaller values of tAA revealing the role of proximal remote bands in quantum geometry enabled nonequilibrium superconductivity in TBG.

Conclusion

In this work we have shown that the quantum geometry of Bloch bands in a flat-band superconductor can enable a distinct mechanism for inducing nonequilibrium dynamics, with the potential for dramatic microwave-enhancement of the superconducting gap. Our work underscores the pivotal role of nontrivial Bloch wavefunction winding in flat bands, while also highlighting the role of remote bands, which are particularly relevant in moiré heterostructures, such as TBG. Though we have considered s-wave pairing for brevity, our formalism can be qualitatively generalized to other forms of nodal-less pairings. While we have concentrated on microwave driving by “classical” light, we emphasize that the features of nonequilibrium flat band superconductivity proposed here are likely also relevant to cavity systems wherein the cavity may enable additional control via the quantum nature of light25. Furthermore, the tunablity of correlated phases in flat band systems suggests that such nonequilibrium functionalities can be extended to other correlated phases, e.g., spontanously generated fractional and integer anomalous Hall excitations in graphene multilayers52,53. It is known that microwave driving may have a dramatic effect on the nonequilibrium physics of Landau levels in magnetic field54,55,56,57,58,59,60,61,62,63, and it could potentially be interesting to extend this to strongly interacting Chern bands in moiré materials. Additionally, details involving electron-phonon dynamics64,65,66, strongly-coupled superconducting channels67,68,69 and interaction modified flat bands70 are open directions for future works. From a technological perspective, this can be used for better control and accessibility of the superconducting phase which can be utilized in superconductor devices for sensing of quantum matter.

Methods

The change in superconducting order δΔ/Δ0 for TBG-heterostructure is calculated numerically using Eq. (9) where the change in distribution function under microwave drive is calculated using collision integral in Eq. (3). Two Riemann sums, over \({\bf{k}}^{\prime}\) and k in Eq. (3) and Eq. (9), respectively are calculated over discrete grid in (kx, ky) plane of mBZ. Two sums make the problem computationally heavy for which we choose a grid of 2500 points, and include only two flat bands (conduction flat and valence flat bands) with the corresponding nearest remote bands in our calculation. Further, we choose Δ0 = 0.1 meV and approximate δ-function as a Lorentzian with phenomenological energy broadening of 0.1 meV.