Introduction

Multiphase flow dynamics within opaque and porous 3D materials or devices is a complicated and ubiquitous phenomenon in Nature. Such processes are key to understanding multiphase flow in porous biological and geological media1,2, in the process industry, and in man-made devices such as batteries and fuel cells3. Micro-computed tomography (μCT) based on X-ray radiation has revolutionized 3D imaging of microscopic structures, including porous media, during the last two decades. Dynamic or 4D (i.e., 3D + time) CT denotes imaging of internal structures in objects that change over time. In geosciences, 4D-CT is used to study a wide range of processes, including mechanical deformation of rocks1,4, multiphase flow5,6, the interaction between CO2 and minerals under reservoir conditions7,8, and drainage and imbibition in rocks9. CT reconstruction with high spatiotemporal resolution can give fundamental insights into pore-level events5,10. The importance of CT in medicine is well known, and numerous efforts are made to reduce the radiation dose with shorter exposures while maintaining a high spatial resolution11.

The analytical and non-iterative Feldkamp-Davis-Kress (FDK) algorithm12 offers fast and accurate high-quality CT reconstructions if given sufficiently many projections, making it the standard workhorse for 3D CT image reconstruction13. Note that FDK requires the number of projections to fulfill the Shannon-Nyquist sampling for faithful image reconstruction. Iterative methods, such as the “simultaneous algebraic reconstruction technique” (SART) algorithm14, are also increasingly used, as they facilitate the incorporation of a priori information, at the cost of a significantly increased computational burden. While these iterative methods can reconstruct sparse-view input with reduced artifacts, they unfortunately also tend to reduce the contrast in the reconstructed images. The naive and simplest approach to 4D-CT is to perform a series of independent subsequent 3D CT scans to create multiple time steps. The natural time limitation of this approach is equal to the time it takes to acquire each full tomogram, typically of the order of 1 h1.

Several groups have during the last decades developed methods for fast CT with time resolution on the order of seconds to tens of seconds, using laboratory-based instruments6,15,16,17,18,19,20,21. A common approach is to reduce the number of projections and compensate for the lacking information through prior information or regularization techniques. In several cases, a temporal resolution of about half a minute is reported, often at the expense of image artifacts and reduced spatial resolution.

Using 3rd and 4th generation synchrotron radiation sources22, the beam brilliance is 10–14 orders of magnitude higher than for laboratory sources, facilitating X-ray imaging, microscopy, and CT experiments with high spatial resolution (~nm)23,24, short exposures25, beam coherence opening for quantitative phase contrast23, diffraction contrast26, energy scanning, and nano-focusing. These developments enable subsecond temporal resolution with thousands of radiographic exposures recorded per second. Such sampling frequencies are not possible with current home laboratory technology, owing to photon flux limitations. To achieve 4D-CT with substantially higher time resolution than the second scale, also with synchrotron radiation, the fast-spinning sample approach becomes impractical, and other methods, such as repeated motion10,27, must be invoked.

Machine learning (ML) is a promising way to reconstruct images from sparse-view input, thus enabling a higher temporal resolution. One approach is to use U-Nets28 trained to perform a mapping from a sub-sampled artifact-rich FDK reconstruction to a final image with the characteristic artifacts removed29. U-Nets can also be used for sinogram inpainting where the U-Net is used to learn the mapping from a subsampled sparse-view sinogram to a complete sinogram30. Generative Adversarial Networks (GANs)31 have also been used to reconstruct CT images32,33, often incorporating U-Nets in the generator network. U-Nets are a type of convolutional neural network (CNN), which require extensive training datasets and hyperparameter fine-tuning, and are also prone to hallucinating34. These black-box procedures are effectively uninformed about the (known) physics and constraints of CT.

In the field of computer graphics, novel-view synthesis, denoting the ability to predict views of a 3D scene based on a (limited) number of other camera views, has made great progress in recent years35,36,37,38,39. A key success has been the development of implicit neural representation (INR), a neural network-based continuous functional representation of the object itself35,39. INR-based reconstruction methods promise to have significant advantages over CNN-based reconstruction methods. Most importantly, they are instance-specific, meaning that no additional external dataset is required for training, strongly reducing their tendency of hallucinating. Moreover, INRs have been found to give realistic reconstructions with few artifacts35,40. However, the reconstruction process is iterative and requires guidance by physics modeling.

Inspired by the progress in novel-view synthesis, INR with Fourier features encoding for correctly capturing sharp features37 has been used to represent 3D CT images41. The INR object representation is refined iteratively using a penalty (loss) function based on comparing the physically modeled CT intensity predictions with the actual CT measurements. See also the study by Zheng and Hatzell42. Zha et al. in their 3D INR implementation “Neural Attenuation Fields” (NAF)43 used “multiresolution hash encoding”36 rather than “Fourier features” to decrease the CT reconstruction time by orders of magnitude while further improving the reconstruction quality. For 4D-CT, a parametric motion field can be learned to warp a 3D INR template44, but this approach does not fully utilize the representational power of INR in 4D. We note that time-resolved lensless imaging has been reported40, as well as 4D INRs for novel-view synthesis45,46,47. Arguably, the full power of INR is invoked when the entire collection of harvested experimental data is used as input to model the full duration of spatiotemporal dynamics, rather than a limited subset of the data to reconstruct each time step independently41,48.

To the best of our knowledge, we report the first holistic, fully INR-based dynamic image reconstruction algorithm for time-resolved 4D-CT, coined NeCT for Neural Computed Tomography. Essentially, the measured CT data together with an idealized physics-based model of the CT instrument used for data acquisition are used to train a neural network to represent the object. Specifically, NeCT predicts the key parameter for attenuation-contrast CT, the local attenuation constant μ = μ(r, t) represented as a continuous field in space r = (x, y, z) and time t by a neural network. As we shall discuss, NeCT enables a temporal resolution of the order of seconds in the home laboratory, combined with excellent spatial resolution, suppressed artifacts, and low storage requirements. We demonstrate both sparse-view 3D and 4D reconstructions of high resolution, surpassing previously reported results, and opening avenues for practical use of ML for CT.

Results

INR architecture

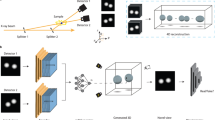
The NeCT pipeline, which consists of three main conceptual parts, is illustrated in Fig. 1. Virtual X-rays are computationally traced from the source through the sample to each pixel on the area detector. Points along each ray are sampled and fed through the neural network, returning the attenuation coefficient field \(\hat{\mu }({{{\bf{r}}}},t)\) associated with each coordinate in space and time. The predicted attenuation coefficients at the points along the ray are summed using Beer-Lambert’s law, giving an estimate of the intensity value \({\hat{I}}_{j}\) for the ray rj that hits the detector pixel j. Finally, the simulated intensity \({\hat{I}}_{j}\) is compared to the measured intensity Ij, and their absolute difference (L1 loss) serves as the cost function. The neural network minimizes this cost through backpropagation, effectively learning the attenuation coefficient field μ = μ(r) for the static case and μ = μ(r, t) for the dynamic case. The network architecture for 3D CT is an improved version of NAF43 (see also Supplementary Notes 3 and 4), optimized for reconstruction of sparsely sampled static 3D structures.

Fig. 1: Overview of the NeCT architecture.
figure 1

a Sampling and intensity comparison. In the illustration, three rays (color coded red, green, blue) propagate from the source, through the object, to the detector. The number of sampled points per ray depends on the length traveled within the object as the distance between each point is set to be constant. b Network block for sparse-view 3D CT image reconstruction, similar to NAF43, with the forward call returning \(\hat{\mu }(x,y,z)\). c Network block for 4D-CT reconstruction, named NeCT QuadCubes. The input data (r, t) is split into 4 separate multiresolution hash encoders, and the feature vectors are concatenated together and sent into a multilayer perceptron (MLP). A forward call to NeCT QuadCubes gives the estimated attenuation coefficient \(\hat{\mu }\) for the space-time position (r, t).

Full size image

Our INR architecture optimized for time-resolved studies, here coined “NeCT QuadCubes”, is inspired by reported efforts to visualize dynamic scenes45,46,47. Formally, our INR is a continuous function \({{\Phi }}:{{\mathbb{R}}}^{4}\to {\mathbb{R}}\). Using four 3D hash encoders instead of either a 3D+4D hash encoder45 or six 2D encoders46,47, can be considered a compromise between a large number of hash collisions and low coupling between the input dimensions in the encoder. The four 3D multiresolution hash encoders, with respective dimensions xyz, xyt, xzt, and yzt, encode the input coordinate and timestamp into a higher dimensional space. The multilayer perceptron (MLP) predicts the attenuation coefficient \(\hat{\mu }({{{\bf{r}}}},t)\) at any desired spatial coordinate and time point.

Conventional cone beam CT proceeds by stepwise angular increments until a complete 360° scan has been performed, giving only marginally new information for each subsequent projection. With the philosophy of harvesting as much complementary information as possible for each new recorded projection, the “golden section” sampling scheme has been proposed49. With golden section scanning, the angular interval between subsequent projection angles is approximately 137.5°. In practice, however, this large angular step has the disadvantage that a significant amount of time is spent on unproductive instrument motor movements. We have thus devised a “hybrid golden section” procedure where a fixed number of equidistant projections (say 25) are collected for each full revolution of the sample, and the golden section is used to decide the starting angle for each subsequent revolution, see also Methods and Supplementary Note 1.

With NeCT QuadCubes, in favorable cases of sufficiently large dynamically changing objects, a temporal resolution approaching the experimental time between subsequent projection acquisitions is achieved. All projections from a dynamic CT experiment comprising multiple sample rotations are used to optimize a single 4D INR object that describes the whole experiment. Using a 4D continuous representation of the object, the algorithm combines the information from all the acquired projections to give the best possible estimate \(\hat{\mu }({{{\bf{r}}}},t)\). Static structures will benefit from the many unique projections to become sharply defined, whereas short-lived features will tend to be less precisely reconstructed as they may be supported by just a couple of projections. Comparisons of NeCT QuadCubes with conventional FDK, demonstrating the large improvement in spatiotemporal resolution, are provided in Supplementary Note 5.

NeCT simulations

Simulations of idealized static 3D sparse-view CT were carried out to benchmark NeCT against the reconstruction schemes FDK12, “ordered subsets - simultaneous algebraic reconstruction technique - total variation” (OS-SART-TV)50,51, and NAF43. For this purpose, several CT datasets were obtained from the Open SciVis Datasets project52. An example of a reconstruction based on 49 projections is shown in Fig. 2a for the Stagbeetle dataset (see also Supplementary Note 4 for several more examples and how the projections are obtained). Using the standard metrics of peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM)53, we demonstrate that NeCT performs better than the competitors for both metrics across all the tested datasets, as illustrated in Fig. 2b.

Fig. 2: Static sparse-view 3D reconstructions.
figure 2

a Panoramic and zoomed sections, and accompanying difference images with respect to the ground truth, are shown for the Feldmann-Davis-Kress (FDK), ordered subsets - simultaneous algebraic reconstruction technique - total variation (OS-SART-TV), neural attenuation field (NAF), and NeCT (our) algorithms. The reconstructions are based on 49 projections of the benchmark Stagbeetle CT dataset52. b Peak signal-to-noise ratio (PSNR) and structural-similarity index measure (SSIM) values for all static datasets are shown. NeCT is seen to outperform the other methods both visually and in terms of PSNR and SSIM for all datasets.

Full size image

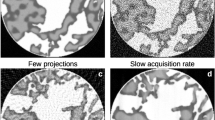
Simulations of dynamic CT, based on 4D datasets of liquid invasion in porous media created with the open source Python package PoreSpy54, were used to estimate the spatiotemporal resolution of NeCT. A slice of the porous rock taken at time T = 0.8, on a normalized time scale ranging from 0 to 1, is shown in Fig. 3. When comparing the ground truth with the reconstruction, there are only small visible differences. The difference image shows that NeCT typically misses by at most 1 pixel when reconstructing the pore boundary edges. Evidently, the dynamic process is almost fully resolved, with NeCT lagging slightly behind the ground truth in a single pore, which happened to be in the middle of a pore-filling event (cf. Supplementary Note 5).

Fig. 3: Simulated porous medium with fluid invasion reconstructed using NeCT.
figure 3

Results at normalized time T = 0.8 are shown. Black = pore w/air, gray = fluid, white=matrix. a Large overview. b–d A region centered on a pore-filling event is shown (the region highlighted in (a)), comparing the ground truth to the reconstruction. There are no errors in the reconstruction except for a few places at the pore boundaries and the highlighted pore. The pore was temporarily in the middle of a pore-filling event and lagged slightly behind the ground truth.

Full size image

In an effort to better understand and quantify the performance of NeCT QuadCubes, we performed two sets of simulations in the same artificial porous framework, with both single on-off and periodically switching domain structures (cf. Supplementary Note 5.3). These simulations demonstrate that NeCT QuadCubes is able to learn periodicity, giving a better resolution for the periodic events. For a cubic domain of size 123 voxels, the dynamics could be discerned if lasting for the time of two projections, and essentially fully resolved if lasting for ten projections.

Dynamic CT of spontaneous imbibition in sandstone

To support the development of NeCT, an in situ dynamic μCT experiment was performed. Rather than a traditional core flooding sequence, a simpler and potentially more dynamic process was selected for this purpose: spontaneous imbibition of brine into a dry porous rock under ambient conditions. Bentheimer sandstone55 is a homogeneous outcrop rock with relatively uniform properties, making it well suited for laboratory testing of multiphase flow. In this study, a cylindrical core sample of Bentheimer, drilled to a diameter of 8.8 mm and a length of 19.6 mm, was used for the dynamic experiments. The permeability of the measured sample was (2.3 ±  0.3) D and the porosity (23.0 ± 2.3)%. The small size of the core plug enabled a μCT setup with the sample placed close to the X-ray source, allowing sufficient geometric magnification for inspecting pore scale effects. The Bentheimer core plug was put in a rubber (VitonTM) sleeve inside an X-ray transparent core holder with an applied confining pressure of about 2 MPa. The sample holder was mounted on the rotary CT stage, with inlet lines for the doped brine supplied by a pump and the confining pressure connected at the bottom of the core holder. To keep the setup simple, no lines were connected at the top of the core holder.

The brine was a synthetic saltwater solution with a concentration of 237 g/L, resembling reservoir conditions. In addition, the brine was doped with CsI (182 g/L) to increase its X-ray attenuation. The pore space of the rock was partially filled with precipitated grains of the salt NaI, to a filling ratio of approximately (20.3 ± 1.0)%, in order to create a richer dynamics with dissolution events to be observed during the brine invasion.

The scanning protocol involved a total of 1400 projections distributed across 14 revolutions using our hybrid golden section sampling scheme, with alternating rotation direction for subsequent revolutions to avoid tangling of the inlet liquid supply lines. After the first full sample revolution of X-ray scanning, the pumping of brine at 5 μL/min was started. Capillary contact between the invading brine and the rock was established during the second rotation. The whole 14-revolution sequence was completed within 40 min, when breakthrough of brine was observed at the top of the core sample. All projections were pre-processed with flat-field and dead pixel corrections. See Methods and Supplementary Notes 1 and 2 for full experimental details.

Because NeCT is a continuous model of the dynamic object represented by its attenuation coefficient in space and time, μ = μ(r, t), explicit 2D or 3D discretized (pixel or voxel-based) instances of the reconstructed object can be realized for any chosen time. Figure 4 gives a sample-scale view with a segmented reconstructed slice of the Bentheimer sandstone 700 seconds into the spontaneous imbibition process (see also Supplementary Movie 1). The areas of highest attenuation are segmented as salt (red), while the difference with respect to t0 was used to segment the incoming brine (blue).

Fig. 4: Segmented dynamic NeCT reconstruction of Bentheimer sandstone, panoramic view.
figure 4

The shown sections are explicitly decoded representations of the NeCT model for the specified times. Black = pore space, gray = matrix, red = salt, blue = brine. a Overview of the full sample at time t2 = 700 s. b–d Magnified view corresponding to the rectangle in (a), at t0 = 0, t1 = 650 and t2 = 700 seconds, respectively. The fluid front is highlighted with broken lines. Scale bars are 2 mm.

Full size image

A detailed visualization of the dynamics in selected regions of the Bentheimer sample is provided in Fig. 5. In low porosity regions, the local attenuation stayed essentially constant with time, as it should in the absence of physicochemical reactions. As the brine front reached and filled open pores, the local attenuation increased. The 4D reconstruction allowed us to investigate the pore-filling events in great detail. In some larger pores, we observed that trapped air bubbles formed when brine entered the pore and wetted the rock surface. Interestingly, NeCT enabled us to directly observe the dissolution of the salt deposits in the sample as the brine front arrived, with a typical dissolution time of the order of 10 s (see also Supplementary Movie 2). CT studies of reactive transport and dissolution are a topic of high current interest; see, e.g., the recent work on carbonate dissolution by Agrawal et al.56.

Fig. 5: Dynamic NeCT reconstruction of Bentheimer sandstone, pore-level view.
figure 5

a, b The filling of an initially empty pore with brine. Note the progressive water invasion leading to a homogeneous filling of the whole pore volume during a time span of about 10 s. c, d A salt grain dissolves, leaving behind an empty pore as capillary forces fail to hold the brine. The dissolution of the entire grain lasted ~30 s. The blue lines in (b) and (d) are NeCT reconstructions, and the red broken lines are error-function fits to the data as described in the legends. Scale bars are 0.1 mm.

Full size image

Note that in both the 3D and 4D NeCT reconstructions, the common CT image artifacts of streaks (arising for undersampled data) and rings (for detector pixel errors)13 are nonexistent (cf. Supplementary Note 5.4). A partial explanation for the smooth appearance of the reconstructions may be that the INR effectively acts as a regularizer by being spectrally biased towards low frequencies37, and presumably also because the information from all the projections is exploited to inform the entire time-span of the model \(\hat{\mu }({{{\bf{r}}}},t)\)40,48. For non-smooth events unfolding over a too low number of projections, NeCT may still yield unphysical solutions to the inverse problem due to the insufficient information provided by the small set of 2D images to fully reconstruct the complete 4D data.

Discussion

Using NeCT, we have successfully repurposed a standard commercially available CT instrument designed for 3D CT scans of typical duration  ~1 hour to enable dynamic “4D-CT” scans with a temporal resolution approaching the time between subsequent projections, i.e., an improvement by 2–3 orders of magnitude as compared to FDK-based reconstruction. This achievement was obtained using a combination of our “hybrid golden section” sampling scheme and the continuous INR representation NeCT QuadCubes of the sample, which exploits all the temporally preceding and succeeding information to concertedly inform the reconstruction at any instance of time. The NeCT architecture is original and has many possibilities for further extensions and improvements. Arguably, NeCT also benefits from being conceptually closer to conventional reconstruction algorithms like SART than to e.g., trained GAN networks, which likely lowers the barrier to user adoption, further convincing us that our approach represents an important step towards new physics-informed measurement methods in the natural sciences.

The capability of resolving 3D movies of events inside an opaque material on a time scale of seconds using home laboratory equipment is a substantial advance of the state-of-the-art in dynamic imaging. Indeed, conventional μCT sampling and reconstruction methods, which give a temporal resolution on the order of an hour, make it practically infeasible to carry out many experiments of high scientific or industrial importance. Many research groups are currently engaged in resolving this challenge, with NeCT providing a continuous representation of the dynamically evolving object on a length scale of micrometers and a time scale of seconds. The spontaneous imbibition experiment with Bentheimer presented in this article revealed dynamics that can currently only be inferred by synchrotron imaging methods.

While significant advantages of the NeCT approach include that the data model is continuous in space and time, does not require external training data, and is memory efficient for storage, these features also come with several limitations that will require significant future efforts to fully understand and mitigate. Most importantly, the spatiotemporal resolution and how the algorithm chooses solutions from solution space are complex questions that require further research. Similarly, the choice of data collection settings, the NeCT hyperparameters, and the training schemes appear to be well-behaved, but their exact influence on the reconstruction performance should be explored further. The long training, i.e., reconstruction times, in particular for 4D datasets, being of the order of tens of hours on advanced graphical processing units (GPUs), can be problematic for some applications. To this end, we envision that perhaps a two-step reconstruction process where a computationally cheaper method, maybe along the lines of van Eyndhoven et al.18 or by Goethals et al.21, can be used to initialize NeCT.

In conventional 4D-CT, the temporal resolution is given by the time it takes to complete each full scan (360°), since each time step is given by an independent reconstruction. This restriction is lifted with the NeCT approach, and because NeCT opens for capturing dynamics with less than a full rotation for each time step, also the fast spinning requirement mentioned in the Introduction is significantly relaxed. Estimating the ability of NeCT to resolve 4D dynamics in space and time is not straightforward. The resolution depends on the sampling scheme, and attention must be paid to the optimization of angular velocity, exposure time, and number of projections per scan. The optimal configuration gathers the most complementary information per time. When reconstructing a 4D model, it is necessary to discuss the spatiotemporal resolution rather than only the temporal resolution. Presumably, the size, location, and type of event will influence the dynamic results, see also Goethals et al.19. Quantifying the exact spatiotemporal resolution and further optimization, performance, and limitations of NeCT are topics to explore in future studies.

In NeCT, the underlying physical model assumes that the X-ray radiation can be described as effectively monochromatic and that scattering can be ignored. These simplifications are commonly made in CT analysis and are known to work well in practice13, as also seen in the current work. Still, it is reasonable to assume that enhancing the physics-based forward model to better capture additional phenomena that can give systematic modifications of the measured signal, such as scattering, polychromatic radiation, and detector nonlinearity, will further improve the reconstructions. Although we have exclusively focused on cone-beam CT in this article, a parallel-beam forward model has been implemented, making NeCT equally applicable to synchrotron and neutron tomography.

An interesting extension of NeCT would be to account for the fact that spectrally (energy) resolved CT is already widely used for medical CT57, and developments are underway for laboratory μCT58. As in the original INR work by Mildenhall et al.35, where three color channels (RGB) are returned for each coordinate, we envision that rather than a single-valued attenuation coefficient \(\hat{\mu }\) from each space-time coordinate (r, t), an energy-dependent \(\hat{\mu }=\hat{\mu }({{{\bf{r}}}},t,E)\) can be foreseen, opening for chemical contrast, see also Wu et al.59. Similar lines of thought apply to the recent developments within tensorial CT, where orientation information about sub-resolution anisotropic texture is retrieved from scattering signals26,60. INR-models could be key to substantially simplifying the heavy data analysis associated with such datasets. Following these ideas, NeCT can be extended to return continuous multi-valued objects for each space-time coordinate (r, t).

Continuous scanning can increase the temporal resolution of CT scanning because the sample is imaged without pause while it rotates at a constant speed, avoiding the angular acceleration and homing at each measurement point1,24. Continuous scanning can provide more information about fast events by recording dynamics that could otherwise take place between exposures. A complication is that continuous scanning inevitably introduces motion smearing because of the constant rotation speed. NeCT can be extended to account for spatial averaging, most directly by approximating each projection angular interval as a series of discrete steps, or by using more elaborate integration schemes. Thereby, the contribution from each point within the object during rotation would be accounted for, potentially further increasing the information harvesting rate and hence the effective temporal resolution of the experiment.

The continuous INR representation of the experimentally measured data is highly storage efficient, allowing complete time-resolved datasets to be represented with just a few GB of data, as compared to several TB of data for the 4D data in conventional voxel representation. Consequently, we envision the sparse sampling and data representation to be a partial answer to the growing demands for data storage in CT experiments. We note that NeCT should be easily adaptable to future improved neural network architectures, which are expected to be developed as a result of the ongoing massive research into artificial intelligence. Similarly, while NeCT has been developed specifically for operating without prior information, incorporating additional data into the reconstruction data is often desirable6,15,40,48. In the context of dynamic CT, such priors could include static high-resolution scans6,15, complementary simultaneous measurements of pressure, temperature, and acoustic emissions, to mention a few.

In summary, NeCT enables dynamic or 4D μCT measurements to be carried out with high spatiotemporal resolution, allowing us to resolve liquid flow in porous media obtained with standard cone-beam CT equipment. Our method is likely to help facilitate laboratory-based measurements of dynamic processes inside 3D structures, which will be of high interest to academia and industry alike.

Methods

Experimental CT acquisition

The dynamic Bentheimer sandstone dataset was acquired at Equinor’s Rotvoll laboratory facility using a North Star Imaging X5000 μCT. The X-ray source was an XRayWorX 225 kV operated at 124 kV and 100 μA with a focal spot of 12.4 μm. The detector was a Varex Imaging PaxScan 2520DX with 1920 × 1536 pixels, with a pixel pitch of 127 μm. The sample was imaged at a source-to-detector distance of 518 mm and a source-to-origin distance of 49.5 mm, corresponding to a conventional voxel size of 12.1 μm. Each radiograph was recorded as an average of 5 exposures, with a total exposure time of 0.42 s. Each full (360°) rotation lasted 165 s.

Raymarcher sampling scheme

The ray marcher was implemented with an equidistant sampling scheme, implying that equidistant points were sampled along each ray within the object. Instead of using a constant number of points per ray, NeCT gradually increases the number of sampled points over time. The number of points per ray n is defined as \(n=\min ({n}_{init}+\lfloor i/j\rfloor ,{n}_{max})\), where i is the number of projections processed, j is the update interval, and ninit and nmax are the initial and maximum number of points per ray, respectively. This adaptive strategy improves reconstruction efficiency by refining the sampling resolution over time. NeCT employs an adaptive number of points per ray, increasing linearly from 100 to \(1.5\times \max ({n}_{{{{\rm{Detector}}}}})\), where \(\max ({n}_{{{{\rm{Detector}}}}})\) denotes the number of pixels along the longest axis of the detector. For the experimental Bentheimer sandstone reconstruction, the maximum was set to be reached after 30% of the reconstruction time.

Hyperparameters

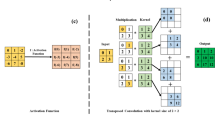
All NeCT reconstructions were made using a single Nvidia A100 or H100 GPU. We have verified that NeCT also works on a multi-GPU setup when NVLink is available. The encoder configuration, used for both NeCT (static and dynamic) and our reproduced NAF results43, consists of a hashmap with 223 entries, 23 levels, a base resolution of 16, and 4 features per level. The MLP has 4 hidden layers, each with 128 neurons. The activation function used is “Leaky ReLU”.

Learning rate scaling

To maintain consistent reconstructions across different batch sizes (B) and number of GPUs used (#GPU), we apply the square root scaling rule61 to scale the base learning rate by the batch size. With the base batch size set to 1 million, the scaling factor becomes \(\sqrt{\#GPU\times B\times 1{0}^{-6}}\), where B represents the batch size.

Optimization

We used a learning rate scheduler that included a linear warm-up phase for the first 5000 batches, followed by a cosine decay schedule with an ending learning rate set at 1% of the initial value after the warm-up phase. The number of training epochs was set at four times the standard value (see Supplementary Note 2.3) in all experiments, except for the Bentheimer sandstone reconstruction, where we used 40 times the standard number of epochs. Although the reconstruction had already converged well before reaching the end, we set the number of epochs this high to ensure that we achieved the best possible reconstruction. We used the Adam optimizer with a base learning rate of 1 × 10−3 for static reconstructions and 2 × 10−4 for dynamic reconstructions. The batch size was set to 5 × 106 points per batch. Finally, L1 loss was used as the loss function in all experiments.