Introduction

Photodissociation refers to the breaking of chemical bonds due to energy absorbed from photons1. It has become a standard technique in photochemical reactions for detaching ligands from coordination complexes and fragmenting supramolecular complexes2,3,4. Additionally, it initiates most oxidation pathways for biogenic and anthropogenic volatile organic compounds in the troposphere5. When coupled with information-rich detection methods, photodissociation can be employed as a type of action spectroscopy to study the structures, dissociation pathways, and spectra of molecules and coordination complexes5,6.

Unveiling the photodissociation branching ratio and its manipulation has long been a focus of photochemical investigations1,7. This interest partly stems from its sensitivity to subtle effects, such as spin-orbit coupling8,9, electronic channel coupling10,11, the isotope effect12,13, roaming dynamics14,15, and others. Consequently, the efficient and precise manipulation of photodissociation becomes vital for applications involving these subtle effects. Changing the radiation wavelength to achieve selective bond-breaking is an effective and enduring strategy10,13,16,17, especially with the use of tunable VUV-FEL facilities18. Vibrational overtone excitation, which can be prepared by infrared (IR) or stimulated Raman excitation, allows for the preferential cleavage of bonds in bond-selected chemistry19. By varying the phases between competing pathways, the products of chemical reactions can be modulated through coherent laser control20. Using aligned or oriented molecules, both selective photoexcitation and directional dynamics have been demonstrated21,22. Nevertheless, these weak-field approaches do not induce any additional physical processes; photodissociation is determined solely by the transition itself.

Advancements in ultrashort and intense laser pulses have provided new physical insights into manipulating molecular dynamics23. The nonadiabatic couplings, which are dynamically modified by IR or THz fields, have enabled the demonstration of dynamic Stark control in nonadiabatic photochemical reactions24,25. Intense IR pulses can couple bound and continuum vibrational states, leading to multi-photon-related nonlinear ionization and dissociation observable in photofragmentation spectra. This includes phenomena such as bond-softening26,27, above-threshold dissociation28, and vibrational trapping29. By creating one-photon or multi-photon light-induced potentials with intense ultrashort IR pulses, the steering of photodissociation dynamics has been successfully observed using a time-delayed probe pulse30,31. Additionally, increasing the intensity of UV pulses for resonant photodissociation can significantly enhance the role of electron-rotation coupling, as evidenced by the angular distribution of photofragments32,33. These unique nonlinear dynamics can efficiently change the molecular dynamics. However, they present challenges for accurate evaluation and pose obstacles for precise selective bond-breaking.

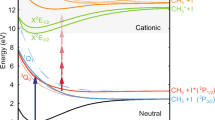
To maintain selective manipulation through weak fields and enable efficient steering via intense pulses, we propose a pump-embedding scenario in which the molecular ground potential is embedded within the dissociative continuum using a UV laser pulse (ωembed) (illustrated in Fig. 1(a)). The overlapping pump UV pulse, with a larger frequency ωpump > ωembed, triggers the transition from the molecular ground state to the continuum. Note that unlike photodissociation induced by the resonant intense pulse involving electronic Rabi flopping34, the non-resonant embedding pulse alone is insufficient to initiate the photoexcitation. It effectively couples the unpopulated vibrationally excited levels of the ground state with the dissociative continuum, resulting in UV pulse-induced vibrational resonances (UIVRs) that are independent of the pump pulse. Note that the current pump-embedding scenario is similar to the schemes used in Raman spectroscopy studies35,36, which focus on passive spectroscopic observations. However, this scenario fundamentally emphasizes the active manipulation of molecular dynamics. In principle, the weak pump with any pulse duration triggering dissociation is viable. In this scheme, a 1 fs short pump pulse with broad energy bandwidth is applied, avoiding the need for repetitive frequency adjustments associated with longer pulses. The 1 fs Gaussian pump pulse (FWHM  ≈ 2.18 eV) centered at 8.25 eV primarily excites the dissociative C1Σ+ state, initiating the fragmentation channel CH+ → C(1D)+H+(1S)37. The energy profile of the reaction probability within these resonances changes dramatically depending on the embedding frequency and intensity. Consequently, the photoexcitation yield can be efficiently manipulated by adjusting the pump wavelength within the resonance. This technique can be further developed to selectively manipulate the branching ratio for desired fragments and pathways, which could be promising for the separation of isotopic molecules.

Fig. 1: Illustration of the pump-embedding scenario.
figure 1

(a) The UV pump (ωpump, gray dashed)-UV embedding (ωembed, red dash-dotted) scenario for a diatomic CH+. The embedding pulse effectively couples the unpopulated vibrationally excited levels of the ground state X1Σ+ with the dissociative continuum C1Σ+, resulting in the formation of UIVRs, which are detected by the pump pulse in photofragment spectra. (b) The pump-embedding scenario in the lowest order of the Floquet frame involves a long embedding field, whose electric envelope couples the lifted potential with the dissociative potential.

Full size image

Below, we demonstrate the proof-of-principle for UIVR on kinetic energy release (KER) spectra using CH+ diatomic and H2O polyatomic molecules as examples. In what follows, the embedding pulse is modeled as a rapid-on and -off trapezoidal pulse, while the 1 fs Gaussian pump pulse overlaps with it (see Methods section). Since the pump pulse sets the time zero of the dissociation dynamics, the remaining time of the interaction with the embedding field is described by τembed. The time-dependent wave functions are propagated using the Heidelberg Multiconfiguration Time-Dependent Hartree package38,39. In the simulations, the intensities of the non-resonant embedding pulse and the weak pump field are insufficient to induce multi-photon processes. The dominant single-photon process does not significantly trigger nonlinear rotational dynamics. The rotational degrees of freedom contribute to the constant coupling matrix element, allowing the system to be reasonably treated with only the vibrational degree of freedom. Actually, the ro-vibrational simulations (see Supplementary Note 1) show quite similar results to those ignoring the rotational degree of freedom.

We start with discussion of a simple CH+ diatomic, allowing to capture clearly a physical picture of the UIVR formation and the concept of photodissociation dynamics manipulation. The embedding UV field couples highly-excited–and thus unpopulated – vibrational states around \(\left\vert \nu =7\right\rangle\) of the ground electronic state X1Σ+ with the vibrational continuum of the first valence excited C1Σ+ state (see Fig. 1a). The short broadband pump pulse ωpump promotes the electron-vibrational ground state molecule to the dissociative excited state C1Σ+ near the UIVR and then the KER is collected. In the case of long pulse duration of the embedding field, we can simplify the picture in the lowest-order Floquet frame schematically shown in Fig. 1(b), where the excited bound potential X1Σ+ + ωembed is achieved by shifting the ground potential and couples the dissociative potential by the electric envelope of the embedding field.

Results and Discussion

KER in embedding pulses

Figure 2 shows the KER spectra for the embedding field intensity Iembed = 1 × 1012 W cm−2 with varied frequency (ωembed=6.05-6.29 eV) and pulse width (τembed=200–800 fs). The simulations are performed using the two-potential system given in Fig. 1a (see Methods section). The gray curves represent the results without the embedding field, where the peaks at 0.53 eV and 0.65 eV correspond to the shape resonance and virtual state of the C1Σ+ potential energy curve, respectively34,37. The effect of UV embedding field changes dramatically the KER profiles and manifests in additional asymmetric spectral structures. These UIVR structures are labeled as UIVRs(ν) in the insets with the energy position \({{{\rm{E}}}}_{\nu }^{{{\rm{UIVR}}}}={{{\rm{E}}}}_{\nu }^{{{\rm{X}}}}+{\omega }_{{{\rm{embed}}}}-{{{\rm{E}}}}_{{{\rm{asymp}}}}^{{{\rm{C}}}}\), where \({{{\rm{E}}}}_{\nu }^{{{\rm{X}}}}\) is the energy of the vibrational level \(\left\vert \nu \right\rangle\) of state X and \({{{\rm{E}}}}_{{{\rm{asymp}}}}^{{{\rm{C}}}}\) is the potential energy of state C at R → ∞. This energy conservation relation shows clearly that the UIVRs position can be manipulated using the frequency of the embedding field ωembed. In the shown spectral range four UIVRs clearly manifest for \(\left\vert \nu \right\rangle =7-10\), whose positions are shifted with the change of ωembed. The UIVR(ν = 8) and UIVR(ν = 7) overlap with virtual state at 0.65 eV for ωembed=6.05 and 6.29 eV, respectively, modifying the peak to a dip and asymmetric profile. In the case of ωembed=6.2 eV, the UIVR(ν = 7) coincides with the shape resonance near 0.53 eV causing splitting and shift of the peak.

Fig. 2: KER spectra in different embedding pulse frequencies.
figure 2

KER spectra for the moderate embedding intensity Iembed = 1 × 1012 W cm−2. Gray curve -- no embedding field, black, blue, and red curves corresponds to τembed = 200, 400, and 800 fs, respectively. a–c correspond to ωembed = 6.05, 6.20, and 6.29 eV), respectively. Labels UIVR(ν) indicates the light-induced vibrational resonance brought by the UV field coupling of the νth vibrational state of the ground state to the continuum. The insets show the local magnification of the spectra.

Full size image

The spectra at a specific embedding frequency but different embedding pulse durations show quite similar structures, but the LIVRs profile becomes slightly sharper. This occurs because a resonance state requires enough time to transition from the discrete channel to the continuum channel to form its natural structure40. The smaller the interaction (or width) correspond to the longer the relaxation time (lifetime). However, the duration of the embedding pulse sets a limit on the maximum time for the relaxation of a resonance state. This will inevitably lead to the broadening for resonances with longer lifetimes. The time window set by the embedding duration also causes the overall modulation in the spectra, making it denser for longer pulses.

The asymmetry of the UIVR profile is very sensitive to the change of the embedding position controlled by ωembed. Indeed, the UIVR(ν = 8) shows a dip at ωembed = 6.05 eV, which transforms into the up-down asymmetric Fano shape at ωembed = 6.20 eV, and becomes a down-up asymmetric profile at ωembed = 6.29 eV. UIVRs(ν = 7, 9) exhibit similar changes of the profile asymmetry with the modification of ωembed. This effect is attributed to the energy-dependent interaction matrix elements TBε and T0ε, resulting in the energy dependence of the Fano asymmetry parameter q41,42. The significant changes observed in the KER spectra within resonances enable highly efficient manipulation of photodissociation. For instance, with an embedding pulse of ωembed=6.2 eV (see Fig. 2b), the spectral intensity around UIVR(8) has increased by approximately a factor of 200. Specifically, the spectral intensities at KER values of 0.793 eV and 0.798 eV are approximately 1.92 and 0.01, respectively, compared to about 0.75 without the embedding pulse.

KER resonance profiles and Fano parameter q

The above behavior can be understood from the long pulse limit solution, using the Floquet frame model (Fig. 1b). The computed dissociation cross section as function of KER and ωembed is shown in Fig. 3a, along with the transition matrix elements TBε and T0ε, and the Fano parameter \({{\rm{q}}}=\frac{{{{\rm{T}}}}_{0{{\rm{B}}}}+{\int}{{\rm{d}}}{\varepsilon }^{{\prime} }{{{\rm{T}}}}_{{\varepsilon }^{{\prime} }{{\rm{B}}}}\frac{{{\rm{P}}}.{{\rm{V}}}.}{\varepsilon -{\varepsilon }^{{\prime} }}{{{\rm{T}}}}_{0{\varepsilon }^{{\prime} }}}{\pi {{{\rm{T}}}}_{0\varepsilon }{{{\rm{T}}}}_{{{\rm{B}}}\varepsilon }}\)41,42 (see Supplementary Note 2). It is worthwhile noting that in the present case of Fano parameter q, the first term T0B=0 due to the forbidden one-photon vibrational excitation, and the whole UIVR effect is explained by the second principal integral term, which becomes strong due to significant energy dependence of the TBε matrix elements (Fig. 3b, c). This is in drastic contrast to the conventional Fano autoionization resonance, where the second integral term is generally negligible since \({{{\rm{T}}}}_{{{\rm{B}}}\varepsilon }\approx {{\rm{const}}}\) in the atomic case, while the first term T0B plays the major role.

Fig. 3: Photodissociation cross section and transition matrix elements.
figure 3

a Photodissociation cross section as a function of the KER and embedding field frequency computed in Floquet frame model (Fig. 1b) with long pulse limit and Iembed = 1 × 1012 W cm−2; (b) The transition matrix elements TBε (left axis) and Fano q parameter (right axis) for UIVR(7); (c) Same as (b) but for UIVR(8); (d) Transition matrix element for the pump absorption T0ε.

Full size image

Figure 3a clearly shows a linear KER dispersion of UIVR with the change of ωembed, as it was discussed above for \({{{\rm{E}}}}_{\nu }^{{{\rm{UIVR}}}}\). The asymmetry of UIVR (ν) profile alters with the change of ωembed, same as it was observed from the full simulations of Fig. 2. This asymmetry change can be explained by the significant energy dependence of the q parameter shown in panels (b) and (c) for \(\left\vert \nu \right\rangle =7\) and 8, respectively. The significant variation and the sign change of q in a limited KER range results in the change of the UIVR asymmetry in full accordance with the Fano formula41,42 (see Supplementary Note 2): the negative and positive q values result in down-up and up-down asymmetric profile, respectively. The observed infinite discontinuities of q profile are due to the fact that TBε = 0 at this energies. Zero transition matrix element TBε means no coupling between the discrete and continuum states, resulting in the absence of UIVR structures (Fig. 3). Symmetric window shape is observed when q ≈ 0, corresponding to the regions where TBε weakly varies thus the numerator of the equation of Fano parameter q becomes zero.

KER in different intense embedding pulses

The effect of the embedding pulse intensity on UIVR formation is illustrated in Fig. 4, where the same model as in Fig. 2 is employed with fixed ωembed = 6.2 eV, when the UIVR(7) coincides with the shape resonance at 0.53 eV. As it shows, increasing the embedding intensity enhances the coupling between discrete and continuum states, resulting in the broadening of the UIVR profile. Additionally, a higher embedding pulse intensity can significantly alter the spectral shape of UIVR structures.

Fig. 4: KER spectra in different embedding pulse intensities.
figure 4

Same as in Fig. 2b with ωembed=6.20 eV, but with variation of the embedding pulse intensity Iembed: a 5 × 1011 W cm−2, b 2 × 1012 W cm−2, c 1 × 1013 W cm−2. The insets show the local magnification of the spectra.

Full size image

When Iembed = 1013 W cm−2, the profiles of UIVR go beyond the Fano picture applicable in the perturbative regime, because of the strong coupling by pulses. Moreover, the increasing of embedding field leads to a distortion and split of the main shape resonance peak at 0.53 eV due to interaction with UIVR(7). At this energy the interaction matrix element TBε takes a sharp maximum (Fig. 3b) that dramatically enlarges the coupling between discrete and continuum states resulting in the field-dependent splitting of the resonance. Indeed, the splitting value increases from 0.031 eV to 0.091 eV with intensity increase from Iembed = 5 × 1011 W cm−2 to 1013 W cm−2. This is a clear indication of Rabi-splitting caused by the strong field interactions. The energy splitting here does not follow directly the Autler-Townes model since the transition matrix element TBε sharply decreases when the KER energy is away from the shape resonance (Fig. 2b). Note that under more intense embedding pulses, the ground molecule may undergo multi-photon ionization or strong field ionization processes. As the current scenario focuses on the coupling effect between discrete and continuum states by embedding pulse, the influence of ionization was not explicitly studied. Future investigations could explore the interplay between these effects.

KER of polyatomic molecules in embedding pulses

To demonstrate the generality of the proposed scheme, the polyatomic molecule H2O is also studied. The simulation uses intramolecular coordinates and including all the vibrational degrees of freedom, both the two O-H stretching modes and H-O-H bending mode. The embedding field couples the unpopulated vibrationally excited levels of the ground state X1A1 with the dissociative continuum \({}^{1}\widetilde{{{\rm{A}}}}(1{b}_{1}^{-1}4{a}_{1}^{1})\) of H2O, while the pump field initiates the photodissociation process H2O → HO + H, exciting the molecule from the ground electron-vibrational state to the vibrational continuum state (see Supplementary Note 4). Note that the dissociation of the electronic state \(\widetilde{{{\rm{B}}}}\) produces complex structures in the high-energy region43, resulting from intricate coupling dynamics. In this scheme, only the purely repulsive state \(\widetilde{{{\rm{A}}}}\) is used to avoid the complex dissociation caused by couplings to state \(\widetilde{{{\rm{B}}}}\) and to highlight the influence of embedding pulse coupling.

The embedding pulses at ωembed = 4.64 (Fig. 5a) and 4.74 eV (Fig. 5b) of duration τembed = 200.0 fs and intensity Iembed = 1013 W cm−244,45 are used in the simulations, and a 1.0 fs UV pump pulse at ωpump = 7.61 eV triggers the transition from the molecular ground state to the dissociative state. The full simulations (Fig. 5a, b), where all three vibrational modes of H2O are taken into account, are compared with that of a single stretching bond model, where one O-H bond and H-O-H angle are fixed at the ground state geometry (the asymmetric-mode of one O-H bond fixed at 1.8 a.u. and the H-O-H angle fixed at 104.5∘). The embedding field-free KER spectra are shown as gray lines in all cases.

Fig. 5: Three-mode and one-mode KER spectra of photodissociation H2O → HO + H by embedding UV pulse.
figure 5

The pulse duration τembed=200.0 fs, intensity Iembed = 1013 W cm−2, and frequency ωembed=4.64 eV (a) and 4.74 eV (b). The KER spectra without embedding field are shown as gray lines.

Full size image

The three-mode calculations show significant modification of the KER spectra by the UIVR structures. Due to higher density of the vibrational excited states in the three dimensional potential energy surface, the UIVR arising from close vibrational levels overlaps, resulting in a more complex KER profile. However, several asymmetric Fano-like structures showing rather strong spectral modulation can still be observed (see vertical dashed lines). For example, the UIVR structure near 2.5 eV in (Fig. 5a) alters the dissociation rate by about three times within a small KER range from about 2.43 to 2.50 eV. With the help of one mode simulations, these structures can be clearly identified as UIVRs resulting from \(\left\vert \nu \right\rangle =7-10\) vibrational levels of the O-H stretching mode. Changing the embedding frequency ωembed from 4.64 eV to 4.74 eV shifts these structures by 0.1 eV according to the dispersion relation of \({{{\rm{E}}}}_{\nu }^{{{\rm{UIVR}}}}\) (Fig. 5b). Note that the UIVR, fully controllable with the help of embedding pulse, allow to decrease or increase the contribution of desirable kinetic energy in the fragmentation process. In a more general sense, this may enable selecting the direction of over-barrier reaction flow in multi-channel photo-chemical reactions with alternative pathways leading to the desired products.

Conclusions

In conclusion, we propose manipulating photodissociation dynamics via embedding UV pulses. In this scenario, a UV pulse with a frequency insufficient for excitation of the molecular ground state but couples the unpopulated excited vibrational levels of the ground bound state with the dissociative state, forming the UIVRs. The overlapping pump UV promotes the ground state molecule to the dissociative state, where the photodissociation probabilities or KER spectra are strongly modified around the UIVRs. With the help of numerical simulations for a single- and multi-mode molecular systems, we show that the profiles of UIVR in continuum can be effectively controlled by the frequency and intensity of the embedding UV pulse.

The key aspect of this scenario is the utilization of resonances to significantly alter the transition probabilities. Since the resonant excitation energy between the vibrationally excited levels of the ground state and the dissociative state lies within the UV region, a frequency-selected UV pulse can effectively mix these states through one-photon coupling, forming fully flexible resonances for manipulation. In contrast, using IR pulses as embedding pulses can lead to unexpected multi-photon excitations and couplings, making selective bond-breaking impossible.

Isotopic molecule separation could be one of the most promising applications. The distinct masses of isotopic molecules lead to different vibrational energy levels, and thus different UIVRs when subjected to the same embedding UV pulse. By using a frequency-tuned pump pulse, we can enhance or suppress the photodissociation probabilities of specific isotopic molecules, thereby achieving effective separation of isotopic molecules or production of desired isotopic atoms/fragments. In a broader context, this scenario may be applied for manipulating photodissociation dynamics, steering the ion-scattering dynamics, and selecting desirable reaction channels in a multidimensional reaction coordinate potential energy surface.

Methods

Computational methods

With the Born-Oppenheimer approximation, the nuclear Hamiltonian of a pump-embedding two-potential molecule can be written as

$${{\bf{H}}}={{{\rm{T}}}}_{{{\rm{v}}}}+\left(\begin{array}{cc}{{{\rm{V}}}}_{{{\rm{X}}}}&{({{{\rm{T}}}}_{{{\rm{embed}}}})}^{{\dagger} }+{({{{\rm{T}}}}_{{{\rm{pump}}}})}^{{\dagger} }\\ {{{\rm{T}}}}_{{{\rm{embed}}}}+{{{\rm{T}}}}_{{{\rm{pump}}}}&{{{\rm{V}}}}_{{{\rm{C}}}}\end{array}\right),$$
(1)

where the first term is the vibrational kinetic operator, the diagonal terms VX and VC represent the potential energy curves/surfaces for the ground bound state X and excited dissociative state C. The off-diagonal terms Tembed and Tpump correspond to the electric dipole interactions by the embedding and pump laser fields, as \({{{\rm{T}}}}_{{{\rm{f}}}}={{{\rm{E}}}}_{{{\rm{f}}}{{{\rm{g}}}}_{{{\rm{f}}}}}({{\rm{t}}}){\mu }_{{{\rm{XC}}}}\cos ({\omega }_{{{\rm{f}}}}{{\rm{t}}})\) (f = {embed, pump}). Ef is the peak intensity of electric field, μXC is the electronic transition dipole moment. A rapid-on and -off trapezoidal envelope gembed(t) is used for the embedding pulse (T=6 fs) as

$${{{\rm{g}}}}_{{{\rm{embed}}}}({{\rm{t}}})=\left\{\begin{array}{ll}{\sin }^{2}(\pi {{\rm{t}}}/{{\rm{T}}})\hfill &0 < {{\rm{t}}} < {{\rm{T}}}/2\hfill \\ 1\hfill & {{\rm{T}}}/2 < {{\rm{t}}} < {{\rm{T}}}/2+{\tau }_{{{\rm{embed}}}}\\ {\sin }^{2}(\pi {{\rm{t}}}/{{\rm{T}}})& {{\rm{T}}}/2 < {{\rm{t}}}-{\tau }_{{{\rm{embed}}}} < {{\rm{T}}}\end{array}\right.$$

A Gaussian envelope with an ultrashort pulse duration of τpump = 1 fs is utilized for the pump pulse represented as \({{{\rm{g}}}}_{{{\rm{pump}}}}({{\rm{t}}})={\exp} (-{({{\rm{t}}}-{{\rm{t}}}_{0})}^{2}/{\tau }_{{{\rm{pump}}}}^{2})\), with a pulse center at t0 = 12 fs in the leading section of the embedding field.

The technique of Complex Absorbing Potential (CAP) is employed to calculate the KER spectra of the dissociative state C from its wavefunction ΦC, as

$${{{\rm{P}}}}_{{{\rm{KER}}}}({{\rm{E}}})=\frac{1}{\pi }\int\limits_{0}^{\infty }\int\limits_{0}^{\infty }\left\langle {\Phi }_{{{\rm{C}}}}({{\rm{t}}})\right\vert {{\rm{W}}}\left\vert {\Phi }_{{{\rm{C}}}}({{{\rm{t}}}}^{{\prime} })\right\rangle {{{\rm{e}}}}^{-{{\rm{i}}}{{\rm{E}}}({{\rm{t}}}-{{{\rm{t}}}}^{{\prime} })}{{\rm{d}}}{{\rm{t}}}{{\rm{d}}}{{{\rm{t}}}}^{{\prime} },$$
(2)

where \(-{{\rm{i}}}W({{\rm{R}}})=-{{\rm{i}}}\eta {({{\rm{R}}}-{{{\rm{R}}}}_{{{\rm{c}}}})}^{3}\Theta ({{\rm{R}}}-{{{\rm{R}}}}_{{{\rm{c}}}})\) is the CAP, with η being the strength. Rc is the point where the CAP is switched on, Θ is Heaviside’s step function39,46.

In the case of a long embedding field, the lowest-order of Floquet frame as a three-potential molecular Hamiltonian is

$${{\bf{H}}}={{{\rm{T}}}}_{{{\rm{v}}}}+\left(\begin{array}{lll}{{{\rm{V}}}}_{{{\rm{X}}}}&0&{({{{\rm{T}}}}_{{{\rm{pump}}}})}^{{\dagger} }\\ 0&{{{\rm{V}}}}_{{{\rm{X}}}}+{\omega }_{{{\rm{embed}}}}&{({{{\rm{T}}}}_{{{\rm{embed}}}}^{{\prime} })}^{{\dagger} }\\ {{{\rm{T}}}}_{{{\rm{pump}}}}&{{{\rm{T}}}}_{{{\rm{embed}}}}^{{\prime} }&{{{\rm{V}}}}_{{{\rm{C}}}}\end{array}\right),$$
(3)

where the off-diagonal is the embedding interaction \({{{\rm{T}}}}_{{{\rm{embed}}}}^{{\prime} }=\frac{1}{2}{{{\rm{E}}}}_{{{\rm{embed}}}}{\mu }_{{{\rm{XC}}}}({{\rm{R}}})\). The photodissociation cross sections from potential VX to the coupled potentials (VX + ωembed and VC) are calculated using Pydiatomic47.

In the analyzing of Fano parameter q (see Supplementary Note 2), the time-independent interaction matrix elements are achieved by integrating the vibrational degrees of freedom as \({{{\rm{T}}}}_{{{\rm{B}}}\varepsilon }={{\rm{X}}}\left\langle \nu \right\vert {\mu }_{{{\rm{XC}}}}{\left\vert \varepsilon \right\rangle }_{{{\rm{C}}}}\) and \({{{\rm{T}}}}_{0\varepsilon }=\,_{{\rm{X}}}\!\!\left\langle 0\right\vert {\mu }_{{{\rm{XC}}}}{\left\vert \varepsilon \right\rangle }_{{{\rm{C}}}}\), where \({\left\vert \nu \right\rangle }_{{{\rm{X}}}}\) is the νth bound vibrational wavefunction of bound electronic state X, \({\left\vert \varepsilon \right\rangle }_{{{\rm{C}}}}\) is the continuum vibrational wavefunction with kinetic energy ε of dissociative electronic state C.

Numerical Simulations

The diatomic CH+ molecule and polyatomic H2O molecule are used as examples to represent the UIVRs on the KER spectra in a embedding field. The X1Σ+ and C1Σ+ states34,37 are coupled by the embedding field for the diatomic CH+ molecule, while the X1A1 and \({}^{1}\tilde{{\rm{A}}}(1{{{\rm{b}}}}_{1}^{-1}4{{{\rm{a}}}}_{1}^{1})\) states44,45 are coupled by the embedding field for the polyatomic H2O molecule, the detailed potential energy curves and surfaces are given in Supplementary Note 3 and Note 4.

The time-dependent wave functions are propagated using the Heidelberg Multiconfiguration Time-Dependent Hartree package38,39. For the simulation of diatomic CH+ molecule, the vibrational degrees of freedom (DOF) is described by 891 sin-DVRs equally distributed in the region of [1.0–90.0] a.u.; 21 basis functions have been used for the rotational DOF β by Legendre polynomials when considering rovibrational excitation. The CAP is applied with η = 3 × 10−5 a.u. and Rc = 80 a.u. For the simulation of polyatomic H2O molecule, the O-H stretching modes DOF is described by 1287 sin-DVRs equally distributed in the region of [1.4-130.0] a.u.; 181 basis functions have been used for the H-O-H bending modes DOF β by Legendre polynomials. The CAP is applied with η = 5 × 10−5 a.u. and Rc = 120 a.u. The total propagation time ensures complete absorption of the disassociated wave packets, and the time step is 0.2 fs.