Introduction

Non-Hermitian physics has remained at the forefront of contemporary research for the past two decades, uncovering a rich landscape of dynamic phenomena with no counterpart in conservative environments1,2,3,4,5,6,7,8,9,10,11,12,13. Among the most intriguing observations is the non-Hermitian skin effect (NHSE), where an extensive number of eigenstates localize at the boundaries of a system, defying the conventional bulk-boundary correspondence observed in Hermitian configurations14,15,16,17,18,19,20,21,22,23,24,25. This effect has opened new avenues for exploring novel topological phases and has profound implications for both theoretical and experimental physics7,14,26,27,28,29,30,31,32.

In classical wave models, such as those describing the harmonic response of optical, acoustic and electronic systems, the NHSE becomes even more intriguing when examined alongside exceptional points (EPs). These points represent critical degeneracies in parameter space where two or more eigenvalues, and their corresponding eigenvectors, coalesce32,33,34,35,36,37,38,39,40. EPs are common in models displaying pseudo-Hermitian features, and are associated with a wide array of novel physical phenomena, including unidirectional invisibility41 and enhanced sensitivity in optical devices42,43. In NHSE systems, EPs can lead to what may be termed a dual singularity, characterized by the simultaneous collapse of both the eigenspectrum and the wave amplitude profile into a single spatial location or port. Such anomalous localization typically requires extreme anisotropy and occurs near the boundaries of the parameter space. For instance, in the archetypal Hatano-Nelson model44, when the ratio of nearest-neighbor couplings κ becomes infinitely asymmetric (i.e., κ21/κ12 â†’ âˆž), the system undergoes a complete spectral collapse into a single exceptional point of maximal order, which equals the system size N45. At this limit, (also referred to as an Infernal Point46,47), the eigenvalues exhibit extreme sensitivity to perturbations, following a characteristic fractional-root dependence on perturbations, scaling as ϵ1/N 48. Finally, when the system is parametrically set exactly at the maximal-order EP, the field amplitude follow a polynomial growth in time or propagation length, with an amplification order of the localized state that scales linearly with N, reflecting the underlying high-order Jordan block structure.

To date, maximal-order exceptional points of the skin-effect type have been predicted only in non-reciprocal models, such as those involving anisotropic couplings49,50. Designing a fully reciprocal system capable of supporting these enhanced degeneracies remains highly challenging, and as a result, existing reciprocal and isotropic Floquet models have been constrained to a limited regime of NHSE localization47,51. For example, certain diatomic lattices have been shown to exhibit edge localization when hosting multiple high-order exceptional points that scale with N52.

In general, Floquet configurations can leverage the interplay between \({{{\mathscr{PT}}}}\)-symmetry5,53,54,55 and Floquet theory56,57,58 to enable novel non-Hermitian designs, unveiling a rich spectrum of phases absent in static settings18,24,25,59,60,61. This naturally raises the question of whether the currently elusive maximal-order NHSE EPs can be realized through a sophisticated integration of Floquet engineering and \({{{\mathscr{PT}}}}\)-symmetry in reciprocal systems. If successful, this could pave the way for a new class of non-Hermitian sensors, harnessing both the extreme sensitivity of higher-order EPs and the pronounced localization of the skin effect. More importantly, it would enable, the observation of this unique interplay in platforms that inherently lack conventional means of reciprocity-breaking, such as waveguide arrays or other classical lattices relying on evanescent couplings.

In response to these challenges, we propose and demonstrate a Floquet model capable of realizing tunable skin localization of arbitrary strength, thereby allowing access to the critical regime of maximal-order NHSE exceptional points. Leveraging the properties of supersymmetric lattices62,63,64,65, we introduce alternating gain and loss in both space and time to create a class of \({{{\mathscr{PT}}}}\)-symmetric non-Hermitian Floquet models capable of exhibiting critical localization. We rigorously prove that EPs of maximum order will manifest at unique periods of the drive, where all eigenstates collapse simultaneously at the Floquet boundary. These Floquet systems demonstrate an unconventional phase transition at a critical coupling strength, delineating a regime characterized by a singular EP collapse and a domain hosting an infinite number of N âˆ’ th order EP solutions. At the transition points, the stroboscopic dynamics reveal a polynomial growth of amplitude at the edge site, a characteristic signature of NHSE EPs.

Results and discussion

Theoretical framework

To develop a model exhibiting high-order NHSE EPs, we apply the principles of \({{{\mathscr{PT}}}}\)–symmetry within a Floquet framework. The evolution dynamics of Floquet configurations, i.e., systems subject to periodic driving, are difficult to analyze directly. Floquet theory tackles this issue by transforming the time-dependent problem into an effective time-independent one, expressed in an extended Hilbert space. In this context, we seek signatures of the NHSE and its EP manifestations within the quasispectra of 1D \({{{\mathscr{PT}}}}\)-symmetric Hamiltonians. The time evolution of such Floquet configurations can be described stroboscopically by the evolution operator

$$U(T,0)={\prod }_{n=1}^{{N}_{F}}\exp \left(i\frac{T}{{N}_{F}}{H}_{{N}_{F}+1-n}\right)$$
(1)

where Hj represents the sequential j âˆ’ th static non-Hermitian Hamiltonian, which remains active for a proportionate time of T/NF, where NF is the number of independent steps over one Floquet period. In turn, the dynamic properties can be captured by the effective Hamiltonian Heff,

$${H}_{{{{\rm{eff}}}}}=-i\frac{\hslash }{T}log(U(T,0))$$
(2)

Non-Hermitian Floquet models that are built on \({{{\mathscr{PT}}}}\)-symmetric principles are known to exhibit signatures of the skin effect, even when the stationary matrices Hj encompass isotropic couplings, tnm = tmn. In these systems, EPs typically manifest when two eigenvalues from different Floquet zones collapse at the Floquet boundary, i.e., at quasienergy  Â± Ï€/T. This condition is satisfied at unique periods of the drive T, giving rise to a rich landscape of second order EPs that are directly tunable via the modulation period. However, one may conjecture that systems of arbitrary size N, could also host skin-effect EPs of higher or even maximum order, while collapsing the entire spectrum into a critically localized eigenstate. We claim that such a scenario would require the simultaneous coalescence of all N eigenstates at the Floquet boundary, a rather demanding prospect.

To address the above question and demonstrate a skin-effect EP of maximally order, we examine a periodic process consisting of two independent steps, NF = 2, involving the static \({{{\mathscr{PT}}}}\)-symmetric Hamiltonian

$${H}_{1} =\,\, \kappa {\sum }_{n=1}^{N-1}\sqrt{n(N-n)}(| n\left.\right\rangle \left\langle \right.n+1| +| n+1\left.\right\rangle \left\langle \right.n| )\\ + i\gamma {\sum }_{n=1}^{N}(N+1-2n)(| n\left.\right\rangle \left\langle \right.n| )$$
(3)

where N represents the total number of elements, and κ and γ the coupling and gain/loss coefficient respectively. This static \({{{\mathscr{PT}}}}\)-symmetric Hamiltonian can be derived using supersymmetric principles63,65 and is known to exhibit an N âˆ’ th order conventional EP at a critical ratio of κ/γ. In the absence of gain and loss (γ = 0), H1 displays equidistant eigenvalues.

The Hamiltonian of Eq. (3) encompasses isotropic couplings and its eigenstates are evenly distributed across the lattice, thus bearing no relation to NHSE models or nonreciprocal localization phenomena. Here, we demonstrate how a modification of this static Hamiltonian into a 2-step Floquet system, transforms the EP into one of the NHSE type, while significantly enriching the system’s response, leading to multiple phase transitions between NHSE dynamical regimes. To this end, we first consider a modulation period T and construct a model governed by H1 from t = 0 to t = T/2 and by its conjugate transpose \({H}_{2}={H}_{1}^{{\mathsf{H}}}\) for the second half of the period. In essence, we employ balanced alternating gain and loss in both space and time.

To obtain the Floquet evolution operator, without loss of generality, we assume γ = 1 and apply equation (1), for NF = 2

$$U(T,0)={e}^{i{H}_{{{{\rm{2}}}}}T/2}\cdot {e}^{i{H}_{{{{\rm{1}}}}}T/2}$$
(4)

Here, we analytically derive the eigenspecta of this Floquet model for a representative case involving N = 4 sites, as illustrated in Fig. 1a. Nonetheless, the results are general and applicable to systems of any size N, as discussed in Supplementary Note 3. In what follows, we will further present an analytical treatment for the N = 5 case and provide numerical results for systems up to N = 50, corroborating fully our theoretical framework.

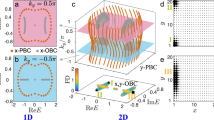
Fig. 1: Four-site Floquet system with periodically modulated gain and loss.
figure 1

a Floquet model featuring four sites with an alternating gain and loss modulation protocol. b Quasispectra of Heff. The exceptional lines are illustrated in red, for κ > 1 as derived from Eq. (9), and in teal for κ ≤ 1. The dashed line and red dot mark the transition between the single-exceptional point (EP) regime and the regime with infinitely many EP solutions. c Floquet quasienergies for κ = 1 and corresponding eigenstates at T = 0.7 and T = 1.5. In the \({{{\mathscr{PT}}}}\)-unbroken regime all four eigenstates become globally localized at the left edge, with their on-site normalized intensities for T = 0.7 and T = 0.5 shown in red color grading below. A non-Hermitian skin effect (NHSE) EP is observed for a T = 2. The red and green curves depict the imaginary and real components of the quasienergy spectrum, respectively, with the dashed lines indicating the Floquet zone boundaries  Â±Ï€/T. The red and green dots correspond to the imaginary and real parts of the fourth-order exceptional point, respectively. d Floquet quasienergy for κ = 1.6 where an infinite set of EP solutions manifest. Yellow and blue shaded areas mark regions of global localization at the left and right lattice edges, respectively. The on-site normalized intensity profiles of all four eigenstates at T = 1.2 are shown below, with red (blue) color grading indicating localization on the left (right) edge.

Full size image

To compute the product of Eq. (4) for N = 4 the Jordan decomposition method is deployed. After applying Eq. (2), the four eigenvectors of Heff are computed analytically. In this respect, the i âˆ’ th normalized eigenvector takes the form

$${{{{\bf{u}}}}}_{{{{\bf{i}}}}}={\left[\begin{array}{cccc}1&f\cdot {g}_{1i}&f\cdot {g}_{2i}&f\cdot {g}_{3i}\end{array}\right]}^{{\mathsf{T}}}$$
(5)

where

$$f=f(\kappa ,T)={\kappa }^{2}{e}^{2iT\sqrt{{\kappa }^{2}-1}}+2{e}^{iT\sqrt{{\kappa }^{2}-1}}({\kappa }^{2}-2)+{\kappa }^{2}$$
(6)

and gli = gli(κ, T) are complex functions associated with the i-th eigenvector having non-zero modulus.

The critical condition for the collapse of the system’s eigenvalues and eigenvectors into the first element, signifying the emergence of an N-th order NHSE EP with singular eigenvector \({{{\bf{u}}}}={\left[\begin{array}{cccc}1&0&0&0\end{array}\right]}^{{\mathsf{T}}}\) for the 4-site case, is given by f(κ, T) = 0. It is important to emphasize that this condition is valid irrespective of the system’s size, considering that coefficient f is not dependent on site index j or N, representing instead a universal model parameter (see in Supplementary Note 3). In this respect, the generalized solution of f(κ, T) = 0 is given by

$${e}^{iT\sqrt{{\kappa }^{2}-1}}=\frac{-2{\kappa }^{2}+4\pm 4\sqrt{1-{\kappa }^{2}}}{2{\kappa }^{2}}$$
(7)

providing a set of points in the (T, Îº) parameter space where the Floquet quasispectra collapse into NHSE EPs.

As evidenced by Eq. (7), depending on the value of κ, the equation can be solved for three distinct cases. In this respect, we identify a phase transition at κ = 1, separating a regime hosting a single EP solution (κ ≤ 1) at a unique value of T, from a domain of infinite solutions (κ > 1) at periodic intervals of T.

At the regime where a single EP is found (κ < 1), the positive-sign solution of Eq. (7) is discarded as it yields a negative period T. Consequently, the value of T where an N-th order EP manifests is derived from the alternate solution

$$T=\frac{-ln(\frac{-{\kappa }^{2}+2-2\sqrt{1-{\kappa }^{2}}}{{\kappa }^{2}})}{\sqrt{1-{\kappa }^{2}}}$$
(8)

For κ > 1, the solutions of Eq. (7) become complex. To solve with respect to the period parameter we proceed by computing the complex logarithm, whose real part equals zero due to Eq. (7) having a modulus of one. Due to the complex nature of the logarithm, it yields periodic solutions with a period of 2π, and thus for each of the two solutions, there is a coupling dependent periodicity of \(\frac{2\pi }{\sqrt{{\kappa }^{2}-1}}\), as can be derived from (9). Consequently, for a given value of κ, an infinite number of NHSE EPs appear at Floquet periods

$$T=\frac{2ta{n}^{-1}(\pm \sqrt{{\kappa }^{2}-1})+2k\pi }{\sqrt{{\kappa }^{2}-1}}$$
(9)

where \(k\in {\mathbb{N}}\). For the critical coupling value of κ = 1, Eq. (7) cannot provide a solution. Therefore, the analysis must be carried out from the beginning, as outlined in Supplementary Note 2. In this case, a single EP manifests at T = 2.

In Fig. 1b we plot the numerically computed eigenvalues of Heff for the 4-site system in the (T, Îº) parameter space. The solutions of Eq. (8) and Eq. (9) define multiple exceptional lines, depicted in red for the infinite solution regime and in teal for the singular solution regime, outlining the points where all 4 quasienergies coalesce at the Floquet Boundary (±π/T). The white dashed line, at κ = 1, demarcates the transition between the two regimes.

Figure 1c illustrates the numerically evaluated quasispectra of Heff at the critical coupling of κ = 1. At T = 0, the 4 quasienergies are symmetrically split around zero. In Floquet systems, an increase in the modulation period typically leads to a collapse of the two outermost quasi-energies at the Floquet boundary (here observed for T = 1), resulting in either a trivial degeneracy or a second-order EP. However, generating an N-th order Floquet EP of the NHSE type is not straightforward. To attain this, our protocol requires all eigenstates to collapse simultaneously at the boundary. Here, the unique spectral properties of Eq. (3) appear to steer the eigenvalues along an optimal trajectory as T increases, leading to their ultimately collapse at T = 2. At first glance, it may appear that two eigenvalues collapse at a positive real value and two at a negative real value. However, this impression is visually misleading due to the Floquet nature of the system, where the quasienergy spectrum repeat infinitely along the vertical axis with a period of Ï€/T (indicated by the black dotted curve). As a result, the apparent negative collapse point is effectively equivalent to the positive one, as it lies precisely on this Floquet boundary. Evidently, in Fig. 1c, this maximal-order EP marks the boundary between a regime where all eigenvalues are real and one where all eigenvalues become complex. In \({{{\mathscr{PT}}}}\)-symmetric systems, this transition is closely associated with the sudden breakdown of pseudo-Hermiticity through a spontaneous breakdown of \({{{\mathscr{PT}}}}\)-symmetry. For T < 2, a closer examination of the local profiles of the 4 eigenstates in Fig. 1c reveals pronounced skin localization at the leftmost element. The strength of localization depends explicitly on T, reaching a maximum critical anisotropy at the EP (T = 2) where the fields collapse entirely onto the leftmost element.

The collapse of the eigenvalues at a maximal-order EP is most transparently illustrated in Supplementary Note 2. In this section, we analytically compute the effective Hamiltonian Heff for this four-site system. Evidently, the effective Hamiltonian is upper triangular, which implies that its eigenvalues are simply the elements of the main diagonal. These diagonal entries all take the value of the Floquet quasi-energy boundary, Ï€/T. Given that the period is T = 2, all 4 eigenvalues are Ï€/2. The appearance of negative values in the Floquet boundary stem mathematically from the complex nature of the logarithm function. Since the complex logarithm is multivalued and periodic with period 2Ï€i, this periodicity translates in our system to an effective periodicity of Ï€/T, thereby explaining the observed structure in the spectra.

Figure 1d depicts a more involved scenario at κ = 1.6 where infinite EP solutions manifest at periodic intervals of T, matching analytical predictions. The regions with broken \({{{\mathscr{PT}}}}\)-symmetry are highlighted with a light gray color. In the regimes where the system exhibits real quasispectra (colored regions), skin localization manifests at the rightmost site of the lattice, near the left EP (blue shaded regions). Conversely, close to the right EP (yellow shaded regions), the eigenstates coalesce towards the leftmost element. Thus, by varying the modulation period T, one can smoothly control both the direction and strength of the effective anisotropy, leading to a complete collapse of all eigenstates at either the rightmost or leftmost element at the NHSE EP solutions.

Dynamics at the exceptional point

The dynamics at an EP exhibit an atypical response that in a Floquet context can be captured by examining the stroboscopic evolution of the system, solving the time-dependent problem \(i\frac{\partial }{\partial t}\left\vert \psi (t)\right\rangle =\hat{H}(t)\left\vert \psi (t)\right\rangle\). At a NHSE EP, excitation of the edge site where the field amplitudes collapse leads to a stable localization of energy throughout the entire duration of stroboscopic evolution. Indeed, this behavior is observed in our 4-site system, at κ = 1 and T = 2, as seen in Fig. 2a, confirming that this fully reciprocal Floquet \({{{\mathscr{PT}}}}\)-symmetric system exhibits a true high-order NHSE EP.

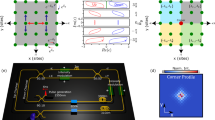
Fig. 2: Dynamical response of the Four-Element System at the Exceptional Point.
figure 2

a–d Polynomial growth at the exceptional point (EP). The amplitude ∣ψ1∣ at the first site is plotted stroboscopically over time when the system is excited independently at different elements, indicated by arrows. The red lines represent the numerical results of the evolution of the time-dependent problem, while the dots correspond to the theoretical solutions. e BPM simulations of a four-site photonic waveguide lattice, excited at individual sites near the EP. In all cases, the optical power is observed to funnel at the leftmost waveguide. The field amplitudes are normalized at each observation step. f Response of the 4-site system at the EP under different excitation conditions, shown as a function of continuous time. Red dots represent the field amplitude at the first site, and black lines show its stroboscopic evolution. In the first case, the amplitude remains constant (c), indicating a stable mode. In the other two, it grows linearly (t) and quadratically (t2) with time, depending on the initial excitation.

Full size image

Figure 2b–d demonstrate the stroboscopic response when energy is injected through elements 2, 3 and 4. When the initial state vector is \(\left\vert \psi (0)\right\rangle ={\left[\begin{array}{cccc}0&1&0&0\end{array}\right]}^{{\mathsf{T}}}\), the dynamic response at the first site exhibits a linear growth with time with a slope of \(2\sqrt{3}\). For excitations at elements 3 and 4, the dynamic response exhibits a quadratic and cubic growth, respectively, with polynomial coefficients indicated in the figure. While this behavior is typical for higher-order NHSE EPs (see Supplementary Note 1), to understand it in the context of our Floquet system we must transition again into the picture of the effective Hamiltonian Heff. As analytically derived in Supplementary Note 2, at κ = 1 and T = 2, the effective Hamiltonian takes the form

$${H}_{{{{\rm{eff}}}}}=\left[\begin{array}{cccc}\frac{\pi }{2}&-2\sqrt{3}&0&0\\ 0&\frac{\pi }{2}&-4&0\\ 0&0&\frac{\pi }{2}&-2\sqrt{3}\\ 0&0&0&\frac{\pi }{2}\end{array}\right]$$
(10)

Evidently, the physical system, despite being composed of two \({{{\mathscr{PT}}}}\)-symmetric isotropic Hamiltonians, H1 and H2, gives rise to an effective Hamiltonian characterized by extreme anisotropy, residing at a 4th-order NHSE EP, as evidenced by the effective next-neighbor couplings. By calculating the effective evolution operator \(\left\vert \psi (t)\right\rangle =U(t,0)\left\vert \psi (0)\right\rangle\), we acquire

$$U(t,0)={e}^{-i{H}_{{{{\rm{eff}}}}}t}=\alpha \left[\begin{array}{cccc}1&i2\sqrt{3}t&-4\sqrt{3}{t}^{2}&-i8{t}^{3}\\ 0&1&i4t&-4\sqrt{3}{t}^{2}\\ 0&0&1&i2\sqrt{3}t\\ 0&0&0&1\end{array}\right]$$
(11)

where \(\alpha ={e}^{-\frac{i\pi t}{2}}\). In a Floquet context, this equation is valid at periodic time intervals t = kT, with \(k\in {\mathbb{N}}\). Equation (11) provides confirmation of the results of Fig. 2, as the polynomial growth factors match precisely with those of the analytically calculated stroboscopic evolution operator. While the system’s response was demonstrated precisely at the EPs, as a unique case of interest, the dynamics unfolding in either the broken or unbroken \({{{\mathscr{PT}}}}\)-symmetric regimes of Fig. 1c, d, are also confirmed to exhibit the characteristic behavior associated with the NHSE. In addition to the stroboscopic visualization of the field amplitude, Fig. 2f presents the dynamic behavior of the system as a function of continuous time for various initial conditions. During each Floquet period, the field oscillates between the elements of the lattice, ultimately exhibiting a corresponding polynomial growth over time. The isotropic nature of the model becomes evident. In other words, despite the apparent non-reciprocal nature of the transmission operator U in Eq. (11), the non-stroboscopic dynamics unfold in an isotropic manner, in contrast to purely non-reciprocal systems that rely on anisotropic couplings to induce NHSE EPs.

To assess the practical feasibility of our Floquet design, we conduct beam propagation method (BPM) simulations on a fused-silica waveguide array engineered to operate near the Floquet NHSE EP. This example demonstrates that NHSE EP dynamics can indeed emerge in systems governed solely by evanescent reciprocal couplings. The design parameters are as follows: wavelength λ = 800 nm, refractive index: ncore = 1.457, nclad = 1.4575, waveguide radius: a = 5 μm, and modulation period Λ = 8.5 cm. While an all-lossy configuration can be implemented, recent experimental advancements have also enabled the realization of longitudinally (z-) modulated gain regions, expanding the scope of such non-Hermitian modulations59. Here the design is set very close to the Floquet EP, where the field localized at the left-most element. The stroboscopic dynamics reveal a funneling-like response – a hallmark of NHSE systems, where irrespective of the excitation site, the field converges and localized at the edge66. Importantly, this is not a lasing effect: the energy does not grow unboundedly at the edge, but instead accumulates and remains localized, with no further increase in the overall field norm.

Scaling of EPs in the generalized model

To generalize the model, we first consider the case where the system consists of an odd number of sites. Figure 3a, illustrates the configuration for N = 5. A key feature in the odd case is the presence of a flat band (indicated by the blue line in Fig. 3b) that spans the entire period T for both the real and imaginary part of its quasienergy. The odd symmetry responsible for this flat band also results in the emergence of a 5-th order EP at zero real quasienergy, unlike in the N = 4 case, where the EP manifests at the Floquet boundaries  Â±Ï€/T. The periodicity of the \({{{\mathscr{PT}}}}\)-unbroken regimes, along with the alternating blue and yellow regions representing skin localization at opposite edges, mirrors the behavior observed in the N = 4 system, consistent with the universality of Eq. (9). Due to the generality of Eq. (8) and (9), these features extend to lattices of any size, with either odd or even number of elements.

Fig. 3: Generalized framework of the model.
figure 3

a Floquet system featuring five sites in which gain and loss are periodically modulated in time, as described by Eq. (3). b For κ = 1, the system hosts a fifth-order exceptional point (EP) at T = 2. The real and imaginary parts of the quasienergy spectrum are plotted in green and red, respectively. A flat band, highlighted in blue, remains pinned at zero eigenvalue across the entire range of T. The black dashed lines denote the Floquet zone boundaries. c Quasienergies at the infinite EP regime (κ = 1.6). The yellow and blue shaded regions correspond to regimes in which all five eigenstates are localized at the left and right edges of the lattice, respectively. Normalized intensities of all eigenstates for left T = 1.2 (on-site red color grading) and right T = 4 (blue color grading) edge localization are shown below. All EPs (gray dots) manifest at zero real quasienergy. d Time evolution of the amplitude at site 1 for independent excitation at each of the five sites, with each excitation shown in a distinct color. Dots denote the theoretically extracted field amplitude at stroboscopic time points. e Time evolution of the amplitude at the first site for 8 different systems ranging from N = 3 to N = 10 total elements. The lattice is always excited at the edge site, opposite of the EP skin mode, leading to a tN−1 growth of amplitude.

Full size image

The 5 × 5 effective Hamiltonian Heff at the EP of Fig. 3d contains only 4 non-zero elements, all located on the upper main diagonal, associated with the left-directional nearest-neighbor couplings, given by \(\left[\begin{array}{cccc}-4&2\sqrt{6}&-2\sqrt{6}&-4\end{array}\right]\). The corresponding evolution operator leads to polynomial growth in the first element, with coefficients \(\left[\begin{array}{ccccc}1&i4t&-4\sqrt{6}{t}^{2}&-i16{t}^{3}&16{t}^{4}\end{array}\right]\) when sites 1 to 5 are independently excited. This behavior is demonstrated in Fig. 3e, where the dynamics are simulated and shown stroboscopically at t = kT. Due to the logarithmic scale, the growth at the first element is represented by straight lines, with the slopes increasing by one unit as the initial excitation shifts by one element to the right.

Figure 3f, shows the dynamic response at the first site for various systems consisting of N elements, where the field is excited at the N-th site. The coupling coefficient and modulation period are set to κ = 1 and T = 2, leading to an N-th EP across all systems. The logarithm of the amplitude appears as a straight line (representing a tN−1 growth), with the slope linearly dependent on N, matching the corresponding order of the N-th order NHSE EP. The Floquet quasispectra for up to N = 10 are shown in Supplementary Note 3 and Fig. S1.

Figure 4 presents the quasienergy spectra as functions of the Floquet period for systems of larger size, at N = 10, 25 and N = 50, evaluated at a coupling value κ = 1. These spectra exhibit characteristics similar to those observed in smaller systems composed of 4 and 5 elements, depending on whether the number of sites is even or odd. A common feature across all cases is the emergence of an N-order exceptional point at T = 2.

Fig. 4: Large size systems.
figure 4

a Dispersion diagrams of the quasienergy spectra as a function of the Floquet period for a system comprising up to N = 50 elements (at κ = 1). The spectral features closely resemble those observed in smaller-sized systems, exhibiting an exceptional point (EP) at T = 2. The real and imaginary parts of the system’s quasienergy spectra are plotted in green and red, respectively. The black dashed lines indicate the Floquet zone boundaries  Â±Ï€/T. Maximal order exceptional points are marked by purple dots. The yellow-shaded region denotes the unbroken \({{{\mathscr{PT}}}}\)-symmetric phase of the system. b Amplitudes of Floquet eigenmodes, for different values of the Floquet period. The red dots mark the modal averages of the amplitude at each site. At the exceptional point (T = 2), in all cases, the field localizes fully at the leftmost site, revealing a maximal-order EP.

Full size image

To the right of each dispersion diagram, the corresponding eigenmode amplitudes are shown for various Floquet period values. In particular, the case T = 0.01 represents the quasi-static regime, where no NHSE is observed. As the period increases and the system enters the periodically modulated regime, the skin effect becomes evident even at relatively small values, at T = 0.5. By further increasing the period to T = 1.9, the system approaches the N-order EP, with a progressively stronger concentration of the field toward the leftmost sites. At the critical point T = 2, a complete collapse of all eigenmodes onto the leftmost site is observed.

Conclusion

In conclusion, by incorporating the principles of \({{{\mathscr{PT}}}}\)-symmetry within a Floquet framework, we have introduced a reciprocal model capable of exhibiting skin-effect exceptional points (EPs) of maximal order. Under open boundary conditions (OBC), our model displays a direct isomorphism to the Hatano-Nelson lattice, as illustrated in Fig. S3 of Supplementary Note 5. The full spectrum of NHSE localization—from its complete absence to the emergence of maximal-order EPs—is accessible within a finite parameter range T ∈ (0, 2), eliminating the need to approach extreme lattice parameter regimes. A key theoretical challenge that remains is the identification of potential topological features associated with conventional NHSE signatures. In Supplementary Note 5 and Fig. S4, we compare the spectra under periodic boundary conditions (PBC) and OBC, highlighting their complex and real-valued nature, respectively. However, a difficulty in identifying a point gap topology arises from the fact that the system does not scale smoothly as N â†’ âˆž, due to the N-dependence of the coupling in Eq. (3).

More broadly, we anticipate that our theoretical framework could open avenues in the field of non-Hermitian Floquet physics, enabling platforms to harness the full spectrum of skin-effect dynamics. The design principles introduced here offer direct access to the regime of maximal-order NHSE EPs, allowing hallmark NHSE phenomena—such as the funneling response shown in Fig. 2—to be observed even in this previously elusive regime. These findings pave the way for a more accessible route toward the experimental realization of the NHSE in fully reciprocal optical, acoustic, and other physical platforms where Floquet engineering is viable.