Introduction

Over the past decade, topological phases have emerged as one of the most rapidly advancing research areas, garnering significant attention across diverse fields such as condensed matter1,2,3, photonics4,5,6, and electrical circuits systems7,8,9. A hallmark feature of topological phases is the presence of topological modes (TMs), typically confined to system boundaries or interfaces, and governed by the bulk-boundary correspondence1. These TMs decay exponentially into the bulk and remain resilient to disorder and perturbations, granting them inherent robustness. However, since the existence of TMs depends on bulk-band topology, their reliance on bulky materials with large lattice structures poses a significant challenge for scalability and integration into compact systems, hindering practical applications and the broader advancement of topological technologies.

A recent study suggests that incorporating non-Hermiticity into the system can overcome the boundary-localized nature of TMs, with the non-Hermitian skin effect (NHSE) facilitating their delocalization10,11,12. The NHSE is characterized by the collapse of bulk-band eigenstates into localized boundary modes, and its discovery has opened new avenues for exploring exotic physics that have no Hermitian counterparts in non-Hermitian systems13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55. By harnessing the NHSE, the wavefunction of the TM can transition from localized to delocalized states when the system parameters satisfy a critical condition11. However, the requirement for such precise parameter tuning imposes practical limitations on the implementation of extended TMs and increases fabrication complexity. To overcome this challenge, we propose a non-Hermitian and nonlinear approach that circumvents these constraints, offering a more robust and scalable solution.

Highly controllable nonlinearity has emerged as a powerful and versatile tool for manipulating next-generation topological devices56. They enable a broad range of novel topological phenomena, including the formation of topological soliton states57,58,59,60,61,62, the nonlinearity-driven topological phase transitions63,64,65,66, and the active control of TMs when combined with non-Hermiticity67,68. Recently, it was demonstrated that the nonlinearity can partially delocalize topological zero modes (TZMs), which are originally confined to the interface between a nonlinear and a linear Hermitian Su-Schrieffer-Heeger (SSH) chains. This effect causes the TZMs to spread throughout the entire nonlinear chain69. Moreover, the wavefunction profiles of TZMs can be tailored to form arbitrary plateaus, opening new avenues for topological state manipulation69.

Despite significant progress, a fundamental question remains unresolved: Can the synergy of nonlinearity, non-Hermiticity, and topology enable fully delocalized and reconfigurable TMs across an entire lattice without strict parameter constraints? Addressing this challenge is crucial for overcoming the limitations of current topological systems that rely on bulky materials, expanding their functional scope, and enabling compact and reconfigurable device architectures. Moreover, achieving fully extended states beyond the continuum could significantly enhance a wide range of topological applications11.

In this work, we explore the intricate interplay between nonlinearity, NHSE, and topology to achieve the delocalization and precise design of TMs. Initially confined to the interface between Hermitian and non-Hermitian lattices, these modes exhibit unusual behavior under the influence of nonlinearity. When the nonlinearity is introduced exclusively in the Hermitian section of the topological interface model, the TM extends across the entire Hermitian part under weak nonreciprocal hopping. As the system parameters approach a critical condition, the mode seamlessly expands over both the Hermitian and non-Hermitian regions. In contrast, strong nonreciprocity localizes the mode at the boundary due to NHSE. When the nonlinearity is applied to both the Hermitian and non-Hermitian regions, the TM becomes fully delocalized across the entire lattice without requiring precise parameter tuning, significantly enhancing its versatility and robustness. Moreover, this approach allows for arbitrary shaping of wavefunction profiles, enabling customized configurations across the entire lattice. The topological protection of these extended non-Hermitian TMs is rigorously verified using the real-space spectral localizer. Additionally, we explore their dynamical stability under external pumping, demonstrating how an initially localized excitation evolves into a predefined wavefunction profile. Furthermore, the nonlinear non-Hermitian model enables the excitation of long-range patterns, an effect unattainable in purely Hermitian systems.

Results and discussion

Model

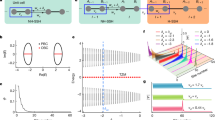
We consider a one-dimensional (1D) topological interface model consisting of a Hermitian nonlinear SSH chain and a non-Hermitian nonlinear SSH chain, as shown in Fig. 1. Both SSH chains contain two sublattices a and b, and their state amplitudes are labeled by aj and bj on the j-th unit cell with j ≤ N for the Hermitian chain, and j > N for the non-Hermitian chain. The real-space eigenvector \(| \psi \left.\right\rangle ={(\cdots ,{a}_{j},{b}_{j},\cdots )}^{T}\) of this hybrid system is captured by the nonlinear Schrödinger equation \(\hat{{{{\mathcal{H}}}}}| \psi \left.\right\rangle =\omega | \psi \left.\right\rangle\), where ω is eigenfrequency, and the Hamiltonian \(\hat{{{{\mathcal{H}}}}}\) is written as

$$\hat{{{{\mathcal{H}}}}}= {\sum}_{j\le N}\left(\tau | {a}_{j}\left.\right\rangle \left\langle \right.{b}_{j}| +{t}_{j-1}| {a}_{j}\left.\right\rangle \left\langle \right.{b}_{j-1}| +\,{\mbox{H.c.}}\,\right)\\ +{\sum}_{j > N}\left[(J-\delta )| {a}_{j}\left.\right\rangle \left\langle \right.{b}_{j}| +(J+\delta )| {b}_{j}\left.\right\rangle \left\langle \right.{a}_{j}| \right]\\ +{\sum}_{j > N}\left({\lambda }_{j}| {a}_{j+1}\left.\right\rangle \left\langle \right.{b}_{j}| +\,{\mbox{H.c.}}\,\right)\\ +{t}_{{{{\rm{d}}}}}\left(| {a}_{N+1}\left.\right\rangle \left\langle \right.{b}_{N}| +\,{\mbox{H.c.}}\,\right).$$
(1)

In Eq. (1), τ is the intracell hopping strength in the Hermitian chain (see Fig. 1), and \({t}_{j}={\tilde{t}}_{j}+\alpha (| {a}_{j+1}{| }^{2}+| {b}_{j}{| }^{2})\) is the intensity-dependent nonlinear intercell hopping strength, with α being the Kerr nonlinear coefficient. J ± δ denote the nonreciprocal intracell hopping amplitudes in the non-Hermitian chain, \({\lambda }_{j}={\tilde{\lambda }}_{j}+\beta (| {a}_{j+1}{| }^{2}+| {b}_{j}{| }^{2})\) is the nonlinear intercell hopping strength, with β being the Kerr nonlinear coefficient, and td represents the inter-chain coupling strength. Such non-Hermitian nonlinear lattices can be feasibly implemented in various experimental platforms, including photonic systems66,70 and electronic circuits71,72,73 [See detailed discussion in Supplementary Note 1]. Unless otherwise specified, we assume that the Hermitian SSH chain is in the topologically trivial regime, while the non-Hermitian chain is topologically nontrivial.

Fig. 1: Non-Hermitian nonlinear topological interface lattice.
figure 1

Tight-binding representation of a one-dimensional topological interface model consisting of a Hermitian nonlinear SSH chain (left) and a non-Hermitian nonlinear SSH chain lattice (right). For the Hermitian chain, τ is the intracell hopping strength (black link), and \({t}_{j}={\tilde{t}}_{j}+\alpha (| {a}_{j+1}{| }^{2}+| {b}_{j}{| }^{2})\) is the intensity-dependent nonlinear intercell hopping strength (orange link) with α being the Kerr nonlinear coefficient. For the non-Hermitian chain, J ± δ denote nonreciprocal intracell hopping amplitudes (blue and red links), and \({\lambda }_{j}={\tilde{\lambda }}_{j}+\beta (| {a}_{j+1}{| }^{2}+| {b}_{j}{| }^{2})\) is the nonlinear intercell hopping strength (green link) with Kerr nonlinear coefficient β. Also, td represents the inter-chain coupling strength (violet link).

Full size image

Nonlinear morphing of TZMs in a critical condition

Without nonlinearity (α = β = 0), a TZM can be delocalized from the interface, occupying only the non-Hermitian SSH chain of the interface model at a critical value11 with δc = λ − J, where we label \({\tilde{\lambda }}_{j}=\lambda\). Here, we demonstrate that the TZM can occupy the entire Hermitian and non-Hermitian chains when the nonlinearity is only applied to the Hermitian chain (α ≠ 0, β = 0). We solve self-consistently the nonlinear Schrödinger equation for different squared amplitudes I = ∑j(∣aj∣2 + ∣bj∣2).

Figure 2 shows eigenfrequency spectrum ω versus I, and the corresponding spatial distributions ∣ψx∣ = {∣a∣, ∣b∣} (x denotes the lattice site) of the TZMs [see red dots in Fig. 2a, c, e] for different δ with α = 0.05. Note that, in addition to TZMs, the nonlinearity can induce in-gap non-zero modes [see gray dots in Fig. 2a]. This work focuses exclusively on TZMs, with detailed discussions of the non-zero in-gap modes provided in Supplementary Note 2.

Fig. 2: Complete delocalization of a topological zero modes (TZMs) under a critical condition.
figure 2

Eigenfrequency spectrum ω versus the squared amplitudes I = ∑j(∣aj∣2 + ∣bj∣2) for Kerr nonlinear coefficient β = 0 with (a) δ = 0.5, (c) δ = δc = 1.0, and (e) δ = 1.5, where red dots indicate the TZMs. In (a), in-gap non-zero modes (gray dots) are shown. The corresponding spatial distributions ∣ψx∣ of TZMs for different I are shown in (b1–b3), (d1–d3) and (f1–f3), respectively. Other parameters used here are J = 1.5, \({\tilde{t}}_{j}=1.0\), \(\tau ={t}_{{{{\rm{d}}}}}={\tilde{\lambda }}_{j}=2.5\), α = 0.05, N = 31 and L = 121.

Full size image

For weak nonreciprocal hopping with δ = 0.5 < δc, a TZM is localized at the interface between the topologically trivial Hermitian nonlinear chain and the nontrivial non-Hermitian linear chain for small I, as shown in Fig. 2(b1). As I increases, the TZM gradually delocalizes towards the Hermitian chain, and eventually spreads uniformly across the entire Hermitian chain at large values of I, e.g., I = 322 [see Fig. 2b2]. Furthermore, as I increases further, the TZM becomes compressed toward the left boundary while maintaining a plateau in the bulk region of the Hermitian lattice at sufficiently large values of I, e.g., I = 502 [see Fig. 2b3]. Note that the same nonlinearity-induced delocalization of TZMs is also observed69 in the Hermitian case with δ = 0.

Distinctive behavior arises at the critical point δ = δc. For the weak nonlinearity, the TZM occupies the whole non-Hermitian chain due to the competition between NHSE localization and topological localization of the in-gap interface state11, as shown in Fig. 2d1. However, as I increases, the TZM gradually spreads to uniformly occupy the entire Hermitian and non-Hermitian lattices due to the interplay of the nonlinearity, NHSE and topology at large values of I, e.g., I = 432 [see Fig. 2d2]. Furthermore, for significantly large values of I, e.g., I = 502 in Fig. 2d3, the TZM is compressed toward the left boundary while maintaining a plateau throughout the entire bulk region of two chains. In the case of strong nonreciprocal hopping [e.g., ∣ψx∣ for δ = 1.5 in Fig. 2f1–f3], the NHSE dominates the nonlinear effects, and the TZM is localized at the right boundary even for strong nonlinearity. These results show that the interplay of nonlinearity, nonreciprocal hopping, and topology determines the morphing of TZM wavefunctions. Note that the delocalized TZM remains robust against disorder (see details in Supplementary Note 3).

Nonlinearity-enabled control of TZMs

The TZM can occupy the entire lattice when δ = δc with β = 0, which can benefit a wide variety of topological applications11. However, the necessary condition with δc = λ − J in the non-Hermitian linear chain restricts its tunability. To overcome this limitation, we introduce the nonlinearity into the non-Hermitian chain, i.e., β ≠ 0 for \(\hat{{{{\mathcal{H}}}}}\) in Eq. (1), and focus on parameters that deviate from the linear critical condition with (J + δ) > λ. Our analysis considers the scenario where the linear non-Hermitian SSH chain resides in the topologically nontrivial regime, characterized by \(J\in [-\sqrt{{\delta }^{2}+{\lambda }^{2}},\,\sqrt{{\delta }^{2}+{\lambda }^{2}}]\) for ∣λ∣≥∣δ∣.

Figure 3 shows the eigenfrequency ω versus I, and the corresponding spatial distributions ∣ψx∣ of TZMs [red dots in Fig. 3a, d] for δ = 1 with β = 0.05 [see Fig. 3b1–b3], and δ = 1.5 with β = 0.075 [see Fig. 3e1–e3]. When δ = 1, in contrast to the case of the non-Hermitian linear chain [see Fig. 2d1], the TZM is initially localized at the right boundary due to the NHSE, and then gradually spreads from the boundary as I increases [see Fig. 3b1]. For large values of I, the TZM occupies the entire lattice [see Fig. 3b2, b3], forming a plateau. The most notable finding is that the delocalization of TZMs, accompanied by the occupation of the entire lattice, occurs without requiring δ = 1 for β ≠ 0. For example, even with unidirectional hopping at δ = 1.5, a uniform distribution of TZMs across the entire lattice is observed [see Fig. 3e2], which does not occur for β = 0. Further details on how δ and β influence the plateau behavior of TZMs are provided in Supplementary Note 4.

Fig. 3: Delocalization and manipulation of topological zero modes (TZMs) without fine parameter tuning.
figure 3

Eigenfrequency ω versus the squared amplitudes I = ∑j(∣aj∣2 + ∣bj∣2) (a) for δ = 1 and β = 0.05, and (d) for δ = 1.5 and β = 0.075, where red dots indicate the TZMs. The corresponding spatial distributions ∣ψx∣ of TZMs for different I, with \({\tilde{t}}_{j}={\tilde{\lambda }}_{j}=1.5\), are shown in (b1–b3) and (e1–e3), respectively. Square, isosceles triangle and cosine profiles of TZMs (c) for δ = 1 and β = 0.05, and (f) for δ = 1.5 and β = 0.075 by designing \({\tilde{t}}_{j}\) and \({\tilde{\lambda }}_{j}\), where the corresponding distributions \({\tilde{t}}_{j}\) and \({\tilde{\lambda }}_{j}\) are provided in Supplementary Fig. S5. Other parameters used here are J = 1.5, α = 0.05, τ = td = 2.5, N = 31, and L = 121.

Full size image

Along the entire lattice, arbitrary wavefunction profiles of TZMs can be achieved by designing site-dependent hopping parameters, \({\tilde{t}}_{j}\) and \({\tilde{\lambda }}_{j}\) [see Supplementary Note 5(A)], without requiring a linear critical condition. Figure 3c, f illustrate square, isosceles triangle, and cosine profiles of TZMs for δ = 1 and δ = 1.5, respectively. Notably, even when the system parameters deviate from the linear critical condition, ideal wavefunction profiles can still be achieved by adjusting β, as demonstrated by comparing Fig. 3c, f. Further details regarding nonlinearity-driven control of TZMs and disorder effects are provided in Supplementary Note 5.

Topological origin of zero modes

Conventional topological invariants are typically characterized by the system’s band structure and associated Bloch eigenstates, and are regarded as global properties of the system. However, nonlinear effects in our model are inherently local, and strong nonlinearity breaks translation symmetry, rendering topological invariants in momentum space ill-defined. To verify the topological origin of the zero modes in our nonlinear non-Hermitian system, we utilize a spectral localizer74,75,76,77,78,79, which is applicable to systems lacking translation symmetry. In order to employ the spectral localizer to our 1D non-Hermitian system (see details in Methods), we map the non-Hermitian Hamiltonian \(\hat{{{{\mathcal{H}}}}}\) to the Hermitian one \({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}\) via a similarity transformation \(\hat{S}\), i.e., \({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}=\hat{S}\hat{{{{\mathcal{H}}}}}{\hat{S}}^{-1}\), with its eigenvector satisfying \(| \bar{\psi }\left.\right\rangle =\hat{S}| \psi \left.\right\rangle\). The spectral localizer of a 1D system at any choice of location x and frequency \(\bar{\omega }\) is written as76

$${L}_{\zeta \equiv (x,\bar{\omega })}(\hat{X},{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}})=\eta (\hat{X}-x{{{\bf{I}}}})\otimes {\Gamma }_{x}+({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}-\bar{\omega })\otimes {\Gamma }_{y},$$
(2)

where Γx and Γy are Pauli matrices, I is an identity matrix, η is a tuning parameter which ensures \(\hat{X}\) and \({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}\) have compatible units, and \(\hat{X}\) is a diagonal matrix whose entries correspond to the coordinates of each lattice site. When the system preserves chiral symmetry, the spectral localizer can be written in a reduced form as76

$${\tilde{L}}_{\zeta \equiv (x,\bar{\omega })}(\hat{X},{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}})=\eta (\hat{X}-x{{{\bf{I}}}})\hat{\Pi }+{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}-i\bar{\omega }\hat{\Pi },$$
(3)

with \(\hat{\Pi }\) being the system’s chiral operator. The eigenvalues of \({\tilde{L}}_{\zeta }\) is labeled by \(\sigma ({\tilde{L}}_{\zeta })\), and the local band gap is given by the smallest value as \({\mu }_{\zeta }=| {\sigma }_{\min }({\tilde{L}}_{\zeta })|\). Furthermore, the local topological invariant is written by76

$${C}_{\zeta }=\frac{1}{2}\,{{\mbox{Sig}}}\,({\tilde {L}}_{\zeta }({\hat {X}},{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}})),$$
(4)

where Sig is the signature of a matrix, i.e., its number of positive eigenvalues minus its number of negative ones.

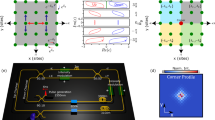
Figure 4 shows spatial distributions \(| {\bar{\psi }}_{x}| =| \hat{S}{\psi }_{x}|\) of TZMs after a similarity transformation \(\hat{S}\), site-resolved \(\sigma ({\tilde{L}}_{\zeta })\), Cζ, and μζ for different I at \(\bar{\omega }=0\), with δ = 1 and β = 0.05. Specifically, \(\sigma ({\tilde{L}}_{\zeta })\), Cζ, and μζ exhibit intensity dependence. Whenever \(\sigma ({\tilde{L}}_{\zeta })\) crosses zero [see red curves in Fig. 4d–f], the value of Cζ changes accordingly [see blue curves in Fig. 4g–i]. Simultaneously, the local gap of μζ closes [see red curves in Fig. 4g–i]. The fact that a zero value of \(\sigma ({\tilde{L}}_{\zeta })\) at ζ = {x0, 0} signifies a zero-frequency mode that is localized near at x0, implies that the change in Cζ at ζ = {x0, 0} reflects the bulk-boundary correspondence. Furthermore, the regions where the local band gap μζ is closest to zero differ for each intensity, signifying the emergence of extended TZMs. Further details on the spectral localizer for different wavefunction profiles are provided in Supplementary Note 6.

Fig. 4: Spectral localizer.
figure 4

a–c Spatial distributions \(| {\bar{\psi }}_{x}| =| \hat{S}{\psi }_{x}|\) of topological zero modes. d–f Eigenvalues of \({\tilde{L}}_{\zeta }\), labeled by \(\sigma ({\tilde{L}}_{\zeta })\), versus x for different I = ∑j(∣aj∣2 + ∣bj∣2), with η = 0.2 and \(\bar{\omega }=0\). g–i Site-resolved topological invariant \({C}_{\zeta }=\,{\mbox{Sig}}\,({\tilde{L}}_{\zeta })/2\), and local band gap \({\mu }_{\zeta }=| {\sigma }_{\min }({\tilde{L}}_{\zeta })|\) for different I. The distributions \({\tilde{t}}_{j}\) and \({\tilde{\lambda }}_{j}\), along with the other parameters, are chosen to be the same as in the case δ = 1 and β = 0.05 shown in Fig. 3.

Full size image

This framework allows us to rigorously assess the topological protection of the TZMs. Specifically, the robustness of a TZM can be guaranteed as long as any perturbation to the system remains below the local band gap. This condition is expressed by69

$$| | \Delta {\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}(W)| | < {\mu }_{\zeta }^{\max },$$
(5)

where \(| | \Delta {\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}(W)| |\) is the largest singular value of \(\Delta {\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}(W)={\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}(W)-{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}\), with \({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}(W)={\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}+W\delta {\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}\) representing the perturbed nonlinear Hamiltonian with perturbation strength W, and \({\mu }_{\zeta }^{\max }=\max [{\mu }_{\zeta }]\) is the maximum value of μζ within the topological region. When this condition is satisfied, a stable TZM exists with topological protection. Further detailed discussion on disorder robustness of TZMs for different wavefunction profiles are provided in Supplementary Note 5(B).

Dynamical evolution under external pumping

Unlike conventional linear topological models, nonlinear models can exhibit distinctive dynamical properties that depend on how intensity levels are reached, enabling intrinsic control on TZMs through external pumping69. Here, we investigate the dynamical evolution under an external pumping scheme, as illustrated in Fig. 5(a), with the evolution governed by the following equation

$$\frac{\partial | \Phi \left.\right\rangle }{\partial t}=-i\left(\hat{{{{\mathcal{H}}}}}+{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{loss}}}}}\right)| \Phi \left.\right\rangle +\xi | {{{\mathcal{P}}}}\left.\right\rangle {e}^{-i\tilde{\omega }t},$$
(6)

where \({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{loss}}}}}={\sum }_{j}(-i{\kappa }_{{{{\rm{a}}}}}| {a}_{j}\left.\right\rangle \left\langle \right.{a}_{j}| -i{\kappa }_{{{{\rm{b}}}}}| {b}_{j}\left.\right\rangle \left\langle \right.{b}_{j}| )\), denotes onsite losses in the two sublattices, which contributes to the stabilizing excitation. The pumping sources \(| {{{\mathcal{P}}}}\left.\right\rangle \equiv {(0,\cdots ,{{{{\mathcal{P}}}}}_{m},\cdots )}^{T}\) (m = 1, 2, ⋯  , (L − 1)/2 − N) are only applied to the a-sites of the non-Hermitian chain [see Fig. 5(a)], with the pumping frequency denoted by \(\tilde{\omega }\), and the pumping strength ξ. We consider a single external pumping source with distribution \({{{{\mathcal{P}}}}}_{m}={\delta }_{m,1}\) for \(\tilde{\omega }=0\), and a complementary discussion on the alternative distribution for \({{{{\mathcal{P}}}}}_{m}\) is provided in Supplementary Note 7(A).

Fig. 5: Dynamical evolution and external excitation of tailored topological zero modes (TZMs).
figure 5

a Schematic showing external pumping applied to the a-sites of the non-Hermitian chain, highlighted by yellow spots. The intensity distributions of the pumping sources are represented by \(\xi {{{{\mathcal{P}}}}}_{m}\), with ξ being the pumping strength. The cyan and red wave arrows indicate staggered onsite losses in the two sublattices, labeled κa and κb, and different colored lines connecting the chain sites correspond to different hopping terms in Fig. 1. b Intensity ∣Φ∣2 of the evolved steady state versus ξ. The circles represent results from the evolution equation (6), which closely match the results (red curve) from self-consistent nonlinear equations in the Supplementary Equation (S10). c Wavefunction profile ∣Re(Φx)∣ of the evolved steady states for different ξ, corresponding to colored circles in (b). d Time- and space-resolved ∣Re(Φx)∣ for ξ = 2.5, with the steady-state result highlighted by red circles in (e). In (e), the steady-state wavefunction profile (red circles) closely matches the designed one (blue line) of the TZM. Evolution of (f) the similarity function χ(t) and (g) the corresponding standard deviations σ(t) for different ξ with 200 independent realizations. ∣Re(Φx)∣ illustrating the excitation of a long-range pattern with a large-size lattice in the (h) Hermitian and (i) non-Hermitian interface models.The parameters are the same as the case of δ = 1 and β = 0.05 in Fig. 3, with \(\tilde{\omega }=0\), κa = 0.01 and κb = 0.5.

Full size image

Figure 5b plots the intensity ∣Φ∣2 of the evolved steady state versus ξ, with the wavefunction profile ∣Re(Φx)∣ for different ξ shown in Fig. 5c. As the pumping strength ξ increases, an initially localized waveform begins to spread and gradually occupies the non-Hermitian chain [see green line in Fig. 5c]. Eventually, this expansion allows the waveform to fill the entire lattice of both the Hermitian and non-Hermitian chains, aligning with the designed profile (indicated by the blue line). Upon further increasing ξ, the steady-state intensity becomes concentrated toward the left boundary while maintaining the plateau in the bulk region (illustrated by the purple line). The steady-state wavefunction profile [red circles in Fig. 5e], with its time- and space-resolved amplitude \(| {{{\rm{Re}}}}({\Phi }_{x})|\) shown in Fig. 5d, closely matches the designed target profile of the TZM [blue lines in Fig. 5e]. A detailed discussion on the evolution into various designed wavefunction profiles is provided in Supplementary Note 7(A). These results demonstrate that, by leveraging dynamical evolution, we can achieve any arbitrarily desired waveform across the entire lattice.

We now examine the stability of the evolved steady state under random noise. To incorporate the effects of noise, we introduce a disturbance \(| \Upsilon \left.\right\rangle\) to the evolved steady state \(| \Phi \left.\right\rangle\) at a certain evolution time. We then solve the dynamical evolution equation for the perturbed state \(| \phi \left.\right\rangle =| \Phi \left.\right\rangle +| \Upsilon \left.\right\rangle\) as

$$\frac{\partial | \phi (t)\left.\right\rangle }{\partial t}=-i\left(\hat{{{{\mathcal{H}}}}}+{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{loss}}}}}\right)| \phi (t)\left.\right\rangle +\xi | {{{\mathcal{P}}}}\left.\right\rangle {e}^{-i\tilde{\omega }t},$$
(7)

where the component of \(| \Upsilon \left.\right\rangle\) is randomly sampled in the range10 [ − 3, 3].

If the perturbed state \(| \phi \left.\right\rangle\) can return to the original steady state \(| \Phi \left.\right\rangle\), it indicates that the evolved steady state is robust against random noise. To examine this return, we calculate the similarity function69, defined as

$$\chi (t)=\frac{| \langle \Phi | \phi (t)\rangle | }{\sqrt{\langle \Phi | \Phi \rangle \langle \phi (t)| \phi (t)\rangle }},$$
(8)

where, when χ(t) reaches 1, it indicates the stability of the evolved steady state under random noise.

We present the evolved similarity function χ(t) and the corresponding standard deviations σ(t) for different pumping strength ξ, as shown in Fig. 5f, g. The results are averaged over 200 independent realizations with a single-site pumping. As time evolves, χ(t) returns to 1, and the corresponding standard deviation σ(t) approaches zero. This confirms the stable and fully-extended TZM achieved through external pumping.

Compared to the Hermitian case, the required pumping strength ξ to achieve the desired long-range plateau is significantly lower in our non-Hermitian nonlinear interface model [see details in Supplementary Note 7(B) for further details on long-range pattern excitations for other wavefunction profiles]. In contrast, for the Hermitian interface model, the external pumping is insufficient to fully excite the predesigned pattern in a large-size lattice [see Fig. 5h]. This highlights how the interplay of nonlinearity, NHSE, and topology facilitates the dynamical preparation of long-range patterns with arbitrary wavefunction shapes. This capability could benefit future applications in reconfigurable topological photonic devices.

Delocalization of TZMs in a 2D non-Hermitian nonlinear lattice

We now extend the 1D non-Hermitian nonlinear model to two dimensions (2D) by stacking 1D topological interface chains along the y direction, as shown in Fig. 6a. The blue dashed box marks a unit cell containing four sublattices, with odd and even indices j distinguishing sites along y. Hopping amplitudes along the y direction are both nonlinear and site-dependent, where dashed purple lines indicate hopping terms with negative signs. The nonlinear intracell coupling is given by

$${u}_{i,j}={u}_{0}+{\gamma }_{1}(| {\eta }_{i,j}{| }^{2}+| {\eta }_{i,j+1}{| }^{2}),\,j\in \,{\mbox{odd}}\,,$$
(9)

where ηi,j ∈ {ai,j, bi,j} represents the state amplitudes of the two sites linked by the corresponding nonlinear coupling, and the intercell coupling, characterized by strength v0, is linear.

Fig. 6: Delocalization of topological zero modes (TZMs) in a 2D non-Hermitian nonlinear lattice.
figure 6

a Schematic of a 2D non-Hermitian nonlinear interface model, formed by stacking 1D topological interface chains with staggered nonlinear hopping along the y direction. Each unit cell, indicated by a blue dashed box, contains four sublattices. The nonlinear intracell hopping, along the y direction, is given by ui,j = u0 + γ1(∣ηi,j∣2 + ∣ηi,j+1∣2) (j ∈ odd), where ηi,j ∈ {ai,j, bi,j} are the state amplitudes of the two sites linked by the corresponding nonlinear coupling. Dashed purple lines indicate hopping terms with negative signs along the y direction. b Eigenfrequency ω versus I = ∑i,j(∣ai,j∣2 + ∣bi,j∣2) for γ1 = 0, where red dots mark TZMs. The corresponding spatial distributions ∣ψx,y∣ (x and y labels lattice site along the x and y directions) of the TZMs for different I are shown in (c1–c3). d ∣ψx,y∣ for γ1 = 0.01, where the TZMs exhibit fully extended spatial distributions at I = 502. Other parameters used are J = 1.5, \({\tilde{t}}_{i,j}={\tilde{\lambda }}_{i,j}=1.5\), α = β = 0.05, τ = td = 2.5, δ = 1.2, u0 = 0.2, v0 = 0.4, N = 6, and Lx = Ly = 21.

Full size image

Along the x direction, for each chain, the intercell couplings, ti,j and λi,j, are nonlinear and given by

$${t}_{i,j}={\tilde{t}}_{i,j}+\alpha (| {a}_{i,j}{| }^{2}+| {b}_{i-1,j}{| }^{2}),$$
(10)
$${\lambda }_{i,j}={\tilde{\lambda }}_{i,j}+\beta (| {a}_{i,j}{| }^{2}+| {b}_{i-1,j}{| }^{2}).$$
(11)

In the absence of both nonlinearity and non-Hermiticity, the system reduces to an interface model based on the Benalcazar-Bernevig-Hughes (BBH) lattice80. The BBH model exhibits a higher-order topological phase characterized by the emergence of TZMs localized at the corners. In the linear Hermitian case, the corresponding 2D interface model supports TZMs localized at the ends of the interface.

When the nonlinearity along the x direction is introduced with γ1 = 0, the 2D non-Hermitian nonlinear interface model supports TZMs, as indicated by the red dots in Fig. 6b. Owing to the strong NHSE, these TZMs are localized from the interface toward the right-bottom corner for weak nonlinearity at I = 52 [see Fig. 6c1]. As the nonlinear intensity increases to I = 202, the TZMs become more extended and predominantly occupy the bottom edge [see Fig. 6c2]. When the nonlinearity is further strengthened to I = 502, the modes do not spread across the entire lattice but instead become localized again [see Fig. 6c3]. In contrast, when nonlinearity is also introduced along the y direction with γ1 = 0.01, the TZMs extend over the entire 2D lattice at I = 502 [see Fig. 6d]. Notably, this extended phase emerges without the need to satisfy the constraint \(\delta ={\delta }_{{{{\rm{c}}}}}={\tilde{\lambda }}_{i,j}-J\). These results demonstrate how the interplay between nonlinearity and non-Hermiticity enables flexible control of topological mode localization in 2D lattices.

Conclusions

In summary, we demonstrate how the intricate interplay of nonlinearity, NHSE and topology enables flexible control over the spatial profile of TMs. By coupling a Hermitian nonlinear SSH chain with a non-Hermitian one, we achieve full delocalization of the TM across the entire lattice. Unlike the delocalization induced by NHSE under critical conditions or the partial delocalization caused by nonlinearity in Hermitian systems, this triple synergy eliminates the need for precise parameter tuning to extend the TM across both chains. Furthermore, the TM waveform can be arbitrarily engineered by independently adjusting the nonlinearity strength in each chain. These extended non-Hermitian TMs exhibit robustness against disorder while maintaining dynamical stability and enabling long-range spatial patterns through external pumping. We also apply our approach to 2D systems, demonstrating its feasibility for delocalizing topological modes in higher-order topological phases. These results open potential avenues for applications in robust wave manipulation and nonlinear topological photonics, where tailored and disorder-resistant states are essential.

Methods

Spectral localizer in the nonlinear non-Hermitian system

Topological band theory establishes that topological invariants are global properties, intrinsically tied to the band structure and Bloch eigenstates of gaped systems. However, nonlinearity poses a significant challenge by introducing local effects that disrupt the spatial periodicity essential to traditional band theory. To establish the topological origin of the zero modes in our nonlinear non-Hermitian system, we turn to the spectral localizer as a diagnostic tool74,75,76,77,78,79,81,82.

The spectral localizer combines a system’s Hamiltonian and position operators through a non-trivial Clifford representation81,82, which is generally applied to Hermitian systems. To extend its application to our 1D non-Hermitian system, we employ a similarity transformation \(\hat{S}\) that maps the non-Hermitian nonlinear Hamiltonian \(\hat{{{{\mathcal{H}}}}}\) to an equivalent Hermitian Hamiltonian \({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}\). This transformation is defined as \({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}=\hat{S}\hat{{{{\mathcal{H}}}}}{\hat{S}}^{-1}\), ensuring compatibility with the spectral localizer framework. The matrix of the similarity transformation is given by

$$\hat{S}=\left(\begin{array}{cc}{{{{\bf{I}}}}}_{2N}&\\ &{0}_{L-2N}\end{array}\right)+\left(\begin{array}{cc}{0}_{2N}&\\ &{{{{\mathcal{R}}}}}_{L-2N}\end{array}\right),$$
(12)

where I is the identity matrix, and \({{{\mathcal{R}}}}\) is a diagonal matrix, with dimensions L − 2N, whose diagonal elements are \(\{1,r,r,{r}^{2},\cdots \,,{r}^{\frac{L-1}{2}-N-1},{r}^{\frac{L-1}{2}-N},{r}^{\frac{L-1}{2}-N}\}\) (where L is odd). Here, \(r=\sqrt{| (J-\delta )/(J+\delta )| }\), and \({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}\) reads

$${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}= {\sum}_{j\le N}\left(\tau | {a}_{j}\left.\right\rangle \left\langle \right.{b}_{j}| +{t}_{j-1}| {a}_{j}\left.\right\rangle \left\langle \right.{b}_{j-1}| +\,{\mbox{H.c.}}\,\right)\\ +{\sum}_{j > N}\left[\sqrt{(J-\delta )(J+\delta )}| {a}_{j}\left.\right\rangle \left\langle \right.{b}_{j}| +\,{\mbox{H.c.}}\,\right]\\ +{\sum}_{j > N}\left({\lambda }_{j}| {a}_{j+1}\left.\right\rangle \left\langle \right.{b}_{j}| +\,{\mbox{H.c.}}\,\right)\\ +{t}_{{{{\rm{d}}}}}\left(| {a}_{N+1}\left.\right\rangle \left\langle \right.{b}_{N}| +\,{\mbox{H.c.}}\,\right).$$
(13)

The original nonlinear Schrödinger equation, \(\hat{{{{\mathcal{H}}}}}| \psi \left.\right\rangle =\omega | \psi \left.\right\rangle\), now takes the form

$${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}| \bar{\psi }\left.\right\rangle =\omega | \bar{\psi }\left.\right\rangle ,$$
(14)

with \(| \bar{\psi }\left.\right\rangle =\hat{S}| \psi \left.\right\rangle\). This allows us to leverage the information from the Hermitian Hamiltonian \({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}\) and its eigenmodes \(| \bar{\psi }\left.\right\rangle\) to characterize the topological properties of the non-Hermitian nonlinear system.

The nonlinear spectral localizer is a composite operator that incorporates the system’s Hamiltonian \({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}\) accounting for its current occupations \(| \bar{\psi }\left.\right\rangle\) and position operators \(\hat{X}\), using a nontrivial Clifford representation. The 1D nonlinear spectral localizer is explicitly written as76,81,82,83,84

$$\begin{array}{l}{L}_{\zeta \equiv (x,\bar{\omega })}(\hat{X},{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}})\\ =\left(\begin{array}{cc}0&\eta (\hat{X}-x{{{\bf{I}}}})-i({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}-\bar{\omega }{{{\bf{I}}}})\\ \eta (\hat{X}-x{{{\bf{I}}}})+i({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}-\bar{\omega }{{{\bf{I}}}})&0\end{array}\right),\end{array}$$
(15)

where the position matrix \(\hat{X}\) is a diagonal matrix whose diagonal elements are {1, 2, 3, ⋯  , L − 1, L}, η > 0 is a scaling factor that ensures that the units of \(\hat{X}\) and \({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}\) are compatible. The pair \(\zeta \equiv (x,\bar{\omega })\) serves as input for locally probing the topology in real space, with x representing the spatial coordinate and \(\bar{\omega }\) being the energy. This pair can be chosen either within or outside the system’s spatial and spectral extent.

The spectral localizer can be used to construct the relevant local topological invariant and to define the associated local gap. For a given \(\zeta \equiv (x,\bar{\omega })\), the spectrum of the nonlinear spectral localizer, \(\sigma ({L}_{\zeta }(\hat{X},{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}))\), provides a measure of whether the system, when linearized around its current state \(| \bar{\psi }\left.\right\rangle\), supports a state \(| \bar{\Phi }\left.\right\rangle\) that is approximately localized near the point \((x,\bar{\omega })\), satisfying \({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}| \bar{\Phi }\left.\right\rangle \approx \bar{\omega }| \bar{\Phi }\left.\right\rangle\) and \(\hat{X}| \bar{\Phi }\left.\right\rangle \approx x| \bar{\Phi }\left.\right\rangle\). In particular, if the smallest singular value of the spectral localizer,

$${\mu }_{\zeta }(\hat{X},{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}})=\min \left[| \sigma ({L}_{\zeta }(\hat{X},{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}))| \right],$$
(16)

is sufficient close to zero, such an approximately localized state exists. Conversely, a large value indicates that the system does not support such a state. Thus, μζ can be heuristically understood as a local band gap76.

If the system respects chiral symmetry, the spectral localizer \({L}_{\zeta }(\hat{X},{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}})\) can be further written in a reduced form as

$${\tilde{L}}_{\zeta \equiv (x,\bar{\omega })}(\hat{X},{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}})=\eta (\hat{X}-x{{{\bf{I}}}})\hat{\Pi }+{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}-i\bar{\omega }\hat{\Pi },$$
(17)

where \(\hat{\Pi }\) is the system’s chiral operator, satisfying \({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}\hat{\Pi }=-\hat{\Pi }{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}\). Then, the local topological invariant Cζ and local band gap μζ are given by76

$${C}_{\zeta }(\hat{X},{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}})=\frac{1}{2}\,{{\mbox{Sig}}}\,({\tilde{L}}_{\zeta }(\hat{X},{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}})),$$
(18)
$${\mu }_{\zeta }(\hat{X},{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}})=\min \left[| \sigma ({\tilde{L}}_{\zeta }(\hat{X},{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}))| \right],$$
(19)

where Sig is the signature of a matrix, i.e., its number of positive eigenvalues minus its number of negative ones, and \(\sigma ({\tilde{L}}_{\zeta })\) is the eigenvalue of the reduced spectral localizer \({\tilde{L}}_{\zeta }\). For a system with an even or odd number of states, Cζ is either integer or half-integer, and the changes in Cζ are always integer-valued. Note that we consider \({C}_{(x,0)}(\hat{X},{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}})\) for \(\bar{\omega }=0\), reflecting the fact that the chiral symmetry can only protect states at the center of the system’s eigenvalue spectrum.

The local band gap μζ and the local topological invariant Cζ provide a consistent and complete description of a system’s topology76. An intuitive physical interpretation of the spectral localizer’s connection to a system’s topology is that the invariant \({C}_{\zeta }(\hat{X},{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}})\) evaluates whether the matrices \({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{S}}}}}\) and \((\hat{X}-x{{{\bf{I}}}})\) can be smoothly deformed to the trivial atomic limit, where the Hamiltonian and position operator commute, without closing the spectral gap and violating a specific symmetry during the deformation. If Cζ = 0, this deformation is possible, indicating the system is topologically trivial at \(\zeta =(x,\bar{\omega })\). However, if Cζ ≠ 0, the deformation is obstructed, implying that the system is topologically nontrivial at \(\zeta =(x,\bar{\omega })\). Furthermore, at the local site x0 for the specific eigenfrequency \(\bar{\omega }\), when \({C}_{\zeta = ({x}_{0},\bar{\omega })}\) changes value, the local band gap \({\mu }_{\zeta = ({x}_{0},\bar{\omega })}\) necessarily closes with \({\mu }_{\zeta = ({x}_{0},\bar{\omega })}=0\). This gap closure corresponds to a state that is approximately localized near x0 at the energy \(\bar{\omega }\), thereby embodying the principle of bulk-boundary correspondence.