Enhanced continuous-variable quantum key distribution protocol via adaptive signal processing

Abstract

Quantum key distribution (QKD) provides secure communication using quantum mechanics, with continuous-variable QKD (CV-QKD) being an attractive solution due to its compatibility with existing telecommunication technology. Its main drawback is susceptibility to signal loss in fibres and free-space links, including satellites, which limits performance. Here we show a software-based protocol enhancing CV-QKD by applying adaptive filters at the transmitter and receiver, allowing the system to dynamically respond to changing channel conditions. Our security analysis avoids relying on Gaussian extremality, giving accurate bounds on an eavesdropper’s information. The protocol can also extract keys in regions that would normally be considered insecure. We demonstrate a threefold increase in secret-key rates compared with the best existing CV-QKD protocol, and in satellite simulations, up to a 400-fold improvement. Because it requires no hardware modifications, our method can be readily integrated into existing systems, paving the way for more practical and robust quantum communication networks.

Introduction

Quantum key distribution (QKD) is a method used to securely establish a secret key between two distant parties, Alice and Bob^1,2,3. One variant of QKD is continuous-variable (CV) protocols, where keys are encoded in the amplitude and phase quadratures of the optical field and measured using heterodyne or homodyne detection^4,5. CV-QKD can be categorised into different types, one of which includes protocols with Gaussian modulation (GM), where coherent states are modulated with a Gaussian distribution^{6,7,8,9,10,11,12,13,14,15,16}. The most commonly used CV-QKD protocol with GM is the GG02 protocol^6,7,8, which optimises the variance of Gaussian modulation for each transmission distance to achieve the best key rates. A key step in QKD is parameter estimation, which is often performed after error reconciliation to assess channel noise and loss, helping to bound Eve’s information¹⁷. This helps optimise experimental parameters, assuming the channel varies slowly. However, if parameter estimation falls within a non-secure region, key data must be discarded, and rapid variations like atmospheric scintillation can render these estimates ineffective.

In CV-QKD, passive methods that do not require feedback loops to optimise experimental parameters can enhance key rates by employing quantum processes such as noiseless linear amplifiers (NLAs)^18,19, phase-sensitive amplifiers²⁰, photon subtraction^21,22, and photon catalysis^22,23,24. While these techniques can increase key rates, they are challenging to implement. Recent post-selection protocols emulate such physical processes using digital filtering, where applying a quantum process becomes equivalent to first detecting the quantum state and then digitally filtering the measured outcomes. This approach is particularly useful for point-to-point applications like QKD. For example, measurement-based NLA (MB-NLA) replaces physical NLAs by employing Gaussian post-selection on detection outcomes. This approach extends the transmission distance of CV-QKD^25,26,27 and also provides overall performance enhancements in CV-based quantum communications^28,29,30,31. Similar approaches have been applied to photon subtraction and photon catalysis protocols, where physical processes are replaced with non-Gaussian virtual photon-subtraction^32,33 and Gaussian zero-photon catalysis post-selection³⁴. However, since these methods still emulate physical processes, the post-selection filters are constrained by the characteristics of those processes. Additionally, these protocols rely on Gaussian extremality, which states that Gaussian states maximise the von Neumann entropy for a given covariance matrix^35,36. This results in an overestimation of Eve’s information with non-Gaussian filters, leading to an underestimation of the key rate.

In this work, we present a CV-QKD protocol using Gaussian modulations and homodyne or heterodyne detection followed by post-selection. The protocol introduces a paradigm shift by eliminating the need to simulate physical processes for filtering. It combines post-selection at both Alice’s and Bob’s stations: Alice’s Gaussian filter optimises modulation variance to achieve key rates near the optimal GG02 performance, while Bob’s non-Gaussian filter emulates a higher-performing channel, surpassing optimal GG02 key rates. To avoid overestimating Eve’s information, we developed a security analysis that tightly bounds Eve’s information after Bob’s filter. The protocol dynamically optimises key rates for rapidly changing channels, such as satellite-to-ground links, where rapid channel changes render any parameter estimation unreliable. Moreover, it can extract keys even in regions where unfiltered channel parameters would not allow secure QKD under the GG02 protocol.

Results

Protocol overview

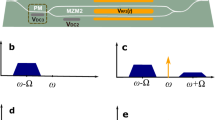
The experimental setup is shown in Fig. 1(a), where Alice generates two variables, x_a and p_a, from a zero-mean Gaussian distribution with variance V_mod in units of vacuum noise using two independent function generators. In our implementation, Alice’s Gaussian-modulated variables are encoded onto the sidebands of a 1064 nm continuous-wave laser using amplitude and phase electro-optic modulators driven at 3-5 MHz. This generates a thermal state with quadrature variance V_mod + 1, as required by the protocol. Alice retains these variables to apply a Gaussian filter to both x_a and p_a after the states have been sent to Bob and measured. The encoded state is sent through a quantum channel with transmittance T and thermal noise W, simulated by a half-wave plate and polarising beamsplitter. Bob performs homodyne detection, randomly measuring the x or p quadrature. The homodyne signal is filtered by a 3 − 5 MHz bandpass filter and then fed to the oscilloscope with a sampling rate of 25 MSamples/s, collecting 10 million samples. Both homodyne data and Alice’s data were digitally filtered with a 3 − 3.5 MHz bandpass filter.

Fig. 1: Experimental schematic and illustrative diagram of the filtering process.

a Alice encodes coherent states $| ({x}_{a}+i{p}_{a})/2\left.\right\rangle$ from a Gausssian distribution with zero mean and variance, V_mod, using white noise generated by function generators (orange box). She samples x_a and p_a simultaneously, then sends the encoded states through a quantum channel with transmittivity T and thermal noise W. Bob performs homodyne detection to measure x_b and p_b, randomly switching between these two quadratures. After data acquisition and once the states have been sent to Bob and measured, Alice applies a Gaussian filter to the data kept on her computer (purple box), followed by Bob applying a non-Gaussian filter to his measurement outcomes (pink box). b Left: The correlation between Alice’s variables x_a and Bob’s measurement outcomes x_b before any post-selection. Middle: The correlation after Alice’s Gaussian post-selection superimposed by the original distribution (orange), which reduces the variance of the Gaussian-modulated variables, effectively creating a thermal state with this reduced variance. Right: The correlations after Bob’s non-Gaussian post-selection, resulting in highly non-Gaussian distributions for x_a and x_b. PM/AM Electro-optic phase/amplitude modulators and LO Local oscillator.

While the experimental setup follows the well-known GG02 protocol^6,7, which utilises Gaussian modulated coherent states and homodyne detection, our protocol diverges at the software level. This software-level protocol can be applied to any system with Gaussian modulated states and coherent detection. After the data acquisition, Alice’s post-selection is applied on the samples x_a and p_a where Alice’s Gaussian post-selection filter is defined by the following expression

$${F}_{A}({x}_{a})={e}^{-{g}_{x}^{2}{x}_{a}^{2}},$$

(1)

where x_a is the randomly generated variable and g_x ≥ 0 represents the filter gain. Each symbol, x_a, is either kept or discarded based on the probability F_A(x_a) (See the Methods section for details on how the filter is applied). The same function applies to p_a, replacing g_x with g_p. This post-selection on x_a and p_a imitates attenuating the modulation variance, as shown in Fig. 1(b). When g_x = 0, no filtering is applied, but as g_x increases significantly (e.g., g_x = 10⁵), the modulation variance approaches zero, effectively turning the state into vacuum. In the GG02 protocol, there is an optimal modulation variance for each distance and noise combination to achieve the best key rates. While Alice’s post-selection does not alter the channel parameters, it reduces the modulation variance to match the optimal GG02. Unlike GG02, which requires modulation variance optimisation, Alice’s approach optimises both the variance and key rates without needing prior channel characterisation. The optimisation also inherently depends on the reconciliation efficiency, β, which quantifies how efficiently Alice and Bob can extract shared bits from their correlated data during classical post-processing (see Eq. (18)). Lower values of β reduce the mutual information between Alice and Bob, shifting the modulation variance that maximises the final key rate. Therefore, when comparing key rates or optimising filters, the effect of β must be taken into account.

The key rates can be further optimised by using a non-Gaussian post-selection performed by Bob. Bob’s post-selection filter can be expressed as

$${F}_{B}({x}_{b})=\left\{\begin{array}{ll}0 &-{c}_{x} < {x}_{b} < {c}_{x}\\ 1 &{{{\rm{elsewhere}}}},\hfill\end{array}\right.$$

(2)

where x_b represents Bob’s homodyne measurement outcome and c_x is the cut-off parameter of the filter which can take values from 0 to the largest measurement outcome of Bob. Bob’s post-selection discards all the numbers within the cut-off, therefore, it creates a highly non-Gaussian distribution as shown in Fig. 1(b). This post-selection effectively simulates a channel with better performance than the original one used by Alice to send the quantum states.

In QKD, Eve holds the purification of Alice and Bob’s joint state σ_AB, meaning her von Neumann entropy matches that of the state shared by Alice and Bob. Therefore, Eve’s information can be bounded by the Holevo bound³⁷, which represents the maximum classical information extractable from a quantum channel. It is expressed as

$${I}_{E}=S({\sigma }_{AB})-S({\sigma }_{A| B}),$$

(3)

where S(σ_AB) and S(σ_A∣B) are the von Neumann entropies of Alice and Bob’s joint state and Alice’s state conditioned on Bob’s measurement outcome x_b, respectively. Since Bob’s post-selection is non-Gaussian, using the covariance matrices σ_AB and σ_A∣B would overestimate Eve’s information due to Gaussian extremality, leading to lower key rates. Instead, we directly calculate Eve’s information from her density matrix, assuming that she performs a general Gaussian attack. In this attack, Eve prepares a two-mode squeezed vacuum (TMSV) state with a variance that mimics the quantum channel³⁸. She replaces the channel between Alice and Bob with a beamsplitter, injecting one mode (E₁) into the beamsplitter to interact with Alice’s state, while retaining the other mode (E₂)³⁹. While the optimal strategy after post-selection is not known, our assumption follows from the intuition that Alice and Bob can verify (within some tolerance) that the channel remains Gaussian by computing higher-order moments from their measurement outcomes such as skewness and kurtosis, thereby restricting Eve to Gaussian attacks. Eve’s information is then calculated using the Holevo bound as follows

$${I}_{E}=S({\rho }_{{E}_{1}{E}_{2}})-S({\rho }_{{E}_{1}{E}_{2}| B}({x}_{b})),$$

(4)

where $S({\rho }_{{E}_{1}{E}_{2}})$ represents the von Neumann entropy of Eve’s average state, and $S({\rho }_{{E}_{1}{E}_{2}| B})$ gives the von Neumann entropy of Eve’s conditional state given Bob measures an outcome x_b. This equation saturates Eq. (3) when Bob performs no post-selection, and everything remains Gaussian. In that case, Eve’s average state is the sum of all Gaussian conditional states measured by Bob. With non-Gaussian post-selection, the conditional states remain Gaussian, but Eve’s average state becomes non-Gaussian. Since Bob can discard measurement outcomes within the filter cut-off, Eve’s average state is no longer obtained by simply summing all the states, but is derived from the filtered results as follows

$${\rho }_{{E}_{1}{E}_{2}}=\sum\limits_{{x}_{i}=-n}^{n}{p}_{b}^{{\prime} }({x}_{i}){\rho }_{{E}_{1}{E}_{2}| B}({x}_{i}),$$

(5)

where n is the maximum number that Bob measures and ${p}_{b}^{{\prime} }({x}_{i})$ denotes Bob’s probability of getting a given outcome, x_i (For a detailed derivation of how to obtain the density matrices ${\rho }_{{E}_{1}{E}_{2}}$ and ${\rho }_{{E}_{1}{E}_{2}| B}$, refer to the Methods section). This method is particularly beneficial because it does not rely on Gaussian extremality to determine key rates. Previously, this reliance limited the performance of some protocols when non-Gaussian post-selection was used³².

It is important to note that post-selection by both parties is not always required. Depending on the channel parameters, either Alice’s post-selection or Bob’s post-selection alone may be sufficient, while in some cases, both may be necessary. The advantage of our protocol lies in its ability to be augmented into existing CV-QKD setups without any hardware modifications, as it operates entirely at the software level.

Experimental results

Fig. 2 shows the experimental results for a transmission of T = 0.26 with thermal noise values of W_x = 1.02 SNU and W_p = 1.01 SNU for the x and p quadratures, respectively. This loss corresponds to an equivalent fibre distance of 29.1 km assuming a fibre loss of 0.2 dB per km. The key rate extracted from the raw data is initially negative, as illustrated in Fig. 2(a). This is because the modulation variance used in the experiment is not optimal for the 29.1 km distance with the given noise parameters. The experimental modulation variances for the x and p quadratures were ${V}_{mo{d}_{x}}=12.73$ SNU and ${V}_{mo{d}_{p}}=13.52$ SNU, while the optimal GG02 modulation variances required for this regime are ${V}_{mo{d}_{x}}=6.14$ SNU and ${V}_{mo{d}_{p}}=5.97$ SNU. The asymmetry in the variances is due to asymmetric noise in the state preparation stage. A portion of this preparation noise, primarily due to modulator electronics, is considered trusted in our security analysis (see the Methods). Alice applies a Gaussian filter with gains of g_x = 0.213 and g_p = 0.259 to reduce the modulation variances. These gains yield the optimal key rate, as indicated in Fig. 2(b) where the reported key rates in bits/use are normalised to the original number of transmitted states, with the filtering success probabilities included in the calculation to account for the reduction in usable states (refer to Eq. (35)). Although the key rate becomes positive after Alice’s post-selection, it does not reach the optimal GG02 key rate as shown in Fig. 2(a) due to the success probability penalty of the post-selection process (${P}_{{A}_{x}}=0.68$ and ${P}_{{A}_{p}}=0.60$ are the probability of success of Alice’s post-selection on the x and p quadratures, respectively, giving a total probability of success of 0.41).

Fig. 2: Experimental results of the protocol at a fixed channel.

The channel has a transmission of T = 0.26, equivalent to a fibre distance of 29.1 km (assuming 0.2 dB loss per km), with a thermal noise of W_x = 1.02 ± 0.001 and W_p = 1.01 ± 0.001 in shot noise units (SNU) in x and p quadratures, respectively. a From left to right, we give the mutual information between Alice and Bob (blue boxes), Eve’s information (orange boxes) and the key rates of the protocol (purple boxes) before any post-selection, after Alice’s post-selection and after Alice and Bob’s post-selection combined, respectively. The key rate is initially negative, indicating that Eve’s information exceeds the mutual information of Alice and Bob, making it a non-secure region. After Alice’s post-selection, the key rate becomes positive but remains below the optimal GG02 rate for that distance. The key rate is further optimised by applying a post-selection on Bob’s side where the key rate achieves the optimal GG02 line. b The top panel shows the contour plot of the key rates after Alice’s post-selection along the x and p quadratures, with gains ranging from 0 to 0.436. The bottom panel illustrates the key rate slices at optimal performance after Alice’s post-selection with fixed gains g_x and g_p. The solid line represents fixed g_x while varying g_p, and the dashed line represents fixed g_p while varying g_x. c Top panel demonstrates the contour plot of the key-rates after Bob’s post-selection with the cut-off parameters ranging from 0 to 8.95, while the bottom panel shows the key rates after Bob’s post-selection with fixed optimal cut-offs in the x (solid line) and p (dashed line) quadratures. The solid line varies the cut-off in the p quadrature while keeping the x cut-off fixed, and the dashed line varies the cut-off in the x quadrature while keeping the p cut-off fixed. KR Key rate, I_AB Mutual information between Alice and Bob, I_E Eve’s information and β Reconciliation efficiency. The reconciliation efficiency is set to 92% throughout the experiment. The error bars indicate the statistical uncertainties in the data. For details on how they are calculated, refer to the Methods section.

To further optimise the key rate, Bob applies a non-Gaussian filter with cut-off parameters of c_x = 0 and c_p = 8.95 which is shown in Fig. 2(c). Bob keeps the x quadrature unchanged as it is already optimal but discards most measurements in the p quadrature where the maximum value is p_b = 9. The key rate increases and saturates at 0.0038 ± 0.001 bits/use, surpassing the optimal GG02 key rate of 0.0036 bits/use. Our protocol turned regions with negative key rates, deemed insecure by the GG02 protocol, into regions with positive key rates. In these regions, we achieved key rates close to the optimal GG02 rates that are only achievable using optimal modulation which requires accurate channel estimations.

Next, we investigate distinct regimes where the system benefits from varying post-selection strategies. Fig. 3(a) and (b) show that at 6 km and 15.1 km, the key rates with Alice’s Gaussian filter match those without post-selection, as the system parameters were already optimal. In this protocol, Alice’s Gaussian filter attenuates the quantum signal by reducing the modulation variance, which is useful at long distances where photon losses require smaller optimal variances for the GG02 protocol. For shorter distances, where higher modulation variances are preferred, an inverted Gaussian filter can be used to increase the effective variance and optimise key rates. In contrast to the 6 km and 15.1 km regimes, Alice and Bob’s post-selection improves the key rate when experimental parameters are sub-optimal. For example, without post-selection, the chosen parameters yield no positive key rate (solid line, Fig. 3(c)), but Alice’s post-selection makes the key rate positive, surpassing the optimal GG02 rate when Bob also applies post-selection. Similarly, at 39.1 km (transmission of T = 0.17), Alice’s post-selection increased the key rate by 1.7 times (Fig. 3(d)), but Bob’s post-selection did not lead to further improvement, as it is more effective in extreme loss regimes where the GG02 protocol approaches negative key rates.

Fig. 3: Experimental key rates for various channel parameters.

Solid lines represent theoretical key rates of the GG02 protocol with fixed modulation variance, while dashed lines show theoretical key rates with optimal variances. Triangle markers indicate raw key rates before post-selection, circles show key rates after Alice’s post-selection, and the square marker represents results after Bob’s post-selection. a, b show the experimental results at d = 6 km (T = 0.76) and d = 15.1 km (T = 0.50), respectively. For d = 6 km, thermal noise is W_x = 1.02 ± 0.004 SNU and W_p = 1.04 ± 0.004 SNU; for d = 15.1 km, W_x = 1.02 ± 0.002 SNU and W_p = 1.03 ± 0.002 SNU. Key rates before and after Alice’s post-selection overlap, indicating optimal operations. c Key rates at d = 29.1 km (T = 0.26) with thermal noise W_x = 1.02 ± 0.001 SNU and W_p = 1.01 ± 0.001 SNU. The post-selections enhance the key rate which is otherwise negative; as a result, the data without post-selection (triangular marker) does not appear on the logarithmic scale. d Key rates at d = 39.1 km (T = 0.17) with thermal noise W_x = 1.00 ± 0.001 SNU and W_p = 1.00 ± 0.001 SNU, where only Alice’s post-selection was applied, as Bob’s post-selection did not lead to any further improvements in this region. The error bars represent statistical uncertainties in the measured data (see Methods for details).

Integration with state-of-the-art demonstrations

Furthermore, we applied our protocol to state-of-the-art CV-QKD experimental demonstrations and showed improved performance (see Fig. 4(a)). Our protocol increased the key rates of the experimental results of Wang et al.¹³ and Hajomer et al.¹⁶, while doubling the key rate of Zhang et al.¹⁴ and achieving a fivefold improvement for Li et al.⁴⁰ using Alice’s post-selection where the percentage improvements are shown in Table 1. We projected their experimental demonstrations to larger distances by simulating their protocols using the parameters listed in Table 1, assuming these parameters remain constant across all distances. Under these conditions, our protocol extended the effective transmission distance by 42 km for Wang et al.¹³ and Zhang et al.¹⁴, while also enhancing the transmission distance for Hajomer et al.¹⁶ and Li et al.⁴⁰ by 19 km and 23 km, respectively as shown in Fig. 5.

Fig. 4: Key rates of the existing experiments after applying our protocol.

Results are based on the original experimental parameters listed in Table 1. a Key rates from various experiments^13,14,16,40 and the experimental data from Data61 using the CV-QKD setup from Quintessence Labs. Orange boxes represent the key rates before post-selection, purple boxes denote the results after Alice’s post-selection, and the pink box shows the key rate after Bob’s post-selection. b Key rates of Data61 at each step, with a reconciliation efficiency of β = 92.5% (Refer to Supplementary Note II for the derivation of the key rate with heterodyne detection). The error bars indicate statistical uncertainties: for data before post-selection and after Alice’s post-selection, they are derived from experimental fluctuations, while for Bob’s post-selection, they correspond to worst and best-case estimates.

Table 1 Experimental parameters of the state-of-the-art CV-QKD demonstrations

Fig. 5: Simulated key rates for state-of-the-art experiments extended beyond their original demonstration distances.

Solid lines indicate the projected key rates using the experimental parameters, while dashed lines show the key rates when applying our protocol with these same parameters. Triangle markers denote the original experimental results from the cited works. Simulation results are presented for Wang et al.¹³ (42 km improvement), Hajomer et al.¹⁶ (19 km improvement), Zhang et al.¹⁴ (42 km improvement), and Li et al.⁴⁰ (23 km improvement) in (a–d), respectively. Refer to Table 1 for the experimental parameters.

Application to a commercial CV-QKD system

Our protocol was also implemented on the Quintessence Labs qOptica system at Data61, CSIRO Sydney, for a fibre distance of 41.71 km, using heterodyne detection with a modulation variance of approximately 4. Since this variance is close to the optimal value, Alice’s post-selection offered little improvement. However, Bob’s post-selection tripled the original key rate, surpassing the optimal GG02 rate by emulating a better performing channel as shown in Fig. 4(b). This improvement can be explained by considering an entanglement-based experiment where Alice creates a two-mode squeezed vacuum state, sending one arm to Bob and measuring the other. With a Gaussian filter, the best achievable key rate is the optimal GG02 rate, as Gaussian operations cannot distill entanglement⁴¹. Non-Gaussian operations, however, enable entanglement distillation, allowing Bob to outperform the GG02 key rate. This was also observed in Hosseinidehaj et al.²⁷ when the MB-NLA filter was made slightly non-Gaussian. However, since their approach emulates a physical filter, it cannot be made highly non-Gaussian without deviating from its intended function as a noiseless amplifier. In contrast, our protocol offers the flexibility to choose any filter cut-off.

Performance in satellite-to-ground CV-QKD links

Our protocol’s applicability extends beyond terrestrial setups and can be applied to improve satellite-to-ground communication links for CV-QKD. Fig. 6(a) and (b) show how our protocol expands the communication window between the ground station and satellite under varying weather conditions, using the satellite-to-ground link model of Sayat et al.⁴². Assuming the satellite is in Low Earth orbit at 500 km altitude, the orange lines represent the conventional GG02 protocol with a modulation variance of V_mod = 8 SNU, while the purple lines show the results of our protocol with Alice’s post-selection. In good weather (Fig. 6(a)), the GG02 protocol supports communication between the optical ground station (OGS) and satellite at angles from 20^∘ to 160^∘. In contrast, Alice’s post-selection enables communication at all angles, boosting key rates by up to 40 times at the extremes where GG02 achieves the lowest key rates. In poor weather (Fig. 6(b)), our protocol further expands the communication window by 76^∘, achieving a 400-fold improvement in key rates under extreme conditions. In addition to higher key rates, our protocol offers a longer active communication window, defined as the time during which a positive key rate above 10⁻⁴ bits/use is maintained. Traditional CV-QKD protocols using LEO satellites allow for windows of 1.28 h in favourable weather and 38 minutes in poor conditions. In contrast, our protocol extends this window to 3 hours in any weather, maintaining a minimum key rate of 10⁻⁴ bits/use. If a higher key rate threshold were used, the GG02 protocol would have even smaller windows, while our protocol would still provide significantly longer active times (For more details, refer Supplementary Note IV). This showcases that our protocol can be particularly useful in free-space channels, such as satellite-to-ground communication links, where rapid changes in the quantum channel are common.

Fig. 6: Key rates for satellite-to-ground communication as a function of elevation angle.

Results are obtained using our protocol applied to the GG02 scheme with homodyne detection, assuming the satellite orbits at an altitude of 500 km in low-Earth orbit and the optical ground station is at an elevation of 0 km. We used the model and parameters from Sayat et al.⁴² with a reconciliation efficiency of β = 90% (Refer to the Supplementary Note IV for the parameters). a The orange lines represent key rates with a fixed modulation variance of V_mod = 8 SNU, while the purple lines show key rates using our protocol with Alice’s post-selection only. This simulation assumes good weather conditions with a visibility of V = 200 km and low turbulence corresponding to ${C}_{n}^{2}=1{0}^{-16}$ m^−2/3. At each elevation angle, the post-selection gain was optimised to achieve the best key rates. b Key rates under bad weather conditions with a visibility of V = 20 km and high turbulence where ${C}_{n}^{2}=1{0}^{-13}$ m^−2/3. c The duty cycle of our protocol and the GG02 protocol in good weather conditions using a key rate threshold of 10⁻⁴ from (a). d The duty cycle of our protocol and the GG02 protocol in bad weather conditions using a key rate threshold of 10⁻⁴ from (b).

Discussion

QKD plays a crucial role in securing communications against potential eavesdropping in the quantum era. However, challenges such as limited key rates and vulnerability to environmental factors have impeded its practical deployment.

Addressing these issues, we introduced a protocol which enhances CV-QKD by combining post-selection at both Alice and Bob’s stations. This protocol utilises a Gaussian filter at Alice’s end and a non-Gaussian box-like filter at Bob’s end to optimise key rates even under non-ideal conditions. Our approach dynamically adjusts to varying quantum channel conditions, making it particularly effective in free-space channels such as ground-to-satellite communication links.

Experimental results demonstrated significant improvements in key rates when applying our protocol to state-of-the-art CV-QKD systems. We observed up to a five-fold increase in key rates using Alice’s post-selection and tripling of the original key rate with Bob’s post-selection on different systems. Additionally, our protocol extended the communication window between ground stations and satellites, showing robustness under both good and adverse weather conditions. Specifically, under poor weather conditions, our protocol expanded the communication window to all elevation angles and achieved a 400-fold improvement in key rates under extreme conditions.

The ability of our protocol to achieve secure key distribution even in rapidly changing quantum channels highlights its potential for practical implementation in challenging environments. By leveraging software-level modifications without the need for hardware changes, our approach provides a flexible and efficient solution for advancing CV-QKD technology.

Our current work focuses on asymptotic key rates, with potential extensions to account for finite-size effects and composable security. In practical applications, data sizes are finite, and smaller block sizes can adversely affect key rates. Nevertheless, our protocol can be effective in scenarios where block sizes degrade key rate quality; however, a full composable security analysis remains an important direction for future work. As Bob’s post-selection involves a non-Gaussian filter, the security analysis cannot follow the Gaussian extremality. Instead, Eve’s information is bounded by representing her state as a density matrix with some finite truncation in the Fock-number basis. This is computationally demanding and can be challenging if Alice’s variance is too high. A recent paper by Denys et al.⁴³ provides an analytical lower bound on the asymptotic secret key rate for CV-QKD with arbitrary modulation schemes. Extending this to include Bob’s post-selection could bypass the need for density matrices, making the security analysis less time-consuming. In this work, we restrict Eve to Gaussian attacks. However, the optimal eavesdropping strategy in the presence of non-Gaussian post-selection remains an open question. Future studies should consider whether Eve could perform a non-Gaussian attack to compromise the key.

Our protocol could potentially be applied to CV-QKD protocols with discrete modulation (DM CV-QKD)^44,45,46, which utilise a constellation of modulated coherent states. In particular, Bob’s non-Gaussian post-selection could enable dynamic switching between different types of DM CV-QKD protocols by selectively combining states from the constellation of modulated coherent states. While Bob’s post-selection filter is similar in shape to those used in the DM CV-QKD protocol proposed by Kanitschar and Pacher⁴⁷, which demonstrated switching between formats like 8PSK and QPSK, our approach differs in that Alice sends Gaussian-modulated states. This allows Bob to emulate a wider range of modulation formats (e.g., BPSK, QPSK, or multiring) through flexible filter design, enabling more general DM or GM CV-QKD switching.

Methods

Alice’s Gaussian post-selection

The random variables generated by Alice’s function generator follow a Gaussian distribution as described below

$${p}_{a}({x}_{a})=\frac{1}{\sqrt{2\pi {V}_{mo{d}_{x}}}}\exp \left[\frac{-{x}_{a}^{2}}{2{V}_{mo{d}_{x}}}\right],$$

(6)

where ${V}_{mo{d}_{x}}$ represents the modulation variance of Alice along the x quadrature with random variables x_a. The modulation variance of the x and p quadratures are not symmetric due to the experimental imperfections. However, as Bob performs a homodyne measurement, Alice’s Gaussian distribution of the x and p quadrature variables can be expressed individually. In the following, we explicitly present the analysis for the x quadrature, which can be similarly applied to the p quadrature. When Alice applies the filter shown in Eq. (1), the probability of success is given by

$${P}_{{A}_{x}}=\int_{-\infty }^{\infty }{F}_{A}({x}_{a}){p}_{a}({x}_{a})\,d{x}_{a}=\frac{1}{\sqrt{2{g}_{x}^{2}{V}_{mo{d}_{x}}+1}},$$

(7)

where g_x is the gain of the Gaussian filter for the x quadrature. Experimentally, Alice’s filter, as described in Eq. (1), is implemented by generating a random number uniformly distributed between 0 and 1. The filter then retains the variables whose corresponding filter function values are greater than or equal to this random number. The probability of success is determined by the ratio of samples kept after filtering to the total number of samples. For our experiment, the gains were optimised to maximise the key rates. For a distance of 29.1 km, we used g_x = 0.213 and g_p = 0.259, while for a distance of 39.1 km, the gains were g_x = 0.178 and g_p = 0.213.

After Alice’s post-selection, the modulation variance of the effective thermal state is reduced. The equivalent modulation variance is expressed as follows

$${\tilde{V}}_{mo{d}_{x}}=\int_{-\infty }^{\infty }\,\,\frac{{x}_{a}^{2}{F}_{A}({x}_{a}){p}_{a}({x}_{a})}{{P}_{{A}_{x}}}\,d{x}_{a}=\frac{{V}_{mo{d}_{x}}}{2{g}_{x}^{2}{V}_{mo{d}_{x}}+1}.$$

(8)

Alice’s post-selection cannot modify the channel parameters. However, Bob’s effective variance also reduces, as he must disregard the data that Alice discards. Therefore, Bob’s variance, using Alice’s new variance ${V}_{x}={\tilde{V}}_{mo{d}_{x}}+1$, can be expressed as

$${V}_{{b}_{x}}=T({V}_{x}+{\xi }_{x})+(1-T){W}_{x},$$

(9)

where ξ_x is trusted excess noise coming from the state preparation, T is the channel transmittance that is introduced experimentally using a half-wave plate followed by a PBS. This loss is equivalent to a distance of $d=-{\log }_{10}T/0.02$ assuming a loss of 0.2 dB per km. W_x denotes the thermal noise from the quantum channel, attributed to Eve. Similarly, the covariance between Alice and Bob after Alice’s post-selection scales to $T{\tilde{V}}_{mo{d}_{x}}$ in the prepare-and-measure (PM) scheme. QKD protocols can be expressed in either entanglement-based (EB) or prepare-and-measure schemes. While mathematically equivalent^38,48, the EB representation is more convenient for security analysis. Therefore, the new covariance between Alice and Bob in the equivalent EB scheme can be expressed as

$${C}_{x}=\sqrt{T({V}_{x}^{2}-1)}.$$

(10)

The EB-based covariance matrix of the quantum state between Alice and Bob can be written as ref. ⁴⁹ (Refer to Supplementary Note I for the derivation of the PM covariance matrix and Supplementary Note III for derivation of the covariance matrices starting from the EB model)

$${\sigma }_{AB}^{{{{\rm{EB}}}}}=\left(\begin{array}{cccc}{V}_{x}&0&{C}_{x}&0\\ 0&{V}_{p}&0&-{C}_{p}\\ {C}_{x}&0&{V}_{{b}_{x}}&0\\ 0&-{C}_{p}&0&{V}_{{b}_{p}}\end{array}\right).$$

(11)

Note that C_p has the same form as C_x, but with a different variance, V_p. Similarly, Bob’s variance ${V}_{{b}_{p}}$ follows the same formula as Eq. (9), with the variance V_p, trusted noise ξ_p, and thermal noise W_p.

The mutual information between Alice and Bob can be calculated using the EB-based covariance matrix shown in Eq. (11). In our protocol, we employ reverse reconciliation, meaning the direction of classical communication is from Bob to Alice¹⁷. While the direction of reconciliation does not affect the mutual information between Alice and Bob, it influences how much information Eve can access. CV-QKD protocols with reverse reconciliation, unlike direct reconciliation, allow key distribution beyond the 3 dB loss limit^7,50. The mutual information between Alice and Bob is calculated from

$${I}_{A{B}_{x}}=\frac{1}{2}{\log }_{2}\frac{{V}_{{A}_{x}}}{{V}_{{A}_{x}| {B}_{x}}},$$

(12)

where ${V}_{{A}_{x}}$ represents Alice’s variance of the classical data in the EB scheme where she performs a heterodyne measurement on the mode she keeps. This variance is given by ${V}_{{A}_{x}}=({V}_{x}+1)/2$ and ${V}_{{A}_{x}| {B}_{x}}={V}_{{A}_{x}}-{C}_{x}^{2}/(2{V}_{{b}_{x}})$ denotes Alice’s variance conditioned on Bob’s measurement outcomes.

Eve’s average covariance matrix also scales after Alice’s post-selection, as Alice and Bob keep fewer states than originally. As previously mentioned, Eve injects a TMSV state with modes E₁ and E₂. Mode E₁ interacts with incoming signal from Alice, while mode E₂ is retained by Eve. After Alice’s post-selection, the variance of E₁ is updated as follows, while the variance of E₂ remains unchanged

$${V}_{{E}_{{1}_{x}}}=T{W}_{x}+(1-T)({V}_{x}+{\xi }_{x}).$$

(13)

Note that the variance of the p quadrature for this mode follows the same formula, but with Alice’s variance V_p, trusted excess noise ξ_p and a thermal noise of W_p. In practice, there exists a slight discrepancy between W_x and W_p due to the asymmetry in the experimental measurements. This implies that Eve introduces slightly different noise in the x and p quadratures, expressed as W_x and W_p, respectively. To achieve this, Eve must create two separate TMSV states³⁸ and combine them at a 50/50 beamsplitter before interacting with Alice’s signal. Based on these, Eve’s average covariance matrix can be expressed as

$${\sigma }_{{E}_{1}{E}_{2}}=\left(\begin{array}{cccc}{V}_{{E}_{{1}_{x}}}&0&{C}_{{E}_{x}}&0\\ 0&{V}_{{E}_{{1}_{p}}}&0&{C}_{{E}_{p}}\\ {C}_{{E}_{x}}&0&{W}_{x}&0\\ 0&{C}_{{E}_{p}}&0&{W}_{p}\end{array}\right),$$

(14)

where ${C}_{{E}_{x}}=0.5(-{{{{\rm{e}}}}}^{2{r}_{1}}+{{{{\rm{e}}}}}^{2{r}_{2}})$ and ${C}_{{E}_{p}}=0.5(-{{{{\rm{e}}}}}^{-2{r}_{1}}+{{{{\rm{e}}}}}^{-2{r}_{2}})$ where r₁ and r₂ are the squeezing parameters of the TMSV states of Eve which are given by ${r}_{1}=0.5\ln ({W}_{x}+\sqrt{{W}_{x}^{2}-{W}_{x}/{W}_{p}})$ and ${r}_{2}=0.5\ln ({W}_{x}/{W}_{p})-0.5\ln ({W}_{x}+\sqrt{{W}_{x}^{2}-{W}_{x}/{W}_{p}})$. Eve’s information is calculated using the Holevo bound³⁷, which is used to upper bound the information leaked to Eve as shown below

$${I}_{{E}_{x}}=S({\sigma }_{{E}_{1}{E}_{2}})-S({\sigma }_{{E}_{1}{E}_{2}| {B}_{x}}),$$

(15)

where $S({\sigma }_{{E}_{1}{E}_{2}})$ and $S({\sigma }_{{E}_{1}{E}_{2}| {B}_{x}})$ represent the von Neumann entropy of Eve’s average state and Eve’s state conditioned on Bob’s measurement outcome x_b, respectively. Eve’s conditional covariance matrix can be found from⁴⁹

$${\sigma }_{{E}_{1}{E}_{2}| {B}_{x}}={\sigma }_{{E}_{1}{E}_{2}}-\frac{1}{{V}_{{b}_{x}}}{\sigma }_{c}{\Pi }_{x}{\sigma }_{c}^{T},$$

(16)

where Π_x = diag(1, 0) if Bob measures x quadrature and Π_p = diag(0, 1) for p quadrature. σ_c is the covariance terms between Eve and Bob, given as

$${\sigma }_{c}=\left(\begin{array}{cc}{C}_{{E}_{1}{B}_{x}}&0\\ 0&{C}_{{E}_{1}{B}_{p}}\\ {C}_{{E}_{2}{B}_{x}}&0\\ 0&{C}_{{E}_{2}{B}_{p}}\end{array}\right),$$

(17)

where ${C}_{{E}_{1}{B}_{x}}=\sqrt{T(1-T)}\left({W}_{x}-({V}_{x}+{\xi }_{x})\right)$, ${C}_{{E}_{1}{B}_{p}}=\sqrt{T(1-T)}\left({W}_{p}-({V}_{p}+{\xi }_{p})\right)$, ${C}_{{E}_{2}{B}_{x}}=\sqrt{(1-T)}{C}_{{E}_{x}}$ and ${C}_{{E}_{2}{B}_{p}}=\sqrt{(1-T)}{C}_{{E}_{p}}$. Refer to Laudenbach et al.⁴⁹ for the full derivation of σ_c.

The secret key rate is calculated using Eqs. (12) and (15):

$$K=\beta {I}_{AB}-{I}_{E},$$

(18)

where β represents the reconciliation efficiency, with 0 ≤ β < 1. In our experiment, we assume β = 92% when calculating the key rates.

As Bob performs homodyne measurements on the x quadrature half of the time and on the p quadrature the other half, and since the variances and noise parameters differ between these quadratures due to experimental imperfections, Alice and Bob’s mutual information, as well as Eve’s information, must be averaged over both quadratures. This leads to ${I}_{AB}=0.5{P}_{{A}_{x}}\times {I}_{A{B}_{x}}+0.5{P}_{{A}_{p}}\times {I}_{A{B}_{p}}$ and ${I}_{E}=0.5{P}_{{A}_{x}}\times {I}_{{E}_{x}}+0.5{P}_{{A}_{p}}\times {I}_{{E}_{p}}$.

Bob’s non-Gaussian post-selection

Bob’s initial distribution before his post-selection can be expressed as

$${p}_{b}({x}_{b})=\frac{1}{\sqrt{2\pi {V}_{{b}_{x}}}}\exp \left[\frac{-{x}_{b}^{2}}{2{V}_{{b}_{x}}}\right],$$

(19)

where x_b corresponds to Bob’s measurement outcome. Following Alice’s post-selection, Bob applies the filter shown in Eq. (2), which gives a probability of success of

$${P}_{{B}_{x}}=\int_{-\infty }^{\infty }{F}_{B}({x}_{b}){p}_{b}({x}_{b})\,d{x}_{b}=1-{{{\rm{erf}}}}\left[\frac{{c}_{x}}{\sqrt{2{V}_{{b}_{x}}}}\right],$$

(20)

where c_x is the cut-off parameter of the filter function.

Following Bob’s post-selection, his output probability distribution becomes

$${\tilde{p}}_{b}({x}_{b})=\left\{\begin{array}{ll}0\hfill &-{c}_{x} < {x}_{b} < {c}_{x}\\ \frac{{p}_{b}({x}_{b})\hfill}{{P}_{{B}_{x}}} &{{{\rm{elsewhere}}}}.\hfill\end{array}\right.$$

(21)

As Bob’s filter is non-Gaussian, we avoid using the Gaussian extremality as this approach underestimates the secret key rate due to overestimating Eve’s information. Therefore, we propose calculating the absolute bound on Eve’s information directly from her density matrix.

To express Eve’s conditional state shown in Eq. (16) as a density matrix, we first use Williamson’s decomposition, which provides a symplectic matrix s and a diagonal matrix ω, following $s{\sigma }_{{E}_{1}{E}_{2}| {B}_{x}}{s}^{T}=\omega$⁵¹. We then decompose the symplectic matrix, s, further using the Bloch-Messiah decomposition⁵², representing s as a series of beamsplitters, squeezers, and phase rotations: s = s_us_is_v in the covariance matrix notation and S = S_U S_I S_V in the density matrix notation. In our case, both s_u and s_v are expressed through phase rotations and beamsplitters: S_U = R(θ₁, θ₂)B(τ_U)R(θ₃, θ₄) and S_V = R(θ₅, θ₆)B(τ_V)R(θ₇, θ₈), where each parameter needs to be solved. The s_i component is expressed through two-mode squeezing operations, S_I = S(r₁, r₂). Therefore, Eve’s overall conditional density matrix is written in terms of the symplectic density matrix S and a mixed thermal state Λ

$${\rho }_{{E}_{1}{E}_{2}| {B}_{x}}({x}_{b}=0)=S\Lambda {S}^{{{\dagger}} },$$

(22)

where Λ = ρ₁ ⊗ ρ₂, with ρ₁ and ρ₂ being thermal states given by ${\sum }_{n = 0}^{\infty }\frac{{\bar{n}}^{n}}{{(\bar{n}+1)}^{n+1}}| n\left.\right\rangle \!\left\langle \right.n|$, having mean photon numbers ${\bar{n}}_{1}$ and ${\bar{n}}_{2}$, respectively. Note that ${\bar{n}}_{i}=({\lambda }_{i}-1)/2$, where λ_i represents the i^th diagonal terms of the diagonal matrix ω. In our case, ω has two unique diagonal terms, λ₁ and λ₂, which are used to calculate the mean photon numbers ${\bar{n}}_{1}$ and ${\bar{n}}_{2}$.

To calculate Eve’s information, we need to determine her average density matrix, which is the sum of her all conditional matrices over Bob’s measurement outcomes weighted by the probability density for the respective outcome. Given that Bob measures an outcome x_b, Eve’s conditional state is

$$\begin{array}{rcl}{\rho }_{{E}_{1}{E}_{2}| {B}_{x}}({x}_{b})&=&D({\alpha }_{1}({x}_{b}),{\alpha }_{2}({x}_{b})){\rho }_{{E}_{1}{E}_{2}| {B}_{x}}({x}_{b}=0)\\ &&{D}^{{{\dagger}} }({\alpha }_{1}({x}_{b}),{\alpha }_{2}({x}_{b})),\end{array}$$

(23)

where D(α₁(x_b), α₂(x_b)) represents the displacement operator for Eve’s modes 1 and 2 in the form of

$$\begin{array}{rcl}D({\alpha }_{1}({x}_{b}),{\alpha }_{2}({x}_{b}))&=&\exp ({\alpha }_{1}({x}_{b}){a}^{{{\dagger}} }-{\alpha }_{1}({x}_{b})a)\otimes \\ &&\exp ({\alpha }_{2}({x}_{b}){a}^{{{\dagger}} }-{\alpha }_{2}({x}_{b})a),\end{array}$$

(24)

where α₁ and α₂ are functions of Eve’s conditional means based on Bob’s measurement outcomes, x_b. The matrix of Eve’s conditional means is calculated from

$${\mu }_{{E}_{1}{E}_{2}}({x}_{b},{p}_{b})={\sigma }_{c}{\left(\begin{array}{cc}{V}_{{b}_{x}}&0\\ 0&{V}_{{b}_{p}}\end{array}\right)}^{-1}\left(\begin{array}{c}{x}_{b}\\ {p}_{b}\end{array}\right),$$

(25)

where p_b = 0 for homodyne detection when x_b is measured and x_b = 0 when p_b is measured. Therefore ${\alpha }_{1}({x}_{b})={\mu }_{{E}_{1}}({x}_{b})/2$ and ${\alpha }_{2}({x}_{b})={\mu }_{{E}_{2}}({x}_{b})/2$ where ${\mu }_{{E}_{1}}({x}_{b})$ and ${\mu }_{{E}_{2}}({x}_{b})$ are obtained from the entries of the ${\mu }_{{E}_{1}{E}_{2}}({x}_{b},0)$ vector as follows: ${\mu }_{{E}_{1}}({x}_{b})={\mu }_{{E}_{1}{E}_{2}}{({x}_{b},0)}_{1}$ and ${\mu }_{{E}_{2}}({x}_{b})={\mu }_{{E}_{1}{E}_{2}}{({x}_{b},0)}_{3}$.

Although each conditional state has the same entropy, they contribute differently to Eve’s average state due to the varying probabilities of obtaining each conditional state. Therefore, we determine Eve’s average density matrix by multiplying each conditional state with their corresponding probabilities from Bob’s post-selected probability distribution followed by summing them all up. Note that Bob’s probability of getting a given outcome is obtained from

$$p_{b}^{\prime} ({x}_{i})=\int_{{x}_{i}-\Delta }^{{x}_{i}+\Delta }{\tilde{p}}_{b}({x}_{i})\,d{x}_{b}.$$

(26)

To calculate the key rates after the non-Gaussian post-selection, we discretise Eve’s information to determine the conditional states for each of Bob’s measurement outcomes. Therefore, Δ in Eq. (26) is the width of the discretised bins and in our results Δ = 0.1. Consequently, Eve’s average state can be calculated from Eq. (5). Eve’s information is then calculated using the Holevo bound which is

$${I}_{{E}_{x}}=S({\rho }_{{E}_{1}{E}_{2}})-S({\rho }_{{E}_{1}{E}_{2}| {B}_{x}}(0)),$$

(27)

where $S({\rho }_{{E}_{1}{E}_{2}})$ represents the von Neumann entropy for Eve’s average state while $S({\rho }_{{E}_{1}{E}_{2}| {B}_{x}}(0))$ gives the von Neumann entropy of Eve’s conditional state which remains the same irrespective of Bob’s measurement outcome x_b.

In order to find Alice and Bob’s mutual information, the new bivariate Gaussian distribution between Alice and Bob following Alice’s post-selection is fitted to the following function

$${f}_{AB}({x}_{a},{x}_{b}) = \frac{1}{2\pi {\sigma }_{a}{\sigma }_{b}\sqrt{1-{\rho }^{2}}}\\ \exp \left[-\frac{1}{2(1-{\rho }^{2})}\left(\frac{{x}_{a}^{2}}{{\sigma }_{a}^{2}}-\frac{2\rho {x}_{a}{x}_{b}}{{\sigma }_{a}{\sigma }_{b}}+\frac{{x}_{b}^{2}}{{\sigma }_{b}^{2}}\right)\right],$$

(28)

where ${\sigma }_{a}=\sqrt{({V}_{x}+1)/2}$ and ${\sigma }_{b}=\sqrt{{V}_{{b}_{x}}}$ are the standard deviations of Alice and Bob, respectively, and $\rho ={C}_{x}/\sqrt{2{\sigma }_{a}{\sigma }_{b}}$ represents the correlation term between them.

Using Eq. (28), we generate a probability table between Alice and Bob for each values of x_a and x_b where x_a = −15, −15 + Δ, ⋯  , 15 and x_b = − 9, − 9 + Δ, ⋯  , 9. The mutual information then is calculated from

$${I}_{A{B}_{x}}={H}_{{A}_{x}}+{H}_{{B}_{x}}-{H}_{A{B}_{x}},$$

(29)

where ${H}_{{A}_{x}}$, ${H}_{{B}_{x}}$, and ${H}_{A{B}_{x}}$ represent the Shannon entropy of Alice’s classical variable, Bob’s classical variable, and the joint entropy of Alice’s and Bob’s classical variables, respectively.

After Bob’s post-selection ${H}_{A{B}_{x}}$ can be computed from

$$\begin{array}{l}{H}_{A{B}_{x}}=-\sum\limits_{{x}_{a}=-{n}_{a}}^{{n}_{a}}\sum\limits_{{x}_{b}=-{n}_{b}}^{-{c}_{x}-\Delta /2}\frac{{f}_{AB}({x}_{a},{x}_{b})}{{P}_{{B}_{x}}}\\ {\log }_{2}\left[\frac{{f}_{AB}({x}_{a},{x}_{b})}{{P}_{{B}_{x}}}\right]-\sum\limits_{{x}_{a}=-{n}_{a}}^{{n}_{a}}\sum\limits_{{x}_{b}={c}_{x}+\Delta /2}^{{n}_{b}}\frac{{f}_{AB}({x}_{a},{x}_{b})}{{P}_{{B}_{x}}}\\ {\log }_{2}\left[\frac{{f}_{AB}({x}_{a},{x}_{b})}{{P}_{{B}_{x}}}\right],\end{array}$$

(30)

where c_x is the cut-off parameter of Bob’s filter function in Eq. (2); where n_a and n_b represent the maximum number that Alice prepares and Bob measures, respectively.

Alice’s probabilities after Bob’s post-selection can be found from

$${f}_{A}({x}_{a})=\sum\limits_{{x}_{b}=-{n}_{b}}^{-{c}_{x}-\Delta /2}\frac{{f}_{AB}({x}_{a},{x}_{b})}{{P}_{{B}_{x}}}+\sum\limits_{{x}_{b}={c}_{x}+\Delta /2}^{{n}_{b}}\frac{{f}_{AB}({x}_{a},{x}_{b})}{{P}_{{B}_{x}}},$$

(31)

which is used to compute ${H}_{{A}_{x}}$

$${H}_{{A}_{x}}=-\sum\limits_{{x}_{a}=-{n}_{a}}^{{n}_{a}}{f}_{A}({x}_{a}){\log }_{2}\left[{f}_{A}({x}_{a})\right].$$

(32)

Similarly, Bob’s probabilities from the probability table after his post-selection can be found from

$${f}_{B}({x}_{b})=\sum\limits_{{x}_{a}=-{n}_{a}}^{{n}_{a}}\frac{{f}_{AB}({x}_{a},{x}_{b})}{{P}_{{B}_{x}}},$$

(33)

which is used to calculate ${H}_{{B}_{x}}$ as

$$\begin{array}{rcl}{H}_{{B}_{x}}&=&-\sum\limits_{{x}_{b}=-{n}_{b}}^{-{c}_{x}-\Delta /2}{f}_{B}({x}_{b}){\log }_{2}\left[{f}_{B}({x}_{b})\right]-\\ &&\sum\limits_{{x}_{b}={c}_{x}+\Delta /2}^{{n}_{b}}{f}_{B}({x}_{b}){\log }_{2}\left[{f}_{B}({x}_{b})\right].\end{array}$$

(34)

Calculating the final key rate

Since both Alice and Bob perform post-selection, we need to consider the probabilities of success and average the key rates over the x and p quadratures. Following Bob’s filtering process, the average mutual information between Alice and Bob becomes ${I}_{AB}=0.5{P}_{{B}_{x}}{P}_{{A}_{x}}{I}_{A{B}_{x}}+0.5{P}_{{B}_{p}}{P}_{{A}_{p}}{I}_{A{B}_{p}}$. Eve’s information is averaged in the same manner as the mutual information. Finally, the key rate is calculated using Eq. (18) as

$$KR\,=\,0.5{P}_{{B}_{x}}{P}_{{A}_{x}}(\beta {I}_{A{B}_{x}}\,\,-\,{I}_{{E}_{x}})\,+\,0.5{P}_{{B}_{p}}{P}_{{A}_{p}}(\beta {I}_{A{B}_{p}}\,\,-\,{I}_{{E}_{p}})$$

(35)

Error bars

In QKD, key rate calculations typically rely on a worst-case estimation of the channel parameters derived from parameter estimation. In our approach, we fit the raw data to a bivariate Gaussian distribution with the same formula as Eq. (28) within a 95% confidence interval to obtain the values of σ_a, σ_b and ρ. In this case, σ_a and σ_b the standard deviations of Alice’s modulation, $\sqrt{{V}_{mo{d}_{x}}}$, and Bob’s measurement outcomes, $\sqrt{{V}_{{b}_{x}}}$, respectively, while ρ denotes the correlation parameter between Alice and Bob’s data.

Since our data sample is finite, the error bars in the key rates represent statistical errors, calculated by bootstrapping the data. We resample the data 100 times, with 10 million samples in each iteration, effectively simulating the experiment 100 times. The variance across these simulations provides the error bars.