Introduction

Communications based on electromagnetic waves are in place since a century. As such, numerous techniques have been developed to enhance the quality and efficiency of data transmission and reception, all relying on wave propagation principles. One of the most widely used technique, beamforming1,2,3,4, initially conceived for free-space applications, has now been extended to complex and scattering media5. As the propagation medium becomes increasingly complex, free-space models fail to provide accurate descriptions of the propagation media, necessitating more sophisticated and global approaches. Time-reversal techniques, known for their simplicity and remarkable focusing capabilities in complex environments, have been extensively studied since the 1990s, first in acoustics6,7, then in electromagnetism8,9, and more recently in optics through spatial light modulators10,11,12.

In parallel, reconfigurable intelligent surfaces4,13,14,15,16,17,18,19,20,21,22,23 have been introduced to dynamically manipulate wavefronts in complex scattering environments, especially in the microwave regime where wireless telecommunications occur. This paradigm shift promises significant advances in telecommunications, especially in the context of multiple-input multiple-output (MIMO) systems. More recently, this concept has been extended to the acoustic domain24,25,26,27, paving the way for new applications in sound control. However, most existing designs of such metasurfaces operate in relatively narrow frequency bands and are not suited for acoustic purposes where the bandwidth spans several decades of frequencies.

Here, we propose an approach designed for broadband operation in the audible range, specifically targeting speech applications—an inherently ultra-wideband communication scenario. In this study, we extend the idea of a transient metasurface tested in an ultrasonic proof of concept experiment28. We introduce an active acoustic metasurface, whose unit cells are pairs of micro-loudspeakers with tunable impulse responses, thereby realizing the ultimate form of a controllable metasurface: providing complete spatio-temporal control over a broad frequency range, and enabling selective sound addressing between multiple users. Thanks to time-reversal robustness, our system overcomes the limitations of passive architectures and provides a versatile platform for advanced acoustic communication in reverberating environments.

Results

Concept

Let us begin by considering the ideal shape of a room that would allow sound emitted by a source E to be efficiently captured and delivered to a receiver R at a different location within the space. If the walls are assumed to be perfect reflectors, the travel time of all acoustic rays from E to R must remain constant. Given the speed of sound c0 inside the room, the total propagation time for a wave reflecting off a point M on the boundary must satisfy:

$$\frac{{\rm{EM}}}{{c}_{0}}+\frac{{\rm{MR}}}{{c}_{0}}={\rm{constant}}$$
(1)

which directly leads to the geometric constraint EM + MR = 2a. This corresponds precisely to the definition of an ellipsoid with a major axis of 2a, where E and R are located at the two foci (see Fig. 1a). One can notice that we added a glass wall between the emitter and the receiver. This is because we chose not to consider the direct path, as it can be less strong than the reflected sound as observed in an old radome29. Such elliptical architectures have been intentionally used in concert halls and whispering galleries since at least the 17th century to enhance acoustic transmission between two fixed points30,31.

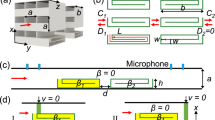
Fig. 1: Focusing sound, physical or electronic concepts.
figure 1

a Classical way to focus sound via reflections (red and green, as examples) coming from an emitter (E) to a receiver (R) using an ellipsoidal room. b Concept of replacing the physical ellipsoidal room by an electronic system made of microphones, speakers and microcontrollers. Two alternative example paths (red and green, respectively) show the sound focusing from the emitter (E) to the receiver (R): the sound is captured by the microphones located at Mj, and transmitted via real time digital convolutions with suited filters \({h}_{{M}_{j}}\) to the receiver room (left room).

Full size image

However, several fundamental limitations arise from this approach. The most immediate is that an ellipsoidal geometry inherently supports only two focal points, restricting its applicability to a single emitter-receiver pair. Another constraint is the structural rigidity of the design, which does not allow for easy adaptation to different focal points. Finally, a more subtle issue is that Equation (1) holds strictly under the assumption of a homogeneous medium; the presence of obstacles, such as furniture, architectural elements, or even the floor, disrupts the perfect focusing of sound waves, significantly altering the intended acoustic behavior.

To overcome all these limitations, we propose replacing the reflective walls of the ellipsoidal room with an electronically controlled system. This system consists of N independent elements, or “atoms” (each referred as Mj), forming a metasurface installed on the walls of the room (see Fig. 1b). Each atom comprises a microphone that records the incoming acoustic wavefield, a digital unit that processes the recorded signal and a speaker that emits the adjusted acoustic waves into the room. Again, we deliberately neglect the uncontrollable direct path between E and R, and we imagine a scenario where the speakers and microphones of each atom are not installed in the same part of the room as shown in Fig. 1b to avoid any spurious feedback loops.

The term of metasurface is appropriate here, despite our particular case implies all the elements being linearly independent since the general concept does not forbid coupling.

To replicate the same time-of-flight conditions as in Equation (1), each atom Mj needs to apply a time delay τj given by:

$${\tau }_{j}=\frac{2a}{{c}_{0}}-\frac{{\rm{E}}{{\rm{M}}}_{j}}{{c}_{0}}-\frac{{{\rm{M}}}_{j}{\rm{R}}}{{c}_{0}}={\rm{constant}}.$$
(2)

However, as previously discussed, this approach remains constrained by the assumption of a homogeneous medium. To generalize beyond this limitation, we introduce the Green’s function \({G}_{E\to {M}_{j}}(t)\), which accounts for wave propagation from the source E to the atom Mj, including all the possible multipath between them. The signal sj(t) recorded by the microphone of atom Mj, given a source signal e(t) emitted at E, can then be expressed as:

$${s}_{j}(t)={G}_{E\to {M}_{j}}(t)* e(t).$$
(3)

Similarly, the propagation from the atom’s speaker to the receiver R is modeled by the Green’s function \({G}_{{M}_{j}\to R}(t)\) which again includes all the reverberation inside the room. Therefore, the received signal at R, assuming that atom Mj emits ej(t), is given by:

$$r(t)=\sum _{{M}_{j}}{G}_{{M}_{j}\to R}(t)* {e}_{j}(t)$$
(4)

By introducing the signal processing operation performed at each atom as a convolution with a finite impulse response filter, \({h}_{{M}_{j}}(t)\), we eventually obtain:

$$r(t)=\sum _{{M}_{j}}{h}_{{M}_{j}}(t)* {G}_{{M}_{j}\to R}(t)* {G}_{E\to {M}_{j}}(t)* e(t)$$
(5)

Thus, rather than relying on the physical shape of the room or fixed time delays, the entire complexity of constructing the desired acoustic pathway is now embedded within the impulse responses \({h}_{{M}_{j}}(t)\) of each atom.

One effective strategy for determining the optimal filters is based on the concept of time reversal7,28. Specifically, convolving a signal g(t) ∗ s(t) with the time-reversed function g(−t) yields ∣G(ω)∣2S(ω) in the frequency domain. This operation modifies the amplitude spectrum of s(t) while preserving its phase, a key property that enables robust focusing without introducing phase distortion. We therefore define the impulse response of each atom’s filter as:

$${h}_{{M}_{j}}(t)={G}_{E\to {M}_{j}}(-t)* {G}_{{M}_{j}\to R}(-t)$$
(6)

This actually corresponds to the convolution of two time-reversal mirrors28: one associated with the receiver R and the other with the emitter E. Beyond their conceptual simplicity, time-reversal techniques have been shown to significantly improve wave focusing in complex and heterogeneous environments9,32,33. By naturally compensating for multipath interference and scattering, this approach enables robust signal focusing where traditional methods often fail. Interestingly, the more complex the propagation medium (e.g., reverberant or multiply scattering), the richer the transient Green’s function between two points, ultimately enhancing focusing performance. Put differently, a longer transient response duration between two points encodes more information, thereby increasing the number of available temporal degrees of freedom34.

However, as shown in equation (6), since the Green’s functions \({G}_{E\to {M}_{j}}(t)\) and \({G}_{{M}_{j}\to R}(t)\) are causal, the corresponding double time-reversal filters \({h}_{{M}_{j}}(t)\) cannot be causal and are therefore unrealizable. The only way we could implement these filters in practice is by introducing a delay of duration T and define \({h}_{{M}_{j}}(t)=0\) for t < 0. This introduces a trade-off between adding delay to the system and preserving as much information from the Green’s functions as possible.

One can also notice the system is not passive and thus, we can amplify the input signal as much as we want.

SISO: Single-input/single-output scenario

To experimentally validate the concept, we use an array of 32 independent “atoms", each consisting of a microphone, a speaker and a microcontroller. Also, note that omnidirectional microphones were deliberately used, as they ensure full reconfigurability and compatibility with multiple sources, even in reverberant environments where no direct path to the source may exist. This sampling rate, together with the hardware bandwidth of the microphones and loudspeakers, sets the practical frequency range of the system, and frequencies up to approximately 22 kHz could thus be supported.

However, the real-time and active nature of this system makes it particularly prone to feedback loops. This undesired effect can be mitigated by reducing the gain of each individual atom, but this would also decrease the signal intensity at the focal point. To address this, as previously explained, we chose to isolate the microphones and speakers of the individual atoms in two separate rooms, effectively eliminating the possibility of feedback.

During an initial calibration step, the Green’s functions \({G}_{E\to {M}_{j}}(t)\) and \({G}_{{M}_{j}\to R}(t)\) need to be measured. To this end, each speaker (both the emitter E and the 32 atoms’ speakers) sequentially emits a frequency sweep (chirp) ranging from 100 Hz to 12 kHz. The responses are recorded at the atom microphones when E emits and at the receiver R when the atoms emit. The recorded transient responses are then correlated with the original chirp to extract the system’s impulse response and approximate the Green’s functions35.

Once extracted, the Green’s functions corresponding to each atom Mj are convolved and subsequently time-reversed to construct the filter functions (Fig. 2). To ensure uniform performance across all frequencies, a frequency equalization step is applied to compensate for variations in the room’s acoustic response and the frequency response of the speakers. The final filter functions \({h}_{{M}_{j}}(t)\) are then loaded into the memory of each microcontroller.

Fig. 2: Making the filters using Green’s functions.
figure 2

a One of the typical Green’s function \({G}_{E{M}_{j}}\) on the emitter side. b One of the typical Green’s function \({G}_{{M}_{j}R}\) on the receiver side. c One of the typical resulting filters. d Photograph of one element, the scale is 20mm.

Full size image

Following acquisition, the processing units switch from recording mode to convolution mode. Each unit continuously convolves the signal received by its microphone with its internal filter function \({h}_{{M}_{j}}(t)\) and immediately retransmits the processed signal through its speaker. This process is executed in real time, without requiring a central clock for synchronization.

To assess the system’s ability to focus acoustic waves, the same chirp is emitted from the emitter E, and the received signals are systematically correlated with the reference chirp, effectively reconstructing an experiment where the emitter would have produced a Dirac delta function (or more specifically, the autocorrelation of the chirp) with an improved signal-to-noise ratio. The resulting transient response (Fig. 3b) exhibits a pronounced peak at t = 0. It needs to be compared to the 350-ms-long coda when the filter functions \({h}_{{M}_{j}}(t)\) are replaced with Dirac delta functions. This confirms successful temporal focusing at the receiver’s location, demonstrating that our system effectively compensates for multipath propagation within the reverberant environment.

Fig. 3: Demonstrating focusing in the Single-input/single-output scenario.
figure 3

a Representative snapshots for five different time of the two-dimensional scan around the receiver’s location consecutive to a Dirac emission from the emitter. The dashed gray circles outline the approximately isotropic spherical wavefront converging toward the focal point x = y = 0 at t = 0. b Measured signal at the focal point revealing a nice broadband temporal focusing. c Cuts along x and y (passing through the focal point) of the two-dimensional scan around the receiver’s location revealing the spatial focusing. d One-dimensional scan around the emitter’s location while the receiver stay at the focal point revealing spatial focusing on the emitter side.

Full size image

To evaluate the spatial focusing properties of the system, we perform a two-dimensional scan around the receiver’s location using a 0.6 m × 0.6 m grid with a step size of 4 mm, while keeping the emitter at the same position. The received signals are again correlated with the reference chirp as before, allowing us to reconstruct instantaneous acoustic field maps near the initial receiver position. Five representative snapshots around t = 0 are shown in Fig. 3a. An approximately isotropic spherical wave (outlined by the dashed gray circle) converging toward the focal point at t = 0 is evidenced. As expected, for positive times, this focused wave transitions into a diverging spherical wave for positive times. While the circular wavefront is visible, a slight asymmetry in energy distribution is observed, with stronger wavefronts propagating from the side facing the wall where the atoms are located (see Supplementary Movie 1 for a video version of this figure).

These observations align well with the theoretical framework of time-reversal acoustics, which predicts that the reconstructed field is the superposition of the advanced and retarded Green’s functions6. The difference here is that the experiment does not refocus back on the initial source position but on a different spot. Consequently, the experiment inherently produces diffraction-limited focal spots36,37. Figure 3C confirms this by demonstrating that the focal width is approximately 11 cm in both the x and y directions. These experimental results alone provide a clear and physically intuitive demonstration of focusing, in full agreement with time-reversal theory, making a full-room numerical simulation both unnecessary and practically unfeasible due to the long reverberation times involved.

The same methodology is applied to analyze the spatial selectivity of sound capture with respect to the emitter position. In this case, we measure the received signal at the initial position of R while systematically scanning the source position around the emitter over a linear displacement ranging from  −15 cm to  +15 cm with a step size of 4 mm while all the atoms are performing their convolution. Figure 3D presents the peak amplitude of the received signals for each source position. The results confirm that the system achieves selective sound capture, with a spatial resolution of ~7.5 cm.

All these results demonstrate the ability of our electronic metasurface to dynamically shape the acoustic field within a reverberant environment, achieving both temporal and spatial focusing of sound in real time. Thanks to the time-reversal robustness, our system effectively compensates for multipath propagation, enabling precise audible sound delivery from one emitter toward one receiver with a resolution of roughly 8 cm, smaller than the human head’s dimension. This is achieved by exploiting the full Green’s functions, allowing precise control of the effective time delays of all virtual sources created by reflections, rather than relying solely on direct paths, which provides ultimate spatio-temporal focusing of broadband sound compared to classical beamforming strategies.

MU-MIMO: multiple-user multiple-input/multiple-output scenario

As previously discussed, one of the main limitations of using ellipsoidal rooms is the inability to accommodate more than one emitter and one receiver. Fortunately, due to its electronic nature, our metasurface is fully capable of establishing communication between multiple sources and receivers. As they operate in real time, we usually refer to as a MU-MIMO (Multiple-user multiple-input/multiple-output) scenario in the context of telecommunications38.

Let us consider two emitters, E1 and E2, and two receivers, R1 and R2. Our system allows to create dedicated links between E1 and R1 as well as E2 and R2 (Fig. 4a). Thanks to the linearity of the underlying equations, we simply propose to sum the corresponding double time-reversal filters:

$${h}_{{M}_{j}}(t)={G}_{{E}_{1}\to {M}_{j}}(-t)* {G}_{{M}_{j}\to {R}_{1}}(-t)+{G}_{{E}_{2}\to {M}_{j}}(-t)* {G}_{{M}_{j}\to {R}_{2}}(-t).$$
(7)

Experimentally, the Green’s functions are recorded and the filters computed exactly as before, with the final filters obtained by summing the individual contributions.

Fig. 4: Demonstrating focusing in the Multiple-user multiple-input/multiple-output scenario.
figure 4

a Establishing independent, selective communication channels between two sources and two receivers (E1 → R1 and E2 → R2). b 2D map of the acoustic energy received around the receivers (R1 and R2 when the two emitters emit white noises. Correlation maps of the two-dimensional scan with the emitted noise by emitter E1 (c) and E2 (d).

Full size image

To test this approach, the speakers E1 and E2 simultaneously emit white noises, while the microcontrollers perform their real-time convolution with the precomputed filters. A microphone scans the 2D transient acoustic field around the two target receiver positions at x = 0, with y = 15 cm for R1 and y = − 15 cm for R2. It is important to note that the noise emitted by each emitter remains the same from point to point in the experimental scan.

The intensity map, obtained by integrating the square of the received signal at each position, is represented as a color-coded image in Fig. 4c. Here, “intensity” denotes the squared envelope of the measured acoustic signals, used as a relative indicator of focusing. Since the system is active and linear, all amplitudes are scalable by a constant factor, and thus the maps reflect spatial selectivity rather than an absolute energy balance. As a result, it reveals two focalization spots at the desired positions of R1 and R2. Furthermore, we can confirm the individual links between E1 → R1 and E2 → R2 by computing the correlation of the measured field with the respective emitted noise signals from E1 (Fig. 4b) and E2 (Fig. 4d). These maps unambiguously demonstrate two distinct focal points: receiver R1 predominantly captures sound from emitter E1, while receiver R2 exclusively receives sound from emitter E2 (see Supplementary Movie 2 for a qualitative demonstration using two musics being played at the same time).

These results confirm the ability of our electronic metasurface to create independent, selective communication channels between multiple sources and receivers within a reverberant environment. The clear separation of the focal spots in Fig. 4 demonstrates that different emitter-receiver pairs can coexist without significant crosstalk, a crucial feature for applications requiring multi-user spatialized sound environments.

Conclusion

In this work, we have demonstrated an electronic approach to sound focusing in a reverberant environment, overcoming the geometric limitations of traditional ellipsoidal architectures. By replacing reflective walls with a metasurface composed of independent acoustic “atoms," we achieved precise temporal and spatial control of sound propagation. Through double time-reversal filtering, our system successfully compensates for multipath propagation and enhances signal focusing, even in highly reverberant conditions.

Experimental validations confirm the ability of our approach to dynamically control the acoustic field, creating well-defined focal points at desired locations. Furthermore, we have shown that multiple independent communication channels can be established between different emitter-receiver pairs without significant interference.

These results pave the way for a range of applications, from immersive audio environments and private communication zones to advanced transient wavefront shaping in complex media. By independently controlling the wavefield at different focal points, and given the focal width observed here, one possible application could be a stereo effect: distinct sound signals can be delivered simultaneously to separate receivers, such as the left and right ears of a listener. Future work will focus on improving real-time adaptability, especially in the case where feedback loops appear when microphones and speakers are in the same room, optimizing filter computation for large-scale implementations, and exploring applications beyond acoustics, such as ultrasound imaging or electromagnetic ultrawide band wireless communications or power transfer.

Methods

Hardware

The microphones used were SPH0645LM4H MEMS, mounted on Adafruit I2S MEMS Microphone Breakout boards, and the speakers were 40-mm-diameter, 4 Ohm, 5 Watt models from Adafruit (model prior to January 22, 2024) with a class D amplifier (MAX98357A mounted on an Adafruit I2S 3W Class D Amplifier Breakout) and an additional  ≈ 4Ω resistor. A custom PCB was used to simplify the assembly of the experiment. The microcontroller used was an ARM Cortex-M7 running at 600 MHz (MIMXRT1062 on a Teensy 4.1 board). To minimize latency, a uniform partitioned convolution algorithm was implemented, with a block size of 128 samples (FFTConvolver C++ library) and a sampling rate of 44.1 kHz.

The sound field was recorded using an AudioBox 44VSL with a t.bone MM-1 microphone and two Creative Inspire T10 speakers.

Signal processing

The system (microphones, speakers, and the room as well) introduces limitations in the bandwidth. To optimize signal dispersion, we need to compensate for the loss at certain frequency values by modifying the spectrum of the filters.

$${h}_{{M}_{j}}(\omega )=H(\omega ){G}_{E\to {M}_{j}}^{* }(\omega ){G}_{{M}_{j}\to R}^{* }(\omega )$$
(8)

with H(ω) being a real quantity. To achieve this, we first perform a focusing test without frequency compensation (using the same chirp as for acquiring the Green’s functions). The recorded sound is then correlated with the chirp, and a moving average with a kernel size of 100 samples is applied to its spectrum, giving a quantity S(ω).

We decided to match the chirp’s spectrum C(ω), so we obtain:

$$H(\omega )=\frac{S(\omega )}{{C}^{2}(\omega )}$$
(9)

An inverse Fourier transform is then applied to return to the time domain.