Abstract
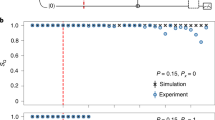
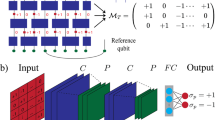
Monitored many-body quantum systems can exhibit a measurement-induced phase transition (MIPT) between entangling and disentangling dynamical phases. Proposed approaches to study the MIPT experimentally typically rely on a classical decoding process, but the complexity of this decoding generally grows exponentially with the system size unless the dynamics is restricted to a fine-tuned set of unitary operators. In this work we overcome this difficulty in the context of tree-shaped quantum circuits. We construct a hybrid circuit with Haar-random unitary operators, and we show that the MIPT can be detected without postselection using a simple decoding process whose complexity grows linearly with the number of qubits. The tree structure also enables a complete theoretical description of the MIPT and all its critical properties. We experimentally realize the MIPT on a trapped-ion quantum computer and show that the results are precisely described by theory without the need for error mitigation.
Similar content being viewed by others
Data availability
Data for this experiment is available at a public Zenodo repository60. We include the measurement outcomes and circuits we used for the experiment.
Code availability
Code for this experiment is available at a public Zenodo repository60. We include code to create the circuits and analyze the data, as well as code for classically simulating the order parameter.
References
Skinner, B., Ruhman, J. & Nahum, A. Measurement-induced phase transitions in the dynamics of entanglement. Phys. Rev. X 9, 031009 (2019).
Li, Y., Chen, X. & Fisher, M. P. A. Quantum zeno effect and the many-body entanglement transition. Phys. Rev. B 98, 205136 (2018).
Chan, A., Nandkishore, R. M., Pretko, M. & Smith, G. Unitary-projective entanglement dynamics. Phys. Rev. B 99, 224307 (2019).
Li, Y., Chen, X. & Fisher, M. P. A. Measurement-driven entanglement transition in hybrid quantum circuits. Phys. Rev. B 100, 134306 (2019).
Choi, S., Bao, Y., Qi, X.-L. & Altman, E. Quantum error correction in scrambling dynamics and measurement-induced phase transition. Phys. Rev. Lett. 125, 030505 (2020).
Gullans, M. J. & Huse, D. A. Dynamical purification phase transition induced by quantum measurements. Phys. Rev. X 10, 041020 (2020).
Bao, Y., Choi, S. & Altman, E. Theory of the phase transition in random unitary circuits with measurements. Phys. Rev. B 101, 104301 (2020).
Jian, C.-M., You, Y.-Z., Vasseur, R. & Ludwig, A. W. W. Measurement-induced criticality in random quantum circuits. Phys. Rev. B 101, 104302 (2020).
Li, Y., Chen, X., Ludwig, A. W. W. & Fisher, M. P. A. Conformal invariance and quantum nonlocality in critical hybrid circuits. Phys. Rev. B 104, 104305 (2021).
Zabalo, A. et al. Critical properties of the measurement-induced transition in random quantum circuits. Phys. Rev. B 101, 060301 (2020).
Gullans, M. J. & Huse, D. A. Scalable probes of measurement-induced criticality. Phys. Rev. Lett. 125, 070606 (2020).
Tang, Q. & Zhu, W. Measurement-induced phase transition: A case study in the nonintegrable model by density-matrix renormalization group calculations. Phys. Rev. Res. 2, 013022 (2020).
Turkeshi, X., Fazio, R. & Dalmonte, M. Measurement-induced criticality in (2+1)-dimensional hybrid quantum circuits. Phys. Rev. B 102, 014315 (2020).
Fan, R., Vijay, S., Vishwanath, A. & You, Y.-Z. Self-organized error correction in random unitary circuits with measurement. Phys. Rev. B 103, 174309 (2021).
Li, Y. & Fisher, M. P. A. Statistical mechanics of quantum error correcting codes. Phys. Rev. B 103, 104306 (2021).
Nahum, A., Roy, S., Skinner, B. & Ruhman, J. Measurement and entanglement phase transitions in all-to-all quantum circuits, on quantum trees, and in Landau-Ginsburg theory. PRX Quantum 2, 010352 (2021).
Li, Y., Vasseur, R., Fisher, M. P. A. & Ludwig, A. W. W. Statistical mechanics model for Clifford random tensor networks and monitored quantum circuits. Phys. Rev. B 109, 174307 (2024).
Lavasani, A., Alavirad, Y. & Barkeshli, M. Measurement-induced topological entanglement transitions in symmetric random quantum circuits. Nat. Phys. 17, 342–347 (2021).
Ippoliti, M., Gullans, M. J., Gopalakrishnan, S., Huse, D. A. & Khemani, V. Entanglement phase transitions in measurement-only dynamics. Phys. Rev. X 11, 011030 (2021).
Lopez-Piqueres, J., Ware, B. & Vasseur, R. Mean-field entanglement transitions in random tree tensor networks. Phys. Rev. B 102, 064202 (2020).
Noel, C. et al. Measurement-induced quantum phases realized in a trapped-ion quantum computer. Nat. Phys. 18, 760–764 (2022).
Ippoliti, M. & Khemani, V. Postselection-free entanglement dynamics via spacetime duality. Phys. Rev. Lett. 126, 060501 (2021).
Li, Y., Zou, Y., Glorioso, P., Altman, E. & Fisher, M. P. A. Cross entropy benchmark for measurement-induced phase transitions. Phys. Rev. Lett. 130, 220404 (2023).
Li, Y., Vijay, S. & Fisher, M. P. Entanglement Domain Walls in Monitored Quantum Circuits and the Directed Polymer in a Random Environment. PRX Quant. 4, 010331 (2023).
Feng, X., Skinner, B. & Nahum, A. Measurement-induced phase transitions on dynamical quantum trees. PRX Quant. 4, 030333 (2023).
Google Quantum AI Collaborators. Measurement-induced entanglement and teleportation on a noisy quantum processor. Nature 622, 481–486 (2023).
Fava, M., Piroli, L., Swann, T., Bernard, D. & Nahum, A. Nonlinear sigma models for monitored dynamics of free fermions. Phys. Rev. X 13, 041045 (2023).
Jian, C.-M., Shapourian, H., Bauer, B. & Ludwig, A. W. W. Measurement-induced entanglement transitions in quantum circuits of non-interacting fermions: Born-rule versus forced measurements (2023). https://arxiv.org/abs/2302.09094.
Agrawal, U. et al. Entanglement and charge-sharpening transitions in u(1) symmetric monitored quantum circuits. Phys. Rev. X 12, 041002 (2022).
Barratt, F., Agrawal, U., Potter, A. C., Gopalakrishnan, S. & Vasseur, R. Transitions in the learnability of global charges from local measurements. Phys. Rev. Lett. 129, 200602 (2022).
Majidy, S. et al. Critical phase and spin sharpening in su(2)-symmetric monitored quantum circuits. Phys. Rev. B 108, 054307 (2023).
Koh, J. M., Sun, S.-N., Motta, M. & Minnich, A. J. Measurement-induced entanglement phase transition on a superconducting quantum processor with mid-circuit readout. Nat. Phys. 19, 1314–1319 (2023).
Ippoliti, M. & Khemani, V. Learnability transitions in monitored quantum dynamics via eavesdropper’s classical shadows. PRX Quantum 5, 020304 (2024).
Akhtar, A. A., Hu, H.-Y. & You, Y.-Z. Measurement-induced criticality is tomographically optimal. Phys. Rev. B 109, 094209 (2024).
Garratt, S. J. & Altman, E. Probing postmeasurement entanglement without postselection. PRX Quantum 5, 030311 (2024).
McGinley, M. Postselection-free learning of measurement-induced quantum dynamics. PRX Quantum 5, 020347 (2024).
Agrawal, U., Lopez-Piqueres, J., Vasseur, R., Gopalakrishnan, S. & Potter, A. C. Observing quantum measurement collapse as a learnability phase transition. Phys. Rev. X 14, 041012 (2024).
Kamakari, H. et al. Experimental demonstration of scalable cross-entropy benchmarking to detect measurement-induced phase transitions on a superconducting quantum processor. Phys. Rev. Lett. 134, 120401 (2025).
Potter, A. C. & Vasseur, R.Entanglement Dynamics in Hybrid Quantum Circuits, 211–249 (Springer International Publishing, Cham, 2022).
Fisher, M. P., Khemani, V., Nahum, A. & Vijay, S. Random quantum circuits. Annu. Rev. Condens. Matter Phys. 14, 335–379 (2023).
Fidkowski, L., Haah, J. & Hastings, M. B. How Dynamical Quantum Memories Forget. Quantum 5, 382 (2021).
Szyniszewski, M., Romito, A. & Schomerus, H. Entanglement transition from variable-strength weak measurements. Phys. Rev. B 100, 064204 (2019).
Szyniszewski, M., Romito, A. & Schomerus, H. Universality of entanglement transitions from stroboscopic to continuous measurements. Phys. Rev. Lett. 125, 210602 (2020).
Côté, J. & Kourtis, S. Qubit vitrification and entanglement criticality on a quantum simulator. Nat. Commun. 13, 7395 (2022).
Feng, X., Fishchenko, N., Gopalakrishnan, S. & Ippoliti, M. Charge and Spin Sharpening Transitions on Dynamical Quantum Trees. Quantum 9, 1692 (2025).
Sommers, G. M., Huse, D. A. & Gullans, M. J. Dynamically generated concatenated codes and their phase diagrams (2024). 2409.13801.
Miller, J. D. & Derrida, B. Weak-disorder expansion for the anderson model on a tree. J. Stat. Phys. 75, 357–388 (1994).
Monthus, C. & Garel, T. Anderson transition on the cayley tree as a traveling wave critical point for various probability distributions. J. Phys. A: Math. Theor. 42, 075002 (2009).
García-Mata, I. et al. Scaling theory of the anderson transition in random graphs: Ergodicity and universality. Phys. Rev. Lett. 118, 166801 (2017).
Shi, Y.-Y., Duan, L.-M. & Vidal, G. Classical simulation of quantum many-body systems with a tree tensor network. Phys. Rev. A 74, 022320 (2006).
Murg, V., Verstraete, F., Legeza, O. & Noack, R. M. Simulating strongly correlated quantum systems with tree tensor networks. Phys. Rev. B 82, 205105 (2010).
Silvi, P. et al. Homogeneous binary trees as ground states of quantum critical hamiltonians. Phys. Rev. A 81, 062335 (2010).
Tagliacozzo, L., Evenbly, G. & Vidal, G. Simulation of two-dimensional quantum systems using a tree tensor network that exploits the entropic area law. Phys. Rev. B 80, 235127 (2009).
Li, W., von Delft, J. & Xiang, T. Efficient simulation of infinite tree tensor network states on the Bethe lattice. Phys. Rev. B 86, 195137 (2012).
Quantinuum H1-1. https://www.quantinuum.com/ (2024).
Derrida, B. & Simon, D. The survival probability of a branching random walk in presence of an absorbing wall. EPL 78, 60006 (2007).
Derrida, B. & Spohn, H. Polymers on disordered trees, spin glasses, and traveling waves. J. Stat. Phys. 51, 817–840 (1988).
Banaszek, K., Cramer, M. & Gross, D. Focus on quantum tomography. N. J. Phys. 15, 125020 (2013).
Sivarajah, S. et al. t∣ket-: a retargetable compiler for NISQ devices. Quantum Sci. Technol. 6, 014003 (2020).
Feng, X., Côté, J., Kourtis, S. & Skinner, B. Data for “postselection-free experimental observation of the measurement-induced phase transition in circuits with universal gates” (2025). https://doi.org/10.5281/zenodo.17516025. Zenodo dataset.
Acknowledgements
We thank Michael Foss-Feig for assistance with running our circuits on the Quantinuum quantum computers and for suggesting the weak measurement circuit construction in Fig. 3c. We thank Zihan Cheng and Matteo Ippoliti for useful discussions. This work was supported by the Ministère de l’Économie, de l’Innovation et de l’Énergie du Québec via its contributions to its Research Chair in Quantum Computing and to the AlgoLab at Institut quantique, Université de Sherbrooke. S.K. and J.C. were supported by a Natural Sciences and Engineering Research Council of Canada Discovery grant. This research used resources of the Oak Ridge Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC05-00OR22725.
Author information
Authors and Affiliations
Contributions
X.F. and J.C. contributed equally. X.F. and J.C. developed the code for the experiment and analyzed the results from numerical simulations and experiment. B.S. and S.K. supervised the project. All authors wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Feng, X., Côté, J., Kourtis, S. et al. Postselection-free experimental observation of the measurement-induced phase transition in circuits with universal gates. Commun Phys (2026). https://doi.org/10.1038/s42005-025-02443-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-025-02443-0