Deep learning for predicting rate-induced tipping

Abstract

Nonlinear dynamical systems exposed to changing forcing values can exhibit catastrophic transitions between distinct states. The phenomenon of critical slowing down can help anticipate such transitions if caused by a bifurcation and if the change in forcing is slow compared with the system’s internal timescale. However, in many real-world situations, these assumptions are not met and transitions can be triggered because the forcing exceeds a critical rate. For instance, the rapid pace of anthropogenic climate change compared with the internal timescales of key Earth system components, like polar ice sheets or the Atlantic Meridional Overturning Circulation, poses significant risk of rate-induced tipping. Moreover, random perturbations may cause some trajectories to cross an unstable boundary whereas others do not—even under the same forcing. Critical-slowing-down-based indicators generally cannot distinguish these cases of noise-induced tipping from no tipping. This severely limits our ability to assess the tipping risks and to predict individual trajectories. To address this, we make the first attempt to develop a deep learning framework predicting the transition probabilities of dynamical systems ahead of rate-induced transitions. Our method issues early warnings, as demonstrated on three prototypical systems for rate-induced tipping subjected to time-varying equilibrium drift and noise perturbations. Exploiting explainable artificial intelligence methods, our framework captures the fingerprints for the early detection of rate-induced tipping, even with long lead times. Our findings demonstrate the predictability of rate-induced and noise-induced tipping, advancing our ability to determine safe operating spaces for a broader class of dynamical systems than possible so far.

Main

Tipping points denote critical thresholds in nonlinear dynamical systems in which changing environmental conditions can lead to a collapse into distinctly different states as a bifurcation point is crossed. This phenomenon has been substantiated through theoretical and observational studies in diverse real-world systems, encompassing the climate system^1,2,3, ecosystems^4,5,6, financial crises⁷ or the human brain⁸. Therefore, a central objective is to detect early warning signals (EWS) that the system may be approaching a tipping point^9,10,11,12.

Dynamical systems theory suggests that when slowly varying external forcing is far from a bifurcation point^2,3,9, often indicated by a threshold value of the forcing, the state of the system remains in the basin of attraction of the quasi-static state. After any minor perturbation, the system will promptly return to its equilibrium state. As a bifurcation-induced tipping approaches, the basin of attraction undergoes a reduction in its curvature (local stability). As a consequence, even slight perturbations begin to exhibit a more prolonged effect in the dynamics, referred to as critical slowing down (CSD)^1,9,13. In particular, in the presence of noise perturbations, this manifests as an increase in variance and lag-1 autocorrelation in the time series data, serving as statistical EWS that often precedes bifurcation-induced tipping events across various systems. Recent advancements have showcased the efficacy of deep learning (DL) techniques in offering EWS for bifurcation-induced tipping^14,15,16,17.

However, in many cases, the changing rate of external forcing is too rapid for the system to maintain its quasi-equilibrium state. In such situations, the collapse can occur unexpectedly, even if there is no bifurcation tipping^2,11. This rate-induced tipping (R-tipping) has been documented across a wide range of dynamical systems^11,18,19. In particular, in the context of anthropogenic climate change, it is probable that the forcing rate is fast compared with the characteristic timescales of key Earth system components that have been suggested to exhibit the tipping potential^3,11,12,20. Unlike bifurcation-induced tipping, R-tipping is not linked to a loss of stability of equilibrium, and the shape of the system’s basin of attraction can remain invariant; no underlying theory exists for anticipating R-tipping, such as CSD in the bifurcation-induced tipping case. R-tipping is characterized by a shift in the attractor occurring at an accelerating rate (Fig. 1). In particular, amid minor disturbances such as noise or within intricate high-dimensional systems, anticipating the occurrence of R-tipping poses a challenge. If the rate of forcing is close to the critical rate required for R-tipping, it depends on the noise realization whether an individual trajectory stays within the basin of attraction of the autonomous system or undergoes a transition across its boundary. Such transitions into an alternative basin can even occur without any change in forcing and have been named noise-induced tipping (N-tipping)². Therefore, the challenge in predicting R-tipping stems from the concurrent involvement of rapidly changing forcing signals and N-tipping mechanisms^11,21,22,23.

Fig. 1: R-tipping visualized through a system represented as a particle in a basin of attraction.

a, Comparison of basins of attraction before (black solid line) and after (black dash line) undergoing a shift due to the change in environmental forcing. When the time-varying rate of environmental forcing change (that is, forcing rate ϵ) is much slower than the critical threshold (ϵ_c), the particle near the basin (its quasi-equilibrium state) can recover and return to the equilibrium state in a timely manner (that is, the stable fixed point). In other words, the forcing rate is sufficiently low for the system to be able to track the basin of attraction associated with that equilibrium. b, When the forcing rate is faster than the critical threshold, the particle cannot track the basin of attraction anymore, and R-tipping occurs. c, When the forcing rate is rapid but stays slightly below the critical threshold, but the system additionally experiences slight noise perturbations, the particle will leave the basin of attraction for some noise realizations, but not for others, establishing a mixture of R-tipping and N-tipping.

As depicted in Fig. 2a, during experimentation on a prototypical R-tipping system, using ensemble simulations with identical time-varying forcing but different instant noise perturbations, part of the realizations exhibit tipping, whereas others do not. The randomness of perturbations precludes the inference of whether a specific realization will undergo tipping based on the system’s equations alone. In this case, the occurrence of R-tipping lacks deterministic dependence on the changing rate of forcing, as evidenced by the broad distribution of R-tipping occurrence times (Methods) (Fig. 2a, bottom). Moreover, on the basis of visual observations, the time series realizations that exhibit R-tipping under noise influence cannot be discriminated from those that do not exhibit tipping before the transition, and it is unreasonable to expect CSD to differentiate between R-tipping and non-tipping realizations. So far, identifying EWS for R-tipping under noise perturbations still proves exceptionally challenging. It is noted that when systems approach tipping points, the phenomena and dynamical mechanisms could become common to both low-dimensional and high-dimensional systems^11,24,25. For instance, the above-mentioned issues about tipping phenomena unexpected by bifurcation theory were also underscored in ensemble simulations of the Atlantic Meridional Overturning Circulation in climate studies^11,26,27. Consequently, these facts raise considerable concern since the concept of a ‘safe operating space’ becomes ambiguous under the risks of R-tipping, especially in policies addressing anthropogenic climate change^11,28,29, and enhancing the resilience of ecosystems^6,18,30. In the context of anthropogenic climate change, the risk of R-tipping may have been greatly underestimated, and so far, no method to anticipate such transitions has been proposed.

Fig. 2: Ensemble simulation results for prototypical R-tipping systems.

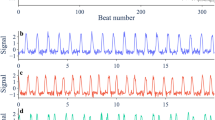
a–c, Ensemble simulations are conducted on the saddle-node system (a), Bautin system (b) and compost-bomb system (c). For each simulated system, the same time-varying forcing parameter is used, but different noise perturbations (sampled from independently and identically distributed white noise) are applied to the simulations. Top panels: the simulated time series that do not tip (blue) and that exhibit R-tipping (red). Middle panels: the time-varying forcing parameter. Bottom panels: the probability density of the observed occurrence time of R-tipping. The blue-shaded area denotes the 99% confidence intervals of the ensemble realizations that do not manifest R-tipping.

Here we aim to improve this situation by predicting R-tipping occurrence among an ensemble of noise perturbations, using DL. We first present a composite analysis to demonstrate that CSD cannot serve as the indicator for discerning R-tipping amidst time-varying external forcing and noise perturbations. Thereafter, we show that the application of an interpretable DL framework can discern the subtle hidden information beyond CSD purely from the data, which enables the detection of the early warning fingerprints preceding R-tipping.

Results

Potential predictability of R-tipping

To reproduce the dynamics of R-tipping, we implement three prototypical example systems from different scientific disciplines. First, we examine a prototypical system for R-tipping introduced in another work² (saddle-node system), incorporating additive white noise perturbations²¹ (Methods). When the system’s basin of attraction shifts slowly due to a time-varying environmental forcing, the system can follow the shifting attraction basin and promptly recover towards equilibrium. Conversely, a very rapid shift in the attractor can cause the system to escape from the basin, leading to R-tipping (Fig. 1b). There exists a theoretical threshold value ϵ_c for the shift rate that triggers R-tipping^2,21. In cases where a shifting basin of attraction and noise perturbations coexist, tipping can manifest even when the shift rate is not as fast as ϵ_c (Fig. 1c). The results presented in Fig. 2a align with such a scenario, and the statistics are derived from 300,000 ensemble realizations, with approximately 37% of them experiencing R-tipping. Specifically, we select 60,000 time series with R-tipping (group A) and an additional 60,000 without tipping (group B) for further analysis.

On the basis of the time of R-tipping occurrences (Methods), for group A, we retain the time series segments before this tipping time. To ensure fairness in statistics, the cut-off point for each time series segment in group B aligns with the corresponding point in group A. Subsequently, we calculate the autocorrelation and variance of the classical CSD indicators (Methods) for each time series and record the composite mean values and 99th percentiles of these metrics within groups A and B, respectively. Results show that the autocorrelations within groups A and B cannot be distinguished over time, evident in both their composite mean values and 99% confidence intervals (Fig. 3a). Regarding the variance, the composite mean values for groups A and B display increasing trends over time, and their 99% confidence intervals substantially overlap. Hence, unlike for the case of bifurcation-induced tipping, CSD cannot discern R-tipping from the non-tipping cases amidst the changing forcing and noise perturbations. CSD can, hence, not serve to anticipate R-tipping. This may be expected since CSD focuses on changes in the linear restoring rate and how that affects the autocorrelation or variance. The underlying assumption that the system remains close to equilibrium and that the linearization around the equilibrium is valid is, by design, broken in the R-tipping context.

Fig. 3: DL-based prediction of R-tipping for paradigmatic systems.

a–c, Saddle-node system (a), Bautin system (b), compost-bomb system (c) and comparison to classical early warning indicators. First row: statistics of simulated time series for indicating the time-varying system states. Second row: estimated autocorrelation evolution. Third row: estimated variance. Fourth row: DL-derived R-tipping probabilities as functions of time. The red solid lines represent the composite mean values of the time series within the class exhibiting R-tipping, and light-red- and red-shaded areas depict the 99% and 75% confidence intervals, respectively. The corresponding non-tipping scenarios are indicated by blue. The unit on the time axis adopts the time step used in numerical integration (Methods).

We also apply two additional prototypical R-tipping systems, each with distinct internal dynamics, to perform similar composite analyses, namely, the Bautin system³¹ and the compost-bomb system³² (see the details in the following sections), revealing that CSD continues to fail to anticipate the transitions (Fig. 3b,c). Note that the increase in autocorrelation and variance may indicate that these two measures reflect the systems’ deviation from equilibrium; however, the way they increase for both tipping and non-tipping cases implies that this information cannot be used to predict if a transition occurs. Moreover, the CSD theory relies on linearizing the dynamics around a given stable equilibrium, so using CSD indicators in cases where the system is not close to equilibrium is not mathematically justified.

Thus, we search for alternative ways to identify a precursor signal in the time series before the R-tipping occurrence. To this end, we first examine the probability distribution of the time series values over 100 time steps preceding the onset of R-tipping for the saddle-node system (Supplementary Fig. 1a), revealing significant differences between R-tipping and non-tipping scenarios preceding the R-tipping occurrence. Although there is overlap in the probability distributions for these two scenarios, distinctions can be observed in the profiles of the probability distributions. We then employ a Kolmogorov–Smirnov significance test to examine whether the probability distribution under the R-tipping scenario is distinguishable from that under the non-tipping scenario. This analysis is performed across various lead times preceding the occurrence of R-tipping (Supplementary Fig. 2a). It is found that significant differences in probability distributions between R-tipping and non-tipping scenarios persist up to 280 time steps before the onset of R-tipping. Similar conclusions are also evident in the analyses conducted for the Bautin system and the compost-bomb system (Supplementary Figs. 1 and 2). This suggests the presence of higher-order statistical information beyond CSD, which can differentiate between R-tipping and non-tipping time series, thereby making R-tipping potentially predictable. We conjecture that these characteristic higher-order statistics represent how far the system in question is away from equilibrium. This encourages us to pursue further investigations to identify valid precursor signals for R-tipping.

DL for predicting R-tipping

Distinguishable features are evident in the probability distributions of ensemble time series before the R-tipping occurrence. However, this information alone does not provide a direct way for determining whether a single time series will exhibit R-tipping under additional noise perturbations. Hence, we hypothesize that feeding these ensemble time series into DL models will enable the extraction of essential features from both probability distributions and time series structures. This, in turn, would facilitate inference on whether a single time series will manifest R-tipping or not. Aiming to establish a DL-based indicator for predicting R-tipping, our DL models integrate a convolutional neural network (CNN) with a fully connected neural network, enabling the extraction of both local and global information from the time series³³. For a specific lead time before the R-tipping occurrence, we correspondingly train a DL model to discern between R-tipping and non-tipping scenarios, such that we can specifically inspect the potential difference between R-tipping and non-tipping scenarios at each forecast lead time. When feeding a time series segment into the trained DL model, the binary outputs represent the probabilities of this time series, at this lead time, to be an R-tipping scenario or a non-tipping scenario (Supplementary Fig. 3). Detailed DL model configurations and training settings are described in the Methods. Here the probability output by the trained DL models is taken to provide a prediction indicator, explaining the real-time probability of the system state to approach R-tipping.

As shown in Supplementary Fig. 4a, comparing two given time series at a given lead time before R-tipping occurs, visual or CSD-based inspection to confirm if they will experience R-tipping is not feasible. CSD indicators show increasing trends in autocorrelation and variance for both R-tipping and non-tipping cases. In contrast, our DL model predicts an increase in R-tipping probability for the time series under the R-tipping scenario, but a decrease for the time series in the non-tipping scenario. Iterating predictions using the trained DL models on time series within the aforesaid groups A and B, the composite results show that this DL-derived R-tipping indicator can clearly distinguish R-tipping (group A) from non-tipping (group B) scenarios, with a long lead time before R-tipping (Fig. 3a, bottom). At each forecast lead time, we employ the Kolmogorov–Smirnov significance test to assess whether the R-tipping probability of group A is distinguishable from those of group B (Supplementary Fig. 2a, bottom). The findings reveal that for up to 290 time steps before the onset of R-tipping in the saddle-node system, the DL-derived R-tipping probabilities in the two groups become distinguishable. This observation aligns with the analysis results regarding the probability distributions of the system states (Supplementary Fig. 2a, top). Consistent conclusions can be drawn regarding the Bautin system and compost-bomb system (Supplementary Fig. 2b,c). According to the Kolmogorov–Smirnov test results, their R-tipping probabilities can be discerned, respectively, at 130 and 1,000 time steps before the onset of R-tipping.

A detailed assessment for the DL prediction results is provided in Supplementary Note 1. By using the trained DL models, the prediction accuracy for R-tipping is enhanced to 60–95%, between 100 and 10 time steps before the onset of R-tipping. It is noteworthy that the prediction accuracy of the DL models shows weak disparity between the training and testing phases (Supplementary Fig. 5), indicating that overfitting is not an issue for our DL model. This observation suggests that the trained DL model has robustly learned the predictive information of R-tipping. Therefore, the predictive capability of our DL model markedly surpasses that of visual inspection on time series and CSD indicators, demonstrating that the model has successfully extracted higher-order statistical information from the time series data.

The feasible predictability of R-tipping can be further substantiated in two additional prototypical systems. The Bautin system features R-tipping in a dynamically different way than the saddle-node system, simulating a periodic attractor that undergoes shifts due to changing external forcing³¹. In addition, the compost-bomb system embodies a prototypical interaction between soil carbon and climate change, capable of exhibiting R-tipping in the context of dynamical feedback³² (Methods). With these two systems, we can investigate R-tipping predictability under conditions with much more internal variability (Supplementary Fig. 4). Despite different internal dynamics compared with the saddle-node system, the combined impact of rapid external forcing and noise perturbations triggering R-tipping is common to all three systems. Similar to the observations in the saddle-node system, the occurrences of R-tipping in the Bautin and compost-bomb systems are subtle and uncertain under their respective dynamics, particularly in the presence of noise perturbations (Fig. 2). Also, for the latter two systems, classical CSD indicators fail to anticipate R-tipping, as expected. Employing a consistent DL configuration and training strategy, the trained DL models, in contrast, provide reliable long-lead forecasts for R-tipping within the Bautin and compost-bomb system (Fig. 3 and Supplementary Fig. 3). This demonstrates that predicting R-tipping probabilities is possible in diverse dynamical systems.

Fingerprints and variability of R-tipping probabilities

Our DL model exhibits a notable ability to differentiate between R-tipping and non-tipping scenarios in advance of the R-tipping occurrence, enabling the prediction of such R-tipping cases. This sparks further interest in understanding the DL model predictions, for example, regarding the question if there is a particular time window during which the system’s state significantly influences the probability of subsequent R-tipping. This hypothesis can be tested by monitoring the pivotal features within the input time series that contribute to the DL model’s ultimate predictions. Here this analysis is facilitated by the layer-wise relevance propagation (LRP) algorithm, guiding the interpretation of DL models^34,35 (Methods). For each forecast lead time, the LRP scores can be considered as a function of time, indicating the relative importance of each time point within the input time series for guiding the prediction of the DL model. We compute the LRP scores for the trained DL models as they process time series from groups A and B. On comparing the 99% confidence intervals of the two groups of LRP scores, evident distinctions emerge in the attention patterns of DL models between R-tipping and non-tipping scenarios (Fig. 4). Regardless of the chosen forecast lead time, the curves of LRP scores consistently exhibit maximum peaks near the end of the time series. This suggests that the R-tipping probability of the system primarily relies on its past neighbouring dynamic states. The position of this R-tipping fingerprint varies with the lead time and depends on the system’s instantaneous dynamical evolution.

Fig. 4: Saliency maps to interpret the fingerprint features that the trained DL models for predicting R-tipping have extracted.

a, Three example time series (from the saddle-node system) approaching R-tipping (red solid, dashed and dotted lines), and the 99% confidence intervals of R-tipping and non-tipping scenarios (red- and blue-shaded areas, respectively). b, Predicted R-tipping probabilities for the three example time series. c, LRP scores for a lead time equal to 0 time steps, indicating the relative importance of each individual time series point for guiding the prediction. The red solid line shows the LRP scores for the time series of example 1. The red- and blue-shaded areas represent the 99% confidence intervals of the LRP scores for the R-tipping and non-tipping scenarios, respectively. The left and right vertical axes denote the LRP values of R-tipping and non-tipping scenarios, respectively. d–f, Mirror configuration of the data in c, corresponding to lead times of 30 (d), 50 (e) and 150 (f) time steps.

For the saddle-node system, another R-tipping fingerprint can be observed: when the forecast lead time is set to 0, 30 and 50, respectively, the curves of LRP scores commonly display peaks within the time window ranging from –100 to –50 time steps (Fig. 4c–e), which are absent in the LRP score profiles of the non-tipping scenario. Further investigation reveals that this fingerprint interprets the dynamical system’s maximum shift rate induced by the instant forcing (Supplementary Note 2). An examination of the LRP scores of a sample time series (Fig. 4, example 1) reveals the close relationship between its temporal R-tipping probability evolution and the pattern of LRP scores: when its LRP score profiles closely resemble those of the R-tipping scenario (Fig. 4c,d), the DL model infers that its R-tipping probability exceeds 50% (Fig. 4b), and vice versa (Fig. 4e). However, when the forecast lead time is extended to 150 time steps, the differences in the LRP scores’ patterns between R-tipping and non-tipping scenarios become smaller (Fig. 4f), and the predictability of R-tipping also gets weaker (Fig. 4b). Similarly, in the Bautin and compost-bomb systems, the LRP analyses also demonstrate informative fingerprints of R-tipping before its onset (Supplementary Figs. 6 and 7), and the changes in LRP scores are consistent with the R-tipping probability.

Prediction accuracy across out-of-sample forcing rates

Next, we assess the performance of our DL models in out-of-sample predictions, that is, to predict R-tipping for forcing rates not encountered during training. Although the above DL models are trained exclusively on time series with a specific forcing rate (ϵ = 1.25), we employ the trained models to predict R-tipping cases with different forcing rates, ranging from ϵ = 0.9 to ϵ = 1.9 (see the forcing time series in Supplementary Fig. 10). The prediction accuracy as a function of the forcing rate and forecast lead time for the saddle-node system (Fig. 5a) demonstrates that the trained DL models can well adapt to the out-of-sample forcing scenarios. With a forecast lead time of 50 time steps, the DL model exhibits higher accuracy in cases featuring lower forcing rates. This can be explained by the fact that time series with lower forcing rates experience earlier increases compared with those with higher forcing rates (Supplementary Fig. 10a). In support of this suggestion, we replace a new training dataset with a higher forcing rate (ϵ = 1.7), and repeat the out-of-sample experiment. As a reference, we also trained the DL models incorporating all the available forcing rates. As shown in Fig. 5a,d,g, the prediction accuracy maps under these three training settings exhibit consistent patterns, demonstrating that the out-of-sample predictions are accurate. Similar conclusions can be drawn from experiments using the compost-bomb system (Fig. 5c,f,i).

Fig. 5: Prediction accuracy of DL models for R-tipping with out-of-sample forcing rates.

a,d, For the saddle-node system, DL models were trained on time series with specific forcing rates of ϵ = 1.25 (a) and ϵ = 1.7 (d), and subsequently used to predict R-tipping cases with previously unseen forcing rates, and the prediction accuracy as a function of forcing rate and forecast lead time is shown. g, For comparison, DL models were trained on time series with all the available forcing rates. b,e,h, For the Bautin system, DL models were trained on forcing rates of r = 0.1 (b), r = 0.06 (e) and all the available forcing rates (h). c,f,i, For the compost-bomb system, DL models were trained on forcing rates of v = 0.1 (c), v = 0.17 (f) and all the available forcing rates (i).

However, in the case of the Bautin system, out-of-sample predictions are not universally successful across all the unseen forcing scenarios. The DL models demonstrate high prediction accuracy primarily for forcing rates that are close to the training forcing rate (Fig. 5b,e). This could be attributed to the Bautin system displaying more complex dynamical modes, as discussed earlier³¹. To improve this situation and constrain the DL models to focus more on R-tipping instead of the complex dynamical modes in the Bautin system, we train the DL models using a specific forcing rate of r = 0.1 in the Bautin system along with additional data from the saddle-node and compost-bomb systems (Fig. 6k). Consequently, the R-tipping predictions for the out-of-sample forcing rates in the Bautin system improved dramatically. This shows that the DL models exhibit transferability and can predict R-tipping probabilities across varying forcing rates and different dynamical systems, even in the presence of timescale separation among these systems (Supplementary Fig. 11). As further evidence for this, the DL models trained with a specific forcing rate of ϵ = 1.25 under the saddle-node system can make skilful predictions for R-tipping cases with previously unseen forcing rates across all the saddle-node, Bautin and compost-bomb systems (Fig. 6a–c). Similar conclusions can be drawn from the experiments with training on the Bautin system and compost-bomb system, too (Fig. 6). We also note that the prediction skills under out-of-sample forcing rates can be further improved when the time series from different dynamical systems were involved during training (Fig. 6j–l). Hence, the trained DL model is able to predict R-tipping probabilities across different forcing rates and different dynamical systems.

Fig. 6: Prediction accuracy of DL models for R-tipping under out-of-sample dynamical systems.

a–c, DL models were trained on time series with a specific forcing rate of ϵ = 1.25 in the saddle-node system, and subsequently used to predict R-tipping cases with previously unseen forcing rates in the saddle-node system (a), Bautin system (b) and compost-bomb system (c). The prediction accuracy is presented as a function of forcing rate and forecast lead time. d–f, DL models trained on data with a forcing rate r = 0.1 in the Bautin system were used to predict R-tipping cases with previously unseen forcing rates in the Saddle-node system (d), Bautin system (e) and Compost-bomb system (f), respectively. g–i, DL models trained on data with a forcing rate v = 0.1 in the compost-bomb system were used to predict R-tipping cases with previously unseen forcing rates in the Saddle-node system (g), Bautin system (h) and Compost-bomb system (i), respectively. j–l, For comparison, DL models were trained on a combined dataset that integrated equal proportions of the above three training datasets, and subsequently used to predict R-tipping cases with previously unseen forcing rates in the Saddle-node system (j), Bautin system (k) and Compost-bomb system (l), respectively.

Discussion

In contrast to the extensive literature on bifurcation-induced tipping, there remains a notable scarcity of methods for anticipating R-tipping. In particular, the well-established CSD framework cannot be used when the rate of forcing is fast compared with the characteristic timescale of the system in question since it assumes that the system dynamics can be linearized around that equilibrium. To fill this gap, we introduced here a skilful DL-based indicator to predict R-tipping amid noise perturbations. To test its performance, we used datasets from prototypical R-tipping systems, affirming the predictability of R-tipping in the presence of noise perturbations with our method. The findings suggest that the DL algorithm can extract high-order statistical information quantifying how far a system is away from equilibrium and, hence, how close it is to crossing the boundary of a given basin of attraction. This information can be readily used to give quantitative probabilities that an R-tipping event is forthcoming and, hence, for predicting such an event.

It is worth noting that two limitations need to be addressed before applying our current DL model to provide ‘generic’ EWS for tipping points in natural systems. On one hand, we conducted predictions for R-tipping and N-tipping on three individual systems. On the other hand, besides R-tipping, there are other tipping phenomena such as global bifurcations^2,36 and tipping transitions from non-equilibrium attractors³⁷ that do not rely on changes to the local stability of equilibrium and would, hence, also not be captured by CSD. We prospect that a comprehensive DL model could be taken to provide precursor signals across diverse tipping phenomena and systems, as well as distinguish between them in terms of their different forcing scenarios, purely based on the data. Achieving this would involve training the model on an extended dataset that encompasses those dynamics. By doing so, such a general DL model for tipping prediction should be expected to better identify the boundary of the safe operating space of a given system, in terms of the position of critical forcing thresholds as well as critical rates of forcing. This would enable a comprehensive quantification of tipping risk in natural systems.

By utilizing interpretable DL techniques, we identified the presence and location of the precursory fingerprint of R-tipping in a time series; however, we did not delve deeply into the characteristics of this fingerprint. This limitation is partly attributed to the one-dimensional nature of the time series data, which restricts visual observations. A more in-depth analysis may necessitate the application of high-order statistical theories and techniques^38,39,40,41. It can be speculated that for a three-dimensional field, such as in studies on the Atlantic Meridional Overturning Circulation^42,43, the characteristics of an R-tipping fingerprint could be presented in both spatial and temporal dimensions, allowing for a more nuanced observation and understanding of its nature and content. The adequate disclosure of precursory fingerprints for tipping points is valuable for further exploring and understanding the subtle dynamics of complex systems^13,43,44,45. Leveraging interpretable DL techniques would greatly benefit these efforts.

For the time series data considered here, our model utilizes a framework based on one-dimensional CNNs and employs the LRP approach for interpreting the results. We also experimented with multilayer perceptron³³, long short-term memory^14,46 and self-attention⁴⁷ architectures for the DL model. Although these architectures achieved satisfactory predictive performance for R-tipping (Supplementary Fig. 12), a comparative analysis showed that our current framework performs better. Nevertheless, this suggests that our results are robust and not specific to the exact model architecture. Furthermore, we extended our model to handle multivariate inputs by incorporating two-dimensional variables from the Bautin and compost-bomb systems (Supplementary Fig. 13). Our DL method successfully predicted R-tipping in these two-dimensional scenarios, too. This indicates that the method can potentially be extended to datasets with multidimensional variables, but in fact also suggests that the DL model is capable of predicting R-tipping, although it only shows one of the two relevant dynamical variables.

An important consideration in our study is that we specifically observe the predictability and fingerprint of R-tipping amidst noise perturbations at different time points before its occurrence. This theoretically allows for a better exploration of the predictability of R-tipping. However, this assumes that we already know the time of R-tipping occurrence. In practical predictions, we may not be aware of how far our prediction time point is from the occurrence of R-tipping. To address this issue in future work, one might focus in more detail on the results of the LRP application, which carry additional information. This approach would require more specific knowledge and description of the characteristics of the fingerprints. Moreover, the DL model framework could be modified by allowing the states of neurons in the model to update continuously with new time points of the input time series, thereby providing continuous predictions of R-tipping probabilities for various time points in the time series. This would place higher demands on the information extraction capabilities of the model framework.

In summary, many real-world systems, such as ecosystems or climate subsystems, may be prone to tipping induced by a combination of rate- and noise-induced effects. For example, given the pace of anthropogenic climate change, it may be argued that combinations of rate- and noise-induced effects are more relevant than bifurcation-induced effects when assessing tipping risk in the climate change context. Noise perturbations may trigger transitions even in cases where the forcing of a system under study is below the critical rate. Bifurcation-induced tipping can be predicted based on the phenomenon of CSD, for which a well-established mathematical theory exists³. DL approaches have recently been shown to outperform CSD-based ones in some cases^14,17,48. In contrast, for R-tipping, no underlying theory exists and DL, as proposed here, is so far the only effective prediction method for R-tipping and N-tipping, independent of specific neural network frameworks. We have shown that the proposed DL model possesses transferability across varying forcing rates and different dynamical systems.

Methods

Prototypical systems for R-tipping

We examined the R-tipping dynamics using data from three paradigmatic systems, each manifesting R-tipping under different internal dynamical variabilities. The equations governing these systems are given here, which have been integrated to provide time series data for our comprehensive analyses. The first system stems from the normal form for saddle-node bifurcation^2,21, incorporating additional noise perturbations:

$${\rm{d}}{X}_{t}=[{({X}_{t}+\lambda (t))}^{2}-1]{\rm{d}}t+\sqrt{2{D}_{1}}d{W}_{1t}.$$

(1)

The system state X_t is shifted by the forcing term λ(t), and it follows λ(t) = 0.5λ_max[tanh(0.5λ_maxϵt) + 1], in which λ_max = 3 and the time-varying rate of λ(t) is controlled by ϵ (that is, the forcing rate). The white noise term dW_1t, increments of a Wiener process W₁, represents the slight perturbation, and D₁ = 0.008 determines its magnitude. In the absence of noise perturbations, ϵ_c = 4/3 determines the threshold of ϵ for triggering R-tipping. But in the presence of noise perturbations, R-tipping can happen by chance when ϵ takes a smaller value than ϵ_c, and here ϵ is set to 1.25 to allow such phenomena.

The employed Bautin system involves a branch of periodic attractors³¹, subjected to additional noise perturbations, as follows:

$$\begin{array}{rcl}{\rm{d}}{Z}_{t}&=&(a+{\rm{i}}\omega )[{Z}_{t}-\varLambda (t)]{\rm{d}}t-b{[{Z}_{t}-\varLambda (t)]}^{2}[{Z}_{t}-\varLambda (t)]{\rm{d}}t\\ &&+{[{Z}_{t}-\varLambda (t)]}^{4}[{Z}_{t}-\varLambda (t)]{\rm{d}}t+{D}_{2}{\rm{d}}{W}_{2t},\end{array}$$

(2)

where the complex number Z_t = X_t + iY_t denotes the system state and Λ(t) is the forcing term, following Λ(t) = 0.5Λ_max[tanh(0.5Λ_maxrt) + 1] . The forcing rate is controlled by r, with r set to a small value of 0.1, far from the threshold required to trigger R-tipping in the absence of noise. D₂ = 0.2 determines the magnitude of white noise dW_2t that slightly perturbs the system. The rest of the parameters are set to Λ_max = 8, a = 0.1, ω = 3 and b = 1.

The third system is the compost-bomb model³², also with additional noise perturbations applied to the system state:

$$\begin{array}{rcl}&&{\rm{d}}{C}_{t}=\Pi {\rm{d}}t-{C}_{t}{r}_{0}{{\rm{e}}}^{\alpha t}{\rm{d}}t\\ &&\mu {\rm{d}}{T}_{t}={C}_{t}{r}_{0}{{\rm{e}}}^{\alpha t}A{\rm{d}}t-\lambda [{T}_{t}-{T}_{{\rm{a}}}(t)]{\rm{d}}t+{D}_{3}{\rm{d}}{W}_{3t}\end{array}.$$

(3)

For this system, T_a(t) denotes the forcing from atmospheric temperature warming, following T_a(t) = vt. T_t is the soil temperature, which undergoes a coupled feedback process with soil respiration rate r₀e^αt and soil carbon C_t. v = 0.1 denotes the time-varying rate of forcing T_a(t), under which R-tipping will not occur in the absence of noise. D₃ = 0.5 determines the magnitude of noise perturbations dW_3t. For the remaining parameters, their definitions and chosen values in this study are provided in Supplementary Table 1.

The stochastic differential equations were numerically integrated by an Euler–Maruyama scheme to obtain the time series data. The integration step for the saddle-node system and Bautin system is 0.01, whereas for the compost-bomb system, it is 0.1. For each of the three systems, we repeated the simulations for 200,000 runs, each run incorporating a different realization of white noise. This enabled ensemble simulations, resulting in 200,000 distinct time series for subsequent analysis.

Data preprocessing

We initially selected the time series from the ensemble simulation dataset that displayed R-tipping, characterized by values abruptly increasing far beyond the upper limit of the distribution range for non-tipping time series. For the saddle-node, Bautin and compost-Bomb systems, the selection criteria are that the end value of the time series exceeds 0, 10 and 30, respectively (Fig. 2). Conversely, the ensemble time series without R-tipping evolve following similar trajectories, in which a time series envelope for the non-tipping scenario can be identified (Fig. 2a, grey-shaded area). To determine the occurrence time of R-tipping for each time series, we identified it as the moment when a time series surpasses the envelope of the non-tipping time series. For each time series that manifests R-tipping, their R-tipping times vary widely. Accordingly, we truncated the time series at the point in time at which R-tipping occurs, and marked that moment as time 0. The time series segment before this point was retained, allowing us to explore common patterns preceding the occurrence of R-tipping. For each dataset generated for the three simulated systems, we categorized them into group A and group B, corresponding to R-tipping and non-tipping scenarios. In the case of the compost-bomb system, all the time series exhibit a common linear trend with the same slope (Fig. 2c). Consequently, we removed this linear trend from each time series before proceeding with subsequent truncation and grouping. For the saddle-node and Bautin systems, we compared the experimental results between detrended and non-detrended data, and found no difference in the prediction skill.

Calculating CSD indicators

Autocorrelation and variance calculations for all the time series followed the same procedure. Each time series underwent nonlinear detrending using a running mean with a window size of 100 time steps. Subsequently, the CSD indicators were computed within a sliding window of 120 time steps, in which the variance and autocorrelation are calculated using the standard way^3,9. We experimented with different sizes for the sliding window, ranging from 60 to 200 time steps. The resulting CSD indicators did not show significant divergence, and the insights for the inferences remained consistent.

Configurations for DL

We utilized a CNN-based framework to construct our DL model for predicting R-tipping. As illustrated in Supplementary Fig. 3, the model is composed of two one-dimensional CNN layers and one fully connected network layer, with average pooling procedures connecting them. The models were implemented using PyTorch 1.12.0. The convolution kernel sizes and filters were uniformly set as 3 and 64, respectively. The cross-entropy loss function and stochastic gradient descent optimizer were adopted, and the learning rate was set to 0.01. When a time series segment is input into the DL model, the sliding convolution process extracts local information from the data, whereas the fully connected network can handle the global information of the data, through which we expect that the DL model can discern predictive information for R-tipping from the data. We provide detailed descriptions of the tasks for each model during the analysis of the results. For training each model, we set the number of samples in the training dataset, validation dataset and testing dataset to 97,200, 10,800 and 12,000, respectively. During training, we experimented with different hyperparameters and selected the settings that achieved optimal performance on the validation dataset. Training is stopped when the model’s performance on the validation set does not improve for five consecutive epochs. We conducted cross-validation on the DL models (Supplementary Fig. 14), demonstrating that the sample size of the used dataset is sufficiently large to ensure that the training converged to a stable configuration.

The prediction accuracy of the DL model is determined by calculating the ratio between correctly predicted cases and the total number of cases of R-tipping and non-tipping groups. A prediction case is considered correct when the predicted R-tipping probability of an R-tipping case is higher than 50%, or that of a non-tipping case is lower than 50%.

We employ LRP to interpret the decision-making process of our DL framework in classifying the time series into tipping and non-tipping cases. For a trained DL model and the input time series, the process begins with a forward pass through the neural network layers to obtain the prediction. Once the prediction is made, relevance scores are initialized at the output layer. The relevance scores are then propagated backwards through the network, layer by layer. During this backward pass, the relevance scores are redistributed from neurons in the current layer to neurons in the preceding layer. The propagation continues through all layers within the DL model, including fully connected, pooling and convolutional layers, until the input layer is reached. The aggregated relevance scores at the input layer (shown as LRP scores in Fig. 4) indicate the contribution of each input feature to the final prediction, providing a clear understanding of which features of the input data were the most influential in the DL model’s output. The process of relevance propagation in LRP is mathematically intricate, involving the application of rules and formulas to distribute relevance backward through the layers. Here we do not present its mathematical content. More detailed information on the LRP algorithm can be found in existing literature^34,35.