Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Kernel approximation using analogue in-memory computing

Nature Machine Intelligence volume 6, pages 1605–1615 (2024)Cite this article

Subjects

An Author Correction to this article was published on 21 January 2025

This article has been updated

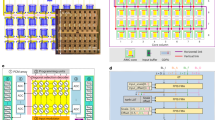
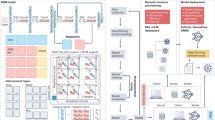
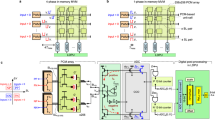
Abstract

Kernel functions are vital ingredients of several machine learning (ML) algorithms but often incur substantial memory and computational costs. We introduce an approach to kernel approximation in ML algorithms suitable for mixed-signal analogue in-memory computing (AIMC) architectures. Analogue in-memory kernel approximation addresses the performance bottlenecks of conventional kernel-based methods by executing most operations in approximate kernel methods directly in memory. The IBM HERMES project chip, a state-of-the-art phase-change memory-based AIMC chip, is utilized for the hardware demonstration of kernel approximation. Experimental results show that our method maintains high accuracy, with less than a 1% drop in kernel-based ridge classification benchmarks and within 1% accuracy on the long-range arena benchmark for kernelized attention in transformer neural networks. Compared to traditional digital accelerators, our approach is estimated to deliver superior energy efficiency and lower power consumption. These findings highlight the potential of heterogeneous AIMC architectures to enhance the efficiency and scalability of ML applications.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Proposed in-memory kernel approximation technique.
Fig. 2: Experimental results for the hardware-accelerated approximations of the RBF and arc-cosine kernel.
Fig. 3: Schematic overview of in-memory kernel approximation for MHA.

Similar content being viewed by others

Data availability

The data that support the plots within this article and other findings of this study are available at https://github.com/IBM/kernel-approximation-using-analog-in-memory-computing. The LRA dataset is available at https://github.com/google-research/long-range-arena. The datasets ‘ijcnn01’, ‘skin’, ‘cod-rna’ and ‘cov-type’ are available at https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html. The datasets ‘magic04’, ‘letter’ and ‘EEG’ are available at https://archive.ics.uci.edu/datasets. The synthetic dataset is available at https://ibm.box.com/shared/static/c3brah3t04o8ruixb4m7z94e2rylsz8o.zip.

Code availability

The code used to generate the results of this study is available at https://github.com/IBM/kernel-approximation-using-analog-in-memory-computing (ref. 78).

Change history

References

  1. Scholkopf, B. & Smola, A. J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond (MIT, 2001).

  2. Hofmann, T., Schölkopf, B. & Smola, A. J. Kernel methods in machine learning. Ann. Stat. 36, 1171–1220 (2008).

    Article  MathSciNet  MATH  Google Scholar 

  3. Boser, B. E., Guyon, I. M. & Vapnik, V. N. A training algorithm for optimal margin classifiers. In Proc. Fifth Annual Workshop on Computational Learning Theory (ed. Haussler, D) 144–152 (ACM, 1992).

  4. Drucker, H., Burges, C. J. C., Kaufman, L., Smola, A. & Vapnik, V. Support vector regression machines. In Proc. Advances in Neural Information Processing Systems (eds Mozer, M. et al.) 155–161 (MIT, 1996).

  5. Schölkopf, B., Smola, A. J. & Müller, K.-R. in Advances in Kernel Methods: Support Vector Learning (eds Burges, C. J. C. et al.) Ch. 20 (MIT, 1998).

  6. Liu, F., Huang, X., Chen, Y. & Suykens, J. A. Random features for kernel approximation: aA survey on algorithms, theory, and beyond. IEEE Trans. Pattern Anal. Mach. Intell. 44, 7128–7148 (2021).

    Article  MATH  Google Scholar 

  7. Rahimi, A. & Recht, B. Random features for large-scale kernel machines. In Proc. Advances in Neural Information Processing Systems (eds Platt, J. et al.) (Curran, 2007).

  8. Yu, F. X. X., Suresh, A. T., Choromanski, K. M., Holtmann-Rice, D. N. & Kumar, S. Orthogonal random features. In Proc. Advances in Neural Information Processing Systems (eds Lee, D. et al.) (Curran, 2016).

  9. Choromanski, K., Rowland, M. & Weller, A. The unreasonable effectiveness of structured random orthogonal embeddings. In Proc. 31st International Conference on Neural Information Processing Systems (eds von Luxburg et al.) 218–227 (Curran, 2017).

  10. Le, Q., Sarlós, T. & Smola, A. Fastfood: Approximating kernel expansions in loglinear time. In Proc. 30th International Conference on Machine Learning (eds Dasgupta, S. & McAllester, D.) III–244–III–252 (JMLR, 2013).

  11. Avron, H., Sindhwani, V., Yang, J. & Mahoney, M. W. Quasi-monte carlo feature maps for shift-invariant kernels. J. Mach. Learn. Res. 17, 1–38 (2016).

    MathSciNet  MATH  Google Scholar 

  12. Lyu, Y. Spherical structured feature maps for kernel approximation. In Proc. 34th International Conference on Machine Learning (eds Precup, D. & Teh, Y. W.) 2256–2264 (JMLR, 2017).

  13. Dao, T., Sa, C. D. & Ré, C. Gaussian quadrature for kernel features. In Proc. 31st International Conference on Neural Information Processing Systems (eds von Luxburg et al.) 6109–6119 (Curran, 2017).

  14. Li, Z., Ton, J.-F., Oglic, D. & Sejdinovic, D. Towards a unified analysis of random Fourier features. J. Mach. Learn. Res. 22, 1–51 (2021).

    MathSciNet  MATH  Google Scholar 

  15. Sun, Y., Gilbert, A. & Tewari, A. But how does it work in theory? linear SVM with random features. In Proc. Advances in Neural Information Processing Systems (eds Bengio, S. et al.) 3383–3392 (Curran, 2018).

  16. Le, Q., Sarlos, T. & Smola, A. Fastfood - computing Hilbert space expansions in loglinear time. In Proc. 30th International Conference on Machine Learning (eds Dasgupta, S. & McAllester, D.) 244–252 (JMLR, 2013).

  17. Pennington, J., Yu, F. X. X. & Kumar, S. Spherical random features for polynomial kernels. In Proc. Advances in Neural Information Processing Systems (eds Cortes, C. et al.) (Curran, 2015).

  18. Avron, H., Sindhwani, V., Yang, J. & Mahoney, M. W. Quasi-Monte Carlo feature maps for shift-invariant kernels. J. Mach. Learn. Res. 17, 1–38 (2016).

    MathSciNet  MATH  Google Scholar 

  19. Ailon, N. & Liberty, E. An almost optimal unrestricted fast Johnson-lLndenstrauss transform. ACM Trans. Algorithms 9, 1–12 (2013).

    Article  MATH  Google Scholar 

  20. Cho, Y. & Saul, L. Kernel methods for deep learning. In Proc. Advances in Neural Information Processing Systems (eds Bengio, Y. et al.) (Curran, 2009).

  21. Gonon, L. Random feature neural networks learn black-scholes type PDEs without curse of dimensionality. J. Mach. Learn. Res. 24, 8965–9015 (2024).

    MathSciNet  MATH  Google Scholar 

  22. Xie, J., Liu, F., Wang, K. & Huang, X. Deep kernel learning via random Fourier features. Preprint at https://arxiv.org/abs/1910.02660 (2019).

  23. Zandieh, A. et al. Scaling neural tangent kernels via sketching and random features. In Proc. Advances in Neural Information Processing Systems (eds Ranzato, M. et al.) 1062–1073 (Curran, 2021).

  24. Laparra, V., Gonzalez, D. M., Tuia, D. & Camps-Valls, G. Large-scale random features for kernel regression. In Proc. IEEE International Geoscience and Remote Sensing Symposium 17–20 (IEEE, 2015).

  25. Avron, H. et al. Random Fourier features for kernel ridge regression: approximation bounds and statistical guarantees. In Proc. 34th International Conference on Machine Learning (eds Precup, D. & Teh, Y. W.) 253–262 (JMLR, 2017).

  26. Sebastian, A., Le Gallo, M., Khaddam-Aljameh, R. & Eleftheriou, E. Memory devices and applications for in-memory computing. Nature Nanotechnol. 15, 529–544 (2020).

    Article  Google Scholar 

  27. Lanza, M. et al. Memristive technologies for data storage, computation, encryption, and radio-frequency communication. Science 376, eabj9979 (2022).

    Article  MATH  Google Scholar 

  28. Mannocci, P. et al. In-memory computing with emerging memory devices: status and outlook. APL Mach. Learn. 1, 010902 (2023).

    Article  Google Scholar 

  29. Biswas, A. & Chandrakasan, A. P. Conv-sram: an energy-efficient sram with in-memory dot-product computation for low-power convolutional neural networks. IEEE J. Solid-State Circuits 54, 217–230 (2019).

    Article  MATH  Google Scholar 

  30. Merrikh-Bayat, F. et al. High-performance mixed-signal neurocomputing with nanoscale floating-gate memory cell arrays. IEEE Trans. Neural Netw. Learn. Syst. 29, 4782–4790 (2018).

    Article  MATH  Google Scholar 

  31. Deaville, P., Zhang, B., Chen, L.-Y. & Verma, N. A maximally row-parallel mram in-memory-computing macro addressing readout circuit sensitivity and area. In Proc. 47th European Solid State Circuits Conference 75–78 (IEEE, 2021).

  32. Le Gallo, M. et al. A 64-core mixed-signal in-memory compute chip based on phase-change memory for deep neural network inference. Nature Electron. 6, 680–693 (2023).

    Article  MATH  Google Scholar 

  33. Cai, F. et al. A fully integrated reprogrammable memristor–cmos system for efficient multiply–accumulate operations. Nature Electron. 2, 290–299 (2019).

    Article  MATH  Google Scholar 

  34. Wen, T.-H. et al. Fusion of memristor and digital compute-in-memory processing for energy-efficient edge computing. Science 384, 325–332 (2024).

    Article  MATH  Google Scholar 

  35. Ambrogio, S. et al. An analog-AI chip for energy-efficient speech recognition and transcription. Nature 620, 768–775 (2023).

    Article  MATH  Google Scholar 

  36. Jain, S. et al. A heterogeneous and programmable compute-in-memory accelerator architecture for analog-AI using dense 2-d mesh. IEEE Trans. Very Large Scale Integr. VLSI Syst. 31, 114–127 (2023).

    Article  MATH  Google Scholar 

  37. Choquette, J., Gandhi, W., Giroux, O., Stam, N. & Krashinsky, R. NVIDIA A100 tensor core GPU: performance and Innovation. IEEE Micro. 41, 29–35 (2021).

    Article  Google Scholar 

  38. Choromanski, K. M. et al. Rethinking attention with performers. In Proc. International Conference on Learning Representations (Curran, 2020).

  39. Browning, N. J., Faber, F. A. & Anatole von Lilienfeld, O. GPU-accelerated approximate kernel method for quantum machine learning. J. Chem. Phys. 157, 214801 (2022).

    Article  MATH  Google Scholar 

  40. Liu, S. et al. Hardsea: hybrid analog-reram clustering and digital-sram in-memory computing accelerator for dynamic sparse self-attention in transformer. IEEE Trans. Very Large Scale Integr. VLSI Syst. 32, 269–282 (2024).

    Article  MATH  Google Scholar 

  41. Yazdanbakhsh, A., Moradifirouzabadi, A., Li, Z. & Kang, M. Sparse attention acceleration with synergistic in-memory pruning and on-chip recomputation. In Proc. 55th Annual IEEE/ACM International Symposium on Microarchitecture 744–762 (IEEE, 2023).

  42. Reis, D., Laguna, A. F., Niemier, M. & Hu, X. S. Attention-in-memory for few-shot learning with configurable ferroelectric fet arrays. In Proc. 26th Asia and South Pacific Design Automation Conference 49–54 (IEEE, 2021).

  43. Vasilopoulos, A. et al. Exploiting the state dependency of conductance variations in memristive devices for accurate in-memory computing. IEEE Trans. Electron Devices 70, 6279–6285 (2023).

    Article  MATH  Google Scholar 

  44. Büchel, J. et al. Programming weights to analog in-memory computing cores by direct minimization of the matrix-vector multiplication error. IEEE J. Emerg. Sel. Top. Circuits Syst. 13, 1052–1061 (2023).

    Article  MATH  Google Scholar 

  45. Vovk, V. in Empirical Inference: Festschrift in honor of Vladimir N. Vapnik (ed. Schölkopf, B. et al.) Ch. 8 (Springer, 2013).

  46. Vaswani, A. et al. Attention is all you need. In Proc. Advances in Neural Information Processing Systems (eds Guyon, I. et al.) (Curran, 2017).

  47. Chen, M. X. et al. The best of both worlds: combining recent advances in neural machine translation. In Proc. 56th Annual Meeting of the Association for Computational Linguistics (eds Gurevych, I. & Miyao, Y.) 76–86 (ACL, 2018).

  48. Luo, H., Zhang, S., Lei, M. & Xie, L. Simplified self-attention for transformer-based end-to-end speech recognition. In Proc. IEEE Spoken Language Technology Workshop 75–81 (2021).

  49. Parmar, N. et al. Image transformer. In Proc. 35th International Conference on Machine Learning (eds Dy, J. & Krause, A.) 4055–4064 (JMLR, 2018).

  50. Tay, Y., Dehghani, M., Bahri, D. & Metzler, D. Efficient transformers: a survey. ACM Comput. Surv. 55, 1–28 (2022).

    Article  MATH  Google Scholar 

  51. Katharopoulos, A., Vyas, A., Pappas, N. & Fleuret, F. Transformers are RNNs: fast autoregressive transformers with linear attention. In Proc. 37th International Conference on Machine Learning (eds Daumé, H. & Singh, A.) 5156–5165 (PMLR, 2020).

  52. Peng, H. et al. Random feature attention. In Proc. International Conference on Learning Representations (Curran, 2021).

  53. Qin, Z. et al. cosformer: Rethinking softmax in attention. In Proc. International Conference on Learning Representations (Curran, 2022).

  54. Chen, Y., Zeng, Q., Ji, H. & Yang, Y. Skyformer: remodel self-attention with gaussian kernel and nyström method. In Proc. Advances in Neural Information Processing Systems (eds Beygelzimer, A. et al.) 2122–2135 (Curran, 2021).

  55. Joshi, V. et al. Accurate deep neural network inference using computational phase-change memory. Nature Commun. 11, 2473 (2020).

    Article  MATH  Google Scholar 

  56. Büchel, J., Faber, F. & Muir, D. R. Network insensitivity to parameter noise via adversarial regularization. In Proc. International Conference on Learning Representations (2022).

  57. Rasch, M. J. et al. Hardware-aware training for large-scale and diverse deep learning inference workloads using in-memory computing-based accelerators. Nature Commun. 14, 5282 (2023).

    Article  MATH  Google Scholar 

  58. Murray, A. F. & Edwards, P. J. Enhanced MLP performance and fault tolerance resulting from synaptic weight noise during training. IEEE Trans. Neur. Netw. 5, 792–802 (1994).

    Article  MATH  Google Scholar 

  59. Tsai, Y.-H. H., Bai, S., Yamada, M., Morency, L.-P. & Salakhutdinov, R. Transformer dissection: a unified understanding for transformer’s attention via the lens of kernel. In Proc. Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (eds Inui, K. et al.) 4344–4353 (ACL, 2019).

  60. Li, C. et al. Three-dimensional crossbar arrays of self-rectifying si/sio2/si memristors. Nat. Commun. 8, 15666 (2017).

    Article  MATH  Google Scholar 

  61. Wu, C., Kim, T. W., Choi, H. Y., Strukov, D. B. & Yang, J. J. Flexible three-dimensional artificial synapse networks with correlated learning and trainable memory capability. Nat. Commun. 8, 752 (2017).

    Article  Google Scholar 

  62. Le Gallo, M. et al. Precision of bit slicing with in-memory computing based on analog phase-change memory crossbars. Neuromorphic Comput. Eng. 2, 014009 (2022).

    Article  MATH  Google Scholar 

  63. Chen, C.-F. et al. Endurance improvement of ge2sb2te5-based phase change memory. In Proc. IEEE International Memory Workshop 1–2 (IEEE, 2009)

  64. Chang, C.-C. & Lin, C.-J. IJCNN 2001 challenge: generalization ability and text decoding. In Proc. International Joint Conference on Neural Networks 1031–1036 (IEEE, 2001).

  65. Slate, D. Letter recognition. UCI Machine Learning Repository https://doi.org/10.24432/C5ZP40 (1991).

  66. Bock, R. MAGIC gamma telescope. UCI Machine Learning Repository https://doi.org/10.24432/C52C8B (2007).

  67. Roesler, O. EEG Eye state. UCI Machine Learning Repository https://doi.org/10.24432/C57G7J (2013).

  68. Uzilov, A. V., Keegan, J. M. & Mathews, D. H. Detection of non-coding RNAs on the basis of predicted secondary structure formation free energy change. BMC Bioinformatics 7, 1–30 (2006).

    Article  MATH  Google Scholar 

  69. Bhatt, R. & Dhall, A. Skin segmentation. UCI Machine Learning Repository https://doi.org/10.24432/C5T30C (2012).

  70. Tay, Y. et al. Long range arena: a benchmark for efficient transformers. In Proc. International Conference on Learning Representations (Curran, 2021).

  71. Paszke, A. et al. Pytorch: an imperative style, high-performance deep learning library. In Proc. Advances in Neural Information Processing Systems (eds Wallach, H. M. et al.) 8024–8035 (Curran, 2019).

  72. Hoerl, A. E. & Kennard, R. W. Ridge regression: biased estimation for nonorthogonal problems. Technometrics 12, 55–67 (1970).

    Article  MATH  Google Scholar 

  73. Ott, M. et al. fairseq: a fast, extensible toolkit for sequence modeling. In Proc. Conference of the North American Chapter of the Association for Computational Linguistics (Demonstrations) (eds Ammar, W. et al.) 48–53 (2019).

  74. Lefaudeux, B. et al. xformers: a modular and hackable transformer modelling library. GitHub https://github.com/facebookresearch/xformers (2022).

  75. Rasch, M. J. et al. A flexible and fast PyTorch toolkit for simulating training and inference on analog crossbar arrays. In Proc. 3rd International Conference on Artificial Intelligence Circuits and Systems 1–4 (IEEE, 2021).

  76. Gallo, M. L. et al. Using the IBM analog in-memory hardware acceleration kit for neural network training and inference APL Mach. Learn. 1, 041102 (2023).

  77. Reed, J. K. et al. Torch.fx: practical program capture and transformation for deep learning in Python. In Proc. of Machine Learning and Systems (eds Marculescu, M. et al.) Vol. 4, 638–651 (2022).

  78. Büchel, J. et al. Code for ‘Kernel approximation using analog in-memory computing’. GitHub https://github.com/IBM/kernel-approximation-using-analog-in-memory-computing (2024).

Download references

Acknowledgements

This work was supported by the IBM Research AI Hardware Center. A.S. acknowledges partial funding from the European Union’s Horizon Europe research and innovation programme under grant no. 101046878 and from the Swiss State Secretariat for Education, Research and Innovation (SERI) under contract no. 22.00029. We would also like to thank T. Hofmann for fruitful discussions.

Author information

Author notes

  1. These authors contributed equally: Julian Büchel, Giacomo Camposampiero.

Authors and Affiliations

  1. IBM Research Europe, Rüschlikon, Switzerland

    Julian Büchel, Giacomo Camposampiero, Athanasios Vasilopoulos, Corey Lammie, Manuel Le Gallo, Abbas Rahimi & Abu Sebastian

Authors
  1. Julian Büchel
    View author publications

    Search author on:PubMed Google Scholar

  2. Giacomo Camposampiero
    View author publications

    Search author on:PubMed Google Scholar

  3. Athanasios Vasilopoulos
    View author publications

    Search author on:PubMed Google Scholar

  4. Corey Lammie
    View author publications

    Search author on:PubMed Google Scholar

  5. Manuel Le Gallo
    View author publications

    Search author on:PubMed Google Scholar

  6. Abbas Rahimi
    View author publications

    Search author on:PubMed Google Scholar

  7. Abu Sebastian
    View author publications

    Search author on:PubMed Google Scholar

Contributions

J.B. and G.C. set up the infrastructure for training and evaluating the various models. J.B., G.C., A.V. and C.L. set up the infrastructure for automatically deploying trained models on the IBM Hermes project chip. J.B. and G.C. wrote the paper with input from all authors. A.R., M.L.G. and A.S. supervised the project.

Corresponding authors

Correspondence to Julian Büchel or Abu Sebastian.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Machine Intelligence thanks Parthe Pandit and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Tables 1–4 and Notes 1–4.

Reporting Summary

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Büchel, J., Camposampiero, G., Vasilopoulos, A. et al. Kernel approximation using analogue in-memory computing. Nat Mach Intell 6, 1605–1615 (2024). https://doi.org/10.1038/s42256-024-00943-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s42256-024-00943-2

This article is cited by

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics