Main

Transition states (TSs) are central to understanding the kinetics and mechanisms of chemical reactions1,2. Accurate TS structures reveal precise elementary reaction steps on the potential energy surface (PES), enabling the construction of large reaction networks for complex chemical reactions3,4 and the design of new catalysts5,6,7,8. However, since they have higher free energy compared with reactants and products (RP) in reaction pathways and are affected by dynamic processes, TSs are transient structures that often live at a timescale of femtoseconds, which makes them impossible to isolate and characterize experimentally. Very few studies have successfully unravelled elusive TS properties or their structures in experiments. Ultrafast millimetre-wave vibrational spectra, for example, were used to analyse characteristic patterns in isomerizing systems where their TS energies and properties are extracted from frequency-domain data9. More recently, ultrafast electron diffraction was used to obtain a more direct observation of TS structures for a photochemical electrocyclic ring-opening reaction10. These experimental techniques, however, are expensive and cannot be universally applied in all types of reaction.

In parallel, defined as a first-order saddle point on the PES, the TS of any chemical reaction can be searched systemically by a suite of optimization algorithms coupled with quantum chemistry calculations (for example, density functional theory (DFT)11). These TS search algorithms have been developed over the past 20 years, with salient examples being string methods12, growing string methods13, nudged elastic band (NEB) methods14, artificial force induced reaction15 and stochastic surface walking methods16. Together with these algorithms, comprehensive reaction networks4,17 can be constructed by either iteratively enumerating potential elementary reactions on-the-fly18,19,20,21,22, exploration PES starting from a local minimum15,16 or propagating biased ab initio molecular dynamics for enhanced sampling23,24,25. For a reasonably sized reaction network, however, thousands of TS structures need to be optimized, requiring millions of DFT single-point calculations26,27,28. The large number of chemical species involved in reaction networks calls for the need to reduce the computational cost of TS search for a single elementary step in chemical reactions.

Recently, machine learning (ML) has demonstrated promise for accelerating the search of TSs. Ideas include developing ML potential as a surrogate for DFT during TS optimizations (for example, in NEB)29,30 and formulating the transition path sampling problem as a shooting game solved by reinforcement learning31. It has also been formulated as a stochastic optimal control problem to learn a controlled stochastic process from the reaction to the product32. The TS search problem can also be viewed as a three-dimensional (3D) structure generation task, which can then be addressed by equivariant graph neural networks33,34, generative-adversarial networks35, a combination of gated recurrent neural networks and transformers36, or denoising diffusion probabilistic models37,38,39,40. Our prior work, OA-ReactDiff39, leverages a diffusion model for elementary chemical reactions, directly generating a set of reactants, TS structure and products jointly. By preserving all required symmetries of chemical reactions, OA-ReactDiff achieves state-of-the-art performance on generated structure similarity. Despite its high accuracy, the stochastic nature of OA-ReactDiff requires multiple runs of sampling for a reaction of interest and the use of a ranking model41,42 to recommend one out of many generated TSs. This workflow leads to both an additional cost of sampling and unfavoured randomness in a double-ended TS search with RP provided, which would be troublesome in its practical usage when replacing or reducing DFT calculations in high-throughput TS searches.

In this work, we developed React-OT, an optimal transport approach to generate TSs of an elementary reaction in a fully deterministic manner. Compared with OA-ReactDiff, React-OT eliminates the need to train an additional ranking model and reduces the number of inference evaluations of the denoising model from 40,000 to 50, achieving a nearly 1,000-fold acceleration. With React-OT, highly accurate TS structures can be deterministically generated in 0.4 s. In addition, React-OT outperforms OA-ReactDiff in both structural similarity and barrier height estimation by 30%. When pretrained on RGD1-xTB43, a dataset containing 760,615 elementary reactions computed with low-cost semi-empirical quantum chemistry methods (that is, GFN2-xTB44), React-OT improves further by 25%, reaching a median root mean square deviation (r.m.s.d.) of 0.044 Å and median error of 0.74 kcal mol−1 in barrier height prediction. To accelerate the TS search, we replace DFT-optimized reactant and product geometries with those optimized using much cheaper GFN2-xTB. In this scenario, React-OT continues to exhibit comparable performance, achieving a median r.m.s.d. of 0.049 Å and median error of 0.79 kcal mol−1 in barrier height calculations. Furthermore, we integrated React-OT in the high-throughput DFT-based TS optimization workflow, where an uncertainty quantification model is used to activate a DFT-based TS search only when the generated TS from React-OT is uncertain. With this workflow, chemical accuracy can be achieved in the generated TS structures using just one-seventh of the computational resources required for full reliance on DFT-based TS optimizations. The high quality of generated TSs, the extremely low cost in sampling and the simplicity of its integration in high-throughput computational workflows characterize React-OT as a promising model in constructing large reaction networks for studying chemical reactions with unexplored mechanisms.

Results

Overview of React-OT

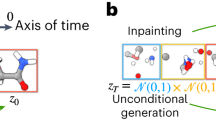
A diffusion model learns the underlying distribution of observed samples through training a scoring network by a denoising objective37,45,46 (see ‘Equivariant diffusion models’ section in the Methods). Our earlier work, OA-ReactDiff39, which satisfies all the symmetries in elementary reactions, essentially learns the joint distribution of paired reactants, TSs and products (Fig. 1a and Supplementary Text 1). With the learned joint distribution, one can either generate a new reaction from scratch or generate only a TS structure conditioned on fixed RP, resembling the set-up of the double-ended TS search problem (Fig. 1b; see ‘Inpainting for conditional generation’ section in the Methods). The standard Gaussian distribution, which is far from a reasonable guess of the TS structure, was used as the starting point for sampling (Supplementary Fig. 2). The fact that initial structures at t = 0 are randomly sampled from a Gaussian also leads to inevitable stochasticity in the final generated TS structures (Fig. 1b).

Fig. 1: Overview of the diffusion model and optimal transport framework for generating TSs.
figure 1

a, Learning the joint distribution of structures in elementary reactions (reactant in red, TS in yellow and product in blue). A forward diffusion process brings the joint distribution at t = T to independent normal distribution at t = 0. Backwards, an object-aware SE(3) GNN is trained with denoising objective to recover the normal distribution to the original joint distribution. b, Stochastic inference with inpainting in OA-ReactDiff. Starting with samples drawn from normal distribution, the trained GNN is applied to denoise the reactant, TS and product. A diffusion process on reactant and product is combined with the denoising process to ensure the end-point reactant and product at t = T are the same as the true reactant and product. c, Deterministic inference with React-OT. Both the reactant and product are unchanged throughout the entire process from t = 0 to t = T. The linear interpolation of reactant and product is provided as the initial guess structure at t = 0, followed by optimal (that is, linear) transport to the final TS. Atoms are coloured as follows: C, grey; N, blue; O, red; H, white.

Full size image

To address this challenge, we reformulate the double-ended TS search problem in a dynamic transport setting and utilize an objective resembling flow matching47 to achieve the optimal transport in reactions48,49 (see ‘Details about React-OT’ section in the Methods). For simplicity, we use the linear interpolation of RP as the guess starting point and keep the RP constant during the transport process (Fig. 1c). This way, we avoid any stochastic processes during the sampling phase. React-OT also uses a transition kernel that is object-aware SE(3) equivariant, thus fulfilling all symmetries required in modelling an elementary reaction (see ‘Equivariance in modelling chemical reactions’ section in the Methods). In essence, the key benefit of React-OT is threefold. First, it simulates the sampling process as an ordinary differential equation instead of as a stochastic differential equation in diffusion models. Therefore, the generated TS with React-OT is deterministic, in line with the fact that there is only one unique TS structure given the paired RP conformations50,51,52. Second, utilizing a relatively reasonable initial guess and pushing the sampling path closer to optimal transport, React-OT generates TS structures with higher accuracy at lower cost. Third, with fully deterministic inference, React-OT needs to be run only once to generate the final TS structure, greatly simplifying its application in realistic computational workflows. These advantages make React-OT a model that is trustworthy and extremely low cost, adequately starting to replace actual DFT calculations in high-throughput computing.

Generating accurate TS structure in 0.4 s

We trained React-OT on Transition1x53, a dataset that contains paired reactants, TSs and products calculated from climbing-image NEB54 obtained with DFT (ωB97x/6-31G(d))55,56. Transition1x contains 10,073 organic reactions with diverse reaction types sampled from enumeration57,58 of 1,154 reactants in GDB759 dataset, which has up to 7 heavy atoms (C, N and O) and 23 atoms in total. For ease of comparison, we use the same train–test partitioning as in OA-ReactDiff, with 9,000 elementary reactions in training and leaving the remaining 1,073 unseen reactions as the test set (see ‘Details for model training’ section in the Methods). In React-OT, the object-aware version of LEFTNet39,60 is used as the scoring network to fit the transition kernel (see ‘LEFTNet’ section in the Methods).

React-OT achieves a mean r.m.s.d. of 0.103 Å between generated and true TS structures on the set-aside test reactions of Transition1x, significantly improving upon previous state-of-the-art results on ML generation for TS structures38,39. The mean structural r.m.s.d. from React-OT is halved compared with a diffusion model that utilizes only two-dimensional (2D) graphs (TSDiff38, 0.252 Å) and that uses 3D structures of RP explicitly (OA-ReactDiff39, 0.180 Å). React-OT also outperforms the combination of 40-shot sampling of OA-ReactDiff and a recommender by 26%, which gives 0.130 Å mean r.m.s.d. at a 40× cost of one-shot OA-ReactDiff. With React-OT, the likelihood of finding a TS below a certain r.m.s.d. is higher than that of both diffusion models, highlighting the excellent accuracy of React-OT across all test reactions regardless of their level of complexity (Fig. 2a). Similarly, React-OT halves the mean absolute error (MAE) on barrier height estimation from 10.37 kcal mol−1 of single-shot TSDiff and 6.26 kcal mol−1 of single-shot OA-ReactDiff to 3.34 kcal mol−1, irrespective of the actual barrier height of different reactions (Supplementary Fig. 10). Among 1,073 reactions, 62% of the TS structures generated by React-OT give a more precise TS structure compared with 40-shot OA-ReactDiff + recommender and 66% for a more accurate barrier height (Fig. 2c and Supplementary Fig. 3). It is found that the r.m.s.d. and barrier height error of the React-OT-generated TS have good positive correlation, demonstrating the effectiveness of both metrics (Supplementary Fig. 12). In chemical reactions, a difference of one order of magnitude in reaction rate is often used as the characterization of chemical accuracy, which translates to 1.58 kcal mol−1 in barrier height error assuming a reaction temperature of 70 °C (refs. 61,62). With this definition, over 64% of TS from React-OT have high chemical accuracy, whereas the number is only 11% for TSDiff and 49% for OA-ReactDiff + recommender.

Fig. 2: Structural and energetic performance of diffusion and optimal transport generated TS structures.
figure 2

a, Cumulative probability for structure r.m.s.d. (left) and absolute energy error (∣ΔETS∣) (right) between the true and generated TS on 1,073 set-aside test reactions. Single-shot OA-ReactDiff39 (blue), 40-shot OA-ReactDiff with recommender (red), single-shot TSDiff38 (green) and React-OT TS (orange) are shown. Both r.m.s.d. and ∣ΔETS∣ are presented in log scale for visibility of the low error regime. b, Reference TS structure, OA-ReactDiff TS sample (red) and React-OT structure (orange) for select reactions. r.m.s.d. and ∣ΔETS∣ for OA-ReactDiff and React-OT structures are shown in text with their corresponding colour. Atoms in the reference TS are coloured as follows: C, grey; N, blue; O, red; H, white. c, Histogram of probability (grey, left y axis) and cumulative probability (blue, right y axis) showing the difference in r.m.s.d. (left) and ∣ΔETS∣ (right) between OA-ReactDiff-recommended and React-OT structures compared with reference TS. Negative Δr.m.s.d. or Δ∣ΔETS∣ suggests that the React-OT structure is of higher quality. A box plot (blue) for Δr.m.s.d. and Δ∣ΔETS∣ is shown above the histogram, correspondingly. A dashed vertical line is shown for no deviation between two structures. d, Inference time in seconds for single-shot OA-ReactDiff (blue), 40-shot OA-ReactDiff with recommender (red) and React-OT (orange). The y axis is presented in log scale for visibility of the extremely low inference time for React-OT. In a and c, the statistics are displayed for 1,073 test reactions, where the median is represented by a solid line, the mean as a dashed line and quarters 1 and 3 as the edges of the box, and the fences correspond to the edges ±1.5 times the interquartile range.

Source data

Full size image

The superior performance in both the structural similarity and barrier height estimation of React-OT can be ascribed to its more reasonable initial guess in combination with the optimal transport objective (Supplementary Table 3). As a result, React-OT has a much higher chance of obtaining the correct intermolecular arrangement for a TS that contains multiple fragments (Fig. 2b, middle). With diffusion models, however, one can take advantage of their stochasticity and keep generating different conformations of TS until obtaining the most desired one38,39. Still, there are only very few reactions, in 40 runs of sampling, where OA-ReactDiff is able to generate much more accurate TS structures, with H-atom transfer in 5H-pyrimidin-5-ide as an example (Fig. 2b, top). Due to the limited size of training data, the parameterization of the scoring network is not perfect, leading to a few reactions where both React-OT and OA-ReactDiff generate the same TS structure that deviates significantly from the true TS (Fig. 2b, bottom). These reactions mostly involve chemical species that are radical or that do not obey octet rule, which are rare in Transition1x and are thus difficult to learn (Supplementary Fig. 6). Starting from a more reasonable TS guess and trained towards optimal transport paths, React-OT requires, on average, only 0.39 s to generate a high-quality TS structure (Fig. 2d). Interestingly, we do not observe a strong correlation between the quality of the initial guess structure and the r.m.s.d. for the React-OT-generated structure, indicating the great effectiveness of React-OT on learning the TS through the transport perspective (Supplementary Fig. 11). Owing to its deterministic character, React-OT generates a TS structure in one shot. Consequently, the 0.39-s inference time corresponds to a 20-fold acceleration to single-shot OA-ReactDiff and near-1,000-fold acceleration to 40-shot OA-ReactDiff with recommender39, drastically accelerating the TS generation process at the same time as improving the precision.

Given that the initial guess of the sampling path deviates significantly from Gaussian distributions but remains relatively close to the TS, React-OT incorporates a rational implicit bias by assuming that the associations between initial guesses and true TSs are in proximity to the optimal coupling. To further investigate the distance between React-OT and the true optimal transport paths, we gradually reduce the number of function evaluation (nfe) during the sampling process. If the learned transition kernel resembles the true optimal transport, the path would be linear and, thus, nfe = 2 should suffice. In practice, React-OT converges at nfe = 6 for the r.m.s.d. of generated TS structures, which corresponds to an inference time of 0.05 s, demonstrating its effectiveness in learning the optimal transport path during structure generation48 (Fig. 3a). However, we observe a much slower convergence at nfe = 50 for the barrier height of generated TS structures (Supplementary Fig. 4). This is probably due to the fact that the energy of TS, which usually contains strained bonds, is extremely sensitive to subtle structural changes in some directions compared with others. Because this non-uniform response relationship between structure and energy is not captured by the scoring network, it is difficult for React-OT to optimize the transport path to obtain the exact energy, resulting in a slower convergence in barrier height. Consequently, React-OT with nfe = 6 and nfe = 200 generates structurally similar TSs, where most of their differences in r.m.s.d. is below a chemically meaningful threshold (that is, 0.01 Å; Fig. 3b). Yet, the two sets of generated TSs exhibit a visible difference in their barrier height, with more than 80% showing a deviation above 0.1 kcal mol−1. As both structural and energetic perspectives for generated TS are equally important, nfe = 50 is found sufficient when using React-OT in practice.

Fig. 3: Performance of React-OT with respect to nfe.
figure 3

a, The distribution of r.m.s.d. (left) and ∣ΔETS∣ (right) between the true and generated TS on 1,073 set-aside test reactions, where the mean is shown in pink and median is shown in yellow. The first and third quarter are bounded by a green box. b, The absolute difference in r.m.s.d. (top) and ∣ΔETS∣ (bottom) for generated structures at nfe = 6 and nfe = 200. Structures where nfe = 200 gives better quality are shown in blue; others are shown in red. A threshold below which the comparison is not chemically meaningful is shown (dashed vertical line). Reference TS structure and React-OT-generated structure at nfe = 6 (pink) and nfe = 200 (sky blue) for a select reaction. Atoms in the reference TS are coloured as follows: C, grey; N, blue; O, red; H, white.

Source data

Full size image

Although React-OT generates the TS structure in a fully deterministic manner, it is important to note that this is a desired behaviour when both reactant and product conformations are fixed. For the same reaction with different reactant and product conformations, React-OT is able to generate TS structures that correspond to the input reaction conformation (Supplementary Fig. 13). With the ability to generate accurate TSs and differentiate reaction conformations, React-OT can be effectively used to explore reaction networks from scratch. For instance, upon integrating React-OT with the Yet Another Reaction Program21,63—a reaction network exploration package that encompasses graph-based reaction enumeration rules and a comprehensive reaction conformational sampling algorithm50—we can explore the well-studied γ-ketohydroperoxide system, a common benchmark in recent research21,63,64,65. The resulting two-step reaction network generated by React-OT was compared with previously published networks, demonstrating a high degree of similarity and successfully capturing all key reactions (Supplementary Section 2).

Pretraining on additional reactions further improves React-OT

Despite the availability of large computational datasets at DFT accuracy for molecular66 and material67 properties, surface-absorbate structures68 and molecular dynamics trajectories69,70, the size of datasets containing paired reactants, TSs and products is often limited43,53,71. This limitation is primarily due to the significantly higher computational cost—two orders of magnitude more expensive—associated with optimizing the minimum energy pathway for chemical reactions43. By contrast, reaction datasets at more affordable levels of theory, such as semi-empirical quantum chemistry, can be much larger. This disparity highlights the importance of developing efficient schemes for pretraining models with lower-accuracy reaction data. For instance, during the generation of DFT-level reactions in RGD1, 760,615 intrinsic reaction coordination calculations were performed at the GFN2-xTB level, resulting in a dataset that can potentially serve as a valuable source of data (henceforth named RGD1-xTB)43. Compared with Transition1x, RGD1-xTB covers a much larger chemical space, with 57% of reactions consisting of both more than seven heavy atoms (that is, the largest system size in Transition1x) and more diverse bond rearrangement schemes during chemical reactions (Fig. 4a). Moreover, the dataset’s reactants originate from PubChem, and generic enumeration rules were applied to construct the dataset, resulting in a more realistic and diverse set of chemical reactions involving multiple RP and breaking and forming of multiple bonds (Fig. 4b).

Fig. 4: React-OT with RGD1-xTB data for pretraining.
figure 4

a, The distribution of the number of heavy atoms (left) and reaction type (right) for Transition1X (red) and RGD1-xTB (blue). The percentages are shown in log scale for better visibility of rare cases. ArBp refers to a reaction that has A reactants and B products where a rule of A ≤ B is set. The percentage of 1r4p and 2r4p is multiplied by 10 to be shown in the plot. b, Examples of reaction types that are presented exclusively in RGD1-xTB. c, A box plot for r.m.s.d. (left) and ∣ΔETS∣ (right) in log scale between the true and generated TS on 1,073 set-aside test reactions evaluated by React-OT trained from scratch on Transition1X (red) and React-OT with RGD1-xTB pretraining (blue). The nfe is 100 for this comparison. The statistics are displayed for 1,073 test reactions, where the median is represented by a solid line, the mean as a dashed line and quarters 1 and 3 as the edges of the box, and the fences correspond to the edges ±1.5 times the interquartile range.

Source data

Full size image

With a dataset 75 times larger than Transition1x at hand, we pretrained React-OT on RGD1-xTB, which was then fine tuned on the training set of Transition1x with a reduced learning rate. RGD1-xTB-pretrained React-OT further improves on its quality of generated TS structures, yielding a 0.098 Å mean r.m.s.d. and 2.86 kcal mol−1 mean barrier height error (Fig. 4c). The mean error improves by only roughly 10%, mostly due to the persistent high-error TSs generated by React-OT both with and without pretraining (Supplementary Fig. 5). By contrast, the median of the structural r.m.s.d. and barrier height error is reduced by more than 25%, suggesting the superior performance of React-OT after pretraining on RGD1-xTB (Table 1). This pretraining scheme is helpful, in particular, in cases where the ground-truth reaction data (either DFT or experiment) are limited. Considering that GFN2-xTB is roughly three orders of magnitude cheaper than DFT, this observation encourages the application of low-level theory on generating reaction datasets coupled with TS search algorithms (such as NEB), especially for large chemical systems where DFT is too computationally demanding. In addition, we find great transferability of React-OT on out-of-distribution reactions, which gives similar performance on 41 Diels–Alde reactions at different substrates and a standard test set of diverse reaction types that Birkholz et al. used to test TS optimization methods72.

Table 1 Summary of statistics for r.m.s.d., barrier height error and inference time of TSDiff, OA-ReactDiff and React-OT TS structures
Full size table

Utilizing xTB-optimized RP in React-OT

Usually the DFT-optimized RP are assumed to be known explicitly in double-ended TS search problems1. This assumption, however, is not practical in ML-accelerated workflows such as React-OT because the time spent on optimizing RP with DFT is several orders of magnitude longer than that for generating the TS structure. Therefore, the robustness of being able to utilize approximate RP structures is of great value in ML-based TS search. Here, we reoptimized RP in Transition1x with GFN2-xTB as an approximation to DFT-optimized structures. These xTB-optimized RP still share some degrees of structural similarity with those optimized by DFT (that is, ωB97x/6-31G(d)), especially for unimolecular reactions, with a mean r.m.s.d. of 0.07 Å (Fig. 5a). Reactions with multiple products, however, show a much larger r.m.s.d. (that is, 0.28 Å) for products optimized by GFN2-xTB and DFT (Supplementary Fig. 7 and Supplementary Table 1). This large r.m.s.d. is mostly ascribed to the error in the alignment of multiple molecules in the product conformer. Consequently, React-OT with xTB-optimized RP generates TS structures with higher structural and energetic errors on reactions with multiple products than unimolecular reactions (Fig. 5b). However, despite using xTB-optimized RP that demonstrate a 0.07–0.28 Å mean r.m.s.d. as input, React-OT still generates TS structures at comparable performance, with a 0.106 Å mean r.m.s.d. and 0.049 Å median r.m.s.d., exhibiting only less than 10% increase in r.m.s.d. compared with that using DFT-optimized RP as input (Table 1). In addition, React-OT still gives a r.m.s.d. as low as 0.12 Å for TSs in multimolecular reactions, although there are large structural differences between xTB- and DFT-optimized products (mean r.m.s.d. of 0.28 Å; Fig. 5b). The same behaviour is observed in estimating barrier height, where React-OT also shows comparable performance when using xTB-optimized RP. Despite a slight reduction in performance using xTB-optimized RP as input, React-OT still maintains state-of-the-art performance compared with ML approaches with various flavours, such as diffusion models of 3D (OA-ReactDiff39) and 2D RP (TSDiff38), ML potential as a surrogate in climbing-image NEB (NeuralNEB29) and transformer-based generative models (PSI36) (Fig. 5c and Supplementary Fig. 8). This observation also suggests that the optimal transport formalism used in React-OT still holds, at least approximately, on RP computed at different levels of theory.

Fig. 5: React-OT with xTB RP as input and its performance in combination with DFT workflow and uncertainty control.
figure 5

a, A 2D contour plot for the structure r.m.s.d. of DFT- and xTB-optimized RP. The single-product (blue) and multiproduct (red) reactions are shown separately. b, Cumulative probability for structure r.m.s.d. (left) and ∣ΔETS∣ (right) between the true and React-OT-generated TS on 1,073 set-aside test reactions. The single-product (blue) and multiproduct (red) reactions are shown separately. Both r.m.s.d. and ∣ΔETS∣ are presented in log scale for visibility of the low error regime. c, The workflow of combining React-OT and conventional DFT-based TS search using a confidence (conf.) model. ML models are shown with orange squares, outputs from ML models are shown with pink triangles (TS) and pink circles (confidence score) and DFT-based TS search shown with the red square, with its output shown as a blue triangle (true TS). d, r.m.s.d. versus ∣ΔETS∣ for different TS generations approached, where the MAE is shown in pink and the median absolute error is shown in yellow. OA-ReactDiff and TSDiff are also evaluated by the best sample among 40 sampling rounds (symbols without colour filling), which, however, is not practical in real application settings. e, Average ∣ΔETS∣ (pink, left y axis) and time cost per reaction (yellow, right y axis) with respect to the fraction of TS generated by React-OT under the control by uncertainty quantification. The dashed lines show the statistics at chemical accuracy (1.58 kcal mol−1). Reference and generated TS structures (pink) for the best and worst test reactions are shown. Atoms in the reference TS are coloured as follows: C, grey; N, blue; O, red; H, white. In a and b, the statistics are displayed for 783 multiproduct (red) and 290 single-product (blue) test reactions, where the median is represented by a solid line, the mean as a dashed line and quarters 1 and 3 as the edges of the box, and the fences correspond to the edges ±1.5 times the interquartile range.

Source data

Full size image

There is often a need to integrate ML models in high-throughput computational workflows to further accelerate data acquisition and chemical discovery7. With its great accuracy in generating TS structures even using xTB-optimized RP, we investigate the performance of React-OT integrated in typical high-throughput computational workflows that mandate TS search. Provided a pair of xTB-optimized RP, we first use React-OT to generate a TS structure (Fig. 5e). This TS structure is then passed through a confidence model to obtain a confidence score on the likelihood of reactants, React-OT-predicted TS and products forming an elementary reaction (see ‘Details for model training’ section in the Methods). One accepts the React-OT structure if the confidence score is higher than a user-defined threshold; otherwise, a conventional TS search calculation with DFT is performed. With a confidence threshold of 0, all React-OT-generated TS structures are preserved, giving a mean inference time of 0.39 s and barrier height error of 3.28 kcal mol−1. With a confidence threshold of 1, none of the React-OT-generated TS structures is considered accurate, and thus one would run explicit TS search for all reactions, taking 12.8 h per reaction on average. By varying the confidence threshold, one can choose between being aggressive and conservative on activating React-OT in the computational workflow. As we reduce the threshold, a larger fraction of TS structures are accepted from React-OT. Meanwhile, the mean barrier height error increases smoothly and monotonically, which indicates that the confidence model can successfully assess the quality of generated TS structures (Fig. 5d and Supplementary Fig. 9). When the chemical accuracy of barrier height prediction (that is, 1.58 kcal mol−1 MAE) is targeted, 86% TSs would be generated by React-OT and the remaining 14% would be searched by climbing-image NEB with DFT, rendering a sevenfold acceleration compared with DFT-only computational workflows. At the same time, an extremely low median structural r.m.s.d. of 0.031 Å and median barrier height error of 0.54 kcal mol−1 would be achieved. These observations showcase the promise of combining React-OT and conventional TS search algorithms in the high-throughput screening of elementary reactions and building of large reaction networks.

Discussion

We developed React-OT, an optimal transport approach for deterministically generating TSs provided RP. React-OT achieves great accuracy on generated TS structures within 0.4 s. Pretrained on a large reaction dataset at GFN2-xTB level, React-OT further improves by 25% in TS structural r.m.s.d. and barrier height. In a practical setting where xTB-optimized RP are used as input, React-OT still shows comparable performance, generating TSs at chemical accuracy with only one-seventh of the cost for a hybrid ML–DFT high-throughput computational workflow.

Despite the use of RP optimized by GFN2-xTB, the preparation of optimized RP is the most time-consuming step (tenfold more expensive than others combined) in React-OT-enabled TS search workflows. Therefore, ML approaches that accelerate RP conformer optimizations, either by an ML potential or with a 2D graph to 3D conformation sampling model, would be desired to unleash the potential of subsecond inference speed of React-OT in large reaction network exploration. There, generic ML interatomic potentials (such as ANI-1xnr (ref. 30), MACE-OFF23 (ref. 73) and DPA-2 (ref. 74)) would be helpful to achieve fast optimization for reactant and product structures. In addition, there are ongoing efforts in benchmarking75 the performance of these ML interatomic potentials systematically for TS optimization problems against diffusion- and transport-based generative modelling. Due to the absence of large reaction datasets with charged species and metals, the demonstration of React-OT is limited to the scope of neutral organic chemical space with CNOH elements. In the future, it would be of great interest to generate more chemical reaction data and train React-OT on more diverse chemistry to enable its application in more realistic chemical systems, such as those involving transition-metal catalysts.

With the optimal transport approach, React-OT does not have any stochasticity in the sampling process, making it tailored for double-ended TS search. To construct reaction networks, however, a model is required to generate products from reactants, which does not have a one-to-one mapping. There, either diffusion models that carry some degree of stochasticity (for example, OA-ReactDiff39) or conventional high-throughput computational workflows that efficiently sample reactant–product pairs under xTB calculations (for example, YARP21), is preferred. Although we demonstrate only React-OT on the TS search problem, there are many scenarios in biology, chemistry and materials science where an optimal transport setting is appropriate, including protein–ligand docking, molecule absorption on metal surfaces, and structural changes of materials in phase transitions. For example, an extended transport approach based on Doob’s Lagrangian was recently developed, finding feasible transition paths on molecular simulation and protein folding tasks76. We anticipate that this optimal transport approach presented here will be useful for applications in other domains of science.

Methods

Equivariance in modelling chemical reactions

As we discussed in our previous work, OA-ReactDiff39, a function f is said to be equivariant to a group of actions G if g∘f(x) = f(g∘x), where g∘ denotes the group element g ∈ G acting on x (refs. 77,78). In this Article, we specifically consider the special Euclidean group in 3D space (SE(3)) which includes permutation, translation and rotation transformations. We intentionally break the reflection symmetry so that our model can describe molecules with chirality. In diffusion models, SE(3) equivariance is achieved by building an SE(3)-invariant prior and an SE(3)-equivariant transition kernel79. However, in the dynamic optimal transport setting, we can design a more informative prior than Gaussian distribution48 (in this case, we use the linear interpolation between the reactant and product as an initial guess). As the paired data (initial guess and TS) are available during training, we align the initial and target geometry for permutation, rotation and reflection and move the centre of mass to the origin to remove the effect of translation. In addition, we have an equivariant transition kernel to transport from the initial to the target distribution.

Equivariant diffusion models

As we discussed in our previous work, OA-ReactDiff39, diffusion models are originally inspired from non-equilibrium thermodynamics37,45,46. A diffusion model has two processes, the forward (diffusing) process and the reverse (denoising) process. The noise process gradually adds noise into the data until it becomes a prior (Gaussian) distribution

$$q({x}_{t}| {x}_{t-1})={\mathcal{N}}\left({x}_{t}| {\alpha }_{t}{x}_{t-1},{\sigma }_{t}^{2}I\right),$$

where αt controls the signal retained and σt controls the noise added. A signal-to-noise ratio is defined as \(\,\text{SNR}\,(t)=\frac{{\alpha }_{t}^{2}}{{\sigma }_{t}^{2}}\). We set \({\alpha }_{t}=\sqrt{1-{\sigma }_{t}^{2}}\) following the variance preserving process in ref. 46.

The true denoising process can be written in a closed form owing to the property of Gaussian noise

$$\begin{array}{rcl}q({x}_{s}| {x}_{0},{x}_{t})&=&{\mathcal{N}}({x}_{s}| {\mu }_{t\to s}({x}_{0},{x}_{t}),{\sigma }_{t\to s}^{2}I\,),\\ {\mu }_{t\to s}({x}_{0},{x}_{t})&=&\frac{{\alpha }_{t| s}{\sigma }_{s}^{2}}{{\sigma }_{t}^{2}}{x}_{t}+\frac{{\alpha }_{s}{\sigma }_{t| s}^{2}}{{\sigma }_{t}^{2}}x\,\,\,\text{and}\,\,\,{\sigma }_{t\to s}=\frac{{\sigma }_{t| s}{\sigma }_{s}}{{\sigma }_{t}},\end{array}$$

where s < t refer to two different timesteps along the diffusion/denoising process ranging from 0 to T, \({\alpha }_{t| s}=\frac{{\alpha }_{t}}{{\alpha }_{s}}\), \({\sigma }_{t| s}^{2}={\sigma }_{t}^{2}-{\alpha }_{t| s}^{2}{\sigma }_{s}^{2}\). However, this true denoising process is dependent on x0, which is the data distribution and not accessible. Therefore, diffusion learns the denoising process by replacing x0 with xt + σtϵθ(xt, t) predicted by a denoising network ϵθ, which predicts the difference of x between two timesteps (that is, ϵ). The training objective is to maximize the variational lower bound on the likelihood of the training data

$$\begin{array}{l}-\log p(x)\le {D}_{{\mathrm{KL}}}(q({x}_{T}| {x}_{0})| | {p}_{\theta }({x}_{T}))-\log p({x}_{0}| {x}_{1})\\+{\Sigma }_{t = 2}^{T}{D}_{{\mathrm{KL}}}(q({x}_{t-1}| {x}_{0},{x}_{t})| | {p}_{\theta }({x}_{t-1}| {x}_{t})).\end{array}$$

where DKL is the Kullback–Leibler divergence. Empirically, a simplified objective has been found to be efficient to optimize37 as follows:

$${{\mathcal{L}}}_{{\rm{simple}}}=\frac{1}{2}| | \epsilon -{\epsilon }_{\theta }({x}_{t},t)| {| }^{2}.$$

However, it is worth noting that the diffusion model follows a protocol that transforms a fixed normal distribution to a target distribution. Therefore, one end of the diffusion model can only be the normal distribution, which limits the use of prior knowledge in formulating the TS problem, motivating us to pursue flow matching and optimal transport formalism.

Details about React-OT

Optimal transport

Optimal transport problems80,81,82,83 investigate the most efficient means of transporting samples between two specified distributions. Originating from Gaspard Monge’s work84 in the eighteenth century, the problem has evolved and gained broader significance through Leonid Kantorovich’s relaxation85. Given a pair of boundary distributions \(\mu ,\nu \in {\mathcal{P}}({{\mathbb{R}}}^{d})\), where \({\mathcal{P}}({{\mathbb{R}}}^{d})\) denotes the space of probability distributions, the problem involves minimizing the, for example, squared Euclidean, transport cost

$${W}_{2}^{2}(\,\mu ,\nu ):=\mathop{\inf }\limits_{\pi \in \Pi (\,\mu ,\nu )}\int\int\parallel x-y{\parallel }^{2}\pi (x,y){\rm{d}}x{\rm{d}}y,$$

where \(\Pi (\,\mu ,\nu ):=\{\pi \in {\mathcal{P}}({\mathcal{X}}\times {\mathcal{Y}}):\int\pi (x,y){\rm{d}}y=\mu ,\int\pi (x,y){\rm{d}}x=\nu \}\) is the set of couplings on \({{\mathbb{R}}}^{d}\times {{\mathbb{R}}}^{d}\) with respective marginals μ, ν. The resulting distance \({W}_{2}^{2}(\,\mu ,\nu )\) between μ and ν, given the optimal transport coupling π⋆, is commonly referred to as the squared Wasserstein-2 distance.

Dynamic optimal transport

Dynamic optimal transport, as introduced by Benamou and Brenier86, presents the squared Wasserstein-2 distance \({W}_{2}^{2}(\,\mu ,\nu )\) in a dynamic formulation. This formulation involves optimizing the squared L2 norm of a time-varying vector field ut(xt), which transports samples from x0 ~ μ(x0) to x1 ~ ν(x1) according to an ordinary differential equation, \(\frac{{\mathrm{d}}{x}_{t}}{{\mathrm{d}}t}={u}_{t}({x}_{t})\). Mathematically, this dynamic formulation is expressed as

$$\begin{array}{r}{W}_{2}^{2}(\,\mu ,\nu ):=\mathop{\inf }\limits_{{q}_{t},{u}_{t}}\displaystyle\mathop{\int}\nolimits_{0}^{1}\displaystyle\int\frac{1}{2}\parallel {u}_{t}({x}_{t}){\parallel }^{2}{q}_{t}({x}_{t}){\rm{d}}{x}_{t}{\rm{d}}t\\ \,\text{s.t.}\,\,\frac{\partial {q}_{t}}{\partial t}+\nabla \cdot ({u}_{t}{q}_{t})=0,\quad {q}_{0}=\mu ,\quad {q}_{1}=\nu \end{array},$$

subject to the continuity equation and the boundary conditions q0 = μ and q1 = ν. This approach describes a fully deterministic transportation process, distinguishing it from previous methods such as OA-ReactDiff, which rely on stochastic processes. The minimal assumptions placed on the distributional boundaries μ, ν in optimal transport problems, in contrast to the Gaussian priors in standard diffusion models37, enable the straightforward incorporation of domain-specific structures, such as the incorporation of pairing information, if available.

Given the optimal transport coupling π⋆(x, y), the optimal time-marginal \({q}_{t}^{\star }\) can be defined using the optimal transport interpolant (equation 7.8 in ref. 87) as

$${q}_{t}^{\star }={P}_{t\sharp }{\pi }^{\star },\,\text{where}\,\,{P}_{t}:(x,y)\mapsto (1-t)x+ty$$

is the mapping of optimal transport interpolant and Pt♯ is its corresponding push-forward operator. In essence, the optimal trajectories between samples drawn from (x0, x1) ~ π⋆ move along straight lines xt = (1 − t)x0 + tx1. Consequently, the optimal vector field can be constructed as a constant velocity \({u}_{t}^{\star }({x}_{t})={x}_{1}-{x}_{0}\).

Formulation of TS finding as optimal transport

Recent advances in flow-matching methods47,88 have introduced an efficient framework for solving dynamic optimal transport problems in high-dimensional Euclidean spaces. To harness this computational efficiency for molecular transportation, we reformulate the TS finding problem in \({{\mathbb{R}}}^{d}\), where the collections of ground-truth TS structures and their initial guesses are treated as \(\nu \in {\mathcal{P}}({{\mathbb{R}}}^{d})\) and \(\mu \in {\mathcal{P}}({{\mathbb{R}}}^{d})\), respectively. The dimensionality d is determined by padding the maximum number of atoms in the collection. For instance, a collection with three carbon atoms, two oxygen atoms and one hydrogen atom corresponds to an 18-dimensional space, as each atom occupies a 3D position. The state of each TS structure is represented by filling in atom coordinates according to their type, with unfilled coordinates set to a default large value. This formulation yields a well-posed optimal transport problem in Euclidean space with an L2 norm, where distances between molecules x0 ~ μ and x1 ~ ν are properly defined. Molecules with different atom compositions incur large distance values, making them suboptimal pairings. Unlike prior approaches for similar data structures, such as point clouds89 and graphs90, which often involve complex extensions to the optimal transport framework, our formulation retains the scalability of the flow matching approach.

Practical implementation of flow matching

In practice, given a tuple of product (P), reactor (R) and TS, we set the initial and terminal states respectively to \({x}_{0}=\frac{P+R}{2} \sim \mu\) and x1 = TS ~ ν. This is due to an implicit bias where the pairing information is assumed to be close to the optimal coupling, that is, \((\frac{P+R}{2},{\mathrm{TS}}) \sim {\pi }^{\star }\). This assumption generally holds when the pairings are sufficiently close to each other without much overlap with others48,49, which is indeed the case in the application being considered. Note that, as R and P may differ by an arbitrary orientation, we always align them with an SE(3) group action by minimizing their r.m.s.d. using the Kabsch algorithm. Given the pair of prealigned (x0, x1) from π⋆, we leverage the construction of optimal transport interpolant (equation 7.8 in ref. 87) and minimize a flow-matching47 objective

$$\mathop{\min }\limits_{\theta }\parallel {u}_{\theta }({x}_{t},t,z)-({x}_{1}-{x}_{0}){\parallel }^{2},$$

where z encapsulates all conditional information required for predicting the flow matching target, such as the conformer structures of R and P. Ablation study was performed to investigate the source of superior performance of React-OT, finding that both a good initial guess TS structure and optimal transport objective are important; leaving either out would result in a reduced performance (Supplementary Table 3). At inference, we can sample x1 ~ ν(x1∣x0) by solving the parametrized ordinary differential equation \(\frac{{\rm{d}}{x}_{t}}{{\rm{d}}t}={u}_{\theta }^{\star }({x}_{t},t,z)\) using off-the-shelf numerical solvers.

Inpainting for conditional generation

As we discussed in our previous work, OA-ReactDiff39, inpainting is a flexible technique to formulate the conditional generation problem for diffusion models.91 Instead of modelling the conditional distribution, inpainting models the joint distribution during training. During inference, inpainting methods combine the conditional input as part of the context through the noising process of the diffusion model before denoising both the conditional input and the inpainting region together. The resampling technique91 has demonstrated excellent empirical performance in harmonizing the context of the denoising process as there is sometimes mismatch between the noised conditional input and the denoised inpainting region. However, at a given total step T, resampling increases the total number of sampling steps in each denoising step by sampling the inpainting region back and forth together with the conditional input. For example, with a resample size of 10 and total step of 100, the number of function evaluation is 1,000 for a single sampling process, which is significantly larger than that in React-OT.

LEFTNet

As we discussed in our previous work, OA-ReactDiff39, we build our equivariant transition kernel on top of a recently proposed SE(3)-equivariant graph neural network (GNN), LEFTNet60. LEFTNet achieves SE(3) equivariance based on building local node- and edge-wise equivariant frames that scalarize vector (for example, position and velocity) and higher-order tensor (for example, stress) geometric quantities. The geometric quantities are transformed back from scalars through a tensorization technique without loss of any information. LEFTNet is designed to handle Euclidean group symmetries including rotation, translation and reflection, as well as the permutation symmetry. To tailor the model for chemical reaction, we adopt the object-aware improvement from our previous work, OA-ReactDiff39. In addition to handling symmetries, LEFTNet has strong geometric and function approximation expressiveness. Specifically, LEFTNet has a local structure encoding module that is proven to distinguish a hierarchy of local 3D isomorphism and a frame transition encoding module that is capable of learning universal equivariant functions. For more detailed descriptions, we refer to the original LEFTNet60 or OA-ReactDiff39 works. It is noted, however, that newly developed model architectures (for example, MACE73) can be incorporated as the scoring network in React-OT as long as they fulfil the object-aware SE(3) symmetry.

Details for model training

React-OT training

We directly fine tuned the OA-ReactDiff model checkpoint with the new optimal transport objective and a reduced learning rate of 0.0001 (see ‘Details about React-OT’ section). The scoring network, LEFTNet, has 96 radial basis functions, 196 hidden channels for message passing, 6 equivariant update blocks and an interaction cut-off of 10 Å. The React-OT model was trained for an additional 200 epochs.

Confidence model training

The confidence model was also fine tuned from the OA-ReactDiff model checkpoint, with the change of the final output layer to a sigmoid function for predicting a probability ranging from 0 to 1 as the confidence score. The OA-ReactDiff was run for 40 rounds of sampling on the 9,000 training reactions, which generated 360,000 synthetic reactions. A reaction was labelled as ‘good’ (that is, 1) if the generated TS structure had a r.m.s.d. <0.2 Å compared with the true TS; otherwise, it was labelled as ‘bad’ (that is, 0). Here, we directly adopted the confidence model trained in OA-ReactDiff without further changes.