Mask-prior-guided denoising diffusion improves inverse protein folding

Abstract

Inverse protein folding generates valid amino acid sequences that can fold into a desired protein structure, with recent deep learning advances showing strong potential and competitive performance. However, challenges remain, such as predicting elements with high structural uncertainty, including disordered regions. To tackle such low-confidence residue prediction, we propose a mask-prior-guided denoising diffusion (MapDiff) framework that accurately captures both structural information and residue interactions for inverse protein folding. MapDiff is a discrete diffusion probabilistic model that iteratively generates amino acid sequences with reduced noise, conditioned on a given protein backbone. To incorporate structural information and residue interactions, we have developed a graph-based denoising network with a mask-prior pretraining strategy. Moreover, in the generative process, we combine the denoising diffusion implicit model with Monte-Carlo dropout to reduce uncertainty. Evaluation on four challenging sequence design benchmarks shows that MapDiff substantially outperforms state-of-the-art methods. Furthermore, the in silico sequences generated by MapDiff closely resemble the physico-chemical and structural characteristics of native proteins across different protein families and architectures.

Main

Proteins are complex, three-dimensional (3D) structures folded from linear amino acid (AA) sequences. They play a critical role in essentially all biological processes, including metabolism, immune response and cell cycle control. The inverse protein folding (IPF) problem is a fundamental structure-based protein design problem in computational biology and medicine. It aims to generate valid AA sequences with the potential to fold into a desired 3D backbone structure, enabling the creation of new proteins with specific functions¹. Its enormous applications range from therapeutic protein engineering, lead compound optimization and antibody design².

Traditional physics-based approaches consider IPF as an energy optimization problem³, suffering from high computational cost and limited accuracy. In recent years, deep learning has emerged as the preferred paradigm for solving protein-structure problems owing to its strong ability to learn complex nonlinear patterns from data adaptively. In deep learning for IPF, early convolutional neural network-based models view each protein residue as an isolated unit or the whole as point cloud data, with limited consideration of structural information and interactions between residues^4,5,6,7. Recently, graph-based methods have represented 3D protein structures as proximity graphs, and then use graph neural networks (GNNs) to model residue representations and incorporate structural constraints. GNNs can aggregate and exchange local information within graph-structured data, enabling substantial performance improvement in graph-based methods.

Despite the advances in graph-based methods, structural information alone cannot determine the residue identities of some challenging structural elements, such as intrinsically disordered regions⁸. In such uncertain, low-confidence cases, interactions with other accurately predicted residues can provide more reliable guidance for mitigating uncertainty in these regions. Moreover, existing deep learning-based IPF methods typically employ autoregressive decoding or uniformly random decoding to generate AA sequences, are prone to accumulating prediction errors^9,10 and are limited in capturing global and long-range dependencies in protein evolution^11,12. Recently, several non-autoregressive alternatives have shown the potential to outperform the autoregressive paradigm in related contexts^9,13,14. In addition, protein-structure prediction methods, such as the AlphaFold series^15,16, often take an iterative generation process to refine non-deterministic structures by integrating well-predicted information. These raise the question: can combining residue interactions with an iterative refinement and an efficient non-autoregressive decoding improve IPF prediction performance to generate more plausible protein sequences?

Recently, denoising diffusion models, an innovative class of deep generative models, have gained growing attention in various fields. They learn to generate conditional or unconditional data by iteratively denoising random samples from a prior distribution. Diffusion-based models have been adopted for de novo protein design and molecule generation, achieving state-of-the-art performance. For example, RFdiffusion¹⁷ fine-tunes the protein structure prediction network RoseTTAFold¹⁸ under a denoising diffusion framework to generate 3D protein backbones, and torsional diffusion¹⁹ implements a diffusion process on the space of torsion angles for molecular conformer generation. In structure-based drug design, DiffSBDD²⁰ proposes an equivariant 3D-conditional diffusion model to generate new small-molecule binders conditioned on target protein pockets. Although diffusion models have a widespread application in computational biology, most existing methods focus primarily on generating structures in continuous 3D space. The potential of diffusion models in inverse folding has not yet been fully exploited.

We propose a mask-prior-guided denoising diffusion (MapDiff) framework (Fig. 1) to accurately capture structure-to-sequence mapping for IPF prediction. Unlike previous graph-based methods, MapDiff models IPF as a discrete denoising diffusion problem that iteratively generates less-noisy AA sequences conditioned on a target protein structure. Owing to the property of denoising diffusion, MapDiff can also be viewed as an iterative refinement that enhances the accuracy of the generated sequences over time. Moreover, we have designed a two-step denoising network to adaptively improve the denoising trajectories using a pretrained mask prior. Our denoising network effectively leverages the structural information and residue interactions to reduce prediction error on low-confidence residue prediction. To further improve the denoising speed and uncertainty estimation, we combine the DDIM²¹ with Monte-Carlo dropout²² in the discrete generative process. DDIM accelerates sequence generation by skipping multiple denoising steps, whereas Monte-Carlo dropout reduces uncertainty by performing multiple stochastic forward passes with dropout enabled during inference. We conducted performance comparisons against state-of-the-art methods for IPF prediction, demonstrating the effectiveness of MapDiff across multiple metrics and benchmarks, outperforming even those incorporating external knowledge. Moreover, when we used AlphaFold2¹⁵ to fold the sequences generated by MapDiff back to 3D structures, such AlphaFold2-folded structures were highly similar to the native protein templates, even for cases of low sequence recovery rates.

Fig. 1: Mask-prior-guided denoising diffusion (MapDiff) for inverse protein folding.

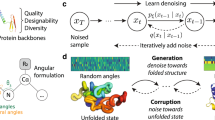
a, The mask-prior pretraining stage randomly masks residues within the AA sequence and pretrains an invariant point attention (IPA) network with the masked sequence and the 3D backbone structure to learn prior structural and sequence knowledge, using BERT-like masked language modelling objectives. b, The mask-prior-guided denoising network ϕ_θ takes an input noisy AA sequence X^aa to predict the native AA sequence ${{\bf{X}}}_{0}^{\rm{aa}}$ by means of three operations in every iterative denoising step. It first initializes a structure-based sequence predictor as an equivariant graph neural network to denoise the noisy sequence X^aa conditioned on the provided 3D backbone structure. Then, combining an entropy-based mask strategy with a mask ratio adaptor identifies and masks low-confidence residues in the denoised sequence in the first step to produce a masked sequence ${{\bf{X}}}_{\rm{m}}^{\rm{aa}}$. Next, the pretrained masked sequence designer in a takes the masked sequence ${{\bf{X}}}_{\rm{m}}^{\rm{aa}}$ and its 3D backbone information for refinement (fine-tuning) to better predict the native sequence ${{\bf{X}}}_{0}^{\rm{aa}}$. c, The MapDiff denoising diffusion framework iteratively alternates between two processes: diffusion and denoising. The diffusion process progressively adds random discrete noise to the native sequence ${{\bf{X}}}_{0}^{\rm{aa}}$ according to the cumulative transition matrix ${\overline{\bf{Q}}}_{t}$ at the diffusion step t so that the real data distribution can gradually transition to a uniform or marginal prior distribution. The denoising process randomly samples an initial noisy AA sequence ${{\bf{X}}}_{T}^{\rm{aa}}$ from the prior distribution and iteratively uses the denoising network ϕ_θ in b to denoise it, learning to predict the native sequence ${{\bf{X}}}_{0}^{\rm{aa}}$ from ${{\bf{X}}}_{t}^{\rm{aa}}$ at each denoising step t. The prediction ${\hat{{\bf{X}}}}_{0}^{\rm{aa}}$ facilitates the computation of the posterior distribution $q({{\bf{X}}}_{t-1}^{\rm{aa}}| {{\bf{X}}}_{t}^{\rm{aa}},{\hat{{\bf{X}}}}_{0}^{\rm{aa}})$ for predicting a less-noisy sequence ${{\bf{X}}}_{t-1}^{\rm{aa}}$.

This work shows the high potential of using discrete denoising diffusion models with mask-prior pretraining for IPF prediction. Our main contributions are three-fold: (1) we propose a discrete denoising diffusion-based framework named MapDiff to explicitly consider the structural information and residue interactions in the diffusion and denoising processes; (2) we have designed a mask-prior-guided denoising network that adaptively denoises the diffusion trajectories to produce feasible and diverse sequences from a fixed structure; and (3) MapDiff incorporates discrete DDIM with Monte-Carlo dropout to accelerate the generative process and improve uncertainty estimation.

Results

MapDiff framework

As shown in Fig. 1, the MapDiff framework formulates IPF prediction as a denoising diffusion problem (Fig. 1c). The diffusion process progressively adds random discrete noise to the native AA sequence according to the transition probability matrices to facilitate the training of a denoising network. In the denoising process, this denoising network iteratively denoises a noisy, randomly sampled AA sequence conditioned on the 3D structural information to predict or reconstruct the native AA sequence. The diffusion and denoising processes iterate alternately to capture the sampling diversity of native sequences from their complex distribution and refine the predicted AA sequences.

We propose a mask-prior-guided denoising network to adaptively adjust the discrete denoising trajectories towards generating more valid AA sequences by means of three operations within each iterative denoising step (Fig. 1b). First, a structure-based sequence predictor employs an equivariant graph neural network (EGNN)²³ to denoise the noisy sequence conditioned on the backbone structure. Second, we use an entropy-based mask strategy²⁴ and a mask ratio adaptor to identify and mask low-confidence or uncertain (for example, structurally undetermined) residues in the denoised sequence in the first operation to produce a masked sequence. Third, a pretrained masked sequence designer network predicts the masked residues to obtain their refined prediction. The pretraining of the masked sequence designer is done before the diffusion and denoising processes by means of an invariant point attention (IPA) network¹⁵ using masked language modelling (Fig. 1a), incorporating prior structural and sequence knowledge. The structure-based sequence predictor and masked sequence designer refine denoising trajectories by leveraging structural information and residue interactions. For efficient sequence generation, the denoising network uses non-autoregressive decoding to generate sequences in a one-shot manner¹³. In addition, we incorporate DDIM²¹ to accelerate inference by skipping multiple denoising steps and Monte-Carlo dropout²² to reduce uncertainty. The Methods provides more details.

Evaluation strategies and metrics

We conducted experiments across diverse datasets to evaluate MapDiff against state-of-the-art protein sequence design methods. We first evaluated two popular benchmark datasets, CATH 4.2 and CATH 4.3 (ref. ²⁵), using the same topology-based data split employed in previous works^13,26,27. In addition to the full test sets, we also studied two subcategories of generated proteins: short proteins up to 100 residues in length and single-chain proteins (labelled with one chain in CATH). We used another two distinct datasets, TS50 (ref. ⁵) and PDB2022 (ref. ²⁴) to evaluate the zero-shot generalization of models. Furthermore, we studied the foldability of the generated protein sequences by means of AlphaFold2 (ref. ¹⁵) by comparing the discrepancy between the AlphaFold2-refolded structures and ground-truth native structures. This is an in silico evaluation rather than definitive proof that the designed sequences can fold into their intended structures. The ‘Experimental setting’ section provides detailed information and statistics about these datasets.

We evaluated the accuracy of generated sequences using three metrics: perplexity, recovery rate and native sequence similarity recovery (NSSR)²⁸. Perplexity measures the alignment between a model’s predicted AA probabilities and the native AA types at each residue position. The recovery rate indicates the proportion of accurately predicted AAs in the protein sequence. The NSSR evaluates the similarity between the predicted and native residues by means of the blocks substitution matrix (BLOSUM)²⁹, where each residue pair contributes to a positive prediction if their BLOSUM score is greater than zero. We used BLOSUM42, BLOSUM62, BLOSUM80 and BLOSUM90 to account for AA similarities at four different cutoff levels for NSSR computation. To evaluate the foldability, that is, the quality of refolded protein structures, we used six metrics: predicted local distance difference test (pLDDT), predicted aligned error (PAE), predicted template modelling (pTM), template modelling score (TM-score), root mean square deviation (RMSD) and global distance test-total score (GDT-TS), where pLDDT, PAE and pTM measure the confidence and reliability of predicted structures produced by AlphaFold2, and TM-score, RMSD and GDT-TS measure the discrepancies between the predicted 3D structures and their native counterparts. Supplementary Information Section 9 provides the technical details for these metrics.

Sequence recovery performance

First, we evaluated MapDiff’s sequence recovery with uniform or marginal priors against state-of-the-art baselines on the CATH datasets. Table 1 presents the prediction perplexity and median recovery rate on the full test set, along with short and single-chain subsets. The results demonstrate that MapDiff achieves the best performance across different metrics and subsets of data, highlighting its effectiveness in generating valid protein sequences. Specifically, we observe that: (1) MapDiff achieves a recovery rate of 61.03% and 60.86% on the full CATH 4.2 and CATH 4.3 test sets, substantially outperforming the baselines by 7.74% and 7.20%, respectively. Furthermore, MapDiff shows recovery improvements of 8.20% and 6.61% on the short and single-chain test sets of CATH 4.2.; (2) MapDiff consistently achieves the lowest perplexity compared with previous methods and produce high-confidence probability distribution to facilitate accurate predictions; (3) MapDiff is a highly accurate IPF model that operates independently of external knowledge. In some of the compared baselines, external knowledge sources, such as additional training data or protein language models, are used to enhance prediction accuracy. Owing to its well-designed architecture and diffusion-based generation mechanism, MapDiff effectively uses limited training data to capture relevant patterns to achieve superior generalizability; and (4) MapDiff’s performance is largely unaffected by the choice of prior distribution. Therefore, we use the marginal prior³⁰ in our experiments, as it is data-driven and better aligns with the true amino acid distribution.

Table 1 Performance comparison on the CATH 4.2 and CATH 4.3 datasets with topology classification split

We further study model performance across different scenarios. Figure 2a presents the mean NSSR scores for MapDiff and the baselines on the CATH datasets. MapDiff consistently achieves the best NSSR scores across different test sets. Figure 2b compares the confusion matrices of MapDiff and LM-Design with the native BLOSUM62 matrix on CATH 4.2. For clearer visualization and comparison, we normalized these matrices to the [0,1] probability range, with the diagonal elements masked. The confusion matrix denotes proportions for specific combinations of actual and predicted amino acid types, with darker cells indicating greater proportion. Many non-diagonal darker cells in MapDiff highlight the alignment between closely related residue pairs, as defined by the BLOSUM62 matrix, indicating that MapDiff can effectively capture the homologous substitutions between residues. In addition, MapDiff’s higher correlation with BLOSUM62 than LM-Design suggests a stronger alignment with substitution preferences.

Fig. 2: Model performance comparison and sensitivity analysis across different scenarios on the CATH datasets.

a, NSSR scores for MapDiff and baseline methods^1,13,38,45 on the full test sets and the short and single-chain protein subsets for four different BLOSUM matrices and no BLOSUM matrix. b, Sum-normalized confusion matrices for MapDiff (left) and LM-Design (right) predictions, and the softmax-normalized native BLOSUM62 matrix (middle). Darker colours indicate a higher predicted likelihood, with diagonal elements masked. The Pearson correlation coefficient (PCC) between the predicted matrix and BLOSUM62 quantifies their similarity and linear correlation. c, Breakdown of the recovery rates into hydrophilic and hydrophobic residues. d, Median sequence recovery rates across different protein lengths. e, Residue recovery performance across different secondary structures visualized in two groups for clarity, defined using the DSSP algorithm⁵⁷. Coils correspond to regions without regular secondary structures and are considered disordered regions. Bends and H-bonded turns are regarded as less ordered regions owing to their flexibility and transient nature. For these regions, MapDiff outperforms the baselines substantially.

Source data

Figure 2c,e shows the sequence recovery performance across different amino acid types, as well as eight secondary structures. Notably, MapDiff is the only model achieving over 50% recovery rate in predicting hydrophobic amino acids and substantial improvements in recovering α-helix and β-sheet secondary structures. Figure 2d presents a sensitivity analysis of the recovery performance for varying protein lengths. For short proteins (less than 100 amino acids in length), several baselines show a marked decrease in performance. For example, the recovery rate of LM-Design falls below 40% for the short proteins. This could be due to the protein language model used in LM-Design being sensitive to protein length. By contrast, MapDiff, which employs a mask-prior-guided denoising network and an iterative denoising process, consistently outperforms all baselines and maintains high performance across all protein lengths.

To validate the zero-shot transferability of our method, we compared the model’s performance on two independent test datasets, TS50 and PDB2022, which do not overlap with the CATH data, as shown in Table 2. The results demonstrate that MapDiff achieves the highest recovery and NSSR scores on both datasets. We can conclude that, even though LM-Design reaches a high recovery (66%) that is approaching our method on PDB2022, the performance gap widens on NSSR62 and NSSR90. By contrast, GRADE-IF and MapDiff can generalize better when considering the possibility of similar residue substitution. This suggests that diffusion-based models more effectively capture residue similarity in IPF prediction. For the TS50 dataset, MapDiff substantially improves state-of-the-art methods by 6.33% on NSSR62, and is the best model, achieving a recovery rate of 68%.

Table 2 Transferability: zero-shot performance comparison on transferability from CATH to PDB2022 and TS50 datasets

Foldability of generated protein sequences

Foldability is a crucial property that evaluates whether a protein sequence can fold into the desired structure. In this study, we evaluated the foldability of generated protein sequences by predicting their structures with AlphaFold2 and comparing the discrepancies against the native crystal structures. Table 2 presents six foldability metrics for the 1,120 structures in the CATH 4.2 test set. The results indicate that the generated protein sequences by MapDiff exhibit superior foldability, the highest confidence and minimal discrepancy compared with their native structures. Notably, the foldability and sequence recovery results do not always positively correlate. For example, although ProteinMPNN performs poorly in sequence recovery, it achieves the best RMSD among baseline methods. Therefore, it is essential to comprehensively evaluate IPF models from both sequence and structure perspectives. Supplementary Information Section 2 and Supplementary Fig. 2 present analysis of the right-skewed RMSD distribution³¹.

In Fig. 3a, we illustrate exemplary 3D structures refolded by AlphaFold2 from IPF-derived sequences generated by MapDiff, GRADE-IF and LM-Design for three different protein folds (PDB ID 1NI8 (ref. ³²), 2HKY (ref. ³³) and 2P0X (ref. ³⁴) with a preselected monomer pTM prediction argument. In addition to estimating the sequence recovery rate and foldability of derived 3D structures using the RMSD metric, we also inspected the alignment of native and generated sequences, including the agreement between refolded secondary structures and individual pairs of amino acids in Fig. 3b. Figure 3c,d presents quantitative analyses of performance on different regions.

Fig. 3: Comparison of three refolded structures (left) and the respective model-designed sequences (right) for proteins with PDB IDs 1NI8, 2HKY and 2P0X.

a, Refolded tertiary structure visualization of the sequences designed by three models MapDiff (red), GRADE-IF (orange) and LM-Design (blue). The refolded structures were generated by AlphaFold2 and superposed against the ground-truth structures (purple). For each model and structure, the recovery rate and RMSD value are indicated for foldability comparison. b, The alignment of the three native sequences and the respective model-designed sequences. The results are shown with secondary structure elements marked below each sequence: α-helices are shown in red cylinders, β-strands in blue arrows, and loops and disordered regions are unmarked. For the native proteins, the secondary structures were derived from their source PDB files. For the predicted proteins, the secondary structures were assigned by first identifying all interbackbone hydrogen bonds and then searching for hydrogen-bonding patterns that represent helices and strands. The refolded structures and sequence alignments are visualized using the Schrödinger Maestro software⁵⁸. c, Recovery rates for loops and disordered regions (left panel) and α-helix and β-strand regions (right panel) across three structures. Bars indicate the recovery rates of three methods (MapDiff, Grade-IF and LM-Design). The percentage composition of regions for each structure is provided below the panel titles. MapDiff consistently achieves the highest recovery rates across different categories of regions for the three structures, with an average improvement of 5.1% in loops and disordered regions and 13.4% in α-helix and β-strand regions compared with Grade-IF. d, Jaccard region intersections between the predicted and ground-truth structures for loops and disordered regions (left panel) versus α-helix and β-strand regions (right panel). The Jaccard index measures the fraction of the overlap between two sets, and the results demonstrate that MapDiff achieves the highest score across both categories of regions.

The first example is a 46-amino-acid-long monomer of the 1NI8 structure (purple) representing an amino-terminal (N-terminal) fragment of the H-NS dimerization domain, a protein composed of three α-helices that is involved in structuring the chromosome of Gram-negative bacteria, and hence acts as a global regulator for the expression of different genes³². Two monomers form a homodimer which requires the presence of K5, R11, R14, R18 and K31 residues to engage in the prokaryotic DNA binding. MapDiff (red) managed to retrieve two out of the three α-helices, with an interhelical turn present at the same position as in the original structure (A17-R18), whereas GRADE-IF (orange) and LM-Design (blue) models only consisted of a single continuous α-helix. Moreover, MapDiff and GRADE-IF obtained four out of five (K5, R11, R14 and R18) amino acids required for DNA binding and LM-Design obtained none. MapDiff and LM-Design generate glutamic acid (E) and GRADE-IF isoleucine (I), which, in comparison with the corresponding positively charged K31 in the original structure, are negatively charged and neutral residues, respectively. The single continuous α-helix displayed by GRADE-IF and LM-Design AlphaFold2 models hence produces much worse RMSD values (14.5 Å and 14.2 Å, respectively) than the MapDiff model, which retrieved two helices at the right positions (RMSD = 4.6 Å). Consistent with this, MapDiff obtained a 10% higher recovery rate than GRADE-IF and LM-Design.

The second example is the 2HKY structure of 109-amino-acid-long human ubiquitous ribonuclease 7 (hRNase7), rich in positively charged residues, that possesses antimicrobial activity³³. This α/β mixed protein contains 22 cationic residues (18 K and 4 R) distributed into three surface-exposed clusters that promote binding to the bacterial membrane, which thus renders it permeable, which consequently elicits membrane disruption and death. In addition, it contains four disulfide bridges (C24–C82, C38–C92, C56–C107 and C63–C70), which are critical for its secondary and tertiary structure, three of which were successfully retrieved by MapDiff, whereas no cysteines were found in either GRADE-IF or LM-Design sequences. Furthermore, all secondary structure elements were nearly entirely recovered by MapDiff, unlike GRADE-IF and LM-Design solutions which contained little resemblance to the native structure, particularly in the carboxy-terminus (C-terminus) half. These structural findings were reflected in a fair recovery rate of 40.3% and an RMSD value of 5.0 Å for MapDiff, which was considerably better than in GRADE-IF and LM-Design structures (14.0 Å and 12.6 Å, respectively).

A third example displays AlphaFold2-refolded structures obtained from generated sequences with relatively low recovery rates that used the 2P0X structure of an optimized non-biological (de novo) ATP-binding protein as a template³⁴. Here MapDiff retrieved all detected secondary structure elements, except for the C-terminus β-strand which was replaced by a loop. LM-Design was the second best with an α-helix substituting the aforementioned β-strand. Even if nearly all secondary structure elements were retrieved by both MapDiff and LM-Design AlphaFold2 models, the MapDiff model obtained by far the best RMSD (3.3 Å as opposed to 8.8 Å). Despite having a better recovery rate than LM-Design, GRADE-IF generated a sequence that folded poorly compared with the experimentally confirmed structure (15.0 Å).

In these cases, MapDiff achieved low RMSD values to successfully replicate the majority of secondary structure elements elucidated through experiments, including other structural features such as the disulfide bonds (2HKY) or positively charged residues that were suspected to participate in protein function (1NI8). By contrast, Grade-IF and LM-Design predicted sequences that not only had lower recovery rates than MapDiff but also exhibited partially or entirely absent secondary structure elements, as shown by the experimentally derived 3D structures, resulting in substantially worse RMSDs. Although the structures predicted by AlphaFold2 cannot entirely substitute the structural elucidation by experimental techniques such as X-ray or NMR (nuclear magnetic resonance), they provide the first glance at the foldability potential of de novo generated protein sequences by IPF models. A natural next step in future work would be to express the de novo designed protein sequences and experimentally determine their tertiary structures.

Supplementary Information Section 1 and Supplementary Fig. 1 study the closest training structures and sequences of the three examples. The highest TM-scores for 1NI8, 2HKY and 2P0X from structures in the training set were 0.57 (1A7W), 0.25 (1V88) and 0.33 (1WIM), respectively, indicating that there are no highly similar structures during training. Similarly, the highest BLAST³⁵ bit-scores for sequences in the training set were 23.1 (4ZEO), 26.6 (2BM8) and 24.6 (3MSR), respectively, indicating that no highly similar sequences are present during training.

Model analysis and ablation study

We performed analysis and ablation studies to assess the effectiveness of key components in MapDiff. We focused on investigating the contributions of edge feature updating, node coordinate updating and global context learning within the base sequence predictor (G-EGNN) to the model performance. In addition, we examined the impact of the mask ratio adaptor and the pretrained IPA network in the residue refinement module on the predictions. As shown in Table 3, we studied five variants of MapDiff, each with different key components removed, and compared their results with the CATH 4.2 test set. The results show that each component positively enhanced the sequence recovery and foldability performance. For example, the IPA-based refinement mechanism (variant 5) achieved the most substantial sequence improvement, increasing recovery by 4.47%, whereas the global context learning and coordinate updating (variants 2 and 4) in G-EGNN improved the recovery by 1.17% and 0.77%, respectively. The impact on foldability increases with sequence recovery performance but remains less pronounced, indicating that AlphaFold2 is robust to these variations and predicts stable protein folds. In addition, Supplementary Information Section 7 and Supplementary Fig. 3 analyse MapDiff’s sensitivity to the number of Monte-Carlo samples and DDIM skipping steps.

Table 3 Ablation study of the denoising network modules in MapDiff

Discussion

In this work, we present MapDiff, a mask-prior-guided denoising diffusion framework for structure-based protein design. Specifically, we regard IPF prediction as a discrete denoising diffusion problem, and developed a graph-based denoising network to capture structural information and residue interactions. At each denoising step, we used a G-EGNN module to generate clean sequences from input structures and a pretrained IPA module to refine low-confidence residues, ensuring reliable denoising trajectories. Moreover, we integrated DDIM with Monte-Carlo dropout to accelerate generative sampling and enhance uncertainty estimation. Experiments demonstrate that MapDiff consistently outperforms the state-of-the-art IPF models across multiple benchmarks and scenarios. At the same time, the generated protein sequences exhibit a high degree of similarity to their native counterparts. Even in cases where the overall sequence similarity was low, these sequences could often refold into their native structures, as demonstrated by the AlphaFold2-refolded models. We also conducted a comprehensive ablation study to analyse the importance of different model components for the prediction results. MapDiff demonstrates transferability and robustness in generating new protein sequences, even with limited training data. Promising future directions include verifying the applicability of MapDiff in practical domains such as de novo antibody design and protein engineering, incorporating predicted structures from structure prediction models as external data for incremental training, integrating physics-informed constraints, leveraging sequential evolutionary knowledge from protein language models to further refine residue predictions, and further validating the foldability of the designed sequences by conducting folding simulations or molecular dynamics simulations.

Methods

Discrete denoising diffusion models

Denoising diffusion models are a class of deep generative models trained to create new samples by iteratively denoising sampled noise from a prior distribution. The training stage of a diffusion model consists of a forward diffusion process and a reverse denoising process. Given an original data distribution q(x₀), the forward diffusion process gradually corrupts a data point x₀ ∼ q(x₀) into a series of increasingly noisy data points x_1:T = x₁, x₂,⋯, x_T over T time steps. This process follows a Markov chain, where $q({{\bf{x}}}_{1:T}| {{\bf{x}}}_{0})=\mathop{\prod}\nolimits_{t=1}^{T}q({{\bf{x}}}_{t}| {{\bf{x}}}_{t-1})$. Conversely, the reverse denoising process, denoted by ${p}_{\theta }({{\bf{x}}}_{0:T})=p({{\bf{x}}}_{T})\mathop{\prod }\nolimits_{t=1}^{T}{p}_{\theta }({{\bf{x}}}_{t-1}| {{\bf{x}}}_{t})$, aims to progressively reduce noise towards the original data distribution q(x₀) by predicting x_t − 1 from x_t. The initial noise x_T is sampled from a predefined prior distribution p(x_T), and the denoising inference p_θ can be parametrized by a learnable neural network. Although the diffusion and denoising processes are agnostic to the data modality, the choice of prior distributions and Markov transition operators varies between continuous and discrete spaces.

In this work, we followed the settings of the discrete denoising diffusion proposed by Austin et al.³⁶ and Clement et al.³⁰. In contrast with typical Gaussian diffusion models that operate in continuous state space, discrete denoising diffusion models introduce noise to categorical data using transition probability matrices in discrete state space. Let x_t $\in$ {1, ⋯ , K} denote the categorical data with K categories and its one-hot encoding represented by ${{\bf{x}}}_{t}\in {{\mathbb{R}}}^{K}$. At time step t, the forward transition probabilities can be denoted by a matrix ${\bf{Q}}_{t}\in {{\mathbb{R}}}^{K\times K}$, where ${[{\bf{Q}}_{t}]}_{ij}=q({x}_{t}=j| {x}_{t-1}=i)$ is the probability of transitioning from category i to category j. Therefore, the discrete transition kernel in the diffusion process is defined as

$$q({{\bf{x}}}_{t}| {{\bf{x}}}_{t-1})={\rm{Cat}}({{\bf{x}}}_{t};{\bf{p}}={{\bf{x}}}_{t-1}{\bf{Q}}_{t}),$$

(1)

$$q({{\bf{x}}}_{t}| {{\bf{x}}}_{0})={\rm{Cat}}({{\bf{x}}}_{t};{\bf{p}}={{\bf{x}}}_{0}{\overline{\bf{Q}}}_{t}),\,{\rm{with}}\,{\overline{\bf{Q}}}_{t}={\bf{Q}}_{1}{\bf{Q}}_{2}\cdots {\bf{Q}}_{t},$$

(2)

where Cat(x; p) represents a categorical distribution over x_t with probabilities determined by ${\bf{p}}\in {{\mathbb{R}}}^{K}$. As the diffusion process has a Markov chain, the transition matrix from x₀ to x_t can be written as a closed form in equation (2) with ${\overline{\bf{Q}}}_{t}={\bf{Q}}_{1}{\bf{Q}}_{2}\cdots {\bf{Q}}_{t}$. This property enables efficient sampling of x_t at arbitrary time steps without recursively applying noise. Following the Bayesian theorem, the calculation of posterior distribution (with the derivation in Supplementary Information Section 3) from time step t to t − 1 can be written as

$$q({{\bf{x}}}_{t-1}| {{\bf{x}}}_{t},{{\bf{x}}}_{0})\propto {{\bf{x}}}_{t}{\bf{Q}}_{t}^{T}\odot {{\bf{x}}}_{0}{\overline{\bf{Q}}}_{t-1},$$

(3)

where ⊙ is a Hadamard (element-wise) product. The posterior q(x_t−1∣x_t, x₀) is equivalent to q(x_t−1∣x_t) owing to its Markov property. Thus, the clean data x₀ is introduced for denoising estimation and can be used as the target of the denoising neural network. In MapDiff, we introduce two simple but effective choices for the transition matrix Q_t: uniform transition³⁶ and marginal transition³⁰. The uniform transition is parametrized by ${\bf{Q}}_{t}=(1-{\beta }_{t}){\bf{I}}+{\beta }_{t}{{\bf{1}}}_{K}{{\bf{1}}}_{K}^{T}/K$, where K = 20 represents the number of native amino acid types and the noise schedule β_t $\in$ [0, 1]. Similarly, the marginal transition is parametrized by Q_t = (1 − β_t)I + β_t1_Kp^T, where ${\bf{p}}\in {{\mathbb{R}}}^{20}$ denotes the marginal probability distribution of AA types in the training data. All matrix values are strictly positive, and each row sums to one, ensuring the conservation of probability mass. Given these properties, along with the condition ${\lim }_{t\to T}{\beta }_{t}=1$, q(x_t) can converge to a stationary uniform or marginal distribution, regardless of the initial x₀.

Residue graph construction

IPF prediction aims to generate a feasible AA sequence that can fold into a desired backbone structure. Given a target protein of length L, we present it as a proximity residue graph ${\mathcal{G}}=(\bf{X},\bf{A},\bf{E})$, where each node denotes an AA residue within the protein. The node features X = [X^aa, X^pos, X^prop] encode the AA residue types, 3D spatial coordinates and geometric properties. The adjacency matrix A $\in$ {0, 1}^N×N is constructed using the k-nearest-neighbour algorithm. Specifically, each node is connected to a maximum of k other nodes within a cutoff distance smaller than 30 Å. The edge feature matrix ${\bf{E}}\in {{\mathbb{R}}}^{{\rm{M}}\times 93}$ illustrates the spatial and sequential relationships between the connected nodes. More details on the graph feature construction are provided in Supplementary Information Section 4. For sequence generation, we define a discrete denoising process on the types of noisy AA residues ${{\bf{X}}}_{t}^{\rm{aa}}\in {{\mathbb{R}}}^{N\times 20}$ at time t. Conditioned on the noise graph ${{\mathcal{G}}}_{t}$, this process is subject to iteratively refine noise ${{\bf{X}}}_{t}^{\rm{aa}}$ towards a clean ${{\bf{X}}}_{0}^{\rm{aa}}={{\bf{X}}}^{\rm{aa}}$, which is predicted by our mask-prior-guided denoising network.

IPF denoising diffusion process

Discrete diffusion process

In the diffusion process, we incrementally introduced discrete noise to the clean AA residues over a number of time steps t $\in$ {1,⋯, T}, which resulted in transforming the original data distribution to a simple uniform or marginal distribution. Given a clean AA sequence ${{\bf{X}}}_{0}^{\rm{aa}}=\{{{\bf{x}}}_{0}^{i}\in {{\mathbb{R}}}^{1\times 20}| 1\le i\le N\}$, we used a cumulative transition matrix ${\overline{\bf{Q}}}_{t}$ to independently add noise to each AA residue at arbitrary step t

$$q({{\bf{x}}}_{t}^{i}| {{\bf{x}}}_{0}^{i})={\rm{Cat}}({{\bf{x}}}_{t}^{i};{\bf{p}}={{\bf{x}}}_{0}^{i}{\overline{\bf{Q}}}_{t}),{\rm{with}}\,{\overline{\bf{Q}}}_{t}={\bf{Q}}_{1}{\bf{Q}}_{2}\cdots {\bf{Q}}_{t},$$

(4)

$$q({{\bf{X}}}_{t}^{{\rm{aa}}}| {{\bf{X}}}_{0}^{{\rm{aa}}})=\prod _{1\le i\le N}q({{\bf{x}}}_{t}^{i}| {{\bf{x}}}_{0}^{i}),$$

(5)

where ${\bf{Q}}_{t}=(1-{\beta }_{t}){\bf{I}}+{\beta }_{t}{{\bf{1}}}_{K}{{\bf{1}}}_{K}^{T}/K$, and K denotes the number of native AA types (that is, K = 20). The weight of the noise, β_t $\in$ [0, 1] was determined by a common cosine schedule³⁷.

Training objective of denoising network

The denoising neural network, denoted by ϕ_θ, is an essential component to reverse the noise process in diffusion models. In our framework, the network takes a noise residue graph ${{\mathcal{G}}}_{t}=({\bf{X}}_{t},\bf{A},\bf{E})$ as input and aims to predict the clean AA residues ${{\bf{X}}}_{0}^{\rm{aa}}$. Specifically, we designed a mask-prior-guided denoising network ϕ_θ to effectively capture inherent structural information and learn the underlying data distribution. To train the learnable network ϕ_θ, the objective is to minimize the cross-entropy loss between the predicted AA probabilities and the real AA types over all nodes.

Reverse denoising process

After the denoising network has been trained, it can be used to generate new AA sequences through an iterative denoising process. In this study, we first used the denoising network ϕ_θ to estimate the generative distribution ${\hat{p}}_{\theta }({\hat{{\bf{x}}}}_{0}^{i}| {{\bf{x}}}_{t}^{i})$ for each AA residue. Then the reverse denoising distribution ${p}_{\theta }({{\bf{x}}}_{t-1}^{i}| {{\bf{x}}}_{t}^{i})$ was parametrized by combining the posterior distribution with the marginalized network predictions as follows:

$${p}_{\theta }\left({{\bf{x}}}_{t-1}^{i}| {{\bf{x}}}_{t}^{i}\right)\propto \sum _{{\hat{{\bf{x}}}}_{0}^{i}}q\left({{\bf{x}}}_{t-1}^{i}| {{\bf{x}}}_{t}^{i},{\hat{{\bf{x}}}}_{0}^{i}\right){\hat{p}}_{\theta }\left({\hat{{\bf{x}}}}_{0}^{i}| {{\bf{x}}}_{t}^{i}\right),$$

(6)

$${p}_{\theta }\left({{\bf{X}}}_{t-1}^{\rm{aa}}| {{\bf{X}}}_{t}^{\rm{aa}}\right)=\prod _{1\le i\le N}{p}_{\theta }\left({{\bf{x}}}_{t-1}^{i}| {{\bf{x}}}_{t}^{i}\right),$$

(7)

where ${\hat{{\bf{x}}}}_{0}^{i}$ represents the predicted probability distribution for the ith residue ${{\bf{x}}}_{0}^{i}$. The posterior distribution is defined as

$$\begin{array}{rcl}q\left({{\bf{x}}}_{t-1}^{i}| {{\bf{x}}}_{t}^{i},{\hat{{\bf{x}}}}_{0}^{i}\right)&=&\frac{q\left({{\bf{x}}}_{t}^{i}| {{\bf{x}}}_{t-1}^{i},{\hat{{\bf{x}}}}_{0}^{i}\right)q\left({{\bf{x}}}_{t-1}^{i}| {\hat{{\bf{x}}}}_{0}^{i}\right)}{q\left({{\bf{x}}}_{t}^{i}| {\hat{{\bf{x}}}}_{0}^{i}\right)},\\ &=&{\rm{Cat}}\left({{\bf{x}}}_{t-1}^{i};{\bf{p}}=\frac{{{\bf{x}}}_{t}^{i}{{\bf{Q}}}_{t}^{T}\odot {\hat{{\bf{x}}}}_{0}^{i}{\overline{{\bf{Q}}}}_{t-1}}{{\hat{{\bf{x}}}}_{0}^{i}{\overline{{\bf{Q}}}}_{t}{({{\bf{x}}}_{t}^{i})}^{T}}\right).\end{array}$$

(8)

By applying the reverse denoising process, the generation of less-noisy ${{\bf{X}}}_{t-1}^{\rm{aa}}$ from ${{\bf{X}}}_{t}^{\rm{aa}}$ is feasible (derivation in Supplementary Information Section 3). The denoised result is determined by the predicted residues from the denoising neural network, as well as the predefined transition matrices at steps t and t − 1. To generate a new AA sequence, the complete generative process begins with a random noise from the independent prior distribution p(x_T). The initial noise is then iteratively denoised at each time step using the reverse denoising process, gradually converging to a desired sequence conditioned on the given graph ${\mathcal{G}}$.

DDIM with Monte-Carlo dropout

Although discrete diffusion models have demonstrated impressive generation ability in many fields, the generative process suffers from two limitations that hinder their success in IPF prediction. First, the generative process is inherently computationally inefficient due to the numerous denoising steps involved, which require a sequential Markovian forward pass for the iterative generation. Second, the categorical distribution used for denoising sampling lacks sufficient uncertainty estimation. Many studies indicate that the logits produced by deep neural networks do not accurately represent the true probabilities. Typically, the predictions tend to be overconfident, leading to a discrepancy between the predicted probabilities and the actual distribution. As the generative process iteratively draws samples from the estimated categorical distribution, insufficient uncertainty estimation will accumulate sampling errors and result in unsatisfactory performance.

To accelerate the generative process and improve uncertainty estimation, we propose a discrete sampling method by combining DDIM with Monte-Carlo dropout. DDIM²¹ is a widely used method that improves the generation efficiency of diffusion models in continuous space. It defines the generative process as the reverse of a deterministic and non-Markovian diffusion process, making it possible to skip certain denoising steps during generation. As discrete diffusion models possess analogous properties, Yi et al. (2023)³⁸ extended DDIM into discrete space for IPF prediction. Similarly, we define the discrete DDIM sampling to the posterior distribution by

$$q\left({{\bf{x}}}_{t-k}^{i}| {{\bf{x}}}_{t}^{i},{\hat{{\bf{x}}}}_{0}^{i}\right)={\rm{Cat}}\left({{\bf{x}}}_{t-k}^{i};{\bf{p}}=\frac{{{\bf{x}}}_{t}^{i}{\bf{Q}}_{t}^{T}\cdots {\bf{Q}}_{t-k}^{T}\odot {\hat{{\bf{x}}}}_{0}^{i}{\overline{\bf{Q}}}_{t-k}}{{\hat{{\bf{x}}}}_{0}^{i}{\overline{\bf{Q}}}_{t}{({{\bf{x}}}_{t}^{i})}^{T}}\right),$$

(9)

where k is the number of skipping steps.

Then we introduce the application of Monte-Carlo dropout within the generative process, a technique designed to enhance prediction uncertainty in neural networks. Specifically, we use dropout not only to prevent overfitting during the training of our denoising network, but also to maintain its activation in the inference stage. By keeping dropout enabled and running multiple forward passes (Monte-Carlo samples) during inference, we generate a prediction distribution for each input, as opposed to a single-point estimation. To improve uncertainty estimation, we aggregate the predictions by taking a mean pooling over all output logits corresponding to the same input. This operation leads to the predicted logits that perform reduced estimation bias, and their normalized probabilities can more accurately reflect the actual distribution. Therefore, we can leverage Monte-Carlo dropout to enhance the generative process towards more reliable samplings.

Mask-prior-guided denoising network

In diffusion model applications, the denoising network plays a crucial role in generation performance. We have developed a mask-prior-guided denoising network, integrating both structural information and residue interactions for enhanced protein sequence prediction. Our denoising network architecture encompasses a structure-based sequence predictor, a pretrained mask sequence designer and a mask ratio adaptor.

Structure-based sequence predictor

We adopt an EGNN with a global-aware module as the structure-based sequence predictor, which generates a full AA sequence from the backbone structure. EGNN is a type of graph neural network that satisfies equivariance operations for the special Euclidean group SE(3). It preserves geometric and spatial relationships of 3D coordinates within the message-passing framework. Given a noise residue graph, we use H = [h₁, h₂, ⋯ , h_N] to denote the initial node embeddings, which are derived from the noisy AA types and geometric properties. The coordinates of each node are represented by ${{\bf{X}}}^{\rm{pos}}=[{{\bf{x}}}_{1}^{\rm{pos}},{{\bf{x}}}_{2}^{\rm{pos}},\cdots {{\bf{x}}}_{N}^{\rm{pos}}]$, whereas the edge features are denoted by E = [e₁, e₂, ⋯ e_M]. In this setting, EGNN consists of a stack of equivariant graph convolutional layers (EGCL) for the node and edge information propagation, which are defined as

$${{\bf{e}}}_{ij}^{(l+1)}={\phi }_{e}\left({{\bf{h}}}_{i}^{(l)},{{\bf{h}}}_{j}^{(l)},\parallel {{\bf{x}}}_{i}^{(l)}-{{\bf{x}}}_{j}^{(l)}{\parallel }^{2},{{\bf{e}}}_{ij}^{(l)}\right),$$

(10)

$${\hat{{\bf{h}}}}_{i}^{(l+1)}={\phi }_{h}\left({{\bf{h}}}_{i}^{(l)},\sum _{j\in {\mathcal{N}}(i)}{w}_{ij}{{\bf{e}}}_{ij}^{(l+1)}\right),$$

(11)

$${{\bf{x}}}_{i}^{(l+1)}={{\bf{x}}}_{i}^{(l)}+\frac{1}{{N}_{i}}\sum _{j\in {\mathcal{N}}(i)}\left({{\bf{x}}}_{i}^{(l)}-{{\bf{x}}}_{j}^{(l)}\right){\phi }_{x}\left({{\bf{e}}}_{ij}^{(l+1)}\right),$$

(12)

where l denotes the lth EGCL layer, ${{\bf{x}}}_{i}^{(0)}={{\bf{x}}}_{i}^{\rm{pos}}$ and ${w}_{ij}={\rm{sigmoid}}$$({\phi }_{w}({{\bf{e}}}_{ij}^{(l+1)}))\left.\right)$ is a soft estimated weight assigned to the specific edge representation. All components (ϕ_e, ϕ_h, ϕ_x, ϕ_w) are learnable and parametrized by fully connected neural networks. In the information propagation, EGNN achieves equivariance to translations and rotations on the node coordinates X^pos, and preserves invariant to group transformations on the node features H and edge features E.

However, the vanilla EGNN only considers local neighbour aggregation while neglecting the global context. Some recent studies^13,39 have demonstrated the importance of global information in protein design. Therefore, we introduce a global-aware module in the EGCL layer, which incorporates the global pooling vector into the update of node representations: that is,

$${{\bf{m}}}^{(l+1)}={\rm{MeanPool}}\left({\left\{{\hat{{\bf{h}}}}_{i}^{(l+1)}\right\}}_{i\in {\mathcal{G}}}\right),$$

(13)

$${{\bf{h}}}_{i}^{(l+1)}={\hat{{\bf{h}}}}_{i}^{(l+1)}\odot {\rm{sigmoid}}\left({\phi }_{m}\left({{\bf{m}}}^{(l+1)},{\hat{{\bf{h}}}}_{i}^{(l+1)}\right)\right),$$

(14)

where MeanPool( ⋅ ) is the mean pooling operation over all nodes within a residue graph. The global-aware module effectively integrates global context into modelling and only increases a linear computational cost. To predict the probabilities of residue types, the node representations from the last EGCL layer are fed into a fully connected classification layer with softmax function, which is defined as

$${{\bf{p}}}_{i}^{\rm{b}}={\rm{softmax}}\left({{\bf{l}}}_{i}^{\rm{b}}\right),\quad {{\bf{l}}}_{i}^{\rm{b}}={{\bf{h}}}_{i}^{(L)}{\bf{W}}_{\rm{o}}+{{\bf{b}}}_{\rm{o}},$$

(15)

where ${\bf{W}}_{\rm{o}}\in {{\mathbb{R}}}^{{D}_{h}\times 20}$ and ${{\bf{b}}}_{\rm{o}}\in {{\mathbb{R}}}^{1\times 20}$ are a learnable weight matrix and a bias vector respectively.

Low-confidence residue selection and mask ratio adaptor

As previously mentioned, structural information alone can sometimes be insufficient to determine all residue identities. Certain flexible regions display a weaker correlation with the backbone structure but are strongly influenced by their sequential context. To enhance the denoising network’s performance, we introduce a masked sequence designer module. This module refines the residues identified with low confidence in the base sequence predictor. We adopt an entropy-based residue selection strategy, as proposed by Zhou et al. (2023)²⁴, to identify these low-confidence residues. The entropy for the ith residue of the probability distribution ${{\bf{p}}}_{i}^{b}$ is calculated as

$${\rm{en{t}}}_{i}^{\rm{b}}=-\sum _{j}{\,\text{p}}_{ij}^{\rm{b}}\log \left({\text{p}}_{ij}^{\rm{b}}\right).$$

(16)

Given that entropy quantifies the uncertainty in a probability distribution, it can be used to locate the low-confidence predicted residues. Consequently, residues with the most entropy are masked, whereas the rest remain in a sequential context. The masked sequence designer aims to reconstruct the entire sequence by using the masked partial sequence in combination with the backbone structure. In addition, to account for the varying noise levels of the input sequence in diffusion models, we designed a simple mask ratio adaptor to dynamically determine the entropy mask percentage at different denoising steps: that is,

$${\rm{mr}}_{t}=\sin {\left(\frac{\uppi }{2}{\beta }_{t}\sigma \right)}+m,$$

(17)

where β_t $\in$ [0, 1] represents the noise weight at step t derived from the noise schedule, and σ and m are the predefined deviation and minimum mask ratio, respectively. With the increase of β_t, the mask ratio is proportional to its time step.

Mask-prior pretraining

To incorporate prior knowledge of sequential context, we pretrained the masked sequence designer by applying the masked language modelling objective proposed in BERT⁴⁰. It is important to clarify that we used the same training data in the diffusion models for pretraining purposes, to avoid any information leakage from external sources. In this process, we randomly sampled a proportion of residues in the native AA sequences and replaced them with the masking procedures: (1) masking 80% of the selected residues using a special MASK type; (2) replacing 10% of the selected residues with other random residue types; and (3) keeping the remaining 10% residues unchanged. Subsequently, we input the partially masked sequences, along with structural information, into the masked sequence designer. The objective of the pretraining stage was to predict the original residue types from the masked residue representations using a cross-entropy loss function.

Masked sequence designer

We used an IPA network as the masked sequence designer. IPA is a geometry-aware attention mechanism designed to facilitate the fusion of residue representations and spatial relationships, enhancing the structure generation within AlphaFold2¹⁵. In this study, we repurposed the IPA module to refine low-confidence residues in the base sequence predictor. Given a mask AA sequence, we denote its residue representation as S = [s₁, s₂,⋯, s_N], which is derived from the residue types and positional encoding. To incorporate geometric information, as with the IPA implementation in Frame2seq⁴¹, we constructed a pairwise distance representation ${\bf{Z}}=\{{{\bf{z}}}_{ij}\in {{\mathbb{R}}}^{1\times {d}_{z}}| 1\le i\le N,1\le j\le N\}$ and rigid coordinate frames ${\mathcal{T}}=\{{T}_{i}:= ({{\bf{R}}}_{i}\in {{\mathbb{R}}}^{3\times 3},{{\bf{t}}}_{i}\in {{\mathbb{R}}}^{3})| 1\le i\le N\}$. The pairwise representation Z was obtained by calculating interresidue spatial distances and relative sequence positions. The rigid coordinate frames were constructed from the coordinates of backbone atoms using a Gram–Schmidt process, providing a consistent local reference for ensuring the invariance of IPA to global Euclidean transformations. Subsequently, we took the residue representation, pairwise distance representation and rigid coordinate frames as inputs, and fed them into a stack of IPA layers for representation learning, which is defined as

$${{\bf{S}}}^{(l+1)},{{\bf{Z}}}^{(l+1)}={\rm{IPA}}({{\bf{S}}}^{(l)},{{\bf{Z}}}^{(l)},{{\mathcal{T}}}).$$

(18)

The IPA network follows the self-attention mechanism. However, it enhances the general attention queries, keys and values by incorporating 3D points that are generated in the rigid coordinate frame of each residue. This operation ensures that the updated residue and pair representations remain invariant by global rotations and translations. More details on the IPA feature construction and algorithm implementation are provided in Supplementary Information Section 6. For the ith residue, the predicted probability distribution and entropy in the masked sequence designer are calculated as

$${{\bf{p}}}_{i}^{\rm{m}}={\rm{softmax}}({{\bf{l}}}_{i}^{\rm{m}}),\quad {{\bf{l}}}_{i}^{\rm{m}}={{\bf{h}}}_{i}^{(L)}{\bf{W}}_{\rm{m}}+{{\bf{b}}}_{\rm{m}},$$

(19)

$${\rm{en{t}}}_{i}^{\rm{m}}=-{\sum _{j}{\,\rm{p}}_{ij}^{\rm{m}}\log ({\rm{p}}_{ij}^{\rm{m}})},$$

(20)

where ${\bf{W}}_{\rm{m}}\in {{\mathbb{R}}}^{{D}_{s}\times 20}$ and ${{\bf{b}}}_{\rm{m}}\in {{\mathbb{R}}}^{1\times 20}$ are the learnable weight matrix and bias vector, respectively. The training objective was to jointly minimize the cross-entropy losses for both the base sequence predictor and masked sequence designer. In the inference stage, we calculated the final predicted probability by weighting the output logits based on their entropy as

$${{\bf{l}}}_{i}^{\,{\rm{f}}\,}=\frac{\exp \left(-{\rm{en{t}}}_{i}^{\rm{b}}\right)}{\exp \left(-{\rm{en{t}}}_{i}^{\rm{b}}\right)+\exp \left(-{\rm{en{t}}}_{i}^{\rm{m}}\right)}{{\bf{l}}}_{i}^{\rm{b}}+\frac{\exp \left(-{\rm{en{t}}}_{i}^{\rm{m}}\right)}{\exp \left(-{\rm{en{t}}}_{i}^{\rm{b}}\right)+\exp \left(-{\rm{en{t}}}_{i}^{\rm{m}}\right)}{{\bf{l}}}_{i}^{\rm{m}}.$$

(21)

$${{\bf{p}}}_{i}^{\,{\rm{f}}\,}={\rm{softmax}}\left({{\bf{l}}}_{i}^{\,{\rm{f}}\,}\right).$$

(22)

By incorporating the mask-prior denoising network into the discrete denoising diffusion process, our framework enhanced the denoising trajectories, leading to more accurate predictions of protein sequences.

Experimental setting

Primary datasets

We evaluated MapDiff on experimentally validated protein structures curated from well-established databases. The CATH database²⁵ is widely used in inverse folding research, enabling fair comparisons across different methodologies. It classifies proteins into hierarchical levels based on class, architecture, topology and homologous superfamily, with filtering to reduce redundancy and ensure structural diversity. Following previous studies^13,26,27, proteins are partitioned based on their CATH topology classification codes, ensuring that the training, validation and test sets contain non-overlapping topologies. This partitioning strategy provided a robust evaluation of the model’s generalization to unseen proteins. For CATH 4.2, the dataset consisted of 18,024 structures for training, 608 for validation and 1,120 for testing. Similarly, in CATH 4.3, we followed the topology classification approach in ESM-IF²⁷, resulting in 16,630 proteins for training, 1,516 for validation and 1,864 for testing. By including both CATH 4.2 and CATH 4.3, we assessed the stability of model performance across dataset versions, ensuring robustness to updates in protein-structure databases.

Zero-shot generalization datasets

To further assess MapDiff’s zero-shot generalization ability, we evaluated it on the two independent TS50 and PDB2022 datasets. TS50 (ref. ⁵) is a commonly used benchmark for protein-sequence design, consisting of 50 diverse protein chains covering different structural classes. PDB2022 includes single-chain structures published in the Protein Data Bank (PDB)⁴² between 5 January 2022 and 26 October 2022, curated by Zhou et al.²⁴, with protein length ≤500 and resolution ≤2.5 Å. This dataset consists of 1,975 proteins published after those in the CATH dataset, ensuring a strict time-based test ‘split’ to evaluate real-world temporal generalization. Both datasets are entirely separate from the CATH-derived training set, minimizing data leakage and providing a robust evaluation of structural and temporal generalization.

Baselines

We compared MapDiff with recent deep-graph models for inverse protein folding, including StructGNN²⁶, GraphTrans²⁶, GVP⁴³, AlphaDesign⁴⁴, ProteinMPNN¹, PiFold¹³, LM-Design⁴⁵ and GRADE-IF¹. To ensure a reliable and fair comparison, we reproduced the open-source and four most state-of-the-art baselines (ProteinMPNN, PiFold, LM-Design and GRADE-IF) under identical settings in our experiments. ProteinMPNN uses a message-passing neural network to encode structure features, and a random decoding scheme to generate protein sequences. PiFold introduces a residue featurizer to extract distance, angle and direction features. It proposes a PiGNN encoder to learn expressive residue representations, enabling the generation of protein sequences in a one-shot manner. LM-Design uses structure-based models as encoders and incorporates the protein language model ESM as a protein designer to refine the generated sequences. GRADE-IF employs EGNN to learn residue representations from protein structures, and it adopts the graph denoising diffusion model to iteratively generate feasible sequences. All baselines were implemented following the default hyperparameter settings in their original papers.

Implementation set-up

MapDiff is implemented in Python v.3.8 and PyTorch v.1.13.1 (ref. ⁴⁶), along with functions from BioPython v.1.81 (ref. ⁴⁷), PyG v.2.4.0 (ref. ⁴⁸), Scikit-learn v.1.0.2 (ref. ⁴⁹), NumPy v.1.22.3 (ref. ⁵⁰) and RDKit v.2023.3.3 (ref. ⁵¹). It consists of two training stages: mask-prior pretraining and denoising diffusion model training, both of which use the same CATH 4.2/4.3 training set. The batch size was set to eight, and the models were trained up to 200 epochs in pretraining and 100 epochs in denoising training. We employed the Adam optimizer with a one-cycle scheduler for parameter optimization, setting the peak learning rate to 5 × 10⁻⁴. In the denoising network, the structure-based sequence predictor consisted of six global-aware EGCL layers, each with 128 hidden dimensions. In addition, the masked sequence designer stacked six layers of IPA, each with 128 hidden dimensions and four attention heads. The dropout rate was set to 0.2 in both the EGCL and IPA layers. A cosine schedule was applied to control the noise weight at each time step, with a total of 500 time steps. During sampling inference, the skip steps for DDIM were configured to 100, and the Monte-Carlo forward passes were set to 50. For the mask ratio adaptor, we set the minimum mask ratio to 0.4 and the deviation to 0.2. All experiments were conducted on a single Tesla A100 GPU. Following the regular evaluation in deep learning, the best-performing model was selected based on the epoch that provided the highest recovery on the validation set. After that, this selected model was subsequently used to evaluate performance on the test set. For the foldability analysis, we applied a single AlphaFold2 pTM model (that is, model_1_ptm) with three recycles to balance accuracy and computational efficiency. Multiple sequence alignment information was generated for each sequence using the MMSeqs2 (refs. ^52,53) server provided by ColabFold⁵⁴. We provide the algorithm details for the training and sampling inference in Supplementary Information Section 5, and the scalability study in Supplementary Information Section 8 and Supplementary Fig. 4.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.