Learning to adapt through bio-inspired gait strategies for versatile quadruped locomotion

Abstract

Legged robots must adapt their gait to navigate unpredictable environments, a challenge that animals master with ease. However, most deep reinforcement learning (DRL) approaches to quadruped locomotion rely on a fixed gait, limiting adaptability to changes in terrain and dynamic state. Here we show that integrating three core principles of animal locomotion-gait transition strategies, gait memory and real-time motion adjustments enables a DRL control framework to fluidly switch among multiple gaits and recover from instability, all without external sensing. Our framework is guided by biomechanics-inspired metrics that capture efficiency, stability and system limits, which are unified to inform optimal gait selection. The resulting framework achieves blind zero-shot deployment across diverse, real-world terrains and substantially outperforms baseline controllers. By embedding biological principles into data-driven control, this work marks a step towards robust, efficient and versatile robotic locomotion, highlighting how animal motor intelligence can shape the next generation of adaptive machines.

Main

Originally inspired by the remarkable adaptability of quadruped mammal locomotion, an ability shaped by innate and environmentally induced factors^1,2,3, the field of quadruped robotics has invested substantial resources into developing equally proficient locomotion frameworks. At present, the most advanced systems rely on end-to-end deep reinforcement learning (DRL), which involves training a multilayer perceptron⁴ capable of navigating diverse environments.

These frameworks demonstrate impressive realization of terrestrial locomotion skills, which can be classified into two groups (further detailed in Supplementary Section 1); Froude-characterized locomotion (no desired velocity normal to the ground plane and hence upholds the assumptions of the Froude number⁵) such as walking or running in real-world^6,7, urban^8,9 and deformable⁷ terrains, and Froude-free locomotion (which features a desired velocity normal to the ground plane) such as jumping between platforms¹⁰, climbing over obstacles¹¹ and sure-footedness¹². Despite these achievements, when it comes to Froude-characterized locomotion, which can account for about 70−90% of daily animal locomotion^13,14, the adaptability of these frameworks remains constrained, as most systems are limited to deploying a single targeted gait or locomotion strategy.

In contrast, biomechanics research has shown that no single gait is universally optimal across all scenarios within Froude-characterized locomotion^15,16,17. Animals adapt their locomotion by employing nominal gaits such as ambling, trotting and running¹⁸, while switching to specialized gaits such as hopping, pronking and bounding for off-nominal tasks such as predator evasion or obstacle navigation¹⁹. Current DRL frameworks fall short of replicating this level of Froude-characterized locomotion versatility. To address this limitation, some approaches have focused on training DRL policies to learn multiple gaits by providing reference motions during training^20,21,22,23 or by learning from policies that specialize in specific gaits²⁴. However, these methods remain insufficient when compared with the extensive capabilities observed in animal locomotion, which include:

• Adaptation of gait style for optimal performance in response to challenging terrains and perturbations, enabled by advanced gait selection strategies.

• Rapid deployment of a diverse set of task- and state-specific gaits, attributable to gait procedural memory.

• Seamless deviation from nominal gait motions to address off-nominal contact states, achieved through precise motion adjustments tailored to the environment.

Although existing DRL frameworks have shown progress in implementing learned gaits, none successfully integrates all three attributes simultaneously. This gap highlights the considerable potential of biomechanics-inspired approaches to advance robotic locomotion.

While bio-inspired methods that leverage central pattern generators²⁵ have realized spontaneous gait transitions²⁶ and mimic certain animal behaviours²⁷, their performance in real-world applications is often limited. Typically, such experiments are constrained to controlled environments^27,28 or, when conducted outdoors, are restricted by low velocities and simple tasks²². Another bio-inspired approach is training locomotion policies from re-targeted animal motion data²⁹. Although this method can achieve natural Froude-free locomotion, there is no guarantee that the exhibited Froude-characterized locomotion is optimal; it is unreasonable to assume that mechanically different systems would perform efficiently with the same low-level behaviour. These limitations suggest that instead of attempting to replicate animal locomotion mechanisms precisely, state-of-the-art DRL frameworks should be augmented with high-level attributes derived from animal locomotion to instil the proficiency observed in nature.

Animal gait transition strategies, which contribute to optimal performance and enable navigation of challenging environments, are believed to emerge from the minimization of metrics related to energy consumption^5,30,31, mechanical work^32,33,34, instability^35,36 and musculoskeletal forces^37,38,39. However, no singular metric has been definitively identified as the sole driver of these transitions. Instead, it is hypothesized that a combination of these factors influences gait transition strategies^35,40,41.

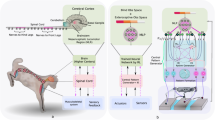
The concept of gait procedural memory, which facilitates the rapid deployment of a range of gaits, is thought to reside within the cerebellum of the animal brain. This region governs the coordination of limb movements for each gait learned by the animal^42,43. Similarly, adaptive motion adjustments, crucial for seamless adaptation to off-nominal contact states, are achieved through coordination between the mesencephalic locomotor region, which oversees locomotion execution⁴⁴, and the cerebellum. These adjustments rely on sensory feedback to modify limb movements in response to the animal’s current state⁴⁵.

Despite these insights, there has been no previous attempt to simultaneously integrate all these attributes—gait transition strategies, procedural memory and adaptive motion adjustments—within existing DRL locomotion frameworks. This leads to the following research questions:

• (1) How can the roles of the mesencephalic locomotor region and the cerebellum inspire the augmentation of an end-to-end DRL locomotion policy to adapt to off-nominal contact states?

• (2) Can a DRL locomotion policy, inspired by gait procedural memory, learn to deploy a diverse set of gaits and perform rapid gait transitions?

• (3) How can metrics that characterize animal gait transition strategies be effectively leveraged within a DRL policy for optimal gait selection? Does the resulting behaviour align with that observed in animals?

• (4) Can the developed framework exhibit exemplary adaptability to traverse real-world terrains not encountered during training? What is the contribution of each metric to this adaptability?

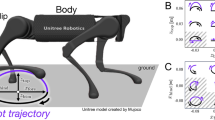
To address these questions, we propose a DRL locomotion framework (Fig. 1) designed to incorporate these key animal locomotion attributes. The framework shows exceptional adaptability through zero-shot deployment in complex, real-world environments, relying solely on interoceptive sensors.

Fig. 1: Instilling the core animal locomotion proficiency attributes within a DRL locomotion framework.

From taking an abstracted view of animal locomotion to determine the attributes of proficient locomotion, we instil animal gait transition strategies within the gait selection policy, π_G, gait procedural memory is embedded within the bio-inspired gait scheduler, and adaptive motion adjustments are realized by the locomotion policy, π_L. π_G has been trained to minimize the animal gait transition metrics applied to the quadruped robot based on the current robot state, s, and relevant bio-inspired gait scheduler output, β_G, to select the optimal gait, Γ*. The bio-inspired gait scheduler then generates the gait references informed by s from encoded high-level gait parameters. The gait references, β_L, are then passed to π_L to inform of any adjustments to the nominal gait motions. The control framework is constant between training and deployment to improve sim-to-real transfer. MLR, mesencephalic locomotor region; PD, proportional derivative controller; IMU, inertial measurement unit.

Results

Within the framework, presented in Fig. 1, a gait selection policy, π_G, is trained for optimal gait selection through minimizing gait transition metrics adopted from biomechanics to generate the output Γ* ∈ [0, 7] which maps to a specific gait within [stand, trot, run, bound, pronk, limp, amble, hop]. This selected gait, coupled with the velocity command within ${{\bf{U}}}^{{\rm{cmd}}}=[{v}_{x}^{{\rm{cmd}}},{v}_{y}^{{\rm{cmd}}},{\omega }_{z}^{{\rm{cmd}}},{\varGamma }^{* }]\in {{\mathbb{R}}}^{4}$, where ${v}_{x}^{{\rm{cmd}}}$, ${v}_{y}^{{\rm{cmd}}}$ and ${\omega }_{z}^{{\rm{cmd}}}$ are base velocities in x, y and yaw, respectively, is passed to the bio-inspired gait scheduler (BGS) to generate gait references (along with transition references between any gait pair), as detailed in ‘Bio-inspired gait scheduler’ in Methods. These gait references are contained within the BGS outputs β_L and β_G for the locomotion policy, π_L, and π_G, respectively, through inclusion within their observation vectors o_L and o_G. In this respect, the BGS acts as pseudo gait procedural memory. The gait references are adjusted based on the robot’s state, s, generated by the state estimator (SE) from the sensor feedback vector, σ, which in turn reflects the relationship between the cerebellum and the mesencephalic locomotor region. To realize the output joint positions of π_L, q*, they are passed through a proportional derivative controller to generate joint torque commands τ*.

We evaluate the proposed framework through a set of studies, demonstrating that it outperforms others by exhibiting quadruped animal locomotion strategies, and validating this gained proficiency on real-world terrain, as presented in Fig. 2 and Supplementary Video 1.

Fig. 2: Snapshots of our framework being deployed in different environments.

Top: simulated terrains ${h}_{{\rm{terr}}}^{0}$ through ${h}_{{\rm{terr}}}^{3}$ are generated with fractal noise with maximum heights of 0 m, 0.06 m, 0.13 m and 0.2 m. a–l, To demonstrate that the adaptability of our framework is transferable to the real world it has been deployed on wood-chip (a), a large step (b), concrete slabs with large cracks (c), tarmac (d), deep rocks (e), grassy terrain (f), overgrown roots (g), fallen leaves (h), loose timber (i), a low-friction ramp (j), flat terrain with perturbations (k) and balanced timber (i).

Achieving adaptive motion adjustment with a diverse set of gaits

To evaluate our method of instilling adaptive motion adjustment and procedural memory for diverse gait deployment, a comparison study is completed between our bio-inspired locomotion policy ${\pi }_{{\mathrm{L}}}^{{\rm{bio}}}$, a standard multi-gait locomotion policy with no pseudo procedural memory ${\pi }_{{\mathrm{L}}}^{{\rm{no}}{{\bf{\upbeta }}}_{{\mathrm{L}}}}$, and a policy trained that also uses β_L within o_L but implements the standard approach of extracting the observations from the simulator, ${\pi }_{{\mathrm{L}}}^{{\rm{noSE}}}$, as shown in Supplementary Video 2. From the results of this study, shown in Fig. 3, the proficiency of ${\pi }_{{\mathrm{L}}}^{{\rm{bio}}}$ over ${\pi }_{{\mathrm{L}}}^{{\rm{no}}{{\bf{\upbeta }}}_{{\mathrm{L}}}}$ and ${\pi }_{{\mathrm{L}}}^{{\rm{noSE}}}$ in terms of velocity tracking error ${v}_{{\mathrm{B}}}^{{\rm{err}}}$, contact schedule tracking error ${c}_{{\rm{avg}}}^{{\rm{err}}}$ and base stability (magnitude of undesirable base angular velocities) ${\omega }_{{\mathrm{B}}}^{{\rm{err}}}$, is stark.

Fig. 3: Locomotion comparison study experiments.

a, Each policy follows a set of command velocities in x and yaw between 0 and 1 m s⁻¹ and between −1 and 1 rad s⁻¹, respectively. During each velocity pair, the commanded gait is cycled through all gaits, switching every 1 s. This repeated five times over flat, ${h}_{{\rm{terr}}}^{0}$, to very rough terrain, ${h}_{{\rm{terr}}}^{3}$ (shown in Fig. 2) with the average performance being plotted. A number rather than a magnitude indicates the count of experiments that the policy failed. b, Each policy follows a sinusoidal trajectory in x (v_x) and in yaw (ω_z) while switching gaits every 2 s, which is repeated 5 times over ${h}_{{\rm{terr}}}^{0}$ and ${h}_{{\rm{terr}}}^{3}$ terrain. The green highlighted areas indicate transition phases, for which the function and formulation are detailed in ‘Bio-inspired gait scheduler’ in Methods, and the black triangles represent points of failure. c, Policies follow a command of just v_x = 0.5 m s⁻¹ while using a constant trot gait while encountering rectangular steps with a height of 0.05 m, where $| {\bar{\omega }}_{{\mathrm{B}}}^{{\rm{err}}}|$ is the magnitude of the desired orientation error, FL is front left, FR is front right, RL is rear left and RR is rear right in reference to the robot’s feet.

As shown in Fig. 3a, on flat terrain, ${\pi }_{{\mathrm{L}}}^{{\rm{bio}}}$ achieves lower ${v}_{{\mathrm{B}}}^{{\rm{err}}}$, ${c}_{{\rm{avg}}}^{{\rm{err}}}$ and ${\omega }_{{\mathrm{B}}}^{{\rm{err}}}$ than ${\pi }_{{\mathrm{L}}}^{{\rm{no}}{\bf{\upbeta }}_{\mathrm{L}}}$ and ${\pi }_{{\mathrm{L}}}^{{\rm{noSE}}}$, averaging 15%, 21% and 10% lower, respectively (excluding failures), with errors increasing at higher velocity commands. This performance gap widens on rough terrain, where ${\pi }_{{\mathrm{L}}}^{{\rm{no}}{\bf{\upbeta }}_{\mathrm{L}}}$ and ${\pi }_{{\mathrm{L}}}^{{\rm{noSE}}}$ fail frequently, especially at higher speeds and rougher surfaces, while ${\pi }_{{\mathrm{L}}}^{{\rm{bio}}}$ succeeds in all trials despite being trained on only flat terrain. This highlights its adaptability to unseen environments (see ‘Policy training’ in Methods for the rationale behind omitting rough terrain in π_L training).

This incompetence of ${\pi }_{{\mathrm{L}}}^{{\rm{no}}{{\bf{\upbeta }}}_{{\mathrm{L}}}}$ and ${\pi }_{{\mathrm{L}}}^{{\rm{noSE}}}$ is caused by a lack of adaptive swing foot motion adjustments captured within β_L based on s and the accumulation of error within the SE respectively. Both of these factors are substantially affected by the instabilities rough terrain inflicts upon the robot. Considering that the nominal swing foot peak height is defined as 25% of the nominal base height and for ${h}_{{\rm{terr}}}^{2}$ and ${h}_{{\rm{terr}}}^{3}$ (as defined in Fig. 2) the peak terrain height is 44% and 67% of the base height, having no data or strategy to account for this harsh terrain results in the rapid deterioration of proficiency.

For ${\pi }_{{\mathrm{L}}}^{{\rm{no}}{\bf{\upbeta }}_{\mathrm{L}}}$, Fig. 3b shows large spikes in ${c}_{{\rm{avg}}}^{{\rm{err}}}$ and ${\omega }_{{\mathrm{B}}}^{{\rm{err}}}$ when encountering ${h}_{{\rm{terr}}}^{3}$, highlighting its inability to adapt swing foot trajectories and overcome an unrefined solution space. Figure 3c further shows sustained instabilities in base height and orientation after contact with steps at 17% of the nominal base height. For ${\pi }_{{\mathrm{L}}}^{{\rm{noSE}}}$, Fig. 3b,c shows that poor reference tracking and stability worsen with velocity command magnitude and time, as it lacks strategies to mitigate error build-up in the SE. Since ${\pi }_{{\mathrm{L}}}^{{\rm{bio}}}$ does not experience any of these limitations, this explicitly demonstrates the effectiveness of implementing β_L and s within o_L; ${\pi }_{{\mathrm{L}}}^{{\rm{bio}}}$ successfully generalizes across gaits and terrain, demonstrating successful instillation of adaptive motion adjustment and gait procedural memory.

Applying biomechanics metrics for optimal gait selection

Directly applying biomechanics metrics to instil animal gait transition strategies is unsuitable due to differences between animals and robots, as well as π_G training requirements. Instead, we use cost of transport (CoT), torque saturation (τ_%), external work (W_ext) and foot contact tracking error (${c}_{{\rm{avg}}}^{{\rm{err}}}$) to minimize energy use, actuator-structural forces, mechanical work and instability, respectively. Details and justification of these metrics are in ‘Biomechanics gait transition metrics’ in Methods.

In accordance with ‘Gait selection policy’ in Methods, these metrics are unified within the training of the gait selection policy ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ to instil the strategies animals use for optimal gait selection to achieve exemplary adaptability. To investigate whether ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ effectively minimizes these metrics through gait selection, the results of competing the highly demanding velocity command trajectory presented in Fig. 4 and Supplementary Video 3 for ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ paired with ${\pi }_{{\mathrm{L}}}^{{\rm{bio}}}$ are collected, along with that for all individual gaits deployable by ${\pi }_{{\mathrm{L}}}^{{\rm{bio}}}$, for flat terrain and terrain ${h}_{{\rm{terr}}}^{2}$.

Fig. 4: Comparative study between each gait and ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$.

For terrains ${h}_{{\rm{terr}}}^{0}$ and ${h}_{{\rm{terr}}}^{2}$, each isolated gait and ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ are given a velocity command to follow to assess their performance in terms of CoT, τ_%, W_ext and ${c}_{{\rm{avg}}}^{{\rm{err}}}$; for each individual gait ${\pi }_{{\mathrm{L}}}^{{\rm{bio}}}$ just run with the gait statically selected and for ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ it is coupled with ${\pi }_{{\mathrm{L}}}^{{\rm{bio}}}$ for autonomous optimal gait selection. In addition, at the bottom of these time-series plots, the contact state of the feet and the gait that ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ realizes is also shown. The average relative performance in terms of these metrics is shown in the radar plots at the bottom of the figure, where each gait’s performance is normalized to that of the best performer for each metric; the higher the value within the radar plot, the more effectively that metric has been minimized.

Figure 4 shows that ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ exclusively uses trotting at low speeds and running at high speeds. When accelerating, ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ oscillates between trotting and running, with an increasing bias towards running, to increase the stride frequency as visualized by the foot contact data in Fig. 4. Consequently, ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ not only reliably tracks the optimal gait but also outperforms individual gaits, which is only aided by its transition to standing during ${v}_{x}^{{\rm{cmd}}}=0,\,{\omega }_{z}^{{\rm{cmd}}}=0$ events for minimal τ_%, W_ext and ${c}_{{\rm{avg}}}^{{\rm{err}}}$. This behaviour, although never targeted, is reflected in animal locomotion strategies, where gait stride frequency increases with speed and transitional phases blend gaits to minimize energy use³³. Under rough terrain and high acceleration, ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ employs additional gaits to manage instability. This leads to a gait classification: trot and run serve as nominal gaits for low and high speeds, while bound, pronk, limp, amble and hop act as auxiliary gaits for off-nominal conditions such as stability recovery.

When inspecting the radar charts in Fig. 4, which depict relative performance in terms of the metrics, the origin of this emerged gait selection strategy becomes clear. Across the gaits, on flat terrain, trot and run gaits achieve the best relative performance. However, when it comes to overcoming rough terrain, bound, hop and limp gaits all gain relative performance in τ_%, W_ext and ${c}_{{\rm{avg}}}^{{\rm{err}}}$, while trot and run gaits show a reduced dominance in relative proficiency. In addition to this observation providing an insight as to why ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ chooses to utilize these auxiliary gaits, it also provides evidence to suggest that τ_%, W_ext and ${c}_{{\rm{avg}}}^{{\rm{err}}}$ can effectively characterize stability. This observation is further investigated and discussed in the following sections. Overall, ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ outperforms all individual gaits across all metrics, with the exception of CoT for trot and run gaits where the difference is negligible, demonstrating the successful minimization of the metrics and successful instillation of gait procedural memory of how to utilize each gait given the robot’s state and task.

Comparison between robot and animal gait selection

When developing metrics to characterize gait transitions in animals, data are collected over intervals of increasing forward velocity on flat terrain^33,35,37,46. Hence, in Fig. 5a we took the same approach. We also repeat this experiment with ${h}_{{\rm{terr}}}^{3}$ to investigate correlations between the metrics and the effects of introducing rough terrain, as presented in Fig. 5b. Additionally, we train four further π_G policies that individually minimize energy consumption ${\pi }_{{\mathrm{G}}}^{{\rm{CoT}}}$, actuator-structural forces ${\pi }_{{\mathrm{G}}}^{{\tau }_{ \% }}$, mechanical work ${\pi }_{{\mathrm{G}}}^{{W}_{{\rm{ext}}}}$ and stability ${\pi }_{{\mathrm{G}}}^{{c}^{{\rm{err}}}}$, in accordance with ‘Biomechanics gait transition metrics’ in Methods, to compare their performance with ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$. One unanimous observation across Fig. 5a is that animals experience a gait transition phase over a range of velocities^35,46,47. This behaviour is reflected in ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$, where we class a transition phase as where no individual gait occupies more than 75% of the gaits used at a specific speed.

Fig. 5: Comparison between animal and robot gait selection policy strategies during increasing linear velocity.

a, The bottom two plots of all robot data indicate the percentage of each gait utilized at that velocity. Magenta, purple and blue shaded regions indicate the transition phases of ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$, ${\pi }_{{\mathrm{G}}}^{{W}_{{\rm{ext}}}}$ and animals, respectively. This study compares transition strategies of ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ and ${\pi }_{{\mathrm{G}}}^{{\rm{CoT}}}$ with data collected from dogs³⁵ and horses^33,46 in terms of CoT (top left), ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ and ${\pi }_{{\mathrm{G}}}^{{\tau }_{ \% }}$ with data collected from horses³⁷ in terms of foot ground reaction forces (top right), ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ and ${\pi }_{{\mathrm{G}}}^{{W}_{{\rm{ext}}}}$ with horses³³ in terms of external work (bottom left), and ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ and ${\pi }_{{\mathrm{G}}}^{{c}^{{\rm{err}}}}$ with opossums and dogs³⁵ (bottom right). b, Mapping the correlation between metrics and the average gait ID selected across velocities for terrains ${h}_{{\rm{terr}}}^{0}$ and ${h}_{{\rm{terr}}}^{3}$, with the dataset of each terrain consisting of 31 data points averaged over 1,000 samples.

Energy expenditure (CoT)

An animal’s gait transition aligns with the CoT-optimal point, ${\lambda }^{{\rm{CoT}}}$, to minimize energy cost^5,33, as shown in Fig. 5a. ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ mirrors this, tracking the lowest-CoT gait with transitions centred on ${\lambda }^{{\rm{CoT}}}$. In contrast, ${\pi }_{{\mathrm{G}}}^{{\rm{CoT}}}$ lacks a defined transition phase and switches earlier, due to training on rough terrain where hopping improves CoT (Fig. 4). Figure 5b further shows ${h}_{{\rm{terr}}}^{3}$ induces similar CoT distributions but with greater gait variance, as auxiliary gaits become more effective. This highlights that CoT-only training reduces generality and diverges from natural gait selection.

Actuator-structural forces (foot contact forces)

Animals are observed to change gait to minimize actuator-structural forces (that is, musculoskeletal forces)³⁷, which in biomechanics is measured through foot ground reaction force, f_grf. Similarly, ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ and ${\pi }_{{\mathrm{G}}}^{{\tau }_{ \% }}$ reduce f_grf through selecting the optimal gait for minimizing τ_%. This supports that τ_% is a suitable alternative to f_grf, which is further validated by a strong correlation between them in Fig. 5b. However, not only does ${\pi }_{{\mathrm{G}}}^{{\tau }_{ \% }}$ maintain a trotting gait past optimal f_grf but also the transition itself is instantaneous. In turn, ${\pi }_{{\mathrm{G}}}^{{\tau }_{ \% }}$ better reflects the animal data from ref. ³⁷ than ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$. This could be explained by the metric being misinterpreted in ref. ³⁷; with a high correlation between τ_% and f_grf with the stability metric ${c}_{{\rm{avg}}}^{{\rm{err}}}$, it suggests that instability causes transition, which is rare on flat terrain, as addressed in ‘Discussion’.

Mechanical work (external work)

Animals transition to preserve external mechanical work, W_ext, but do so before ${\lambda }^{{W}_{{\rm{ext}}}}$, indicating relaxed minimization (Fig. 5a). ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ reflects this behaviour; transition occurs before ${\lambda }^{{W}_{{\rm{ext}}}}$ yet minimal W_ext is preserved. While ${\pi }_{{\mathrm{G}}}^{{W}_{{\rm{ext}}}}$ can reduce W_ext, its transition phase is extended over a larger range of velocities compared with animals, occurring just after ${\lambda }^{{W}_{{\rm{ext}}}}$. In turn, this suggests that switching gaits between trotting and running offers minimal reductions in W_ext, resulting in a less definitive transition. However, W_ext also seems to capture stability due to its high correlation with the stability metrics on ${h}_{{\rm{terr}}}^{3}$ in Fig. 5b, providing insight into its reduced role in Fig. 5a where only flat terrain is present.

Stability (stride duration coefficient of variation)

In ref. ³⁵, animals were shown to reduce their stride duration coefficient of variation (CV) to preserve stability as high gait periodicity indicates stability. This behaviour is presented in Fig. 5a, where animals are seen to initiate a transition phase when there is a considerable increase in stride CV, consequently leading to a decrease in CV and an increase in stability. ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ inherits the same strategy as only when a spike in stride CV is experienced does a transition phase begin, resulting in improved stability through lowering stride CV. However, this is not the case with ${\pi }_{{\mathrm{G}}}^{{c}^{{\rm{err}}}}$ as it acts to reduce stride CV much more aggressively by mixing both slow, fast and auxiliary gaits, which results in no clear transition phase being produced.

Only ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ consistently reflects all animal datasets and demonstrates the successful instillation of animal gait transition strategies. This also supports the notion that no singular metric can characterize animal gait selection and only through unification can similar behaviour in robots arise; the minimization of the metrics is expected and is seen across all π_G policies, but the intricacies of animal gait transition strategies are only seen in ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$. In addition, we have verified this behaviour transfers to real-world deployment in Supplementary Section 2; ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ achieves an 18% and 30% reduction in CoT compared with trotting and running on grassy terrain, respectively, while also preventing the failure cases trotting exhibits.

Adaption to real-world terrain

Although we have instilled animal gait transition strategies, gait procedural memory and adaptive motion into our framework, its real-world proficiency without hardware deployment is uncertain. Grassy terrain may trap swing feet, and the ground often features irregularities. However, despite ${\pi }_{{\mathrm{L}}}^{{\rm{bio}}}$ observing only flat terrain during training, during hardware experiments it successfully realizes all seven gaits on this terrain, as illustrated in Fig. 6a, demonstrating that gait procedural memory and adaptive motion adjustment successfully transfer to real-world environments, providing a high level of adaptability, as shown in Supplementary Video 4.

Fig. 6: Framework deployment in real-world environments to evaluate adaptability.

a, The deployment of ${\pi }_{{\mathrm{L}}}^{{\rm{bio}}}$ on uneven grassy terrain with manual gait selection to cycle through all gaits with a ${v}_{{\rm{x}}}^{{\rm{cmd}}}$ of 0.5 m s⁻¹, where the red shaded regions indicate a transition period. b–d, Our framework is deployed on loose timber (b), muddy grass (c) and a low-friction board (d), with maximum velocity magnitudes of 1 m s⁻¹, 2 m s⁻¹ and 1.7 m s⁻¹, respectively, where the event of critical loss of stability is indicated by the red dashed line, the bottom subplot uses the same gait colour code as Fig. 4, and the heatmaps show the magnitudes of each metric increasing from purple to yellow. e, Snapshots showing how animals also use a mixture of auxiliary gaits to overcome challenging terrain⁵⁵, where red circles are swing feet and green circles are stance feet.

Terrain that causes states of instability presents a substantial risk to the robot, hence we test the limits of our framework through deployment on loose timber, muddy grass and a low-friction board, as presented in Fig. 6b–d, respectively, and consolidated in Supplementary Video 5, with an additional experiment for external perturbations included within Supplementary Section 3. Each of the presented experiments showcases an off-nominal stability recovery event; however, in the nominal scenario, the framework can maintain stability without changing gaits. In the case of loose timber, critical instability is caused when one rear foot slips on a plank, causing it to collide with another. In response, ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ utilizes auxiliary gaits pronk and bound to recover, as depicted in Fig. 6b. This strategy of utilizing the auxiliary gaits for stability recovery is seen across all experiments and reflected in animals as highlighted in Fig. 6e where a horse is observed to utilize bounding and limping gaits to traverse down complex rock formations.

In all experiments presented, a considerable increase in a combination of W_ext, τ_% and ${c}_{{\rm{avg}}}^{{\rm{err}}}$ is experienced before a gait transition, while a weaker correlation is observed with CoT; spikes in W_ext, τ_% and ${c}_{{\rm{avg}}}^{{\rm{err}}}$ directly coincide or even preempt gait changes while CoT peaks lag. This is expected with ${c}_{{\rm{avg}}}^{{\rm{err}}}$ and W_ext as they capture periodicity and base height, respectively. However, this is less expected for τ_% to correlate with stability; this was never a factor investigated in ref. ³⁷. However, the correlation observed in these experiments and in Fig. 5b provides strong evidence that this is the case.

Discussion

By taking inspiration from animal locomotion proficiency attributes, we have developed a locomotion framework capable of traversing complex and high-risk terrain despite the robot not utilizing exteroceptive sensors nor experiencing any rough terrain during the training of ${\pi }_{{\mathrm{L}}}^{{\rm{bio}}}$. For ${\pi }_{{\mathrm{L}}}^{{\rm{bio}}}$, this is achieved through including the BGS output β_L (which encodes state-dependent pseudo gait procedural memory and adaptive motion adjustments) within the observation space o_L. This proves to be effective at overcoming rough terrain within Fig. 3 as without the presence of β_L within o_L, increased failure and instability are observed. This is the equivalent of removing an animal’s cerebellum functionality (resulting in reduced limb coordination and stability⁴⁵) in turn supporting the claim that β_L effectively encodes pseudo gait procedural memory.

${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ for optimal gait selection greatly expands adaptability through instilling gait selection strategies used by animals. As shown in Fig. 6, ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ can maintain stability in the event of the terrain undergoing radical structural or friction coefficient adjustments. These scenarios pose risks to robots with vision systems, as they typically cannot detect ground friction or terrain changes beyond their front legs. Through the use of ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$, this limitation is mitigated without implementing resource-heavy exteroceptive sensors. Comparing Fig. 6b–e showcases that animals and ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ utilize multiple auxiliary gaits to prevent failure. This behaviour, untargeted during training, suggests that unifying these metrics encodes the intricacies of animal gait transitions.

One provoking observation is that actuator-structural forces appear to characterize instability. Considering that ref. ³⁷ validates by applying increased loads that could cause instability, it suggests that this metric was initially misunderstood. Additionally, despite the employed biomechanics metrics being tested only on animals completing a linear forward trajectory on flat terrain, ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ upholds animal gait transition strategies across a wide range of terrains and base velocity commands. This supports that these metrics successfully characterize gait transitions and the notion that robots can indeed test biomechanics hypotheses, avoiding the resource, compatibility and ethical challenges of animal testing. Moving forward, we aim to integrate our work with those that focus on Froude-free locomotion, such as refs. ^11,12,29, to achieve exemplary adaptability and efficiency at both Froude-characterized and Froude-free locomotion levels.

Methods

Control framework overview

At the core of this work, the Unitree A1 quadruped robot used in all experiments features 12 degrees of freedom, n, which are all modelled as revolute joints, with their angular positions denoted as ${\bf{q}}\in {{\mathbb{R}}}^{n}$ and its base orientation represented as a rotation matrix R_B ∈ SO(3). As discussed in ‘Achieving adaptive motion adjustment with a diverse set of gaits’ and outlined in Fig. 1, both π_L and π_G are integrated within a control framework and supported by the SE and BGS for generation of the robot’s state data and gait references, respectively. The final output of π_L is target joint positions, q*, which are converted into joint torques, τ*, through the following proportional derivative controller that gets sent to the motors

$${{\bf{\uptau }}}^{* }={K}_{{\mathrm{p}}}({{\bf{q}}}^{* }-{\bf{q}})-{K}_{{\mathrm{d}}}\dot{{\bf{q}}},$$

(1)

where K_p and K_d are the proportional and derivative gains, respectively. Throughout this work, a constant K_p = 25 N m⁻¹ and K_d = 1 Ns m⁻¹ are used while running at 1,000 Hz, while π_L and π_G are run at 500 Hz and 100 Hz, respectively.

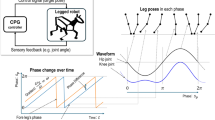
Bio-inspired gait scheduler

The BGS primary output, ${{\bf{\upbeta }}}_{{\mathrm{L}}}=[{{\bf{c}}}^{{\rm{ref}}},{{\bf{p}}}_{x}^{{\rm{ref}}},{{\bf{p}}}_{y}^{{\rm{ref}}},{{\bf{p}}}_{z}^{{\rm{ref}}}]\in {{\mathbb{R}}}^{16}$, defines the reference contact state of each foot, ${{\bf{c}}}^{{\rm{ref}}}\in {{\mathbb{B}}}^{4}$, and their reference Cartesian position in the world frame x axis, ${{\bf{p}}}_{x}^{{\rm{ref}}}\in {{\mathbb{R}}}^{4}$, y axis, ${{\bf{p}}}_{y}^{{\rm{ref}}}\in {{\mathbb{R}}}^{4}$, and z axis, ${{\bf{p}}}_{z}^{{\rm{ref}}}\in {{\mathbb{R}}}^{4}$, which are calculated online using the Raibert heuristic⁴⁸ to account for the current state of the robot. Throughout this paper, the limits enforced on the generation of ${{\bf{p}}}_{x}^{{\rm{ref}}}$, ${{\bf{p}}}_{y}^{{\rm{ref}}}$ and ${{\bf{p}}}_{z}^{{\rm{ref}}}$ are 0.3 m, 0.2 m and 0.1 m from the nominal local foot position, respectively. An adjusted version of the BGS output, β_G, is used for π_G as not all the information in β_L is required. This has the form of ${{\bf{\upbeta }}}_{{\mathrm{G}}}=[{{\bf{c}}}^{{\rm{ref}}},{{\bf{p}}}_{z}^{{\rm{ref}}},{\varOmega }_{{\rm{stab}}},\kappa ]\in {{\mathbb{R}}}^{10}$ where ${\varOmega }_{{\rm{stab}}}\in {\mathbb{R}}$ characterizes the inherent stability of a gait⁵, and $\kappa \in {\mathbb{B}}$ is a logical flag to indicate a state of gait transition. We originally developed the BGS in ref. ⁴⁹ where the Froude number⁵, Ω, is used to trigger gait transition based exclusively on CoT, which results in a set order of transitions. However, when applied to this work, this method is not entirely suitable as now multiple biomechanics metrics and a set of auxiliary gaits need to be considered. One issue is that Ω > 1 values are not compatible when calculating how many gait cycles, C, should a transition occur over. With this work investigating higher velocities than in ref. ⁴⁹, this has been resolved through calculating C through

$$C={{\mathrm{e}}}^{-2\varOmega }$$

(2)

This relationship ensures an almost instantaneous transition at Ω ≥ 2, which is the typical value that quadruped animals transition to a run⁵ instantaneously. Another limitation is that the calculation of the transition resolution, δ (how quickly a transition should be progressed each time step), only enables the transition between set gait pairs; this was not an issue in ref. ⁴⁹ as CoT efficiency was the only metric considered. As π_G requires any gait transition pair to be possible, Ω_stab = g/hf² (ref. ⁵) is utilized, where g is gravitational field strength, h is hip height and f is gait frequency. Through the use of Ω_stab, we are able to determine an indication of the inherent stability of any gait, hence a transition between a higher Ω_stab gait to a lower one should have smaller values of δ to increase the smoothness of the transition to promote stability. In the reverse scenario, a more harsh transition is more feasible, hence larger values of δ should be produced for rapid transition. As such, δ is now calculated by

$$\delta=1+\frac{{\varOmega }_{{\rm{stab}}}}{{\varOmega }_{{\rm{stab}}}^{{\rm{next}}}}$$

(3)

where ${\varOmega }_{{\rm{stab}}}^{{\rm{next}}}$ is the Ω_stab of the gait that is being transitioned to. In essence, f of the current and next gait dictates the harshness of the transition. This behaviour is also reflected in animal gait transitions, where transitioning from running (higher f) to trotting (lower f) the transition is slower compared with the opposite scenario⁵⁰. Overall, this augmented version of the BGS can achieve transition between any designed gait, while considering the inherent stability of the transition. Complete details of how c^ref is generated for each gait can be found in Supplementary Section 5.

Policy training

To simplify the training process, for both the locomotion policy, π_L, and gait selection policy, π_G, the training method, environment and network architecture are kept constant. Both policies are modelled as a multilayer perceptron with hidden layer sizes [512, 256, 128] and LeakyReLU activations. Subscripts L and G represent the specific parameters for the locomotion policy and gait selection policy respectively. The model-free DRL training problem for the policies is represented as a sequential Markov decision process, which aims to produce a policy that maximizes the expected return of the policy π

$$J(\pi )={{\mathbb{E}}}_{\xi \sim p(\xi | \pi )}\left[\mathop{\sum }\limits_{t=0}^{N-1}{\gamma }^{t}r\right],$$

(4)

in which $\gamma \in \left[0,1\right)$ is the discount factor, ξ is a finite-horizon trajectory dependent on π with length N, p(ξ∣π) is the likelihood of ξ, and r is the reward function. The proximal policy optimization algorithm⁵¹ is used to train all policies and the hyperparameters used are detailed in Supplementary Section 6, which were selected through the standard method of parameter tuning. As discussed in ‘Achieving adaptive motion adjustment with a diverse set of gaits’, we estimate the state of the robot during training using an SE. Hence, in terms of applying state feedback noise for domain randomization to improved sim-to-real transfer, we only need to implement this on the input sensor data vector of the SE, ${\bf{\upsigma }}=[{{\bf{\upomega }}}_{{\mathrm{B}}},{\dot{{\bf{v}}}}_{{\mathrm{B}}},{\bf{q}},\dot{{\bf{q}}},{\bf{\uptau }},{{\bf{f}}}_{{\rm{grf}}}]$. This vector includes base angular velocity, ${{\bf{\upomega }}}_{{\bf{B}}}\in {{\mathbb{R}}}^{3}$, base linear acceleration, ${\dot{{\bf{v}}}}_{{\mathrm{B}}}\in {{\mathbb{R}}}^{3}$, joint positions, q, joint velocities, $\dot{{\bf{q}}}$, joint torques, τ, and foot ground reaction forces, ${{\bf{f}}}_{{\rm{grf}}}\in {{\mathbb{R}}}^{4}$. As the initial state of the robot and its performance can never be guaranteed during real-world deployment, we also randomize the initial configuration of the robot, the mass of the robot’s base, K_p and K_d. In addition, to ensure that a rich variation of U^cmd is experienced during training randomly sampled gaits, velocity commands and velocity change durations (to achieve random acceleration) are implemented. For all details regarding the noise and sampling used within training, refer to Supplementary Section 7. Although sim-to-real transfer can pose a considerable challenge when training DRL policies, we have found that through using domain randomization, realistic and diverse velocity commands, and generating all robot state observations from the SE, our framework is able to achieve zero-shot traversal in all experiments and environments shown in Figs. 2 and 6, hence demonstrating that our methods sufficiently bridge the gap between simulation and the real world. The environment itself is constructed using RaiSim⁵², as the vectorized environment set-up allows for efficient training of policies. In addition, the observation normalization functionality offered by RaiSim is also used for improved training.

During the training of π_L only flat terrain is present within the environment to isolate and highlight the effect of implementing β_L. A core claim of this work is that the implementation of β_L aims to impart gait procedural memory within ${\pi }_{{\mathrm{L}}}^{{\rm{bio}}}$; hence if rough terrain was observed during training, it will become ambiguous if the improved performance is a direct result of implementing β_L. However, for training π_G, flat to very rough terrain is implemented using fractal noise, enabling the policy to learn to employ the use of each gait minimizing biomechanics metrics on a variety of terrains. We train all variations of π_L and π_G for 20,000 iterations, taking 6 hours and 9 hours respectively, on a standard desktop computer with one Nvidia RTX3090 graphics processing unit with a training frequency of 100 Hz. It is also important to note that the training of all π_G policies only utilize our final proposed bio-inspired locomotion framework ${\pi }_{{\mathrm{L}}}^{{\rm{bio}}}$.

Locomotion policy

The goal of the locomotion policy π_L is to realize the input U^cmd while exhibiting stable and versatile behaviour. As such, π_L is trained to generate the action, q*, from an input observation, ${{\bf{o}}}_{{\mathrm{L}}}=[{{\bf{\upbeta }}}_{{\mathrm{L}}},{\bf{s}},{{\bf{v}}}_{{\mathrm{B}}}^{{\rm{cmd}}}]\in {{\mathbb{R}}}^{69}$, where ${{\bf{v}}}_{{\mathrm{B}}}^{{\rm{cmd}}}=[{v}_{x}^{{\rm{cmd}}},{v}_{y}^{{\rm{cmd}}},{\omega }_{z}^{{\rm{cmd}}}]\in {{\mathbb{R}}}^{3}$ is the high-level velocity command of the robot’s base within U^cmd, as outlined in Fig. 1. s is generated from the output of the SE and is defined as ${\bf{s}}=[{\bf{\upalpha }}{{\it{R}}}_{{\mathrm{B}}}^{T},{\bf{q}},{{\bf{\upomega }}}_{{\mathrm{B}}},\dot{{\bf{q}}},{{\bf{v}}}_{{\mathrm{B}}},{z}_{{\mathrm{B}}},{\bf{\uptau }},{\bf{c}}]\in {{\mathbb{R}}}^{50}$, where α = [0, 0, 1]^T is used to select the vertical z axis, ${{\bf{\omega }}}_{{\mathrm{B}}}\in {{\mathbb{R}}}^{3}$ is the base angular velocity, ${{\bf{v}}}_{{\mathrm{B}}}\in {{\mathbb{R}}}^{3}$ is the base linear velocity, z_B is the current base height, and ${\bf{c}}\in {{\mathbb{B}}}^{4}$ is the contact state of the feet. The locomotion reward function, r_L, is formulated so that the the output of the policy can realize the reference gait patterns and velocity commands stably, smoothly and accurately

$${r}_{{\mathrm{L}}}={\text{w}}_{\eta }{r}_{\eta }+{\text{w}}_{\bf{v}^{{\rm{cmd}}}}{r}_{\bf{v}^{{\rm{cmd}}}}+{\text{w}}_{f}{r}_{f}+{\text{w}}_{{\rm{stab}}}{r}_{{\rm{stab}}},$$

(5)

where r_η, ${r}_{\bf{v}^{{\rm{cmd}}}}$, r_f and r_stab are the grouped reward terms focusing on efficiency, velocity command tracking, gait reference tracking and stability, respectively. w_η, ${\text{w}}_{\bf{v}^{{\rm{cmd}}}}$, w_f and w_stab are the weights of each reward and are valued at −1.5, 15, −10 and −5 respectively. r_η aims to minimize joint jerk, $\dddot{{\bf{q}}}$, joint torque, and the difference between q* and the previous action, ${{\bf{q}}}_{t-1}^{* }$

$${r}_{\eta }=\parallel \dddot{{\bf{q}}}{\parallel }^{2}+\parallel {\bf{\uptau }}{\parallel }^{2}+\parallel {{\bf{q}}}^{* }-{{\bf{q}}}_{t-1}^{* }\parallel$$

(6)

${r}_{\bf{v}^{{\rm{cmd}}}}$ minimizes the difference between the commanded base velocity and the current base velocity

$${r}_{\bf{v}^{{\rm{cmd}}}}=\psi \left({\left\Vert {{\bf{v}}}_{{\mathrm{B}}}-{{\bf{v}}}_{{\mathrm{B}}}^{{\rm{cmd}}}\right\Vert }^{2}\right),$$

(7)

in which the function $\psi :x\to 1-\tanh \left({x}^{2}\right)$ is used to normalize the reward term so that their maximum value is 1 to prevent bias towards individual rewards, ${{\bf{v}}}_{{\mathrm{B}}}=[{v}_{x},{v}_{y},{\omega }_{z}]\in {{\mathbb{R}}}^{3}$ is the current base x, y and yaw velocities. r_f ensures that the robot realizes the commanded gait references within β_L

$${r}_{f}=| {{\bf{c}}}^{{\rm{err}}}| +\mathop{\sum }\limits_{i=1}^{4}{\left\Vert {{\bf{p}}}_{i}-{{\bf{p}}}_{i}^{{\rm{ref}}}\right\Vert }^{2},$$

(8)

where ${{\bf{c}}}^{{\rm{err}}}\in {{\mathbb{B}}}^{4}$ defines the feet that do not meet the desired contact state, with ${{\bf{p}}}_{i}\in {{\mathbb{R}}}^{3}$ and ${{\bf{p}}}_{i}^{{\rm{ref}}}\in {{\mathbb{R}}}^{3}$ being the current and reference Cartesian positions of the ith foot. r_stab aims to prevent contact foot slip, large hip joint motions and undesirable base orientations

$$\begin{array}{rcl}{r}_{{\rm{stab}}}&=&\mathop{\sum }\limits_{i=1}^{F}\parallel \dot{{{\bf{p}}}_{i}}{\parallel }^{2}+\parallel {{\bf{\upomega }}}_{{\mathrm{B},xy}}{\parallel }^{2}+\psi \left(\parallel {\bf{\upalpha }}{{\it{R}}}_{{\mathrm{B}}}-{\bf{\upalpha }}{{\it{R}}}_{{\mathrm{B}}}^{{\rm{des}}}{\parallel }^{2}\right)\\ &&-\psi \left({\left({z}_{{\mathrm{B}}}-{z}_{{\mathrm{B}}}^{{\rm{nom}}}\right)}^{2}\right)+\parallel {{\bf{q}}}_{{\rm{hip}}}{\parallel }^{2},\end{array}$$

(9)

where ${{\bf{p}}}_{i}\in {{\mathbb{R}}}^{3}$ is the velocity of the ith foot scheduled to be in stance, F is the number of stance feet, ${{\bf{\upomega }}}_{{\mathrm{B},xy}}=[{\omega }_{x},{\omega }_{y}]\in {{\mathbb{R}}}^{2}$ where ω_x and ω_y are roll and pitch base velocities, respectively, ${{\it{R}}}_{{\mathrm{B}}}^{{\rm{des}}}\in {\mathrm{SO}}(3)$ is the desired base orientation, ${z}_{{\mathrm{B}}}^{{\rm{nom}}}$ is the nominal base height, and ${{\bf{q}}}_{{\rm{hip}}}\in {{\mathbb{R}}}^{4}$ is the hip angular joint positions. Overall, this reward function enables deployment of all targeted gaits with rapid transitions between them, even at high speeds, as shown in Figs. 3, 4 and 6.

Biomechanics gait transition metrics

Although the set of biomechanics metrics applied in this work were designed to accommodate different animals of the same morphology, even when animal body size and weight vary considerably, the fact still remains that they were designed for the analysis of animal locomotion. Hence, several adjustments to how they are calculated needs to be implemented; for example, energy consumption in animals is often measured through the rate of consumption of O₂, which is unsuitable for the application of robotics. In addition, as robots provide a wide array of feedback data, some of the metrics have also been augmented to better reflect the characteristic that these biomechanics metrics are attempting to characterize. That being said, for Fig. 5a, only the original biomechanics metrics are applied to allow for direct comparison between robot and animal data.

Energy efficiency

The calculation of CoT takes the general form of

$$\,\text{CoT}\,=\frac{P}{mgv},$$

(10)

where P is power consumed and m is the system’s mass. When studying animal locomotion, P is found through measuring how much CO₂ is generated and O₂ is consumed and v is assumed to be the speed of the treadmill the animal is running on^5,30,31. For the case of the robot, we calculate P from τ and $\dot{{\bf{q}}}$ with an adjustment term, adopted from ref. ⁵³, and v is assumed to be the magnitude of the robot base velocity command to take a similar approach to animal studies and for consistent metric use between simulation and real-world deplopyment; completely accurate measurement of the robot’s linear base velocity is impossible during real-world deployment due to the accumulation of error within the SE. As such, calculation of the robot’s CoT is formulated as

$$\,\text{CoT}\,=\mathop{\sum }\limits_{i=1}^{n}\frac{\max ({\tau }_{i}{\dot{q}}_{i}+0.3{\tau }_{i}^{2},0)}{mg| {{\bf{v}}}_{{\mathrm{B}}}| },$$

(11)

where m is the robot’s mass and g is gravity. It should be noted that CoT is only calculated and applicable when $| {{\bf{v}}}_{{\mathrm{B}}}^{{\rm{cmd}}}| > 0$.

Actuator-structural forces

As gaining an exact understanding of the actuator-structural forces within animals is infeasible, researchers have opted instead to measure the peak ground reaction forces of the animal’s stance feet during locomotion using force plates³⁷. Other methods include adding strain gauges to the bones of the animals³⁸. However, in the case of robots, we have the privilege of having access to joint state feedback while also knowing the exact limitations of the hardware. Therefore, when considering the biomechanics hypothesis that animals aim to minimize actuator-structural forces to prevent injury and that torque is proportional to strain and force, in the case of the robot we chose to characterize the actuator-structural forces through joint torque saturation, τ_%, which is calculated by

$${\tau }_{ \% }=\left\vert \frac{{\bf{\uptau }}}{{{\bf{\uptau }}}_{\lim }}\right\vert \frac{1}{n},$$

(12)

where ${{\bf{\uptau }}}_{\lim }\in {{\mathbb{R}}}^{n}$ is the joint torque limits (assumed based on manufacturers specification), which proves particularly usefully when considering that the hip joints of most quadruped robots, including the A1, are often more sensitive to forces at the foot due to their distance from the point of ground impact and the only motor of the leg set in this plane; this would not be considered if just ground reaction force was used to characterize actuator-structural forces.

Mechanical work efficiency

During animal locomotion, if they were to have perfect mechanical work efficiency there would be a net-zero change in external work over the duration of a gait cycle as there would be perfect exchange between kinetic and potential energy³². As expected, perfect mechanical work is never seen in nature; hence, mechanical work efficiency in animals is characterized by the sum of the change in kinetic and potential energy³² or the sum of the external work of the animal³³ over the duration of a gait cycle. As this is typically calculated through measuring the O₂ uptake, for the case of robots we formulate the calculation of the external work, W_ext, through

$${W}_{{\rm{ext}}}=\mathop{\sum }\limits_{i=0}^{{t}_{{\rm{gait}}}}\left(\Delta {E}_{{\rm{k}},i}-\Delta {E}_{{\rm{p}},i}\right)$$

(13)

where t_gait is the duration of the current gait cycle, and ΔE_k,i and ΔE_p,i are the changes in kinetic and potential energy over a control time step, respectively. The primary difference between the metrics seen in biomechancis and our formulation of W_ext is that ΔE_k,i accounts for not only forward linear velocity but also lateral and angular velocity, whereas originally only forward linear velocity was considered.

Stability

The best indication of stability in animals is their stride duration CV. This metric characterizes periodicity, which is a primary indication of stable locomotion³⁵. However, to accurately calculate this, the mean and standard deviation of the stride duration needs to be taken over an extended period of time for appropriate data generation. This is sufficient for undertaking analysis similar to that presented in Fig. 5a, but this presents an issue when it comes to analysing the performance of the proposed control framework as it is common for multiple speed commands being used within the duration of one stride. Hence, to overcome this limitation we instead use ${c}_{{\rm{avg}}}^{{\rm{err}}}=| {{\bf{c}}}^{{\rm{err}}}| /4$, which can be measured every time step rather than just at each foot touchdown event; the gait references generated by the BGS have a constant and periodic stride duration; therefore, an accurate tracking of this reference would in turn indicate high periodicity, which is further supported by the correlation between the two metrics in Fig. 5b.

Gait selection policy

To achieve optimal gait selection for a given state, we leverage the biomechanics metrics within the reward function of π_G, r_G. For the different variations of π_G used in Fig. 5a, each policy’s reward function features only the metric that its focusing on within r_G but ${\pi }_{{\mathrm{G}}}^{{\rm{uni}}}$ unifies all metrics and hence uses the full form of r_G with all metrics. In addition, as the biomechanics metrics all describe characteristics that animals try to minimize through changing gaits, they can be directly applied within r_G with some normalization where appropriate. The full form of r_G is

$${r}_{{\mathrm{G}}}={\text{w}}_{{\rm{u}}}{r}_{{\rm{u}}}+\psi (\,\text{CoT}\,)+\psi ({\tau }_{ \% })+\psi ({c}_{{\rm{avg}}}^{{\rm{err}}})+\psi ({W}_{{\rm{ext}}}),$$

(14)

where r_u is the utility reward term that all π_G use and w_u is its weight with a value of 0.4. r_u aims to ensure the smoothness of the output Γ*, the standing gait is used only when appropriate and any select gait is still able to follow ${{\bf{v}}}_{{\mathrm{B}}}^{{\rm{cmd}}}$. To achieve this, r_u has the form of

$${r}_{{\rm{u}}}={r}_{\bf{v}^{{\rm{cmd}}}}+{r}_{{\rm{stand}}}+{r}_{{\rm{smooth}}},$$

(15)

in which ${r}_{\bf{v}^{{\rm{cmd}}}}$ is taken from equation (7), and r_stand is set to 10 if a stand gait is used when $| {{\bf{v}}}_{{\mathrm{B}}}^{{\rm{cmd}}}| > 0$ or not used when $| {{\bf{v}}}_{{\mathrm{B}}}^{{\rm{cmd}}}| =0$. For r_smooth, the reward aims to penalize unnecessary changes in Γ* to remove rapid gait changes when two gaits could achieve similar metric minimization for a given task and state. As such, if there is a gait change between time steps it is calculated as ${r}_{{\rm{smooth}}}=-\psi (\,\text{CoT}\,+{\tau }_{ \% }+{c}_{{\rm{avg}}}^{{\rm{err}}}+{W}_{{\rm{ext}}})$ otherwise it is set to 0. To generate Γ*, π_G takes in input observation vector ${{\bf{o}}}_{{\mathrm{G}}}=[{\bf{s}},{{\bf{\upbeta }}}_{{\mathrm{G}}},{{\bf{v}}}_{{\mathrm{B}}}^{{\rm{cmd}}},{\dot{{\bf{v}}}}_{{\mathrm{B}}}^{{\rm{cmd}}},{\varGamma }_{t-1}^{* }]\in {{\mathbb{R}}}^{66}$ in which ${\varGamma }_{t-1}^{* }$ is the previous output action to aid in action smoothing. Appropriate selection of the data provided to π_G is critical to achieve targeted minimization of the biomechanics metrics. As such, the inclusion of s coupled with c^ref, ${{\bf{p}}}_{z}^{{\rm{ref}}}$, ${{\bf{v}}}_{{\mathrm{B}}}^{{\rm{cmd}}}$, ${\dot{{\bf{v}}}}_{{\mathrm{B}}}^{{\rm{cmd}}}$ and Ω_stab informs the policy of its current and demanded stability, while the terms τ and $\dot{{\bf{q}}}$ within s capture the power consumption of the robot and the forces to which it is subjected. Overall, through the formulation of the biomechanics metrics within this reward function, we are able to not only fully investigate the effects in gait selection when minimizing each metric but also instil the intrinsics of animal gait transition strategies within a DRL gait selection policy, as detailed in Fig. 5.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.