UnitedMet harnesses RNA–metabolite covariation to impute metabolite levels in clinical samples

Abstract

Comprehensively studying metabolism requires metabolite measurements. Such measurements, however, are often unavailable in large cohorts of tissue samples. To address this basic barrier, we propose a Bayesian framework (‘UnitedMet’) that leverages RNA–metabolite covariation to impute otherwise unmeasured metabolite levels from widely available transcriptomic data. UnitedMet is equally capable of imputing whole pool sizes and outcomes of isotope tracing experiments. We apply UnitedMet to investigate the metabolic impact of driver mutations in kidney cancer, identifying an association between BAP1 and a highly oxidative tumor phenotype. We similarly apply UnitedMet to determine that advanced kidney cancers upregulate oxidative phosphorylation relative to early-stage disease, that oxidative metabolism in kidney cancer is associated with inferior outcomes to anti-angiogenic therapy and that kidney cancer metastases demonstrate elevated oxidative phosphorylation. UnitedMet provides a scalable tool for assessing metabolic phenotypes when direct measurements are infeasible, facilitating unexplored avenues for metabolite-focused hypothesis generation.

Main

Changes to metabolite pool sizes and metabolic flux are fundamental to numerous diseases and biological phenomena¹; consequently, measurement of metabolites themselves is critical to the discovery of disease biomarkers, therapeutic vulnerabilities and mechanisms of action^2,3,4,5,6,7. However, despite the translational value of metabolite measurement, large-scale profiling of metabolite levels in clinical specimens remains scarce because of the technical challenges associated with metabolomic measurements (for example, the need for fresh, snap-frozen tissue and the analytical challenges of measuring chemically diverse compounds)⁸. Overcoming this data scarcity, therefore, comes with the potential reward of expanded access to the large space of underexplored, metabolite-centered biological hypotheses.

Two simultaneous and recent developments have now poised the metabolism field to overcome the lack of large-scale metabolite measurements. First, recent developments in machine learning have demonstrated the promise of using reference multimodal data (that is, measurements of two or more distinct data modalities) to ultimately impute measurements of interest in single-modality data^9,10. For example, multimodal learning methods for single-cell multiomics^9,10,11 have been successful at cross-modal prediction for single-modality datasets (for example, protein prediction by jointly modeling with single-cell RNA sequencing (RNA-seq) in TotalVI (ref. ¹²) and single-cell ATAC prediction through modeling with single-cell RNA-seq in MultiVI (ref. ¹³)). Second, we and other groups have identified both cancer-type-specific and lineage-agnostic patterns of RNA–metabolite covariation^{14,15,16,17,18,19}. Together, these developments suggest that suitably designed machine learning models may, by leveraging strong covariation between transcripts and metabolite pools, be able to predict otherwise unmeasured metabolite levels from matched single-modality transcriptomic data. Such a joint framework for modeling metabolic and RNA measurements would also produce a unified, low-rank representation of multimodal metabolite and RNA data, enabling downstream sample clustering, visualization and integration in a latent space.

Three key quantitative challenges must be addressed by multimodal models of metabolite and RNA levels. First, mass-spectrometry-derived metabolomics and isotope labeling data are predominantly reported in semiquantitative relative abundances, impeding comparisons of identical metabolites and isotopologs across datasets (and of different metabolites within the same dataset). Second, different metabolomic measurement platforms often detect a subset of metabolites with limited overlap. As a result, each metabolic reference dataset exhibits a varying degree of missing measurements. Third, both metabolic and RNA modalities possess distinct sources of technical errors and noise that need to be suitably modeled. Prior attempts at predicting metabolic profiles from RNA-seq data had limited success, in part because of their inefficacy in addressing the aforementioned challenges. One method, reliant on correlation networks, struggled with missing values, resulting in a limited ability to predict cross-dataset outcomes for only 34 metabolites, with the highest Pearson’s ρ below 0.5 (ref. ²⁰). Similarly, a different approach using multivariate Lasso regression yielded poor performance, with a median R² value of 0 for within-dataset prediction and an inability to perform cross-dataset prediction²¹.

Here, we present UnitedMet, a Bayesian probabilistic method for joint modeling of metabolic and RNA-seq data. UnitedMet addresses the above challenges by mapping both RNA and metabolite data onto a shared rank-transformed scale and inferring missing metabolic measurements in reference datasets. UnitedMet operates as a comprehensive framework at two levels. In the latent space, it learns a unified representation for both metabolic and RNA data, facilitating tasks such as sample clustering and dataset integration. At a higher level, UnitedMet seizes on the strength of RNA–metabolite covariation to impute either metabolite pool sizes or isotopolog distributions from isotope labeling experiments directly from RNA abundance. We demonstrate that UnitedMet performs well on both imputation of pool sizes and imputation of isotope tracing experiments. We subsequently apply UnitedMet to identify the metabolite phenotypes of driver mutations in clinical specimens from persons with clear cell renal carcinoma (ccRCC) and study the metabolic phenotypes associated with metastatic disease in ccRCC.

Results

UnitedMet: a Bayesian model for multimodal metabolic data analysis

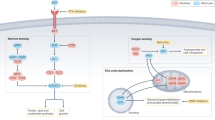
UnitedMet is a Bayesian generative method that jointly models RNA-seq and metabolite data. The input to UnitedMet comprises the paired matrices of RNA counts (X) and total ion counts of metabolites or isotopologs (Y) from samples with both RNA-seq and metabolite data measured (defined as reference datasets) and single-modality matrices with only RNA-seq data available (defined as target datasets) (Fig. 1a). To map metabolite relative abundances and gene expression levels onto a shared measurement scale, we rank-transform the metabolite or isotopolog and gene expression levels across all the samples within each dataset. Such a rank transformation places the distribution of values for metabolite features onto a common, nonparametric scale that naturally accounts for the semiquantitative nature of mass-spectrometry-based metabolomics data. UnitedMet then takes in an aggregate multiple-dataset matrix (R) containing the rankings data from both paired and single-modality samples. UnitedMet assumes observations are generated from a Plackett–Luce ranking distribution of a latent variable Z, which is the matrix product of a latent sample embedding matrix (W) and a latent feature embedding matrix (H) (Fig. 1b). UnitedMet infers posterior distributions of gene expressions and metabolic profiles for all samples in the aggregate matrix and predicts metabolic profiles for single-modality samples using stochastic variational inference (SVI). A hyperparameter λ, the number of latent embedding dimensions, is selected by grid search. The output of UnitedMet is a fully imputed multimodal data matrix, where any missing measurements from single-modality data in the input matrix R are replaced with their posterior estimates.

Fig. 1: Overview of the UnitedMet method.

a, Workflow of a metabolite imputation pipeline with UnitedMet. UnitedMet takes paired matrices of RNA counts ($X$) and total ion counts of metabolites or isotopologs ($Y$) (defined as reference datasets) and single-modality matrices with only RNA-seq data available (${X}_{0}$) (defined as target datasets) as inputs. UnitedMet then normalizes and rank-transforms both RNA-seq and metabolic data. By probabilistic modeling, UnitedMet infers posterior distributions of metabolic profiles for single-modality target samples, which can be used in downstream analysis for biological hypothesis testing. b, Architecture of the UnitedMet model. An aggregate matrix ($R$) containing ranking data from both paired and single-modality samples is modeled with a Plackett–Luce ranking distribution based on latent variables derived from embedding matrices $W$ and $H$. UnitedMet integrates transcriptomic and metabolic data into a common low-dimensional space for tasks such as clustering and visualization. Next, UnitedMet imputes missing metabolite levels from gene expression data, offering predictions and uncertainty quantification (some icons in the figure were created with BioRender.com).

UnitedMet provides a unified solution for multimodal metabolomic data analysis at two levels. First, UnitedMet learns a shared representation of both transcriptomic and metabolic data, including from samples where one type of measurement is missing, and integrates these data into a common low-dimensional latent space. Such a low-dimensional, integrated representation facilitates downstream tasks such as sample clustering and data visualization (Fig. 1b). Second, by learning a unified representation of metabolomic and transcriptomic features from reference data, UnitedMet enables the imputation of otherwise unmeasured metabolite levels and/or isotopolog distributions from gene expression data alone and delivers these predictions along with a quantification of their uncertainty. Together, these functions of UnitedMet enable the interrogation of metabolism and the evaluation of hypotheses relying on metabolite measurements in large, deeply profiled cohorts of tumors otherwise lacking metabolomic data.

UnitedMet accurately predicts metabolite levels from RNA-seq data in human tumor samples

To evaluate UnitedMet’s capacity to predict metabolite abundances on real-world patient-derived data, we first applied UnitedMet to four datasets of ccRCC samples with fully paired RNA-seq and metabolomics profiles. The aggregated data contained two datasets from the NIH Clinical Proteomic Tumor Analysis Consortium (CPTAC) project, CPTAC (n = 50, no. of metabolites = 183, no. of genes = 60,483)and CPTAC_val (n = 71, no. of metabolites = 130, no. of genes = 60,483), and two in-house datasets RC18 (n = 144, no. of metabolites = 783, no. of genes = 22,937) and RC20 (n = 76, no. of metabolites = 1,012, no. of genes = 22,987) (Supplementary Table 1). These data represented a typical use case for UnitedMet; while 20,171 genes were represented in all four datasets (corresponding largely to protein-coding genes uniformly measured across all data), only 86 (7% of the 1,148 unique metabolites in the entire dataset) were measured in all four datasets.

We designed a benchmarking experiment to evaluate the performance of UnitedMet and comparator methods for the imputation of otherwise unmeasured metabolites. At each iteration of our benchmarking experiment, we treated three of the four ccRCC datasets as ‘reference’ datasets for UnitedMet (in which both metabolomic and transcriptomic data were available) and treated the remaining ccRCC dataset as a ‘target’ dataset (where only transcriptomic data were available). We subsequently trained four distinct UnitedMet models (one for each iteration of the benchmarking experiment, each with different hyperparameters λ) (Extended Data Fig. 1a) and evaluated the accuracy of UnitedMet metabolite predictions in the target dataset. For each metabolite, predicted levels from UnitedMet were compared to their ground-truth values by Spearman correlation (Fig. 2a). We considered a metabolite well predicted if the correlation between ground-truth and imputed abundance for that metabolite was positive and statistically significant (false discovery rate (FDR)-adjusted P value < 0.1). By calculating the percentage of well-predicted metabolites among the total number of available metabolites in the target dataset that were also measured in at least one other training dataset, UnitedMet successfully imputed between 48% and 67% of metabolites in the four target datasets (Fig. 2b and Supplementary Table 2). We compared the performance of UnitedMet to two existing methods for prediction of metabolite abundance from gene expression with the same datasets: multivariate Lasso regression²¹ and MIRTH^22,23 (Methods). We used two metrics to quantify how well each method predicted metabolite abundance: the Spearman ρ among all predicted metabolites and the number of well-predicted metabolites. UnitedMet outperformed the other methods in all four cross-validation datasets by both metrics (Fig. 2c, Extended Data Fig. 1b and Supplementary Table 2). From these experiments, we conclude that UnitedMet can successfully impute a subset of metabolites directly from RNA-seq and that the accuracy of this imputation varies significantly across metabolites.

Fig. 2: UnitedMet achieves high accuracy predicting metabolite levels in human tumor samples.

a, Schematic of the benchmarking experiment to evaluate model performance in a cross-validation scenario. Each time, three of four ccRCC datasets were designated as reference datasets, while the fourth dataset served as the target dataset with only transcriptomic data. The accuracy of UnitedMet’s predictions was then evaluated by comparing predicted metabolite abundances to their ground-truth levels. $X$, RNA-seq data; $Y$, metabolomics data. b, The imputation performance for each dataset was assessed by Spearman ρ values between predicted values and their ground truths across all simulated missing features. Metabolites with predicted ranks that showed a significant positive correlation (two-sided FDR-adjusted P < 0.1 and Spearman ρ > 0) with the actual ranks are labeled red. c, Performance of UnitedMet, multivariate Lasso regression and MIRTH based on the Spearman ρ among all predicted metabolites. Significance was assessed using a two-sided Wilcoxon signed-rank test. (CPTAC, n = 156 participant samples, P_{Lasso_UnitedMet} = 2.1 × 10⁻¹¹, P_{MIRTH_UnitedMet} = 2.7 × 10⁻⁸; CPTAC_val, n = 129 participant samples, P_{Lasso_UnitedMet} = 6.4 × 10⁻¹², P_{MIRTH_UnitedMet} = 6.8 × 10⁻⁴; RC18, n = 709 participant samples, P_{Lasso_UnitedMet} = 6.6 × 10⁻⁶, P_{MIRTH_UnitedMet} = 2.1 × 10⁻¹¹; RC20, n = 718 participant samples, P_{Lasso_UnitedMet} = 1.7 × 10⁻³³, P_{MIRTH_UnitedMet} = 4 × 10⁻³). In the box plots, the center line represents the median, the bounds of the box indicate the interquartile range (25th to 75th percentiles) and the whiskers extend to the minima and maxima within 1.5 times the interquartile range. Data points outside this range are shown as individual outliers. d, Correlation between actual and predicted metabolite ranks for two reproducibly well-predicted metabolites: kynurenine (top) and N-acetylneuraminate (bottom). Each point represents one sample in which the metabolite was measured and predicted. e, The imputation performance for each metabolite is summarized across datasets, with average Spearman ρ values plotted. A subset of consistently well-imputed metabolites is labeled and those that are reproducibly well predicted are marked in blue.

Source data

As targeted mass spectrometry can only measure a specific class of metabolites, a related challenge is imputing a large panel of metabolites from a subset of measured metabolites and RNA-seq data. To address this, we extended UnitedMet’s capabilities by introducing a weighted loss function to address the imbalanced metabolomics and RNA-seq modalities. To benchmark the imputation accuracy, we randomly selected 50% of all measured metabolites as simulated missing in each dataset. Once again, we found UnitedMet was the top performer on all datasets in terms of the same metrics mentioned above (Extended Data Fig. 1c,d and Supplementary Table 3).

We next investigated the consistency of prediction accuracy across the four ccRCC datasets in UnitedMet. For each pair of two datasets from the four, we observed strong correlation between their metabolite-level prediction performances (Spearman ρ = 0.32–0.83 in all pairwise comparisons, P < 0.001 in all pairwise comparisons; Extended Data Fig. 2a). The highest concordance was observed between the two in-house datasets, likely because of the larger overlap in measured metabolites that could be used for training and the larger sample sizes in these datasets. These results together confirmed that well-predicted metabolites were highly consistent across all four datasets. For instance, kynurenine (average Spearman ρ = 0.64, FDR-adjusted P value < 0.1 in all four datasets) and N-acetylneuraminate (average Spearman ρ = 0.64, FDR-adjusted P value < 0.1 in all four datasets) exhibited robust prediction results across four datasets (Fig. 2d). Combining these prediction results in four datasets, we labeled 59 metabolites as ‘reproducibly’ well-predicted metabolites, indicating that they were well predicted in at least three of four target datasets (Supplementary Table 4). Reproducibly well-predicted metabolites were enriched for amino acids and carbohydrates but depleted of lipids relative to the full panel of metabolites (Fig. 2e). We also explored UnitedMet’s capacity to estimate model uncertainty by evaluating the s.d. of 1,000 draws from the posterior distribution of metabolite levels. We found that prediction uncertainty was negatively correlated with the prediction accuracy (Extended Data Fig. 2b), indicating that posterior uncertainty could guide the selection of reliable predictions for downstream analyses.

To further validate UnitedMet’s reliability, we conducted an external validation using three independent breast cancer cohorts^24,25,26. Training on two breast cancer datasets^24,25 and testing on a triple-negative breast cancer (TNBC) dataset^26,27, UnitedMet successfully predicted 42% of available metabolites in the TNBC dataset (Extended Data Fig. 2c), demonstrating its ability to generalize across different cancer types. Importantly, these predictions preserved well-characterized metabolic alterations of TNBC subtypes, such as elevated lipid metabolism in the C1 subtype and increased carbohydrate and glutathione metabolism in the C2 subtype (Extended Data Fig. 2d), highlighting the biological relevance of the model.

UnitedMet can predict isotopolog distributions from RNA-seq data in vitro and in vivo

Unlike measurements of metabolite pool sizes, isotopolog distributions produced from steady-state isotopic labeling experiments capture the flow of nutrients through cellular metabolism. However, labeling experiments are technically challenging; consequently, there are even less publicly available isotopic labeling data (both in cell lines and in tissue specimens) compared to conventional metabolomic data. Motivated by the ability of UnitedMet to predict metabolite levels by jointly modeling metabolomics and RNA-seq data and the generalizability of our model, we hypothesized that UnitedMet might be able to predict isotopolog distributions from RNA-seq data. To test this hypothesis, we obtained three datasets with paired RNA-seq data and isotopic labeling data (measured by mass spectrometry). Dataset RCC contained RCC tumor samples obtained from 76 participants receiving infusions of [U-¹³C]glucose before surgery²⁸. A total of 64 isotopologs and 12,300 genes were measured in the RCC dataset²⁸. The other two datasets were composed of human non-small cell lung cancer (NSCLC) cell lines labeled with either [U-¹³C]glucose or [U-¹³C]glutamine: NSCLC-G (n = 85, no. of isotopologs = 28, no. of genes = 16,383) and NSCLC-Q (n = 85, no. of isotopologs = 21, no. of genes = 16,383) (Supplementary Table 1)³.

To evaluate UnitedMet’s performance of predicting isotopolog distributions, we conducted a simulation where 50% of the samples in a given dataset were randomly selected and treated as target data for UnitedMet (that is, with isotopolog measurements masked) (Fig. 3a). The remaining 50% of samples were treated as a reference dataset for UnitedMet. We trained three distinct UnitedMet models (one for each dataset) with different hyperparameters λ (Extended Data Fig. 3a). UnitedMet was able to successfully impute 52% (RCC), 56% (NSCLC-G) and 63% (NSCLC-Q) of the held-out isotopologs (Spearman ρ > 0, FDR-adjusted P value < 0.1) (Fig. 3b and Supplementary Table 5). Citrate M + 2, which reflects the contribution of glucose-derived carbon to the tricarboxylic acid (TCA) cycle through pyruvate in [U-¹³C]glucose-labeled data, was reproducibly predicted with high accuracy in both the in vitro NSCLC dataset (Spearman ρ = 0.44, P = 0.003) and the in vivo RCC dataset (Spearman ρ = 0.39, P = 0.01) (Fig. 3c). In contrast, gene expression scores of either oxidative phosphorylation signature or TCA cycle signature, calculated directly from RNA-seq data, were not correlated to citrate M + 2 labeling in these datasets (oxidative phosphorylation signature: Spearman ρ = 0.16, P = 0.3 (NSCLC) and Spearman ρ = 0.22, P = 0.19 (RCC), Fig. 3c; TCA cycle signature: ρ = 0.06, P = 0.3 (NSCLC) and ρ = 0.25, P = 0.13 (RCC); Extended Data Fig. 3b). Similarly, lactate M + 3, which reflects glucose contribution to glycolysis in [U-¹³C]glucose-labeled data, was accurately predicted in the RCC dataset (Spearman ρ = 0.43, P = 0.007), while a glycolysis gene expression signature was not correlated to lactate M + 3 (Spearman ρ = 0.05, P = 0.8; Extended Data Fig. 3c). Together, these results demonstrate that UnitedMet can accurately predict isotopologs that characterize specific metabolic phenotypes, an achievement not possible with standard gene set enrichment analysis of RNA-seq data.

Fig. 3: UnitedMet accurately predicts isotopolog distributions from RNA-seq data.

a, Schematic of the benchmarking experiment to assess model performance on isotopolog predictions. Here, 50% of the samples in a given dataset were randomly selected and treated as target data for UnitedMet (that is, simulated as unmeasured). The remaining 50% of samples were treated as a reference dataset for UnitedMet. $X$, RNA-seq data; $Y$, Isotopolog data. b, Imputation performance for each dataset was evaluated using Spearman ρ values between predicted values and their ground truths across all simulated missing features. Isotopologs with predicted ranks that exhibited a significant positive correlation with the actual ranks are marked in red. c, True ranks of citrate M + 2 were well predicted by UnitedMet but not by the gene expression signature of the Hallmark oxidative phosphorylation pathway. For each sample in the [U-¹³C]glucose-labeled NSCLC (top) and RCC (bottom) datasets, true ranks of citrate M + 2 were compared to predicted ranks from UnitedMet (left) and oxidative phosphorylation pathway scores calculated from gene expressions in the corresponding Hallmark gene set (right). Significance was assessed using a two-sided Spearman correlation. d, Uniform manifold approximation and projection plots of sample embedding matrix W (posterior means) learned by UnitedMet reveal integration of batches (top) and clustering across renal cell carcinoma subtypes in TCGA KIPAN batch (bottom). Each dot represents a participant sample. RCC and TCGA KIPAN samples overlap in the latent space. e, UnitedMet captures histology-associated differences in metabolism across RCC subtypes. DA of imputed isotopologs across RCC subtypes in TCGA KIPAN were compared to ground-truth differences in the measured RCC cohort. Significance was assessed using a two-sided Spearman correlation. Isotopologs in blue were consistently and significantly enriched (FDR-adjusted P < 0.1, two-sided Wilcoxon rank-sum test) in both measured and predicted cohorts. f, UnitedMet captures mutation-driven metabolic reprogramming in ChRCC. For each sample in the ChRCC cohort (n = 61), predicted levels of lactate M + 3/glucose M + 6 (left) and citrate M + 2/glucose M + 6 (right) are shown. Error bars represent ±1 s.d. The x axis is sorted by predicted abundances of corresponding isotopologs. Samples with complex I insertions or deletions are labeled red. Samples with complex I single-nucleotide variations are labeled green. P values show the results of a two-sided Wilcoxon rank-sum test between complex I indel samples and the other samples.

Source data

Human kidney cancer arises in a variety of subtypes, including ccRCC, papillary RCC (pRCC) and chromophobe RCC (ChRCC), presenting with functionally distinct metabolic activity. To further benchmark the capacity of UnitedMet to impute isotopolog distributions, we assessed its capacity to capture histology-associated differences in metabolism across RCC subtypes. To do so, we applied UnitedMet, using multimodal RNA-seq and isotopolog data from Bezwada et al.²⁸ as a reference dataset and 1,020 RCC tumor and adjacent normal samples from The Cancer Genome Atlas (TCGA) pan-kidney cohort (KIPAN) (encompassing ccRCC, pRCC and ChRCC) as a target dataset (Extended Data Fig. 3d and Supplementary Table 6). At the low-dimensional latent space learned by UnitedMet, we found that UnitedMet successfully embedded samples in both the reference and the target datasets according to their subtype, despite missing measurements of isotopologs in TCGA KIPAN (Fig. 3d). Furthermore, imputed labeling patterns in TCGA KIPAN dataset preserved ground-truth differences between ChRCC and ccRCC samples (Spearman ρ = 0.85, P = 4.2 × 10⁻¹⁵) and between pRCC and ccRCC samples (Spearman ρ = 0.79, P = 5.0 × 10⁻¹²) (Fig. 3e). Consistent with prior findings²⁸, ccRCC samples demonstrated higher glycolytic labeling, such as lactate M + 3/glucose M + 6, while ChRCC and pRCC samples displayed higher ratios of TCA cycle labeling, such as citrate M + 2/glucose M + 6 and succinate M + 2/glucose M + 6 (Fig. 3e and Supplementary Table 7). While ChRCC displays increased use of the TCA cycle, loss-of-function alterations to mitochondrial DNA (mtDNA)-encoded complex I genes can result in loss of oxidative phosphorylation and metabolic reprogramming in favor of glycolysis²⁹. Consistent with these findings, we found that ChRCC samples with complex I alterations demonstrated a shift to an alternative glycolytic metabolic pathway with higher levels of lactate M + 3/glucose M + 6 (P = 0.02) and lower levels of citrate M + 2/glucose M + 6 (P = 0.04), evaluated using the Wilcoxon rank-sum test) (Fig. 3f and Supplementary Table 8). This suggested that UnitedMet captured mutation-driven metabolic reprogramming in ChRCC, which further validated UnitedMet’s capability to generate biologically meaningful predictions.

In total, the analysis presented in Figs. 2 and 3 demonstrates that UnitedMet is capable of accurately imputing both metabolite levels and isotopolog distributions from RNA-seq data through joint, multimodal modeling with reference datasets.

BAP1 mutations are associated with an oxidative metabolic phenotype in ccRCC

Although both oncogenes (such as MYC and PIK3CA) and tumor suppressor genes (PTEN and VHL) are well-recognized regulators of metabolism^30,31, the functional consequences of driver alterations on tumor metabolism in vivo are poorly studied^32,33. In fact, the lack of population-scale metabolomic profiling in contemporary cohorts of molecularly profiled tumors renders a direct evaluation of the association of either metabolite levels or metabolic flux with the presence of specific driver alterations infeasible. We reasoned that we could apply UnitedMet to impute both metabolite levels and isotope labeling patterns in richly profiled cohorts of tumors, such as those from TCGA, to assess whether genomic alterations were associated with specific metabolite changes.

We focused our efforts on understanding the genome–metabolome covariation in ccRCC, for which we have several reference datasets with both transcriptomic and metabolomic or labeling data. The canonical founder mutation in ccRCC is the biallelic inactivation of the tumor suppressor gene VHL (affecting between 50% (ref. ³⁴) and 80% (ref. ³⁵) of ccRCC cases) and the subsequent activation of a pseudohypoxic transcriptional and metabolic program. The subsequent evolution of ccRCC includes the acquisition of secondary driver mutations in genes (such as PIK3CA, PTEN, MTOR and BAP1), whose functions are (at least in part) metabolic². To understand the associations between genetic mutations and metabolic variations in ccRCC, we applied UnitedMet to large-scale multiomics TCGA kidney ccRCC (KIRC) cohort (n = 606), which has paired RNA-seq and whole-exome sequencing (WES) data. Training the RNA-seq data from TCGA KIRC with four ccRCC reference datasets (CPTAC, CPTAC_val, RC18 and RC20; n = 341) containing paired RNA-seq and metabolomics data, UnitedMet predicted metabolite levels for TCGA KIRC samples (Fig. 4a and Supplementary Table 9).

Fig. 4: BAP1 mutations in ccRCC are associated with a unique metabolic phenotype.

a, Schematic of the metabolite-level prediction and downstream analysis for TCGA KIRC samples with UnitedMet. RNA-seq data (${X}_{\rm{TCGA}}$) of TCGA KIRC cohort (target dataset) were trained with four ccRCC reference datasets (CPTAC, CPTAC_val, RC18 and RC20; n = 341) containing paired RNA-seq and metabolomics data. $X$, RNA-seq data; $Y$, metabolomics data. Predicted metabolite levels (${Y}_{\rm{TCGA}}$) are leveraged for association analysis with ccRCC driver mutations. b, BAP1 mutation demonstrates the strongest association with a broad range of predicted metabolites. Top, distribution of the total number of significantly associated metabolites across 14 key driver mutations in ccRCC. The x axis is sorted by the number of significantly associated metabolites. Bottom, mutation frequency of 14 driver genes. The x axis is sorted by mutation frequency. c, Pathway-based analysis of predicted metabolic changes in BAP1-mutant versus BAP1 wild-type samples in TCGA KIRC cohort. MUT, mutant; WT, wild type. d, Predicted metabolite-level changes in BAP1-mutant versus BAP1 wild-type samples in TCGA KIRC cohort. Left, diagram of glucose metabolism pathways: glycolysis and TCA cycle (created with BioRender.com). α-KG, α-ketoglutarate. Right, box plots comparing predicted unphosphorylated glucose, citrate, fumarate and malate levels in mutant BAP1 (n = 38) versus wild-type BAP1 (n = 330) participant samples. P values were calculated using unpaired two-tailed parametric t-tests. In the box plots, the center line represents the median, the bounds of the box indicate the interquartile range (25th to 75th percentiles) and the whiskers extend to 1.5 times the interquartile range. Individual data points are shown as dots. e, Schematic of the isotopolog distribution prediction for TCGA KIRC samples with UnitedMet. RNA-seq data (${X}_{\rm{TCGA}}$) of TCGA KIRC cohort (target dataset) were trained with ccRCC samples in the [U-¹³C]glucose-labeled RCC dataset containing paired RNA-seq and isotope labeling data. $X$, RNA-seq data; $Y$, isotopolog data. f, Predicted isotopolog changes in BAP1-mutant versus BAP1 wild-type samples in TCGA KIRC cohort. Box plots compare the predicted citrate M + 2/pyruvate M + 3, succinate M + 2/pyruvate M + 3 and malate M + 2/pyruvate M + 3 ratios in mutant BAP1 (n = 38) versus wild-type BAP1 (n = 330) participant samples. P values were calculated using unpaired two-tailed parametric t-tests. In the box plots, the center line represents the median, the bounds of the box indicate the interquartile range (25th to 75th percentiles) and the whiskers extend to 1.5 times the interquartile range. Individual data points are shown as dots.

Source data

We first studied associations between the predicted metabolite abundances and genetic mutations in TCGA KIRC cohort. For each of the 14 key driver mutations in ccRCC (VHL, PBRM1, SETD2, BAP1, MTOR, KDM5C, PTEN, TP53, PIK3CA, TSC2, TCEB1, TSC1, PIK3R1 and SDHB), we compared metabolite levels (considering only reproducibly well-predicted metabolites) between mutant and wild-type samples, using an FDR-corrected Wilcoxon test (Fig. 4b). We identified significantly higher or lower mutation-specific abundance of metabolites in BAP1 (n = 38 metabolites), PBRM1 (n = 37), VHL (n = 22), SETD2 (n = 15) and TP53 (n = 3) mutations. The BAP1 mutation showed the strongest association with the largest variety of predicted metabolites despite a relatively low mutation rate (~10%) in participants with ccRCC (Fig. 4b). For example, BAP1-mutant samples exhibited lower levels of β-alanine, glutamine, glutamate and oxidized glutathione, which aligns with the loss of BAP1 impairing cellular redox homeostasis and weakening antioxidant defense mechanisms^36,37,38. Additionally, prior studies showed that BAP1 mutations have a role in several aspects of cellular metabolism including glucose metabolism^37,38,39. Mass spectrometry measurements demonstrated that germline BAP1 mutations induced the Warburg effect in human fibroblasts, including depleted TCA cycle activity and increased aerobic glycolysis⁴⁰. Additionally, transcriptome analysis showed that BAP1-mutant ccRCC samples were enriched in glycolytic gene expression⁴¹. To gather insight into the interplay between BAP1 mutation and metabolite abundance, we performed a pathway-based differential abundance (DA) analysis of predicted metabolic changes in BAP1-mutant and wild-type samples in TCGA KIRC. BAP1-mutant samples showed significant depletion in the TCA cycle metabolism (DA score = −1), including drops in the levels of citrate (P = 0.03), fumarate (P = 0.007) and malate (P = 0.008) (Fig. 4c,d). BAP1-mutant samples also demonstrated lower levels of free, unphosphorylated glucose (P = 3 × 10⁻⁷), suggesting that these tumors may upregulate glucose uptake from the microenvironment (Fig. 4d). Consistent with these findings, similar trends of BAP1 mutation-specific changes were observed in the directly measured metabolite abundances from both CPTAC and CPTAC_val datasets, further validating the metabolite-level differences between BAP1-mutant and wild-type samples (Extended Data Fig. 4a,b).

To more granularly understand the metabolic flux patterns associated with the above-described pool size changes, we trained the RNA-seq data from TCGA KIRC with the [U-¹³C]glucose-labeled reference dataset RCC (Fig. 4e and Supplementary Table 10) and leveraged imputed [U-¹³C]glucose-labeled isotopolog distribution data from TCGA KIRC. Relative to BAP1 wild-type tumors, BAP1-mutant tumors demonstrated increased levels of citrate M + 2/pyruvate M + 3 (P = 3 × 10⁻⁴), succinate M + 2/pyruvate M + 3 (P = 0.003) and malate M + 2/pyruvate M + 3 (P = 0.03) (Fig. 4f), indicating an elevated contribution of glucose to TCA cycle activity in BAP1-mutant ccRCC. These data indicated that pool size drops in TCA cycle metabolites are not caused by decreased entry of glucose into the TCA cycle. Instead, they suggest that BAP1-mutant tumors undergo reduced entry of other anapleurotic sources of TCA cycle intermediates, such as glutamate, or alternatively increase diversion of TCA cycle intermediates into alternate pathways, such as the use of acetyl-CoA for fatty acid synthesis. Such hypotheses are directly testable by analogous infusion experiments using, for example, labeled glutamine, and suggest that BAP1 tumors may harbor metabolically distinct (and potentially therapeutically targetable) metabolic alterations.

Lastly, we sought to evaluate whether other diseases may similarly display associations between genotype and metabolic phenotype. To do so, we trained UnitedMet on a reference dataset containing paired RNA-seq and [U-¹³C]glucose-labeled isotopolog distribution data from 42 NSCLC samples⁴² and used TCGA lung adenocarcinoma (LUAD) cohort (n = 576) as a target dataset (Supplementary Table 11). Partitioning the reference data into 50% training and 50% testing, we found that UnitedMet was able to successfully impute 7/29 isotopologs. We subsequently studied associations between the well-predicted isotopolog distributions and genetic mutations in TCGA LUAD cohort. Consistent with a prior study³, EGFR-mutant tumors demonstrated decreased levels of citrate M + 2/pyruvate M + 3 (P = 2 × 10⁻⁶) and glutamate M + 2/pyruvate M + 3 (P = 2 × 10⁻⁴) (Extended Data Fig. 5a) relative to EGFR wild-type tumors, indicating a diminished contribution of glucose to the pool sizes of TCA cycle constituents in EGFR-mutant LUAD. Functionally, this suggests that EGFR mutations in persons with cancer are associated with a less oxidative phenotype, although additional data from tracing of other nutrient sources such as glutamine and acetate are necessary to more completely resolve TCA cycle flux. Together, our findings suggested that, in diverse settings, driver mutations induce specific metabolic phenotypes.

Shift to oxidative metabolism correlates with disease progression and poorer clinical outcome

Recent work suggested that, although ccRCC tumors generally downregulate mitochondrial gene expression and limit entry of glucose-derived carbon into the TCA cycle relative to normal tissue, distant metastases in ccRCC upregulate oxidative phosphorylation and glucose entry into the TCA cycle²⁸. However, there are no large-scale data available on the metabolism of metastatic tumors. We reasoned that high-stage, aggressive ccRCC tumors, which ultimately seed distant metastases, should exhibit signatures of upregulation of oxidative glucose metabolism. To test this hypothesis, we again leveraged predicted isotopolog distribution data from TCGA KIRC and compared isotopolog levels of [U-¹³C]glucose-labeled TCA cycle intermediates normalized by pyruvate M + 3 in ccRCC tumors from different pathological stages. Aggressive ccRCCs with a higher stage demonstrated higher levels of citrate M + 2/pyruvate M + 3 (P = 3 × 10⁻⁴), succinate M + 2/pyruvate M + 3 (P = 7 × 10⁻⁶) and malate M + 2/pyruvate M + 3 (P = 2 × 10⁻⁴), evaluated using the Kruskal–Wallis test (Fig. 5a), consistent with increased glucose-derived carbon entry into the TCA cycle. Motivated by this finding, we sought to evaluate whether high-stage, aggressive tumors in other cancers also displayed a similar shift to oxidative glucose metabolism. We leveraged predicted isotopolog distribution data from TCGA LUAD and found no significant associations between TCA cycle labelings such as citrate M + 2/pyruvate M + 3 (P = 0.8), glutamate M + 2/pyruvate M + 3 (P = 0.8) and malate M + 2/pyruvate M + 3 (P = 0.3) and pathological stages, evaluated using the Kruskal–Wallis test (Extended Data Fig. 5b). This suggested that metabolic reprogramming in aggressive tumors is cancer-type-specific.

Fig. 5: Shift to oxidative metabolism correlates with disease progression and poorer clinical outcome.

a, Aggressive ccRCCs with higher pathological stage demonstrate higher ratios of predicted citrate M + 2/pyruvate M + 3 (left), succinate M + 2/pyruvate M + 3 (middle) and malate M + 2/pyruvate M + 3 (right) in TCGA KIRC cohort (stage 1, n = 267 participant samples; stage 2, n = 57 participant samples; stage 3, n = 123 participant samples; stage 4, n = 84 participant samples). The significance between any two stages was assessed using a pairwise two-sided t-test. P values are FDR adjusted. Citrate M + 2/pyruvate M + 3, P₁_₃ = 0.0014 and P₁_₄ = 0.0014; succinate M + 2/pyruvate M + 3, P₁_₂ = 0.04, P_{1_3} = 0.0011 and P_{1_4} = 3 × 10⁻⁵; malate M + 2/pyruvate M + 3, P_{1_3} = 0.067 and P_{1_4} = 0.00015. In the box plots, the center line represents the median, the bounds of the box indicate the interquartile range (25th to 75th percentiles) and the whiskers extend to 1.5 times the interquartile range. Individual data points are shown as dots. b, Samples from metastatic sites in participants with ccRCC show higher ratios (compared to samples from primary tumor sites) of predicted citrate M + 2/pyruvate M + 3 (left), succinate M + 2/pyruvate M + 3 (middle) and malate M + 2/pyruvate M + 3 (right) in the IMmotion151 cohort (primary ccRCC, n = 625 participant samples; metastatic ccRCC, n = 198 participant samples). Significance was assessed using two-sided Wilcoxon rank-sum tests. In the box plots, the center line represents the median, the bounds of the box indicate the interquartile range (25th to 75th percentiles) and the whiskers extend to 1.5 times the interquartile range. Individual data points are shown as dots. c, Kaplan–Meier plot showing PFS of ccRCC participants with a high level of citrate M + 2/pyruvate M + 3 (based on median level) versus a low level of citrate M + 2/pyruvate M + 3 in both the atezolizumab + bevacizumab arm (top) and the sunitinib arm (bottom). Significance was assessed using a log-rank test. d, Same as c but for succinate M + 2/pyruvate M + 3. e, Same as c but for malate M + 2/pyruvate M + 3.

Source data

We then applied UnitedMet to predict isotopolog distribution data for 823 primary or metastatic tumor samples from a publicly available advanced ccRCC clinical trial (IMmotion151) (Supplementary Table 12). We trained RNA-seq data from IMmotion151 with the ccRCC samples from the RCC reference dataset. Predicted isotopolog levels of [U-¹³C]glucose-labeled TCA cycle intermediates normalized by pyruvate M + 3 were compared between primary and metastatic ccRCC tumors in IMmotion151. Metastatic ccRCC tumor samples demonstrated higher levels of citrate M + 2/pyruvate M + 3 (P = 5 × 10⁻¹³), succinate M + 2/pyruvate M + 3 (P = 3 × 10⁻¹⁰) and malate M + 2/pyruvate M + 3 (P = 2 × 10⁻⁹), evaluated using the Wilcoxon rank-sum test (Fig. 5b). This finding was further validated in a second set of trials (the CheckMate cohort⁴³), where predictions for metastatic ccRCC tumors also showed increased oxidative TCA cycle labeling (Extended Data Fig. 5c). Together, these results indicated that, in ccRCC, increased TCA cycle activity is associated both with (1) high stage or disease progression and (2) the establishment of metastasis itself.

We next interrogated whether this oxidative metabolic phenotype may be linked to poor clinical outcomes. Participants with ccRCC in the IMmotion151 trial were treated with either atezolizumab plus bevacizumab (a combination of tyrosine kinase inhibitor and immunotherapy) or sunitinib (an antiangiogenic tyrosine kinase inhibitor). We evaluated the association between isotopolog levels of TCA cycle intermediates and progression-free survival (PFS) using multivariate Cox proportional hazard models (evaluating different treatment arms separately). In the atezolizumab + bevacizumab arm, participants with high levels of citrate M + 2/pyruvate M + 3, succinate M + 2/pyruvate M + 3 and malate M + 2/pyruvate M + 3 did not exhibit a significant survival difference (Fig. 5c–e). In the sunitinib arm, we observed that participants with high succinate M + 2/pyruvate M + 3 (P = 4.4 × 10⁻⁵) Fig. 5d) and malate M + 2/pyruvate M + 3 (P = 1.6 × 10⁻⁶) (Fig. 5e) had significantly poorer PFS. These data highlighted oxidative metabolism of glucose as a potential druggable target to diminish cancer progression and metastasis in persons receiving antiangiogenic agents in ccRCC.

Discussion

This work presents an advanced methodology for the joint, probabilistic modeling of multimodal metabolic data. In doing so, it addresses the numerous challenges associated with the analysis of metabolomics data (including but not limited to semiquantitative data and batch effects) and its joint modeling with transcriptomics data. After establishing that UnitedMet accurately imputes metabolite features with estimates of uncertainty in benchmark datasets, we applied UnitedMet to study the metabolic consequences of key driver mutations and the metabolic adaptations associated with aggressive disease and metastatic competency.

The era of cancer genomics has revealed that only a small number of metabolic enzymes (including, for example, IDH1, IDH2, FH and SDH) are recurrently mutated or otherwise lost in cancer. However, a much larger number of recurrently altered genes are so-called regulators of metabolism (for example, PIK3CA, MTOR and MYC) or other proteins indirectly drawing on metabolites as substrates for their action (for example, epigenetic regulators such as DNA methyltransferases). Our observations here suggest that certain molecular subtypes of cancer, associated with the presence or absence of key driver mutations such as BAP1 in ccRCC or EGFR in LUAD, may themselves be associated with unique metabolic features. Whether these associations between genotype and metabolism are gene intrinsic or potentially extend across cancer lineages (for example, to BAP1-mutant mesothelioma) is an open question. While such observations have been made in the past^24,44, the growing number of metabolomics datasets in primary tumors and, now, the availability of UnitedMet suggest that the field is now poised to carry out a more comprehensive analysis of the metabolic impact of driver mutations.

Several key limitations underlie UnitedMet and represent important challenges in the development of next-generation methods for joint modeling of multimodal metabolic data. First, the accuracy of UnitedMet varied widely across metabolites (Fig. 2), rendering a large fraction of the metabolite nonimputable. The successive addition of relevant data for training for UnitedMet is the most direct route to addressing this limitation, although the possibility remains that a subset of metabolites will remain nonimputable with even very large training data. Nonetheless, UnitedMet’s ability to estimate the uncertainty of the model for each imputed metabolite enables users to filter reliable predictions, which can help mitigate the variability in performance and ensure robust downstream analyses. Second, while rank transformation has proven useful in both UnitedMet and MIRTH²³ for the comparison of semiquantitative metabolite data produced in distinct batches, the process of rank transformation produces a loss of information, where large effect sizes (that is, large fold changes between pairs of samples) in one metabolite feature can be equated to small effect sizes in another metabolite feature in the rank-transformed space. Third, the vast majority of the training data for UnitedMet are derived from single-site tissue biopsies, leaving open the possibility that fluctuations in the global tumor nutrient milieu may be incompletely captured by RNA-seq from a single site. Multiregional sampling of both metabolites and RNA (or coregistered spatial metabolomics and transcriptomics) is likely necessary to address this limitation. Fourth, UnitedMet requires at least one reference dataset of sufficient size to carry out imputation. For the majority of diseases, such a dataset does not exist^14,45. One potential avenue to overcoming this challenge is to train disease-agnostic models to impute metabolite features. This seems feasible for at least some metabolite features that demonstrate lineage-agnostic covariation with gene expression, such as IDO1 and kynurenine^14,22. However, while our own prior studies focused on analyzing lineage-agnostic covariation between individual genes and individual metabolites, such interactions are rare. Conversely, it remains unknown whether generalized, multivariate patterns of gene–metabolite covariation (for example, a multidisease implementation of UnitedMet) could be used to impute metabolite levels in different contexts. It is reasonable to speculate that certain fundamental and common metabolic phenotypes (such as hypoxia or aerobic glycolysis) may be associated with shared transcriptomic signatures across diseases, whereby cross-disease or cross-tissue imputation would be feasible. Encoding tissue site as an additional factor in future versions of UnitedMet may improve model performance in this setting. Lastly, while UnitedMet demonstrates high accuracy in predicting metabolic phenotypes, we acknowledge that further reference data with paired measurements of RNA-seq and metabolomics are required to expand its predictive capabilities comprehensively. Given the abundance of gene expression data in the field, we advise cautious interpretation to prevent overreliance on imputed metabolite predictions without adequate empirical validation.

UnitedMet harnesses the covariation between the transcriptome and metabolome to impute otherwise unmeasured metabolite features. In doing so, it enables the inference of pool size and tracing patterns (and, consequently, the evaluation of metabolite-centered hypotheses) in valuable clinical samples where metabolite profiling is difficult or otherwise infeasible. Several valuable clinical use cases come to mind as natural applications of the UnitedMet framework where ancillary transcriptomic data are available. For instance, one may seek to infer metabolite levels in archival formalin-fixed, paraffin-embedded samples of inadequate quality for metabolite profiling or in biopsy samples with an inadequate quantity of material for metabolite profiling. Such data are commonly generated in the pursuit of genomic and transcriptomic biomarkers of response to targeted and immunotherapies (and, indeed, form the basis of our analysis in Fig. 5). Separately, in isotope tracing experiments where one is interested in more than one tracer (for example, ¹³C-glucose and ¹³C-glutamine tracing, where the infusion of both tracers in the same person is infeasible or does not provide useful data), UnitedMet could be used to impute the outcome of the counterpart tracer as long a common data modality (for example, RNA-seq) was collected. This would overcome fundamental limitations in the ability to resolve tracers using a common isotope in a single person and, in doing so, facilitate a more complete description of metabolic flux patterns in pathways driven by multiple nutrient sources. UnitedMet, therefore, democratizes metabolomics data for scientific discovery.

Methods

Data preprocessing

This study complies with all relevant ethical regulations and was approved by the institutional review board at Memorial Sloan Kettering Cancer Center (MSKCC).

The input to UnitedMet consists of reference datasets with paired measurements of RNA counts and total ion counts of metabolites or isotopologs and a single-modality target dataset with RNA-seq data only (Fig. 1a). We assume that there are N different reference datasets, each with an RNA-seq sample × gene matrix of raw counts ${X}_{n}\in {{\mathbb{R}}}^{{S}_{n}\times {G}_{n}}(n=1,2,\ldots ,N)$ and a paired sample × metabolite or sample × isotopolog ion count matrix ${Y}_{n}\in {{\mathbb{R}}}^{{S}_{n}\times {M}_{n}}(n=1,2,\ldots ,N)$. Let ${X}_{0}\in {{\mathbb{R}}}^{{S}_{0}\times {M}_{0}}$ be the RNA-seq sample × gene matrix in a single-modality target dataset.

Normalization

We first normalized all input data with distinct techniques. We implemented total ion count normalization to raw ion count matrices of metabolomics data (Y) and transcripts per million (TPM) normalization to raw count matrices of RNA-seq data (X). In metabolomics experiments, ion counts below a threshold were not detected by the mass spectrometry. This ended up with missing metabolite measurements in some samples. We treated these left-censored values as half of the minimum value across all metabolite measurements when calculating the total ion count normalizer.

For sample × isotopolog ion count matrices (Y) of isotope labeling data, we first calculated the fractional labeling (namely, the proportion of each isotopolog relative to the sum of all isotopologs in that metabolite). We then divided all fractions by the fraction of pyruvate M + 3 or glucose M + 6. Normalization by pyruvate M + 3 allowed us to establish the labeling ratio of each isotopolog to pyruvate M + 3, providing insights into the contribution of glucose-derived pyruvate to that specific isotopolog.The labeling ratio of citrate M + 2 to pyruvate M + 3, for instance, suggested the contribution of glucose through the pyruvate dehydrogenase reaction. Normalization by glucose M + 6 instead revealed the contribution of glucose carbon to other metabolites.

Rank transformation

As metabolomics and isotope tracing data generated using mass spectrometry are reported as semiquantitative relative abundances, we are only able to compare measurements of the same metabolite or isotopolog from different samples in the same dataset. To map metabolic relative abundances and gene expression levels into a shared measurement scale across all features and datasets, we rank the metabolite or isotopolog and gene expression levels across all the samples within each dataset. Ranks enable the comparison of features across datasets and transfer learning from RNA-seq modality to metabolic modality. Samples exhibiting the maximum level for a specific feature within the provided dataset are assigned the highest rank. Conversely, samples displaying the minimum level for the same feature are allocated the lowest rank. Left-censored samples are tied, sharing the last rank in the ranking hierarchy. While we use unnormalized rankings for modeling, we normalize ranks by their total number of samples S in downstream analyses, mapping them to a comparable scale of ranks [0, 1) in all datasets. Here, we use 𝑆 to refer to the number of samples within a dataset in a general sense, without referring to a specific dataset. For each feature j, the normalized rank of a measurement ${f}_{{ij}}(i=\mathrm{1,2},\ldots ,S\;)$ in that dataset is defined by ${\rm{rank}}_{{ij}}=\frac{{\sum }_{k=1}^{S}P [\;{f}_{{ij}} > {f}_{{kj}}]}{S}$. Importantly, rank transformations are performed separately for each metabolite, ensuring that comparisons are made only within the same metabolite across samples. The ranked values are specific to each metabolite and are not directly comparable between different metabolites.

Data aggregation

Rankings data of RNA-seq matrices X_n and metabolic matrices ${Y}_{n}(n=\mathrm{1,2},\ldots ,N)$ in reference datasets are aggregated into a single data matrix R along with the rankings data of metabolic matrix X₀ in the target dataset. While we take in the common genes shared across datasets to save computation costs, we aggregate metabolic modalities by taking the union of relevant features (namely, the aggregated matrix $R\in {{\mathbb{R}}}^{{S}_{R}\times {F}_{R}}$, where ${S}_{R}={S}_{0}+{\sum }_{i=1}^{N}{S}_{n}$ and ${F}_{R}=|{G}_{R}|+|{M}_{R}|,{G}_{R}={G}_{0}\bigcap{\cap }_{i=1}^{N}{G}_{i},{M}_{R}={\cup}_{i=1}^{N}{M}_{i}$). In the benchmarking test on four ccRCC datasets, R contained measurements of 1,148 metabolites and 20,171 genes for 341 samples.

The UnitedMet model

UnitedMet is a probabilistic generative method that jointly models RNA-seq and metabolic data. UnitedMet assumes that the rankings in R are generated by a Plackett–Luce ranking distribution of a latent variable matrix Z, where $Z=WH$ is the product of the latent sample embedding matrix $W\in {{\mathbb{R}}}^{{S}_{R}\times \lambda }$ and the latent feature embedding matrix $H\in {{\mathbb{R}}}^{\lambda \times {F}_{R}}$. The hyperparameter λ is the number of embedding dimensions. We suppose all latent variables in both latent embedding matrices are generated by normal prior distributions: ${W}_{{ik}}\overset{\text{iid}}\sim {\rm{Normal}}(\mathrm{0,1}),{H}_{{kj}}\overset{\text{iid}}\sim {\rm{Normal}}(\mathrm{0,1}),$ where W_ik is the entry in the ith sample and the kth embedding column in embedding matrix W and H_kj is the entry in the kth embedding row and the jth feature in embedding matrix H.

Plackett–Luce ranking distribution

The Plackett–Luce distribution^46,47 models a ranking of T items as an ordered series of choices. It begins by choosing the top-ranked item from the entire set of T options, followed by choosing the second-ranked item from the remaining options and so on⁴⁸. Given a set of T options $\{{Q}_{1},\ldots ,{Q}_{T}\}$, the probability of selecting the ith item Q_i is defined as $P(i|\{1,\ldots ,T\})=\frac{{u}_{i}}{{\sum }_{t=1}^{T}{u}_{t}}$ by the Luce choice axiom, where u_i represents the utility score of Q_i. The probability of a full ordering $\{{\sigma }_{1},\ldots ,{\sigma }_{T}\}$, where we assume ${Q}_{{\sigma }_{1}} > \ldots > {Q}_{{\sigma }_{T}}$, is then given by recursively applying the Plackett–Luce distribution, choosing σ₁ from $\{1,\ldots ,T\}$, σ₂ from $\{1,\ldots ,T\}\backslash \{{\sigma }_{1}\}$ and σ₃ from $\{1,\ldots ,T\}\backslash \{{\sigma }_{1},{\sigma }_{2}\}$, yielding $P(\{{\sigma }_{1},\ldots ,{\sigma }_{T}\}|\{1,\ldots ,T\})={\prod }_{i=1}^{T}\frac{{u}_{{\sigma }_{i}}}{{\sum }_{r=i}^{T}{u}_{{\sigma }_{r}}}$. Given the latent variable matrix $Z=WH$ in UnitedMet, we suppose the utility score of the item in the ith sample and the jth feature is defined as ${\rm{exp}}({Z}_{ij})={\rm{exp}}({{W}_{i}}{H}_{j})$. Extending this to censored rankings in UnitedMet, the likelihood of observing a censored ordering $\{{\sigma }_{1},{\sigma }_{2},\ldots ,{\sigma }_{K},\{{\sigma }_{K+1},\ldots ,{\sigma }_{S}\}\}$ in the jth feature of a batch is then defined by $P\left({R}_{\!j}=\left\{{Z}_{{\sigma }_{1},\,j} > {Z}_{{\sigma }_{2},\,j} > \ldots > {Z}_{{\sigma }_{K},\,j} >\right.\right.$ $\left.\left.\{{Z}_{{\sigma }_{K+1},\,{j}},\ldots ,{Z}_{{\sigma }_{S},\,{j}}\}\right\}|\{{Z}_{1,\,{j}},\ldots ,{Z}_{S,\,{j}}\}\right)$$={\prod }_{i=1}^{K}\frac{{\rm{exp}}({Z}_{{\sigma }_{i},\,{j}})}{{\sum }_{r=i}^{S}{\rm{exp}}({Z}_{{\sigma }_{r},\,{j}})}$. Detailed definitions of UnitedMet are described below.

$$\begin{array}{c}({i}{\rm{th}}\;{\rm{sample}},\,{k}{\rm{th}}\;{\rm{column}}\,{\rm{in}}\,{\rm{embedding}}\,{\rm{matrix}}\,{{W\;}})\,{W}_{ik} \overset{\text{iid}}\sim {\rm{Normal}}(0,1)\\ ({k}{\rm{th}}\;{\rm{row}},\,{j}{\rm{th}}\;{\rm{feature}}\,{\rm{in}}\,{\rm{embedding}}\,{\rm{matrix}}\,{{H\;}})\,{H}_{kj} \overset{\text{iid}}\sim {\rm{Normal}}(0,1)\\ ({\rm{Transformed}}\,{\rm{parameter}}\,{\rm{matrix}}\,{{Z}})\,Z=WH\\ \left({\rm{PL}}\,{\rm{model}}\,{\rm{return}}\,{\rm{a}}\,{\rm{probabilistic}}\,{\rm{permutation}}\,{R}_{\!j}\,\right.\\\left.{\rm{for}}\,{j}{\rm{th}}\,{\rm{column}}\,{\rm{in}}\,{\rm{batch}}\,{\rm{b}}\right)\,{R}_{\!j} \sim {\rm{PL}}({Z}_{\!j}),\\ {\rm{where}}\,{R}_{\!j}=({Z}_{{\sigma }_{1},\;j},{Z}_{{\sigma }_{2},\;j},\ldots ,{Z}_{{\sigma }_{K},\;j},{Z}_{{\sigma }_{K+1},\;j},\ldots ,{Z}_{{\sigma }_{S},\;j}),\\ {\rm{and}}\,{\rm{we}}\,{\rm{assume}}\,{Z}_{{\sigma }_{1},\;j} > {Z}_{{\sigma }_{2},\;j} > \ldots > {Z}_{{\sigma }_{K},\;j} > {Z}_{{\sigma }_{K+1},\;j},\ldots ,{Z}_{{\sigma }_{S},\;j}.\\ \begin{array}{ccc}p({R}_{\!j}) & = & \mathop{\prod }\limits_{i=1}^{K}\frac{\exp ({R}_{ij})}{{\sum }_{r=i}^{S}\exp ({R}_{rj})}\\ & = & \mathop{\prod }\limits_{i=1}^{K}\frac{\exp ({Z}_{{\sigma }_{i},\;j})}{{\sum }_{r=i}^{S}\exp \left({Z}_{{\sigma }_{r},\;j}\right)}\\ & = & \mathop{\prod }\limits_{i=1}^{K}\frac{\exp \left({W}_{{\sigma }_{i}}{H}_{\!j}\right)}{{\sum }_{r=i}^{S}\exp\left({W}_{{\sigma }_{r}}{H}_{\!j}\right)}\end{array}\end{array}$$

Cross-validation

To determine the optimal number of embedding dimensions ($\lambda$) of latent matrices $W$ and $H$, we use tenfold cross-validation. The range of $\lambda$ to be tested is contingent on the total number of samples ${S}_{R}$. For instance, performance evaluation spans a $\lambda$ range of [1, 351] with a step of 10 in the benchmarking test on ccRCC datasets. For each batch, cross-validation features that are used to test model performance are selected separately. Only metabolic features (metabolites or isotopologs) that are measured in at least one other batch are included. These features are then randomly distributed into ten folds. We treat one fold at a time as unmeasured and hold out the fold’s features in the corresponding batch. Masked features are then predicted by UnitedMet. In the end, we calculate the mean absolute error (MAE) between the true ranks of held-out features in the fold and their predicted ranks. The MAE scores across all folds are averaged to obtain a final performance score. We evaluate the MAE scores for all $\lambda$ values and the one resulting in the elbow of the MAE score curve is chosen as the optimal number of embedding dimensions for the factorization.

Inference

The likelihood is computed from observed rankings in both paired modalities of reference datasets and only in the respective RNA-seq modality of the target dataset. We use SVI within the Pyro⁴⁹ package for inference. Variational distributions are generated using the AutoNormal function. Optimization is executed through the Adam optimizer, with a default learning rate set to 0.001. Convergence is ascertained when the relative change in evidence lower bound (ELBO) falls below 0.01. To address the inherent imbalance between the RNA-seq and metabolomics modalities in scenarios where we want to impute a large panel of metabolites from a subset of measured metabolites and RNA-seq data, we introduced a weighted loss function in UnitedMet. Typically, RNA-seq data contains measurements for approximately 20,000 genes, whereas metabolomics data comprises around 1,000 measured metabolites. This large difference in the number of features between the two modalities can disproportionately affect the likelihood computation, leading to biases in the inferred rankings. To mitigate this issue, we applied modality-specific weighting when computing the log-likelihood using the Plackett–Luce distribution. Specifically, we assigned equal weight to the metabolomics features, while down-weighting the gene features proportionally by the ratio of the number of metabolites to genes. Given a log-likelihood matrix L of shape (n_genes + n_metabolites) × S, where S is the number of samples. We defined a weight matrix C of the same shape such that: C_:,j = 1, if j corresponds to a metabolite; C_:,j = n_metabolites/n_genes, if j corresponds to a gene. The weighted log-likelihood matrix was computed as: L_weighted = C ⊙ L. The final total log-likelihood was obtained by summing over all observed values in L_weighted.

Posterior prediction

UnitedMet estimates the joint posterior distribution of the latent embedding matrix $W$ and $H$. For every latent variable in $W$ and $H$, we draw 1,000 samples from their estimated posterior distribution. Given posterior samples of the latent matrix $Z(=WH)$, posterior rankings are then generated by the Plackett–Luce ranking distribution. To sample in a computation-efficient way, we implemented the Gumbel–Max trick⁵⁰, which generates ordered samples from the Plackett–Luce ranking distribution by sorting the perturbed log probability through the addition of independent variables from the Gumbel distribution⁵¹ (${G}_{1,\,j},\ldots ,{G}_{S,\,j}\sim {\rm{Gumbel}}(0),{\rm{iid}}$). Let ${Z}_{,\;j}$ be the ${j}{\rm{th}}$ column of the latent matrix $Z$. Set perturbed log probability ${U}_{i,j}$ = ${Z}_{i,j}+{G}_{i,j}$. The ordered indices of the ${j}{\rm{th}}$ column returned by sorting the perturbed log probabilities $\{{U}_{1,\,j},\ldots ,{U}_{S,\,j}\}$ are equivalent to the orderings generated by the Plackett–Luce model given probabilities (utility scores) $\{{Z}_{1,\;j},\ldots ,{Z}_{S,\;j}\}$. Specifically, if $\{{U}_{{\sigma }_{1},\,j} > {U}_{{\sigma }_{2},\,j} > \ldots > {U}_{{\sigma }_{K},\,j} > \{{U}_{{\sigma }_{K+1},\,j},\ldots ,{U}_{{\sigma }_{S},\,j}\}\}$, then we observe $\{{Z}_{{\sigma }_{1},\;j} > {Z}_{{\sigma }_{2},\;j} > \ldots > {Z}_{{\sigma }_{K},\;j} > \{{Z}_{{\sigma }_{K+1},\;j},\ldots ,{Z}_{{\sigma }_{S},\;j}\}\}$.

Estimates of the rankings can be found as the mean of the 1,000 posterior draws, while the s.d. of posterior samples represents a quantification of the prediction uncertainty.

Benchmarking

Multivariate Lasso regression

We implemented multivariate Lasso regression on four ccRCC datasets according to Li et al.²¹. In each dataset, metabolomics data were preprocessed by total ion count normalization, while transcript levels were converted into TPM units. At each time in the benchmarking experiments, one ccRCC dataset was treated as the testing set while the other three were training sets. All RNA-seq data were scaled before training or testing. For every metabolite (y), we used gene expressions (x) to predict it in the training set. LassoCV in Python package scikit-learn was used to select the best penalizer α by fivefold cross-validation. The maximum number of iterations fitting along the regularization path was set to default 1,000. After selecting the best model for each metabolite, we assessed model accuracy by calculating Spearman correlation coefficients between predicted metabolite levels and their ground truths.

MIRTH

MIRTH is a matrix factorization approach aimed at predicting the levels of unmeasured metabolites by collectively analyzing the covariation of metabolites across multiple datasets²³. We extended MIRTH to the cross-modality prediction problem as previously described²². Metabolomics and RNA-seq data were preprocessed in the same way mentioned above.

MSKCC ccRCC datasets

We obtained two datasets, RC18 (n = 144) and RC20 (n = 76), each with matched RNA-seq and mass spectrometry metabolomics measurements from fresh frozen high-quality tumor or adjacent normal specimens of persons with ccRCC that underwent partial or radical nephrectomies at MSKCC²². Samples were collected under the approval of MSKCC’s institutional review board. The alignment of RNA-seq reads was performed using STAR two-pass alignment against human genome assembly hg19. Metabolites were identified on the basis of the criteria according to Benedetti et al.¹⁴. RC18 had measurements for 783 metabolites and 22,937 genes. RC12 had measurements for 1,012 metabolites and 22,987 genes.

CPTAC ccRCC datasets

Metabolite raw count matrices of CPTAC (n = 50) and CPTAC_val (n = 71) were downloaded from Li et al.¹. Transcriptomic and WES data were downloaded from Genomic Data Commons (https://portal.gdc.cancer.gov/projects/CPTAC-3; project: CPTAC-3, primary site: kidney). CPTAC contained only ccRCC tumor samples, while CPTAC_val contained tumor and adjacent normal samples of persons with ccRCC. Mass spectrometry peaks were quantified using Thermo Scientific Compound Discoverer software to generate raw counts. HTSeq version 0.11.2 was implemented to calculate the gene-level stranded read count. We then performed total ion count normalization and TPM normalization on metabolite and gene expression count matrices, respectively. CPTAC had measurements for 183 metabolites and 60,483 genes. CPTAC_val had measurements for 130 metabolites and 60,483 genes.

Breast cancer datasets

Matched TPM-normalized RNA-seq and bulk metabolomic data (raw count matrices) of two breast cancer datasets BrCa1 (ref. ²⁴) (n = 108, no. of metabolites = 533, no. of genes = 20,032), BrCa2²⁵ (n = 18, no. of metabolites = 397, no. of genes = 21,773) were downloaded from Benedetti et al.¹⁴. RNA-seq data of primary tumor tissues from the TNBC cohort (n = 360, no. of genes = 23,211) were downloaded from the National Omics Data Encyclopedia (https://www.biosino.org/node/analysis/detail/OEZ00000398) according to Jiang et al.²⁷. Bulk metabolomics data of the TNBC cohort (n = 479, no. of metabolites = 594) were downloaded from Xiao et al.²⁶. There were 258 tumor samples with paired RNA-seq and metabolomics data after matching.

Human RCC RNA-seq and isotopic labeling data infused with [U-¹³C]glucose in vivo

Paired RNA-seq and isotopic labeling data from 76 primary tumor or adjacent normal kidney samples of persons with RCC were downloaded from Bezwada et al.²⁸. The RCC dataset had measurements for 64 isotopologs and 12,300 genes. Because small fluctuations of isotopolog levels that are not biologically interpretable can be quantified as signals in mass spectrometry, we set a criterion to filter out isotopologs whose average fraction over all samples was less than 10%. This ended with a total of 23 isotopologs including biologically meaningful isotopologs such as citrate M + 2 and malate M + 2.

Human NSCLC cell line RNA-seq and isotopic labeling data

We downloaded two human NSCLC cell line datasets with paired RNA-seq and isotopic labeling data from Chen et al.³: NSCLC-G (n = 85, no. of isotopologs = 28, no. of genes = 16,383) and NSCLC-Q (n = 85, no. of isotopologs = 21, no. of genes = 16,383). A total of 85 NSCLC cell lines were cultured with medium containing the isotopically enriched nutrient under identical conditions. The isotopic data in NSCLC-G were labeled with [U-¹³C]glucose, while the isotopic data in NSCLC-Q were labeled with [U-¹³C]glutamine. After filtering out isotopologs whose average fraction over all samples was less than 10%, there were nine and eight isotopologs in the NSCLC-G and NSCLC-Q datasets, respectively.

TCGA datasets

We downloaded paired RNA-seq, WES and clinical data of 1,020 RCC tumor and adjacent normal samples in TCGA KIPAN from the Genome Data Analysis Center (GDAC) at Broad Institute. A total of 606 TCGA KIRC samples were included in TCGA KIPAN. mtDNA mutation calls using a PCR-based amplification approach for 61 ChRCC cases in TCGA KICH were downloaded from Davis et al.²⁹. Paired RNA-seq, WES and clinical data of TCGA LUAD (n = 576) were also downloaded from GDAC.

Annotation of MAF files from WES data

We downloaded MAF files of WES data for CPTAC, CPTAC_val, TCGA KIPAN and TCGA KIRC from the corresponding websites mentioned above. We annotated all molecular variations to 0 or 1 in a gene-wise way, where 0 represented wild-type or silent variations and 1 represented nonsilent variations. Missense mutation, nonsense mutation, frame-shift deletion, splice site mutation, frame-shift insertion, in-frame deletion, splice-region variant, translation start site mutation, in-frame insertion and nonstop mutation were considered as nonsilent molecular variations. Silent mutations, intron mutation, 3′ UTR mutation and 5′ UTR mutation were considered as silent variations, because they were not able to change gene functions.

DA score

The DA score assesses the distinct regulation of a metabolic pathway between two groups. Calculated through a Wilcoxon rank-sum test applied to all pathway metabolites, the score undergoes P-value correction using the Benjamini–Hochberg method (FDR-corrected P value < 0.1). For each pathway, the DA score is derived as follows: (no. of significantly enriched metabolites − no. of significantly depleted metabolites)/no. of total metabolites. Scoring is exclusively applied to pathways exhibiting three or more significantly altered metabolites.

Survival analysis

We collected RNA-seq data and participant-level clinical information from IMmotion151 (refs. ^35,52) (n = 823), a published trial exploring immunotherapeutic versus systemic agents in advanced ccRCC. To account for diverse drug effects in clinical trials, we conducted separate statistical analyses for the immunotherapy arm (atezolizumab + bevacizumab) and the sunitinib arm. The survival regression analysis was performed using the Python package lifelines.

Statistical and reproducibility

Statistical analyses were conducted using either R or Python. Differential distribution comparisons were implemented with the Wilcoxon rank-sum test or t-test. All statistical tests were two-sided by default, unless specified otherwise, with P values corrected using the Benjamini–Hochberg method⁵³. No statistical method was used to predetermine sample size and no data were excluded from the analyses. Blinding and randomization were not relevant because this was an observational study.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.