Introduction

The ground state of cuprate high-critical-temperature superconductors (HTS) exhibits a fascinating interplay of quantum phases, where charge, spin and orbital orders are intertwined1,2,3,4. Superconductivity emerges from a metallic state, named “strange metal”5, with properties that cannot be accounted for by the Fermi liquid theory. In this state, the quasiparticle picture breaks down and a robust T-linear dependence of the resistivity is observed, as if the details of the scattering events become irrelevant in a certain temperature range6,7,8,9,10.

Modeling the strange metal state is challenging due to the strong electron-electron interactions. Recent work has addressed the problem of T-linear resistivity within advanced computational methods applied to the two-dimensional Hubbard model11,12. Other approaches, involving critical fluctuations in the vicinity of a quantum critical point13,14,15,16, e.g., based on short ranged dynamical charge density fluctuations17,18, were also able to reproduce the fingerprint of this state of matter19,20. Holographic duality, which maps the physics of strongly interacting systems onto the classical theory of gravity in higher dimensions, is a further pathway to obtain the T-linear resistivity21,22.

Though encouraging, these theoretical attempts require further developments. The tuning of the ground state of HTS beyond oxygen doping, demonstrated in recent mechanical strain experiments23,24,25,26,27,28,29,30,31, can give additional information about the strange metal phase, its origin and the intertwining with the various local orders, including charge density waves (CDW)32,33,34,35,36,37. These new inputs could be fed into theories to discriminate between different scenarios.

In a recent experiment38, where we studied the transport properties of ultrathin films as a function of doping, we have shown that the substrate-induced strain strongly modifies the ground state of the material affecting the Fermi surface topology, the strange metal phase and the CDW order. It is therefore natural to ask what the role of strain is in nm-thick films. Is it just the strain-induced geometrical modification of the unit cell that is important or does the substrate-film interface coupling induce subtler effects, possibly intertwined with other orders?

To answer these questions, we compare the resistivity measurements of 10 nm thick YBa2Cu3O7−δ (YBCO) films grown on (110) MgO and (001) SrTiO3 (STO) substrates, extensively studied in ref. 38, having different lattice parameters and surface morphologies. Using as input the experimental data from atomic force microscopy (AFM), we develop a model which describes different film-substrate coupling, depending on the extension and morphology of the surface facets. The results can nicely reproduce the nematic Fermi surface in the case of MgO, while confirming an unaltered ground state with STO. Starting from a nematic Fermi surface we retrieve the unidirectional CDW observed in the experiment38 and discuss the possible implication on the strange metal state.

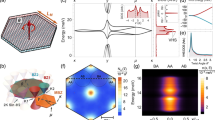
Figure 1 summarizes the transport properties at p = 0.12 of our 10 nm thick YBCO films, on both MgO and STO, as we have shown in ref. 38. Here, the doping level has been calibrated through measurements of the c-axis length and of the critical temperature, according to the procedure extensively discussed in ref. 39. Figure 1a shows the temperature dependence of the resistivity ρ, measured in two devices oriented along the YBCO a- and b-axis, realized in an untwinned film grown on MgO. The anisotropy ratio at T = 290 K, defined by ρa(290 K)/ρb(290 K), exceeds 2, a value much higher than that measured in our thicker YBCO films, cf. Supplementary Note 4. The slopes of ρa(T) and ρb(T) are quite different, indicating different Fermi velocities along a- and b-axis, and thus a nematic Fermi surface38. In these samples, both the strange metal state and the CDW become very anisotropic. The T-linear behavior along b is extended down to TL = 187 K, while along a TL is the same as in bulk samples. Simultaneously, the CDW measured by resonant inelastic X-ray scattering (RIXS) becomes unidirectional along b38. These anisotropies are doping dependent, being observed only within the range 0.11 ≲ p ≲ 0.16; for p < 0.11, the typical isotropic behavior seen in bulk samples, e.g., \({T}_{{{\rm{L}}}}^{a}={T}_{{{\rm{L}}}}^{b}\), is restored38.

Fig. 1: Strain dependence of the in-plane resistivity of underdoped YBCO films (thickness t = 10 nm).
figure 1

a ρ(T) along the a- and b-axis of a film grown on MgO. The dashed lines are the linear fits of the curves for T > 260 K. Close to these lines, the temperatures below which the resistivity deviates by 1% from the linear behaviour are reported. b Same as a, but for a film grown on a 1° vicinal angle STO.

Full size image

In underdoped, untwinned, 10 nm thick YBCO films grown on (001) STO substrates with a vicinal angle, the transport properties along a- and b-axis are more conventional and resemble bulk samples. Here, at p = 0.12, the slopes of the T-linear resistivity are very similar for ρa(T) and ρb(T) [see Fig. 1b], indicating comparable Fermi velocities along both axes and therefore a rather isotropic Fermi surface. Moreover, the strange metal state and the CDW exhibit no anisotropy, unlike the MgO case38.

The large difference in transport properties between films grown on MgO and on STO, despite the identical doping levels, suggests that the nematicity, conspicuous only in films grown on MgO, cannot be solely attributed to the CuO chains along the b-axis, since these are present and equally filled in both systems. To shed light on this peculiar anisotropic state, we investigated the substrate surface structure and its interface with the YBCO films.

The surface of (110) oriented MgO substrates exhibits elongated nanofacets, running along the [001] direction. They are due to surface reconstruction, achieved through substrate annealing, which is instrumental to get untwinned YBCO films40. Tapping mode (TM) AFM investigation demonstrates that these nanofacets have an average height of about 1.5 nm and a nearly triangular profile [see Fig. 2(a-c)]. This results in a very anisotropic atomic lattice, where large areas along the facet edges consist of under-coordinated atoms. This picture is confirmed by peak force quantitative nanomechanics (PFQNM) AFM adhesion analysis [see Fig. 2(a)], where the chemical contrast at the surface of the MgO substrate can be investigated. The difference in coordination between the atoms in the valleys and along the facet edges is very large, and affects a substantial area of the substrate surface. When YBCO is deposited on top of this surface [see the scanning electron microscopy image in Fig. 2(a)], it is subject to a very anisotropic strain, resulting in an untwinned film, with the a-axis and the b-axis respectively aligned perpendicular and parallel to the MgO facets40. At the interface, the film is embedded in this articulated and anisotropic substrate matrix, with its unit cell height comparable to the nanofacet height. It is then natural to expect a strong film-substrate coupling, mainly occurring in the areas where the substrate atoms are under-coordinated. This strong coupling is based on the hybridization between the two layers to saturate these bonds and therefore only affects few YBCO layers adjacent to the substrate. It is thus particularly relevant for the transport properties of the 10 nm films analyzed in this paper.

Fig. 2: Analysis of the substrate surface and modeling of the interface with the YBCO film.
figure 2

a From the bottom: TM AFM image of a 250 × 250 nm2 region of the annealed MgO (yellow-brown map). The chemical contrast caused by the elongated and rather high nanofacets is detected in the very same area by PFQNM AFM adhesion image (bluish map). The YBCO film grown on top is represented by a scanning electron microscopy image. The planar tight-binding structure of the YBCO planes is the topmost enlargement at the interatomic scale (red dots) with the nearest neighbor hopping parameter t and the next nearest neighbor hopping parameter \(t^{\prime}\). These atoms are those coupled to the under-coordinated regions of the substrate by a coupling parameter t⊥ (see the wide red slabs). b Same as a, but for a film grown on STO. c TM AFM linescan along the [\(1\bar{1}0\)] MgO direction. d Same as c, but along the [100] STO direction.

Full size image

Results and Discussion

Effective model for the coupling between thin film and substrate

Our model for this heterogeneous structure is depicted in Fig. 2 where the YBCO layer is represented by the red-dot lattice. The chemical coupling between CuO2 plane and MgO substrate is described by a hopping t⊥ to the elongated regions of the substrate having under-coordinated atoms. Consequently, only the elongated (actually 1D) regions of the CuO2 lattice along the b-axis are endowed by this additional t⊥. The virtual hopping of charge carriers to the substrate atoms induces an effective repulsion between the atomic levels of film and substrate, leading to an effective potential \({V}_{{{\rm{eff}}}}=\frac{1}{2}(\sqrt{{V}_{{{\rm{sub}}}}^{2}+4{t}_{\perp }^{2}}-{V}_{{{\rm{sub}}}})\) for the coupled film atoms, where Vsub is the on-site energy of the coupled substrate atoms. The strips of atoms with the added t⊥ hopping are randomly distributed on the lattice, and can therefore be treated by a standard coherent potential approximation (CPA), see Supplementary Note 1.

For the YBCO/STO system, the 1° vicinality of the substrate results in step edges, having an average height of 3.9 Å [STO lattice parameter, see Fig. 2(b-d)]. These steps induce an anisotropic strain, favoring the growth of untwinned YBCO films with the b-axis (a-axis) parallel (perpendicular) to the elongated steps. An effective, but much weaker, potential Veff can again be used to describe the film-substrate coupling. Indeed, the atomic-scale-high steps of the STO substrates result in a tiny chemical contrast [see Fig. 2(b)], involving much narrower areas of the substrate surface (they are much sharper and reduced in height compared to the smooth slopes of the MgO nanofacets). In our model, the main difference between the two substrates is therefore given by the substantial different values of Veff: ∣Veff∣ ~ t, i.e., is of the order of the in-plane hopping t in case of MgO, playing a significant role in building up the YBCO electronic structure; for the STO substrate, instead, ∣Veff∣ ≪ t.

The model hamiltonian reads

$$H={\sum}_{ij,\sigma }{t}_{ij}{c}_{i,\sigma }^{{\dagger} }{c}_{j,\sigma }+{V}_{{{\rm{eff}}}}{{\sum}_{n}}^{\prime} {\sum }_{iy=1}^{L}{c}_{{{{\bf{R}}}}_{n}+iy{{\bf{b}}}}^{{\dagger} }{c}_{{{{\bf{R}}}}_{n}+iy{{\bf{b}}}}\,.$$
(1)

where, tij includes hopping processes between nearest ( ~ t) and next-nearest (\(\sim t{\prime}\)) neighbors, Veff is the effective potential along the b-oriented strips with length L starting at a random site Rn and the sum over these random sites is denoted by the primed sum. Given the large anisotropy of nanofacets and steps we further set L → ∞ and encode the fraction of regions affected by the nanofacets or steps (the red slabs in Fig. 2) by the parameter f. In Eq. (1)f corresponds therefore to the fraction of sites on which the potential Veff acts, i.e. \(f=1/N{\sum}^{\prime} {\sum }_{iy = 1}^{L}\) where N denotes the total number of sites. In the Supplementary Note 1 we also show that the modulation of the hopping in Eq. (1) can be neglected.

Owing to the random character of the strips and the expected smooth variation of the effective potential on atomic scales, we use a standard CPA (see Supplementary Note 1 for additional details). This allows to compute the self-energy and hence determine the Fermi surface for this disordered system. Figure 3 shows the Fermi surfaces, as obtained from an intensity plot of the momentum dependent spectral function at the Fermi energy, that result upon varying Veff/t while keeping f = 0.15 constant. For small Veff/t = 0.2 the Fermi surface [see Fig. 3(b)] remains unchanged from the unperturbed one [see Fig. 3(a)] and preserves the C4 symmetry. Instead, when Veff/t becomes significant, i.e., of the order as the in-plane hopping t (as in films on MgO), the Fermi surface becomes nematic, i.e., anisotropic and distorted in the regions around the points (0, π) and (π, 0) of the first Brillouin zone [see Fig. 3(c)]. This resembles the Fermi surface inferred in ref. 38 to explain the in-plane transport anisotropy observed in ultrathin YBCO films on MgO [see Fig. 1(a)].

Fig. 3: Fermi surface within the CPA for different values of effective potential Veff/t.
figure 3

a Veff/t = 0; b Veff/t = 0.2; c Veff/t = 1. In all cases, the concentration of one-dimensional strips is f = 0.15, the next-nearest neighbor hopping is \(t{\prime} /t=-0.15\) and the doping is p = 0.12. The red dashed line corresponds to a tight-binding parametrization derived from tb,a = t(1 ± α) and anisotropy parameter α = 0.015.

Full size image

CDW instabilities in the anisotropic effective model

This nematic Fermi surface has strong implications for the symmetry of the resulting charge collective excitations, which can affect the anisotropic transport properties of the films. In the following, we demonstrate that the Fermi surface in Fig. 3c, resulting from the anisotropy imposed by the MgO nanofacets, leads to a unidirectional CDW along the b-axis, consistent with observations in underdoped (p = 0.12) 10 nm thick YBCO films grown on MgO38. To this purpose we adopt the framework of frustrated phase separation, where the charge instability is not driven by nesting properties of the Fermi surface, but merely results from the electron-electron Coulombic repulsion frustrating the phase separation induced by a variety of attractive mechanisms on a strongly correlated electron system41,42,43,44,45.

This theory does not rely on strong coupling between spin and charge degrees of freedom, unlike the stripe phase of 214 cuprates. Hence, it provides an appropriate starting point for describing CDW in YBCO (as well as Bi- and Hg-based cuprates, where the magnitude of the CDW wave vector qCDW decreases with doping). A minimal model for this scenario is given by43,44,45,46

$$H= \mathop{\sum}_{{{\bf{k}}},\sigma }{\varepsilon }_{k}\, {f}_{{{\bf{k}}},\sigma }^{{\dagger} }{f}_{{{\bf{k}}},\sigma }-\frac{g}{\sqrt{N}}{\sum}_{{{\bf{q}}}}({a}_{{{\bf{q}}}}+{a}_{-{{\bf{q}}}}^{{\dagger} }){\rho }_{{{\bf{q}}}}\\ +{\omega }_{0}{\sum}_{{{\bf{q}}}}{a}_{{{\bf{q}}}}^{{\dagger} }{a}_{{{\bf{q}}}}+\frac{1}{2N}{\sum}_{{{\bf{q}}}}[{V}_{{{\rm{coul}}}}({{\bf{q}}})+{V}_{{{\rm{res}}}}({{\bf{q}}})]{\rho }_{{{\bf{q}}}}{\rho }_{-{{\bf{q}}}}$$
(2)

where operators \({f}_{{{\bf{k}}}}^{({\dagger} )}\) annihilate (create) quasiparticles that correspond to the low-energy sector of a strongly correlated (U → ∞) model. The dispersion εk contains the nematicity via a parametrization of the nearest-neighbor hopping tb,a = t(1 ± α) [see Fig. 3c], \({\rho }_{{{\bf{q}}}}={\sum }_{{{\bf{k}}},\sigma }{f}_{{{\bf{k}}}+{{\bf{q}}},\sigma }^{{\dagger} }{f}_{{{\bf{k}}},\sigma }\) is the density operator in momentum space and N denotes the number of lattice sites. The hamiltonian Eq. (2) includes a coupling ( ~ g) to a dispersionless phonon (frequency ω0) which yields an effective attractive interaction between quasiparticles  −λ ≡ −g2/ω0. The latter is counteracted by a long-range Coulomb repulsion Vcoul and a residual repulsion between quasiparticles \({V}_{{{\rm{res}}}}({{\bf{q}}})\) as it customarily occurs in Landau Fermi liquids.

In a Fermi liquid only subject to a constant (in momentum space) attractive interaction Vtot(q) = −λ, a CDW transition occurs when the random-phase-approximation (RPA) condition \(1/{\chi }_{\rho \rho }^{0}({{\bf{q}}})-{V}_{{{\rm{tot}}}}({{\bf{q}}})=0\) is satisfied. Here, \({\chi }_{\rho \rho }^{0}({{\bf{q}}})\) is the charge susceptibility of the non-interacting quasiparticle system. Therefore, this instability occurs at the dominant nesting wave vector, i.e., where the charge susceptibility is maximum (kink in the black curve of Fig. 4). However, in a strongly correlated system, the electron dynamics can be mapped onto an effective low energy hamiltonian43,44,45,46, see Eq. (2), where, according to the Fermi liquid paradigm, the large Hubbard repulsion U among electrons is turned into a residual repulsion between quasiparticles, \({V}_{{{\rm{res}}}}({{\bf{q}}})\) (red curve in Fig. 4), which is maximum at large wave vectors (short distances). Together with an attractive contribution  − λ, the total interaction is minimum (and negative) at small momenta, satisfying the RPA criterion in general at q = 0, corresponding to a phase separation instability. On the other hand, the long-range Coulomb repulsion Vcoul(q) (green curve in Fig. 4) spoils the zero-momentum charge instability, shifting qCDW to finite and in general incommensurate values. In a nematic system, all these contributions, determining the CDW instability, acquire an anisotropic character (analyzed in detail in the Supplementary Note 3). As specified in Eq. (2), we consider an attractive contribution solely due to a momentum independent ‘Holstein-type’ electron-phonon interaction Vph(q) ≡ − λ. This parameter must overcome a critical value (orange dashed arrow in Fig. 4) to trigger the CDW instability.

Fig. 4: CDW instability within the frustrated phase separation scenario (sketch).
figure 4

The effective random-phase-approximation (RPA) expression \(1/{\chi }_{\rho \rho }^{0}(q)-{V}_{{{\rm{tot}}}}(q)=0\) where \({\chi }_{\rho \rho }^{0}(q)\) is the charge susceptibility of the non-interacting quasiparticle system. The total interaction Vtot(q) (blue dashed line) is given by the sum of a long-range Coulomb interaction Vcoul(q) (green line), a residual short-range repulsion between quasiparticles \({V}_{{{\rm{res}}}}(q)\) as customary in Fermi liquid theory (red line), and an attractive interaction \({V}_{{{\rm{attr}}}}(q)\), which for simplicity we suppose momentum independent (\({V}_{{{\rm{attr}}}}=-\lambda\)), providing the vertical shift highlighted by the orange dashed arrow. All these interactions have the symmetry of the electronic system and in the nematic state therefore acquire C2 symmetry as discussed in the Supplementary Note 3 where in Supplementary Fig. S6 we also show an actual plot for a representative doping.

Full size image

Over the whole doping range the nematic Fermi surface leads to an enhanced charge susceptibility \({\chi }_{\rho \rho }^{0}({{\bf{q}}})\) along the b-axis. Three distinct doping regimes can be identified:

- At low doping, due to the effect of strong correlations, the residual repulsion \({V}_{{{\rm{res}}}} \sim 1/p\) dominates the anisotropy of Vtot(q), cf. Supplementary Note 3. Within a standard slave-boson approach46,47, which is also outlined in the Supplementary Note 2, \({V}_{{{\rm{res}}}}({{\bf{q}}})\) is proportional to the quasiparticle kinetic energy. Since the magnitudes of the hoppings along the a- and b-axis are ∣tb∣ > ∣ta∣, the repulsion is stronger along the b-axis, so that this term forces the instability to occur along the a-axis [see Fig. 5(a), and corresponding Fermi surface in Fig. 5(b)].

Fig. 5: Doping dependent orientation of the CDW instability.
figure 5

a Angle (with respect to b-axis) of the CDW wave vector as a function of doping for a Holstein electron-phonon coupling Vph(q) ≡ − λ. The other parameters used in the model, built in the frustrated phase separation scenario, are the following: a/b = 0.98, \(t{\prime} /t=-0.17\), Vcoul/t = 0.5, and the anisotropy parameter α = 0.015. In the three insets, the nematic Fermi surfaces obtained using these parameters are shown as a function of doping, in case b p = 0.08, c p = 0.13 [similar to the one of Fig. 3c] and d p = 0.20. See Supplementary Note 3 for the discussion of the anisotropy of Vcoul(q) and Vres(q) in the nematic system.

Full size image

- Increasing the doping reduces the contribution of \({V}_{{{\rm{res}}}}\) to Vtot, causing the strongly enhanced \({\chi }_{\rho \rho }^{0}({{\bf{q}}})\) along the b-axis, starting at p ≈ 0.12, to rotate qCDW from the a- to the b-axis of the YBCO unit cell [see Fig. 5a]. Notably, the magnitude of qCDW remains constant across the transition, as the minimum of Vtot(q) is only weakly dependent on the orientation of q, cf. Supplementary Note 3. For the considered parameters, the Fermi surface is closed at (π, 0) while remaining open at (0, π) [see Fig. 5c]. Consequently, the CDW modulation maintains its orientation along the b-direction in the doping range 0.12 ≲ p ≲ 0.15. A strong nesting indeed occurs along the b-axis, arising from the small Fermi velocity vkb around (π, 0) and the concomitant enhanced density of states.

- At p ≈ 0.15, the Fermi surface gets closed also at (0, π), while still being nematic [see Fig. 5d]. Upon increasing doping from p = 0.15 to p = 0.20, its topology favors a finite angle between qCDW and the orthorhombic b-axis. Consequently, the instability vector qCDW rotates from the b- back to the a-axis, where it remains for p ≳ 0.20. In this regime, anisotropic interactions again dominate the orientation of qCDW over the reduced nesting along the b-axis.

Three points regarding the validity of these results should be added: (a) We do not consider pinning effects which would turn the continuous rotation of the CDW vector again into an abrupt transition from the b- to a- axis (and vice versa); (b) The model Eq. (2) includes neither magnetism nor the effect of CDW fluctuations45 which suppress the CDW instability at low and large doping, respectively; (c) Our treatment of correlations with U → ∞ might overestimate the anisotropy of Vtot(q), suggesting a larger doping regime for the b-axis oriented CDW for a more realistic repulsive interactions with U/t ≈ 8. These points collectively imply that our model predicts a b-axis oriented unidirectional CDW, consistent with measurements in ref. 38, across the majority of the doping range where experimental evidence of CDW is detected in cuprates (0.08 < p < 0.16).

Conclusions

In summary we have developed a model that accounts for interface effects between HTS thin films and substrate. The nanostructured morphology of the substrate surface creates strong bonds between the films and the substrate, introducing an additional substrate potential that modifies the Fermi surface and induces a CDW instability. The model successfully reproduces the nematic Fermi surface and unidirectional CDW observed in the experiment38. Our finding opens new prospective to tune the ground state of HTS by properly nanopatterning the substrate surface to induce a substrate potential with well-defined symmetries.