Introduction

Alloying is the primary method by which new metals are designed. In most alloys, solute distribution is heterogeneous as individual atoms segregate to different atomic configurations present along grain boundaries (GBs) or other material defects. Although segregation of atomic species often leads to desirable properties, the atomic origins of such segregation behavior are not fully understood. Properties of metal alloys can be significantly changed through alloying and subsequent processing1,2,3. The modern design of metals relies on alloying as a critical aspect of material design to achieve unique, application-specific properties4,5,6. Another key aspect of material design is microstructure. Stabilizing material microstructure is vital for retaining alloy properties7,8,9,10. This is particularly important when considering nanostructured alloys, which are more susceptible to microstructural evolution11,12,13. These effects stem from both solute strengthening and microstructural stabilization13. Highly-processed materials with nanograin structures often have significantly improved mechanical response, but often exhibit microstructural instability13,14.

Microstructural stabilization stems from complex, interface-driven behaviors of segregation energy (Eseg), which are in turn determined by the character of atomic environments at microstructural defects such as interfaces15,16,17,18. Through alloying and control of the subsequent segregation behavior, nanocrystalline (NC) systems can be stabilized, effectively unlocking their potential benefits19,20. To better design advanced alloys and take advantage of unique properties and microstructures obtainable under segregating conditions, improving our understanding of atomic Eseg is critical.

Computational studies of microstructural stability have mainly focused on thermodynamic and solute partitioning effects to guide alloy design21,22,23,24. Microstructural stability is significantly increased under specific thermodynamic conditions, resulting in solute partitioning between the grain and GB regions14,24. While not directly calculating segregation behavior, the alloying effects investigated by previous studies result from localized segregation. Improved properties originating from solute segregation have been demonstrated both computationally and experimentally14,25.

Numerous segregation models have been developed to capture the broad thermodynamics and kinetics of solute segregation in various alloy systems and predict the extent of segregation26,27,28,29,30,31,32,33. While such studies improve our understanding of the global segregation behavior, they lack information regarding the atomic origins of this behavior. Atomistic segregation studies focusing on bicrystalline GB behavior for studying Eseg using molecular force-field based models32,33,34,35,36,37,38,39, which limits the scope of application for resultant findings. Polycrystalline atomic simulations utilizing a combination of Molecular Statics (MS) and Monte-Carlo (MC) techniques can more accurately reproduce experimental segregation behavior in NC alloys, but are computationally expensive and usually limited to small NC samples25,30,40.

Atomic-scale ML models demonstrate the ability for predicting site Eseg in GB bicrystals31,41. The accuracy of input Eseg data calculated from interatomic potentials has been indicated to be within expected error compared to a DFT reference42. These models indicate that simple scalar atomic descriptors such as excess volume, coordination number, and Voronoi polyhedra parameters are insufficient for achieving appropriate accuracy. Improved accuracy can be achieved through the use of more complex atomic descriptors such as the Steinhardt order parameters43. Further improvements can be made by implementing more advanced local atomic descriptors such as the smooth overlap of atomic positions (SOAP)44,45. Although the use of the SOAP features improves prediction accuracy, it requires a large number of descriptors to attain such accuracy. Other studies utilize larger active-learning approaches, where the per-atom descriptors are often physically undefined31,32,33. When implementing a dimensionally-reduced ML model, the atomic accuracy is likewise hampered, eliminating many of the gains realized by utilization of a more advanced descriptor set.

Here, we study the complex relationships between disordered atomic environments within GBs and their segregation energies in the dilute limit. The focus of this study is on the P-doping of Ni (Ni-P), chosen since it has been the subject of previous works regarding segregation behavior25,41. Furthermore, the agreement between computational and experimental results by Gupta et al.25 indicates that the NiP potential is applicable for a wide range of NiP simulations. To accurately quantify the link between local atomic environments and their properties, a set of 24 rotationally-invariant higher-order atomic descriptors (known as the Strain Functional Descriptors (SFDs)46) are combined with modern ML methods. The resultant model allows for rapid calculation of preferential atomic sites for segregation, enabling much larger structures to be appropriately populated with segregates, rather than the current best approach of a computationally expensive random sampling of sites through methods such as MC. Such alloyed structures can be further utilized in studies investigating the fundamental mechanisms of alloy strengthening due to solute segregation, without the significant computational cost of generating the initial alloyed microstructure.

The SFDs improve upon prior higher-order descriptors due to their tuning to key characteristics of local atomic environments, which allows for classification with a minimal number of parameters and eliminates the need for post-processing the descriptors through dimensionality-reduction techniques. This isolation of individual local atomic characteristics in the SFD fingerprint helps elucidate the complex relationship between local atomic structure and segregation potential since each SFD feature isolates a single aspect of the local atomic environment. Model feature analysis is used to indicate these key structural elements, identifying critical aspects of the atomic ’fingerprint’ governing segregation behavior.

Results presented here are demonstrated to be relevant across multiple grain sizes at the nanoscale, indicating their ability to identify the fundamental structural elements driving changes in atomic Eseg. Extending beyond the dilute limit (thus enabling the full-scale implementation of this approach for creating more accurate atomic structures with the desired solute concentration) must await further developments to accurately capture behavioral changes when considering solute-solute interactions, a challenge shared by similar studies which predict Eseg values. The problem of addressing solute behavior beyond the dilute limit has been initially analyzed in regards to GB spectra47, but detailed analysis of the evolution of such spectra and energies from an atomic perspective remains yet unrealized.

Results and Discussion

Atomic segregation energies for Ni-P systems comprised of symmetric tilt grain boundaries (STGBs), bulk amorphous metal, and GBs taken from a 6nm average grain size polycrystal were compared to determine the most appropriate training data for developing transferable predictions of Eseg. From ML models developed with each of these three datasets, performance is evaluated for predicting Eseg behavior for NC structures at larger grain sizes, demonstrating the applicability of the models used for accelerated computation. ML model behaviors are then analyzed using SHapley Additive exPlanations (SHAP) values48,49 to identify critical structure-property relationships used by the models.

Overview of Strain Functional Descriptors (SFDs)

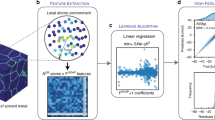
Efficient prediction of segregation behavior necessitates using only a-priori structural information. Relying only on the existing arrangement of atoms in the system provides orders of magnitude faster computation than MS simulations since computationally-expensive energetic relaxation steps and evaluation of acceptance criterion are bypassed. By utilizing the SFD framework to create a detailed fingerprint for each atom, a maximal amount of information regarding the local atomic environment can be encoded with a minimal number of features necessary for identifying key structure-property relationships (Fig. 1).

Fig. 1: Schematic of atomic Structure-Property Relationships enabled by SFDs.
figure 1

Outlining structure-property linkage process with SFD feature calculation and ML prediction for individual atomic sites. Atoms colored by a Common Neighbor Analysis (CNA)56, b Gaussian overlap function, and c Eseg. Large groups of green (FCC) points in CNA visualization are considered Grain regions. Gaussian overlap visualization is created using the Gaussian Kernel Surface method and rendered by Mayavi82.

Full size image

To calculate the set of SFDs for each atomic environment, the Gaussian-overlap approximation method45 was utilized to describe the local environment of each atom as an overlap of 3-D Gaussian fields with each of its neighboring atoms (Fig. 1b). From this atomic overlap, a set of spatial tensors are created to describe the density field which makes up the local environment. These tensors are subsequently decomposed into rotational and rotationally-invariant polynomial components. The orthogonality of each underlying polynomial function is verified for the relevant spherical-harmonic decomposition, such that each tensor environment can be described in the fewest possible number of polynomial functions (see section III C for further details)46. When applied to a specific local Gaussian environment from a single atom, each polynomial function results in a single value which indicates the degree of specific spatial character for that environment.

The number of SFDs is naturally constrained by the order ℓ of the spherical harnomics used in each order of the expansion, where this can be achieved with 2ℓ + 1 terms. Identifying these terms to create an appropriate minimally-spanning set is a mathematical challenge, but this ensures that the structural features each SFD element captures are unique.

ML models using the SFDs of each atomic environment as input features are developed and subsequently analyzed using advanced analysis techniques for explaining model behavior. This enables complex structural relationships underlying atomic segregation behavior to be readily interpreted. Model interpretability combined with isolation of unique atomic features by the SFD fingerprint enables the relationships between specific atomic characteristics and segregation behavior. This improvement in the interpretability of predictive atomic behavior models is critical for furthering our understanding of underlying atomic behaviors beyond accurate predictions.

Training data analysis

When developing ML models, choice of training data is crucial for determining the proper underlying relationships between the input (SFD fingerprint), and output (Eseg). By investigating a variety of datasets independently, the most efficient and accurate method for developing a ML model for a new segregation system can be determined. The differences in accuracy between the models can then be evaluated relative to the expense of generating appropriate training data. Here, optimized gradient boosted machine (GBM) models were developed from Eseg data calculated on three different training sets: (1) a set of 36 STGBs (STGB model (Fig. 2a)), (2) an amorphous cube (Amorphous model (Fig. 2b)), and (3) GB atoms from a polycrystal with 6nm average grain size (6nm model (Fig. 2c)). These datasets were chosen to span a range of atomic structural order when considering non-crystalline environments present within FCC metallic systems.

Fig. 2: ML Model Evaluation.
figure 2

ML test accuracy fits predicting Eseg using a STGB b Amorphous c 6nm Polycrystal data. Individual data points are indicated by single plot points, areas with higher point density are indicated by combined kernel density estimate and frequency histogram. Coefficient of determination (R2) indicated compared to perfect predictions (x=y). Root mean squared error (RMSE) is indicated in units of eV/atom. Number of samples (atomic environments) in testing set are indicated.

Full size image

Comparing these three models, the STGB model has the highest Coefficient of determination (R2), initially indicating that the model provides the best fit of the atomic sites within the training data to their Eseg. In other words, the SFD fingerprint provides enough distinction between atomic environments to uniquely identify each atomic site present in the dataset, given the high R2 of the STGB model. Due to the very specific GB relationship of STGBs, the number of unique atomic sites is limited and does not form a continuous set in the SFD feature space - an aspect that will be discussed in more detail in sections II C and II F.

The Amorphous model dataset has significant outliers, indicating that some of the atomic environments within the amorphous system do not follow the predicted pattern regarding their Eseg as a function of the SFD fingerprint. This leads to a lower R2 value for this model, though the root mean squared error (RMSE) still compares favorably to previously published results41,44. Outliers in the model prediction are likely due to highly-disordered atomic environments where the structural (and thus energetic) changes initiated by single-atom segregation swaps extend significantly beyond the local atomic environment.

Finally, the 6nm model appears to have accurately reproduced the Eseg of each site with minimal variation, as no significant outliers are present in the dataset. This leads to both high R2 and low RMSE values. The 6nm polycrystalline dataset has both a continuous distribution of segregation energies and eliminates significant outliers that are present in the bulk amorphous region.

For comparison, SOAP parameters were calculated for the 6nm polycrystalline dataset using the same parameters as Wagih and Schuh44,45,50,51. This dataset has 1015 input features, compared to only 24 for the SFDs. This increase in input dimensionality greatly increases the computational cost of training, as noted by Wagih and Schuh44 in the development of their dimensionally-reduced model. Despite the larger number of input parameters, this model achieved an RMSE of 0.0567eV, compared to 0.0273eV for the SFD-based model (Supplementary Fig. 1). This highlights the advantage of the SFDs being a minimally-spanning and complete descriptor set52, which likewise translates into greater model interpretability due to the reduced input dimensionality.

An advantage of GBM-type models is their ability for interpretability through feature analysis of the final model. Recent methods such as the SHAP approach focus on aggregating the effects of individual data points to explain tree-based model behavior48,49. Such analysis methods provide a more detailed picture of the decisions and relationships being interpreted by the model. Each input data point is evaluated independently to determine the degree to which each feature in the input vector (atomic fingerprint) increases or decreases the final output value. This allows for further analysis and comparison between models since the effect of input features on the final model performance can be evaluated in more detail than simply ranking their final effect on total model behavior.

Across the ML models, P0_I0, P2_I2, and P4_I8 are generally among the most important features used for predicting Eseg. These features are all related as the purely radial descriptors of the SFD set, while the majority of other features describe non-radial or rotational aspects of the geometry. Due to this radial nature, the polynomial expansion of these features in Cartesian space is fairly straightforward (see Section II G for the functional forms). P0_I0 is 0th order radial node, which here is the total spherical Gaussian weight of the neighboring atoms. P2_I2 is derived from the 2nd order radial node, which here is a spherical Gaussian weighted by radial distance to the 2nd power (r2). P4_I8 is derived from the 4th order radial node, which here is a spherical Gaussian weighted by radial distance to the 4th power (r4). They capture different aspects of the radial distribution of atoms in each neighborhood.

In this analysis, the atomic fingerprint input features are most similar between the 6nm and Amorphous models, with less similarity to the STGB model (Fig. 3). For the STGB model, there is a disparate distribution of SHAP values for each feature. The majority of data points have a singular SHAP value, with the remaining SHAP values distributed evenly over the total range. This indicates that the output Eseg is most often adjusted by a constant, rather than properly correlated with the relevant feature input. From this interaction, the STGB model appears to be fitting directly to the Eseg of specific sites, rather than extracting the fundamental relationships between site character and Eseg. This site-specific fitting is likewise supported by the significant number of data points that have high SHAP values for features outside of the top six features.

Fig. 3: ML Model Feature Importances.
figure 3

Top six feature SHAP impacts for each ML model a STGB, b Amorphous, and c 6nm sorted by mean absolute SHAP value. The SHAP value of each point indicates the effect of the indicated feature on the final model prediction for that atom48. When correlated with changes in the feature value across the model, this indicates the effect of changes in the feature value on the output value (Eseg). X-axis indicates the SHAP value for each point, Y-axis indicates which SFD feature is being considered, and coloring indicates the relevant feature value. Y-axis deviation along each feature row indicates areas of higher and lower density for the corresponding feature and SHAP value.

Full size image

In the Amorphous and 6nm models, SHAP values for a given feature are more continuously distributed, indicating a smoother transition between the identified behaviors of segregating and anti-segregating sites. Additionally, the majority of predictive variance is extracted from fewer features in both the Amorphous and 6nm models. With the Amorphous model, however, there are still several outliers with high magnitude SHAP values where the model has tried to adjust to the outlying atomic environments which do not necessarily represent the bulk trend in behavior.

Critically, with the continuous distribution and low variance of SHAP values beyond the first four features coupled with the high degree of accuracy determined by the training data comparison, the 6nm model appears to be accurately uncovering fundamental relationships between the atomic SFD fingerprint and resultant Eseg. This is vital for using ML relationships to identify physical structure-property relationships.

Since the SHAP values indicate the direction of change caused by each feature and not just the magnitude, the relationship of individual features to the resultant Eseg is directly determined. For the 6nm model, P4_I8 and P2_I2 both have a positive correlation with Eseg, while the P3_I0 has a primarily negative correlation. The primary features selected by the Amorphous and 6nm models of the P4_I8 and P2_I2 features are SFD measures of the radial density of the atomic environments (in 4th and 2nd respectively), while the P3_I0 measures the net 3rd order distortion (strain gradient). This determination of the radial behavior and further details on the nature of various SFD functions is discussed in more detail in the interpretability section. Key findings from leveraging the SHAP analysis include:

  • 6nm Model most accurately predicts Eseg

  • P4_I8 and P2_I2 positively correlate with Eseg

  • P0_I0 negatively correlates with Eseg

Application to Larger Structures

The creation and analysis of a ML model in isolation is only of limited value since without further application the model is of little practical use. The primary use of ML models predicting Eseg is to enable calculation of larger atomic systems which are otherwise computationally expensive with traditional MS techniques. To this end, each of the models developed was tested on a set of new polycrystalline samples of varying grain size from 6 to 16nm with a new random distribution of texture so as not to bias towards a possible texture-dependent Eseg relationship that would potentially skew results from the 6nm model53. These grain sizes represent the majority of GB character studied by molecular dynamics techniques where such models are the most applicable. For evaluation of model performance, Eseg of all relevant GB sites was calculated with MS for these larger-grain structures. In both the MS simulation and ML predicted configurations, all polycrystals maintained a consistent distribution of segregation energies over the GB sites (Supplementary Fig. 2).

Evaluating the ML models on a common polycrystalline dataset allows for evaluation of model performance if they were to be used to evaluate Eseg of new structures. Comparing the performance of each model on the 10 nm polycrystal data, the 6 nm model is the most accurate, followed by the Amorphous and STGB models. Although R2 correlation values only improve moderately between the Amorphous and 6 nm models, the RMSE is nearly halved indicating a significantly improved model performance (Fig. 4). This provides confidence that the 6 nm model is most appropriate for predicting the Eseg behaviors of unknown polycrystalline systems (and thus captures the underlying structure-property relationships most appropriately), which is consistent with the previous analysis of each model.

Fig. 4: ML Model Prediction Accuracy.
figure 4

Predictive fit of the three ML models a STGB, b Amorphous, and c 6 nm on unseen 10 nm polycrystal GB sites compared to Eseg calculated by MS. Individual data points are indicated by single plot points, areas with higher point density are indicated by combined kernel density estimate and frequency histogram.

Full size image

Investigating the changes in predictive accuracy over the range of grain sizes demonstrates the limits of the three ML models. Across all grain sizes tested, the 6nm model consistently resulted in the highest R2 accuracy (Fig. 5). For each model, accuracy did not decrease with increasing grain size but stayed consistent throughout the range tested. This consistency in predictive power across grain sizes for each model indicates that the fundamental SFD atomic features relating to segregation energy are not changing with grain size.

Fig. 5: ML Model Accuracy.
figure 5

R2 accuracy for each of the 3 tested ML models (STGB, Amorphous, and 6nm), on completely unseen polycrystalline samples with grain sizes in 2 nm increments from 6 nm to 16 nm.

Full size image

It does not appear that any suspected changes in GB character with increasing grain size significantly influence the Eseg distributions of the GBs in these polycrystalline systems (Fig. 5). Thus, the atomic characteristics which govern Eseg are consistent throughout the grain sizes investigated in this study. Despite this consistency at the per-site level, significant variability in Eseg between discrete boundaries in the polycrystal or localized variation within a single GB can still be expected and is known to occur both computationally and experimentally25. How grain size effects may be related to these GB-level differences has not been investigated in detail. Likewise, such variability in GB-level Eseg behavior likely plays an important role in determining segregation behavior beyond the dilute limit. Fully addressing this level of detail with regards to independent atomic motion driving continuous segregation from the bulk to the GB region awaits advances in computation and/or simulation procedure which will allow for more rapid determination of a complete segregation spectrum including dilute and non-dilute effects.

Computational efficiency is greatly increased utilizing the SFDs and ML approach, with per-atom computation times improved by over 150,000× (compared to the traditional MS approach) for systems with grain sizes over 10 nm (Supplementary Table 1). This drastic decrease of computational cost is critical, as these grain sizes encompass polycrystalline behavior where the largest variation in GB character would be expected to occur, given the large changes in GB curvature and energy required for even moderate change in overall grain size. By first training on a smaller dataset of atomic environments which encompass the appropriate variation typically found in a polycrystalline sample, the ML model allows for an increase in computational efficiency by avoiding both MC random sampling and MS energetic minimization steps, vastly improving scaling efficiency to larger systems.

Visualization

Although the Gaussian neighborhood utilized by the SFDs has been well-defined previously45,54,55, the connection to individual SFD functions can be difficult to visualize. To address this challenge and illustrate the differences in segregating and anti-segregating atomic sites, surfaces representing the local atomic Gaussian density surrounding the central atom are illustrated for different sites from the 6 nm Ni polycrystal (Fig. 6). These surface representations were generated by first using a sphere around the central atom with a size scaled to the total local atomic density (P0_I0). The sphere is subsequently distorted by each Gaussian overlap vector generated to neighboring atoms, scaled by the corresponding Gaussian weighting and using a spherical Gaussian decay relative to the central atom (Gaussian Kernel Surface method, Supplementary Section 1). This visualization provides a qualitative method to compare distinct atomic environments and visualize SFD numerical features in complex local arrangements such as those found in a GB.

Fig. 6: Visualization of SFD featurization of Atomic Environments Exhibiting Segregation.
figure 6

Illustration of atomic shapes generated with Gaussian Kernel Surface method for representative a minimum, b equilibrium FCC, and c maximum Eseg sites of the 6nm Ni polycrystal with values for the two most relevant SFD features indicated. Coloring indicates relative intensity of Gaussian overlap, with each figure colored and scaled to the same reference. Plots of Gaussian Kernel Surface rendered using Mayavi82.

Full size image

Local atomic features

To visualize the relationships between the key identified SFD elements and Eseg behavior, minimum Eseg (segregating), equilibrium FCC, and maximum Eseg (anti-segregating) environments are compared using this Gaussian surface representation (Fig. 6). Since these shapes represent local Gaussian density, it is important to remember that a larger structure visually represents a more compacted atomic core spatially.

Qualitatively comparing the equilibrium FCC structure to the minimum and maximum Eseg environments, the maximum Eseg structure appears closest to FCC (Fig. 6). However, relative neighbor contributions are significantly decreased, as noted by the lack of clear ’peaks’ on the surface. In the highly segregating minimum Eseg case, there several neighbors closer to the central atom as indicated by the large peak intensity, with only a marginal increase in total local atomic density (P0_I0). This indicates that the first nearest neighboring atoms are quite close to the central atom (Fig. 6b). For the FCC environment, natural slip-planes created by the triangular faces between neighbors on parallel 111 planes are readily identified on the top and front face of the image (Fig. 6b). Likewise, the 12 nearest neighbors are readily apparent in the surface representation due to the Gaussian distance scaling and their primary contribution to the local neighborhood.

Quantitatively, P0_I0 decreases from minimum to equilibrium to maximum, following what we would intuit for the base ’size’ of the environment (0th order ’radius’, r). Compared to equilibrium conditions, both minimum and maximum atomic environments increase P2_I2 magnitude, indicating that they both have increased radial distortion compared to FCC where all of the nearest neighbors are the same distance (2nd order r2 measure). Identified as the most important feature for determining Eseg (Fig. 3), P4_I8 is decreased in the minimum environment and increased in the maximum environment, and indicates the sharpness of variation in local Gaussian density (4th order r4 kurtosis measure). In the maximum energy case, variation between high and low density is relatively small compared to that of the minimum energy case, with the equilibrium lying somewhere in the middle (Fig. 6).

In terms of the local atomic environment, changes in various functions of the radial density can be summarized to indicate that Eseg is minimized in a compact environment, and maximized for a more expanded environment. By isolating various components of this variation in local density through the SFD atomic fingerprint, feature analysis indicates that localization (P4_I8) and radial distortion (P2_I2) of the local Gaussian environment outweigh the environment density (P0_I0) when determining Eseg (Fig. 6).

Fingerprint Feature Relationships

Since P4_I8 and P2_I2 have been identified as the most important local features for determining Eseg, direct comparisons between datasets can be more easily made by isolating these specific elements from the high-dimensionality atomic fingerprint composed of the entire SFD descriptor set. Conveniently, identification of precisely two atomic features from the 6nm model as carrying the majority of variation in Eseg allows for simple 2-D plots for comparison between datasets (Fig. 7).

Fig. 7: Distribution of Atomic Environments Across SFD Features.
figure 7

Distribution of atomic GB site character in P4_I8 and P2_I2 for the three training data sets; 6 nm Phase Field generated polycrystal, Amorphous, and STGBs. Density regions are indicated for every 10% of the relevant dataset.

Full size image

Comparing the three datasets used for training data (6nm Polycrystal, Amorphous, and STGB), key differences in their distributions of atomic environments support the differences already identified in the ML model analysis. The STGB dataset has a larger range in both relevant axes, but the occupation of atomic sites is not continuous over the two-dimensional space (Fig. 7). Instead, there are isolated ’islands’ of specific atomic character with few atomic environments spanning the space between these highly occupied areas. Furthermore, the highest density location in the STGB dataset is close to the equilibrium FCC conditions, indicating that a large portion of atoms in that dataset are similar to an FCC occupancy. This is partially due to more FCC-like atoms near the GB being selected as part of the STGB region and illustrates the challenges with a binary selection of GB regions such as through Common Neighbor Analysis56. These characteristics of the STGB dataset define the ML results discussed earlier, where the STGB model can accurately predict Eseg values within the testing data but is significantly less accurate when determining the energies of atomic sites within polycrystals (Figs. 4a, 5).

In comparison to the STGB dataset, the Amorphous and 6 nm Phase-Field datasets are more continuous in their distribution across the P2_I2-P4_I8 space (Fig. 7). Both of these distributions have a single maximum-density area from which the density of atomic environments decreases towards the maximum range of the distribution. This continuous nature of the distributions enables the most relevant atomic fingerprint features to be more easily discovered by the model. Instead of fitting primarily to the Eseg of select environments which are largely distinct from each other as in the STGB dataset, the Amorphous and 6 nm models can identify the continuous distribution of potential atomic sites as given by each of these datasets. Thus, the Eseg function identified by the Amorphous and 6nm models has a more continuous distribution based on the underlying distribution of atomic fingerprints, which more directly relates to the underlying physical phenomenon that determine the atomic Eseg landscape.

Comparing the Amorphous and 6 nm datasets, while both distributions have similar shapes, the Amorphous distribution has a smaller range (Fig. 7). This is a primary factor contributing to the decreased accuracy of the Amorphous model when predicting Eseg for polycrystalline GB environments. Although this decreased extent of the Amorphous distribution may be initially perplexing since the amorphous bulk is generally considered to be more ’disordered’ than GB environments, we note that the comparison is focused on P2_I2 and P4_I8. Since P2_I2 and P4_I8 are radial density functions, they do not fully capture all characteristics of atomic disorder which may be more significant in an amorphous structure than that of a polycrystal. In addition, the maximum density region of the Amorphous distribution is shifted slightly towards an FCC character compared to that of the 6 nm dataset. This indicates that the structural relaxation allowed in the amorphous bulk causes the local atomic environments to minimize their energy by making their local radial density of neighbor atoms as similar to FCC as possible. In the 6nm polycrystal, however, local structural re-arrangements are more restricted, leading to a slight increase in radial distortion. Although such re-arrangements of an atomic environment may be less energetically favorable individually, they enable nearby atoms to occupy a more favorable energetic state, causing the energy of the entire system to be decreased.

Radial feature analysis

In the feature analysis of the ML models, the P0_I0, P2_I2, and P4_I8 features stood out with significantly higher SHAP values, indicating their higher importance in determining Eseg behavior (Fig. 3). These features are determined as radial density components of local atomic environments in 0th, 2nd, and 4th orders, respectively. By establishing their importance in dictating the segregation behavior, the feature impact analysis reveals a well-established feature of metallic systems that stems from their delocalized bonding character. This is the reason why the embedded atom method (EAM) potential forms of these systems are still widely accepted today, despite the lack of angular dependence in the EAM formulation. If a system best described by a potential form that included more significant angular behavior (and thus a system which intrinsically has important atomic radial components) was analyzed, other SFD elements of the atomic fingerprint would be expected to have higher importance when predicting trends in that system.

The complete functional form of P0_I0 is indicated by equation (1), as a simple Gaussian radial density function.

$${{{\rm{P}}}}0\_{{{\rm{I}}}}0(i)={(\sqrt{2\pi }\sigma )}^{-3} {\sum}_{j\ne i}\exp \left(-\frac{{r}_{ij}^{2}}{2{\sigma }^{2}}\right)$$
(1)

In all equations (1) through (4), rij is the distance between atoms i and j, and σ is the Gaussian width, which is determined such that the corresponding 3-D Gaussian volume is equal to the volume of a primitive unit cell of the reference crystal structure. P2_I2 and P4_I8 are outlined in equations (2) and (3) respectively, where constants A, B, and C are constructed to ensure orthogonality between the terms by removing the contributions of lower-order radial nodes in each term.

$${{{\rm{P}}}}2\_{{{\rm{I}}}}2(i)={(\sqrt{2\pi }\sigma )}^{-3} {\sum}_{j\ne i}\sqrt{\frac{2}{3}}\left(\frac{{r}_{ij}^{2}}{2{\sigma }^{2}}-\frac{3}{2}\right)\exp \left(-\frac{{r}_{ij}^{2}}{2{\sigma }^{2}}\right)/{{{\rm{P}}}}0\_{{{\rm{I}}}}0(i)$$
(2)
$${{{\rm{P}}}}4\_{{{\rm{I}}}}8(i)={(\sqrt{2\pi }\sigma )}^{-3} {\sum}_{j\ne i}\sqrt{\frac{2}{15}}\left(\frac{{r}_{ij}^{4}}{2{\sigma }^{4}}-5\frac{{r}_{ij}^{2}}{2{\sigma }^{2}}+\frac{15}{4}\right)\exp \left(-\frac{{r}_{ij}^{2}}{2{\sigma }^{2}}\right)/{{{\rm{P}}}}0\_{{{\rm{I}}}}0(i)$$
(3)

The polynomial forms of P2_I2 and P4_I8 are defined to provide orthogonality between the original r2 and r4 forms and P0_I0. In general terms, such functions would define the mean, variance, and kurtosis of a distribution. However, given the limited number of points (neighbor atoms) in these functions as applied to atomic environments, the quantities can’t be readily interpreted in such a manner. However, they do capture distinct aspects of the Gaussian-weighted radial distribution.

Given these terms, it is not surprising that radial density is primarily identified to be an important factor in predicting Eseg. This can at least partially be explained by looking at the functional form of the EAM and EAM-FS potentials utilized to calculate the Eseg data on which the models were trained (4).

$${E}_{i}={F}_{\alpha }\left({\sum}_{j\ne i}{\rho }_{\alpha \beta }({r}_{ij})\right)+\frac{1}{2} {\sum}_{j\ne i}{\phi }_{\alpha \beta }({r}_{ij})$$
(4)

The functional form of both the EAM and EAM-FS models is purely radial, as indicated by equation (4), originally proposed by Daw and Baskes57, with modification by Finnis-Sinclair58. In summary, the most important SFD features selected by the ML models have purely radial dependence. This is consistent with the underlying computation of Eseg based on an EAM potential, which also considers purely radial terms. Since EAM potentials have been widely shown to accurately reproduce atomic energies in a large number of metallic systems, we can be confident that this relationship is representative of the underlying physics. If a system in which non-radial features dominated the energetic landscape was investigated, non-radial SFD features would be expected to have a primary contribution. This ability of the SFD and ML analysis to identify the critical elements of atomic structure is a significant advantage of this approach over previous methods.

Non-radial feature analysis

While the primary features of the 6 nm model are largely radial, one non-radial feature (P3_I0, which measures the net third order distortion, i.e., strain gradient) has a small but non-negligible impact on the model prediction. To investigate the nature of this relationship in the 6 nm model further, a joint effect of two input features can be compared to the SHAP value across the input dataset (Fig. 8). Investigating this joint effect with the feature with the highest overall SHAP values (P4_I8), we observe that the relative impact of P3_I0 increases as the value of P4_I8 increases. This effect serves to increase the Eseg when P3_I0 is low, and decrease the Eseg when P3_I0 is high (Fig. 8). Therefore, the degree of tetrahedral distortion serves to tune the model performance primarily at lower atomic densities (Fig. 6), decreasing the Eseg when there is large trigonal distortion and increasing the Eseg when distortion is small.

Fig. 8: Joint Behavior Predictions.
figure 8

Change in SHAP value for P3_I0 based on feature value, with joint effect of variation in P4_I8 indicated by color.

Full size image

This Eseg dependence on non-radial components for an EAM-based potential calculation demonstrates the power of using advanced structural descriptors for mapping complex atomic properties. Although the EAM function does not directly model the effects of non-radial behaviors for a single atom, the combined effect of multi-body system behaviors over a complex energy landscape leads to effects from non-radial features of the local atomic environment. Such features are readily captured by higher-order descriptor sets, among which the SFDs are uniquely capable of deconstructing the contributions from distinct aspects of complex atomic arrangements. For non-radial contributions to Eseg, the key elements are:

  • P3_I0 measures net 3rd-order distortion

  • High P3_I0 impact when P4_I8 is large

  • Low P3_I0 impact when P4_I8 is small

  • P3_I0 negatively correlates with Eseg

It should be noted that the total SFD atomic fingerprint utilized in this work has a majority of non-radial angular terms which are utilized to uncover these more complex atomic trends. Such non-radial components are expected to be of increased importance when determining atomic behaviors in other systems where angular dependence plays a larger role in atomic behavior, such as systems with a higher degree of non-metallic or directional bonding (such as systems best described by other (angular dependent) potential formulations such as modified embedded atom method (MEAM) or Tersoff).

Implementation of the SFD atomic fingerprint coupled with the ML models investigated here illustrates this approach’s capability for uncovering complex atomic interactions. By isolating purely radial terms from terms with angular dependence, the SFD fingerprint allows a ML model to appropriately identify metallic systems as having a majority of radial behavior, with only small contributions from angular configurations. This isolation of local atomic features is particularly useful for model interpretability, enabling key relationships to be uncovered.

Methods

Simulations

Polycrystalline microstructures were initialized through a phase-field to atomic structure generation method developed by Gruber et al59. This method results in more physically-representative microstructures which have improved grain, interface, and triple junction structure, resulting in more accurate deformation behavior. In this method, the microstructural information taken from the phase-field model is then given a random texture and grain regions populated accordingly. Polycrystals used in this study were initialized with around 40 grains, resulting in around 250 unique GBs, to sample a larger degree of GB texture. Once the initial system is populated with atoms, the polycrystalline structures are thermally equilibrated to ensure that they are in an appropriate metastable equilibrium. This process is done by a recently developed method utilizing a two-step equilibration methodology from Gupta et al.60, which identifies and isolates the GB and near-GB regions from the inter-grain atoms. This methodology was shown to expedite the equilibration process without eliminating the selected grain topology while resulting in GB structures and associated properties comparable to structures equilibrated through traditional techniques, but with a significant reduction in required simulation time53,59.

Atomic site Eseg in each polycrystalline system was calculated by setting a single solute atom inside an FCC grain and subsequently swapping that solute atom to each GB site, taking the difference in energy of the structures after minimization as the Eseg(5), (Fig. 9). All MS calculations were performed using LAMMPS61,62. GB regions were identified by selecting non-FCC regions as identified by a common neighbor analysis algorithm60. An EAM potential from Sheng was used to represent the Ni-P behavior63. For the 12 nm, 14 nm, and 16 nm average grain size systems, a randomized set of 100,000 GB atoms were selected to minimize the computational time required for testing all the GB atoms present in these systems.

Fig. 9: Schematic of Eseg Calculation.
figure 9

Illustration of the computational approach for calculating Eseg. a Atomic view of 6nm average grain size polycrystal. GB atoms for which Eseg are calculated shown in red, P atom is blue, with transparent gray atoms indicating FCC grain containing P atom. Swaps occur for every GB atomic site as illustrated by green arrows, with close-up images c–e of detailed GB structure colored by the resultant Eseg. Rendered in OVITO56. b Site potential energy vs Eseg for 6 nm grain size Ni polycrystal obtained from atomistic simulation. Linear regression fit indicated by dashed lines, along with respective R2 value.

Full size image

In the Ni-P system, site energy is well-correlated with segregation energy (Fig. 9). However, this correlation alone is a similar strength to the STGB model and alone is not a sufficient descriptor. This further highlights the significant limitations when training only on STGB data for fully describing polycrystalline GB environments. To verify that this procedure applies to a range of segregation systems and is not limited to the Ni-P system and demonstrate the capability of the SFDs for prediction when site energy has a worse correlation with the segregation energy, six previously studied Al-alloy systems were studied with 6 nm polycrystals generated by the same method. ML models developed for these systems showed similar accuracy to the results presented here, even for systems where the site energy has a significantly worse correlation with segregation energy than Ni-P (Supplementary Figs. 3, and 4).

The amorphous structure utilized a 12 × 12 × 12 nm simulation cube with 1,000,000 atoms which was homogenized at 1.8Tm before applying conjugate-gradient energy minimization to generate a single-species amorphous metallic region. The set of 36 STGBs used were generated from 〈100〉 and 〈110〉 tilt-axis symmetric boundaries64.

Eseg in the STGB and Amorphous systems was calculated by directly changing the atom type at each reference site. This is necessary since no appropriate equilibrium FCC segregation sites are present in these simulations. Since this procedure changes the atomic makeup of the system, the difference in equilibrium energy between the solute and solvent must be taken into account by calculating reference energy values for single Ni and P atoms in perfect Ni FCC lattices. This is illustrated in Equation (5), where ΔE is the total change in system energy, ΔNP is the change in the number of P atoms, ΔNNi is the change in the number of Ni atoms, and \({E}_{Ni}^{P}\) and \({E}_{Ni}^{Ni}\) are the equilibrium energies of a P and a Ni atom in an equilibrium FCC lattice, respectively.

$${E}_{seg}^{i}={{\Delta }}E+{{\Delta }}{N}^{P}{E}_{Ni}^{P}+{{\Delta }}{N}^{Ni}{E}_{Ni}^{Ni}$$
(5)

Similar formulations for calculating Eseg of individual atomic sites within a bulk system have been described by many previous authors studying segregation behavior16,25,27,35.

Machine learning

ML models were trained using the XGBoost GBM architecture using a 5-fold cross-validation scheme65. All model implementation and data analysis were completed with the use of python packages numpy, pandas, matplotlib, and scipy66,67,68,69. Hyperparameters for the number of trees and maximum search depth were investigated, with default parameters from the XGBoost library found to provide accurate results (Supplementary Figs. 5, 6). Tested models were seen to be relatively robust at avoiding overfitting. When comparing the STGB, Amorphous, and 6 nm models, a linear offset term was utilized to find the best-fit line comparing the true and predicted values. This was done to account for the difference in segregation potential intrinsic to each of these calculation methods. The values were not scaled, however, keeping a slope of unity for all fit comparisons to ensure that the predicted and true distributions were not modified in shape, but only shifted in value where the shift represents the change in chemical potential between calculation methods.

SOAP parameters were calculated using QUIP and the quippy python interface50,51. A cutoff of 6Åwas used, along with 12 radial basis functions (nmax), a maximum spherical harmonic degree (lmax) of 12, and a gaussian width (σat) of 1 Å, which results in 1015 SOAP features.

Utilizing these ML models for calculating Eseg provides significant speed-up for calculating atomic Eseg behavior of subsequent systems. As a reference, calculating initial Eseg training data on the 6nm polycrystal GBs took 520 core-hours while calculating SFDs and predicting Eseg of the entire 6nm polycrystal took 0.70 core-minutes. With larger systems, the efficiency improves further, with 9000 core-hours taken for the 10nm GBs and only 3.46 core-minutes for the SFDs and ML prediction (Supplementary Table 1). SHAP values used for analysis and model interpretation were calculated using the relevant TreeExplainer functions from Lundberg and Lee48,49. Each model was evaluated with the entire dataset utilized for train/test splits.

Strain functional descriptors (SFDs)

To devise a unique descriptor of local atom environments, techniques were adapted from many different areas of atomic physics, chemistry, computer science, and computational materials science46. The first step in describing a local atomic environment is first to identify the characteristics of local atomic neighborhoods which can then be translated into discrete descriptors of that environment. For the SFDs, the atomic mathematical framework is based on a Gaussian overlap method developed initially by Bartok et al., where each atomic neighbor is represented by a vector pointing from the central atom of interest with a length scaled by a Gaussian function of the distance between the two atoms45,55,70. Here, we define the 3-D Gaussian with a σ such that the volume for a single Gaussian is equal to the atomic space-filling volume in the reference crystalline structure at its energetic minimum. Each atom each atom around the central atom inside a cutoff distance of 5σ is considered according to this weighting. For the NiP system used here, a σ of 0.881 Å is used. From this vector-based description of the atomic positions, a Taylor series expansion of nth order terms (corresponding to rank n) is used to construct spatial tensors of rank 0 to 4 (representing \({{\mathbb{R}}}^{0}\) to \({{\mathbb{R}}}^{4}\)) which describe the overall Gaussian geometry. Higher-order terms can be constructed, but expansion to rank 4 is sufficient for the majority of atomic environments. This construction leads to a set of 24 atomic descriptors which describe the complete nature of the local atomic environment captured by the 0th to 4th order Gaussian tensors.

This tensor-based description is then decomposed to form scalar values that represent various atomic distortions in geometric terms (i.e, tetrahedral or octahedral character, net shear). For the rank 0 tensor, this is trivial as it is already a scalar that represents the local Gaussian density of the atomic neighborhood (1). When considering all higher-order tensors, the Cartesian tensor formed from the initial construction (from the Gaussian overlap vectors) is first converted into a spherical-harmonic tensor. This spherical harmonic tensor is subsequently converted into a set of rotationally-invariant scalars using Clebsch-Gordan coefficients71,72,73,74,75. The redundant set of all possible scalars representing a given spherical harmonic tensor is down-sampled to a unique and complete set of descriptors pre-defined for each tensor order. Finally, radial orthogonality is established (as in equations (2) and (3)) between similar scalar terms originating from different tensor orders such that each scalar carries a maximum amount of information when considering the entire set of SFDs across all orders. This independence between similar scalar features of different orders represents another advantage of the SFD formulation over previously published descriptors76,77,78,79. Further representation of the mathematics behind these principles underlying our SFDs requires more in-depth discussion than relevant to this manuscript and awaits further publication46.

The SFD approach follows an established method for describing physical properties in terms of irreducible spherical tensors71,72,73,74,75. This step is somewhat different from the bispectrum approach of Bartok et al.70 (SOAP) and produces a tensor representation that is very analogous to the principal quantum representation of atomic orbitals [see80 for examples]. In the framework illustrated by Levine, the n = 4 expansion terms would be primarily described by shapes analogous to the g orbitals (l = 4). Additional lower order terms (l = 2 and l = 0 with radial nodes) are also generated that describe orthogonal subspaces in the rotationally invariant SO(3) space75. These scalar functions can then be further reduced to rotationally invariant descriptors70,75,76,77,78,79. The application of Clebsch-Gordan coupling is a useful means of achieving this rotational invariance based on the harmonic polynomial basis70,79,81. As noted by Lo and Don79, a large number of invariants that contain redundant information can be generated, and the reduction of these to a minimal set with compact geometric information is described by Kober et al.46. This results in a set of 24 rotationally-invariant descriptors with an additional 12 indicating the local rotationally-dependent character of each tensor relative to a global coordinate frame. Only the 24 rotationally-invariant descriptors were used in this study.