Introduction

The kagome motifs, which are composed of two-dimensional honeycomb networks of alternating corner-sharing triangles, are attracting enormous interest as they provide a fascinating platform for exploring the emergence of many topological and correlated electronic phenomenon1,2,3. The kagome structure allows the possibility of flat bands, Dirac-like dispersions, and van Hove singularities (vHSs), resulting in a complex interplay of geometry, topology, and electronic correlation effects4,5,6,7,8,9,10,11,12,13,14,15,16,17,18. For example, a class of kagome superconductors, AV3Sb5 (A = K, Rb, and Cs), was discovered recently and found to host non-trivial band topology, charge density wave order and a superconducting ground state19,20,21,22,23,24,25,26,27,28,29.

The intertwining of magnetism with the electronic states in the kagome materials has yielded notable discoveries such as the massive Dirac fermions in Fe3Sn27, antiferromagnets Mn3Sn and Mn3Ge that showcase giant anomalous Hall effect30,31 and the Weyl semimetal state in Co3Sn2S232,33. The RMn6Sn6 kagome family (R = rare-earth element) has garnered special attention due to its unique magnetic tunability and large Berry curvature fields10,14,34,35,36,37,38,39,40,41,42,43. TbMn6Sn6 hosts massive Dirac fermions at the K point owing to Landau quantization and the presence of Landau fan diagram10,34. Flat bands and Dirac fermions have been reported in RMn6Sn6 (R = Gd–Dy, Y)14,35,36 family, topological Hall effect has been observed in YMn6Sn6, ErMn6Sn6, and HoMn6Sn639,40,41,42, and a large anomalous Hall effect has been reported in LiMn6Sn644.

Recently, two kagome metals, YbV3Sb4 and EuV3Sb4, were reported, introducing a new family of vanadium-based kagome materials45. It was found that YbV3Sb4 is a Pauli paramagnet with no clear thermodynamic phase transition between 300 K and 60 mK, whereas EuV3Sb4 displays a ferromagnetic transition below Tc of roughly 32 K and a signature of spin-texture under low-fields. The larger LnM3X4 (MX: VSb, TiBi) family is growing rapidly46,47, providing a new kagome materials platform.

Here we discuss our comprehensive investigation of the electronic structure of the YbTi3Bi4 kagome material. Our approach involves magneto-transport and angle-resolved photoemission spectroscopy (ARPES) measurements, in combination with parallel density-functional theory (DFT) based calculations. YbTi3Bi4, like its structural analog YbV3Sb4 is a nonmagnetic (Yb2+) kagome metal, which does not exhibit any electronic or structural phase transitions down to 60 mK47. Our ARPES measurements on YbTi3Bi4 indicate the presence of several flat bands spanning a large area of the Brillouin zone (BZ), multiple vHSs at the \(\overline{\,{\mbox{M}}\,}\) point, and a linear Dirac-like state at the \(\overline{\,{\mbox{K}}\,}\) symmetry point, and are consistent with our DFT calculations. Our study establishes YbTi3Bi4 as a fertile playground for exploring exotic physics in an easily exfoliable Ti-based nonmagnetic kagome material.

Results

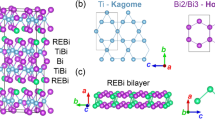
YbTi3Bi4 crystallizes in the orthorhombic space group Fmmm (No. 69) with a = 5.91(4) Å, b = 10.3(4) Å, c = 24.9(4) Å, and α = β = γ = 90∘. Figure 1a, b shows that the structure consists of Ti kagome layers stacked along the c-axis between the Bi and Yb layers. To emphasize the kagome lattice formed by the Ti atoms and the zig-zag chains formed by the Yb atoms, we highlight only the Ti–Ti, and Yb–Yb bonds in Fig. 1. Kagome layers formed by the Ti atoms are better visualized in Fig. 1c, where each unit cell consists of four kagome layers. However, unlike AV3Sb5, the kagome layers formed by the Ti atoms in YbTi3Bi4 exhibit slight buckling (Fig. 1b, d). Figure 1e illustrates the zig-zag chains formed by the Yb atoms extending in the a-direction. The Yb–Yb distance in the chains is ~3.9 Å, which is significantly shorter than the nearest neighbor Yb–Yb interchain distance of ~5.7 Å.

Fig. 1: Crystal structure and DFT results for YbTi3Bi4.
figure 1

a Crystal structure of YbTi3Bi4 where the blue, red, and green solid spheres denote Yb, Ti, and Bi atoms, respectively. The crystal structure is orthorhombic (Fmmm) with a zig-zag sublattice of Yb atoms. b The kagome lattice, which is formed by the Ti atoms, c is slightly distorted and it is not coplanar. d A view of the structure perpendicular to the b–c plane, which highlights the relatively small out-of-plane distortion of about ( ~2°). e Zig-zag chain formed by the Yb atoms. f Bulk Brillouin zone (BZ) and its projection onto the (001) surface BZ; high-symmetry points are marked. g DFT-based energy bands along the various high-symmetry directions without the inclusion of spin–orbit coupling (SOC). h Same as (g) except that these results include SOC. Purple and black arrows in (g and h) point to vHSs and flat bands, respectively.

Full size image

The bulk BZ and its projection on the (001) surface (labeled with the pseudo-hexagonal \(\overline{\,{\mbox{M}}\,}\), \(\overline{\,{\mbox{K}}\,}\), and \(\overline{\Gamma }\) nomenclature) is presented in Fig. 1f. To gain insight into the electronic structure of YbTi3Bi4, we performed band structure calculations without (Fig. 1g) and with the inclusion of the spin–orbit coupling effects (Fig. 1h); see Supplementary Note 1 and Supplementary Fig. 1 for orbital-resolved band structures. Multiple bands are seen to cross the Fermi level (EF) consistent with the metallic nature of YbTi3Bi4. Effects of SOC are generally small, except for the Dirac-like crossing along the Γ–X direction which becomes gapped with the inclusion of SOC. We observe three vHS points at Y (purple arrows) along with the presence of dispersionless bands below the EF (black arrows), indicating a high degree of localization of the associated electronic states. The dispersionless or “flat” bands are seen to extend over a large portion of the BZ. The flat bands at  ~ −0.5 eV and  ~ −0.7 eV predominantly arise from the kagome-based Ti dxy and \({d}_{{x}^{2}-{y}^{2}}\) orbitals, see Supplementary Note 1 and Supplementary Fig. 1.

For experimental work, we grew high-quality single crystals of YbTi3Bi4 using the flux method. Temperature-dependent molar magnetic susceptibility χ(T) = M/H measured under magnetic field of H = 0.1 T is presented in Fig. 2a for H ∥ c. Essentially temperature-independent Pauli paramagnetism is seen with a weak Curie tail from the impurity spins. The extremely weak nature of the susceptibility (10−3 emu Oe−1 mol−1) is evident from Fig. 2a, which does not display any signature of a bulk magnetic moment. No qualitative difference is observed when H is applied ∥ versus ⊥ to the c-axis. The inset compares magnetization as a function of the magnetic field at 300 and 1.8 K, and shows no saturation up to 7 T. Note that the scale of the M versus H plot is of the order of 10−2 μB per Yb, consistent with the polarization of impurity spins.

Fig. 2: Bulk electronic properties and characterization of a YbTi3Bi4 single crystal specimen.
figure 2

a Magnetic susceptibility (χ) versus temperature under a magnetic field of H = 0.1 T. Inset shows magnetization as a function of magnetic field M(H) up to 7 T at 300 and 1.8 K. b Temperature-dependent zero-field electrical resistivity. c Temperature dependence of the specific heat (Cp) over 2–300 K. Inset highlights Cp/T versus T2 in the low-temperature regime.

Full size image

Figure 2b shows the electrical resistivity ρ as a function of temperature, where the current is flowing in the ab-plane. The typical metallic behavior is seen until the lowest temperature of 2 K used in the measurements. The residual resistivity is ~20 μΩ cm and the residual resistivity ratio is around 4. The resistivity data at low temperatures (<80 K) is modeled using the Fermi liquid picture, which yields the simple quadratic form, ρ = ρ0 + aT2 (red dotted line), where ρ0 = 19.7 μΩ cm and a = 1.6 × 10−3 μΩ cm K−2. We also measured the specific heat (Cp) of the sample from 200 K down to 2 K without a magnetic field (Fig. 2c). We have fitted the Cp data over the limited temperature range of 2–12 K using the Sommerfeld model. Recall that the Cp for nonmagnetic metals consists of of electronic Ce and lattice Cph contributions, and at low temperature it is given by: Cp(T) = γT + βT3, where Ce = γT and Cph = βT3. Here, γ is the Sommerfeld coefficient, and β = 12\({\pi }^{4}NR/5{\Theta }_{D}^{3}\) with N, R, and ΘD representing the number of atoms per unit cell, the ideal gas constant, and the Debye temperature, respectively. The inset of Fig. 2c shows that the Cp/(T) scales linearly with T2 at low temperatures. The resulting least-squares fit yields the parameters γ = 1.78 × 10−2 J mol−1 K−2 and β = 1.46 × 10−3 J mol−1 K−4. These results indicate that YbTi3Bi4 is a nonmagnetic kagome metal with no clear thermodynamic phase transitions up to 300 K.

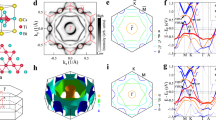
We turn now to discuss our ARPES measurements from YbTi3Bi4. Note that our DFT calculations indicate that the density of states (DOS) at the EF in YbTi3Bi4 is dominated by the Ti and Bi orbitals. With the Yb-orbitals lying away from the EF, ARPES is expected to show an apparent sixfold symmetry, although the underlying structure is orthorhombic. We focus first on the Fermi surface (FS) topology. Figure 3a presents the FS measured using a photon energy of 90 eV as a function of kx and ky. Several pockets can be seen at the EF, with a circular pocket near the BZ center \(\overline{\Gamma }\), a pocket with hexagonal symmetry which is anticipated due to the underlying symmetry of the kagome lattice along the \(\overline{\Gamma }\)–\(\overline{\,{\mbox{M}}\,}\) direction, and two pockets around the \(\overline{\,{\mbox{K}}\,}\) point, where the inner pocket seems to show a circular shape and the outer pocket is triangular; see Supplementary Note 2 and Supplementary Fig. 2a for additional results of FS measurements. The DFT-based bulk FS including surface states, presented in Fig. 3b, is in good agreement with our experimental results, see Supplementary Note 2 and Supplementary Fig. 2b for bulk FS without the surface states. Discrepancies between the theory and experiment may be attributed to the effects of the ARPES matrix element48,49 and the intrinsic limitations of the DFT in capturing electronic correlations50,51,52.

Fig. 3: Fermi surface (FS) and band dispersion along the \(\overline{\,{\mbox{M}}\,}\)–\(\overline{\Gamma }\)–\(\overline{\,{\mbox{M}}\,}\) high-symmetry line.
figure 3

a ARPES measured FS using a photon energy of 90 eV. High-symmetry points are labeled. b DFT calculated FS. c, d Constant-energy contours at various binding energies as noted on the top of each plot. e Experimental band dispersion measured along the \(\overline{\Gamma }\)–\(\overline{\,{\mbox{M}}\,}\)–\(\overline{\Gamma }\)–\(\overline{\,{\mbox{M}}\,}\)–\(\overline{\Gamma }\) high-symmetry line with a photon energy of 90 eV. f Same as (e) except that the measurements are with a photon energy of 75 eV. g Projected bulk band structure along the \(\overline{\,{\mbox{M}}\,}\)–\(\overline{\Gamma }\)–\(\overline{\,{\mbox{M}}\,}\) high-symmetry line. h Same as (g) except that this panel includes the surface states.

Full size image

ARPES measured constant-energy contours (CECs) are presented in Fig. 3c, d at various binding energies. With increasing binding energy, the circular pocket at \(\overline{\Gamma }\) contracts to a point-like feature around  ~ −370 meV indicating its electron-like nature, whereas the pocket at \(\overline{\,{\mbox{K}}\,}\)/\(\overline{\,{\mbox{M}}\,}\) increases in size with increasing binding energy, indicating its hole-like nature. Note that the underlying orthorhombic structure naturally imparts small distortions to the kagome lattice, which result in the apparent sixfold symmetry in the ARPES FS and CECs. Although we refer to the data using the hexagonal nomenclature, the underlying symmetry is twofold.

Band dispersions along the \(\overline{\Gamma }\)–\(\overline{\,{\mbox{M}}\,}\)–\(\overline{\Gamma }\)–\(\overline{\,{\mbox{M}}\,}\)–\(\overline{\Gamma }\) high-symmetry line using photon energies of 90 and 75 eV are shown in Fig. 3e and f, respectively. In agreement with our measured FS and CECs, an electron-like pocket can be seen at the \(\overline{\Gamma }\) point. However, a closer examination of the band dispersion at \(\overline{\Gamma }\) in the second BZ reveals the presence of two distinct pockets. This is also evident in the band-dispersion plot obtained with 75 eV photons along the \(\overline{\Gamma }\)–\(\overline{\,{\mbox{M}}\,}\)–\(\overline{\Gamma }\)–\(\overline{\,{\mbox{M}}\,}\)–\(\overline{\Gamma }\) line, see Fig. 3f. [For detailed analysis of the bands, labeled α and β, see Supplementary Note 3 and Supplementary Fig. 3a, b]. We also obtained momentum distribution curves (MDCs) by integrating over an energy window of 10 meV below the Fermi level around the \(\overline{\Gamma }\) point in the second BZ and fitted the spectra using two Gaussian peaks (see Supplementary Note 3 and Supplementary Fig. 3c) to further confirm the presence of two peaks (α and β) at \(\overline{\Gamma }\). Additionally, two hole-like bands (γ and δ) are visible in Fig. 3e, f, which exhibit hole-like characteristics consistent with the FSs and CECs presented in Fig. 3a, c, d. Our projected (bulk) DFT calculations in Fig. 3g are in good agreement with the results of ARPES measurements in Fig. 3e, f, reproducing the two electron-like pockets α and β, and the hole-like pocket around the γ point, indicating their bulk origin. However, the band denoted as δ in the ARPES spectra is not reproduced in our DFT calculations. When surface states are included in the calculations, Fig. 3h shows the appearance of the hole-like pocket δ (green arrow), suggesting its surface origin.

Figure 4a presents the experimental ARPES band structure along \(\overline{\Gamma }\)–\(\overline{\,{\mbox{M}}\,}\)–\(\overline{\,{\mbox{K}}\,}\)–\(\overline{\Gamma }\). The most prominent feature is the presence of the vHSs, denoted vHS1 and vHS2 (purple arrows), along with four dispersionless flat bands (black arrows) that extend across a large region of the BZ, which lie at binding energies of  ~ −0.3 eV,  ~ −0.5 eV,  ~ −0.7 eV, and  ~ −1.1 eV. The flat bands at  ~ −0.3 eV and  ~ −0.5 eV are attributed to the destructive interference of wavefunctions within the Ti kagome motif, with interlayer coupling between the two kagome layers resulting in bonding (with a decreased energy at around  ~ −0.5 eV) and antibonding (with an increased energy at around  ~ −0.3 eV) splittings7,53. Orbital-resolved DFT calculations suggest that these flat bands predominantly consist of a mixture of Ti dxy and Ti \({d}_{{x}^{2}-{y}^{2}}\) orbitals, see Supplementary Note 1 and Supplementary Fig. 1. The discrepancy of ~200 meV between the DFT calculations and the ARPES results may be due to the neglect of Yb 4f states in our calculations48,49,50,51,52. The flat band observed at  ~ −0.7 eV is associated with Yb surface atoms, while the flat band around  ~ −1.1 eV originates from bulk Yb2+ 4f5/2 states54, see Supplementary Note 4 and Supplementary Fig. 4 for additional photon energy dependent measurements. vHS2 mostly involves Ti \({d}_{{x}^{2}-{y}^{2}}\) and Ti \({d}_{{z}^{2}}\) orbitals, whereas vHS1 mainly involves the Ti dxy orbital. The vHS above the EF seen in DFT calculations, which is not accessible to ARPES, mostly consists of Ti dxy orbital, see Supplementary Note 1 and Supplementary Fig. 1. Except for the flat bands contributed by Yb 4f states, the DFT calculated bulk band structure along \(\overline{\Gamma }\)–\(\overline{\,{\mbox{M}}\,}\)–\(\overline{\,{\mbox{K}}\,}\)–\(\overline{\Gamma }\) in Fig. 4b reproduces the ARPES measured vHSs (vHS1 and vHS2) and flat bands. The vHSs near the EF have been implicated in driving exotic physics (e.g., charge ordering and superconductivity) in AV3Sb5 (A = K, Rb, and Cs) kagome metals. Since the vHSs in YbTi3Bi4 lie away from the EF, this could explain the absence of charge ordering and superconductivity in this material.

Fig. 4: Visualization of multiple vHSs and flat bands.
figure 4

a Experimental photoelectron intensity plot of the band structure along the \(\overline{\Gamma }\)–\(\overline{\,{\mbox{M}}\,}\)–\(\overline{\,{\mbox{K}}\,}\)–\(\overline{\Gamma }\) line with 90 eV photons. The white-dashed curves serve as guides to the eye to help visualize the two vHSs. Purple and black arrows in (a) and (b) point to the vHSs and flat bands, respectively. b DFT-based bulk band structure along the \(\overline{\Gamma }\)–\(\overline{\,{\mbox{M}}\,}\)–\(\overline{\,{\mbox{K}}\,}\)–\(\overline{\Gamma }\) line. c Experimental band dispersion and the associated integrated energy distribution curves (EDCs) along the \(\overline{\Gamma }\)–\(\overline{\,{\mbox{K}}\,}\)–\(\overline{\,{\mbox{M}}\,}\)–\(\overline{\,{\mbox{K}}\,}\)–\(\overline{\Gamma }\) line measured using 58 eV photons. Peak positions in the EDCs (black arrows) denote flat bands at  ~ −0.3 eV,  ~ −0.5 eV, and  ~ −0.7 eV, with the most intense peak lying at around ~ − 1.1 eV. d Same as (c) except these results are for measurements using 55 eV photons. e Integrated intensity of the EDCs (over the momentum range of −0.8 Å−1 to 0.8 Å−1) along the \(\overline{\Gamma }\)–\(\overline{\,{\mbox{K}}\,}\)–\(\overline{\,{\mbox{M}}\,}\)–\(\overline{\,{\mbox{K}}\,}\)–\(\overline{\Gamma }\) line. The EDCs used to obtain integrated intensities plotted were taken at photon energies ranging from 40 to 60 eV as indicated by the color bars on the right side of (f). Peak positions in the EDCs (black arrows) correspond to flat bands. f Same as (e) except that here the integration involves EDCs along the \(\overline{\,{\mbox{K}}\,}\)–\(\overline{\Gamma }\)–\(\overline{\,{\mbox{K}}\,}\) line.

Full size image

To further examine the flat bands, we present the band dispersion along \(\overline{\Gamma }\)–\(\overline{\,{\mbox{K}}\,}\)–\(\overline{\,{\mbox{M}}\,}\)–\(\overline{\,{\mbox{K}}\,}\)–\(\overline{\Gamma }\) high-symmetry using 58 and 55 eV photons in Fig. 4c and d, respectively. Four dispersionless bands at binding energies of  ~ −0.3 eV,  ~ − 0.5 eV,  ~ −0.7 eV, and  ~ − 1.1 eV can be seen as before at both photon energies. The associated DOS can be visualized by examining the momentum-integrated EDCs in Fig. 4c and d, which exhibit several distinct peaks (black arrows) that arise from flat bands. Figure 4e, f shows the momentum-integrated EDCs as a function of photon energy along \(\overline{\Gamma }\)–\(\overline{\,{\mbox{K}}\,}\)–\(\overline{\,{\mbox{M}}\,}\)–\(\overline{\,{\mbox{K}}\,}\)–\(\overline{\Gamma }\) and \(\overline{\,{\mbox{K}}\,}\)–\(\overline{\Gamma }\)–\(\overline{\,{\mbox{K}}\,}\); see Supplementary Note 4 and Supplementary Figs. 5, 6 for additional data. The peaks related to the four flat bands in these integrated spectra also occur at the four aforementioned energies, as expected (black arrows). A closer examination of the spectra reveals a slight dispersion in the flat bands around  ~ −0.3 eV and  ~ −0.5 eV, which could be attributed to hopping between the nearest and/or next-nearest-neighbor atoms within the same or adjacent kagome planes53.

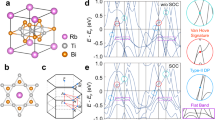
It is interesting to further consider band dispersions along \(\overline{\,{\mbox{K}}\,}\)–\(\overline{\Gamma }\)–\(\overline{\,{\mbox{K}}\,}\). Results at 50 and 60 eV photon energies presented in Fig. 5a, b show the presence of a linear Dirac-like state formed by the innermost band (dashed blue lines culminating in the blue arrow), which looks like a hole pocket that merges near the EF. For additional related ARPES results, see Supplementary Note 4 and Supplementary Fig. 6. The linear Dirac-like band is better resolved at 60 eV photon energy and is identified by symbol ζ for clarity. The asymmetry seen in the spectra around \(\overline{\,{\mbox{K}}\,}\) is likely due to well-known photoemission cross-section effects, in ARPES measurements. To gain further insight into the nature of the innermost linear Dirac-like band (blue arrow in Fig. 5a, b), we consider MDCs obtained by integrating the spectra over a narrow 10 meV binding energy range below the Fermi level. The results obtained from spectra taken at various photon energies are presented in Supplementary Notes 4, 5 and Supplementary Figs. 6, 7. The innermost band at the \(\overline{\,{\mbox{K}}\,}\) is seen to show dispersion, indicating its bulk origin, see Supplementary Note 5 and Supplementary Fig. 7 for details. The bulk bands plotted in Fig. 5c also show a linear Dirac-like band around the \(\overline{\,{\mbox{K}}\,}\) point (blue arrow) in reasonable accord with our experimental results. The band characters in Fig. 5c indicate that the linear Dirac-like state is dominated by the Ti \({d}_{{x}^{2}-{y}^{2}}\) orbitals.

Fig. 5: Observation of a Dirac-like state at the \(\overline{\,{\mbox{K}}\,}\) point.
figure 5

Experimental band dispersions along \(\overline{\,{\mbox{K}}\,}\)–\(\overline{\Gamma }\)–\(\overline{\,{\mbox{K}}\,}\) using a photon energy of a 50 eV, and b 60 eV. c Orbital-projected bulk band structure along \(\overline{\,{\mbox{K}}\,}\)–\(\overline{\Gamma }\)–\(\overline{\,{\mbox{K}}\,}\). Color scale provides relative contributions from various orbitals. d DFT-based (bulk) projected band structure including the surface states.

Full size image

Interestingly, there are many band inversions in the bulk band structure of Fig. 5c. To unravel the topology of YbTi3Bi4, we have calculated the Z2 invariant by following the evolution of the Wannier charge center and also via the parity-based methods, see Supplementary Fig. 8. In this way, we found the strong Z2 invariant to vanish (ν0 = 0) and the weak invariants to be: ν1 = 0, ν2 = 1, ν3 = 1. Figure 5d presents a DFT-based projection in which both the bulk and surface bands are included. These results are in line with much of the discussion above of bulk and surface states and their signatures in the experimental ARPES spectra, and exhibit complex hybridization of the bulk and surface states at the \(\overline{\,{\mbox{K}}\,}\) point, see Supplementary Note 6 and Supplementary Fig. 9 for further details.

Discussion

Defining features of the valence electronic structure of YbTi3Bi4 include: (i) a linear Dirac-like state near EF at the \(\overline{\,{\mbox{K}}\,}\) point; (ii) based on DFT calculations, a saddle-point vHS at \(\overline{\,{\mbox{M}}\,}\) lying about 150 meV above EF, along with other two vHSs about 250 meV below the EF; and (iii) four flat bands spanning across a large region of the BZ, with two of these originating from Yb 4f states and the other two from the Ti 3d kagome states. These features should be contrasted with the low-energy electronic spectrum of vanadium-based kagome materials such as AV3Sb5 in which the physics responsible for producing exotic phenomena, such as superconductivity, is dominated by the interplay of the saddle-point vHSs and a topological surface state, both located at \(\overline{\,{\mbox{M}}\,}\) in close proximity to the EF55,56,57,58. Absence of vHSs near EF could be the reason for lack of superconductivity and charge ordering in YbTi3Bi4. Flat bands have been predicted theoretically in AV3Sb5: one flat band lies about 1 eV above the EF (inaccessible to ARPES), while the other flat band around 1.2 eV below EF is not well resolved in ARPES experiments20,58. In contrast, we have clearly shown the presence of several flat bands in YbTi3Bi4. It should be possible to tune the chemical potential in YbTi3Bi4 so that it lies near the vHSs and the flat bands. Magnetism in YbTi3Bi4 can also be tuned by replacing Yb with other rare-earth elements47. Our work thus sets the stage for further exploration of YbTi3Bi4, including studies involving its exfoliation down to few monolayers.

Conclusions

In summary, we have synthesized a nonmagnetic Ti-based kagome material (YbTi3Bi4) and analyzed its electronic structure in-depth using a combination of magneto-transport, ARPES, and parallel first-principles calculations. The ARPES measured FS and band dispersions are in good accord with our theoretical predictions. We provide compelling evidence for the presence of multiple flat bands and vHSs in YbTi3Bi4. The flat bands originate from both the Ti-based kagome lattice and the Yb2+4f orbitals. Our work highlights the importance of the Ti-based LnTi3Bi4 kagome family as a potential platform for exploring exotic phases.

Note added to proof

While the manuscript was under review, several related studies have been published47,59,60,61.

Methods

Experimental details

YbTi3Bi4 single crystals were grown through bismuth self-flux. Elemental reagents of Yb (Alfa 99.9%), Ti (Alfa 99.9% powder), and Bi (Alfa 99.999% low-oxide shot) were combined in 2:3:12 ratio into 2 mL Canfield crucibles fitted with a catch crucible and a porous frit62. The crucibles were sealed under ~0.7 atm of argon gas in fused silica ampoules. Each composition was heated to 1050 °C at a rate of 200 °C/h. Samples were allowed to thermalize and homogenize at 1050 °C for 12–18 h before cooling to 500 °C at a rate of 2 °C/h. Excess bismuth was removed through centrifugation at 500 °C.

Synchrotron-based ARPES experiments were performed at the ALS beamlines 10.0.1.1 and 4.0.3 at a temperature of 15 K equipped with R4000 and R8000 hemispherical electron analyzers. Additional ARPES experiments were carried out at the Stanford Synchrotron Radiation Lightsource end station 5-2 at 15 K. The angular and energy resolution were set at better than 0.2° and 15 meV, respectively. High-quality single crystals were cut into small pieces and mounted on a copper post using silver epoxy. Ceramic posts were attached on top of the samples. To avoid oxidation, samples were prepared in a glove box, and loaded into the main chamber which was cooled and pumped down for a few hours. Measurements were carried out at 11 K. Pressure in the UHV chamber was maintained at around 10−11 Torr.

Computational methods

Electronic structure calculations were performed within the DFT framework using a plane-wave basis set as implemented in the Vienna Ab initio Simulation Package (VASP)63,64. Standard projector-augmented-wave (PAW) pseudopotentials were used65. The kinetic energy cutoff for the plane-wave basis was set to 500 eV. A Γ-centered 10 × 10 × 10 k mesh was used for k-space integrations. The SCAN (strongly-constrained and appropriately-normed) functional was used to treat exchange-correlation effects66,67. Yb_3 pseudopotential was used, where the Yb 4f electrons are taken to be core electrons. The lattice parameters were fully relaxed by optimizing atomic positions until the force on each atom became less than 0.001 eV Å. The relaxed lattice parameters are a = 5.862 Å, b = 10.385 Å, c = 24.838 Å, which are very close to the corresponding experimental values.