Introduction

Materials in which the electrical and magnetic properties are intertwined are of considerable interest from a fundamental point of view as well as for applications, specifically in spintronics1,2. Here, correlated materials are of particular significance because of their often inherent coupling of lattice, charge, orbital and/or spin degrees of freedom. As a consequence of these multiple interactions electronically inhomogeneous states can arise3. Moreover, these multiple interactions may give rise to large responses upon small perturbations, a desired scenario for possible applications. Prime examples of electronically correlated, spatially inhomogeneous materials are the cuprate superconductors with high transition temperatures4,5 or manganites exhibiting colossal magnetoresistance (CMR) effects6.

Eu-based compounds are often prone to coupled charge and spin degrees of freedom: A strong exchange interaction between charge carriers and the localized spin of the Eu2+ ions7,8 may result in a localization of these charge carriers at Eu2+ sites. The resulting quasiparticle made up of the localized charge carriers and the Eu moment is referred to as a magnetic polaron9,10 and exemplifies the interplay between electrical and magnetic properties, the hallmark of spintronics11,12. A prerequisite for polaron formation is a low enough carrier concentration, which assures polarons remain localized and do not populate the materials volume. In this respect, Zintl phases13 emerge as a promising playground. In particular, Eu5In2Sb6 has been recently reported14,15,16 as a narrow-gap semiconductor17,18 whose properties are consistent with polaron formation. Notably, this material is a magnetic counterpart to Ba5In2Sb619, which crystallizes in the non-symmorphic space group Pbma (No. 55) and has been predicted to display topological surface states20,21. Hence, Eu5In2Sb6 may combine topologically nontrivial surface states with magnetism and polaron formation, albeit only the latter two properties have been experimentally established so far14,15,16. Also, a remarkably large negative magnetoresistance, comparable to the best CMR manganites, was observed in Eu5In2Sb614,16. The price to be paid for this potentially interesting combination of properties is the complex orthorhombic structure of Eu5In2Sb6 with three crystallographically different Eu sites17, resulting in a complicated magnetic phase diagram with at least two antiferromagnetic phases (TN1 ≈ 14.1 K, TN2 ≈ 7.2 K) and entangled magnetization processes14,15,22,23. It must also be pointed out that despite an orbital angular momentum of L = 0 of the Eu2+ ions in this compound, strong anisotropies of the transport properties and the magnetic susceptibility in the magnetically ordered phase have been observed indicating competing magnetic interactions. In particular, the low symmetry of the Eu sublattices allows for the existence of Dzyaloshinskii-Moriya interactions and spin canting15. Thus, the magnetic structure of Eu5In2Sb6 is highly complex15,22,23 and not yet fully resolved in all detail.

In an effort to shed light on the intriguing properties of Eu5In2Sb6 we conducted thermal expansion and magnetostriction measurements along the different crystallographic directions of single crystals. The results provide further evidence for the formation of non-spherical polarons far above the Néel temperature TN. These polarons give rise to an extraordinarily rich and anisotropic magnetoresistive behavior. Within the antiferromagnetically ordered phase, our results are in excellent agreement with the established phase diagrams. Additionally, however, these dilatation data reveal a crossover which is associated with the coexistence of ferromagnetic (fm) polarons and antiferromagnetic (afm) long-range order. Surprisingly, these polarons become more stable upon lowering the temperature. This crossover could not be traced by any other, i.e., magnetic, transport or specific heat measurement, a fact that points to magnetoelastic coupling effects as its origin and that underscores the remarkable sensitivity of expansion measurements, establishing them as pivotal tool to unveil subtle phenomena.

Results

Paramagnetic regime

We start off by considering the paramagnetic regime before discussing the magnetically much more complex afm low-temperature regime. Thermal expansion data up to room temperature for measurements along the c axis are presented in Fig. 1. For T ≳ 175 K, the relative length change ΔL(T)/L0 increases linearly with T within experimental resolution (Fig. 1b), as expected for a material with a Debye temperature θD ≈ 197 K16. Here, L0 is the sample length at a reference temperature. Between 35 K ≲ T ≲ 130 K, Fig. 1a, ΔL(T)/L0 can be well described by a model in which electronic and phononic contributions are considered24,25, see Supplementary Note 2 and Supplementary Table I. For simplicity, we relied on our specific heat results16 and conducted the fits with θD = 197 K and without Einstein modes. For measurements along the a axis, the fits hold down to about 25 K, and with an applied field of 4 T even to slightly lower T, cf. Fig. 1c. We note that using different fitting procedures does not change our findings qualitatively (see Supplementary Figs. 2 and 3).

Fig. 1: Fits of thermal expansion data.
figure 1

a ΔL(T)/L0 can very well be fitted to a model containing electronic and phononic contributions24 for 35 K ≲ T ≲  130 K and b is linear in T above 175 K, respectively. c Fits to the model24 for ΔL(T, H)/L0 measured along the a axis and at selected fields (same data as in Fig. 4a, units of 10−6). All dashed lines are fit results.

Full size image

Since thermodynamic, magnetic and electronic transport properties of Eu5In2Sb6 all indicate a clear impact of magnetic polarons below 40–50 K14,16,26,27, the deviations of ΔL(T)/L0 from the modeled T-behavior can safely be associated with such polarons. In Eu5In2Sb6, these nanoscale clusters are likely anisotropic in shape with the shortest direction along c and fm alignment of the Eu2+ moments within the polaron in the ab plane15,26,27. It is well established that magnetic polarons can induce lattice distortions28,29,30. In Fig. 2a, we focus on T ≤ 40 K and present the relative length changes ΔL(T)/L0 as measured along the three main crystallographic directions of Eu5In2Sb6. Clearly, there are large anisotropies observed, as already seen in magnetic, transport and piezoresistive measurements14,16,26 and treated by density functional theory calculation15. For all directions, however, a kink is observed at  ≈14.3 K in zero magnetic field, a temperature associated with TN114,16. The transition near TN2 ≈ 7.2 K is most pronounced for ΔL100(T)/L0 along the a axis. In fact, the strong length increase with increasing T below 7.2 K and the subsequent decrease up to 14.3 K mimics very nicely the strongly T-dependent magnetization M(T) measured along the a axis, as shown in Fig. 2b. Similarly, thermal expansion and magnetization exhibit the smallest change with temperature for measurements along the c axis. Here we emphasize again that L = 0 for Eu2+ and hence, crystalline electric field effects are negligible to first order. This implies that magnetic interactions not only determine the anisotropic magnetization behavior in Eu5In2Sb6 but also its thermal expansion in magnetic fields and magnetostrictive behavior25,31.

Fig. 2: Comparison of thermal expansion and magnetization.
figure 2

a Relative length change ΔL(T)/L0 measured along the three main crystallographic directions of Eu5In2Sb6. Inset: Low-temperature thermal expansion coefficient α(T, H) along the b axis and for representative magnetic fields μ0H = 0, 1.5, 2.0, 2.5 T. The feature near 8 K evolves non-monotonically with H. b Zero-field cooled (ZFC) magnetization of Eu5In2Sb6 measured in μ0H = 0.1 T for the three directions. For comparison, the field-cooled (FC) curve along the a axis is also shown. Arrows mark TN1 and TN2, respectively. Sketch: spin configuration just below TN1 in phase I, as suggested in ref. 15.

Full size image

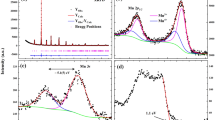
We now attempt to interpret the resistive behavior of Eu5In2Sb6, Fig. 3. In order to minimize dependencies on specific samples on the one hand, and focus on the anisotropy of the polarons on the other hand, we consider the ratio of resistivities along different directions, r = ρI∥a/ρI∥c, where ρI∥a and ρI∥c are the resistivities measured for I∥a (H∥c) and I∥c (H∥b), respectively16. The infinite \({[{{{{{\rm{In}}}}}}_{2}{{{{{\rm{Sb}}}}}}_{6}]}^{10-}\) ribbons of the Eu5In2Sb6 structure along c support preferred charge transport along this direction17 upon lowering T below 50 K, and r(T) increases strongly at zero field. This increase of r(T) is intercepted below 30 K by the interaction of the polarons which are more extended in the ab plane. This results in a shoulder of ρI∥a and a pronounced maximum in r(T). The sharp increase of r(T) below T = 14.4 K reflects the onset of afm ordering at TN1.

Fig. 3: Analysis of resistivities.
figure 3

Ratio r of resistivities ρ measured along I∥a, H∥c versus I∥c, H∥b for fields μ0H = 0 T ( × ), 3 T (∘) and 9 T ( + ). The dotted line is a guide to the eye. Inset: individual ρ values; I∥a bluish, I∥c reddish for 0 T ( × ) and 3 T (∘). T+ marks the crossover into an inhomogeneous, polaronic state upon lowering T, here shown for H = 0.

Full size image

In a magnetic field of 3 T parallel to c, the polarons grow in size along c and hence, abate their anisotropy, such that the differences in ρI∥a and ρI∥c (for fields along c and b, respectively) are much less pronounced; likely the maximum in r(T) is then shifted close to TN1. In the nearly field-polarized state at 9 T (saturation of magnetization is achieved near 10 T at 2 K16), the fm polarons have grown further, overlapped and likely merged into their surroundings. In consequence, only a weak temperature dependence of r(T) is observed.

Antiferromagnetically ordered regime

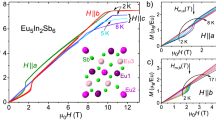
Considering the formation of polarons well above the afm ordered phase as being established we now investigate the fate of these polarons upon cooling to below TN1. The transitions at TN1 and TN2 can easily be recognized in the dilatation data along the different crystallographic directions, Figs. 2 and 4, particularly from the coefficients of thermal expansion α(T) = (1/L0)(dL/dT) and magnetostriction λ = (1/L0)∂L/∂H. In Fig. 5 we include these results into the T–H phase diagrams obtained from magnetic, specific heat and transport measurements (faint data points and lines from Ale Crivillero et al.16) for the three main crystallographic directions. In order to allow for such a comparison the samples’ demagnetizing effects were taken into consideration. HN1 and HN2 describe the field dependencies of TN1 and TN2, respectively. Clearly, our dilatation data trace the transitions at HN1 (red) and HN2 (blue) very well. This emphasizes again that the effects observed in thermal expansion and magnetostriction are primarily related to the magnetic structure of Eu5In2Sb6. Further support for such an assignment comes from the magnetostriction measurement ΔL(H)/L0 at T = 7.5 K along the crystallographic b direction which exhibits a jump at \({\mu }_{0}{H}_{{{{{\rm{m}}}}}}^{b}\approx\) 2 T, red and orange data in Fig. 6b. Here, \({H}_{{{{{\rm{m}}}}}}^{b}\) marks the metamagnetic behavior associated with a spin flop16 as sketched in Fig. 5b.

Fig. 4: Detailed thermal expansion and magnetostriction along a axis.
figure 4

a Length change ΔL(T)/L0 and b thermal expansion coefficient α(T) measured at different magnetic fields H along the a axis. Inset: α(T, H = 0) along the c axis. c Magnetostriction ΔL(H)/L0 and (d) magnetostriction coefficient λ for H∥a at different T.

Full size image
Fig. 5: H–T phase diagrams of Eu5In2Sb6 for the three main crystallographic directions.
figure 5

a along a axis, b along b and c along c. The faint lines and data points, reproduced16 for direct comparison, result from specific heat and magnetic measurements. Thermal expansion and magnetostriction results are indicated by ⋆ and ▵, respectively (dotted triangles for H∥b indicate results obtained with a different setup, see Supplementary Note 4 and Supplementary Fig. 5). \({H}_{{{{{\rm{m}}}}}}^{b}\) marks a metamagnetic behavior. The three regions I, II and III between HN1 and HN2, below HN2, and between HN1 and H+, respectively, are marked in (c). Here, HN1 and HN2 mark antiferromagnetic (afm) phase transitions while H+ signals a crossover. In (a), an anisotropic ferromagnetic polaron at zero field is sketched within afm global order, a situation expected in region I. The polarons' shortest dimension is expected along the crystallographic c direction and the Eu moments are aligned in the ab plane.

Full size image
Fig. 6: Magnetostriction data.
figure 6

a ΔL(H)/L0 for H∥c and three exemplary temperatures. The dotted black line at 4 K is a fit to ΔL(H)/L\({}_{0}={a}^{{\prime} }{H}^{2}\) (see text), and the dashed one to \({a}^{{\prime\prime} }{H}^{2}+{c}^{{\prime\prime} }\), see Supplementary Note 5. b ΔL(H)/L0 for H∥b. Data for field sweep up (red) and down (orange) show a tiny hysteresis. A spin-flop takes place at \({H}_{{{{{\rm{m}}}}}}^{b}\approx\) 2 T.

Full size image

Analysis of magnetostrictive behavior

As clearly seen in α(T, H) along the a and the c axis these data reveal another, field-dependent feature just below TN1 denoted as H+ in Fig. 5 (orange data). In the following, we inspect this feature by considering the magnetostriction for H∥c within the three regions marked in Fig. 5c. Note that c is the magnetically hard direction and applying H∥c rotates the local moments out of the ab-plane without spin-flop.

As shown in Fig. 6a, at T = 4 K and below HN2, region II, where Eu moments at all three lattice sites are ordered22,23, the sample contracts with increasing H in an impeccable H2-fashion. This results from32,33\(\Delta {{{{\rm{L}}}}}(H) \sim -{[M(H)/{M}_{s}]}^{2}\) (Ms is the saturation magnetization) and M(H) ~ H in this regime16. In the same phase space, the sample contracts not only with H, but also with increasing T, cf. Figs. 2a and 4. This is, however, outweighed by a much larger extension along a, both with increasing T and H, such that the total sample volume increases. These effects are reversed upon entering region I for fields above HN2: the sample now expands along c with increasing H or T. We emphasize that the H2-dependence of the magnetostriction inside region I, dashed line in Fig. 6a, is consistent with an expected expansion of fm polarons, see Supplementary Note 5. Unfortunately, with a maximum field of 9 T along the c axis we do not reach HN1 at 4 K.

At 8.5 K, ΔL(H)/L0 is negligibly small up to  ~2.5 T. This can be explained by a concurrence of sizeable moment fluctuations at zero field in this T-range, seen e.g., by muon spin rotation measurements (μSR)23, and a fm alignment of magnetic moments with field, as will be discussed below. The latter prevails at higher fields and the sample expands with H, as expected for region I from the 4 K-data. Between 5 T ≲ μ0H ≲ 7.4 T, a H2-law holds again. Above HN1, i.e., in the paramagnetic regime, fluctuations are suppressed by magnetic field and the sample contracts.

An intriguing behavior is observed at T = 12.5 K. The sample initially contracts, but crosses over into expansion at H+ before a sharp transition into contraction is observed for H > HN1. According to these dilatation data the minimum at H+ indicates a crossover from region III into I of the phase diagram Fig. 5c, in contrast to the sharp transitions at HN1 and HN2. Likely, it is this crossover behavior that hindered a clear-cut assignment in other measurements16,23. It should be noted that the slopes of ΔL001(H)/L0 just below H+ as well as above H+ are comparable for the different temperatures.

Thermal expansion at low temperatures

The values of α100 and α001(T, H = 0) show a qualitatively similar behavior but with opposite sign, cf. Fig. 4b and its inset (see also Supplementary Note 3 and Supplementary Fig. 4). Likewise, the magnetostrictions along a and c, Figs. 4c and 6a, exhibit qualitatively very similar behavior, yet again with opposite sign. However, the effects are much larger along a compared to c. In addition, the magnetostriction ΔL100(H) does not follow an H2-dependence even below TN2 as can be inferred from the coefficient λ in Fig. 4d. This behavior can be attributed to the complex magnetic structure of Eu5In2Sb6. The magnetization M100(H) exhibits a metamagnetic behavior16; in case of the example at 4 K this takes place just below 1.5 T, see Fig. 7a. HN2 may then be related to a spin-flop transition within the additional afm order below TN2 with ordered moments along a22,23. The very sharp, almost jump-like increase of ΔL100(H) near HN2 at lowest temperatures supports such a scenario which, in turn, explains the deviation of ΔL100(H) from a H2-dependence.

Fig. 7: Magnetization curves M(H) for selected T and H.
figure 7

a At 4 K, a metamagnetic transition is observed for H∥a. b Low-field zoom of data with H∥a and linear slope subtracted showing hysteresis. c M(H) at low fields for H∥b. A tiny hysteresis is seen at 8.5 K, as is more obvious once a linear slope is subtracted, right scale.

Full size image

Fully relativistic density functional theory (DFT) calculations predict the ground state of Eu5In2Sb6 to be close to an afm A-type configuration with the Eu spin moments in the ab-plane and antiparallel stacking along c15. The easy magnetization direction is along b14,16. Recent neutron data are consistent with this picture, particularly for TN2 ≤ T ≤ TN122,23. Given the aforementioned relation of our dilatation data to the magnetic properties, it is then not surprising that α010(T) is small, see inset to Fig. 2a. The magnetostriction at 7.5 K is similarly small, red data in Fig. 6b. The magnetic structure facilitates a spin-flop transition which is clearly seen in ΔL010(H) at \({H}_{{{{{\rm{m}}}}}}^{b} \sim\) 2 T. M(H) data revealed this spin-flop to occur at all T < TN116. In addition, ΔL010(H) again follows an H2-dependency up to HN1 ~ 7.4 T except near \({H}_{{{{{\rm{m}}}}}}^{b}\). The small offset in length after a cycle of field up- and down-sweeps possibly results from different configurations of magnetic domains34.

Discussion

The thermal expansion coefficients α010(T, H), inset to Fig. 2a, do not show an additional feature between TN2 ≤ T ≤ TN1 as it was seen along the a and c directions. With the Eu moments aligned along b, this provides a hint toward the origin of the additional crossover H+ in the a- and c-phase diagrams. As mentioned, there is sufficient evidence for polaron formation in Eu5In2Sb6 well above TN114,15,16,26,27. However, unlike in fm materials where the polarons are simply taken up with the onset of magnetic order30,35,36,37,38, in antiferromagnets the polarons may coexist with the material’s global (long-range) order35,39,40,41,42,43. Upon cooling Eu5In2Sb6 to below TN1, the already existing polarons with their short-range fm interaction in the ab plane can most easily embed into the afm ordered environment with their magnetic moments oriented along b, as suggested by the fm chains along b, see sketch of moments in Fig. 2. Along b and in region I of the phase diagram, the fm polarons simply include a few reversed moments around the trapped conduction electron, cf. sketch in Fig. 5a and ref. 41. Of course, the alignment of magnetic moments between different fm polarons can still be opposite and hence, a net antiferromagnetism can be observed along b. Note that, despite the afm ground state, short-range fm interactions are relevant in Eu5In2Sb6 as evidenced by Curie–Weiss fits of the high-temperature susceptibility14,16. It is this delicate balance of the two interactions—along with the gain in exchange energy—which allows fm polarons to easily form above TN144,45.

The situation is different for the a direction, Fig. 4. Below TN1, the sample expands with decreasing T, a behavior observed in a few afm materials upon entering the ordered state46,47. As a result of the intermediate magnetic anisotropy along a, the magnetization processes of the afm states are different compared to the b direction. In a simplified, two-sublattice picture of an antiferromagnet, a magnetic field along a or c results in a canting of the moments, and polarons with moment parallel H will experience a different change of its surface energy as compared to those antiparallel moments. In consequence, the effective size of these polarons and their stability against thermal or quantum mechanical fluctuations will be changed. (Note that such differences in polaron-moment alignment do not take hold for field applied in easy b direction.) Such a stabilization is reflected by the suppression of the negative α100(T, H) just below TN1 with increasing fields up to μ0H = 4 T. Essentially, this picture of embedded ferromagnetic polarons should also hold for the more complex afm state of Eu5In2Sb6 in applied fields perpendicular to the easy axis. Hence, these high-field data suggest that in region I, fm polarons coexist with afm long-range order. This is corroborated by the negative magnetostriction ΔL100 at higher fields in Fig. 4c indicating a suppression of afm fluctuations. The larger jump of α100(T, H) at TN1 and small fields, i.e., upon going from the paramagnetic into region III in the phase diagram, is then consistent with a prevailing afm transition at HN1 while the crossover at H+ marks the additional impact of fm polarons. The different afm order below HN2 with the magnetic moments along a22,23, region II, terminates the signatures of polaron existence as seen by the very strong changes in both thermal expansion and magnetostriction. The suggestion of a relieved competition between afm and fm correlations23 is consistent with this scenario.

The twofold change of slope of the magnetostriction ΔL(H)/L0 in Fig. 6a clearly indicates competing interactions and highly likely magnetic inhomogeneity. The resulting phase diagrams exhibit an unusual H+-crossover line with increasing H-values for increasing T which cannot be explained by anisotropy effects alone31,33. Rather, such an unexpected thermal behavior is predicted by a phenomenological model introduced in Supplementary Note 5. This model considers anisotropic polarons in an antiferromagnet and finds an increased stability of the fm polarons inside the global afm order upon decreasing temperature, i.e., upon going from region III to I. Concomitantly, the polarons’ volume decreases. As a consequence of these two effects, the decreasing magnetization of the low-field hysteresis in Fig. 7b, c, which indicates a fm polaronic component, can be rationalized. In contrast, in the more common case of fm polarons in an eventually fm ordered material, the polarons would just dissolve upon entering the globally ordered state.

For fields along a and c large enough to drive the system close to the field-polarized paramagnetic state, polarons with moments opposite to the field direction cease to exist, leaving only polarons with parallel components along the field direction. The fact that the H+-crossover lines end on the HN1-lines in the magnetic phase diagrams, Fig. 5, in a field range comparable to the spin-flop field \({H}_{{{{{\rm{m}}}}}}^{b}\) for H∥b corroborates such a simple picture. Here, the Zeeman energy compensates the magnetic anisotropy.

The qualitatively complementary behavior along the a and c axis below TN1, best seen in Fig. 4b and its inset, suggests similar short-range fm and long-range afm competition in the phase diagrams of these two directions. Hence, the above assignments of the regions I–III can be cross-compared with the magnetostriction results ΔL(H) for H∥c in Fig. 6a. At 4 K, the initial decrease of ΔL(H) marks afm region II, while its increase above HN2 in region I (a behavior similar to the one observed before48) signals the incorporation of fm polarons. At 8.5 K, long-range afm and short-range fm correlations coexist and compete, which causes the initially negligible ΔL(H). Increasing H favors the fm arrangement and ΔL(H) increases. An increasing volume upon going from a preferred afm to a fm moment configuration was observed e.g., in (Hf,Ta)Fe249. In the paramagnetic regime beyond HN1 the field suppresses magnetic fluctuations and ΔL(H) decreases. At 12 K, the afm order gives rise to the contraction of the sample in region III, which smoothly crosses over into an expansion above H+, where polarons appear to exist more easily. The paramagnetic state above HN1 is again accompanied by a negative λ.

Interestingly, the temperature T+ corresponds to the steepest decrease in r(T) upon decreasing T (Fig. 3) consistent with its assignment as a crossover. A strong decrease of resistivity near 10.5 K in zero field was also reported earlier23. We emphasize that the slopes of r(T) just above TN1 and somewhat below T+ coincide, as indicated by the dotted line in Fig. 3. This is highly suggestive of polarons continuing to exist below the onset of afm order at TN1 and both phenomena operating relatively independent of each other.

A physical picture of electronic transport in Eu5In2Sb6 has to incorporate the existence of self-trapped fm polarons within the afm phases, which generates a magnetically and electronically inhomogeneous behavior. DFT results15 suggested Eu5In2Sb6 to be a semimetal with small Fermi sheets. The availability of charge carriers was found to depend strongly on the spin configuration, with the fm state having a strongly enhanced density of states (DOS) at the Fermi level EF compared to (collinear) afm configurations. The suppression of the fm polaron volume towards lowest T decreases the availability of charge carriers, while the magnetically inhomogeneous and noncollinear configuration in the ground state impedes electronic transport. This explains both the strong increase of ρ(T) at lowest temperatures and the remarkably large magnetoresistance. In particular, the magnetoresistive properties appear to be similar to those observed in metallic granular magnetoresistive materials50,51. An alternative picture arises in insulating or semiconducting materials where charge carriers (stemming solely from defects) are dressed as fm polarons and are exclusively responsible for electronic transport. The observed behavior of ρ(T) upon lowering T should then be explained by the density of polarons and eventually by increased magnetic scattering of the mobile fm polarons in the afm matrix. We emphasize that both scenarios rely on the existence of fm polarons and the self-trapping of charge carriers both in the paramagnetic and within the afm-ordered states. Further investigations of electronic band structure are needed here.

Our thermal expansion measurements reveal a strongly anisotropic behavior of Eu5In2Sb6 and nicely confirm the existence of anisotropic polarons well above TN1. In particular, an enhanced DOS at near EF inside the ferromagnetically ordered polarons15 provides an explanation for the huge negative magnetoresistance in Eu5In2Sb6 which differs from the double-exchange mechanism in CMR manganites6. In the antiferromagnetically ordered phase below TN1(H) the magnetostriction results point to a coexistence of global afm order with fm polarons, with the latter being stabilized upon decreasing temperature. In contrast, there is no indication for polarons below TN2(H). The insight into polaronic behavior provided here may help in advancing CMR effects in materials suited for applications.

Methods

Single crystals of Eu5In2Sb6 were grown by a combined In-Sb self-flux technique14. Here we report results obtained on the same crystals as those investigated earlier16 (additional samples investigated here came from the same batch). The crystallographic orientation of the single crystals was determined by a real-time Laue X-ray system (Laue-Camera GmbH52), see also Fig. 1e in ref. 15 and Supplementary Note 1 and Supplementary Fig. 1.

For thermal expansion and magnetostriction measurements a dilatometer cell was employed53. The cell was equipped with a Cernox temperature sensor providing an accuracy of better than  ±(10 mK + T/1000). The measurements were conducted in a Physical Property Measurement System (PPMS) by Quantum Design Inc.54 with a maximum magnetic field of 9 T applied parallel to the sample direction along which the dilatation was measured. Special attention was paid to minimize electrical noise55. Thermal expansion measurements were conducted upon warming the sample (if not stated otherwise) and repeated at least once for comparison. The error of the measured relative length changes ΔL/L0 in thermal expansion and magnetostriction was estimated to ≤10−6. The error bar of the calculated absolute values of the thermal expansion coefficients α amounts to about 5⋅10−7 K−1. This may account for the apparent low-temperature offsets, particularly along the b direction for which the sample dimension was smallest (see Supplementary Fig. 1). Before each magnetostriction measurement the sample was heated up to at least 100 K to avoid any influence of the magnetic history of the sample. Unfortunately, the samples often broke inside our measurement cell, specifically upon applying magnetic fields, a fact that severely limited the number of results obtained at higher fields.

Magnetization measurements were conducted in a Magnetic Property Measurement System (MPMS3) by Quantum Design Inc.54 with an accuracy of better than 0.004 μB/Eu.