Introduction

Ultrafast optical manipulation of ferroelectricity1,2,3 and magnetism4,5 in transition-metal-based materials has attracted much attention for developing the next-generation electric and magnetic devices working in the tera-to-petahertz regime. It is the natural idea that utilizing the photoinduced phase transition (PIPT) to modify the long-range orders of electric dipoles and spins is effective. However, observing photoinduced long-range structural changes with ultrafast speeds in real crystals is challenging. Another way is to look for materials in which rather localized photoinjected excited states modify the electronic dipoles and spin exchange interactions around them via strong electron-lattice coupling. In this work, we demonstrate that this idea is practical for modifying the electric dipole and spin exchange of the BiFeO3 thin film at room temperature in the femtosecond time region.

The magnitude of the polarization, optical nonlinearity, and magnetic exchange interaction are strongly coupled with the crystal structure in the materials with strong electron-lattice-spin interaction, and intensive research has been performed on the coupling mechanisms as the origin of multiferroics6,7,8,9,10. Suppose high-frequency phonons in the THz range associated with proper structural modification are generated by optical excitation; the control of the electric polarization, magnetization, and both at once in the femtosecond region can be expected. Very recently, THz field-induced ferroelectricity was found on quantum paraelectric SrTiO311,12, and the THz-induced structural instability due to the combined dynamics between the ferroelectric (FE) and antiferrodistortive (AFD) modes of the perovskite has been under intensive discussion13,14,15. These works stimulate the exploration of the crystalline displacements or phonons generated by optical excitation on the femto-to-picosecond time scale in transition-metal-based multiferroic materials.

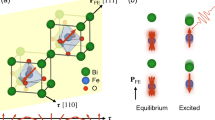
Under such a background, a displacive-type multiferroic perovskite oxide BiFeO3 (BFO), which exhibits ferroelectricity, canted antiferromagnetism, and ferroelasticity at room temperature, has been selected as the target material6,16,17,18,19(See Fig. 1). In this system, we have confirmed the ultrafast polarization change within a few 100 fs (equivalent to several THz) induced by the charge transfer (CT) excitation from the O 2p to Fe 3d bands in the measurement of the photoinduced change of the second harmonic generation (SHG) yield19. The ground state of BFO is a (d5 high-spin of Fe3+) half-filled Mott insulator with the CT gap around ~ 2.5 eV from the O 2p to Fe 3d bands20,21,22. The pump laser around 3.1 eV (λ ~ 400 nm) always introduces the electrons into the minority-spin orbitals of the Fe 3d bands, as schematically described in Fig. 1b. Therefore, the CT excitation and its relaxation process are expected to disturb the magnetic order at local of the Fe sites. In contrast, the 6s and 6p bands for the Bi electronic states lie far below and above the Fermi level, respectively20,21,22,23,24. Then, the present CT excitation will not directly affect the band structure or polarization of the Bi sites. However, as discussed later, ultrafast polarization reduction was confirmed in the SHG measurements. Therefore, the coupling between the magnetic exchange and ferroelectric polarization in the photoexcited state is highly expected.

Fig. 1: Schematics of the crystal and band structure of BFO/STO(111) thin film.
figure 1

a Crystal structure of BFO/STO(111) thin film with R3c symmetry. The blue arrows on the Bi3+- and Fe3+- atoms denote the displacements from the ideal cubic perovskite which arise the electric polarization (P) along the [111]pc or [0001]h direction (pc and h denote pseudocubic and hexagonal notation, respectively) (QFE). The FeO6 octahedra have an antiphase rotation around the polar axis which couples with the magnetic ordering (QAFD). b Schematics of the band structure and optical excitation. c Optical absorption spectrum of BFO/STO thin film in the ground state and the one observed just after the pump pulse irradiation (t = 0.2 ps). The in-gap absorption observed in the current transient optical spectroscopy just after the CT excitation can be assigned as the electron excitation in the Fe2+-like excited state to the unoccupied Fe 3d bands from the theoretical calculation shown later. At the same time, it corresponds to a self-trapped CT exciton due to the strong CT instability in the scenario suggested by Pisarev et al.21,22.

Full size image

BFO’s phonon mode, causing FE polarization, is observed at around 4.2 THz10,25,26,27,28,29,30,31,32. In contrast, the AFD phonon mode modulating the antiferromagnetic interaction is around 6.6 THz. Therefore, the observation of coupling between one of the above two phonons and a photocarrier, i.e., dynamical changes in phonon modes induced by the photoexcitation in several THz region, is a key experiment for confirming the possibility of the photo-control of the electric polarization and magnetization in this system. Lately, we have developed a laboratory-based system for observing ultrafast electron diffraction (UED) with a time resolution shorter than 100 fs33 to probe structural dynamics in several THz range. Here, we report the simultaneous occurrence of the photoinduced change of the nonlinear optical property, strong lattice modulation, and generation of the in-gap absorption within a few 100 fs after photoexcitation of BFO at room temperature.

The comparison with the theoretical study shows that the origin of the observed intense lattice vibration induced by photoexcitation can be attributed to the unexpectedly softened phonons strongly coupling with polarization and magnetic exchange. The theoretical study also reveals that the observed extreme softening of the phonon modes is due to the coupling of the phonons and localized photodoped carriers, namely the phonon-photocarrier-coupled (PPCC) effect similar to the phonon-dressed-exciton state3,34,35. In addition, both experimental and theoretical results show that photocarrier injection never induces a clear-cut insulator-metal transition in this system, though photoinduced metallization is widely observed in transition-metal oxides3,36.

Physical properties of BiFeO3

BFO belongs to a ferroelectric perovskite with spontaneous polarization over ~100 μC cm−2, having the rhombohedral distortion below Tc ~ 1120 K and a cycloidal spin modulation superimposed on a G-type antiferromagnetic order at the Fe sites below TN ~ 640 K37,38. The ferroelectric polarization and magnetism are coupled with lattice distortions of the centrosymmetric breaking (QFE) and rotation in/around the FeO6 octahedral sites (QAFD), respectively (see Fig. 1a)10,37. The thin film of BFO can be grown on various substrates. In particular, the thin film fabricated on SrTiO3(111) substrate [BFO/STO(111)] has the same structural symmetry of trigonal R3c as that of the bulk crystal. Then, the electric polarization aligns perpendicular to the film surface19,38, confirmed by the piezoresponse force microscopy (PFM) as shown in Supplementary Information A.

Photoinduced exotic effects on the BFO-based materials have also been well studied, such as the visible-light-induced giant photovoltaic effects39,40, photoinduced crystal size change17, and domain switching/melting41,42 utilizing the ferroelastic and flexoelectric effects, THz emissions that depend both on the magnetic-field and light polarization43,44 and prominent electrochromic behavior45. Several pump-probed optical studies have revealed the photo generation of acoustic phonons with large amplitude and coherent magnons in the range below 100 GHz46,47 and 2.4 THz48. Despite these previous intensive studies, the initial stage of the light-induced dynamics in the crystal structure and elementary electronic excitation in BFO relating to the ultrafast modulation of electric dipole remains to be solved.

As described earlier, the ground state of BFO is a half-filled Mott insulator with a CT gap around ~ 2.5 eV (Fig. 1b,c). In addition, the characteristic absorption for BFO is observed below 2.2 eV, which corresponds to the on-site d-to-d crystal field excitations (6A1g → 4T1g and 6A1g → 4T2g) of the Fe3+ ions and arises from the intense mixture of Fe 3d and O 2p bands owing to the central symmetry breaking of the FeO6 octahedra (or displacement/polarization of the Fe atoms)20,22. It should be noted that this structure is indistinct on the BFO/STO(111) film, as shown in Fig.1c, compared to those reported on the (100) plane of the film20 and single crystal22, probably because the electronic polarization/displacement of the Fe atoms is always perpendicular to the in-plane polarization of the probe light for the BFO/STO(111) film. One may expect this absorption to decrease upon photo excitation with a decrease in electronic polarization since it simply arises from the degree of hybridization between the Fe 3d and O 2p orbitals.

However, in contrast, F. Meggle et al. reported that the absorption below 2.2 eV always increases upon photoexcitation and with the temperature increase22. Therefore, the CT-type excitonic effect21,22 and the crystal-field effect must be considered to explain the photoinduced effect of this material. The photoinduced absorption observed in this study can be classified as the lowest-energy extension (below 0.8 eV) of this crystal-field excitonic state reported in ref. 22. This photo-excited and trapped carrier in BFO has been controversial referred to as exciton or carrier. In this paper, they are referred to as photocarriers.

Results

Transient changes on second harmonic generation (SHG) yield and optical density (OD)

The upper panel of Fig. 2a shows temporal profiles of the relative change of SHG (ΔISH/ISH) with 3.1 eV excitation on BFO/STO(111) thin film, reported previously19. Here, the intensity of SH (ISH) reflects the degree of QFE and QAFD (Fig.1a). Just after the photoirradiation, ΔISH/ISH suddenly decreases by ~30% at the fluence of 5.2 mJ cm−2, indicating that a kind of photoinduced transient state with less electric dipoles immediately forms within the experimental time resolution of ~200 fs after the photoexcitation and exponentially relaxes with the time constant of τ ~ 220 ± 15 fs19. The τ value scarcely varied with changing the pump fluence.

Fig. 2: Photoinduced dynamics of BFO.
figure 2

a Temporal profiles of relative change of the SH intensity (upper, ΔΙSH/ΙSH) derived from ref. 19, and optical absorption (lower, ΔOD) at the selected photon energies (0.2, 0.5, 0.6, and 0.7 eV) after the 0.1 ps light pulse irradiation of 3.1 eV at room temperature (T = 300 K). The solid lines show fittings according to the function: I(t) = I1exp(-t/τ) + I2, convoluted of the instrument response function ~0.2 ps (t > 0) (See, Supplementary Information B). b ΔOD spectrum at around t ~ 0.2 ps. c Excitation-fluence dependence of the relative change of the ΔΙSH/ΙSH (left) and ΔOD of 0.5 eV (right) at around t ~ 0.2 ps after the photoexcitation.

Full size image

The photo-absorption (or optical density: OD) of the BFO/STO(111) thin film was examined to confirm the transient change of the electronic state occurring with ΔISH/ISH. The lower panel of Fig. 2a shows the temporal profile of photoinduced change in OD (ΔOD) at 0.2, 0.5, 0.6, and 0.7 eV after the pump laser excitation (The temporal profiles probed at different photon energies, and details of the analysis are given in Supplementary Information B). A quick increase of ΔOD within the time resolution of ~200 fs and subsequent relaxation into the long-lived state with a time constant around τ ~ 210 ± 20 fs are observed. The relaxation time constant of ΔOD is consistent with that of ΔISH/ISH. In contrast, scarce absorption is observed in the ground state at this low-energy region (Fig. 1c). Figure 2b shows the ΔOD spectrum observed at around 0.2 ps after the photoexcitation, which can be assumed as the spectrum of the photoinduced transient state.

The ODs at all energy regions increase after the photoexcitation. However, the change is maximized around 0.6 eV and becomes very small at the photon energy lower than 0.2 eV. Therefore, no Drude-like response is observed, unlike the dynamics for Insulator-Metal transition found in photoinduced dynamics for the various transition-metal compounds3,36, suggesting that no-free-photocarrier with high density exists after the photoinduced dynamics for this system. It is the reasonable idea that the origin of this photoinduced absorption will be a lowest-energy extension of the crystal-field exciton reported previously22. More details will be discussed later.

It should be noted that the changes of both SH intensity and OD observed at t ~ 0.2 ps just after the photoexcitation linearly depend on the excitation fluence in a wide fluence range between 0–8 mJ cm−2 as shown in Fig. 2c. No threshold-like dependence nor unreversible effect has been observed up to 8 mJ cm−2. Thus, the photoinduced domain structure melting41,42 and transition to the cubic phase cannot explain the observed photoinduced SH intensity and OD changes in the BFO/STO(111) film. By contrast, the slower component (t > 1 ps) observed in the SHG experiment saturates at around ~3 mJ cm−2 19. Further study will be needed to clarify this specific response.

Ultrafast electron diffraction (UED)

We survey the photoinduced structural dynamics on the BFO/STO(111) thin film by the table-top UED system with the sub-100 fs time resolution33. Figure 3 summarizes the results obtained by UED. The diffraction patterns were taken in the \({[01\bar{1}1]}_{{{{\rm{h}}}}}\) (or [132]pc) zone (See Methods). All the diffraction intensities at \({30\bar{3}0}_{{{{\rm{h}}}}}\), \({4\bar{131}}_{{{{\rm{h}}}}}\), \({5\bar{232}}_{{{{\rm{h}}}}}\), and \({2\bar{2}0\bar{2}}_{{{{\rm{h}}}}}\) immediately and almost simultaneously decrease >30% within 200 fs after the femtosecond laser irradiation, consistent with the timescale in the decrease of the SHG intensity and increase of ΔOD, i.e., the formation of the less-electric dipole transient state. Moreover, the relaxation dynamics (t > 150 fs) of the diffraction intensities involve an intense oscillation with periods around 300 fs. It should be noted that the diffraction of \({4\bar{131}}_{{{{\rm{h}}}}}\) includes information on QAFD along [0001]h and diffraction spots of \({30\bar{3}0}_{{{{\rm{h}}}}}\), \({5\bar{232}}_{{{{\rm{h}}}}}\), and \({2\bar{2}0\bar{2}}_{{{{\rm{h}}}}}\) reflects QFE or expansion/shrinking of perovskite unit cell. All the diffraction intensities show almost the same oscillation periods.

Fig. 3: Result of the time-resolved UED.
figure 3

Time-evolution of the intensities of \({30\bar{3}0}_{{{{\rm{h}}}}}\), \({4\bar{131}}_{{{{\rm{h}}}}}\), \({5\bar{232}}_{{{{\rm{h}}}}}\), and \({2\bar{2}0\bar{2}}_{{{{\rm{h}}}}}\)-types diffraction spots (left panel) after the 3.1 eV pulse irradiation with 1.8 mJ cm−2 fluence at room temperature (T = 300 K), indicated by the red, blue, orange, and green circles, respectively, on the diffraction patterns (right panels). The shades at each plots indicate the statistical error. The solid lines in time evolution represents a fitting used to estimate the frequency and decay times of the oscillatory structure (See Supplementary Information C in detail). Dashed lines in the patterns indicate the 1st Brillouin zone. The lattice-type absences of the diffraction peaks for symmetry of R3c are marked by crosses on the simulation, where multiple scatterings are possibly observed (Details are given in Fig. S9).

Full size image

The frequency of the oscillation and its decay time are estimated to be ~3.3 ± 0.1 THz (or ~110 cm−1) and 180 ± 40 fs, respectively (Details about the data analysis are shown in Supplementary Information C). The decay time is almost consistent with those observed in SHG and absorption experiments, indicating that the oscillation will relate to the electric dipole change. However, the frequency of this vibration does not correspond to any significant phonon mode in the ground state reported in the Raman scattering experiments and calculations10,25,26,27,28,29,30,31,32. The defect-induced small peak around 3.3 THz (~105 cm−1) was reported and assigned as an A2 mode25,28. However, this mode cannot induce the change of the electric polarization (nor antiferromagnetic order).

The observed frequency seems to be 20–50% softened from the A1 modes at ~4.2 and 6.6 THz as the FE- and AFD-vibrations along the polarization, respectively10,25,26,27,28,29,30,31,32. Such phonon softening realized under photoexcitation is crucial for explaining the observed strong lattice vibration. Later, theoretical model calculation reveals that the coupling effect between these phonons and localized photocarriers (PPCC effect), similar to the phonon-dressed-exciton state, can explain the observed results.

One may feel curious that the oscillation around ~3.3 THz was only pronounced on UED and scarcely observed on the absorption and SHG measurements. It is notable that the modulation caused by the photocarriers should remain trapped around the excited local site, and the photoinduced long-range structural change to the cubic phase does not occur as discussed previously. Consequently, while this mode is distinct in the dynamics of the diffraction intensity, which can reflect the local structural disorder, its manifestation remains unclear in the dynamics of SH intensity (reflecting the overall crystal symmetry) and optical conductivity (reflecting band structure). As given in Supplementary Information F, the numerical simulations also exhibit a distinct behavior concerning the dynamics for QFE and QAFD in the polarization and optical conductivity dynamics. Still, the photoinduced softened mode around 3.3 THz is ‘indistinct’ in the polarization and optical conductivity dynamics. In addition, additional discussions about temporal profiles at lower excitation fluence (0.9 mJ cm−2) and in a longer time scale, as well as resolution time effects on the oscillation intensity, are given in Supplementary Informations C and F.

It is a natural idea that a possible origin of observed abrupt decreases in the intensity of UED and SHG may be the effect of the screening induced by the carriers generated by photoinduced Insulator-Metal phase transition. However, the emergence of the ‘free photo-carriers’ with high density was neglected based on the result of the transient absorption, as previously discussed. In addition, the shift of the diffraction spot positions, which reflects the change of the lattice constants or the symmetry of the whole unit cell, is scarcely observed in the UED experiment.

In addition, the results observed by UED measurement cannot be attributed to simple photothermal effects. Even if 100% photon energy was absorbed in 50 nm thick BiFeO3 film, the expected value for the average temperature rise was estimated to be less than ~150 K under the condition with density49 of 8 g cm–3 and specific heat50 of 0.3 J g–1 K–1. The decrease of the diffraction intensity due to this temperature increase is estimated to be <5%, much smaller than the observed value (~30%) under the photoexcitation of 1.8 mJ cm–2. Moreover, the diffraction change starts at 0.1 ps, which is too fast to be considered a simple photothermal effect (typical timescales of 2–3 ps). And, if the observed results by UED measurement were due to simple photothermal effects, a permanent change in SHG intensity by domain wall injection due to the 150 K rise of the sample temperature could be expected, which was also not confirmed by the experiment.

Suppose the observed results by UED measurement were due to ordinal coherent phonon generation induced by photoexcitation51,52. In that case, the coherent oscillation of other Raman-active major modes, such as E mode around ~2.4 THz25,26,27,28,29,30,31,48 should be prominent in the photoinduced dynamics rather than a peculiar coupling of the two A1g modes as observed ~3.3 THz.

As a result, we can conclude that the photoinduced motion of Fe sites induces disorder or randomness in the whole structure of BFO. It decreases the UED and SH intensities via strong coupling between localized photocarrier and lattice, leading to the extraordinary softening of FE and AFD modes without symmetrical change or significant changes on the lattice constants as discussed in the theoretical part (Further details about the estimation of atomic motions are discussed in Supplementary Information D).

Model calculation

As discussed in the previous sections, the suppression in the SHG yield and the suppression in the electron diffraction intensity with the strong oscillation were observed just after photoexcitation. We performed numerical simulations using a theoretical model for BFO to examine the dynamical changes in lattice vibration by photocarrier injection. In BFO, the occupied electrons in Fe3+ ion are localized in a high spin state, (t2g)3(eg)2, and O 2p electrons are most itinerant near the Fermi level20,21,22,23,24 (see Fig. 4). In this model, we consider the itinerant electrons with spin degrees of freedom, two sublattice degrees of freedom corresponding to two FeO6 sites along the c-axis, and two intra-site orbital degrees of freedom for electric polarization. Thus, the electron system has eight bands in the reduced Brillouin zone. In addition to these itinerant electrons, we incorporated two localized spins of Fe3+ and two types of lattice distortions: QFE, which couples to the electronic polarization, and QAFD, which is proportional to the magnetization of the localized canted spins (see Fig. 1a). In the ground state, the itinerant electrons occupy the lower four bands, stabilizing a ferroelectric canted-antiferromagnetic insulating state. The injection of electrons into the four unoccupied bands triggers the real-time dynamics, mimicking the CT excitation from oxygen to iron atoms. Details about our model and calculations are indicated in Fig. 4 and Methods.

Fig. 4: Theoretical model for coupled dynamics of electrons, spins, and lattice distortions in BiFeO3.
figure 4

a Schematic of the density of states for BiFeO3. Fe(1) and Fe(2) denote Fe atoms on each sublattice of the spin-polarized FeO6 octahedra. The localized, spin-polarized Fe 3d electrons are described by the Landau-Lifshitz-Gilbert equation. Itinerant electrons below the Fermi level are primarily composed of O 2p electrons, which are simplified into a one-dimensional, two-orbital, two-sublattice tight-binding model. b Energy diagram of the theoretical model. The itinerant electrons hop to neighboring sites by a transfer integral of \(-h\) (indicated by orange double-headed arrows) and an electron-lattice coupling of \(\pm {\alpha }_{{\mbox{FE}}}{Q}_{{\mbox{FE}}}\) (green solid/dashed arrows). The ferroelectric distortion QFE lifts the degeneracy of the two orbitals in each sublattice and modulates the transfer integrals of the electrons. The chain direction of the tight-binding model is parallel to the z axis, corresponding to the c axis in the real material. The spacing of the two FeO6 sites is denoted by a. The electric polarization is proportional to the expectation value of the orbital pseudospin operator \(\left\langle {\upsilon }^{z}\right\rangle\) when a finite displacement δz of the Wannier center is considered. See Methods section for details of the model.

Full size image

Figure 5a shows the temporal profiles of QFE and QAFD after carrier injection at \(t=0\). FE and AFD lattice distortions are initially suppressed and subsequently relaxed to their equilibrium positions, aligning with the observations from the UED and SHG experiments. The reduction in lattice distortions is ascribed to a sudden decrease in the electron-lattice coupling energy proportional to \({\alpha }_{{\mbox{FE}}}\) (See Fig. S10 of Supplementary Information E). Notably, QFE and QAFD exhibit coherent, synchronized oscillation at an energy of \(\hslash \omega =0.0091h\) (see Fig. 5b), consistent with the oscillation observed in the UED experiment, corresponding to 3.3 THz of the experiment if we read the electron transfer integral h as 1.5 eV. Surprisingly, this energy newly appearing on the photoinduced dynamics independent of Q is ~70% lower than both of the bare energies for the FE mode \((\hslash {\widetilde{\omega }}_{{\mbox{FE}}}=0.0264h)\) and AFD mode \(({\hslash \widetilde{\omega }}_{{\mbox{AFD}}}=0.0310h)\). Even considering the reduction in QFE and QAFD in the transient states, the bare energies of QFE and QAFD (plotted as solid and dashed curves in Fig. 5b) do not align with the numerical results. This behavior can be explained by analyzing the linearized equations of motion for the lattice distortions (see Fig. S12). These results suggest that the low-frequency oscillation observed in the numerical calculations can be attributed to the appearance of a new eigenmode of the lattice distortions, itinerant electrons, and localized spins on the energy surface of the excited state (denoted as the mode along QPPCC in Fig. 6, as discussed in the later part).

Fig. 5: Simulated real-time dynamics in a theoretical model for BiFeO3.
figure 5

a Temporal profiles of the ferroelectric and antiferrodistortive distortions, QFE (top panel) and QAFD (bottom panel). ΔQX = (QX − QX,0)/QX,0 (X = FE, AFD) represents the relative displacement measured from its equilibrium position QX,0. b Spectrograms of QFE (top) and QAFD (bottom), using their time derivatives to remove the dc (ω = 0) component. The solid and dotted curves illustrate the eigen-energies of the ferroelectric (QFE) and antiferrodistortive (QAFD) modes, respectively, calculated from the instantaneous values of QFE and QAFD in the absence of the couplings to the electrons and the localized spins. c Optical conductivity around the in-gap state (ℏω ≈ 2 h) at different times t.

Full size image
Fig. 6: Schematic of the energy potential surface after the CT excitation.
figure 6

a Schematic energy surface on the QAFD and QFE plane before (blue) and just after (red) photoexcitation. Photoexcited itinerant electron (photocarrier) is coupled with the localized electrons on the ground state surface. b Time evolution of the quartic potential surface cutting along the direction of QPPCC mode shown in (a). The circles and the arrows in the local minima of the potential curves indicate the electrons and spins, respectively. The CT excitation by laser induces the excitation into the different potential surface as the Fe2+ itinerant electrons which is distinct from that of the localized electrons on the ground state energy surface. The excited itinerant and localized electrons are tightly bound with each other and relaxed into to a metastable state within a few ps through the combined energy potential surfaces. Due to coupling between phonon modes and localized photocarrier (PPCC effect) similar to the phonon-dressed-exciton, phonon modes are strongly softened.

Full size image

Figure 5c shows the optical conductivity at various delay times after carrier injection. The in-gap absorption around \(\hslash \omega \approx 2h\) just below the original absorption levels appears by the carrier injection (t = 0), similar to the experiment, and almost relaxed within 2 ps on the calculation. This in-gap absorption corresponds to the excitation between the unoccupied bands of Fe 3d itinerant electrons with the energy difference ~2gFEQFE (Fig. 1b), activated by carrier injection. The estimated energy level of the photoinduced absorption band by model calculation at 2 h = 3 eV for h = 1.5 eV is higher than the observed one. This discrepancy can be explained by the excitonic effects between the photoinjected itinerant electrons and localized holes, as discussed in the following section.

Discussion

It is the reasonable idea that the observed ultrafast and drastic softening of the phonon modes in the present UED reflects the tight coupling between the dielectricity and magnetic interaction via the lattice distortions in/around the FeO6 octahedra. Our model calculation assumes that the energy potential surface in multiferroic BFO has two minima against both order parameters of QFE and QAFD10 (Fig. 6a). The results show that the energy surface of the excited itinerant electron is distinct from that of the localized electrons in the ground state. Due to the strong electron-lattice interaction on the excited state energy surface, an eigenmode of the lattice distortions, itinerant electrons, and localized spins (mode along QPPCC) appear as indicated in Fig. 6 (PPCC effect). Based on the calculation, the estimated frequency of these new modes seems relatively lower than the original ones in the ground state. In other words, passing through the potential surfaces of the excited itinerant electrons, the instability between QFE and QAFD makes a significant and softened oscillation of the lattice structure in/around the FeO6 octahedra during the relaxation process through the electron-lattice coupling. This estimation is consistent with the observed results of UED. Then, we can conclude that carrier injection to the Fe 3d band effectively causes the local lattice distortion at the FeO6 sites.

The emergence of a low-energy, in-gap trapping state in BFO has been suggested in the higher-energy pump-probe study47. In addition, Pisarev et al. predicted that BFO is classified as a CT insulator with strong charge fluctuation between the occupied O 2p and unoccupied Fe 3d orbitals21. The ‘self-trapped CT exciton’ describes the lowest in-gap response smearing of the fundamental absorption edge in their scenario. The photon energy of the observed in-gap state utilizing the transient spectroscopy (at t ~ 0.2 ps) is similar to the self-doped state for Fe2+ or oxygen’s defect level in the FeO6 sites observed in the static experiments24,53, and theoretical calculations54,55. Therefore, the reasonable idea is that the present CT excitation creates holes in the O 2p band and is immediately trapped by a Fe2+-like state, forming a CT exciton of which the absorption band is around 0.6 eV. Our model calculation also shows the appearance of the low-energy in-gap state after photocarrier injection. However, as discussed earlier, the energy is slightly higher than the experimental photoinduced in-gap state shown in the inset of Fig. 1c. If electronic correlations such as the excitonic effect between the localized hole and itinerant electron are taken into account more precisely, these states could become a kind of bound state as experimentally observed.

Moreover, the previous model calculation shows that the electric dipole induced by such a trapping hole at oxygen vacancy can cancel out a few 10% of the spontaneous polarization55. This model calculation seems to be consistent with a few 10 % suppression on the SH signal in the transient state observed in the present study (Fig. 1b). Since the CT excitation in BFO directly disturbs their CT instability, the self-trapping state will be formed immediately just after photoexcitation as the exciton rather than polaron.

Furthermore, the appearance of the exciton is consistent with the result of UED. In the UED experiments, the intensity of the diffusive scattering increases after the pump-pulse excitation against the decrease of the diffraction intensities with the oscillation, as shown in Figs. S3 and S4 of Supplementary Information C. Such increases in diffusive scattering have also been observed in the recent UED studies for SnSe56 and WSe257. For SnSe, the diffusive scattering is assigned to an anisotropic polaron formation56. In the survey for WSe2, the diffusive scattering is observed at the whole of the Brillouin zone and regarded as an indication of a non-thermal energy transfer from the electrons to phonons57. In this regard, it is reasonable to consider that the excitonic state in BFO will be bound around the localized oxygen holes in the transient state and subsequently relax within a few ps accompanied by the coherent phonon. The exciton has been known to become a good phonon-trapping center. Thus, the observed drastic softened phonon vibration due to the PPCC effect seems analogous to the phonon-dressed-exciton state3,34,35.

To summarize, we have demonstrated the emergence of an itinerant and localized electron-bounded transient state (excitonic state) within 200 fs in the photoinduced dynamics of BFO/STO(111) thin film by combining the femtosecond UED and optical spectroscopy. The numerical calculation reveals that oscillation around 3.3 THz newly observed in the relaxation process from the transient state to the metastable state probed by UED reflects the PPCC effect, which induces unexpected and extraordinary softening of the phonon modes. The results demonstrate that the trapped photocarrier (exciton-like state) strongly couples with the phonon in BFO, and thus, photo modulation of both QFE and QAFD, i.e., the ferroelectricity and magnetic interaction via the observed structural modification can be realized in the ultrafast time scale, even in the THz region at once. As reported here, the combined use of spectroscopic and structural probes in the femtosecond time region strongly suggests the realization of electric dipole and magnetic switching at once with ultrafast speed by light in multiferroic materials based on a robust electron-lattice coupling effect. In addition, the results may provide clues to explain the highly efficient responses to the optical excitation reported in the various studies for BFO-based materials based on ultrafast structural modifications39,40,41,42,43,44,45,46,47,48. Further ultrafast studies about magnetic order combined with UED are promising for developing the ultrafast control of dipoles and spins in multiferroic materials.

Methods

Synthesis of BiFeO3 thin films on SrTiO3 (111) substrate

Thin films of BiFeO3 with a thickness of about 40 nm and 100 nm were grown on a SrTiO3 (111) substrate 500 μm thick using a pulsed laser deposition method with some adjustments described in ref. 30. The substrate temperature and oxygen pressure were set to 600–640 °C and 15 Pa, respectively. The film area for the optical measurements was about  × 10 mm2.

Transient optical spectroscopy

Transient second harmonic generation (SHG)-yield measurement was performed on the 100 nm-thick BFO/STO(111) at room temperature. The details are described in ref. 19. Transient transmission and reflectivity measurements were performed on the 40 nm-thick BFO/STO(111) at room temperature. To estimate the absorption or optical density (OD) of BFO, the probe pulse’s transmission and reflectivity were simultaneously measured, and their transient changes with photo-irradiation were obtained by a pump-probe method. A Ti:sapphire regenerative amplifier system (center wavelength, 792 nm; pulse width, 90 fs; repetition rate, 1 kHz; Spectra-Physics Solstice Ace) was used as the light source. The polarization of the pump pulses is parallel to \({[11\bar{2}]}_{{{{\rm{pc}}}}}\) The pump pulse wavelength was set to 396 nm using a BBO crystal, and that of the probe pulse was varied from 650 nm (1.8 eV) to 6200 nm (0.2 eV) by the optical parametric amplifier (OPA) and BBO crystals. The pump and probe optical pulses were focused on the sample, and the transmitted and reflected probe lights were detected with adequate photodiodes, depending on the wavelength. The incident fluence of the pump light was ~6.4 mJ cm−2.

The repetition rate of the pump pulse was reduced to 500 Hz using a synchronized optical chopper to compare the intensity of the transmitted/ reflected light with/without photoexcitation. The dimension of the ellipse pump light was typically 320 × 280 μm2, and the diameter of the probe light was about 40 μm. The repetition rate of the probe light was 1 kHz, and a gated integrator obtained the intensity of the transmitted/ reflected light.

We also measured the ΔOD of the SrTiO3(111) substrate with the same setup immediately after BFO was measured. Then, the energy and their pump- and probe-pulses overlapping should be almost similar. Only the fluence was changed from 6.4 mJ cm−2 for BFO and 4.3 mJ cm−2 for bare STO, correcting the absorption of pump-light in BFO at 3.1 eV, and the results are shown in Supplementary Information B.

Ultrafast Electron Diffraction experiments

Ultrafast Electron diffraction (UED) experiments with sub 100 fs time-resolution were performed on the home-built 100 keV UED system with the electron pulse compression technique by ~3 GHz RF33 at room temperature.

The light source for UED was another Ti:Sapphire regenerative amplifier (pulse duration time, approximately 35 fs; center wavelength, 800 nm; repetition rate, 1 kHz). Part of these light pulses is upconverted to 266 nm pulses and generates bunches of 106 to 107 electrons through the photocathode of the thin gold film deposited on the Al2O3 substrate. These electrons are then accelerated to 100 keV in a DC electric field. Electron bunches are compressed with a radio frequency (RF) cavity with low energy to counterbalance space charge repulsion, resulting in a time resolution shorter than 100 fs at the sample. The pulsed electrons pass through the sample, and a CCD camera detects diffracted electrons. The other part of the pulses is upconverted to 400 nm and is used to photoexcite the sample, almost collinearly with the electron propagation axis (∼5°). The polarization of the pump pulse is parallel to \({[11\bar{2}]}_{{{{\rm{pc}}}}}\) similar to optical experiments. Experiments were repeated for up to 50 h to maximize signal-to-noise ratio, which was made possible by improvements in RF cavity-laser synchronization.

Five samples were used for the UED measurements to ensure reproducibility. Mechanical grinding and Ar+ ion beam milling were used to narrow the BFO/STO(111) with 100 nm thickness so that the electron beam could penetrate the film with the substrate. The films were hollowed from the backside of the substrate, and the ion beam was tilted a few degrees from the surface. Then, the film thickness of BFO is estimated to be ~50 nm on average but nonuniform. The size of the thin area of BFO was a few μm2, and the beam size was ~100\(\times\)100 μm2, enough to cover all narrow regions of the fabricated BFO/STO sample. To investigate the lattice dynamics along the electric polarization, the samples were tilted ~21° from the normal of the film surface against the electron beam, then the diffraction patterns were taken in the \({[01\bar{1}0]}_{{{{\rm{h}}}}}\) (or [132]pc) zone. The diffraction signals from the SrTiO3(111) substrate also seem to be overlapped with the diffraction of BFO. Because the intensities of SrTiO3 scarcely change during the time-resolved experiments against the laser irradiation (not shown), the intensities of other diffraction spots from BFO are normalized using these intensities.

Theoretical calculation

We construct a theoretical model describing the itinerant electrons, localized spins \({{{\boldsymbol{S}}}}_{{\mbox{A}}}\) and \({{{\boldsymbol{S}}}}_{{\mbox{B}}}\), and lattice distortions \({Q}_{{\mbox{FE}}}\) and \({Q}_{{\mbox{AFD}}}\). The electron spin, sublattice, and orbital degrees of freedom are represented by the Pauli matrices \({{\boldsymbol{\sigma }}}\), \({{\boldsymbol{\tau }}}\), and \({{\boldsymbol{\upsilon }}}\), respectively. The Hamiltonian consists of seven parts: \(H={H}_{{\mbox{el}}}+{H}_{{\mbox{el}}-{\mbox{el}}}+{H}_{{\mbox{lat}}}+{H}_{{\mbox{sp}}} +{H}_{{\mbox{el}}-{\mbox{lat}}}+{H}_{{\mbox{el}}-{\mbox{sp}}}+{H}_{{\mbox{sp}}-{\mbox{lat}}}\). The first term, \({H}_{{\mbox{el}}}=-2h\cos \left(k\right){\tau }^{x}\), describes the one-dimensional inter-sublattice hopping of electrons with momentum \(k\), where h represents the nearest-neighbor transfer integral. The second term, given by \({H}_{{\mbox{el}}-{\mbox{el}}}=\left(U/2\right)\,{\sum }_{\tau ,\upsilon =\uparrow ,\downarrow }[\left\langle {\tau }^{\tau }{\upsilon }^{\upsilon }\right\rangle {\tau }^{\tau }{\upsilon }^{\upsilon }-\left\langle {{\boldsymbol{\sigma }}}{\tau }^{\tau }{\upsilon }^{\upsilon }\right\rangle \cdot {{\boldsymbol{\sigma }}}{\tau }^{\tau }{\upsilon }^{\upsilon }]\) with \({\tau }^{\uparrow /\downarrow }=({\tau }^{0}\pm {\tau }^{z})/2\) (and similarly for \(\sigma \) and \(\upsilon \)), represents the on-site, intra-sublattice, and intra-orbital repulsive interaction in the Hartree-Fock approximation. The lattice part, inclusive of an anharmonic term and an inter-mode coupling term, is given by \({H}_{{{\rm{lat}}}}={\omega }_{{{\rm{FE}}}}^{2}{Q}_{{{\rm{FE}}}}^{2}/2+{\omega }_{{{\rm{AFD}}}}^{2}{Q}_{{{\rm{AFD}}}}^{2}/2+{b}_{{{\rm{FE}}}}{Q}_{{{\rm{FE}}}}^{4}/4+{b}_{{{\rm{AFD}}}}{Q}_{{{\rm{AFD}}}}^{4}/4-{c}_{{{\rm{FE}}}-{{\rm{AFD}}}}\times{Q}_{{{\rm{FE}}}}^{2}{Q}_{{{\rm{AFD}}}}^{2}/2\). The single ion anisotropy is introduced via \({H}_{{\mbox{sp}}}=-K[{({S}_{{\mbox{A}}}^{z})}^{2}+{({S}_{{\mbox{B}}}^{z})}^{2}]\). The electron-lattice, electron-spin, and spin-lattice couplings are given by \({H}_{{{\rm{el}}}-{{\rm{lat}}}}=-{g}_{{\mbox{FE}}}{Q}_{{\mbox{FE}}}{\upsilon }^{z}-2{\alpha }_{{\mbox{FE}}}{Q}_{{\mbox{FE}}}\sin \left(k\right){\tau }^{x}{\upsilon }^{y}\), \({H}_{{\mbox{el}}-{\mbox{sp}}}=-J({{{\boldsymbol{S}}}}_{{\mbox{A}}}\cdot {{\boldsymbol{\sigma }}}{\tau }^{\uparrow }+{{{\boldsymbol{S}}}}_{{\mbox{B}}}\cdot {{\boldsymbol{\sigma }}}{\tau }^{\downarrow })\), and \({H}_{{\mbox{sp}}-{\mbox{lat}}}=-{g}_{{\mbox{AFD}}}{Q}_{{\mbox{AFD}}}({S}_{{\mbox{A}}}^{x}+{S}_{{\mbox{B}}}^{x})\), respectively. The model parameters are set as follows: \(h=1\), \(U=3\), \(J=1.5\), \(K=1\), \({\omega }_{{\mbox{FE}}}=0.002\), \({\omega }_{{\mbox{AFD}}}=0.003\), \({g}_{{\mbox{FE}}}=0.01\), \({\alpha }_{{\mbox{FE}}}=0.005\), \({g}_{{\mbox{AFD}}}=0.005\), \({b}_{{\mbox{FE}}}=2\times {10}^{-8}\), \({b}_{{\mbox{AFD}}}=6\times {10}^{-8}\), and \({c}_{{\mbox{FE}}-{\mbox{AFD}}}=3\times {10}^{-8}\). In numerical results, time is expressed in units of \(\hslash /h\). The bare frequencies of \({Q}_{{\mbox{FE}}}\) and \({Q}_{{\mbox{AFD}}}\) are evaluated as \({\widetilde{\omega }}_{{\mbox{FE}}}={\left({\omega }_{{\mbox{FE}}}^{2}+3{b}_{{\mbox{FE}}}{Q}_{{\mbox{FE}}}^{2}-{c}_{{\mbox{FE}}-{\mbox{AFD}}}{Q}_{{\mbox{AFD}}}^{2}\right)}^{1/2}=0.0264h/\hslash \) and \({\widetilde{\omega }}_{{\mbox{AFD}}}={\left({\omega }_{{\mbox{AFD}}}^{2}+3{b}_{{\mbox{AFD}}}{Q}_{{\mbox{AFD}}}^{2}-{c}_{{\mbox{FE}}-{\mbox{AFD}}}{Q}_{{\mbox{FE}}}^{2}\right)}^{1/2}=0.0310h/\hslash \), respectively (see Supplementary Information E). Note that the energy and time scales of the lattice system can be arbitrarily tuned without affecting those of the electron and spin systems through a scale transformation: \({Q}_{X}\mapsto {Q}_{X}^{{\prime} }=\beta {Q}_{X}\), \({\omega }_{X}\mapsto {\omega }_{X}^{{\prime} }={\omega }_{X}/\beta \), \({g}_{X}\mapsto {g}_{X}^{{\prime} }={g}_{X}/\beta \), \({\alpha }_{{\mbox{FE}}}\mapsto {\alpha }_{{\mbox{FE}}}^{{\prime} }={\alpha }_{{\mbox{FE}}}/\beta \), \({b}_{X}\mapsto {b}_{X}^{{\prime} }={b}_{X}/{\beta }^{4}\), and \({c}_{{\mbox{FE}}-{\mbox{AFD}}}\mapsto {c}_{{\mbox{FE}}-{\mbox{AFD}}}^{{\prime} }={c}_{{\mbox{FE}}-{\mbox{AFD}}}/{\beta }^{4}\) for \(X={\mbox{FE}},\,{\mbox{AFD}}\).

The time evolution of the system is governed by the von Neumann equation for the itinerant electrons, \({\dot{\rho }}_{k}=-\left(i/\hslash \right)\left[H,{\rho }_{k}\right]-{\gamma }_{{\mbox{el}}}[{\rho }_{k}\left(t\right)-{\rho }_{k}^{{\mbox{gs}}}\left(t\right)]\), the Landau-Lifshitz-Gilbert equation for the localized spins, \({\dot{{{{\boldsymbol{S}}}}}}_{X}=-{{{{\boldsymbol{S}}}}}_{X}\times \left\langle \partial H/\partial {{{{\boldsymbol{S}}}}}_{X}\right\rangle -{\gamma }_{{\mbox{sp}}}{{{{\boldsymbol{S}}}}}_{X}\times {\dot{{{{\boldsymbol{S}}}}}}_{X}\) for \(X={{{\rm{A}}}},{{{\rm{B}}}}\), and the equation of motion for the distortions, \({\ddot{Q}}_{X}+{\gamma }_{{\mbox{lat}}}{\dot{Q}}_{X}=-\langle \partial H/\partial {Q}_{X}\rangle\) for \(X={{{\rm{FE}}}},{{{\rm{AFD}}}}\). Here, \({\rho }_{k}\) represents the one-body density matrix of electrons, \({\rho }_{k}^{{\mbox{gs}}}\) is that for the ground state with the given \({Q}_{X}(t)\) and \({{{{\boldsymbol{S}}}}}_{X}(t)\), and \(\langle \cdot \rangle\) denotes the expectation value defined by \(\left\langle \cdot \right\rangle ={N}^{-1}{\sum }_{k}{{{\rm{Tr}}}}[{\rho }_{k}\cdot ]\). We take \(N=256\) points in reciprocal space and set the damping constants to \({\gamma }_{{\mbox{el}}}={\gamma }_{{\mbox{sp}}}={\gamma }_{{\mbox{lat}}}=0.0005\). These coupled equations are solved using the fourth-order Runge-Kutta method with a time step of \(\delta t=0.01\). At time \(t=0\), among the four unoccupied bands, the number of electrons in each of the upper two bands is changed to \(0.9\times \delta {n}_{{\mbox{e}}}\), and in each of the lower two bands to \(1.1\times \delta {n}_{{\mbox{e}}}\), where \(\delta {n}_{{\mbox{e}}}=0.5\) denotes the average injected carrier density; consequently, the electron density per unit cell is changed from 0.5 to \(0.5+2\times \left(0.9+1.1\right)\delta {n}_{{\mbox{e}}}/8=0.75\). The transient optical conductivity, \(\sigma (\omega ,{t}_{{\mbox{p}}})\), is calculated from the electric current \(J(t)=\langle \partial H/\partial k\rangle\) induced by a probe pulse with a vector potential of \(A(t,{t}_{{\mbox{p}}})=-{A}_{{\mbox{p}}}\Theta (t-{t}_{{\mbox{p}}}){e}^{-\eta (t-{t}_{{\mbox{p}}})}\), where \(\Theta\) is a unit step function, and \({A}_{{\mbox{p}}}=0.0001\) and \(\eta ={\gamma }_{X}=0.0005/\beta\) [See, e.g., ref. 58 for details]. In the calculation of \(\sigma (\omega ,{t}_{{\mbox{p}}})\), we applied the scale transformation by a factor of \(\beta ={10}^{-2}\) to reduce the computational cost.