Intoroduction

The quantum superposition states (QSS) of electron and nuclear spins in point defects in wide-gap semiconductors are stable at room temperature1. These superposition states in semiconductors can prospectively be used for various quantum applications such as quantum computation2, and quantum sensing1,3,4. In quantum sensing, a type of quantum technology, the magnitude of external fields such as magnetic fields, electric fields, and temperature are measured by detecting phase changes of the QSS. In general, QSS reflecting quantum effects are expected to provide higher-sensitivity measurements than classical sensing1. To achieve higher sensitivity in quantum sensing using QSS, extending both the number of sensors and the spin-dephasing time, T2*, are essential.

The QSS of the electron spins of NV− centres formed in diamond are attractive quantum systems because the ensemble of electron spins has an extremely long T2* of tens of microseconds at room temperature5. For NV− centres, T2* is relatively long even at room temperature because of the extremely small nuclear spin concentration of 1.1% in diamond6,7. The value of T2* has been extended using 12C isotopically enriched diamond with [13C] <500 ppm8,9,10, and a quantum sensor for measuring weak magnetic fields has been demonstrated using optically excited NV− centres created in 12C-enriched diamond11. In addition to the elongation T2* of the NV− centre, the crystal size of optically excited diamond, which determines the total number of excited NV− centres, must be enlarged to achieve high magnetic sensitivity. In recent research12, a minimum detectable magnetic field sensitivity (MDMFS) of 9.4 pT Hz−1/2 was reported in a relatively small excitation volume of 0.004 mm3. This sensitivity was the best reported value in the DC frequency range of 5‒100 Hz. In the previous report, a long T2* of the NV− centre ensemble (~2 μs) was achieved by 12C isotopic enrichment. The achieved sensitivity corresponds to the shot noise limit, which is a quantum-limiting MDMFS. The long T2* and reduction in PL intensity noise by laser mainly contributed for the achieved the best reported sensitivity. Here, we proposed that enlargement of the reported excitation volume: 0.004 mm3 could lead to higher sensitivity while maintaining the factors contributing to the best reported sensitivity; long T2* (~2 μs) and PL intensity noise cancelling. Arai et al. reported a relatively large excitation diamond crystal volume of 0.19 mm3 for NV sensing13. The excitation volume was achieved by laser beam spot size being ~0.4 mm in diameter with high laser power (2 W) and constructing a reflection pass of excitation laser in a diamond crystal13. Here, the increase in excitation volume contributes to improve the shot noise limit1. Based on the relationship that the shot-noise limit theoretically improves by a factor of the square root of the excitation volume increase rate, NV sensing using the reported large excitation volume of 0.19 mm3 with high laser power and NV− centre with a long T2* of ~ 2 μs could lead to higher magnetic sensitivity (<1 pT Hz−1/2). There are several factors that substantially reduce magnetic sensitivity when the excitation volume is increased. One of them is significant increase of PL intensity noise due to larger laser power. To increase the excitation volume while maintaining the higher emission rate of each NV− centre, the laser power has to be increased. The PL intensity noise by high laser power is expected to be cancelled by a balanced photon detection technique12,13. Another is the strain distribution, which becomes more pronounced as the excitation volume increases. The estimation of the improvement in sensitivity due to the increase in the excitation volume was based on a condition that the NV centres in the increased excitation volume have a long T2* with uniformed spatial distribution. Here, imperfection of diamond crystal such as strain inhomogeneities1 and magnetic noise by spin bath1 cause shorten of T2*. For example, defects such as dislocations and plastic deformation defects distributed over sub-millimetre-sized areas are formed during the synthesis of diamonds with millimetre-sized volumes14. These defects cause inhomogeneous strain distribution and reduce the T2* of the NV− centre in the excitation volume14. Therefore, we concluded that increasing the excitation volume and spatial homogeneity of T2* by reducing the imperfection of diamond crystal in the excitation volume at the same time would be the key to constructing highly sensitive magnetometers.

For example, the achievement of human magnetoencephalography under ambient conditions is a major milestone in quantum sensing using a NV− centres12. An MDMFS of less than 10 fT15 is required for human magnetoencephalography measurements. Herein, the crystal size needed to obtain a sensitivity of 10 fT is estimated. The sensitivity is expressed as the DC shot noise limit \(({\eta }_{{{\rm{sp}}}}^{{{\rm{ensemble}}}})\) as represented by Eq. 11,13,

$${\eta }_{{{\rm{sp}}}}^{{{\rm{ensemble}}}}=\frac{1}{{\gamma }_{{{\rm{NV}}}}}\frac{1}{C\times \sqrt{{n}_{{{\rm{avg}}}}}\times \sqrt{\beta }}\frac{1}{\sqrt{V{\times \left[{{{\rm{NV}}}}^{-}\right]\times T}_{2}^{* }}}$$
(1)

γNV, C, navg, β and V are gyromagnetic ratio of the NV− centre spin of 1.76 × 1011 Hz T−1, the spin-dependent NV− centre PL contrast, average number of photons collected per NV− centre per measurement, photon collection efficiency, and excitation diamond crystal volume, respectively. The product of V and [NV−] represents the total number of NV− centres in the excitation volume of the diamond crystal. The concentration of NV− centres is typically limited by the total nitrogen concentration in the diamond. The reported maximum efficiency for the conversion of nitrogen to NV− centres is about 50%16,17. The T2* value of the NV− centre ensemble was limited by the total nitrogen concentration when the 13C concentration and strain spatial distribution were significantly small18. T2* was found to be inversely proportional to the total nitrogen concentration, with an inverse coefficient of 9.9 μs ppm (corresponding to dephasing rate per density: 101 kHz ppm−1)10. Using the maximum conversion efficiency [NV−]/[N] of 0.5 and the T2* value limited by the total nitrogen concentration expressed as 9.9/[N], the shot noise limit equation (Eq. 1) can be transformed to Eq. 2.

$${\eta }_{{{\rm{sp}}}}^{{{\rm{ensemble}}}}=\frac{1}{{\gamma }_{{{\rm{NV}}}}}\frac{1}{C\times \sqrt{{n}_{{{\rm{avg}}}}}\times \sqrt{\beta }}\frac{1}{\sqrt{V\times 0.5\times 9.9}}$$
(2)

The product of the PL contrast and square root of the average photon counts of the NV− centre ensemble shown in Eq. 2, C × navg1/2 is an indicator of the photon readout fidelity for the NV− centre. This readout fidelity is unity under ideal condition, which is the spin projection limiting value1. However, in the typical photon readout fidelity for NV− centres, C × navg1/2 was reported to have a significant lower value 1/5000‒1/10001 than the spin projection limiting value. By using the total reflection of the photon emission of the NV− centre in diamond, a value of 1/67 as C × navg1/2 was achieved19, which is two orders of magnitude larger than the typical reported values. This two-magnitude improvement in the photon readout fidelity contributed to enhancing the magnetic sensitivity19. For the excitation of millimetre-sized diamond volumes, this total internal reflection method is thought to be essential. And photon collection efficiency can be improved to 65% by using a trapezoidal-cut diamond crystal and a parabolic concentrator20. Using the shot noise limits in Eq. 2 with photonic parameters as C × navg1/2 = 1/67 and β = 0.65, to achieve a magnetic sensitivity below 10 fT, the minimum excitation diamond volume V was estimated to be ~ 2.6 mm3.

The estimation of the minimum excitation diamond volume for human magnetoencephalography using the shot noise limit equation does not consider high-fidelity spin-rotation operations for high-precision quantum sensing. During quantum sensing, the protocol of spin half-rotation in a Bloch sphere is essential for preparing QSS. The phase of the QSS fluctuates when the half π-rotation time (Tπ/2), that is, the generation time of the QSS, is significantly larger than the spin-dephasing time, T2*. To avoid phase fluctuation, in general, Tπ/2 must be set to a value significantly shorter than T2*. This criterion suggests that the spin rotation is completed well before phase coherence is lost. In order to perform high-fidelity spin rotation, the value of T2* needs to be over two orders of magnitude longer than Tπ21. For achieving high sensitivity using NV sensing, so far, some previous reports showed spin π-rotation time of ~ 50 ns22 and ~ 100 ns23,24. Because the spin π-rotation time of the NV− centre in this study is approximately 100 ns, the minimum spin-dephasing time required for high-fidelity spin rotation is estimated to be 10 μs. To achieve a π rotation time of ~ 100 ns, a driving microwave (MW) magnetic field amplitude of 0.18 ~ 0.21 mT23,24 was applied to the NV− centre ensemble. The spin-rotation time is determined by the strength of the microwave magnetic field applied to the NV− centre. The larger the amplitude of the microwave magnetic field applied to the NV− centre, the faster the spin rotation is. A T2* of over 10 μs is expected when the total nitrogen concentration is below 1 ppm because the total nitrogen concentration and T2* are inversely proportional in this nitrogen doping range. From the shot noise limit and criteria for high-fidelity spin rotation, millimetre-sized diamond crystals and T2* > 10 μs are essential for 10 fT human magnetoencephalography.

Previous research has been conducted using diamonds synthesised by chemical vapour deposition (CVD), a common diamond growth method, to increase the T2* of NV− centres formed in millimetre-sized diamond single crystals and improve their spatial uniformity. Indeed, T2* spatial mapping has reportedly been carried out within an area of 1 mm × 1 mm in the {001} plane of 0.1 µm thick diamond, where non-uniform T2* spatial distribution was observed18. In that study, the T2* inhomogeneity was caused by a strain gradient in the diamond crystal. One of the factors contributing to the spatial distribution of strain in CVD diamonds is the dislocation distribution. In a previous report, high-density dislocation distributions ranging from 104 to 106 cm−2 were observed in CVD diamond crystals using X-ray topography25. Furthermore, Kehayias et al. reported the distribution of NV− centres with a short and non-uniform T2* in the dislocation area in CVD diamond crystals14. High-pressure, high-temperature (HPHT) synthesis is another common method for diamond growth. In the HPHT method, diamond is synthesised under equilibrium conditions; therefore, it is thought that the formation of high-density dislocation defects as observed in CVD diamond is unlikely, as there have been reports of millimetre-sized HPHT diamond single crystals with low dislocation densities of less than 102 cm−2 26,27. Therefore, NV− centres with a uniformly distributed, long T2* are expected to be obtained in HPHT nitrogen-doped diamonds. In previous report, strain imaging by NV sensing were carried out with millimetre-sized nitrogen doped CVD diamond18. The imaging cross-sectional area was 1 mm2 and the doped nitrogen concentration was 0.75 ppm. The obtained strain imaging indicated partial sub-millimetre-sized large strain distributions. This sub-millimetre-sized distribution caused degradation of T2* and a significant large variation of T2* (1‒10 μs) was also reported in that previous study. The large variation of T2* could cause degradation of the averaged T2* in excited millimetre-sized diamond crystal volume. Therefore, expected millimetre-sized homogeneous T2* distribution in HPHT diamond crystal is essential for human magnetoencephalography.

In this study, low-strain, nitrogen-doped diamond crystals are synthesised using HPHT synthesis method. These low-strain HPHT diamond crystals are used for millimetre-size T2* imaging and to clarify the millimetre-size distributed dephasing factor of NV− centre spin coherence. Finally, high uniformity of the spin dephasing time of NV− centres in millimetre-scale area was achieved using 12C-enriched nitrogen doped HPHT diamond crystals, and in region of nitrogen impurity concentrations less than ~ 1 ppm, it was found that the strain gradient in HPHT diamond crystals partially limits spin dephasing time.

Results and discussion

Synthesis of HPHT diamond crystals

In order to form an ensemble of NV− centres that contributes to magnetoencephalography, it is necessary to extend T2* to over 10 μs. To achieve this, the density of the doped nitrogen must be controlled, and the nitrogen concentration should be reduced to less than 1 ppm. In general, the nitrogen concentration can be controlled by adding nitrogen-getter metals such as Ti and Al to the solvent-metal during HPHT synthesis. The nitrogen-getter metal and solvent-metal are described in the sample preparation of Methods section. Precise nitrogen concentration control ranging from 0.2 to 100 ppm was achieved by controlling the amount of the nitrogen-getter metal28. During HPHT synthesis of diamond, when the growth rate was higher than 6‒7 mg h−1, the solvent-metal used in HPHT synthesis was incorporated into the growing diamond, resulting in the formation of metal inclusions29. These metal inclusions become a source of strain gradients distributed over millimetre-sized areas. To suppress the formation of metal inclusions and synthesis large diamond crystal, the lower growth rate than 6‒7 mg h−1 and long growth time: over several tens of hours are required29. When growing diamond crystals for a long time to obtain high-quality crystals, changes in growth rate due to temperature fluctuations can be a problem. To avoid the temperature fluctuation, a modified belt-type, high-pressure apparatus was used28,30,31, in which cooling water was available for temperature stabilisation. In this study, HPHT diamond crystals were synthesised using a modified belt-type, high-pressure apparatus, in the temperature range of 1300‒1350 °C. The temperature fluctuation was less than ± 7.5 °C. The growth time and growth rate were 40‒80 h and ~1 mg h−1, respectively in this study.

Sequence of T 2 * spatial mapping for NV− centres

T2* was measured in the millimetre-scale region of the diamond. A columnar excitation fluorescence microscope23 was used to excite the NV− centres throughout the thickness direction of the diamond crystal, which is typically 400 μm. Because the 532 nm laser diameter and depth of the excitation region in the employed microscope are designed to be 20 and 500 μm23, respectively, the ensemble of NV centres was excited at the same time, as shown in Fig. 1a. The spatial distribution of T2* in the {111} plane was evaluated as follows: (1) Optically detected magnetic resonance (ODMR) measurements were performed at each excited position. During the measurements, an external magnetic field of 2.5 mT was applied along the direction of the [111] diamond crystal. The obtained ODMR frequency was generally ~ 2.8 GHz. (2) Subsequently, spatial Rabi measurements were performed at the same excited position. The MW frequency was set to the ODMR frequency obtained at the same excited position. The typical duration of the microwave π/2 pulse in the Rabi oscillation was ~ 50 ns. (3) Finally, free-induction decay (FID) measurements were performed at the same excited position, where the duration of the microwave π/2 pulse was obtained from Rabi measurement at the same excited position. A typical FID signal was shown in Fig. 1c. T2* was estimated by fitting the obtained FID signal to the damped oscillation function18, shown in Eq. 3:

$${S}_{{{\rm{FID}}}}\left(\tau \right)=\exp \left(-\frac{\tau }{{T}_{2}^{* }}\right){\sum}_{{{\rm{i}}}=1,2,3}{A}_{{{\rm{i}}}}\sin \left(2{{\rm{\pi }}}\, {f}_{{{\rm{i}}}}+{\delta }_{{{\rm{i}}}}\right)$$
(3)

where f1, f2 and f3 are the frequencies of the hyperfine splitting magnetic field due to the 14N atom in the NV− centres. The typical values of f1, f2 and f3 are 0.9, 3 and 6 MHz, respectively.

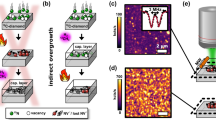
Fig. 1: T2* spatial mapping in {111} plane of diamond using columnar excitation fluorescence microscope.
figure 1

a 532 nm laser excitation volume in diamond for one excited position using columnar excitation fluorescence microscope. b Schematic of spatial T2* mapping in {111} plane of diamond. c Circle symbol indicates representative FID signal respective to free precision time and solid line shows damping oscillation curve as per Eq. 3 for fitting the FID signal. d Spatial distribution of PL intensity of NV− centre mapped in {111} plane of diamond crystal. Red square region indicated as (i) shows {111} growth sector in diamond crystal. The lower PL intensity area indicated as (ii) was the {110} or {113} growth sector. The tapered area indicated as (iii) was {110} or {113} growth sector. e Spatial T2* mapping in {111} growth sector within the red square (1.1 mm × 1.1 mm) as shown in this figure. f Histogram of T2* from spatial T2* mapping in {111} growth sector of diamond, as shown in this figure. g Histogram of Mz obtained from spatial Mz mapping in {111} growth sector, as shown in this figure. ΔMz represents FWHM of Mz.

Full size image

As shown in Fig. 1b, the distance between each laser excited position was set to 100 µm for T2* spatial mapping within the millimetre-scale {111} growth sector.

T 2 * spatial mapping in the millimetre-scale {111} plane

Figure 1d shows the PL intensity imaging for the NV− centre in the HPHT diamond with [Ns0]initial = 1.3 ppm. The HPHT diamond crystal has flat-areas indicated as Fig. 1d-i, ii, and also has tapered-area indicated as Fig. 1d-iii. The growth sector indicated as Fig. 1d-i including the red square area (1.1 mm × 1.1 mm for T2* spatial mapping below) was primarily the {111} growth sector. In this red square area, the distribution of PL intensity was nearly homogeneous, and the PL intensity was significantly larger than that of the other growth sectors as indicated in Fig. 1d-ii except for growth sectors in tapered-area as indicated in Fig. 1d-iii. From the relationship between the reported uptake of nitrogen for different growth sectors32 and the obtained PL intensity from the growth sector in Fig. 1d-ii was {110} or {113} growth sector. The details for PL intensity in multi-growth sectors in flat-areas and the relationship between PL intensity and growth sector in the tapered area were explained in PL intensity of NV− centres in multi-growth sectors of Methods section.

Next, T2* spatial mapping was performed in the millimetre-scale {111} plane region of the red square (1.1 mm × 1.1 mm) in Fig. 1d. Figure 1e shows the T2* spatial distribution in this 1.1 mm × 1.1 mm region. T2* presented here is the average value of four T2* measurements at the same position (for details, see the Supplementary Note 1). No significant low T2* region was detected in the mapped millimetre-scale area shown in Fig. 1e. This means that the number of millimetre-scale structural defects, such as dislocation bundles and plastic deformation zones observed by Kehayias et al.14, is quite small in the millimetre-scale {111} growth sector of the present specimens. On the surface of a diamond crystal, ubiquitous defects cause magnetic noise at the NV− centre located within 100 nm of the surface33. In the present study, most of the detected NV− centres were located inside the diamond crystal with ~400 μm thickness, far away from the surface. Therefore, the degradation of the examined T2* caused by the surface magnetic noise was neglected in this study. PL intensity imaging can provide information on the distribution of non-radiative defects near the NV− centre because NV− photons are transferred from the excited-state level of the NV− centre to the non-radiative defect level. This photon transfer caused by non-radiative defects leads to a decrease in the PL intensity. In addition, non-radiative defects may shorten T2* of the NV− centre due to magnetic noise or lattice strain from these defects. The PL imaging of {111} growth sector as indicated red square in Fig. 1d showed no area with significantly low PL intensity, demonstrating that the distribution of high-density, non-radiative defects was negligible. Furthermore, there was no obvious correlation between the PL intensity and T2* image in the {111} growth sector, as shown in Fig. 1d and e. This result suggests that non-radiative defects primarily do not limit the T2* distribution in the {111} sector. Birefringence imaging detects microdefects such as dislocations and dislocation bundles. The birefringence imaging in the {111} growth sector is presented in Supplementary Note 2. In birefringence imaging, the distributions of dislocations and dislocation bundles cannot be resolved. This birefringence image also shows that the examined HPHT diamond crystal has high crystallinity (see Supplementary Note 2). Figure 1f shows a histogram of T2* obtained from T2* spatial mapping in the millimetre-scale {111} growth sector. The solid line represents the Gaussian curve fitted to the histogram. The median <T2*> of this Gaussian distribution was 4.5 µs, with a standard deviation of less than 10% of <T2*>. The 10% variation in T2* indicates that the HPHT diamond used in this study has a highly uniform spatial distribution of T2*. The obtained spatial variation in T2* was significantly smaller than the previously reported T2* variation of 35 %. The reported variation was obtained by T2* mapping in 150 µm × 150 µm region in {001} plane of CVD diamond with [NT] ~ 20 ppm34.

The phase of the QSS of the NV− centre fluctuates owing to the dipole-dipole interaction (DDI) from the electron-spin bath of nitrogen impurities1,10,18. The fluctuation of the QSS phase led to a decrease in T2*. This phenomenon becomes dominant when the nitrogen concentration exceeds 1 ppm. The spin-dephasing rate, 1/T2*{NT}, due to this DDI from the electron-bath of nitrogen impurities is described as follows:

$$\frac{1}{{T}_{2}^{* }\{{{{\rm{N}}}}_{{{\rm{T}}}}\}}={D}_{{{{\rm{N}}}}_{{{\rm{T}}}}}\times \left[{{{\rm{N}}}}_{{{\rm{T}}}}\right]$$
(4)

where \({D}_{{{{\rm{N}}}}_{{{\rm{T}}}}}=101\pm 12{{{\rm{ms}}}}^{-1}{{{\rm{ppm}}}}^{-1}\) and [NT] is the total concentration of nitrogen impurities in the diamond. The experimentally obtained <T2*> was 4.5 μs which is smaller than T2*{NT} = 7.6 ± 0.9 μs estimated from Eq. 4 with [NT] = [Ns0]initial = 1.3 ± 0.4 ppm for the examined HPHT diamond sample, as seen in the filled orange area in Fig. 1f. This result indicates that the dephasing rate for T2* is affected by sources other than the electron-spin bath of nitrogen impurities. Previous studies reported that the strain gradient in diamond crystals reduces T2* through the interaction between the electronic dipole and the electron spin of the NV− centre14,35. The dephasing rate due to this strain gradient, which is termed 1/T2*{strain gradient} in this study, corresponds to the spatial dispersion of the interaction Mz between the electron spins and diamond crystal strain. In general, Mz is one component of the ODMR resonance frequency \(({f}_{\!\!\!{\pm }})\) of the NV− centre (Eq. 5).

$${f}_{\!\!\!{\pm }}=D+{M}_{{{\rm{z}}}}\pm {\gamma }_{{{\rm{NV}}}}{B}_{{{\rm{z}}}}$$
(5)

\({f}_{\!\!\!{\pm }}\) is composed of the zero-field splitting (D) of the electron spin (S = 1) of the NV− centre, the spin-strain interaction (Mz), and the Zeeman splitting caused by the external magnetic field (Bz)18,35. Strain gradients in diamond crystals have been observed as resonance frequency shifts in ODMR14,35. In this study, Mz was obtained from Eq. 6 using the value of \({f}_{\!\!\!{\pm }}\) obtained from the ODMR measurements.

$${M}_{{{\rm{z}}}}=(\,{f}_{\!\!{+}}+{f}_{\!\!{-}})/2-D$$
(6)

Here, 2.87 GHz was used for D1,36 in Eq. 6. Mz mapping in the {111} sector area was used to study the strain gradient in the HPHT diamond, as indicated by the red rectangle in Fig. 1d. The PL intensity image of the NV− centre, T2*, Mz, and birefringence in the {111} sector are compared in Supplementary Note 2. There was no obvious correlation between the imaging data. In future studies, other defect imaging methods such as X-ray topography and cathodoluminescence will be used to determine the causes of the partial distribution of the relatively low T2* observed in Fig. 1e. Figure 1g shows the histogram obtained from Mz spatial mapping in the {111} growth sector, where T2* mapping was performed. The solid line represents the Gaussian function fitted to the histogram. The result indicates that the diamond crystal strain was uniformly distributed throughout the HPHT diamond. The full width at half maximum (FWHM) of Mz in the Gaussian distribution, that is, ΔMz, was 0.06 MHz. Note that the calculated ΔMz includes not only in-plane variance of the strain, but also depth variance of the strain. The depth variance arises from the examined excited depth of ~400 μm. Assuming that strain is hydrostatic, the strain gradient in the depth direction of the examined HPHT diamond is expected to be comparable to that obtained by in-plane Mz imaging in this study. In future studies, the strain gradient in the depth direction should be directly observed by ODMR using a conventional confocal microscope having a depth resolution of 1 μm. Here, the spatial dispersion of the strain related ODMR shift, ΔMz, induces inhomogeneous broadening of the ODMR spectrum of the NV− centre18. Thus, ΔMz corresponds to the dephasing rate of the strain gradient 1/T2*{strain gradient}18 in the whole T2* spatial mapping region (Fig. 1e). The slope of the strain gradient in the {111} plane direction of the diamond crystal was estimated to be 0.06 MHz/1100 μm = 0.05 kHz μm−1. This value is approximately one order of magnitude smaller than the strain gradient of 2.8 kHz µm−1 for nitrogen-doped CVD diamond with [NT] = 0.75 ppm reported by Bauch and coworkers18. In this study, the critical synthesis parameter for improvement of homogeneity of T2* and strain gradient in examined HPHT diamond crystals were not clear. It is possible that reducing the growth rate to ~1 mg h−1, which is smaller than reported value29, led to the high quality of the diamond single crystal. This low growth rate may cause reduction of defects such as dislocation. In future works, an investigation of the relationship between formation of defect and various synthesis parameters such as growth rate is expected.

Here, strain gradients in diamond crystals caused by high doping with impurities such as boron and phosphorus have been reported37,38,39. Therefore, in the next section, the dependence of the strain gradient observed in this study on the nitrogen impurity concentration is discussed.

Dependence of strain gradient in diamond on concentration of nitrogen impurities

The dependence of the strain gradient in diamond crystals on the concentration of nitrogen impurities was investigated. The green triangles in Fig. 2a show the relationship between ΔMz and [Ns0]initial. To determine the strain gradient, ΔMz, in-plane {111} spatial Mz mapping was carried out for nine 12C-enriched HPHT diamond crystals with different [Ns0]initial. The resulting ΔMz ranged from 0.06 to 0.1 MHz and did not have a strong dependence on [Ns0]initial, indicating that the strain gradient in the diamond crystal was not caused by uptake of nitrogen under the [Ns0]initial ranging from 0.7 to 14 ppm. When strain gradient is independent of nitrogen concentration, dephasing effect due to strain gradient becomes negligible when nitrogen concentration is larger, e.g., 10 ppm, leading to improvement of shot-nose limit. But, in practical sensing, as well as improving shot noise, spin manipulation with high fidelity is also one of essential key technology for high sensitivity as explained in the introduction part. In the case of spin rotation time ~100 ns in this study, T2* over 10 μs is needed for high fidelity of spin manipulation. Therefore, the reduction of strain gradient in diamond with lower nitrogen concentration less than 1 ppm is desirable for practical sensing. The obtained strain gradient ΔMz ranging from 0.06 to 0.1 MHz corresponds to stress ranging from 5 to 8 MPa, assuming that the strain is hydrostatic40. Sumiya et al. reported that an Ib-diamond containing several tens to hundreds of ppm of nitrogen impurities has a larger inhomogeneous strain distribution41. This fact suggests that nitrogen-doped diamond has relatively large strain gradient. This inhomogeneous strain distribution could shift the resonance frequency of the NV− centre. Therefore, in Ib-diamond crystals, the inhomogeneous strain distribution shortens T2* of the NV− centre. To determine the effect of the nitrogen-impurity concentration and strain gradient on T2*, the spin-dephasing rates 1/T2*{NT} estimated using Eq. 4 were superimposed on Fig. 2a, as indicated by the black dotted line. As shown in Fig. 2a, 1/T2*{NT} was approximately 10 times larger than the strain-gradient dephasing rate, ΔMz, at [Ns0]initial ≈ 10 ppm. The difference between ΔMz and 1/T2*{NT} became smaller as [Ns0]initial decreased, and the values of both were comparable at [Ns0] ≈ 1 ppm. This suggests that in the region of a relatively small [Ns0]initial (~1 ppm), T2* is expected to be governed not only by DDI from the electron-spin bath of nitrogen impurities but also by the strain gradient in the diamond crystal. To verify this T2* dephasing model, the relationship between the experimentally-obtained spin-dephasing time of the 12C-enriched HPHT diamond crystal (T2*{exp. 12C}) and [Ns0]initial was investigated. Here, T2*{exp. 12C}, which is plotted in Fig. 2b as red rectangles, is the median value of T2*, <T2*>, in a Gaussian distribution, as shown in Fig. 1f. The vertical error bars for T2*{exp. 12C} indicate the standard deviation of the Gaussian distribution; they are much smaller than the marker size. T2*{exp. 12C} decreased with increasing [Ns0]initial (Fig. 2b). This suggests that the DDI from the electron-spin bath of nitrogen impurities was significant dephasing contribution respect to the other dominant contributions including strain gradient. The T2*{exp. CNat. Abu.} data obtained from carbon natural-abundance HPHT diamond samples were plotted in the figure as orange rhombuses. T2*{exp. CNat. Abu.} also decreased with an increase in [Ns0]initial. Furthermore, T2*{exp. CNat. Abu.} became significantly smaller than T2*{exp. 12C} with a decrease in [Ns0]initial. This significant decrease of T2*{exp. CNat. Abu.} from T2*{exp. 12C} was caused by the presence of magnetic noise from the 13C nuclear spin in carbon natural-abundance HPHT diamond samples. It means that 12C enrichment is indispensable for obtaining T2* of larger than 1 μs. The relationship between T2*{NT} and [Ns0]initial shown in Eq. 4 is superimposed on Fig. 2b using a black dashed line. The difference between T2*{exp. 12C} and T2*{NT} became significantly larger with a decrease in [Ns0]initial. As discussed above, one possible mechanism that shortens T2*{exp.} is the strain gradient of the diamond crystals. To eliminate the strain-gradient dephasing rate (ΔMz) from 1/ T2*{exp. 12C}, T2*{strain subtract} was estimated, as defined below:

$$\frac{1}{{T}_{2}^{* }\{{{\rm{strain}}}\; {{\rm{subtract}}}\}}\equiv \frac{1}{{T}_{2}^{* }\left\{\exp .{\scriptstyle{{12}}\atop}\!{{\rm{C}}}\right\}}-{\Delta M}_{{{\rm{z}}}}$$
(7)
Fig. 2: Effect of concentration of nitrogen impurities on spin-dephasing rate.
figure 2

a Dependence of initial neutral substitutional nitrogen concentration, [Ns0]initial, on two-spin dephasing rate component. Black dashed line and green triangles show dipole-dipole interaction (DDI) from electron-spin bath of nitrogen impurities and strain gradient in diamond crystal, respectively. b Dependence of initial neutral substitutional nitrogen concentration [Ns0]initial on spin-dephasing time, T2*. Red square, orange rhombus, and blue triangle, respectively, show experimental spin-dephasing time as T2*{exp. 12C} and T2*{exp. CNat. Abu.} from 12C-enriched and carbon natural-abundance HPHT diamond, and spin dephasing time obtained by subtracting spatial strain gradient in diamond crystal from T2*{exp. 12C}: T2*{strain subtract}. The black dashed line shows the dephasing time limited by DDI from the electron-spin bath of nitrogen impurities, T2*{NT}. The vertical error bars for T2*{exp. 12C} and T2*{exp. CNat. Abu.} indicate the standard deviation of the Gaussian distribution. The horizontal error bars for T2*{exp. 12C}, T2*{exp. CNat. Abu.} and T2*{strain subtract} indicate the EPR estimation error for initial Ns0 concentration.

Full size image

T2*{strain subtract}, which is plotted as blue triangles in Fig. 2b, had approximately the same value as T2*{NT} (Fig. 2b), as indicated by the black dashed line, based on Eq. 4. This result shows that reducing the strain gradient extends T2* to a value limited by DDI from the electron-spin bath of nitrogen impurities, as shown in Eq. 8:

$$\frac{1}{{T}_{2}^{* }\{{{\rm{strain}}}\; {{\rm{subtract}}}\}} \sim \frac{1}{{T}_{2}^{* }\{{{{\rm{N}}}}_{{{\rm{T}}}}\}}$$
(8)

Reducing the strain gradient in diamond crystals is essential for further improving T2*, especially in the nitrogen-impurity concentration range below 1 ppm. Furthermore, reducing strain and strain gradient in the lower nitrogen impurity concentration is essential for high-performance quantum computation and quantum telecommunication using a single NV− centre. The electronic noise from the strain shifts the ODMR frequency and zero phonon line wavelength42 of a single NV− centre, and this shift causes fluctuation of the quantum state of a single NV− centre, leading to the degradation in the performance of these quantum applications. Here, T2*{strain subtract} at an [Ns0]initial of <1 ppm was slightly larger than T2*{NT}, as indicated by the black dashed line as shown in Fig. 2b. T2*{NT} was obtained from N-doped CVD diamond crystals6,10 with [13C] ~ 500 ppm. The dephasing rate by 13C nuclear spin with [13C] ~ 500 ppm was ~ 1/20 μs−1 using the reported coefficient between [13C] and 13C dephasing rate1. This rate is significant for the NV− centre spin dephasing in diamond crystals with [Ns0]initial of less than 1 ppm. In this study, the dephasing rate by 13C nuclear spin with [13C] ~ 50 ppm was ~ 1/200 μs−1. The one order of magnitude higher isotopically 12C enrichment may cause the observed slight elongation of T2*{strain subtract} relative to T2*{NT} with [Ns0]initial of less than 1 ppm in Fig. 2b. Furthermore, we considered the effects of defects inherent in the CVD growth on T2*. Previous studies have demonstrated that nitrogen-doped CVD diamond crystals with nitrogen-impurity concentrations below 1 ppm contain various vacancy-impurity complexes43,44,45,46. To date, these defects have not been observed in nitrogen-doped HPHT diamond crystals, including those examined in this study. The non-formation of the vacancy-impurity complexes in HPHT diamond crystals may cause a slight elongation of T2*{strain subtract} from T2*{NT}at an [Ns0]initial of <1 ppm in Fig. 2b.

In conclusion, high uniformity of the T2* of NV− centres in millimetre-scale area was demonstrated using 12C-enriched HPHT diamond crystals. The median value of T2*, <T2*>, for the NV− centres formed in the high-pressure, high-temperature diamond was 4.5 μs when the nitrogen concentration in diamond crystal was 1.3 ppm. The spatial variance of T2* was as small as 10% over a millimetre-scale region (1.1 × 1.1 mm2) within the {111} growth sector with a thickness of 0.4 mm. The value of <T2*> was approximately 2/3 times the value limited by the DDI from the electron-spin bath of the nitrogen impurities, suggesting that the strain gradient in the diamond crystal partially limits T2*. The strength of the interaction between the electron spins of the NV− centre and strain in the diamond crystal, Mz, was measured within the {111} growth sector, where T2* was estimated. The spatial variance of Mz, which corresponds to the strain gradient, was 0.06 MHz. The dephasing rate originating from the strain gradient was comparable to that originating from the electron-spin bath of nitrogen impurities. The effect of the nitrogen-impurity concentration on the strain gradient was investigated using several HPHT diamond crystals with [Ns0]initial ranging from 0.7 to 14 ppm. The strain gradient was independent on the nitrogen impurity concentration ranged in over one order of magnitude. Especially, T2* is limited by the electron-spin bath of nitrogen impurities with [Ns0] > 2 ppm because the dephasing rate due to the electron-spin bath of the nitrogen impurities is larger than the obtained dephasing rate of the strain gradient. On the other hand, T2* was limited by the strain gradient in the diamond crystals when [Ns0]initial <~1 ppm. Thus, reducing the strain gradient is essential for further improvement of T2* when the nitrogen-impurity concentration is relatively small (<1 ppm), which is a requirement for achieving high-sensitivity magnetometry by NV quantum sensing.

Methods

Sample preparation

12C isotopically enriched HPHT synthesized diamond was examined in this study28. 12C-enriched CVD polycrystalline diamond was used as the starting material (carbon source) because 12C isotopically enriched graphite is not commercially available47. The reduced 13C concentration was assumed to be 50 ppm. The concentration of nitrogen impurities in the examined diamonds was controlled by the amount of Ti or Al (nitrogen-getter metal) added to the solvent-metals such as Fe and Co28. Diamond single-crystals were grown on (001) plane seed crystals in Co-Ti-Cu, Fe-Co-Ti-Cu, Fe-Al, Fe-Co-Al (99.98%–99.999%, RARE METALLIC Co., Ltd.) solvents via a temperature-gradient method at 5.5 GPa in the temperature range of 1300‒1350 °C for 40‒80 h. A small temperature fluctuation less than ± 7.5 °C was achieved by using cooling water in the modified belt-type, high-pressure apparatus. When Ti was added as a nitrogen getter, Cu was added to the solvent. The Cu additive suppressed the formation of Ti-C inclusion defects in the grown HPHT diamond48. The synthesised diamonds were then laser-cut parallel to the {111} plane. The spin coherence time was maximised when the external magnetic field was parallel to NV− centre’s dipole-oriented axis of [111]. For NV sensing, {111} oriented diamond crystal is typically used12,49,50,51 because the precise alignment of the external magnetic field parallel to the NV axis of [111] is easier than that of {001}, {110} oriented diamond crystal. A magnet can be arranged in a compact manner using a {111}-oriented diamond, leading to the miniaturisation of the NV sensing system49. Laser cutting caused non-diamond phase carbon such as graphite and amorphous carbon defects to form on the surfaces of the diamond samples. The amorphous carbon defect has paramagnetic properties52 and could cause degradation of T2* of NV− centre distributed in surface of diamond crystal. After laser cutting, acid treatment (H2SO4:HNO3 = 1:1 at 360 °C for 2 h) was used to remove the graphite and the surface amorphous carbon from the diamond samples. The in-plane size of the cut diamonds was approximately 2 mm × 2 mm and the thickness in the [111] direction was 400 ± 100 µm. In this study, nine HPHT diamonds were laser-cut. The concentration of nitrogen impurities was then quantified for these nine diamond samples. Most of the nitrogen impurities in the diamonds synthesized by the HPHT method are in the form of neutral substitutional nitrogen (Ns0)53. Electron paramagnetic resonance (EPR) was used to determine the concentration of NV centres and Ns0 53,54. Here, the concentration of NV− centres and Ns0 obtained by EPR were lower than those in the {111} sector because EPR was performed with HPHT diamonds containing multiple sectors, as shown in Fig. 1d. The multisector composed of not only the {111} growth sector but also contains {110} and {113} growth sectors. The Ns0 concentration in the {110} and {113} growth sectors was one order of magnitude smaller than that in the {111} growth sector32. Thus, the EPR intensity obtained from the examined multi growth sector HPHT diamonds mainly originated from Ns0 and NV− centres in the {111} growth sector. To correct the underestimation of [Ns0] and [NV−], the volume of the multi-sectors (that is, the {110} and {113} growth sectors) was subtracted from the total volume of the examined HPHT diamond samples. For some HPHT diamond samples in this study, the {111} growth sector was isolated by laser cutting and [Ns0] and [NV−] were directly estimated. The estimated error in [Ns0] and [NV−] for the {111} growth sector was within ± 30%. Here, the concentration of the NV centres formed during the HPHT synthesis was the detection limit for the EPR measurements in the examined HPHT diamond samples. In HPHT synthesis, the formation of vacancies is less likely to occur than in CVD synthesis. In the CVD synthesis, NV and NVH centres were typically observed54,55. The concentration of neutral substitutional nitrogen, [Ns0]initial, before formation of the NV centres in these crystals ranged from 0.7 to 14 ppm. Electron-beam irradiation followed by post-annealing (1000 °C 2 h) was carried out to form NV centres in the examined diamond54. The examined fluence was ranged from 1 × 1017 to 5 × 1017 e cm−2. The concentrations of NV− centres formed by this post-process ranged from 0.1 to 2 ppm. The obtained maximum conversion efficiency [NV−]/[Ns0]initial was approximately 20% in this study. The ideal conversion efficiency is 50%16,17. By using electron-beam irradiation during high-temperature annealing, the best reported conversion efficiency of 45% was obtained for the Ib-diamond sample with [Ns0]initial = 100 ppm16,17. The enhancement of conversion efficiency has been investigated with only over nitrogen concentration of 30 ppm56. In future work, in diamond samples with nitrogen concentrations less than 1 ppm, the conversion efficiency is expected to be enhanced by electron-beam irradiation during high-temperature annealing.

Experimental setup

Free induction decay measurements were conducted using a home-built PL system with a pulsed microwave module (Synth NV PRO; Windfreak Technologies, LLC/arbitrary waveform generator M3202A; Keysight Inc.). A 532 nm laser (gem 532; Laser Quantum Inc.) was pulsed using an acoustic–optic modulator (#35 250-0.2-0.53-XQ; Gooch & Housego). Red fluorescence emitted from the NV− centre by pulsed green laser excitation was collected using an achromatic lens (AC254-030-AB-ML; Thorlabs, Inc.) and detected using an avalanche photodiode (APD410A/M; Thorlabs, Inc.).

PL intensity of NV− centres in multi-growth sectors

Here, we additionally explained the relationship between PL intensity and growth sectors as indicated in Fig. 1d-ii, iii.

The PL intensity distributed around the three triangular vertices indicated as Fig. 1d-ii is over one order of magnitude lower than that in the {111} growth sector indicated as Fig. 1d-i, indicating that the three triangular vertex areas was corresponding to the {113} or {110} sectors. It has been reported that the nitrogen density in the {113} and {110} growth sector is one order of magnitude lower than that in the {111} growth sectors32. The tapered area indicated as Fig. 1d-iii is {110} or {113} growth sector as following general HPHT diamond text. But PL intensity distributed in the tapered area was comparable to or slightly larger than {111} growth sector in Fig. 1d-i. The PL intensity in the tapered area was not corresponding to typical variation of uptake of nitrogen impurities between multi-sectors. This controversial result in this study was caused by the excitation laser reflecting and refracting at the tapered area. The laser reflecting and refracting at the tapered area, entered a {111} growth sector in central area, and the PL emission from the {111} growth sector returned to the entry-pass and was subsequently detected.