Dynamics of nanoscale phase decomposition in laser ablation

Abstract

Laser ablation is a process that bears both fundamental physics interest and has wide industrial applications. For decades, the lack of probes on the relevant time and length scales has prevented access to the highly nonequilibrium phase decomposition processes triggered by laser excitation. In this study, a close integration of time-resolved probing by intense femtosecond X-ray pulses with large-scale atomistic modeling has yielded unique insights into the ablation dynamics of thin gold films irradiated by femtosecond laser pulses. The emergence and growth of nanoscale density heterogeneities in the expanding ablation plume, predicted in the simulations, are mapped to the rapid evolution of distinct small angle diffraction features. This mapping enables identification of the characteristic signatures of different phase decomposition processes occurring simultaneously in the plume, which are driven by photomechanical and thermodynamic driving forces. Beyond the specific insights into the ablation phenomenon, this study demonstrates the power of joint X-ray probing and atomistic modeling of material dynamics under extreme conditions of thermal and mechanical nonequilibrium.

Introduction

Pulsed lasers have become a routine tool for materials processing, synthesis, and analytics. In particular, precise surface texturing and microstructure modification can be achieved with lasers, as well as the synthesis of advanced materials that cannot be obtained by conventional techniques¹. Most of these applications involve laser ablation, the removal of macroscopic amounts of material from a laser-irradiated surface.

In this context, ultrashort laser pulses of femtosecond to picosecond duration have demonstrated some remarkable advantages. Surface- and three-dimensional modification/functionalization of materials down to the nanometer scale, pulsed-laser-deposition of extremely smooth, particulate free films and tailored production of nanoparticles represent just a few examples (see ref. ², which provides a comprehensive overview, and references therein).

Besides its importance for applications, the phenomenon of laser ablation provides a fertile playground for the exploration of fundamental questions on material behavior under conditions of extreme levels of electronic, mechanical, and thermodynamic nonequilibrium. Again, ultrashort laser pulses provide a unique way to induce ablation, as the energy deposition—initially only to the electronic degrees of freedom of the system—is essentially decoupled in time from the subsequent thermal processes. The non-thermal processes caused by strong electronic excitation³, the kinetics of energy transfer from the excited electrons to atomic vibrations⁴, and the subsequent melting and explosive phase decomposition driven by an interplay of extreme thermodynamic (strong superheating) and mechanical (pressure gradients) driving forces⁵ are the aspects of laser ablation that are not yet fully understood at the fundamental level.

The relevant processes, from the initial energy deposition up to the formation of the final microstructure and/or deposition of ablation products, occur over an extremely large time range from fs to ms (12 orders of magnitude!). Similarly, the spatial scales of the associated structural changes also cover many orders of magnitude—from Å (atomic scale) to hundreds of µm (e.g., the diameter of the ablation crater). This massively multi-scale nature of laser ablation poses a major challenge for its experimental investigation, theoretical description, and modeling.

On the experimental side, the discussion of the ablation dynamics is often based on indirect evidence drawn from ex situ observations, e.g., analysis of crater shapes, ablation rates as a function of laser parameters such as fluence, pulse duration, and a number of applied pulses, as well as size distributions of emitted nanoparticles. Time-resolved studies are scarcer, but provide more direct insights into the ablation dynamics. Of particular relevance to this study are experiments employing femtosecond time-resolved optical microscopy^6,7,8,9,10, which have revealed a universal ablation behavior at fluences not too far above the ablation threshold, leading to the formation of a characteristic optical interference pattern (Newton rings). These observations provide clear evidence that the ablation plume (i) is largely confined to a region with optically steep (length-scale < λ/10) boundaries and (ii) exhibits low effective absorption⁶. The extreme steepness of the ablation front towards the vacuum has been confirmed by time-resolved interferometric studies¹¹.

From a theoretical/modeling perspective, molecular dynamics (MD) simulations have provided so far the most detailed insight into the microscopic processes underlying laser ablation^{12,13,14,15,16}. In particular, these investigations have revealed that, with sufficiently short laser pulses, when the conditions for so-called “stress confinement” are satisfied¹⁷, the material ejection at fluences close to the ablation threshold is largely driven by photomechanical effects, where the relaxation of laser-induced stresses leads to the separation (or spallation) of a thin liquid layer from the bulk of the target. This mechanism is not only universal (i.e., can occur in almost any material), but could also readily explain the experimental observation of transient Newton rings as the result of interference of light reflected at the spalled layer and the boundary of the non-ablating material^6,13,14,16. At higher laser fluences, significantly above the spallation threshold, the simulations reveal the transition to the regime of “phase explosion”^5,12,14,18, when the top part of the target is superheated close to the critical temperature and undergoes a rapid (i.e., explosive) decomposition into vapor, atomic clusters, and small liquid droplets.

Each regime is characterized by a specific evolution of nanoscale density heterogeneities leading to the material disintegration and ejection, from the nucleation, growth, and coalescence of subsurface nanovoids in the spallation regime^13,14,15,16, to the rapid volumetric release of vapor in the phase explosion regime^14,16. These initial dynamic processes occurring on the timescale of hundreds of picoseconds set the stage for the long-term evolution of the ablation plume and have direct implications for practically relevant aspects of the ablation process, such as the size distribution of the generated nanoparticles or the structure/morphology of new surfaces produced by ablative micro-/nanomachining. Despite the fundamental interest and practical relevance, the direct experimental verification of the computational predictions on the initial stage of laser ablation is still lacking due to the absence of suitable characterization techniques.

The ultrafast optical imaging discussed above provides sufficient temporal resolution for tracking both the initial ablation dynamics and slower processes of ablation plume expansion and target resolidification but lacks the spatial resolution in the deep sub-µm to nm range required to probe the onset of phase decomposition. X-ray diffraction and scattering techniques at synchrotrons, on the other hand, have been widely used to determine the structure of materials down to atomic resolution. Regarding the application of these techniques to laser ablation, the relatively low X-ray flux per pulse and the long X-ray pulse duration only allowed investigation of slow dynamics, e.g., nanoparticle agglomeration in laser-induced cavitation bubbles in liquids¹⁹, or the final ablation product²⁰.

During the past decade, the advent of ultrashort pulsed, short wavelength free electron lasers (XFELs) revolutionized the X-ray probing of structural dynamics by adopting the pump-probe scheme, which is well established in the optical domain: a femtosecond optical laser pumps a sample, while a synchronized short-pulse X-ray probe measures the resulting structural changes after a given delay between pump and probe with sub-ps resolution²¹. This scheme has been used to study processes that are also relevant to short pulse laser ablation, namely solid-to-liquid phase transitions following ultrafast laser excitation^22,23. However, these studies focused on the structural response on atomic length scales, i.e., the transition from the ordered solid to the disordered liquid, by measuring the transient changes of Bragg diffraction peaks, the diffuse scattering, and the formation of liquid phase scattering rings. The power of combining the wide- and small-angle X-ray scattering (WAXS and SAXS) probing with atomistic modeling was recently demonstrated in a study of laser fragmentation of colloidal nanoparticles²⁴, where the WAXS signal was used to determine the nanoparticle melting threshold and the SAXS signal provided information on the fragmentation products.

In our work, by utilizing ultrashort, hard X-ray pulses from an XFEL, we apply a combination of time-resolved WAXS and SAXS probing to follow the structural evolution of the material from the initial solid phase into the volatile, ablating state. Our measurements reveal that the material first undergoes a transition to the liquid state, where the loss of long-range order is evidenced by the decay of the wide-angle Bragg peaks, before a dramatic increase of the SAXS signal. The latter exhibits a rich, rapidly evolving structure and signifies the fluence-dependent nanoscale phase decomposition driven by superheating and relaxation of laser-induced pressure waves.

Comparing the experimental data to the results of large-scale atomistic simulations, we are able to analyze the complex SAXS profiles in terms of the different ablation regimes and the corresponding characteristic pathways of phase decomposition. As such, we arrive at a comprehensive view of the energy deposition and redistribution, the kinetics of the phase transformations, as well as the thermodynamic driving forces behind the spatially heterogeneous and highly nonequilibrium ablation process, which, for the first time, is supported by both the direct experimental and modeling data.

Results

Experimental results

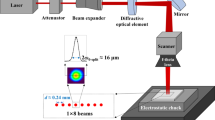
To trigger the ablation process, 100 nm and 250 nm thick gold (Au) films deposited on arrays of free-standing silicon nitride (Si₃N₄) membranes (100 nm thickness) in a silicon wafer frame were irradiated with 50 fs, 800 nm laser pulses and subsequently probed with ultrashort X-ray pulses at 9.5 keV in a normal-incidence transmission geometry (as sketched in Fig. 1a, b).

Fig. 1: Experimental setup with simultaneous small- and wide-angle scattering measurements.

a Schematic of the femtosecond laser pump, X-ray FEL probe experiment. The samples are 100 nm thick Au films deposited on ${{\rm{S}}}{{{\rm{i}}}}_{3}{{{\rm{N}}}}_{4}$ membranes made from 4 in. silicon wafers. The wafer is mounted on translation stages for 2D rastering. The SAXS scattering pattern shown in the schematic is detected by one of the four ePix100s placed at small angles. A JungFrau-1M detector is used to capture the WAXS from the sample. At negative delays (${{\rm{\delta}}} {{\rm{t}}} \, < \, 0$ ps), it captures Au (111) and Au (200) polycrystalline Bragg peaks from the film, as shown in the schematic. b A zoomed-in view of the cross-section of a membrane window. c The difference scattering pattern measured by all four ePix100 detectors. The small-angle images in a and c are measured at 250 ps after laser excitation at an incident laser fluence of 6.3 J/cm².

The small-angle scattering from the sample was captured by four X-ray area detectors (ePix100 detectors²⁵; see an example displayed in Fig. 1c). The finite size of the detector housing resulted in gaps between the detector sensors and gave rise to “blind zones” shown as dark blue regions in the SAXS pattern. The direct X-ray beam was incident on the lower right detector and blocked by a beam stop right before the detector. The detector pixels in the shadow of the beam stop were also removed from the analysis and colored dark blue in the displayed SAXS patterns. The SAXS image shown in Fig. 1c was obtained by averaging over 20 independent measurements performed at a fixed laser fluence of 6.3 J/cm² and an X-ray laser delay of ${{\rm{\delta}}} {{\rm{t}}}$ = 250 ps with respect to the optical laser pulse. Each measurement was performed on a new sample, as detailed in Supplementary Material Section 1 “Experimental Setup”.

Complementary to the SAXS measurement, another X-ray area detector (JungFrau detector²⁶) was used to collect the wide-angle diffraction signal around the (111) and (200) Bragg peaks, which enabled monitoring of the melting process. Examples of the normalized (for details, see Supplementary Material Section 1) wide-angle scattering patterns measured at selected delays between the laser and X-ray pulses are displayed in the first row of Fig. 2. The corresponding radially averaged WAXS profile evolution is summarized in Fig. 3b. At ${{\rm{\delta}}} {{\rm{t}}}$ = −5 ps, the profile features well-defined powder rings corresponding to the (111) and (200) Bragg peaks of Au. Upon laser excitation, the decrease in the intensity of the Bragg peaks and the simultaneous rise of a broad diffuse scattering contribution (apparent as the elevated background on which the Bragg peaks reside) on ps timescales indicate rapid heating and disordering/melting²⁷. After about 20–50 ps, the melting process is complete, as the WAXS does not change at later delay times (see Supplementary Material Section 3, where the Au (111) peak remains unchanged after 50 ps).

Fig. 2: Temporal evolution of the WAXS and SAXS patterns measured for a 100 nm film irradiated at an incident laser fluence of 6.3 J/cm².

First row: Time-resolved WAXS signal. Second and third rows: SAXS intensity measurement on the detector at the smallest angle. The pattern labeled as −5 ps shows the S(Q) pattern used as the reference in the evaluation of the difference patterns ΔS(Q, δt)) = S(Q, δt) − S(Q, −5 ps) plotted in all other SAXS images. The arrow corresponds to a wavevector of 0.01 ${{\text{\AA}}}^{-1}$.

Fig. 3: Measurement on 100 nm Au film.

Time-resolved radially averaged difference SAXS signal in a and WAXS signal in b obtained at an incident laser fluence of 6.3 J/cm². The two plots share the same y-axis. The white vertical column in a indicates the absent Q coverage due to the gaps between the detectors. It is used as the boundary to separate the two regions defined as low Q region (Q from 0.005  ${{\text{\AA}}}^{-1}$ to 0.026 ${{\text{\AA}}}^{-1}$) and high Q region (Q from 0.031 ${{\text{\AA}}}^{-1}$ to 0.096 ${{\text{\AA}}}^{-1}$). Note that the range of Q covered by the SAXS detectors extends up to 0.096 ${{\text{\AA}}}^{-1}$, and a shows an enlarged region. The magenta arrow in a indicates the tilt of the stripe on the low Q side of the arrow. The additional x-axis at the top of a and b represents the length scale corresponding to the Q values, calculated as 2π/Q. c Difference signal averaged over the low-Q and the high-Q ranges plotted as functions of the delay time δt. The dashed and dotted lines serve as guides to the eye, highlighting the different trends. d Change of the integral intensity of the Au (111) Bragg peak as a function of the delay time.

The second and third rows in Fig. 2 show the difference SAXS signal, which was obtained by subtracting the normalized reference pattern measured prior to laser excitation (at a negative delay ${{\rm{\delta}}} {{\rm{t}}}$ = −5 ps) from the normalized SAXS patterns measured at ${{\rm{\delta}}} {{\rm{t}}}\ge 0$. The reference pattern is labeled as −5 ps in the second row of Fig. 2. The small-angle scattering observed in the reference pattern can be mainly attributed to the grainy structure of the polycrystalline films (see Supplementary Fig. S1). By subtracting this reference pattern, we retrieve the net intensity change, ΔS(Q, δt) = S(Q, δt) − S(Q, −5 ps), where Q is the scattering vector). This intensity change is used in the analysis of the SAXS signal in the remaining part of this paper.

Immediately after the melting process is complete, the intensity of the SAXS signal starts to increase and gradually evolves into a pattern with several ring-like features observed on the detector tuned to the smallest scattering angles, i.e., the lower right detector in Fig. 1c. The intensity increase also extends to the other three detectors as well, albeit on a smaller level. Starting from 75 to 100 ps, the whole detector lights up, and the ring-like pattern becomes more pronounced. The diffraction pattern rapidly evolves, with the rings shifting to smaller scattering vectors and merging with each other as time progresses from 100 to 500 ps. After 500 ps, the total intensity moves towards the beam stop area and finally decreases at delays from 750 to 1500 ps.

The rapid rise of the small-angle intensity provides direct evidence for the formation of nanoscale density heterogeneities with characteristic length scales on the order of tens of nanometers. The rapidly evolving ring pattern suggests a complex nature of the transient laser-generated structures characterized by several dominant length scales, while the increase of the signal intensity and the evolution of the ring pattern toward smaller scattering angles indicate a continuous growth and coarsening of the nanostructures within the expanding ablation plume.

Since the scattering signal is isotropic, we performed an azimuthal average on the net scattering intensity change, denoted here as $\Delta {{\rm{S}}}({{\rm{Q}}} , \, {{\rm{\delta}}} {{\rm{t}}})$. This allows us to summarize the time evolution of the SAXS signal using a two-dimensional (2D), false-color representation displayed in Fig. 3a. The multiple rings mentioned above are visible as stripes. The stripes are tilted with respect to the vertical direction (see the magenta arrow), which reflects their shift towards smaller Q as time progresses. To quantify the onset time of the small-angle scattering signal, the SAXS Q range is divided into two regions, denoted here as “low Q” (0.005 ${{\text{\AA}}}^{-1}$ – 0.026  ${{\text{\AA}}}^{-1}$) and “high Q” (0.031 ${{\text{\AA}}}^{-1}$ – 0.096 ${{\text{\AA}}}^{-1}$). The time dependencies of the intensity averaged over the two Q regions are shown in Fig. 3c. In the low Q region, the signal increases gradually with time, while it exhibits an abrupt change at around 50 ps in the high Q region. The simultaneous WAXS measurement is shown in Fig. 3b, and the changes of the integrated intensity of the Au (111) peak extracted by fitting the signal with a Gaussian on a linear baseline (see Supplementary Material Section 3) are shown in Fig. 3d. The black line in Fig. 3d represents an exponential fit to the derived integrated peak signal and yields a decay time of (4.4$\pm$0.1) ps. Comparing the two curves plotted in Fig. 3c, it is clear that the completion of the melting process precedes the increase of the SAXS signal.

The fluence dependence of the evolution of the SAXS profiles is illustrated for the 100 nm film by the 2D Q-resolved maps in Fig. 4a–d and the Q-averaged plots in Fig. 4e for several incident laser fluences. It is noteworthy that the overall intensity of the small angle scattering is the highest at the lower incident fluences of 2.5 and 4.2 J/cm², Fig. 4a, b, suggesting the appearance of relatively large density heterogeneities on the timescale of about 100 ps. In comparison, the intensity increase of the SAXS signal for incident fluences of 6.3 and 7.7 J/m² is smaller, but the SAXS patterns exhibit a modulation of the broad SAXS peak intensity, as shown in Fig. 4c, d. The latter observation hints at the emergence of a more complex structure of the ablation plume characterized by multiple length-scales. The temporal evolution of the low/high Q-averaged SAXS signal for the four fluences is summarized in Fig. 4e. As discussed above, the intensity is the highest at a fluence of 4.2 J/cm² in both Q-regions, and there is a protracted response of the SAXS onset time at higher laser fluence, i.e., at 7.7 J/cm². Interestingly, the drop of the intensity with increasing fluence is less pronounced in the higher Q region, where the contribution comes from smaller structural features.

Fig. 4: Examples of time resolved difference SAXS signal ΔS(Q, δt).

a–d Difference SAXS signals measured for 100 nm films irradiated at incident laser fluences of 2.5 J/cm², 4.2 J/cm², 6.3 J/cm², and 7.7 J/cm². f–i Difference SAXS signals measured for 250 nm films irradiated at incident laser fluences of 1.7 J/cm², 2.9 J/cm², 4.2 J/cm², and 7.0 J/cm². The color bar shown in a is shared by all eight false color plots. Using the same definition for the low and high Q regions as in Fig. 3, the Q-averaged intensity changes are plotted as functions of the delay time δt in e for the 100 nm films and in j for the 250 nm films. Note that the dark blue stripe in g at 300 ps corresponds to an X-ray beam drop during the measurement.

For the 250 nm Au film, the fluence dependence of the scattering intensity is less pronounced, especially in the low-Q region, as can be seen from Fig. 4f–j. Nevertheless, the scattering intensity extends to higher Q values with increasing laser fluences, leading to the formation of a broader peak of the scattering intensity. These results point to the formation of transient density heterogeneities with broader size distributions in the course of the ablation process.

The fluence dependence of the WAXS and SAXS signals is further visualized in Fig. 5, where the incident laser fluence F_inc is scanned in a wide range, from 0 to 11 J/cm². The delay δt is set to 250 ps for the 100 nm film and 200 ps for the 250 nm film, after completion of the melting process and the appearance of the SAXS signal in all the experiments discussed above.

Fig. 5: Laser fluence dependence.

Radial average of the difference SAXS in (a) and WAXS in (b) measured with different laser fluences at a delay ${{\rm{\delta}}} {{\rm{t}}}$ = 250 ps for the 100 nm Au film. The corresponding intensity changes in the low and high Q regions, and the Au (111) Bragg peak integrated intensity are displayed in (c, d). The magenta arrows in a highlight the sub-peaks in the SAXS profile and in b indicate the shift of the (111) and (200) peaks. Radial average of the difference SAXS in (e) and WAXS in (f) measured with different laser fluences at a delay ${{\rm{\delta}}} {{\rm{t}}}$ = 200 ps for the 250 nm Au film. The corresponding intensity changes in the low and high Q regions, and the normalized Au (111) Bragg peak integrated intensity are displayed in (g, h).

As can be seen from Fig. 5c, d for the 100 nm film, the difference SAXS signal appears only when the film is completely molten, i.e., above 1.1 J/cm². Below the fluence threshold for complete melting, the film expands due to laser heating. This is the reason why the (111) and (200) peaks in Fig. 5b shift towards smaller Q values, as indicated by the magenta arrows. This shift becomes more pronounced as the laser fluence increases. Above the threshold for complete melting, the SAXS intensity increases rapidly, reaching the maximum at around 3 J/cm² for the low Q region and at around 4 J/cm² for the high Q region. Figure 5a gives more information regarding the Q dependent nanoscale ablation dynamics: with increasing laser fluence, the single peak broadens, shifts to higher Q values, and subsequently develops a structure featuring several low-intensity modulations or sub-peaks. The SAXS intensity eventually diminishes (faster at low Q), indicative of a progressive homogenization of the ablation plume.

For the 250 nm film, as shown in Fig. 5e–h, the increase of the SAXS signal starts at about 1.7 J/cm², while complete melting occurs only above 3 J/cm², indicating that the ablation starts even before the film melts through its full thickness. The film thickness in this case is substantially larger than the range of the ballistic energy transport by the excited electrons, estimated to be about 100 nm for Au at low levels of excitation^28,29. Moreover, the sharp increase of the electron–electron scattering with increasing level of excitation³⁰ can further constrain the energy redistribution during the initial state of strong electron–phonon nonequilibrium, leading to an inhomogeneous heating over the depth of the film. Therefore, ablation can take place in a near-surface region, where the deposited energy density is highest, while the deeper regions of the film are still solid. Correspondingly, the threshold fluence for the ablation onset at the surface is smaller than that required for the complete melting of the film. Compared to the data for the 100 nm film (Fig. 5a), the SAXS-pattern of the 250 nm film exhibits a broader peak without any pronounced sub-structure. We also attribute this to the non-uniform energy distribution throughout the thickness of the film, where the depth dependence of the material decomposition dynamics leads to the emergence of density inhomogeneities over a continuous range of length scales. The superposition of scattering contributions from different parts of the film can then produce a broad featureless SAXS peak observed for the thicker film.

The interpretation of the rich data obtained from the time-resolved SAXS measurements in terms of the actual dynamics of the film disintegration is not straightforward and requires assistance from the atomistic modeling, as discussed in the following section.

Simulation results

The links between the dynamics of phase decomposition in laser ablation and its manifestation in the evolution of SAXS patterns are established in this study by performing large-scale atomistic modeling of laser ablation of Au films and calculating the SAXS patterns for the atomic configurations predicted in the simulations. The computational setup is detailed in Supplementary Material Section 4. The simulations are performed for a 100 nm Au film deposited on a 100 nm thick ${{\rm{S}}}{{{\rm{i}}}}_{3}{{{\rm{N}}}}_{4}$ membrane and irradiated with a 50 fs laser pulse at a wavelength of 800 nm. Two values of the absorbed fluence F_abs, 0.1069 J/cm² and 0.2014 J/cm², considered in the simulations are chosen to be in the range where the film disintegration is characterized by the appearance of nanoscale density heterogeneities, which can be probed in SAXS measurements. The lower fluence is in the regime of photomechanical spallation, while the higher fluence corresponds to the transition from spallation to phase explosion. Outside this fluence range, the laser-induced processes, such as melting at lower fluences and an explosive phase decomposition into a mixture of vapor and small nanodroplets at higher fluences, do not involve the formation of structural features that contribute to the small angle scattering, thus making the results of SAXS probing less informative.

As a reference, using experimental properties of Au^31,32, the energy density required for uniformly heating the film from 300 K to T_m = 1337 K and fully melting it at T_m is 41.8 kJ/mol (corresponding to an absorbed fluence of 0.041 J/cm² for a 100 nm film), while heating the film to the thermodynamic critical temperature T_c = 7400 K³² requires the deposition of 241.7 kJ/mol or 0.24 J/cm² (see Supplementary Material Section 8). The corresponding values calculated with the thermodynamic properties predicted by the embedded atom method (EAM) interatomic potential³³ used in the simulations are 42.3 kJ/mol or 0.0415 J/cm² for the complete melting of the film at ${T}_{m}^{{\mathrm{EAM}}}$ = 1318 K and 328.9 kJ/mol or 0.323 J/cm² for heating the film to ${T}_{c}^{{\mathrm{EAM}}}$ = 9250 K (see Supplementary Material Section 9). Thus, the deposited energy density in the lower-fluence simulation (109.0 kJ/mol) exceeds the threshold for complete melting by a factor of 2.6, while the deposited energy density in the higher-fluence simulation (205.3 kJ/mol) is 1.6 times lower than the energy needed for homogeneously heating the film to T_c. While the laser-induced heating is not fully uniform even for 100 nm Au films, the analysis provided above still gives useful upper-bound estimates of the fluence values required for melting and explosive phase decomposition of the film material.

We note that the relatively weak electron–phonon coupling in Au^28,34 makes it possible to clearly distinguish the conventional thermal melting from any non-thermal effects driven directly by the strong electronic excitation. The timescale of thermal melting is controlled by the energy transfer from the excited electrons to the atomic vibrations and, in the case of gold, is on the order of several picoseconds or longer, depending on the level of excitation^4,5,35. The non-thermal processes, however, are activated immediately after the femtosecond laser excitation and occur faster than the usual electron-lattice equilibration, i.e., on sub-picosecond timescales^3,36. Indeed, it has been established experimentally^37,38,39,40 and confirmed in ab initio simulations^41,42,43,44 that excitation of ~10% of the valence electrons to the conduction band in semiconductors or dielectrics can induce the so-called “bond softening,” leading to rapid, within hundreds of femtoseconds, collapse of the crystal lattice, i.e., non-thermal melting. However, it needs to be stressed that upon the non-thermal disordering, the energy stored in the electronic subsystem is very effectively transferred to the ionic degrees of freedom⁴¹. Thus, the final state corresponds to a hot liquid with electrons and nuclei essentially in equilibrium.

For Au, however, an opposite effect of “bond hardening” in response to the strong electron excitation has been predicted in ab initio calculations^45,46. The “bond hardening” manifests itself by a sharp increase in the melting temperature, from 1337 K to 3604 K upon an isochoric increase of the electron temperature to 69,636 K (6 eV)⁴⁵, as well as an order of magnitude increase in the enthalpy of vacancy formation for the same electron temperature increase⁴⁶. The computational prediction of the increased lattice stability under conditions of strong electronic excitation has been confirmed by the results of ultrafast electron diffraction probing⁴⁷, where a noticeable increase of the melting time with respect to predictions of TTM calculations is reported for 20 nm Au films at deposited energy densities ranging from 240 and 561 kJ/mol. In an apparent contradiction with these results, a sharp drop of the Bragg peak intensities, by about 50% in 1 ps, is reported in another electron diffraction study performed for 35 nm Au films at a lower deposited energy density of 72.8 kJ/mol⁴⁸. It was suggested in this study that the electron temperature dependence of interatomic interaction can explain the early sup-picosecond onset of the melting process.

In the present study, the decay time of the (111) peak intensity, about 4.4 ps (Fig. 3d), is substantially longer than that reported for (200) peak in ref. ⁴⁸, even though the deposited energy density in the experiment illustrated in Fig. 3d is higher. On the other hand, the timescale of the diffraction peak intensity decay in Fig. 3d is similar to the decay of about 4.1 ps observed in ref. ⁴⁷ for (220) peak at a deposited energy density of 240 kJ/mol. This energy density is comparable to that used in the higher-fluence simulation (205.3 kJ/mol), which, as discussed below, corresponds to the physical regime of the experiment performed at F_inc = 6.3 J/cm². Therefore, while the debate on the role of non-thermal processes in the kinetics of melting in Au is still ongoing⁴⁹, we note that the melting time observed in the present study does not suggest a major contribution of non-thermal processes at energy densities in the vicinity of ablation threshold. We also note that the exact melting pathway is not important for the disintegration dynamics addressed in the present study. The experimental data clearly shows that ablation occurs after the transition to the disordered/molten state is complete, i.e., as discussed above, from an (almost) equilibrated hot liquid.

Snapshots of atomic configurations from the lower-fluence simulation are provided in Fig. 6a, while the evolution of pressure, density, and temperature is shown in the form of contour plots in Fig. 7a, c, e. Following laser excitation at the start of the simulation, the rapid electronic heat transfer and the electron-phonon coupling determine the initial energy redistribution and lattice heating, Fig. 7e. The temperature rises above the limit of lattice stability against melting, ~1.25T_m⁴, throughout the thickness of the film, and the film fully melts by 14 ps. The rapid heating occurring under stress confinement conditions^12,13,14, i.e., faster than the film expansion can occur, leads to the generation of high compressive stresses (up to a maximum level of 28 GPa detected at a depth of 56 nm at 14 ps) in the interior of the film, Fig. 7a. The subsequent ejection and disintegration of the film is largely driven by the dynamics of the relaxation of these initial compressive stresses. Here and below, the stress level is characterized by the pressure, which is the negative one-third of the first invariant of the stress tensor.

Fig. 6: Snapshots of atomic configurations from simulations of laser ablation of Au films.

The simulations are performed for 100 nm films deposited on a 100 nm thick ${{\rm{S}}}{{{\rm{i}}}}_{3}{{{\rm{N}}}}_{4}$ membrane and irradiated by a 50 fs laser pulses. The absorbed laser fluence is 0.1069 J/cm² in (a) and 0.2014 J/cm² in (b). The Au atoms are colored by potential energy in the range of −3.5 to −1 eV, so that the solid and molten Au is blue, surface atoms are green, and the vapor-phase atoms are red. The gray boxes show the position of the substrate at the early stage of the ablation process. The vapor density represented by red dots is evenly distributed laterally, with the visual appearance of higher vapor density in the center being the result of capturing the snapshots at an angle.

Fig. 7: Contour plots of pressure, density, and temperature predicted in simulations of laser ablation of Au films.

The simulations are performed for 100 nm films deposited on a 100 nm thick ${{\rm{S}}}{{{\rm{i}}}}_{3}{{{\rm{N}}}}_{4}$ membrane and irradiated by a 50 fs laser pulses. The absorbed laser fluence is 0.1069 J/cm² in (a, c, e) and 0.2014 J/cm² in (b, d, f), and the snapshots of the simulations are shown in Fig. 6. In the contour plots for F_abs = 0.1069 J/cm² (panels a, c, e), the dashed and dotted magenta lines represent the −1 GPa and −3 GPa isobaric lines, respectively. In the contour plots for F_abs = 0.2014 J/cm² (panels b, d, f), the dotted, dashed, dash-dotted and solid lines represent the 0.6T_c, 0.7T_c, 0.8T_c, and 0.85T_c isothermal lines, respectively, where T_c is the critical temperature of model Au. The density contour plots c, d are normalized by the room temperature density of Au (${\rho }_{0}$). Since the heat transfer to the ${{\rm{S}}}{{{\rm{i}}}}_{3}{{{\rm{N}}}}_{4}$ layer is not represented in the simulations, the layer is not colored in the temperature plot. The initial position of the Au film is from 0 to −100 nm, and the substrate is located under the film, from −100 to −200 nm. The evolution of the melting fronts in the simulations is shown by the gray dotted curves in all contour plots.

The stress relaxation in the presence of a free surface leads to the generation of a bipolar pressure wave consisting of a compressive component followed by a tensile one, Fig. 7a. When the compressive component of the wave reaches the substrate, it is partially reflected from the gold-substrate interface, with the nature of the reflection defined by the acoustic mismatch between the two materials. Using the values of the elastic moduli and densities of Au³³ and ${{\rm{S}}}{{{\rm{i}}}}_{3}{{{\rm{N}}}}_{4}$^50,51, the values of the specific acoustic impedance of the two materials can be estimated as ${Z}_{{\mathrm{Au}}}$ = 64 × 10⁶ Pa s/m and ${Z}_{{{\mathrm{Si}}}_{3}{{{\rm{N}}}}_{4}}$ = 25×10⁶ Pa s/m. For a pressure wave coming to the Au–Si₃N₄ interface from the Au side, the reflection and transmission coefficients for stress amplitudes can be calculated as ${{R}_{{\mathrm{Au}}\to {{\mathrm{Si}}}_{3}{{{\rm{N}}}}_{4}}} = (Z_{{{\mathrm{Si}}}_{3}{{{\rm{N}}}}_{4}}-{Z}_{{\mathrm{Au}}})/({{Z}_{{\mathrm{Au}}}+Z}_{{{\mathrm{Si}}}_{3}{{{\rm{N}}}}_{4}})=-0.44$ and ${T}_{{\mathrm{Au}}\to {{\mathrm{Si}}}_{3}{{{\rm{N}}}}_{4}}=2{Z}_{{{\mathrm{Si}}}_{3}{{{\rm{N}}}}_{4}}/ ({{Z}_{{\mathrm{Au}}}+Z}_{{{\mathrm{Si}}}_{3}{{{\rm{N}}}}_{4}})=0.56$.

The partial transmission of the compressive wave to the substrate layer (${T}_{{\mathrm{Au}}\to {{\mathrm{Si}}}_{3}{{{\rm{N}}}}_{4}}$ = 0.56) accelerates the layer away from the Au film, while the interfacial spallation prevents the layer from being pulled back by the tensile component of the bipolar wave. As a result, the ${{\rm{S}}}{{{\rm{i}}}}_{3}{{{\rm{N}}}}_{4}$ layer acquires momentum in the negative direction and moves away from the Au film with a constant velocity of ~612 m/s. The transmission of the pressure wave into the substrate layer triggers long-term elastic oscillations of the layer, with the maximum tension reaching −8 GPa. The ${{\rm{S}}}{{{\rm{i}}}}_{3}{{{\rm{N}}}}_{4}$ layer is “unbreakable” in its coarse-grained representation used in the model, but can be expected to disintegrate in the experiments.

Due to the negative sign of ${R}_{{\mathrm{Au}}\to {{\mathrm{Si}}}_{3}{{{\rm{N}}}}_{4}}$, the compressive component of the stress wave is partially reflected from the interface as a rarefaction wave. This reflected wave combines with the stronger tensile wave propagating from the surface, leading to the concentration of tensile stresses inside the Au film and at the gold-substrate interface. The tension at the interface is sufficient for the separation/spallation of the Au film from the substrate layer, which can be seen to occur at ~50 ps from the density contour plot in Fig. 7c.

Inside the Au film, the tensile stress concentration is observed at 40-50 ps in a broad region outlined by the −3 GPa isobar in Fig. 7a. The highest tensile stress reaches −5.6 GPa in the lower part of the film at 48 ps. The combination of heating and tension results in massive nucleation of multiple voids throughout a broad central region of the film. As discussed in ref. ⁵², the region affected by the void nucleation can be described within the framework of classical nucleation theory, as a region where the free energy barrier for the void nucleation drops below a certain threshold value. Following the nucleation at ~50 ps, the voids grow and coalesce, leading to the formation of a continuous foamy structure of interconnected liquid regions, which can be seen in the snapshot shown in Fig. 6a for 100 ps.

As the Au film continues to expand, two distinct regions emerge from the evolving foamy structure. The expansion of the upper and hotter part of the foamy structure is faster, and the liquid regions are gradually stretched into filaments elongated in the direction of the film expansion. The expansion of the lower part is slower, and the liquid structure evolves into an arrangement of large voids sandwiched between two liquid layers. The upper of these two layers, marked by the black arrow in the snapshots shown for 500 ps in Fig. 6a, separates the two distinct regions of the foamy structure. The upper part features a more fine-grained structure of liquid filaments extending to the upper liquid layer, while the lower part has a coarser structure of large voids. While the film ejection and disintegration produce a pronounced density variation along the direction normal to the film surface, this variation cannot be probed by an X-ray beam pointed in the same direction. However, the SAXS patterns should be sensitive to the emergence of the two regions of the transient foamy structure featuring distinct length scales of the density variation in the lateral (parallel to the surface) directions. The analysis of the connections between the computational predictions and the experimental observations provided in the next section will therefore focus on the lateral density variations emerging in different parts of the film during the spallation process.

The results of the higher-fluence simulation, performed at almost twice the energy density deposited by the laser pulse, are illustrated by snapshots of atomic configurations shown in Fig. 6b as well as the contour plots of pressure, density, and temperature shown in Fig. 7b, d, f. While the deposited energy is 1.6 times lower than that required to uniformly heat the film to T_c, the maximum temperature at the film surface exposed to the laser pulse reaches 0.947T_c at about 15 ps. The top layer of the film rapidly heated up to and above ~0.85T_c undergoes a rapid decomposition into vapor and liquid droplets in a process commonly referred to as phase explosion^5,12,53. The recoil pressure generated by the phase explosion at the top of the film pushes the underlying material down and is responsible for the formation of a thin liquid layer marked by the black arrow in a snapshot shown for 500 ps in Fig. 6b.

As can be seen from the snapshots, this liquid layer separates the upper region directly affected by the explosive phase decomposition from a larger underlying region where the formation and uniaxial expansion of a foamy structure is observed. While the evolution of the foamy structure and the formation of vertically aligned liquid filaments has some similarity to those discussed above for the lower-fluence simulation, there are some notable differences. In particular, the filaments have a much finer scale and are surrounded by vapor phase atoms represented in the snapshots in Fig. 6b as red dots. The presence of a substantial amount of vapor throughout the thickness of the expanding film indicates the transition to a film disintegration regime where both the relaxation of laser-induced stresses and the rapid release of the vapor phase contribute. Indeed, the level of tensile stresses supported by a part of the film outlined by the 0.7T_c isotherm in Fig. 7b does not exceed −0.8 GPa, and the pressure remains positive at all times in the upper region undergoing the phase explosion. The tensile stresses are still generated in the lower and colder part of the film, although the stress magnitude decreases significantly with respect to the lower fluence simulation, Fig. 7a, due to a combined effect of the ablation recoil generated by the phase explosion and the reduced ability of the hot molten material to support the dynamic tensile loading.

The observation of the foamy nanostructure evolving into an interconnected network of elongated liquid filaments is of direct relevance for the interpretation of the data obtained by SAXS probing of the ablation dynamics. Similar to the lower-fluence simulation, the transient nanostructures generated in the course of the phase decomposition exhibit a range of characteristic length scales of the density variation in the lateral directions. The mapping of the transient nanoscale structures predicted in the simulations to the SAXS patterns measured in the experiments is discussed next.

Discussion

The atomistic simulations described above provide detailed information on the dynamics of the film decomposition and ejection in the regime of photomechanical spallation (F_abs = 0.1069 J/cm²) and at the transition to the phase explosion regime (F_abs = 0.2014 J/cm²). The conversion of the absorbed fluence F_abs to the incident fluence F_inc used in the experiments is not straightforward due to the uncertainty in the fluence dependence of the effective (integrated over the duration of the laser pulse) reflectance of the Au films. While the intrinsic normal incidence reflectance calculated for Au at a wavelength of 800 nm using Fresnel’s equations is 0.974⁵⁴, the effective surface reflectance under experimental conditions can be altered by surface roughness and the electronic excitation during the laser pulse. The experiments are performed for polycrystalline films, as evidenced by the two powder diffraction rings in the WAXS-signal of the unpumped sample in Fig. 1a. The SEM and AFM images in the Supplementary Fig. S1 show that the average grain size is about 50 nm and the peak-to-peak surface roughness is about 8 nm. This surface roughness results in a small reduction of the surface reflectance down to 0.968, as predicted by electromagnetic calculations performed with a model described in Section 7 of the Supplementary Material for computational samples reproducing the surface morphology of the experimental 100 nm films. An additional and stronger reduction of the reflectance is expected from the transient increase in the electron temperature and the associated changes in the electron scattering rates during the laser pulse. However, this reduction is difficult to quantify theoretically, as it has been demonstrated that the experimental data for Au cannot be adequately described by a Drude–Lorentz model without the introduction of empirical ad hoc corrections⁵⁵. Indeed, the direct application of the Drude model converts the absorbed fluences used in the simulations to incident fluences of 1.0 J/cm² and 1.4 J/cm², which is comparable to the experimental threshold for melting of the film, about 1.1 J/cm² (see Fig. 5d).

Given the uncertainty of the theoretical conversion between F_inc and F_abs, we resort to an approximate matching of the fluence ranges using the thresholds for film melting and disintegration. Assuming that the deposited energy at the incident fluence threshold for the complete melting of the 100 nm film (1.1 J/cm², as determined from WAXS probing) corresponds to the deposited energy density needed for the complete melting of the film (0.041 J/cm², as estimated in the previous section), the effective reflectance is about 0.963. This value is higher than that predicted theoretically and measured in previous experiments at this fluence, where the reflectance was reported to be below 0.8⁵⁵, suggesting either an uncertainty in the experimental fluence calibration or the existence of energy loss channels activated during and immediately after laser excitation. According to the simulations, the energy transfer to the ${{\rm{S}}}{{{\rm{i}}}}_{3}{{{\rm{N}}}}_{4}$ substrate (energy of the center-of-mass motion of the substrate away from the film and energy of the elastic wave generated in the substrate, Fig. 7a, b) accounts for 0.007 and 0.017 J/cm² at F_abs of 0.1069 and 0.2014 J/cm², respectively. The energy loss due to electron emission has been estimated to be negligible at fluences near the melting threshold⁴ and, in the absence of other obvious channels of energy loss, we have to assume that the effective reflectance remains surprisingly high up to the melting threshold of the 100 nm film. As the incident fluence increases above the melting threshold, a substantial drop in the effective reflectance is expected, leading to a highly nonlinear scaling of the absorbed fluence with the incident one. Based on these considerations, we approximately match the conditions of the low-fluence (F_abs = 0.1069 J/cm²) and high-fluence (F_abs = 0.2014 J/cm²) simulations with the experimental data measured at F_inc of 4.2 J/cm² and 6.3 J/cm², respectively.

The X-ray scattering profiles calculated for the atomic configurations predicted in the simulations for different delays after the laser excitation are compared with the corresponding profiles obtained in the experimental measurements in Fig. 8a, b, d, e. The computational and experimental SAXS profiles exhibit similar shapes and shape evolution with time. The appearance of broad small-angle scattering peaks gradually shifting towards lower Q values is observed in all cases. To quantify the time evolution of the scattering profiles, the Q-averaged intensity evolution is calculated for the low- and high-Q regions defined above, in the discussion of the experimental results, Fig. 8c, f. The trends show a remarkable quantitative agreement between the computational predictions and the experimental observations. The striking similarities include the delayed onset times for the increase of the low-Q region intensity and the drop of the high-Q intensity at delays larger than about 250 ps. The increase in fluence leads to a slightly delayed increase in the low-Q intensity (cf. Fig. 8c and f) and the formation of a broader peak at low Q values at larger delays.

Fig. 8: Comparison of the simulated and experimental SAXS signals for 100 nm Au films.

The panels in the top row show the radially averaged difference SAXS profiles a predicted in a simulation at an absorbed laser fluence of 0.1069 J/cm² and b measured in experiments at an incident laser fluence of 4.2 J/cm². The corresponding Q-averaged intensity changes in the low and high Q regions are shown in (c). The panels in the bottom row show the radially averaged difference SAXS profiles d predicted in a simulation at an absorbed laser fluence of 0.2014 J/cm² and e measured in experiments at an incident laser fluence of 6.3 J/cm². The corresponding Q-averaged intensity changes in the low and high Q regions are shown in (f).

The good agreement between the computational and experimental SAXS profiles gives us confidence in the realistic representation of the film disintegration dynamics in the simulations and encourages a more detailed analysis of the specific transient features of the film disintegration responsible for the evolution of the SAXS profiles. As noted in the discussion of the simulation results, at both fluences, the phase decomposition proceeds differently in parts of the expanding film located at different depths below the film surface. While the SAXS probing in normal-incidence transmission geometry contains information averaged over the depth of the film, analysis of the computational results can help to disentangle the contributions from different depths, where the phase decomposition produces nanostructures with distinct length scales of the density variation in the lateral directions. To resolve the depth-dependent contributions to the SAXS profiles, we first identify regions of distinct evolution of the transient nanoscale structures and then perform calculations of the “partial” SAXS profiles contributed by these regions.

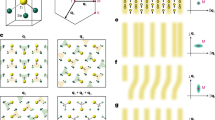
In the low-fluence simulation (F_abs = 0.1069 J/cm²), the two regions of distinct nanostructure are separated by a molten layer marked by the black arrow in Fig. 6a. The 2D real-space projected density maps for these two regions for a time delay of ${{\rm{\delta}}} {{\rm{t}}}$ = 200 ps are shown in Fig. 9a₂ and a₃, while the total density map combining the two contributions is shown in Fig. 9a₄. Despite the clear visual difference between the regions in a snapshot shown for 200 ps in Fig. 6a, the projected density distributions in Fig. 9a₂ and a₃ are quite similar. Apparently, the 2D projections of the larger vertically elongated voids in the upper region of the expanding film and smaller closer-to-spherical voids in the lower region yield similar density distributions when projected on the plane of the film. As a result, the partial contributions to the SAXS profile from the upper and lower regions, shown by the dotted and dashed lines in Fig. 9a₁, have similar shapes. When combined, they yield a single peak shown in blue in Fig. 9a₁. The peak is centered at about ${{\rm{Q}}}=0.021{{\text{\AA}}}^{-1}$ (marked by the blue arrow in Fig. 9a₁), which corresponds to a length-scale of $d=\frac{2\pi }{{{\rm{Q}}}} \approx 30\,{{\mathrm{nm}}}$ (shown by the length of the magenta segment in Fig. 9a₄).

Fig. 9: Depth-resolved dynamics of nanoscale phase decomposition as revealed by the simulations.

The left panels a₁ and b₁ show the radially averaged difference SAXS intensity profiles predicted for 200 ps and 500 ps after the laser pulse in simulations performed for absorbed laser fluences of 0.1069 J/cm² and 0.2014 J/cm². The shaded areas show the total intensity, while the dotted and dashed lines show the contributions to the scattering intensity from regions located above and below the corresponding liquid layers marked by the black arrows in Fig. 6. The contribution from above the layer in b₁ is magnified by a factor of 10. The projected density distributions in regions above the liquid layer, below the liquid layer, and for the whole system are shown for 200 ps and 500 ps in a₂-a₇ for the lower fluence simulation and in b₂-b₇ for the higher fluence simulation. The blue and red arrows in a₁ and b₁ correspond to the lengths indicated by the magenta bars shown in a₄, a₇, b₄, b₅, and b₆. The size of the simulation box in a₂-a₇ and b₂-b₇ is 200 × 200 nm².

At ${{\rm{\delta}}} {{\rm{t}}}$ = 500 ps, both regions expand and coarsen (Fig. 6a), which is reflected in the 2D density maps shown in Fig. 9a₅, a₆. The structure is somewhat coarser in the lower region, which is also reflected by the relative positions of the corresponding peaks of the partial SAXS profile. Namely, the peak produced by the lower region, shown by the dashed orange line in Fig. 9a₁, is shifted to the lower-Q direction with respect to that produced by the upper region. This shift, however, is relatively small, and the two partial profiles merge into a single broader peak of the total SAXS profile shown by light orange color in Fig. 9a₁. The peak position marked by the orange arrow in Fig. 9a₁ is Q = 0.0091 Å⁻¹, which corresponds to the characteristic length-scale of $d \approx 69\,{{\mathrm{nm}}}$, shown by the length of the magenta segment in Fig. 9a₇. Therefore, the computational prediction for the SAXS signature of ablation in the spallation regime is the appearance of a relatively narrow single peak shifting in the direction of smaller Q with time. This behavior is consistent with the experimental data obtained at laser fluences close to the threshold for film disintegration, Fig. 8b, although the Q values of the peak positions are smaller in the experiment (Q = 0.012 Å⁻¹ and Q = 0.008 Å⁻¹ at ${{\rm{\delta}}} {{\rm{t}}}$ = 200 ps and ${{\rm{\delta}}} {{\rm{t}}}$ = 500 ps, respectively). The shift of the SAXS peaks in the lower Q direction in the experiments can be traced back to the early appearance of a strong low-Q signal as early as 100 ps after the laser excitation, Fig. 8b, which is absent in the simulations, Fig. 8a. This effect is common for the lower and higher fluence conditions and is briefly discussed below.

In the high fluence simulation (F_abs = 0.2014 J/cm²), the two regions that can be distinguished in the snapshots shown in Fig. 6b are the region above the molten layer marked by the black arrow in the snapshot shown for 500 ps and the lower region located between the two thin liquid layers. The upper region is generated by an explosive release of vapor. It consists of nanodroplets and small liquid filaments attached to the liquid layer. The lower region, generated by a combined effect of mechanical stretching and vaporization, develops into a foamy structure of vertically elongated interconnected liquid filaments. The difference in the dynamics of the phase decomposition in these two regions is more prominent as compared to the lower-fluence simulation, which is reflected in the corresponding 2D density maps shown in Fig. 9b₂, b₃ for a delay of 200 ps and Fig. 9 b₅, b₆ for 500 ps. Already at ${{\rm{\delta}}} {{\rm{t}}}$ = 200 ps, the top layer undergoing the explosive phase decomposition features a finer-grained density distribution, as reflected by the partial SAXS profile shown by the dotted blue line in Fig. 9b₁. Due to the small mass fraction of this layer, however, it makes only a minor contribution to the total SAXS profile, which is dominated by the large lower region of the expanding film. The total SAXS profile is centered at Q = 0.024 Å⁻¹, which corresponds to the characteristic length-scale of $d=26\,{\mathrm{nm}}$, shown by the length of the magenta segment in Fig. 9b₄.

The difference in the characteristic length-scales of the density distributions in the upper and lower layers further increases with time, as can be seen from the 2D density maps for ${{\rm{\delta}}} {{\rm{t}}}$ = 500 ps shown in Fig. 9b₅ and b₆. In this case, despite the low mass fraction of the upper layer, its contribution turns the shoulder of a broad partial SAXS profile of the dominant lower layer into the second peak in the total SAXS profile. The two peaks of the total SAXS profile, marked by two orange arrows in Fig. 9b₁, are located at Q values of 0.0147 Å⁻¹ and 0.008 Å⁻¹, which corresponds to the characteristic length-scales d of 43 nm and $79\,{\mathrm{nm}}$, respectively. The smaller length-scale and the corresponding peak in the SAXS signal has a substantial contribution from the upper layer.

The broadening of the SAXS peak with increasing laser fluence is consistent with experimental observations, Fig. 5a. According to the simulations, this broadening can be attributed to the transition from spallation to the phase explosion regime of film disintegration, with the latter producing a mixture of vapor and small liquid droplets that contribute to the scattering at larger Q. Indeed, the overall drop in the SAXS signal at the maximum fluences probed in the experiments, Fig. 5a, may indicate the completion of the transition to the phase explosion regime of film disintegration throughout the film thickness.

The splitting of the SAXS profile into sub-peaks in the simulated SAXS profiles, Fig. 8d and 9b₁, is a consequence of the coexistence of different regimes of material decomposition activated at different depth below the irradiated surface. Again, this is (at least qualitatively) consistent with the experimental observations, i.e., the appearance of rings in the 2D SAXS patterns in Fig. 2, the corresponding stripes in Fig. 3a, and sub-peaks in Fig. 8e. However, the quantitative difference in the Q-positions and the larger magnitude of the sub-peaks in the experimental profiles, as well as their persistent presence in a broad range of fluences (Fig. 5a), indicate that additional processes/effects not considered in the simulations contribute to the experimental SAXS patterns.

One of the effects not accounted for in the simulations is the nanoscale surface roughness of the polycrystalline Au film (see Supplementary Material Section 2). This roughness may lead to a spatial variation of the energy deposition due to plasmonic effects^56,57, while the results of large-scale atomistic modeling⁵⁸ suggest that a 20% spatial modulation of the energy deposition can lead to a modulation of density in the ablation plume on length scales beyond 100 nm persevering for hundreds of picoseconds. It was also suggested by recent hydrodynamic simulations that the melt flow driven by Marangoni surface tension forces can produce redistribution of material along the irradiated surface on the length scale of ~150 nm within just 100 ps after the laser irradiation⁵⁹. As illustrated by the Supplementary Fig. S3, the electromagnetic simulation of laser interaction with a model system reproducing the surface roughness of an experimental film reveals an uneven energy deposition leading to the formation of “hot” and “cold” spots in the electron and lattice temperature distributions. The analysis of the implications of the energy deposition on the dynamics of phase decomposition and its SAXS signature is the subject of our current work, which will be reported elsewhere. We would like to emphasize that time-resolved scattering experiments carried out on laser-excited Si in the ablative regime using VUV probe pulses^60,61 have revealed scatterings signals at Q-values well below 0.01 Å⁻¹ over a time range from a few tens of ps up to a few ns—the same time range addressed here. In fact, the rapid rise of the low-Q SAXS signal observed in Fig. 8b, e already at ${{\rm{\delta}}} {{\rm{t}}}$ = 100 ps represents the most striking difference with the computational profiles shown in Fig. 8a, d. The contribution of processes responsible for the rapid emergence of the low-Q signal can be expected to persist at longer delays, leading to the quantitative differences between the experimental and simulated SAXS profiles. Finally, we also note that, in general, due to the small lateral size of the computational cell (200 nm), processes occurring on length-scales beyond 100 nm (Q ≤ 0.006 Å⁻¹) cannot be reliably described in our simulations.

In summary, in this work we demonstrate that the combination of X-ray probing and large-scale atomistic modeling of ultrashort pulse laser ablation of thin Au films represents a powerful approach to characterize the rapid spatially heterogeneous nanoscale phase decomposition driven by a combination of extreme photomechanical and thermodynamic driving forces. In agreement with the simulations, the WAXS measurements show that ablation and phase decomposition are preceded by melting and occur from the liquid state. Furthermore, they allow to establish the threshold for the loss of crystalline order in the film, thus enabling the alignment of the scales of energy deposition in modeling and experiments. The direct and quantitative comparison of the SAXS profiles predicted for the simulated atomic configurations with the measured ones enables the identification of the characteristic SAXS signatures for the photomechanical spallation and phase explosion regimes of laser ablation, thus confirming the predicted coexistence of different processes in different parts of the irradiated films.

The insights into the origins of the SAXS profiles provided in this work open a new avenue for the investigation of rapid phase transformations in materials subjected to ultrafast energy deposition and brought to extreme states of thermal and mechanical nonequilibrium. Future work will include X-ray probing at non-normal incidence to access the emergence of density variations in both the lateral and axial directions at the initial stage of the ablation process.

Methods

Experimental setup

The experiment was performed at the X-ray Pump Probe instrument of the Linac Coherent Light Source⁶². Figure 1a shows a schematic of the experimental setup. The 800 nm optical laser and 9.5 keV X-ray pulse are focused to the sample in a close to colinear geometry. The laser’s focal spot size is 28 µm (RMS), and the estimated pulse duration is 50 fs. The X-ray focal spot size is 1.2 µm (RMS), and the estimated pulse duration is 30-50 fs (see Supplementary Material Section 1 for a more detailed description of the experimental setup). The samples were deposited using a technique known as anodic vacuum arc⁶³ onto arrays (120 by 120) of 100 nm-thick ${{\rm{S}}}{{{\rm{i}}}}_{3}{{{\rm{N}}}}_{4}$ membrane windows, fabricated from 4-in. silicon wafers. The wafer is mounted on translation stages perpendicular to the incoming X-ray beam, and each laser and X-ray pulse pumps and probes a new window. A JungFrau detector²⁶ and four ePix100 detectors²⁵ are placed 0.15 m and 5.05 m downstream to record the WAXS and SAXS from the sample.

Computational model

The laser ablation simulations of an Au film deposited on a ${{\rm{S}}}{{{\rm{i}}}}_{3}{{{\rm{N}}}}_{4}$ membrane are performed with a hybrid atomistic-continuum computational model combining the two-temperature model (TTM) to represent the electron-phonon equilibration and energy redistribution by the electron thermal conductivity, classical atomistic molecular dynamics (MD) to simulate laser-induced nonequilibrium phase transformations and Au film disintegration dynamics, and a one-dimensional (1D) coarse-grained (CG) MD representation of the mechanical interaction of the Au film with the ${{\rm{S}}}{{{\rm{i}}}}_{3}{{{\rm{N}}}}_{4}$ substrate. The hybrid model and the details of the computational setup are described in the Supplementary Material Section 4. The laser energy deposition on the Au film is simulated with an electromagnetic (EM)  model based on the solution of Maxwell’s equations and coupled with TTM, as briefly described in the Supplementary Material Section 5. The TTM-EM calculations are also used to evaluate the effect of surface roughness measured for the polycrystalline films used in the experiments on the surface reflectance and the lateral variation of the laser energy deposition, as discussed in the Supplementary Material Section 7. The method used for the calculation of SAXS profiles for the transient atomic configurations generated in the atomistic simulations is described in the Supplementary Material Section 6.